Efficient-Scheduling Parallel Multiplier-Based Ring-LWE Cryptoprocessors

Abstract

This paper presents a novel architecture for ring learning with errors (LWE) cryptoprocessors using an efficient approach in encryption and decryption operations. By scheduling multipliers to work in parallel, the encryption and decryption time are significantly reduced. In addition, polynomial multiplications are conducted using radix-2 and radix-8 multiple delay feedback (MDF) architecture-based number theoretic transform (NTT) multipliers to speed up the multiplication operation. To reduce the hardware complexity of an NTT multiplier, three bit-reverse operations during the NTT and inverse NTT (INTT) processes are removed. Polynomial additions in the ring-LWE encryption phase are also arranged to work simultaneously to reduce the latency. As a result, the proposed efficient-scheduling parallel multiplier-based ring-LWE cryptoprocessors can achieve higher throughput and efficiency compared with existing architectures. The proposed ring-LWE cryptoprocessors are synthesized and verified using Xilinx VIVADO on a Virtex-7 field programmable gate array (FPGA) board. With security parameters $n=512$ and $q=$ 12,289, the proposed cryptoprocessors using radix-2 single-path delay feedback (SDF), radix-2 MDF, and radix-8 MDF multipliers perform encryption in 4.58 $\mathsf{\mu }$s, 1.97 $\mathsf{\mu }$s, and 0.89 $\mathsf{\mu }$s, and decryption in 4.35 $\mathsf{\mu }$s, 1.82 $\mathsf{\mu }$s, and 0.71 $\mathsf{\mu }$s, respectively. A comparison of the obtained throughput and efficiency with those of previous studies proves that the proposed cryptoprocessors achieve a better performance.

1. Introduction

The internet of things (IoT), with billions of connected devices currently in use, has been developed dramatically during the past decades; therefore, a stronger cryptosystem with the goals of confidentiality, integrity, and authentication has become a necessity. There exist two types of cryptosystems named symmetric cryptography and asymmetric or public key cryptography. The former uses a single key between two parties to enable a secure communication, where the key is kept private from all other parties. Owing to its simplicity, this scheme is widely used. However, a symmetric key algorithm can be used only when the sender and receiver have agreed on the secret key. Asymmetric, or public key cryptosystems use two keys, including one private key and one public key. Whereas the private key is kept secret for the decryption process, the public key is used for encryption and can be revealed to all other parties. The encryption operation is conducted using a public key, and the encrypted message can only be decrypted using the corresponding private key. The security level of these algorithms depends on the difficulty of deriving a private key from a public key. Existing cryptographic primitives such as the symmetric advanced encryption standard (AES) and asymmetric elliptic curve cryptosystems (ECC) [1,2,3] can be applied to achieve the aforementioned security goals. For example, the encryption and decryption operations conducted in ECC are based on an elliptic curve and computation over a Galois field GF$\left(p\right)$ or GF$\left(2^m\right)$, where p and m are prime numbers. In the key generation operation, the receiver selects a random number for its private key $k_S$ and a base point $P_S$ to calculate ECC point multiplication $Q_S=k_S·P_S$. The public key goes to the sender, who encrypts the input data before sending them to the receiver. At the receiver, the original data can be recovered using the secret key of the receiver and ECC point multiplication operations. However, recent advances in quantum computing intimidate the security of existing cryptographic schemes. The security of ECC and that of Rivest, Shamir, and Adleman (RSA) cryptosystems [4] are based on the difficulty of solving the elliptic-curve discrete logarithm problems and the difficulty of solving certain number theoretic problems, respectively. As early as 1994, Shor [5] proposed an algorithm to solve the integer factorization problem and the discrete logarithm problems in polynomial time when using quantum computers. Therefore, the National Institute of Standards and Technology (NIST) is planning to standardize quantum-resistant cryptosystems such as lattice-based cryptography because the security proofs of lattice-based cryptography are based on the worst-case hardness of the lattice problems, and there are no known algorithms that can efficiently solve them. Learning with errors (LWE) is a well-known lattice-based problem that has attracted significant intention in recent years. In this context, the ring-LWE cryptosystems described in [6,7,8,9,10,11,12] are the most studied lattice-based cryptosystems in terms of both software and hardware. A block diagram of the ring-LWE cryptosystem is described in Figure 1.

The ring-LWE public-key cryptosystem operations are conducted in a polynomial ring, normally $R_q={\mathbb{Z}}_q\left[x\right]/f\left(x\right)$. These operations include polynomial addition, polynomial multiplication, and modulo reduction. Among them, polynomial multiplication is the most computationally intensive [9] and can be efficiently executed using a number theoretic transform (NTT) based polynomial multiplication. In addition to the significant progress made regarding the theory of lattice-based cryptography, practical implementations of this cryptosystem have recently gained the attention of the research community. Some software implementations of ring-LWE cryptosystems can be found in the literature. In [6], the authors presented efficient techniques to obtain a high-speed computation in ring-LWE encryption and decryption. A high-speed, low-latency software-based ring-LWE cryptographic scheme is introduced in [8] to perform biomedical image storing and transmission. In addition, the processing time of ring-LWE cryptosystems can be considerably improved by employing parallel operations on a graphics processing unit (GPU) [10]. The aforementioned software demonstrations show that the ring-LWE cryptographic scheme offers a higher level of security with lower latency compared with previous cryptosystems. To prove the practicality and efficiency of ring-LWE cryptoprocessor, many hardware deployments have also been conducted in [7,9,13,14]. The study in [13] illustrates that ring-LWE cryptoprocessors require less hardware resources than conventional cryptosystems such as ECC to carry out encryption and decryption operations. In addition, a ring-LWE scheme can operate at a higher frequency than ECC scheme. Therefore, a ring-LWE cryptosystem outperforms ECC in terms of throughput and efficiency. In the design of an NTT multiplier, SDF-architecture based and multiple-path delay commutator (MDC) architecture based schemes have been deployed. An SDF-architecture based multiplier requires less hardware than an MDC-architecture based multiplier; however, it offers lower throughput than an MDC-architecture based multiplier. In [7], high-throughput ring-LWE cryptoprocessors using SDF and MDC-architecture based multipliers are discussed. The results in [7] show that, for ring-LWE encryption and decryption, the throughputs achieved are at gigabits and megabits per second, respectively. However, this architecture requires a significant number of hardware resources and a long computation time because the NTT multipliers operate separately and the NTTs work serially.

In this paper, we present an efficient scheduling architecture to conduct ring-LWE cryptography encryption and decryption operations. To decrease the encryption time, the multipliers used in the proposed ring-LWE encryption operation are scheduled to work concurrently. The adders in the encryption phase also operate simultaneously. Therefore, the encryption latency is reduced by the computation time of one polynomial multiplication and one polynomial addition. In addition, the NTT multipliers are designed using a multiple delay feedback (MDF) architecture to lessen the hardware complexity and speed up the encryption and decryption operations. As a result, with a lower hardware complexity, the proposed ring-LWE cryptoprocessors provide higher throughput and efficiency compared with other designs.

The rest of this paper is organized as follows: Section 2 provides background information on ring-LWE cryptography and an NTT multiplier. In Section 3, the proposed ring-LWE cryptoprocessors using efficient-scheduling parallel multipliers are presented. A performance analysis and comparison are discussed in Section 4. Finally, some concluding remarks are given in Section 5.

2. Ring-LWE Cryptography

2.1. Operations in Ring-LWE Cryptography

The ring-LWE cryptography, a public key cryptosystem introduced by Regev [15] in 2005, is a machine learning problem that is equivalent to the worst-case lattice problems. The ring-LWE cryptosystem is built on a polynomial ring $R_q={\mathbb{Z}}_q\left[x\right]/f\left(x\right)$, where $q\equiv 1mod2n$ is a sufficiently large public prime number, and $f\left(x\right)$ is the irreducible polynomial. Normally, $f\left(x\right)=x^n+1$, where the security parameter n is a power of 2. The ring-LWE distribution on $R_q\times R_q$ consists of pairs $(a,t)$ with $a\in R_q$ chosen uniformly random, and $t=a\times s+e\in R_q$, where s is a fixed secret element and e is sampled from a discrete Gaussian distribution ${\chi }_{\sigma }$ with a standard deviation $\sigma$. The procedures of a ring-LWE cryptosystem, including the key generation, encryption, and decryption, are described as follows.

2.1.1. Key Generation

This process generates a private key $r_2$ and public key $(a,p)$. The polynomial a is chosen uniformly, and two polynomials $r_1$ and $r_2$ are sampled from the Gaussian distribution ${\chi }_{\sigma }$. The polynomial $r_2$ becomes the private key, and two polynomials $r_1$ and $r_2$ participate in the public key generation process.

$$p\leftarrow r_1-a\times r_2.$$

(1)

2.1.2. Encryption

The ring-LWE encryption operation encrypts the input message m to the cipher-text $(c_1,c_2)$. Initially, the input message m is encoded into the polynomial $m_e$ using an encoder. Depending on the i-th coefficient of m, it is encoded as $(q-1)/2$ (if $m\left[i\right]=1$) or 0 (if $m\left[i\right]=0$). The cipher-text $(c_1,c_2)$ is calculated based on the public key $(a,p)$, the encoded message, and three error polynomials $e_1$, $e_2$, and $e_3$ sampled from the Gaussian distribution.

$$\begin{array}{c}{c}_1\leftarrow a\times e_1+e_2\hfill \\ c_2\leftarrow p\times e_1+e_3+m_e.\hfill \end{array}$$

(2)

2.1.3. Decryption

The decryption operation recovers the original message m from the cipher-text $(c_1,c_2)$. This operation starts with the calculation of the pre-decoded polynomial $m_d$

$$m_d\leftarrow c_1\times r_2+c_2.$$

(3)

The original message m is recovered from the pre-decoded polynomial $m_d$ using a decoder. The i-th coefficient of the message m is converted to 1 if and only if its corresponding value $m_d\left[i\right]$ satisfies the condition $q/4\le m_d\left[i\right]\le 3q/4$; otherwise, it is converted to 0.

2.2. Arithmetic Operations over a Ring

The operations over ring $R_q={\mathbb{Z}}_q\left[x\right]/f\left(x\right)$ include polynomial multiplication, polynomial addition, and modulo reduction. Given $a_i$ and $b_i$ in $R_q$, two polynomials $a\left(x\right)$ and $b\left(x\right)$ over the ring can be expressed as follows.

$$\begin{array}{c}a\left(x\right)=a_0+a_{1}x+a_2{x}^2+\dots +a_{n-1}{x}^{n-1}\hfill \\ b\left(x\right)=b_0+b_{1}x+b_2{x}^2+\dots +b_{n-1}{x}^{n-1}\hfill \end{array}$$

(4)

The polynomial multiplication over ring $R_q$ is the arithmetic requiring the longest processing time. Among existing approaches used to execute polynomial multiplication introduced in [7,9,16], the NTT-based algorithm is efficient. If the root of unity in the fast Fourier transform (FFT) is taken from a finite ring instead of a complex number, the NTT can be viewed as a variation of the FFT. Given a primitive n-th root of unity $\omega$, the NTT of each coefficient of $a\left(x\right)$ is calculated as follows:

$${\displaystyle A_i=\sum _{j=0}^{n-1}{a}_j{\omega }^{ij}modq.}$$

(5)

Thus, the inverse number theoretic transform (INTT) is defined as

$${\displaystyle a_i=n^{-1}\sum _{j=0}^{n-1}{A}_j{\omega }^{-ij}modq.}$$

(6)

Assume that $\alpha$ and $\beta$ are extended vectors of $a\left(x\right)$ and $b\left(x\right)$ by filling n zero elements. The multiplication of two polynomials $a\left(x\right)$ and $b\left(x\right)$ can be expressed as forms of NTT and INTT, where ⊙ is a point-wise multiplication.

$${\displaystyle c\left(x\right)=a\left(x\right)·b\left(x\right)=INT{T}_{\omega }^{2n}(NT{T}_{\omega }^{2n}\left(\alpha \right)\odot NT{T}_{\omega }^{2n}\left(\beta \right)).}$$

(7)

The negative wrapped convolution can be implemented to avoid zero padding in an NTT multiplication. Considering c to be the negative convolution of $a\left(x\right)$ and $b\left(x\right)$, the negative wrapped convolution can be described as

$${\displaystyle c_i=\sum _{j=0}^i{a}_j{b}_{i-j}-\sum _{j=i+1}^{n-1}{a}_j{b}_{n+i-j}}$$

(8)

Define $a^{\prime }=(a_0,\psi a_1,\dots ,\psi a_{n-1})$, $b^{\prime }=(b_0,\psi b_1,\dots ,\psi b_{n-1})$, and $c^{\prime }=(c_0,\psi c_1,\dots ,\psi c_{n-1})$, where $\psi \equiv \omega modq$, the NTT polynomial multiplication becomes

$${\displaystyle c^{\prime }=a^{\prime }·b^{\prime }=INT{T}_{\omega }^n(NT{T}_{\omega }^n\left(a^{\prime }\right)\odot NT{T}_{\omega }^n\left(b^{\prime }\right)).}$$

(9)

Using the negative wrapped convolution, the NTT multiplication can be calculated based solely on the n-coefficient. Detail operations of NTT-based polynomial multiplication are described in Algorithm 1.

Algorithm 1: Number theoretic transform (NTT)-based polynomial multiplication using negative wrapped convolution.

The polynomial addition $d\left(x\right)$ of two polynomials $a\left(x\right)$ and $b\left(x\right)$ is simply adding the corresponding coefficients of two polynomials and then applying modulo reduction (MR).

$$d_i=(a_i+b_i)modq$$

(10)

In an MR operation, the coefficients of the resulting polynomial should be reduced by modulus q. To execute this operation, a few MR algorithms are presented in [7,9,17]. Since security parameters used in this study are $n=512$ and $q=$ 12,289, the SAMS2 algorithm for $q=$ 12,289 presented in [7] is applied to perform the MR reduction.

2.3. Discrete Gaussian Sampler

In the operations of ring-LWE cryptosystems, polynomials sampled from a discrete Gaussian distribution ${\chi }_{\sigma }$ with a standard deviation $\sigma$ are required. In [16,18,19,20,21], the authors present several methods to conduct discrete Gaussian sampling. Among these methods, rejection sampling and inversion sampling are popular choices. In practice, rejection sampling for a discrete Gaussian distribution is slow owing to the high rejection rate for the sampled values, which are far from the center of distribution. The inversion method first generates a random probability and then selects a sample value such that the cumulative distribution up to that sample point is just larger than the randomly generated probability. Since the random probability should be of high precision, this method also requires a large number of random bits. The Knuth–Yao algorithm [16] uses a random walk model for sampling from any non-uniform distribution. However, the output of Knuth–Yao is generated within an unpredictable amount of time [7], and it is therefore not a reliable sampler. In this work, we deploy the linear feedback shift registers (LFSRs) method proposed in [21] because it offers a low complexity with an approximated uniform pseudo-random distribution; hence, it can be exploited to generate an accurate approximation of a Gaussian distribution with a low maximum auto-correlation.

2.4. Ring-LWE Encryption and Decryption Algorithm

In this paper, we use the ring-LWE encryption and decryption algorithms discussed [7]. Furthermore, in the encryption operation, multipliers and adders are scheduled to work in parallel to optimize the computation latency. The detailed algorithms used to perform ring-LWE encryption and decryption operations are presented in Algorithms 2 and 3, respectively. In an encryption operation, the input message m in binary form is converted into a ring polynomial $m_e$ using an encoder. This encoder compares each bit $m\left[i\right]$ of the input message m to decide if it is encoded as 0 or $(q-1)/2$. To compute the cipher-text $(c_1,c_2)$, three error polynomials $e_1$, $e_2$, and $e_3$ generated from a discrete Gaussian sampler are required. In addition, the public key $(a,p)$ and error polynomial $e_1$ are transformed using NTT cores. The main part of the encryption algorithm is calculating cipher-texts $c_1$ and $c_2$ using polynomial addition and polynomial multiplication. In this work, we use two temporary variables $c_{10}$ and $c_{20}$ to store the multiplication results of two scheduled NTT multipliers $Mult1$ and $Mult2$. At the same time, adder $Add1$ calculates the addition between encoded information $m_e$ and error polynomial $e_3$. The multiplication result $c_{10}$ is used to compute cipher-text $c_1$ through adder $Add2$, which adds $c_{10}$ and error polynomial $e_2$, whereas $c_{20}$ is assigned to adder $Add3$ to add with $c_{21}$ and obtain cipher-text $c_2$. Note that the additions through two adders $Add2$ and $Add3$ are executed in parallel to speed up the encryption operation.

Algorithm 2: Ring-learning with errors (LWE) encryption algorithm.

Algorithm 3 describes the ring-LWE decryption process. Initially, cipher-text $c_1$ is transformed using the NTT and driven to multiplier $Mult3$ to compute the multiplication between $c_1$ and $r_2$. The pre-decoded message $m_d$ is calculated using adder $Add4$ whose inputs are $m_{d1}$ and cipher-text $c_2$. The original message m is recovered by decoding message $m_d$. Depending on the value of the i-th coefficient of $m_d$, the corresponding value of m is decoded as 1 or 0.

Algorithm 3: Ring-LWE decryption algorithm.

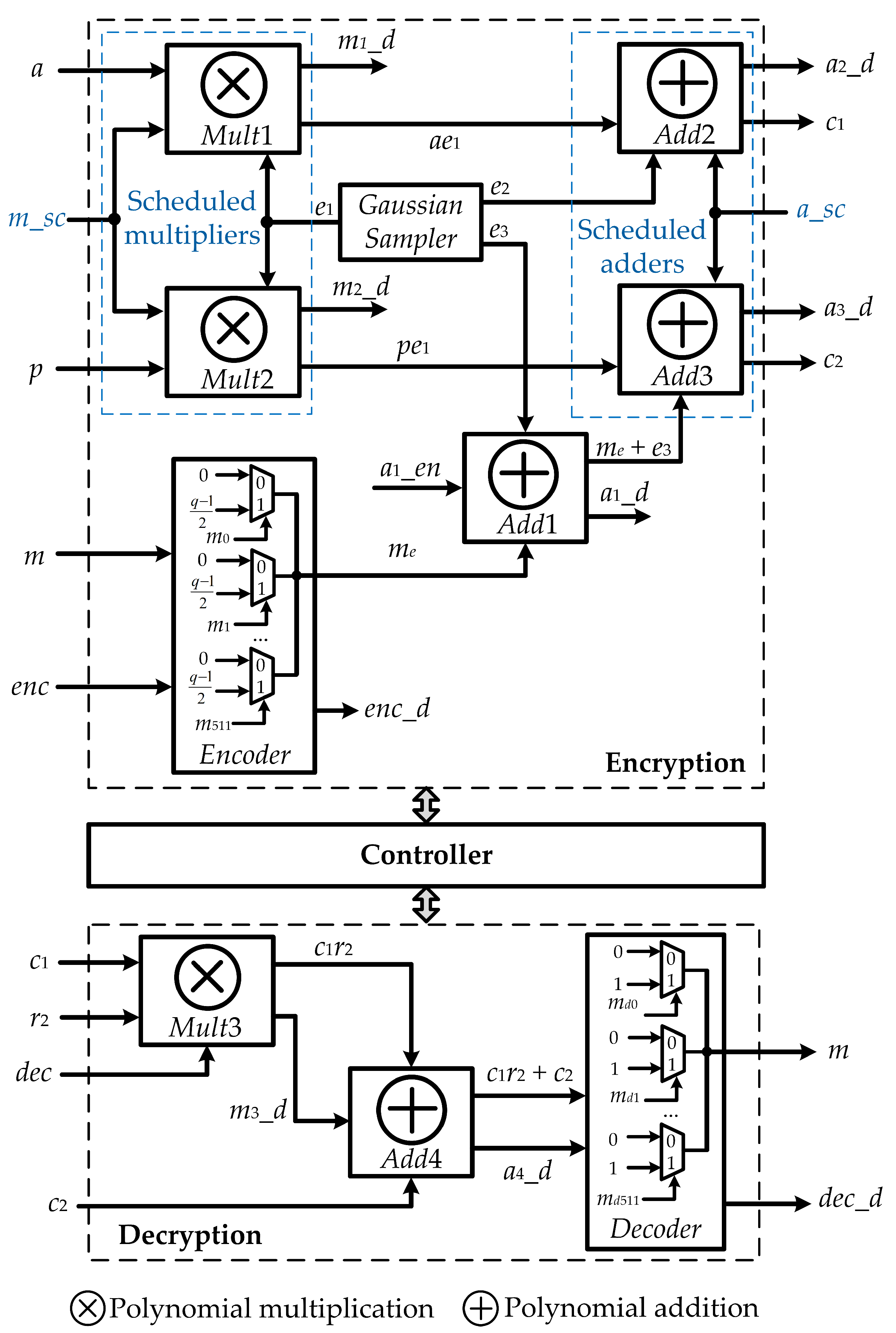
3. Proposed Ring-LWE Cryptoprocessor Architectures

3.1. Proposed Ring-LWE Encryption and Decryption Architectures

Figure 2 describes the top module of the proposed ring-LWE cryptoprocessors. The whole processor is directed by control signals generated from a controller. The system includes a Gaussian sampler to generate error polynomials, an encoder to encode the input message m, a decoder that decodes message $m_d$ to recover the original message m, multipliers, adders, and modulus to perform arithmetic operations over ring.

To conduct ring-LWE encryption and decryption, the efficient-scheduling parallel multiplier-based architectures shown in Figure 3 is proposed. As can be seen, the ring-LWE encryption architecture used to encrypt the input message m with the public key $(a,p)$ is illustrated. When the encryption signal is enabled, the input message m is initially encoded using an encoder. A two-input MUX matrix encodes the message m to the ring polynomial $m_e$. Each bit $m\left[i\right]$ of the input message m becomes the control signal of each MUX deciding whether bit $m\left[i\right]$ should be converted into 0 or $(q-1)/2$. The encoded message $m_e$ is then added with the error polynomial $e_3$ generated from a discrete Gaussian distribution through adder $Add1$. The public key $(a,p)$ is multiplied with error polynomial $e_1$ using MDF architecture-based multipliers $Mult1$ and $Mult2$. These multipliers are controlled by the scheduling signal $m\_sc$. When the signal $m\_sc$ is enabled, two multipliers work simultaneously to reduce the multiplication time. When the multiplications at $Mult1$ and $Mult2$ are accomplished, two signals $m_1\_d$ and $m_2\_d$ are assigned to 1. The scheduling signals $a\_sc$ triggers two adders $Add2$ and $Add3$, where the additions $(a\times e_1)+e_2$ and $(p\times e_1)+(m_e+e_3)$ are executed in parallel, respectively. Once these additions are completed, two signals $a_2\_d$ and $a_3\_d$ are assigned to 1. The output of adder $Add2$ is cipher-text $c_1$, and the output of adder $Add3$ is cipher-text $c_2$. The encryption process is thus accomplished.

The decryption architecture is used to recover the original message m from the cipher-text $(c_1,c_2$) when needed. This process starts when the decryption control signal $dec$ is enabled. The proposed MDF-architecture based multiplier $Mult3$ calculates the multiplication between cipher-text $c_1$ and private key $r_2$. The signal $m_3\_d=1$ indicates that this multiplication has been carried out. The output of multiplier $Mult3$ is then added with cipher-text $c_2$ through adder $Add4$ enabled by signal $m_3\_d$. The pre-decoded message $m_d$ is available when signal $a_4\_d$ of adder $Add4$ equals to 1. To recover message m from the pre-decoded message $m_d$, a decoder with a two-input MUX matrix is used. Each value of the polynomial $m_d$ is compared with $q/4$ and $3\times q/4$ to obtain the control signal of the corresponding MUX. If i-th value of $m_d$ is within this range, the corresponding value of m is decoded as 1; otherwise, it is decoded as 0. Finally, the original message m is completely recovered. The timing diagram of the operations in encryption and decryption phases is described in Figure 4.

3.2. Proposed NTT Multiplier Architecture

As mentioned previously, polynomial multiplication is an important operation in ring-LWE cryptosystems. Theoretically, an NTT-based polynomial multiplication consists of NTT, INTT, point-wise multiplication, and three bit-reverse processes. To decrease the latency and hardware complexity of the polynomial multiplier, we use the reverse Cooley–Tukey algorithm [22] to remove three bit-reverse operations. The design of the MDF-architecture based NTT multiplier is presented in Figure 5. In detail, Figure 5a describes the top level of the proposed MDF-architecture-based NTT multiplier to conduct the multiplication of two polynomials $a\left(x\right)$ and $b\left(x\right)$. Figure 5b presents the radix-8 MDF-architecture-based NTT multiplier. The multiplication of two input polynomials $a\left(x\right)$ and $b\left(x\right)$ is processed using NTT operations NTT$\left(a\right)$ and NTT$\left(b\right)$, followed by a point-wise multiplication. The result from the point-wise multiplication is then processed by the INTT block to get the polynomial multiplication result $c\left(x\right)$. For the radix-k MDF-architecture based NTT multiplier, n-coefficients of the input polynomial are divided into k paths. Each path consists of $n/k$ coefficients with the indexes of $(i+j\times ({log}_{2}n-1))$, where $i=0,\cdots ,k-1$, and $j=0,\cdots ,n/k-1$. The input polynomial with $n=512$ coefficients is allocated as Figure 5c.

4. Simulation Results and Comparison

The proposed efficient-scheduling parallel multiplier-based ring-LWE cryptoprocessors were modeled in Verilog HDL, synthesized and implemented in Xilinx VIVADO on a Virtex-7 FPGA platform. Three architectures, namely, radix-2 SDF (radix-2S), radix-2 MDF (radix-2M), and radix-8 MDF (radix-8M) were developed. The simulation results are shown in

Table 1. Implementation results and performance comparison of the proposed ring-learning with errors (LWE) cryptoprocessors.

	Proposed Radix-2S	R2S [7]	Proposed Radix-2M	R2M [7]	Proposed Radix-8M	R8M [7]	[13]	[16]
Devices	Virtex-7	Stratix IV	Virtex-7	Stratix IV	Virtex-7	Stratix IV	Virtex-6	Virtex-6
LUTs (enc.)	23,015	28,977	29,802	31,890	61,154	62,994	5,595	1,536
LUTs (dec.)	6,623	6,761	7,252	7,272	25,160	27,313	–	–
Slices (enc.)	13,588	29,290	18,933	31,540	42,374	56,435	4,760	953
Slices (dec.)	6,354	7,616	7,657	8,641	23,495	32,019	–	–
Cycles (enc.)	1,832	2,207	651	1,194	240	391	13,769	13,300
Cycles (dec.)	1,754	1,145	612	644	224	225	8,883	5,800
Time (enc.) ($\mathsf{\mu }$s)	4.58	9.33	1.97	5.16	0.89	1.73	54.86	47.90
Time (dec.) ($\mathsf{\mu }$s)	4.35	4.59	1.82	2.78	0.71	1.04	35.39	21.00
Thr. (enc.) ${}^a$ (Mbps)	1,565.07	824.03	3,638.58	1,491.26	8,053.93	4,465.12	130.66	149.64
Thr. (dec.) ${}^a$ (Mbps)	117.70	111.55	281.32	184.17	721.13	492.31	14.47	24.38
Eff. (enc.) ${}^b$ (Kbps/LUT)	68.00	28.41	122.09	46.69	131.70	70.88	23.35	97.42
Eff. (dec.) ${}^b$ (Kbps/LUT)	17.77	16.50	38.79	25.33	28.66	18.02	2.29	15.87

^a Throughput (Thr.) = (Working frequency × No. of bits)/No. of clock cycles. ^b Efficiency (Eff.) = Throughput/No. of LUTs.

.

As can be seen from Table 1, the proposed cryptoprocessors achieved a higher throughput than the architectures in [7,13,16]. It can be explained that the proposed NTT multipliers, as well as adders, were scheduled to work in parallel to speed up the computation time, resulting in an increase in the system throughput. The proposed radix-2S cryptoprocessor required the least amount of hardware resources, whereas the radix-8M architecture provided the highest throughput. Specifically, the proposed radix-2S architecture used only 74.43% and 46.39% of the number of lookup tables (LUTs) and slices in [7] to perform the encryption, respectively. For the ring-LWE encryption, the radix-2S and radix-8M crytoprocessors offered an improvement in throughput of up to 90% compared with the similar architecture presented in [7], while the radix-2M architecture outperformed its predecessor R2M in [7] by approximately 1.5 times in terms of throughput. Although the ring-LWE architectures in [13,16] required a small number of LUTs and slices, the encryption and decryption latencies of these architectures were extremely large. Therefore, these architectures provided a very low throughput. As described in Table 1, the throughput of the proposed radix-2S architecture was about ten times larger than that in [13,16].

The system efficiency was a parameter used to evaluate the performance of the proposed cryptoprocessors and existing studies. This parameter was presented in [23]. As shown in Table 1, the proposed radix-8M architecture achieved the highest encryption efficiency, followed by the radix-2M architecture. The efficiency of the proposed architectures outperformed that of other architectures in general.

5. Conclusions

This paper presents an efficient-scheduling parallel multiplier-based cryptoprocessor architecture to perform the ring-LWE encryption and decryption. By exploiting MDF-architecture based NTT multipliers and scheduling operations of multipliers and adders, the encryption and decryption times are significantly decreased. In addition, the bit-reverse processes in an NTT multiplier are removed to reduce the system hardware complexity. As a result, the proposed cryptoprocessors can lead to a significant reduction in hardware complexity and achieve a much higher throughput and efficiency compared to existing architectures. Therefore, the proposed ring-LWE cryptoprocessors are promising solutions for the security systems that require high throughput, high efficiency, and low latency.