AN-Aided Secure Beamforming in Power-Splitting-Enabled SWIPT MIMO Heterogeneous Wireless Sensor Networks
Abstract
:1. Introduction
- Firstly, we establish the system model of a two-tier MIMO HWSN, where SWIPT technique is performed at the femtocell sink node to recharge the HP-SNs and LP-SNs. To be specific, each HP-SN is equipped with power splitter. We consider a general system case where both the M-SNs and HP-SNs are faced under threat of secrecy leakage from the LP-SNs, where each LP-SN act as a malicious user.
- To promote the security performance and harvest more power, the AN is injected designedly into the transmit beamforming at the femtocell sink node. To achieve secrecy enhancement, a joint design problem is formulated for the MSC maximization while considering the fairness among multiple M-SNs. The original problem is non-convex and hard to solve directly.
- In order to reduce the performance loss of the rank relaxation from the SDR technique while solving the non-convex max–min program [38], we apply SCA technique, first-order Taylor series expansion and SPCA method, and then the recast problem can be converted to an SOCP problem [39] which can be directly solved to achieve a near-optimal solution. Moreover, we propose a novel SCA-SPCA-based iterative algorithm, while its convergence property of the proposed algorithm is proved.
2. System Model and Problem Formulation
3. Proposed Algorithm
| Algorithm 1 Proposed SCA-SPCA-based iterative Algorithm |
|
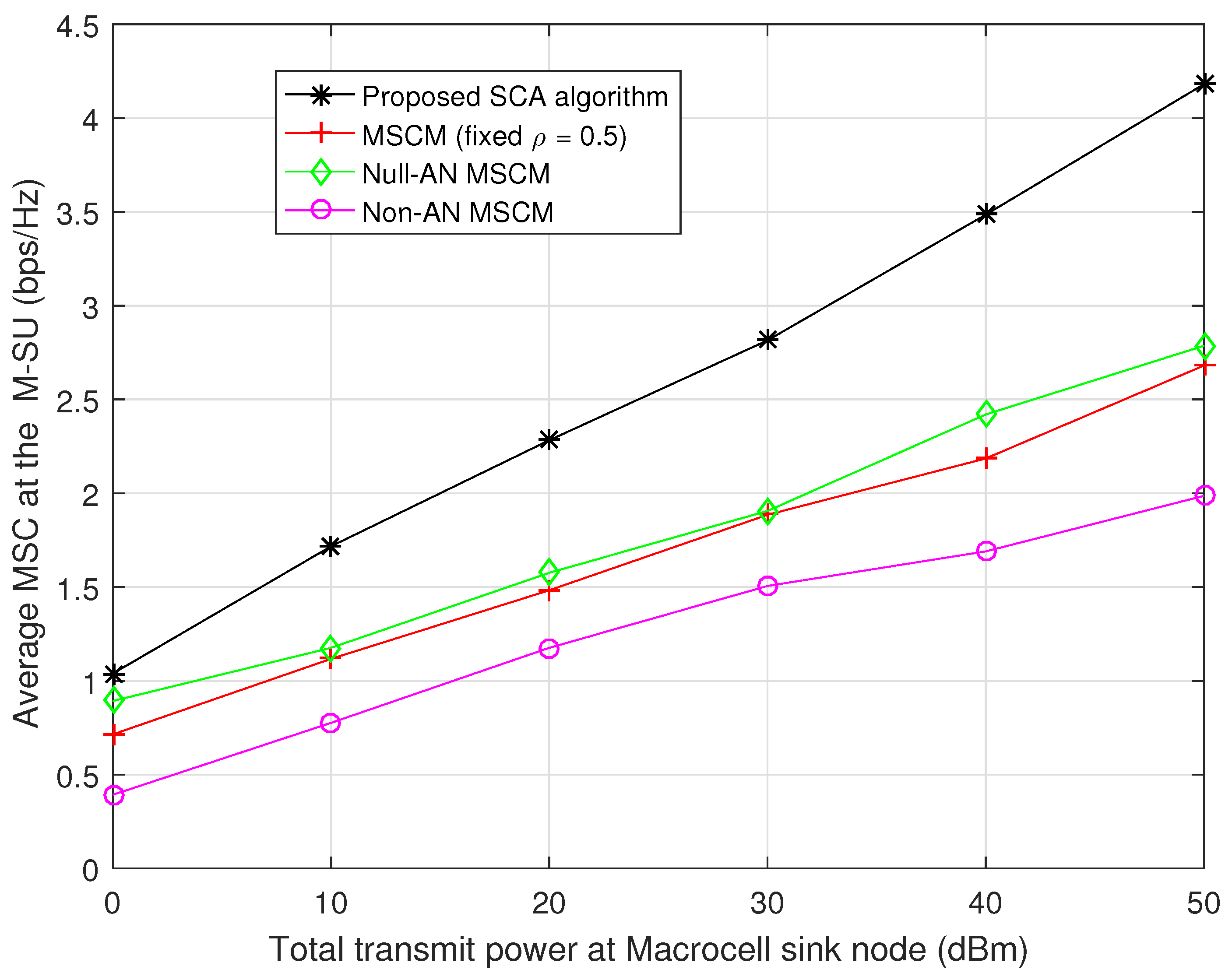
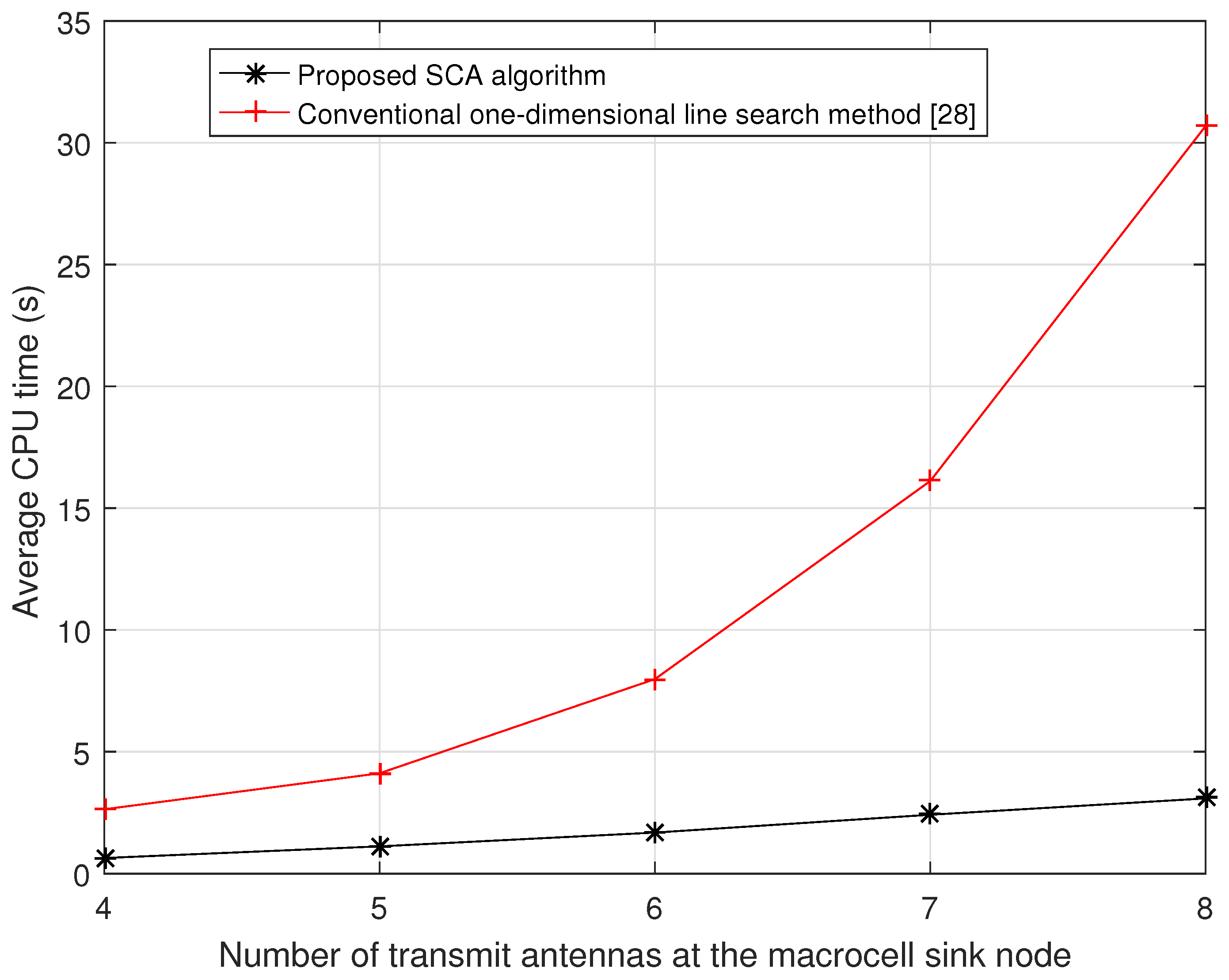
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| HWSN | heterogeneous wireless sensor networks |
| SWIPT | simultaneous wireless information and power transfer |
| AN | artificial noise |
| SCA | successive convex approximation |
| SPCA | sequential parametric convex approximation |
| SOCP | second order cone programming |
| IoT | Internet-of-Things |
| WSN | wireless sensor network |
| MBS | macrocell base station |
| FBS | femtocell base station |
| SN | sensor node |
| HP-SN | high-priority sensor node |
| LP-SN | low-priority sensor node |
| M-SN | macrocell sensor node |
| HetNet | heterogeneous networks |
| WPT | wireless power transmission |
| WIT | wireless information transmission |
| MISO | multiple-input single-output |
| MIMO | multiple-input multiple |
| CoMP | coordinated multi-point |
| CSI | channel state imformation |
| PLS | physical-layer security |
| PS | power splitting |
| MSC | minimal secrecy capacity |
| MSCM | MSC maximization |
| AWGN | additive white Gaussian noise) |
| ID | imformation decoding |
| EH | energy harvesting |
| QoL | quadratic-over-linear |
Appendix A
Appendix B
References
- Wang, S.; Wan, J.; Zhang, D.; Li, D.; Zhang, C. Towards smart factory for industry 4.0: A self-organized multi-agent system with big data based feedback and coordination. Comput. Netw. 2016, 101, 158–168. [Google Scholar] [CrossRef]
- Williams, J.M.; Khanna, R.; Ruiz-Rosero, J.P.; Pisharody, G.; Qian, Y.; Carlson, C.R.; Liu, H.; Ramirez-Gonzalez, G. Weaving the wireless Web: Toward a low-power, dense wireless sensor network for the industrial IoT. IEEE Microw. Mag. 2017, 18, 40–63. [Google Scholar] [CrossRef]
- Khan, I.; Belqasmi, F.; Glitho, R.; Crespi, N.; Morrow, M.; Polakos, P. Wireless sensor network virtualization: A survey. IEEE Commun. Surv. Tutor. 2015, 18, 553–576. [Google Scholar] [CrossRef]
- Liu, H.-H.; Su, J.-J.; Chou, C.-F. On energy-effcient straight-line routing protocol for wireless sensor networks. IEEE Syst. J. 2017, 11, 2374–2382. [Google Scholar] [CrossRef]
- Chincoli, M.; Liotta, A. Self-learning power control in wireless sensor networks. Sensors 2018, 18, 375. [Google Scholar] [CrossRef]
- Wang, C.X.; Haider, F.; Gao, X.; You, X.-H.; Yang, Y.; Yuan, D.; Aggoune, H.M.; Haas, H.; Fletcher, S.; Hepsaydir, E. Cellular architecture and key technologies for 5G wireless communication networks. IEEE Commun. Mag. 2014, 52, 122–130. [Google Scholar] [CrossRef] [Green Version]
- Xiong, K.; Zhang, Y.; Fan, P.; Yang, H. Evaluation framework for user experience in 5G systems: On systematic rateless-coded transmissions. IEEE Access 2016, 4, 9108–9118. [Google Scholar] [CrossRef]
- Damnjanovic, A.; Montojo, J.; Wei, Y.; Ji, T.; Luo, T.; Vajapeyam, M.; Yoo, T.; Song, O.; Malladi, D. A survey on 3GPP heterogeneous networks. IEEE Wirel. Commun. 2011, 18, 10–21. [Google Scholar] [CrossRef]
- Dhillon, H.S.; Ganti, R.K.; Baccelli, F.; Andrews, J.G. Modeling and analysis of K-tier downlink heterogeneous cellular networks. IEEE J. Sel. Areas Commun. 2012, 30, 550–560. [Google Scholar] [CrossRef]
- Lopez-Perez, D.; Guvenc, I.; de la Roche, G.; Kountouris, M.; Quek, T.Q.S.; Zhang, J. Enhanced intercell interference coordination challenges in heterogeneous networks. IEEE Wirel. Commun. 2011, 18, 22–30. [Google Scholar] [CrossRef] [Green Version]
- Bi, S.; Ho, C.K.; Zhang, R. Wireless powered communication: Opportunities and challenges. IEEE Commun. Mag. 2015, 53, 117–125. [Google Scholar] [CrossRef]
- Xiong, K.; Fan, P.; Zhang, C.; Letaief, K.B. Wireless information and energy transfer for two-hop non-regenerative MIMO-OFDM relay networks. IEEE J. Sel. Areas Commun. 2015, 33, 1595–1611. [Google Scholar] [CrossRef]
- Xiong, K.; Chen, C.; Qu, G.; Fan, P.; Letaief, K.B. Group cooperation with optimal resource allocation in wireless powered communication networks. IEEE Trans. Wirel. Commun. 2017, 16, 3840–3853. [Google Scholar] [CrossRef]
- Zhang, R.; Ho, C. MIMO broadcasting for simultaneous wireless information and power transfer. IEEE Trans. Wirel. Commun. 2013, 12, 1989–2001. [Google Scholar] [CrossRef]
- Xiong, K.; Wang, B.; Liu, K.J.R. Rate-energy region of SWIPT for MIMO broadcasting under nonlinear energy harvesting model. IEEE Trans. Wirel. Commun. 2017, 16, 5147–5161. [Google Scholar] [CrossRef]
- Erol-Kantarci, M.; Mouftah, H.T. Radio-frequency-based wireless energy transfer in LTE-A heterogenous networks. In Proceedings of the IEEE Symposium on Computers and Communications (ISCC), Funchal, Portugal, 23–26 June 2014; pp. 1–6. [Google Scholar]
- Tang, J.; Shojaeifard, A.; So, D.K.C.; Wong, K.; Zhao, N. Energy efficiency optimization for CoMP-SWIPT heterogeneous networks. IEEE Trans. Commun. 2018, 66, 6368–6383. [Google Scholar] [CrossRef]
- Jiang, R.; Xiong, K.; Fan, P.; Zhang, Y.; Zhong, Z. Optimal design of SWIPT systems with multiple heterogeneous users under non-linear energy harvesting model. IEEE Access 2017, 5, 11479–11489. [Google Scholar] [CrossRef]
- Chen, X.; Ng, D.W.K.; Chen, H. Secrecy wireless information and power transfer: Challenges and opportunities. IEEE Wirel. Commun. 2016, 23, 54–61. [Google Scholar] [CrossRef]
- Khisti, A.; Wornell, G.W. Secure transmission with multiple antennas I: The MISOME wiretap channel. IEEE Trans. Inf. Theory 2010, 56, 3088–3104. [Google Scholar] [CrossRef]
- Shiu, Y.; Chang, S.Y.; Wu, H.; Huang, S.C.; Chen, H. Physical layer security in wireless networks: A tutorial. IEEE Wirel. Commun. 2011, 18, 66–74. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, R.; Chua, K.C. Secrecy wireless information and power transfer with MISO beamforming. IEEE Trans. Signal Process. 2014, 62, 1850–1863. [Google Scholar] [CrossRef]
- Zhu, Z.; Chu, Z.; Wang, Z.; Lee, I. Outage constrained robust beamforming for secure broadcasting systems with energy harvesting. IEEE Trans. Wirel. Commun. 2016, 15, 7610–7620. [Google Scholar] [CrossRef]
- Zhu, Z.; Chu, Z.; Wang, N.; Huang, S.; Wang, Z.; Lee, I. Beamforming and power splitting designs for AN-aided secure multi-user MIMO SWIPT systems. IEEE Trans. Inf. Forensics Secur. 2017, 12, 2861–2874. [Google Scholar] [CrossRef]
- Lu, Y.; Xiong, K.; Fan, P.; Ding, Z.; Zhong, Z.; Letaief, K.B. Global energy efficiency in secure MISO SWIPT systems with non-linear power-splitting EH model. IEEE J. Sel. Areas Commun. 2019, 37, 216–232. [Google Scholar] [CrossRef]
- Ng, D.W.K.; Lo, E.S.; Schober, R. Robust beamforming for secure communication in systems with wireless information and power transfer. IEEE Trans. Wirel. Commun. 2014, 13, 4599–4615. [Google Scholar] [CrossRef]
- Lu, Y.; Xiong, K.; Fan, P.; Zhong, Z.; Letaief, K.B. Robust transmit beamforming with artificial redundant signals for secure SWIPT system under non-linear EH model. IEEE Trans. Wirel. Commun. 2018, 17, 2218–2232. [Google Scholar] [CrossRef]
- Li, B.; Fei, Z.; Chu, Z. Optimal transmit beamforming for secure SWIPT in a Two-Tier HetNet. IEEE Commun. Lett. 2017, 21, 2476–2479. [Google Scholar] [CrossRef]
- Ren, Y.; Lv, T.; Gao, H.; Li, Y. Secure wireless information and power transfer in heterogeneous networks. IEEE Access 2017, 5, 4967–4979. [Google Scholar] [CrossRef]
- Guo, S.; Wang, F.; Yang, Y.; Xiao, B. Energy-efficient cooperative Tfor simultaneous wireless information and power transfer in clustered wireless sensor networks. IEEE Trans. Commun. 2015, 63, 4405–4417. [Google Scholar] [CrossRef]
- Guo, S.; Shi, Y.; Yang, Y.; Xiao, B. Energy efficiency maximization in mobile wireless energy harvesting sensor networks. IEEE Trans. Mob. Comput. 2018, 17, 1524–1537. [Google Scholar] [CrossRef]
- Pan, G.; Lei, H.; Yuan, Y.; Ding, Z. Performance analysis and optimization for SWIPT wireless sensor networks. IEEE Trans. Commun. 2017, 65, 2291–2302. [Google Scholar] [CrossRef]
- Liu, G.; Sun, Z.; Jiang, T. Joint time and energy allocation for QoS-aware throughput maximization in MIMO-based wireless powered underground sensor networks. IEEE Trans. Commun. 2019, 67, 1400–1412. [Google Scholar] [CrossRef]
- Ha, D.B.; So-In, C.; Tran, H.; Nguyen, T.G.; Baig, Z.A.; Sanguanpong, S. Performance analysis of DF/AF cooperative MISO wireless sensor networks with NOMA and SWIPT over nakagami-m fading. IEEE Access 2018, 6, 56142–56161. [Google Scholar]
- Hu, X.; Huang, K.; Chen, Y.; Xu, X.; Liang, X. Secrecy analysis of UL transmission for SWIPT in WSNs with densely clustered eavesdroppers. In Proceedings of the 9th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 11–13 October 2017. [Google Scholar]
- Chae, S.H.; Jeong, C.; Lim, S.H. Simultaneous wireless information and power transfer for Internet-of-Things sensor networks. IEEE Internet Things J. 2018, 5, 2829–2843. [Google Scholar] [CrossRef]
- Yi, B.; Xiang, M.; Yao, W.; Qiu, K.; Huang, T.; Xie, Q. Simultaneous wireless information and power transfer in wireless sensor networks with fountain codes. In Proceedings of the IEEE International Conference on Internet-of-Things (iThings), Devon, UK, 21–23 June 2017; pp. 516–521. [Google Scholar]
- Luo, Z.-Q.; Ma, W.-K.; So, A.-C.; Ye, Y.; Zhang, S. Semidefinite relaxation of quadratic optimization problems. IEEE Trans. Signal Process. Mag. 2010, 27, 20–34. [Google Scholar] [CrossRef]
- Lobo, M.S.; Vandenberghe, L.; Boyd, S.; Lebret, H. Applications of Second Order Cone Programming. Linear Algebra Appl. 1998, 284, 193–228. [Google Scholar] [CrossRef]
- Ding, Z.; Zhong, C.; Ng, D.W.; Peng, M.; Suraweera, H.A.; Schober, R.; Poor, H.V. Application of smart antenna technologies in simultaneous wireless information and power transfer. IEEE Commun. Mag. 2015, 53, 86–93. [Google Scholar] [CrossRef] [Green Version]
- Beck, A.; Ben-Tal, A.; Tetruashvili, L. A sequential parametric convex approximation method with applications to nonconvex truss topology design problems. J. Glob. Optim. 2010, 47, 29–51. [Google Scholar] [CrossRef]
- Li, Q.; Ma, W. Optimal and robust transmit designs for MISO channel secrecy by semidefinite programming. IEEE Trans. Signal Process. 2011, 59, 3799–3812. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Chu, Z.; Cumanan, K.; Ding, Z.; Johnston, M.; le Goff, S. Secrecy rate optimizations for a MIMO secrecy channel with a cooperative jammer. IEEE Trans. Veh. Technol. 2015, 64, 1833–1847. [Google Scholar] [CrossRef]
- Vishwanathan, A.S.; Smola, A.J.; Vishwanathan, S.V.N. Kernel methods for missing variables. In Proceedings of the 10th International Workshop on Artificial Intelligence and Statistics, Bridgetown, Barbados, 6–8 January 2005; pp. 325–332. [Google Scholar]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming. 2012. Available online: http://cvxr.com/cvx (accessed on 8 August 2018).





| Variables | Definition |
|---|---|
| M-SN | the m-th M-SN |
| HP-SN | the k-th HP-SN |
| LP-SN | the l-th LP-SN |
| the transmit signal from macrocell sink node to M-SN | |
| the transmit signal from femtocell sink node | |
| the transmit beamforming vector from macrocell sink node aiming at M-SN | |
| the transmit beamforming vector from femtocell sink node aiming at HP-SN | |
| , | the information-bearing signal intended for M-SN and HP-SN |
| the energy-carrying AN | |
| the channel between macrocell sink node and M-SN | |
| the channel between macrocell sink node and HP-SN | |
| the channel between macrocell sink node and LP-SN | |
| the channel between femtocell sink node and M-SN | |
| the channel between femtocell sink node and HP-SN | |
| the channel between femtocell sink node and LP-SN | |
| , , | the complex Gaussian noise at the M-SN, the HP-SN and the LP-SN |
| the additional noise introduced from the RF-to-signal conversion in the ID part at the HP-SN |
| Number of M-SN, M | 3 |
|---|---|
| Number of HP-SN, K | 2 |
| Number of LP-SN, L | 2 |
| Number of LP-SN antenna, | 2 |
| Number of transmit antenna at macrocell sink node, | 4 |
| Number of transmit antenna at femtocell sink node, | 16 |
| Distance between the macrocell sink node and the M-SN, | 10 m |
| Distance between the macrocell sink node and the HP-SN, | 5 m |
| Distance between the macrocell sink node and the LP-SN, | 3 m |
| Distance between the femtocell sink node and the M-SN, | 6 m |
| Distance between the femtocell sink node and the HP-SN, | 5 m |
| Distance between the femtocell sink node and the LP-SN, | 2 m |
| Speed of light, c | |
| Carrier frequency, | 900 MHz |
| Path loss exponent, | |
| Gaussian noise power at all the M-SN, | |
| Gaussian noise power at all the HP-SN, | |
| Gaussian noise power of all the LP-SNs, | |
| Additional noise power of all the HP-SNs, | |
| Energy conversion efficiency at all the HP-SN and LP-SN, | 0.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, W.; Zhu, Z.; Hao, W.; Wang, Y.; Wang, Z.; Wu, Q.; Chu, Z. AN-Aided Secure Beamforming in Power-Splitting-Enabled SWIPT MIMO Heterogeneous Wireless Sensor Networks. Electronics 2019, 8, 459. https://doi.org/10.3390/electronics8040459
Ge W, Zhu Z, Hao W, Wang Y, Wang Z, Wu Q, Chu Z. AN-Aided Secure Beamforming in Power-Splitting-Enabled SWIPT MIMO Heterogeneous Wireless Sensor Networks. Electronics. 2019; 8(4):459. https://doi.org/10.3390/electronics8040459
Chicago/Turabian StyleGe, Weili, Zhengyu Zhu, Wanming Hao, Yi Wang, Zhongyong Wang, Qiong Wu, and Zheng Chu. 2019. "AN-Aided Secure Beamforming in Power-Splitting-Enabled SWIPT MIMO Heterogeneous Wireless Sensor Networks" Electronics 8, no. 4: 459. https://doi.org/10.3390/electronics8040459
APA StyleGe, W., Zhu, Z., Hao, W., Wang, Y., Wang, Z., Wu, Q., & Chu, Z. (2019). AN-Aided Secure Beamforming in Power-Splitting-Enabled SWIPT MIMO Heterogeneous Wireless Sensor Networks. Electronics, 8(4), 459. https://doi.org/10.3390/electronics8040459





