Chaotic Pattern Array for Single-Pixel Imaging

Abstract

Single-pixel imaging (SPI) is an emerging framework that can capture the image of a scene via a single-point detector at a considerably low cost. It measures the projection at the detector of the scene under view with certain patterns. One can reconstruct the image of the scene via post-processing the measurements modulated by the patterns. However, the most commonly-used random patterns are not always desirable in many applications, especially for real-time, resource-limited occasions, due to their high memory requirement and huge cost in software and hardware implementation. In this paper, a chaotic pattern array is proposed for the SPI architecture. Compared with random patterns, the proposed chaotic pattern array can not only promise to increase the capabilities of the SPI device, but can also reduce the memory cost and complexity of hardware implementation in the meantime. Moreover, convincing experiment results are given to illustrate that the proposed pattern array is suitable for single-pixel cameras, as well as other compressive imaging applications.

1. Introduction

Compressive sampling (CS) theory implies that one can reconstruct a signal of interest from only a small set of projections, which has brought a revolution in various fields [1,2,3,4,5,6,7]. Motivated by CS theory, Duarte et al. proposed a novel single-pixel imaging (SPI) architecture, which is also known as a single-pixel camera, based on a single-point detector at a considerably low cost [8]. On the surface, imaging via a single-pixel imaging device is counterproductive, as we know that an ordinary sensor-array-based camera (i.e., a CMOS or CCD (CMOS and CCD are complementary metal-oxide-semiconductor transistor and charge coupled device, respectively.) camera) in today’s world can have millions of embedded pixels.

However, the SPI architecture can measure the images of interest while implementing hardware compression of the data without additional cost [9]. Compared to CMOS or CCD cameras, the SPI camera has several outstanding advantages: (1) the single-point detector is typically sensitive to weak light intensity change [10]; hence, it is efficient; (2) using an SPI device has intrinsic hardware compression [11]; therefore, it just requires small memory; (3) the cost of building a single-pixel camera is much lower than that of an ordinary camera [12], so it is economical, as well. As a result, the SPI architecture is of interest for various applications, such as color imaging [13], Terahertz imaging [14], infrared imaging [15], hyperspectral imaging [16], and video acquisition [17].

From a hardware perspective, an SPI device is made up of a single-point detector and a spatial light modulator (SLM). More specifically, the single-point detector essentially uses certain patterns pre-loaded on the SLM hardware to modulate the image of a scene and then integrates the corresponding measurements. By post-processing these measurements, the image of the scene can be exactly restored with high probability. The methods of restoring images are conventional CS recovery algorithms, such as ${\mathbf{l}}_0$ or ${\mathbf{l}}_1$ norm minimization. In fact, there are two other acquisition and restoration strategies for the generalized single-pixel imaging, i.e., basis scan [18] and adaptive basis scan [19,20,21]. The characteristics of these methods can be summarized in

Table 1. Comparison of the main characteristics of the three strategies.

Approach	Sampling Patterns	Image Reconstruction	Required Measurements
Compressive sampling	Sensing matrix	${\mathbf{l}}_0$/${\mathbf{l}}_1$ norm minimization	Few
Basis scan	Basis	Inverse transform	Large
Adaptive basis scan	Basis	Inverse transform	Few

. Each strategy has its benefits, but also some drawbacks. The CS method is efficient because it only needs a few measurements at the expense of the high computational cost of the reconstruction. Basis scan benefits from fast inverse transform, but this method is impractical yet, as it requires a large number of measurements. Adaptive basis scan introduces adaptivity to overcome this drawback, but it cannot offer a perfect image reconstruction. Moreover, it still requires more measurements than the CS method, although this approach greatly reduces the measurement requirements compared to basis scan. Considering that the CS method is attractive because of its high efficiency and simplicity in practical applications, we mainly discuss the commonly-used SPI technique, i.e., the SPI with the CS method.

It is widely agreed that one critical idea of the SPI architecture is to design the SLM patterns. In fact, there have been many different random SLM patterns for SPI over the years. Among them, the most common one is the random Bernoulli pattern whose elements obey the Bernoulli distribution with mean zero and probability $\frac{1}{2}$. To date, researchers have introduced four common hardware architectures to load random patterns, i.e., the digital micromirror device (DMD) (such a device was invented by Hornbeck in 1987, and Duarte et al. firstly introduced this device into the SPI camera) [8], liquid crystal display (LCD) [22], liquid crystal on silicon (LCS) [23], and metamaterial absorber (MMA) [14]. Depending on the desired applications, the DMD is widely used in the SPI device, as it is easy to implement and can provide rapid refreshing rates, as well. Therefore, the DMD together with a random Bernoulli pattern is quite popular [9]. In addition, many particularly useful strategies, such as pattern shifting [8] and pattern generalization [24], have been proposed to improve the performance of random SLM patterns.

Although random patterns are of extraordinary importance for the image modulation in the SPI device, they are not always desirable in many applications because of their high memory requirement and huge cost in software and hardware implementation. Promising approaches to solve these challenges can be found in [25,26,27] and the references therein. These proposed patterns have their benefits, but also some disadvantages. The theoretical guarantees of these deterministic patterns are much more rigorous than those of the random patterns. Moreover, only most of sparsifying signals, but not all general signals, can be exactly recovered using the deterministic approaches. In particular, Jie et al. [28] showed that a chaotic sensing matrix can lead to remarkable improvements of the restoration effect and advantages in hardware and storage in a single-pixel color imaging system. The ingenuity of the work is very appealing, but the method lacks some detailed theoretical perspective such that it may not be general and limits its application in the SPI architecture.

Motivated by the chaotic sensing matrix, a chaotic pattern array (CPA) is proposed for the SPI architecture from a theoretical viewpoint in this paper. Specifically, we first employ the chaotic bipolar sequence ($\{1,-1\}$ elements) to build the CPA and then implement the generated construction for the single-pixel camera. In addition, we show that the proposed CPA is verified to satisfy CS theory via an argument together with Chernoff’s inequality. Based on this work, the bipolar sequence can be generalized to all other chaotic sequences that are independent realizations of $\pm 1$ binarization elements. Compared with random patterns, the CPA is hardware-friendly, and it can save significant memory by only storing the seed. Because of these features, the proposed CPA with $\pm 1$ elements is convenient for any SLM hardware, such as the DMD. The experimental results show that our proposed CPA performs similarly to or better than its random counterparts. The CPA not only works in single-pixel cameras, but also has a promising application in other imaging techniques, such as ghost imaging.

The rest of the work is arranged as follows. In Section 2, we review the related work about the SPI architecture and CS theory. In Section 3, we develop the chaotic pattern array for the SPI architecture. In Section 4, simulation results are illustrated and analyzed to investigate the efficiency of the chaotic pattern array. Finally, we conclude the work with some remarks in Section 5.

2. Related Work

2.1. Simple Modeling of the SPI Architecture

The simplest design of the SPI device can be sketched as in Figure 1. The object image under view is modulated by the predefined SLM pattern to obtain the sequential measurements (or modulated light rays), and then, these corresponding measurements are collected via the single-point detector, wherein the lens is used to focus the measurements. After that, we obtain the numerical data from the single-point detector through an analog-to-digital (A/D) converter.

For simplicity and formal description, we here treat an image of interest as a one-dimensional column vector by vectorizing it. Let $\mathit{x}\in {\mathbb{R}}^{N\times 1}$ denote the image of a scene, where the size of the image is $N=H\times D$. Assume that the predefined SLM pattern is represented by ${\mathit{m}}_k\in {\mathbb{R}}^{1\times N}$ and the collected measurement is denoted by $y_k$. Therefore, mathematically, we have:

$$\begin{array}{c}\hfill y_k=\sum _{j=1}^N{\left\{{\mathit{m}}_k\right\}}_j·{\mathit{x}}_j=<{\mathit{m}}_k,\mathit{x}>withj\in [1,N],\end{array}$$

(1)

where ${\{{\mathit{m}}_k\}}_j$ and ${\mathit{x}}_j$ denote the jth element of ${\mathit{m}}_k$ and $\mathit{x}$, respectively. Equation (1) shows that the predefined SLM pattern ${\mathit{m}}_k$ is used to scan over the full object $\mathit{x}$ and then obtain one measurement $y_k$.

Obviously, restoring the image of the scene $\mathit{x}$ from one single measurement $y_k$ is absolutely impossible, and thus, sequential measurements with a set of SLM patterns should be implemented. Let $\mathit{M}=[{\mathit{m}}_1;{\mathit{m}}_2;\dots ;{\mathit{m}}_S]\in {\mathbb{R}}^{S\times N}$ denote the sequence of S SLM patterns. Thus, the corresponding sequence of measurements $\mathit{y}={[y_1,y_2,\dots ,y_S]}^T\in {\mathbb{R}}^{S\times 1}$ can be modeled by:

$$\begin{array}{c}\hfill \mathit{y}=\mathit{M}·\mathit{x}.\end{array}$$

(2)

Equation (2) implies that the SPI architecture needs to address the following two key points:

• Modulation: how to design or select the predefined SLM patterns $\mathit{M}$?
• Reconstruction: With known $\mathit{y}$ and $\mathit{M}$, how is the image of the scene $\mathit{x}$ reconstructed?

To answer these issues, we have to review the mathematical tool behind this, i.e., CS theory, as the SPI technique is based on the CS framework.

2.2. Basics of CS Theory

The CS framework indicates that one can reconstruct a sparse signal from only a small set of projections, which offers a perfect theoretical framework for the SPI architecture. Assume that the image of a scene is sparse on a transform basis $\mathsf{\Psi }\in {\mathbb{R}}^{N\times N}$. Fourier, discrete cosine transform, and the wavelets basis are several common choices for $\mathsf{\Psi }$. Mathematically,

$$\begin{array}{c}\hfill \mathit{x}=\mathsf{\Psi }·\mathit{\alpha },\end{array}$$

(3)

where $\mathit{\alpha }$ is the K-sparse coefficient vector, i.e., ${\Vert \mathit{\alpha }\Vert }_{{\mathbf{l}}_0}\le K$. Based on CS theory, we know that one can reconstruct the image of the scene $\mathit{x}$ from only K-sparse coefficients. In order to better understand this, we need to make the following review.

With a collection of vectors $\mathit{M}\in {\mathbb{R}}^{S\times N}$ (also called sensing matrix), the holy grail of CS is to obtain $S\ll N$ measurements of the image $\mathit{x}$, i.e.,

$$\begin{array}{c}\hfill \mathit{y}=\mathit{M}·\mathit{x}=\mathit{M}·\mathsf{\Psi }·\mathit{\alpha }=\mathsf{\Theta }·\mathit{\alpha },\end{array}$$

(4)

where $\mathsf{\Theta }=\mathit{M}·\mathsf{\Psi }\in {\mathbb{R}}^{S\times N}$ is called the transform matrix. The ratio $\frac{S}{N}$ is the sampling rate, and we use ♮ to denote it. As there is a linear dimensionality reduction from ${\mathbb{R}}^{N\times 1}$ to ${\mathbb{R}}^{S\times 1}$, it is vital to build the matrix $\mathit{M}$ such that it seizes and possesses enough information to restore $\mathit{x}$. Certain properties of the collection matrix $\mathit{M}$, such as the mutual coherence [29] and the restricted isometry property (RIP) [30], have been proposed to measure $\mathit{M}$.

Definition 1.

The coherence of a matrix $\mathit{M}\in {\mathbb{R}}^{S\times N}$, $\mu \left(\mathit{M}\right)$, is the maximum inner product, i.e.,

$$\mu \left(\mathit{M}\right)=\underset{1\le i\ne j\le N}{max}\frac{|\langle {\mathit{m}}_i,{\mathit{m}}_j\rangle |}{\Vert {\mathit{m}}_i{\Vert }_2·\Vert {\mathit{m}}_j{\Vert }_2},$$

(5)

where ${\mathit{m}}_i$ and ${\mathit{m}}_j$ are any two columns of $\mathit{M}$.

We can prove that $\mu \left(\mathit{M}\right)\in [\sqrt{\frac{N-S}{S(N-1)}},1]$, where $\sqrt{\frac{N-S}{S(N-1)}}$ is also known as the Welch bound [31]. In addition, it can be observed that the lower bound is close to $\frac{1}{\sqrt{S}}$ when $S\ll N$. Much research has extended the concept of coherence to certain structured sparsity models [32]. The coherence is a commonly-used property to measure the matrix $\mathit{M}$, but it may lack an intuitive and visual explanation. Another common property is the RIP, which is an elegant geometrical description for the dimensionality reduction with distance preserving.

Definition 2.

A matrix $\mathit{M}\in {\mathbb{R}}^{S\times N}$ meets the (K,ϵ)-RIP if:

$$(1-ϵ){\Vert \mathit{v}\Vert }_{{\mathbf{l}}_2}^2\le {\Vert \mathit{M}·\mathit{v}\Vert }_{{\mathbf{l}}_2}^2\le (1+ϵ){\Vert \mathit{v}\Vert }_{{\mathbf{l}}_2}^2$$

(6)

holds for all $\mathit{v}\in \{\mathit{v}:\Vert \mathit{v}\Vert {\mathbf{l}}_0\le K\}$ with some $ϵ>0$.

The RIP can guarantee that the distance between $\mathit{y}=\mathit{M}\mathit{v}$ and ${\mathit{y}}^{\prime }=\mathit{M}{\mathit{v}}^{\prime }$ is proportional to the distance between the two original signals $\mathit{v}$ and ${\mathit{v}}^{\prime }$. This distance preserving ensures that any two sparse signals that are far apart from each other will not result in the same measurements $\mathit{y}$. Actually, one can connect the RIP and the coherence via the Geršgorin circle theorem, and we refer the reader to [33,34] and the references therein.

It is well known that an independent identically distributed (i.i.d) random matrix has the (K,$ϵ$)-RIP; thus, random SLM patterns are generally selected for the single-pixel camera. In particular, a random Bernoulli pattern with elements $\pm 1$ loaded on the hardware architecture is quite popular [9], as this pattern can easily modulate the pixels to $+1$ in phase or $-1$ out of phase via a reference. With the Johnson–Lindenstrauss lemma, Baraniuk et al. proposed an algorithmically-simple proof of the RIP for random SLM patterns [35]. By combining the concentration inequalities, they introduced the following theorem.

Theorem 1

([35]).If a matrix $\mathit{M}\in {\mathbb{R}}^{S\times N}$ meets the concentration inequalities and $S\ge (c_0·K·log(N/K))$, then $\mathit{M}$ meets the (K,ϵ)-RIP with probability $\ge 1-2exp\left(-c_1·S\right)$, where $c_0$ and $c_1$, relying only on ϵ, are two constants.

Provided that $\mathit{M}$ meets the (K,$ϵ$)-RIP, then $\mathit{x}$ can be restored from $\mathit{y}$ via CS recovery algorithms. Strategies for CS recovery include the ${\mathbf{l}}_0$ norm, ${\mathbf{l}}_1$ norm, and greedy algorithms. For the SPI recovery, we need first to address that:

$${\mathit{\alpha }}^{*}=arg\underset{\mathit{\alpha }\in {\mathbb{R}}^N}{min}{\Vert \mathit{\alpha }\Vert }_{{\mathbf{l}}_p}\mathrm{such} \mathrm{that}\mathsf{\Theta }\mathit{\alpha }=\mathit{y},$$

(7)

where $0\le p\le 1$ and ${\Vert \mathit{x}\Vert }_{{\mathbf{l}}_p}$ denotes the ${\mathbf{l}}_p$ norm of $\mathit{\alpha }\in {\mathbb{R}}^{N\times 1}$. After that, by virtue of:

$${\mathit{x}}^{*}=\mathsf{\Psi }·{\mathit{\alpha }}^{*},$$

(8)

we can restore the image $\mathit{x}$ from the measurements $\mathit{y}$. In addition, Li demonstrated that total variation (TV) minimization is also suitable for the SPI recovery, as it can offer efficient reconstruction performance in terms of recovery quality and speed [36].

3. Single-Pixel Imaging with the Chaotic Pattern Array

In this section, we introduce the modulation and reconstruction mechanisms using an SPI device with the chaotic pattern array.

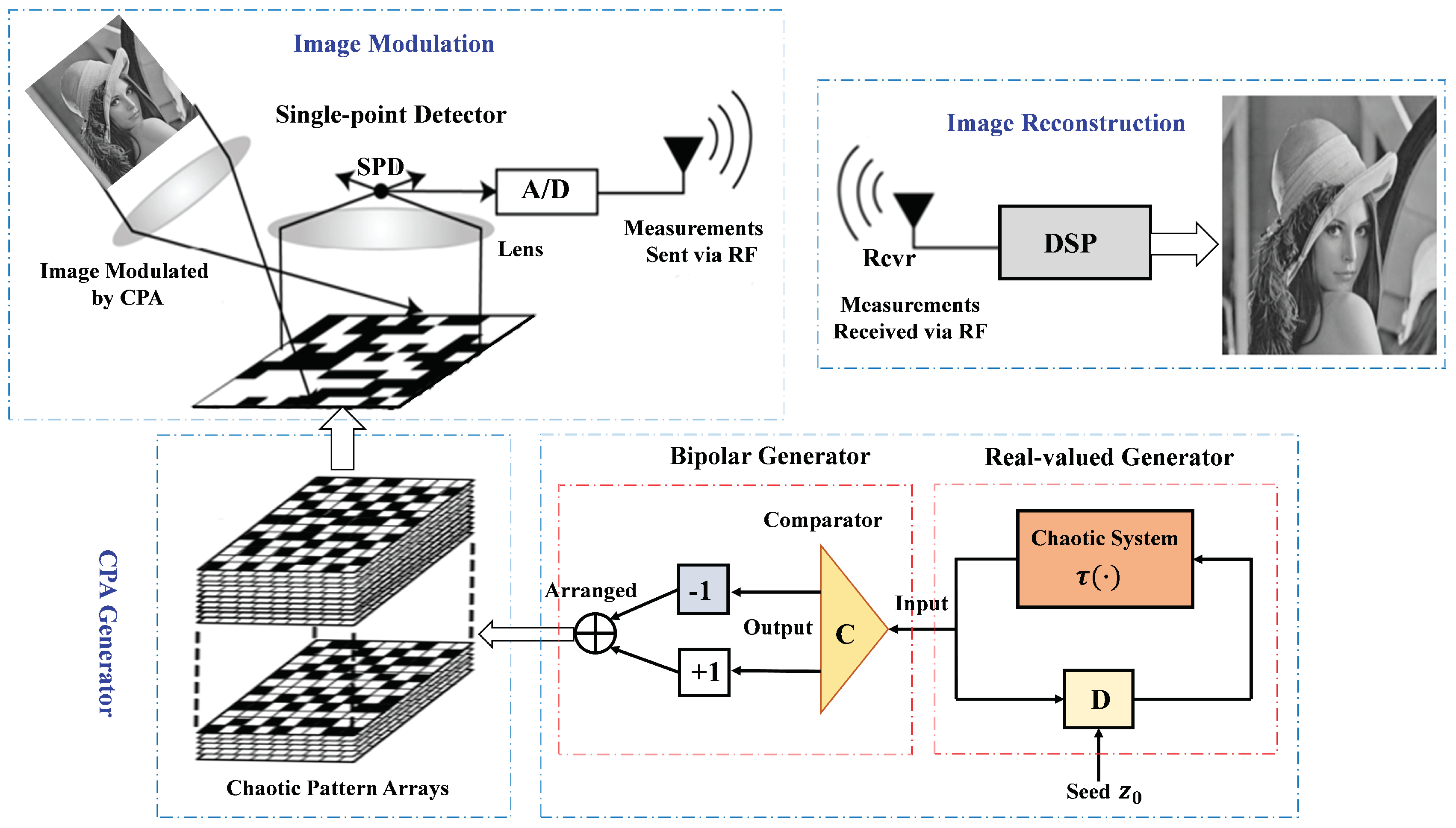
3.1. Overall Framework

For a traditional SPI device, a random SLM pattern is commonly used to modulate the image of a scene. Then the modulated light rays, i.e., the corresponding measurements, are integrated via a single-point detector. As we know, random SLM patterns are of extraordinary importance to modulate the image of the scene in an SPI device. However, random patterns are difficult to load on an SLM hardware, and they also require huge memory cost because we need to store every element of the random patterns in both the modulation and reconstruction side for exact image recovery. To address these shortcomings, we introduce a chaotic pattern array (CPA), which is a simple construction of the desired patterns for the SPI architecture.

The sketch of an SPI device with the CPA can be schematized as in Figure 2. The image of a scene under view is modulated by a CPA pre-loaded on the SLM plane, and then, the single-point detector collects the modulated light rays focused by a lens. After analog-to-digital conversion, the collected measurements are sent via a radio frequency (RF) circuit. By post-processing these measurements, the image of the scene can be exactly restored. The generation of the CPA is shown in the lower half of Figure 2. In the next subsection, we focus on the construction of the CPA such that it meets the RIP.

3.2. Construction of the Chaotic Pattern Array

3.2.1. Reviews for the Chaotic Bipolar Sequence

Chaos is a deterministic dynamical system with special properties. For example, a special case of the well-known Logistic chaotic system is:

$$z_{k+1}=\tau \left(z_k\right)=4z_k(1-z_k),k=0,1,2,\dots ,$$

(9)

where $z_k\in (0,1)$ and $z_0$ is a seed(It should be noted that there are some singularities (only one rational number is 0.5; the others are all irrational numbers, such as $\frac{(2\pm \sqrt{2})}{4}$) for Equation (9). Although these singularities will lead to the chaotic system meeting the degradation phenomenon and yielding a periodic chaotic sequence, we can obtain a sequence that meets the actual needs if we do not use the rational number 0.5 as the initial seed in practical applications. This will also be confirmed in later experiments.). For the special case, the invariant measure of Logistic chaotic system is $f^{*}\left(z\right)dz=dz/\left(\pi \sqrt{1-z^2}\right)$. With a seed $z_0$, a Logistic chaotic real-valued sequence ${\left\{{\tau }^k\left(z_0\right)\right\}}_{k=0}^{\infty }$, i.e., ${\left\{z_k\right\}}_{k=0}^{\infty }$, can be obtained via the recurrence of Equation (9).

We introduce a threshold function $⊺\left(z\right)$ defined as:

$$\begin{array}{c}\hfill ⊺\left(z\right)=\left\{\begin{array}{c}+1\mathrm{if}0.5\le z_k<1\hfill \\ -1\mathrm{if}0<z_k<0.5\hfill \end{array}\right.,\end{array}$$

(10)

with its complementary function:

$$\overline{⊺}\left(z\right)=1-⊺\left(z\right).$$

(11)

Based on the threshold function $⊺\left(z\right)$, we can obtain a Logistic chaotic bipolar sequence ${\{⊺\left({\tau }^k\left(z_0\right)\right)\}}_{k=0}^{\infty }$, i.e., ${\{⊺\left(z_k\right)\}}_{k=0}^{\infty }$. By virtue of the invariant measure of the Logistic system, the ensemble-average of ${\{⊺\left({\tau }^k\left(z_0\right)\right)\}}_{k=0}^{\infty }$ can be attained by:

$$\begin{array}{c}\hfill {\langle ⊺\rangle }_{\tau }={\int }_{[0,1]}⊺\left(z\right)·f^{*}\left(z\right)dz=\frac{1}{2}.\end{array}$$

(12)

Let ${\overrightarrow{Q}}_b=Q_0{Q}_1\cdots Q_{b-1}$ be a binarization string, where $Q_k\in \{1,-1\}$ $(k=0,1,\dots ,b-1)$. Suppose that ${\overrightarrow{q}}_b^{\left(j\right)}=q_0^{\left(j\right)}{q}_1^{\left(j\right)}\cdots q_{b-1}^{\left(j\right)}$ is the jth string, where $q_k^{\left(j\right)}\in \{1,-1\}$. Based on the ensemble-average technique, Kohda et al. investigated the statistical properties of bipolar sequences generated by the ergodic chaotic system with some symmetric properties [38]. Since the Logistic chaotic bipolar sequence is a special case of their work, we have the following lemma.

Lemma 1.

The probability of ${\overrightarrow{q}}_b^{\left(j\right)}$ in an infinite Logistic chaotic binarization sequence ${\{⊺\left(z_k\right)\}}_{k=0}^{\infty }$ is:

$$\begin{array}{c}\hfill \forall j,Pro({\overrightarrow{q}}_b^{\left(j\right)};⊺)={\langle ⊺\rangle }_{\tau }^{\gamma }{(1-{\langle ⊺\rangle }_{\tau })}^{b-\gamma }=\frac{1}{2^b},\end{array}$$

(13)

where γ is the number of $-1^{\prime }s$ in ${\left\{q_k^{\left(j\right)}\right\}}_{k=1}^{b-1}$.

More details about this lemma can be found in [38,39,40,41]. This lemma indicates that ${\{⊺\left(z_k\right)\}}_{k=0}^{\infty }$ is a sequence of i.i.d. binarization random variables. In fact, the i.i.d. property constitutes a good modulation performance for our proposed patterns.

3.2.2. Construction and Performance Analysis

Using ${\{⊺\left(z_k\right)\}}_{k=0}^{\infty }$, we can construct a chaotic pattern array that is arranged in a matrix $\mathit{M}\in {\mathbb{R}}^{S\times N}$ row by row, written as:

$$\mathit{M}=\frac{1}{\sqrt{S}}\left[\begin{array}{llll}⊺\left(z_0\right)& ⊺\left(z_1\right)& \dots & ⊺\left(z_{N-1}\right)\\ ⊺\left(z_N\right)& ⊺\left(z_{N+1}\right)& \dots & ⊺\left(z_{2N-1}\right)\\ ⋮& ⋮& \ddots & ⋮\\ ⊺\left(z_{(S-1)\times N}\right)& ⊺\left(z_{(S-1)\times N+1}\right)& \dots & ⊺\left(z_{(S\times N-1)}\right)\end{array}\right]\begin{array}{l}\leftarrow {\mathit{m}}_1\\ \leftarrow {\mathit{m}}_2\\ ⋮\\ \leftarrow {\mathit{m}}_S\end{array},$$

where ${\mathit{m}}_k$ denotes the kth row vector of the CPA and $\frac{1}{\sqrt{S}}$ is a scalar for normalization. It is worth noting that a seed $z_0$ determines a CPA, and different seeds will result in completely different CPAs. With a given $z_0$ and S, the CPA is constructed once and for all. Moreover, the time cost of generating a CPA is very low, mainly due to the following two aspects: (1) the binary sequence used to construct the CPA is generated by a quadratic iterative equation together with a hard threshold equation; hence, it does not require complex calculations; (2) the generated CPA only needs a simple row-by-row arrangement, so it can be implemented simply and quickly. Figure 3 gives four examples of chaotic pattern arrays $\in {\mathbb{R}}^{20\times 50}$ with different seeds, where $z_0\in \{0.17,0.27,0.67,0.87\}$. It can be seen that the generated CPA is highly non-symmetric. Moreover, as shown in Figure 3, the densities of the four generated CPAs (the ratio of the total number of ones to the total number of elements) are 0.5045, 0.4925, 0.5075, and 0.4865, respectively, i.e., the number of −1’s and the number of ones are almost equal. In other words, the validity of Lemma 1 is also verified from an experimental perspective.

Mathematically, $\mathit{M}$ is a sub-Bernoulli random matrix, as ${\{⊺\left(z_k\right)\}}_{k=0}^{\infty }$ are independent realizations of $\pm 1$ binarization elements. Achlioptas et al. [42] showed that a matrix with elements drawn independently from random variables satisfies the concentration inequalities. In fact, the concentration inequalities are useful and important tools in probability and analysis. Baraniuk et al. [35] used the concentration inequalities together with covering arguments to verify that random matrices have the RIP (see Theorem 1). Following their work, we can easily prove the RIP for our constructions. We now introduce the following lemma for CPAs.

Lemma 2.

Given a generated CPA $\mathit{M}$, for any vector $\mathit{v}\in {\mathbb{R}}^{N\times 1}$, the variable ${\Vert \mathit{M}·\mathit{v}\Vert }_{{\mathbf{l}}_2}^2$ is highly concentrated about ${\Vert \mathit{v}\Vert }_{{\mathbf{l}}_2}^2$, i.e., we have:

$$\begin{array}{c}\hfill \forall \mu \in (0,1),Pro\left[\mid {\Vert \mathit{M}·\mathit{v}\Vert }_{{\mathbf{l}}_2}^2-{\Vert \mathit{v}\Vert }_{{\mathbf{l}}_2}^2\mid \ge \mu {\Vert \mathit{v}\Vert }_{{\mathbf{l}}_2}^2\right]\le 2exp(-S·c\left(\mu \right)),\end{array}$$

(14)

where $c\left(\mu \right)=\frac{{\mu }^2}{4}-\frac{{\mu }^3}{6}$ is a positive constant.

Thanks to the moment conditions, the proof of this lemma can be derived using Chernoff inequalities. We give out this proof procedure in Appendix B. Lemma 2 shows that the proposed CPA meets the concentration inequalities with reasonable bounds on the constants. Based on Theorem 1, the following theorem can be obtained.

Theorem 2.

With probability exceeding $1-2exp\left(-c_2·S\right)$, chaotic pattern array $\in {\mathbb{R}}^{S\times N}$ meets the (K,ϵ)-RIP if $S\ge (c_3·K·log(N/K))$, where $c_2$ and $c_3$ are two constants.

Theorem 2 theoretically guarantees that the proposed Logistic CPA satisfies CS theory; thus, it can also be used as an SLM pattern for the SPI architecture. Besides the Logistic system, we can employ other chaotic systems (e.g., the Chebyshev system) to generate chaotic bipolar sequences and use the generated sequences to construct CPAs for the SPI device.

3.3. Mechanism of the Chaotic Pattern Array

As illustrated in the lower half of Figure 2, the chaotic pattern array generator consists of a real-valued generator and a bipolar generator. Once we input an initial seed for the real-valued generator, it outputs a Logistic chaotic real-valued sequence. After that, we input the real-valued sequence into the bipolar generator. This generator converts the real-valued sequence to a bipolar one through a comparator. Finally, we re-arrange the bipolar sequence into a CPA row by row. Each row of the CPA is a pattern, which is used to scan over the full image of a scene and then obtain one measurement. With one generated CPA, we can modulate the image of the scene, i.e., the generated CPA is used as a basis to generate illumination patterns to modulate the image.

With a given $z_0$ and S, we can construct a CPA once and for all. In other words, we can store the CPA by only storing the seed $z_0$. Moreover, the CPA with $\pm 1$ elements is convenient for any SLM hardware, such as the DMD. We give an example for which the CPA is loaded on a DMD. This hardware consists of thousands of tiny mirrors, which are arranged in a matrix $\in {\mathbb{R}}^{S\times N}$ with $768\le S\le 1600$ and $1024\le N\le 2560$ (The size mentioned here is only a classic value. In fact, it can be an arbitrary size.). The mirror pitch relying on the model ranged from 7–14 μm. We independently controlled each of these mirrors and set them into two states according to the CPA. That is, an element of one of the CPA corresponds to the on state and an element $-1$ to the off state. When the mirror is in the on state, the light is sent to the detector and then collected by this device. While the mirror is off state, the light is reflected in the opposite direction.

After the CPA is loaded on the SLM in an SPI device, we can obtain the measurements one by one. More specifically, using the predefined SLM pattern ${\mathit{m}}_1$, we can obtain the measurement $y_1$, then use ${\mathit{m}}_2$ to get $y_2$, and after repeating the above step S times, we finally obtain S measurements $\mathit{y}={\{y_1,y_2,\dots ,y_S\}}^T\in {\mathbb{R}}^{S\times 1}$. This completes the modulation procedure, and we obtain the corresponding measurements.

It is worth noting that in many applications, we hope to be able to switch the modulation mode flexibly. In these cases, random patterns are not available as they require a lot of memory. Actually, chaotic pattern arrays (CPAs) are especially suitable for these scenarios, because of the following four aspects: (1) each CPA in the CPAs can be easily loaded on SLM; (2) each CPA can modulate the image of the scene very well; (3) it can easily switch between different CPAs; (4) the CPAs will benefit memory cost automatically. There are two ways to generate CPAs. One is that we first used a seed to produce a long sequence and then filled a single CPA via the sequence row by row until the entire CPAs was filled. The other is that we first used different seeds to generate different CPAs and then integrated them into one complete CPAs. In what follows, we will give an interesting application of CPAs.

As mentioned before, an initial seed $z_0$ determines all the elements of the CPA. As distinctly illustrated in Figure 3, with a different seed, the generated CPA is completely different from the other one. In other words, if we want to change the modulation style of the SLM, we only need to change the seed to obtain the corresponding CPA. This property is quite suitable for encryption and privacy [43,44,45,46]. Considering this property, we can construct CPAs for the single-pixel camera. Such a device with CPAs is well suited for these applications that require encryption and privacy, such as medical care and wireless body area networks. Moreover, we only need to store these seeds; thus, the CPAs can be stored with a small storage cost.

4. Numerical Experiments

In this section, some numerical experiments are performed to investigate the performance of the CPA. We first used different recovery algorithms to demonstrate that the CPA is well-suited for CS theory. Then, the comparisons between our proposed construction and existing random patterns were carried out. In addition, recovery time (RecTime), mean squared error (MSE), and peak signal-to-noise ratio (PSNR) were used to assess these patterns. The MSE and PSNR are respectively defined as:

$$\begin{array}{c}\hfill \mathrm{MSE}=\frac{1}{H\times D}\sum _{i=1}^H\sum _{j=1}^D{({\mathit{x}}_{i,j}-{\mathit{x}}_{i,j}^{*})}^2,\end{array}$$

(15)

and:

$$\begin{array}{c}\hfill \mathrm{PSNR}=10{log}_{10}\left(\frac{(H-1)\times (D-1)}{\mathrm{MSE}}\right)dB.\end{array}$$

(16)

where $\mathit{x}\in {\mathbb{R}}^{H\times D}$ and ${\mathit{x}}^{*}$ denote the original image and the restored image, respectively. The software and hardware environments for the simulation were MATLAB 2017a and Intel(R) Core(TM) i5-7500 [email protected] GHz with RAM 16 GB memory, respectively.

In the simulation, six standard testing images $\in {\mathbb{R}}^{256\times 256}$ including “House”, “Camera”, “Baboon”, “Mena”, “Starfish”, and “Straw”, which are illustrated in Figure 4a–f, were the original signals of interest. All testing data were sparse in the well-known discrete cosine transform. In addition, we constructed a CPA $\in {\mathbb{R}}^{S\times 256}$ using ${\{⊺\left(z_k\right)\}}_{k=0}^{\infty }$ with $z_0=0.17$. Note that we did not have to vectorize the testing images as we could process these images column by column.

4.1. CPA with Different Recovery Algorithms

Using eight generated CPAs $\in {\mathbb{R}}^{S\times 256}$, the image “House” was modulated to get measurements of size $S\times 256$ at different sampling rates, ♮s, where $S=[256\times ♮]$ and $♮\in \{0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8\}$. For example, if the size of the generated CPA was $26\times 256$, the sampling rate ♮ was 0.1. Based on these measurements $\in {\mathbb{R}}^{S\times 256}$, we then respectively restored the image “House” via the Newton smoothed ${\mathbf{l}}_0$ (NS${\mathbf{l}}_0$) algorithm [47]. This algorithm is two orders of magnitude faster than linear programming methods, while providing similar reconstruction accuracy. Figure 5a–h illustrates the restored images corresponding to the sampling rates ranging from 0.1–0.8 with increments of 0.1. The corresponding MSEs, PSNRs, and recovery time for Figure 5a–h are shown in

Table 2. The recovery results for reconstructing “House”. RecTime, recovery time.

	Sampling Rate ♮
	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8
MSE	0.923	0.689	0.215	0.054	0.038	0.027	0.020	0.014
PSNR (dB)	4.852	6.762	17.89	27.99	31.32	34.20	36.92	39.82
RecTime (s)	0.077	0.196	0.215	0.276	0.287	0.323	0.350	0.412

. The recovery errors in Figure 5 are very asymmetric between axes, because CS theory considers each pixel in an image to be equally “important” or equally “unimportant”. If ♮ was greater than 0.4, the MSE was dramatically decreased, and the PSNR was rapidly improved. As observed in Figure 5 and Table 2, we know that the CPA can be used to modulate images for the SPI architecture.

Moreover, we utilized different recovery algorithms (i.e., OMP, subspace pursuit (SP), gradient projection for sparse reconstruction (GPSR), NS${\mathbf{l}}_0$, and TV minimization) to restore the image “House”. The OMP and the SP stand for orthogonal matching pursuit algorithm [48] and subspace pursuit algorithm [49], respectively. The former is a typical greedy algorithm for sparse approximation, but it takes a long time to process the image signal. The later has low computational complexity and high reconstruction precision, which is at the same order as that of linear programming methods. The GPSR is the gradient projection for sparse reconstruction algorithm [50], which is suitable for solving convex non-smooth unconstrained optimization problems, especially in large-scale settings. The TV minimization denotes the total variation minimization algorithm, which is especially suitable for image reconstruction. With the aforementioned recovery algorithms, we obtained the corresponding PSNRs and RecTimes, which are plotted in Figure 6a,b, respectively.

As illustrated in Figure 6, we know that the aforementioned algorithms can restore the image “House” from the measurements when we use the CPA to modulate the image “House”. More specifically, the NS${\mathbf{l}}_0$ and TV minimization algorithm performed better than the other methods while using less recovery time. The OMP algorithm took a long time to restore the image “House”, and it was proportional to the sampling rate. However, overall, it can be seen that the CPA was suitable for the SPI architecture with various CS recovery algorithms.

4.2. CPA vs. Different Modulation Patterns

In this part, three SLM modulation patterns $\in {\mathbb{R}}^{S\times 256}$, i.e., random Gaussian pattern (RGP), random Bernoulli pattern (RBP), and Hadamard pattern (In fact, the original Hadamard matrix cannot be directly used as SLM modulation patterns for two reasons. The first is that it is a square matrix, so it cannot achieve compressive imaging. Second, it does not meet the CS matrix property very well. In the simulation, we first generated an original Hadamard matrix $\in {\mathbb{R}}^{256\times 256}$ and then randomly selected S rows and randomly confused its column arrangement to form an underdetermined Hadamard matrix $\in {\mathbb{R}}^{S\times 256}$, and finally, we used the generated matrix as the SLM modulation patterns.) (HMP), are considered to make a comparison. Compared to the CPA, these three patterns require a lot of memory for exact image reconstruction. More specifically, we can store the generated CPA by only storing the seed. However, the random patterns need to store each of their elements, i.e., the storage cost of RGP or RBP is $\mathcal{O}(S\times N)$. The HMP requires to remember its row selection and column arrangement.

The images “House”, “Camera”, “Baboon”, “Mena”, “Starfish”, and “Straw”, shown in Figure 4a–f, were modulated by the proposed CPA and the other three SLM patterns. Using the NS${\mathbf{l}}_0$ algorithm, we obtained the corresponding MSEs, PSNRs, and recovery time, which are reported in

Table 3. Comparison results of recovery using various modulation patterns.

Modulation Pattern	Sampling Rate	Index	Image
			“House”	“Camera”	“Baboon”	“Mena”	“Starfish”	“Straw”
CPA	0.2	MSE	0.689	0.643	0.714	0.514	0.554	0.731
		PSNR (dB)	6.762	8.261	7.272	10.51	9.354	5.083
		RecTime (s)	0.196	0.278	0.190	0.207	0.228	0.237
	0.4	MSE	0.054	0.083	0.104	0.066	0.110	0.126
		PSNR (dB)	27.99	24.78	23.29	27.79	22.98	19.89
		RecTime (s)	0.251	0.329	0.287	0.354	0.282	0.362
	0.6	MSE	0.027	0.049	0.075	0.039	0.063	0.087
		PSNR (dB)	34.20	29.41	26.01	32.40	27.81	23.08
		RecTime (s)	0.323	0.417	0.378	0.384	0.391	0.415
	0.8	MSE	0.014	0.024	0.047	0.019	0.030	0.051
		PSNR (dB)	39.82	35.77	29.94	38.29	34.00	27.64
		RecTime (s)	0.412	0.465	0.407	0.540	0.431	0.526
RGP	0.2	MSE	0.769	0.611	0.532	0.689	0.643	0.808
		PSNR (dB)	6.101	8.729	9.462	7.519	8.282	4.162
		RecTime (s)	0.214	0.252	0.224	0.213	0.225	0.257
	0.4	MSE	0.078	0.107	0.106	0.067	0.114	0.128
		PSNR (dB)	25.49	23.03	23.10	27.56	22.71	19.79
		RecTime (s)	0.286	0.342	0.311	0.296	0.326	0.373
	0.6	MSE	0.028	0.049	0.075	0.038	0.064	0.091
		PSNR (dB)	34.09	29.13	26.01	32.54	27.58	22.85
		RecTime (s)	0.360	0.397	0.381	0.362	0.396	0.446
	0.8	MSE	0.014	0.023	0.046	0.019	0.031	0.052
		PSNR (dB)	39.63	35.85	30.14	38.12	33.93	27.16
		RecTime (s)	0.432	0.469	0.403	0.396	0.461	0.513
RBP	0.2	MSE	0.759	0.476	0.795	0.739	0.705	0.761
		PSNR (dB)	5.771	10.63	6.302	7.304	7.292	4.995
		RecTime (s)	0.285	0.252	0.235	0.247	0.248	0.278
	0.4	MSE	0.057	0.084	0.107	0.063	0.112	0.128
		PSNR (dB)	27.45	24.64	23.07	27.99	22.80	19.78
		RecTime (s)	0.304	0.334	0.302	0.284	0.320	0.364
	0.6	MSE	0.027	0.047	0.075	0.039	0.064	0.089
		PSNR (dB)	34.26	29.80	26.07	32.33	27.65	22.86
		RecTime (s)	0.346	0.413	0.371	0.356	0.373	0.449
	0.8	MSE	0.013	0.023	0.047	0.019	0.030	0.050
		PSNR (dB)	40.09	35.97	29.85	38.23	34.03	27.84
		RecTime (s)	0.416	0.490	0.430	0.439	0.483	0.505
HMP	0.2	MSE	0.484	0.434	0.878	1.120	0.849	0.558
		PSNR (dB)	8.964	10.90	4.953	3.090	5.230	7.046
		RecTime (s)	0.264	0.320	0.357	0.374	0.341	0.402
	0.4	MSE	0.054	0.084	0.105	0.066	0.109	0.126
		PSNR (dB)	28.00	24.29	23.15	27.50	22.90	19.86
		RecTime (s)	0.363	0.405	0.457	0.360	0.356	0.424
	0.6	MSE	0.027	0.047	0.075	0.039	0.064	0.088
		PSNR (dB)	34.25	29.80	25.97	32.45	27.38	22.99
		RecTime (s)	0.453	0.413	0.462	0.419	0.462	0.542
	0.8	MSE	0.014	0.023	0.047	0.019	0.031	0.050
		PSNR (dB)	38.80	35.60	29.77	38.17	33.77	27.58
		RecTime (s)	0.585	0.524	0.623	0.439	0.534	0.559

. In particular, we compared the reconstruction of “House” using the proposed CPA, RGP, RBP, and HMP, which is shown in Figure 7. It shows that the proposed CPA has almost the same performance while saving roughly 5–35% reconstruction time, compared with the popular modulation patterns. From Table 3 and Figure 7, it can be seen that the recovery algorithms were getting better in reconstructing with increased sampling rate. For all cases, these patterns offered similar MSE and PSNR at the same sampling rate. However, the CPA took less time than the other three SLM patterns. This is because the proposed CPA is a totally deterministic binarization construction. Moreover, the CPA administrating $\pm 1$ as entries can accelerate image modulation and reconstruction. Overall, the proposed CPA performs better in most of the cases assessed.

4.3. Encryption Property of CPA

To figure out the effect of the seed $z_0$, we constructed five CPAs using ${\{⊺\left(z_k\right)\}}_{k=0}^{\infty }$ with various seeds, where $z_0\in \{0.17,0.37,0.55,0.77,0.97\}$, and then employed these CPAs to modulate the image “House”. Finally, the image “House” reconstruction was conducted via the NS${\mathbf{l}}_0$ algorithm. The resulting PSNRs and recovery time are respectively plotted in Figure 8a,b. As can be seen, the initial seed $z_0$ did not have a dramatic influence on the recovery performance.

We now focus on the encryption property of the CPA. As mentioned before, a seed $z_0$ determines a CPA, and different seeds will result in completely different CPAs. Thus, we can imagine the single-pixel camera with a CPA as an encryption system. In this scheme, we integrated compression and encryption into only one step using the CPA during the modulation procedure. More specifically, the image of a scene, $\mathit{x}$, was the original data, the measurements represented the encrypted information, and the CPA was the encrypted compression operator, where the seed $z_0$ denotes the security key (If the attacker accidentally finds a seed that creates the generalized inverse matrix of the original CPA, then cracking the encryption of the CPA is a breeze. However, the probability of the occurrence is extremely low, due to two reasons: (1) the original CPA is unknown; (2) the probability of a seed that can directly construct the generalized inverse matrix of the CPA is very low.). Note that the security key was only known by the sender and the authorized receiver. In fact, we can analyze the key space and the key sensitivity of the SPI with a CPA scheme. The key space T and the key sensitivity were determined by the seed $z_0$. Specifically, the key space and the key sensitivity were ${10}^{E_0}$ and ${10}^{-E_0}$, respectively, where $E_0$ denotes the decimal digits of $z_0$. Theoretically, $E_0$ can take any large number so that the key space T will be infinite and the key sensitivity will tend to zero. However, $E_0$ cannot be too large in practice because of the limited precision of electronic devices. For our experimental setup, the maximum of $E_0$ of the Logistic system was 15, resulting in $T={10}^{15}$, and the initiation sensitivity was ${10}^{-15}$.

For example, we considered the image “Lena” $\in {\mathbb{R}}^{256\times 256}$ as the original image of a scene, which is depicted in Figure 9a. Then, we generated a CPA $\in {\mathbb{R}}^{128\times 256}$ with security key $z_0=0.17$ to modulate and encrypt the image “Lena”. Using the NS${\mathbf{l}}_0$ algorithm, we restored the image “Lena” via CPAs $\in {\mathbb{R}}^{128\times 256}$ with incorrect seeds (keys). Figure 9b,c illustrates the recovery images, which corresponds to the CPAs with $z_0=0.171$ and $z_0=0.169$, respectively. The PSNRs of Figure 9b,c were $2.518$ dB and 3.146 dB, respectively, which imply that the original image of the scene cannot be restored by the CPA with an incorrect key. Figure 9d shows the restored image with the right key. The corresponding MSE and PSNR were $0.058$ and $30.11$ dB, respectively, which indicates that the quality of the restored “Lena” is acceptable. Based on this advantage, the proposed CPAs are especially suitable for special CS applications, such as medical imaging and wireless body area networks.

5. Conclusions

Considering that random patterns are difficult to implement and require huge memory cost, we have proposed a chaotic pattern array for single-pixel imaging architecture in this study. The proposed pattern array was directly built by a chaotic bipolar sequence (elements $-1$ or one) based on a chaos system. With this simple construction, the proposed pattern array (CPA) was convenient for any SLM hardware, such as the DMD. Moreover, the CPA can save significant memory since it only needs to store the initial seed of chaotic sequence while the random patterns need to store each of their elements. The results obtained from numerical experiments showed that our chaotic pattern array performed similarly or superior to the conventional random ones. Meanwhile, it can save roughly 5–35% reconstruction time compared with other popular patterns. Moreover, our proposed pattern array is well-suited for those applications that require encryption and privacy.

In the future, we will apply the chaotic pattern array to adaptive basis scan and the hybrid method in a generalized single-pixel imaging device to further improve the performance. The main challenge is to investigate a fast and efficient prediction algorithm that can perfectly reconstruct the image of interest.