Compact Printable Inverted-M Shaped Chipless RFID Tag Using Dual-Polarized Excitation
Abstract
:1. Introduction
2. Proposed Chipless RFID Tag
3. Simulation Results
4. The 20-Bit Dual Polarized Tag
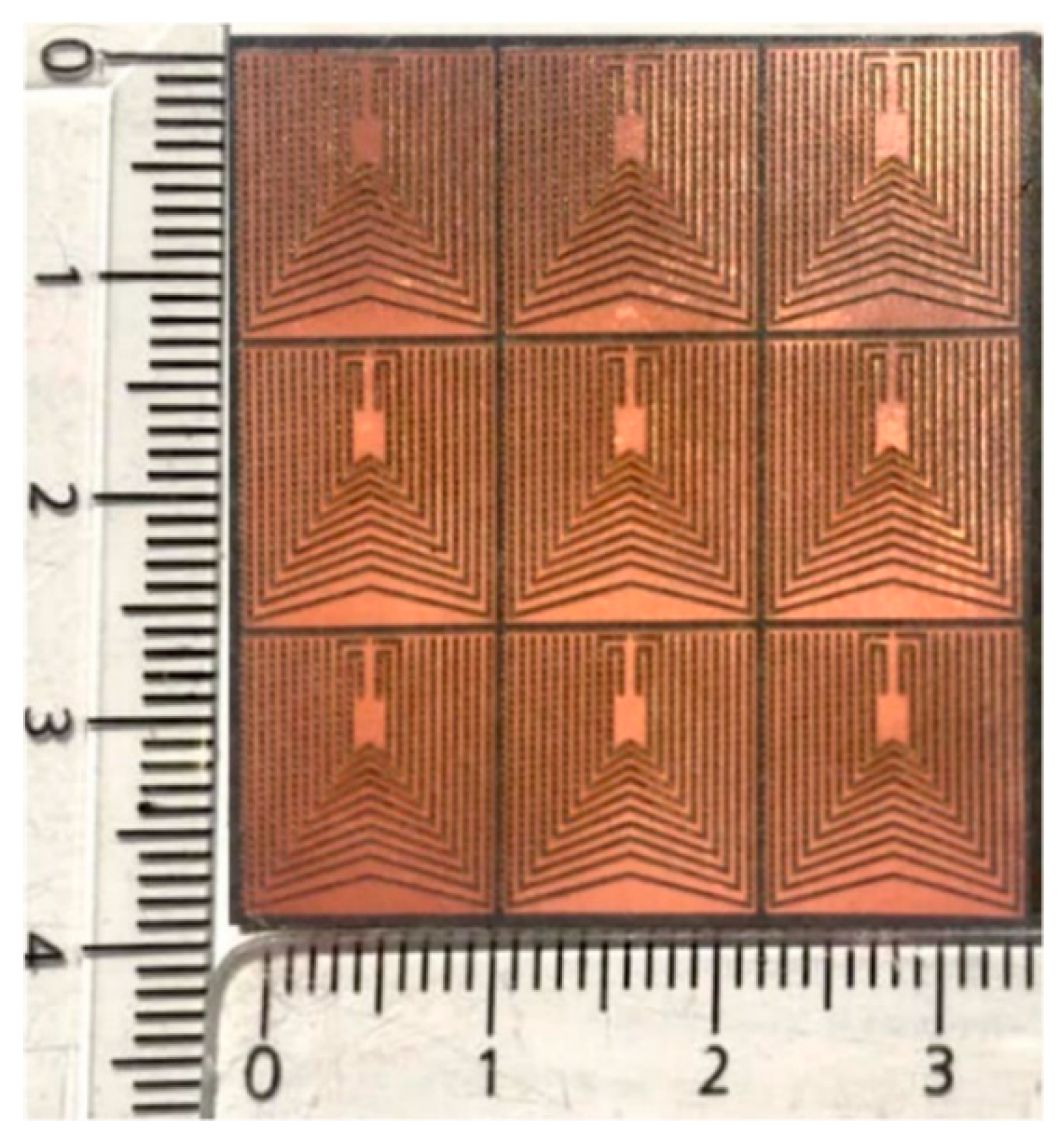
5. Experimental Validation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Preradovic, S.; Karmakar, N.C. Multiresonator-Based Chipless RFID: Barcode of the Future; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Pöpperl, M.; Parr, A.; Mandel, C.; Jakoby, R.; Vossiek, M. Potential and practical limits of time-domain reflectometry chipless RFID. IEEE Trans. Microw. Theory Tech. 2016, 64, 2968–2976. [Google Scholar] [CrossRef]
- Herrojo, C.; Mata-Contreras, J.; Paredes, F.; Núñez, A.; Ramon, E.; Martín, F. Near-Field Chipless-RFID System With Erasable/Programmable 40-bit Tags Inkjet Printed on Paper Substrates. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 272–274. [Google Scholar] [CrossRef]
- Islam, M.A.; Karmakar, N. A compact printable dual-polarized chipless RFID tag using slot length variation in ‘I’ slot resonators. In Proceedings of the IEEE European Microwave Conference (EuMC), Paris, France, 7–10 September 2015. [Google Scholar]
- Adbulkawi, W.M.; Sheta, A.A. A Compact Chipless RFID Tag Based on Frequency Signature. In Proceedings of the 9th IEEE-GCC Conference and Exhibition (GCCCE), Manamah, Bahrain, 8–11 May 2011. [Google Scholar]
- Islam, M.A.; Karmakar, N.C. Real-World Implementation Challenges of a Novel Dual-Polarized Compact Printable Chipless RFID Tag. IEEE Trans. Microw. Theory Tech. 2015, 63, 4581–4591. [Google Scholar] [CrossRef]
- Adbulkawi, W.M.; Sheta, A.-F.A. Printable Chipless RFID Tags for IoT Applications. In Proceedings of the 1st International Conference on Computer Applications & Information Security (ICCAIS), Riyadh, Saudi Arabia, 4–6 April 2018. [Google Scholar]
- Balbin, I.; Karmakar, N.C. Phase-Encoded Chipless RFID Transponder for Large-Scale Low-Cost Applications. IEEE Microw. Wirel. Compon. Lett. 2009, 19, 509–511. [Google Scholar] [CrossRef]
- Babaeian, F.; Karmakar, N.C. Hybrid Chipless RFID Tags—A Pathway to EPC Global Standard. IEEE Access 2018, 6, 67415–67426. [Google Scholar] [CrossRef]
- Vena, A.; Perret, E.; Tedjini, S. Chipless RFID tag using hybrid coding technique. IEEE Trans. Microw. Theory Tech. 2011, 59, 3356–3364. [Google Scholar] [CrossRef]
- Preradovic, S.; Karmakar, N.C. Chipless RFID: Barcode of the future. IEEE Microw. Mag. 2010, 7, 87–97. [Google Scholar] [CrossRef]
- Abdulkawi, W.M.; Sheta, A.F.A. Multi-Resonator Structure for Small Size Chipless Radio Frequency Identification Tag. Int. J. Comput. Digit. Syst. 2018, 7, 43–49. [Google Scholar] [CrossRef]
- Bhuiyan, M.S.; Karmakar, N.C. An efficient coplanar retransmission type chipless RFID tag based on dual-band McSrr. Prog. Electromagn. Res. 2014, 54, 133–141. [Google Scholar] [CrossRef]
- Costa, F.; Genovesi, S.; Monorchio, A. Normalization-Free Chipless RFIDs by Using Dual-Polarized Interrogation. IEEE Trans. Microw. Theory Tech. 2016, 64, 310–318. [Google Scholar] [CrossRef]
- Marindra, A.M.J.; Tian, G.Y. Chipless RFID Sensor Tag for Metal Crack Detection and Characterization. IEEE Trans. Microw. Theory Tech. 2018, 66, 2452–2462. [Google Scholar] [CrossRef]
- Bibile, M.A.; Karmakar, N.C. Moving Chipless RFID Tag Detection Using Adaptive Wavelet-Based Detection Algorithm. IEEE Trans. Antennas Propag. 2018, 66, 2752–2760. [Google Scholar] [CrossRef]
- Islam, M.A.; Karmakar, N.C. Compact Printable Chipless RFID Systems. IEEE Trans. Microw. Theory Tech. 2015, 63, 3785–3793. [Google Scholar] [CrossRef]
- Islam, M.A.; Karmakar, N.C. A novel compact printable dual-polarized chipless RFID system. IEEE Trans. Microw. Theory Tech. 2012, 60, 2142–2151. [Google Scholar] [CrossRef]
- Issa, K.; Ashraf, M.A.; AlShareef, M.R.; Behairy, H.; Alshebeili, S.; Fathallah, H. A Novel L-Shape Ultra Wideband Chipless Radio-Frequency Identification Tag. Int. J. Antennas Propag. 2017, 2017, 2823565. [Google Scholar] [CrossRef]
- Huang, H.-F.; Su, L. A compact dual-polarized chipless RFID tag by using nested concentric square loops. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 1036–1039. [Google Scholar] [CrossRef]
- Islam, M.A.; Yap, Y.; Karmakar, N. ‘Δ’ slotted compact printable orientation insensitive chipless RFID tag for long range applications. In Proceedings of the 2016 9th International Conference on Electrical and Computer Engineering (ICECE), Dhaka, Bangladesh, 20–22 December 2016. [Google Scholar]
- Vena, A.; Perret, E.; Tedjini, S. High-capacity chipless RFID tag insensitive to the polarization. IEEE Trans. Antennas Propag. 2012, 60, 4509–4515. [Google Scholar] [CrossRef]
- Laila, D.; Thomas, R.; Nijas, C.M.; Mohanan, P. A novel polarization independent chipless RFID tag using multiple resonators. Prog. Electromagn. Res. 2015, 55, 61–66. [Google Scholar] [CrossRef]
- Dissanayake, T.; Esselle, K.P. Prediction of the Notch Frequency of Slot Loaded Printed UWB Antennas. IEEE Trans. Antennas Propag. 2007, 55, 3320–3325. [Google Scholar] [CrossRef]
- Islam, M.A.; Karmakar, N. Design of a 16-bit ultra-low cost fully printable slot-loaded dual-polarized chipless RFID tag. In Proceedings of the Asia-Pacific Microwave Conference 2011, Melbourne, VIC, USA, 5–8 December 2011. [Google Scholar]
- Khan, M.M.; Tahir, F.A.; Cheema, H.M. High capacity polarization sensitive chipless RFID tag. In Proceedings of the 2015 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Ancouver, BC, Canada, 19–24 July 2015. [Google Scholar]
- Nijas, C.M.; Deepak, U.; Vinesh, P.V.; Sujith, R.; Mridula, S.; Vasudevan, K.; Mohanan, P. Low-cost multiple-bit encoded chipless RFID tag using stepped impedance resonator. IEEE Trans. Antennas Propag. 2014, 62, 4762–4770. [Google Scholar] [CrossRef]
- Sajitha, V.R.; Nijas, C.M.; Roshna, T.K.; Vasudevan, K.; Mohanan, P. Compact cross loop resonator based chipless RFID tag with polarization insensitivity. Microw. Opt. Technol. Lett. 2016, 58, 944–947. [Google Scholar] [CrossRef]
- Costa, F.; Genovesi, S.; Monorchio, A. A chipless RFID based on multiresonant high-impedance surfaces. IEEE Trans. Microw. Theory Tech. 2013, 61, 146–153. [Google Scholar] [CrossRef]
- Rance, O.; Siragusa, R.; Lemaitre-Auger, P.; Perret, E. Toward RCS magnitude level coding for chipless RFID. IEEE Trans. Microw. Theory Tech. 2016, 64, 2315–2325. [Google Scholar] [CrossRef]
- Svanda, M.; Polivka, M.; Havlicek, J.; Machac, J. Chipless RFID tag with an improved magnitude and robustness of RCS response. Microw. Opt. Technol. Lett. 2017, 59, 488–492. [Google Scholar] [CrossRef]
















| Parameter | l | W | dx | dy | ws | sx |
|---|---|---|---|---|---|---|
| Value (mm) | 12.4 | 11.4 | 0.2 | 0.2 | 0.2 | 0.3 |
| Parameter | sy1 | sy2 | sy3 | sy4 | sy5 | sy6 | sy7 | sy8 | sy9 |
|---|---|---|---|---|---|---|---|---|---|
| Value (mm) | 0.69 | 0.49 | 0.44 | 0.49 | 0.44 | 0.44 | 0.34 | 0.39 | 0.29 |
| Total Length | Calculated Resonant Frequency (GHz) | Simulated Resonant Frequency (GHz) | Δ (MHz) | ||
|---|---|---|---|---|---|
| Parameter | Value (mm) | Vertical | Horizontal | ||
| l1 | 35.36 | 3.351 | 3.256 | 3.272 | 16 |
| l2 | 33.02 | 3.589 | 3.536 | 3.568 | 32 |
| l3 | 30.56 | 3.878 | 3.872 | 3.904 | 32 |
| l4 | 28.08 | 4.220 | 4.328 | 4.336 | 8 |
| l5 | 25.66 | 4.618 | 4.928 | 4.936 | 8 |
| l6 | 23.18 | 5.112 | 5.384 | 5.280 | 104 |
| l7 | 20.74 | 5.714 | 5.880 | 5.848 | 32 |
| l8 | 18.18 | 6.518 | 6.536 | 6.544 | 8 |
| l9 | 17.62 | 6.726 | 6.896 | 6.872 | 24 |
| l10 | 16.7 | 7.270 | 7.400 | 7.384 | 16 |
| Configuration | Possible States | Resonance Frequency | Code |
|---|---|---|---|
| Resonator with short circuits | First state | No resonance | 00 |
| Normal resonator | Second state | 11 | |
| The slot length l increased by factor of | Third state | 10 | |
| The slot length l decreased by factor of | Fourth state | 01 |
| Existing Frequencies | Decreasing Frequencies | Increasing Frequencies | Δ− (MHz) | Δ+ (MHz) | |||
|---|---|---|---|---|---|---|---|
| Parameter | Value (GHz) | Parameter | Value (GHz) | Parameter | Value (GHz) | ||
| 3.24 | 3.168 | 3.296 | 72 | 56 | |||
| 3.512 | 3.472 | 3.568 | 40 | 56 | |||
| 3.896 | 3.816 | 4.008 | 80 | 112 | |||
| 4.376 | 4.288 | 4.496 | 88 | 120 | |||
| 4.944 | 4.848 | 5.04 | 96 | 96 | |||
| 5.384 | 5.216 | 5.64 | 168 | 256 | |||
| 6.0 | 5.824 | 6.28 | 176 | 280 | |||
| 6.784 | 6.6 | 6.976 | 184 | 192 | |||
| 7.168 | 7.04 | 7.36 | 128 | 192 | |||
| 7.656 | 7.472 | 7.856 | 184 | 200 | |||
| Resonator | Frequency Range (GHz) | Coding Capacity (bits) | Coding Density (bits/cm2) | Spectral Capacity (bits/GHz) | Coding Density bits/(GHz·cm2) | Read Range (cm) |
|---|---|---|---|---|---|---|
| Square loop [29] | 2–8 | 5 | 1.23 | 0.83 | 0.21 | 55 |
| Stepped impedance [27] | 3.1–10.6 | NA | 7.9 | NA | NA | 50 |
| U strips [6] | 7–12 | 16 | 16.67 | 3.2 | 3.33 | 20 |
| C-shaped [30] | 2–5 | 15 | 1.25 | 5 | 0.416 | 80 |
| U-folded dipoles [31] | 2–4 | 20 | 0.77 | 10 | 0.385 | 25 |
| Multiple L [23] | 3.1–10.6 | 6 | 0.3 | 0.8 | 0.04 | 40 |
| Plus loop [28] | 3.8–8.8 | 20 | 1.25 | 4 | 0.25 | 25 |
| L-shaped [19] | 4.8–10 | 9 | 12 | 3.46 | 2.31 | 10 |
| Proposed tag | 3–8 | 20 | 15.15 | 4.44 | 3.37 | 60 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulkawi, W.M.; Sheta, A.-F.A.; Issa, K.; Alshebeili, S.A. Compact Printable Inverted-M Shaped Chipless RFID Tag Using Dual-Polarized Excitation. Electronics 2019, 8, 580. https://doi.org/10.3390/electronics8050580
Abdulkawi WM, Sheta A-FA, Issa K, Alshebeili SA. Compact Printable Inverted-M Shaped Chipless RFID Tag Using Dual-Polarized Excitation. Electronics. 2019; 8(5):580. https://doi.org/10.3390/electronics8050580
Chicago/Turabian StyleAbdulkawi, Wazie M., Abdel-Fattah A. Sheta, Khaled Issa, and Saleh A. Alshebeili. 2019. "Compact Printable Inverted-M Shaped Chipless RFID Tag Using Dual-Polarized Excitation" Electronics 8, no. 5: 580. https://doi.org/10.3390/electronics8050580
APA StyleAbdulkawi, W. M., Sheta, A.-F. A., Issa, K., & Alshebeili, S. A. (2019). Compact Printable Inverted-M Shaped Chipless RFID Tag Using Dual-Polarized Excitation. Electronics, 8(5), 580. https://doi.org/10.3390/electronics8050580






