Overview of Binary Locally Repairable Codes for Distributed Storage Systems

Abstract

This paper summarizes the details of recently proposed binary locally repairable codes (BLRCs) and their features. The construction of codes over a small alphabet size of symbols is of particular interest for efficient hardware implementation. Therefore, BLRCs are highly noteworthy because no multiplication is required during the encoding, decoding, and repair processes. We explain the various construction approaches of BLRCs such as cyclic code based, bipartite graph based, anticode based, partial spread based, and generalized Hamming code based techniques. We also describe code generation methods based on modifications for linear codes such as extending, shorting, expurgating, and augmenting. Finally, we summarize and compare the parameters of the discussed constructions.

1. Introduction

Efficient distributed storage systems (DSSs) are considered to be crucial infrastructure for handling big data. These systems must be able to reliably store data over a long duration by introducing redundancy and storing data in a distributed manner across several storage nodes, which may be individually unreliable and could generate failures. Large data centers and peer-to-peer storage systems such as OceanStore [1] from Berkeley and BigTable from Google [2] are famous examples of distributed storage systems.

Owing to cost issues, large data centers also use many commercial hardware storage devices such as hard disk drives/solid state devices (HDDs/SSDs). As a result, device failure occurs regularly, rather than as an exception. The data are typically stored in a redundant manner to effectively protect valuable data against potential failures. The traditional storage method for large storage services such as cloud storage is triplication, i.e., triple replication of each symbol. For example, the Google file system [3] and Hadoop [4] adopt this approach. However, given that triplication requires thrice the storage space, a $(14,10)$ Reed–Solomon code is deployed in their warehouse cluster in the case of Facebook [5]. Although RS codes are efficient for handling specified numbers of erasures, all of the code symbols must be communicated and reconstructed to repair erasures. Thus, more efficient storage methods have been actively researched, including regeneration codes (RCs), fractional repetition codes (FRCs), and locally repairable codes (LRCs) [6,7,8,9,10,11,12]. RC attempts to minimize the number of transmitted symbols, while the objective of LRC is to optimize the number of disk reads required to repair a single lost node. In some respects, LRC is essentially a block code with an additional parameter referred to as locality. There have been excellent reviews on the distributed storage codes (e.g., [13,14,15,16]). Moreover, a review article on this topic has recently been published [17]. However, to the best of the authors knowledge, no review paper deals only with the binary LRC (BLRC) constructions, which are practically useful.

In most of the early suggestions for LRC constructions, the alphabet size of the stored symbols is very large. However, for efficient and convenient hardware implementation, the construction of codes over a small alphabet size for the stored symbols is of particular interest. For example, BLRCs are of special interest because multiplication is not necessary during the encoding, decoding, and repair processes.

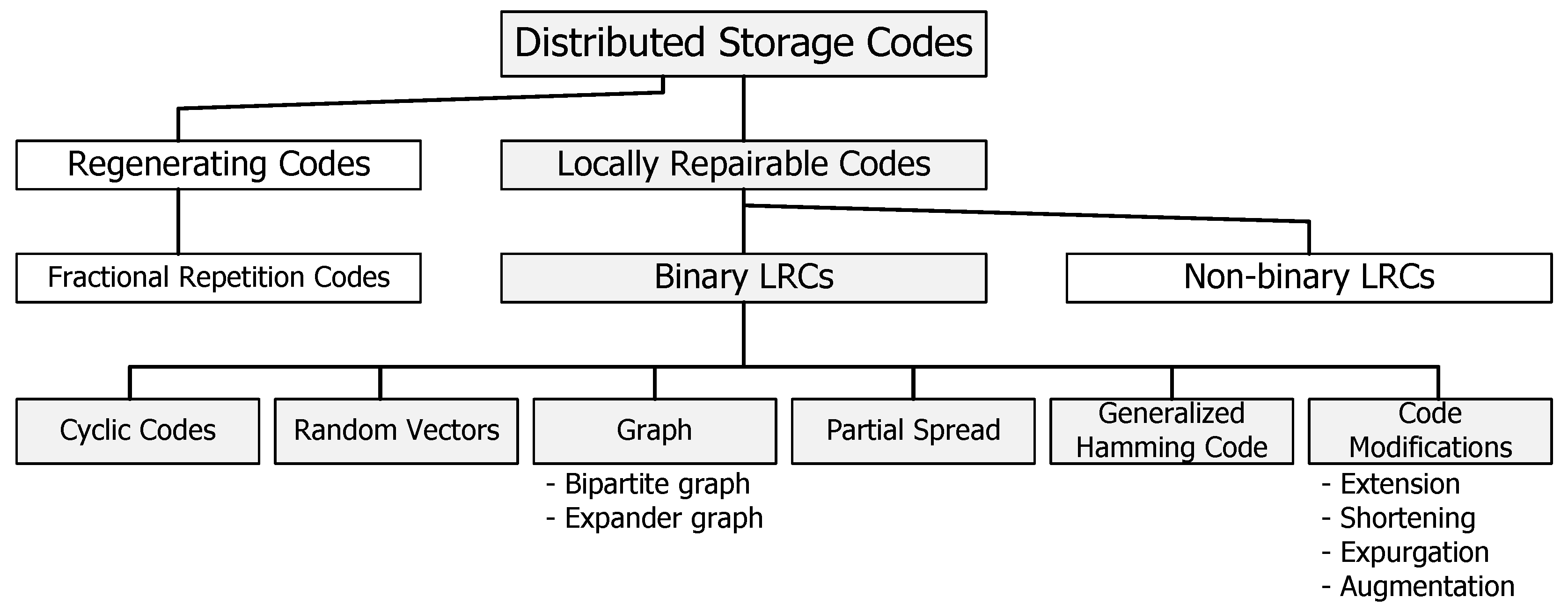
This paper summarizes the recently proposed construction of BLRCs and their features. The code construction methods discussed in this paper are categorized as in Figure 1. The construction methods of BLRCs are explained using cyclic code based, bipartite graph based, anticode based, partial spread based, and generalized Hamming code based approaches. In addition, the construction of BLRCs using modification methods for linear codes such as extending, shorting, expurgating, augmenting, and lengthening are discussed. This paper is organized into several sections. In Section 2, the basic concepts used in the coding techniques for distributed storage systems are introduced. In addition, the characteristics of RC, LRC, and FRC are explained, including the meaning of locality and availability. In Section 3, generation methods of LRCs are summarized with respect to individual types and features, with a focus on BLRC. Finally, the main conclusions are summarized in Section 4.

2. Preliminaries

2.1. Classification of Storage Codes for DSS

There are several types of codes for data storage systems such as regeneration codes, locally repairable codes, and fractional repetition codes. Regeneration codes are a class of codes that enhance data reliability and facilitate the efficient repair of failed nodes in distributed storage systems [18,19]. The key metric of these codes is the network bandwidth, which is intended to optimize the amount of data communicated to repair a single failure node. In the case of node failure, it is necessary to recover the data stored in the failed node or restore them in the replacement node. This is called repair or regeneration of a node. During the repair process, data are typically downloaded from the remaining nodes. In this case, downloading the entire message is a waste of network resources. Therefore, regeneration codes are introduced to reduce the amount of downloaded data during the repair process while retaining the storage efficiency of traditional maximum distance separable (MDS) codes.

The earliest LRCs were proposed as pyramid codes [20,21,22]. The formal definition of LRC with a tradeoff between locality r and the minimum distance d first appears in [23]. LRCs focus on optimization of the number of nodes accessed for node repair and reconstruction. These codes are introduced in [24] and developed further in [25,26]. In addition, LRCs were recently utilized in distributed storage systems, such as Windows Azure storage [27] and Facebook HDFS-RAID [28].

There are several approaches for the construction of efficient storage codes for distributed storage systems as follows:

–

nonlinear codes [25,29];

–

vector codes [30,31,32];

–

codes over bounded alphabets [33];

–

codes with short local MDS [24,30]; and

–

codes with local regeneration [30,32].

A more detailed review of each method can be found in [17].

2.2. Locality, Recoverability, and Availability for Hot Data

Several criteria are used to evaluate the performance of distributed storage codes. This subsection introduces the concepts and definitions of the most important ones, including locality, reliability, and availability.

Let $\mathcal{C}$ be an $(n,k)$ q-ary code of length n and dimension k over a finite field $F_q$. The locality of the ith coordinate of $\mathcal{C}$ is r if the value of the ith symbol of a codeword of $\mathcal{C}$ is represented as a function of r other coordinates, and no such set of coordinates with cardinality less than r exists. This means that a coordinate in a linear code has locality r if it can be expressed as a linear combination of r other coordinates. The set of such r coordinates that can repair the ith symbol is called a “repair set”. An $(n,k)$ code $\mathcal{C}$ with locality r is denoted as an $(n,k,r)$ locally repairable code. In addition to maximizing the distance of codewords, the maximal recoverable LRC (MR-LRC) is defined as a code that can modify all theoretically correctable erasure patterns under locality constraints.

If the ith symbol $c_i$ in a codeword is lost, it can be recovered by reading r other symbols in the codeword. In this case, the locality can be classified into two cases: “information locality r” if all information symbols have locality r, and “all-symbol locality r” if all symbols have locality r. In the case of node failure, the decoding complexity of LRCs can be decoupled from the code length n.

Other construction schemes for LRCs are intended to build codes with maximal recoverability (MR) called MR-LRCs, or partial MDS codes. Some examples are found in [34,35,36,37]. For MR-LRCs, it is important to not only maximize the global distance but also to correct any erasure patterns within a theoretical bound. Therefore, they are considered as a stronger class of LRCs than optimal LRCs [37].

Another important performance criterion is availability [38,39,40,41]. Availability is a very important feature when “hot data’ are accessed. Hot data are data that aere frequently accessed simultaneously by many users in front-end systems. A binary linear code $\mathcal{C}$ of length n is called a t-available r-locally repairable code if every coordinate i for $1\le i\le n$ has at least t parity checks of disjoint $r+1$ nonzero elements. A symbol has availability t if it can be read in parallel by t disjoint groups of symbols. These t reads have locality r if each read involves up to r symbols. Replication provides high availability for hot data. For example, considering that replication is performed three times and each symbol can be read in parallel three times, the availability is then $t=3$ and the locality of these reads is $r=1$. One possible solution is LRC with multiple disjoint recovery sets.

There are two types of availabilities, namely information-symbol availability and all-symbol availability. If an $(n,k,r,d)$ LRC supports availability t for local repair on each of k information symbols, it is referred to as an $(n,k,r,t,d)$ LRC with information symbol availability. If an $(n,k,r,d)$ LRC supports availability t for all n symbols, it is referred to as an $(n,k,r,t,d)$ LRC with all-symbol availability [42].

3. Binary Locally Repairable Codes

When the LRCs are first introduced, there is no restriction on the field size. For the Singleton-like bound in [31], there is an optimal construction matching for the bound of field size $q>n+1$, where the optimal LRCs are constructed using an algebraic structure. However, the coding complexity can be significantly reduced using BLRC.

Compared to q-ary LRCs, BLRCs are known to be advantageous in terms of implementation in practical systems. In [43], the advantages of $(n,k,d,r)=(15,10,4,6)$ BLRC are discussed and compared with $(16,10,4,5)$ non-binary LRC, (14,10) RS code, and three-replication with four metrics including encoding complexity, repair complexity, mean time to data loss, and storage capacity. The authors of [43] further analyzed the advantages of BLRCs with a high Hamming distance and average locality [44,45]. In this section, we introduce bounds for BLRCs and various construction methods of BLRCs.

3.1. Bounds for the Binary Locally Repairable Codes

The bounds and constructions of BLRCs are quite different from those of q-ary LRCs. For the bound, the maximum code dimension of BLRCs is smaller than that of q-ary LRC and the corresponding optimal construction of the former should be made by different motivations such as easy implementation. Initially, we discuss the useful bounds for BLRCs.

Let us start with a general bound on LRC that shows a tradeoff relationship between rate $k/n$, minimum distance d, and locality r [23]. For linear LRCs with information locality r, there are tradeoffs among n, k, d, and r. Let $\mathcal{C}$ be an $(n,k,r)$ LRC. Assuming that $r|k$ and $(r+1)|n$, the rate is bounded as follows:

$$\begin{array}{c}\hfill \frac{k}{n}\le \frac{r}{r+1}.\end{array}$$

In addition, the minimum distance is bounded by [31]

$$\begin{array}{c}\hfill d\le n-k-⌊\frac{k}{r}⌋+2,\end{array}$$

which is called a Singleton-like bound because it is a generalization of the classical Singleton bound for linear codes and we have the Singleton bound if $r=k$. It is well-known that a q-ary $(n,k,d)$ MDS code can achieve a Singleton bound. An optimal $(n,k,r)$ LRC achieves the bound with equality. We can consider two extreme cases when $r=k$ and $r=1$. For $r=k$, we have $d\le n-k+1$ and an $(n,k)$ RS code is an $(n,k,r=k)$ optimal LRC. For $r=1$, we have $d\le n-k-\lfloor k\rfloor +2=2(\frac{n}{2}-k+1)$ and the duplication of an $(n/2,k)$ RS code is an $(n,k,r=1)$ optimal LRC. Therefore, we are interested in the case of $1<r<k$.

For the bounds of BLRCs, Cadambe–Mazumdar (C-M) [33], linear programming [46], and $\mathcal{L}$-space bounds [47,48] are introduced. The first bound, considering the alphabet size, is given as

$$\begin{array}{c}\hfill k\le \underset{t\in Z^{+}}{min}[tr+k_{opt}^{(q)}(n-(r+1)t,d)],\end{array}$$

(1)

where $k_{opt}^{(q)}(n,d)$ denotes the largest possible dimension of an $(n,k,d)$ linear code over $F_q$. The C-M bound is often used to determine whether the given BLRC with short code length is optimal [32]. However, because the exact value of $k_{opt}^q(n,d)$ can only be obtained in a limited case with relatively short code length, it is difficult to apply the C-M bound to evaluate the optimality of general BLRCs.

In addition, a linear programming bound was proposed using the Delsarte linear programming method, which is known to be tighter than the C-M bound for BLRCs for some parameters [49]. However, both bounds are expressed in the implicit forms and, thus, it is difficult to apply these bounds to BLRCs with long code lengths.

For an $(n,k,d)$ linear LRC $\mathcal{C}$, $\mathcal{L}$-space bound was recently proposed using sphere packing [47,48]. The $\mathcal{L}$-space is defined as the dual of the linear space generated by a minimum set of local parity checks of $\mathcal{C}$ with overall support covering all coordinates. For an $(n,k,d,r)$ BLRC with disjoint repair groups, where $d=2t+2$ and $n=(r+1)l$, the following bound holds for the parity of $t+1$ [50].

(i)

If $t+1$ is odd, we have

$$\begin{array}{c}\hfill k\le \frac{rn}{r+1}-⌈{log}_2\left(\sum _{0\le i_1+\dots +i_l\le \lfloor \frac{d-1}{4}\rfloor }\prod _{j=1}^l\left(\genfrac{}{}{0pt}{}{r+1}{2i_j}\right)\right)⌉.\end{array}$$

(2)

(ii)

If $t+1$ is even, we have

$$\begin{array}{c}\hfill k\le \frac{rn}{r+1}-⌈{log}_2\left(\sum _{0\le i_1+\dots +i_l\le \lfloor \frac{d-1}{4}\rfloor }\prod _{j=1}^l\left(\genfrac{}{}{0pt}{}{r+1}{2i_j}\right)+\frac{{\sum }_{i_1+\dots +i_l=\frac{d}{4}}{\prod }_{j=1}^l\left(\genfrac{}{}{0pt}{}{r+1}{2i_j}\right)}{\lfloor \frac{n}{t+1}\rfloor }\right)⌉.\end{array}$$

(3)

These bounds are advantageous in two ways compared to the previous bounds. Firstly, the $\mathcal{L}$-space bound is known to be tighter than the C-M bound for BLRCs with long code lengths. In addition, the inequality of the bound is expressed in an explicit form, i.e., the value of the bound is easily derived for BLRCs with long code lengths. Furthermore, the improved $\mathcal{L}$-space bound is induced with the refined packing radius for BLRCs with $4|d$ [50].

A bound in an explicit form for $d\ge 5$ is given in [48]. For an $(n,k,d)$ linear BLRC with locality r, such that $d\ge 5$ and $2\le r\le \frac{n}{2}-2$, it follows that

$$\begin{array}{c}\hfill k\le \frac{nr}{r+1}-min\left\{{log}_2\left(1+\frac{rn}{2}\right),\frac{rn}{(r+1)(r+2)}\right\}.\end{array}$$

(4)

In the next subsection, we introduce the construction of BLRCs with various parameters and motivations, some of which are optimal or near-optimal with respect to the aforementioned bounds.

3.2. Classification of Binary Locally Repairable Codes

For the construction of BLRCs, various methods have been proposed based on the following:

(i)

cyclic codes [51,52,53,54];

(ii)

random vectors [42];

(iii)

bipartite graph [44,55,56];

(iv)

anticodes [57];

(v)

partial spread [50,58];

(vi)

generalized Hamming code [47,48]; and

(vii)

modification of codes [53,59].

In the following subsections, the various types of constructions of BLRCs are summarized.

3.3. BLRCs from Cyclic Codes

Goparaju and Calderbank proposed several constructions of BLRCs from cyclic codes [51]. Cyclic codes inherently enjoy efficient structures for encoder and decoder implementation. The q-cyclotomic coset $M_{i,n}$ is defined as

$$\begin{array}{c}\hfill M_{i,n}=\{i{q}^{j}modn|1\le j<a\},\end{array}$$

where a is the smallest positive integer that satisfies $i{q}^a\equiv imodn$. The defining set of an $(n,k,d)$ cyclic code $\mathcal{C}$ is defined as

$$\begin{array}{c}\hfill D_{\mathcal{C}}=\{i|g({\alpha }^i)=0,0\le i\le n-1\},\end{array}$$

where $g(x)$ has roots in the splitting field $F_{q^s}$, $n|(q^s-1)$. Using optimal cyclic codes in terms of the Singleton bound, three BLRC constructions are suggested as follows.

Construction (CC1) [51]:

Let $n=2^m-1$, $r+1$ be a factor of n and α be a primitive element of $F_{2^m}$. Let $\mathcal{C}$ be a cyclic code with the generator polynomial $g(x)$ with the defining set as

$$\begin{array}{c}\hfill D_{\mathcal{C}}=\{jmod(r+1)|0\le j\le n-1\}.\end{array}$$

Then, $\mathcal{C}$ is an LRC with locality r and dimension $k=rn/(r+1)$.

Construction (CC2) [51]:

Let $n=2^m-1$ with even m, and locality $r=2$. Let $\mathcal{C}$ be a cyclic code in which the generator polynomial $g(x)$ has the defining set

$$\begin{array}{c}\hfill D_{\mathcal{C}}=\{jmod3|0\le j\le n-1\}\cup M_{1,n}.\end{array}$$

Then, $\mathcal{C}$ is an LRC of dimension $k=\frac{2}{3}(2^m-1)-m$ and a distance $d\ge 6$.

Construction (CC2) is shown to be distance-optimal among the set of linear codes that have disjoint locality parity checks.

Construction (CC3) [51]:

Let $n=2^m-1$. Let α be a primitive element of $F_q$. The generator polynomial with the defining set

$$\begin{array}{c}\hfill D_{\mathcal{C}}=\{jmod3|0\le j\le n-1\}\cup M_{1,n}\cup M_{-1,n}\end{array}$$

can construct a BLRC that satisfies the following inequality $k\le \frac{2}{3}(2^m-1)-2m$ for even k, $d=10$, and $r=2$.

The BLRC construction from the $(7,4,3)$ binary Hamming code is expressed in the following construction.

Construction (CC4) [51]:

For $3|m$, we have $7|n$ when $n=2^m-1$. Let $\mathcal{C}$ be a cyclic code in which the generator polynomial $g(x)$ has the defining set

$$\begin{array}{c}\hfill D_{\mathcal{C}}=\{j|j(mod7)\in \{0,3,5,6\},0\le j\le n-1\}.\end{array}$$

Then, $\mathcal{C}$ is a three-available two-local LRC with dimension $k=3n/7$ and minimum distance $d=4$. The corresponding parity check polynomial $h(x)$ is then given as

$$\begin{array}{c}\hfill h(x)=1+x^{n/7}+x^{3n/7}.\end{array}$$

Extending the results in [51], Zeh and Yaakobi proposed several construction methods for BLRC in [52]. These constructions generate BLRCs with locality 2. Construction (CC5) was based on binary reversible codes. Let $D_{\mathcal{C}}^{[l]}$ be the set given as $\{(i+l)|i\in D_{\mathcal{C}}\}$. Let $D_{\mathcal{L}}$ be the defining set of $(r+1,r,2)$ single parity check code with one erasure correctional capability in a block of length $r+1$. Then, a BLRC can be obtained as in Construction (CC5).

Construction (CC5) [52]:

For odd m, let $n=2^m+1$ and $3|n$. Let $\mathcal{L}$ be a $(3,2,2)$ single parity check code with $D_{\mathcal{L}}=\{0\}$, where the defining set is given as:

$$\begin{array}{c}\hfill D_{\mathcal{C}}=D_{\mathcal{L}}\cup D_{\mathcal{L}}^{[3]}\cup \cdots \cup D_{\mathcal{L}}^{[n-3]}\cup M_{1,n}=\{jmod3|0\le j\le n-1\}\cup M_{1,n}.\end{array}$$

The corresponding code $\mathcal{C}$ is then an $(n,k,d,r)$ BLRC, where $k=\frac{2}{3}(2^m+1)-2m$, $d\ge 10$, and $r=2$.

In addition, Construction (CC4) was extended to obtain codes with a higher Hamming distance at the cost of a small reduction of the rate as follows:

Construction (CC6) [52]:

Let $n=2^m-1$ and $7|n$ (i.e., $3|m$). Let $D_{\mathcal{C}}$ be the defining set given as

$$\begin{array}{cc}\hfill D_{\mathcal{C}}& =\{j|j(mod7)\in \{0,3,5,6\},0\le j\le n-1\}\cup M_{1,n}\hfill \\ & =\{\dots ,-9,-8,-7,-4,-2,-1,0,3,5,6,7,10,12,13,\dots \}\cup M_{1,n}.\hfill \end{array}$$

Then, the corresponding code $\mathcal{C}$ is a BLRC with $k=3n/7-m$, $d\ge 12$, locality $r=2$, and availability $t=2$.

This construction was extended to the construction of $(2^a-1,a,2^{a-1})$ simplex code $\mathcal{L}$ with available $(2^{a-1}-1)$ and locality 2 as follows.

Construction (CC7) [52]:

Let $n=2^m-1$, which is divisible by $2^a-1$ (i.e., $a|m$). Let $\mathcal{L}$ be a $(2^a-1,a,2^{a-1})$ cyclic simplex code with the defining set given as

$$\begin{array}{c}\hfill D_{\mathcal{L}}=\{0,3,5,6,2^{a-1+1},\dots ,2^a-1\}\cup M_{1,n}.\end{array}$$

The corresponding code $\mathcal{C}$ is then a BLRC with $d\ge 2^a+2^{a-1}$, $r=2$, $t=2^{a-1}-1$, and dimension $k=\frac{a}{2^a-1}(2^m-1)-m$.

Another example of BLRCs was proposed by Tamo, Barg, Goparaju, and Calderbank in 2016 as in the following construction.

Construction (CC8) [54]:

Let α be an nth root of unity and let z be an integer such that $(2^z-1)|n$ and $z\ge 1$. Then, $\mathcal{D}$ is an $(n,k)$ binary cyclic code with the defining set D with the coset $\alpha G_{2^z-1}$ of the group $G_{2^z-1}=<{\alpha }^{2^z-1}>$. Then, the locality of $\mathcal{D}$ is bound as $r\le 2^{z-1}-1$. Moreover, each symbol of the codewords in $\mathcal{D}$ has at least $2^{z-1}$ recovery sets $A_i$ of size $2^{z-1}-1$.

A BLRC that can satisfy the explicit bound given in Equation (4) is also proposed in [60] as follows:

Construction (CC9) [60]:

For $(r+1)|n$, let $v=\frac{n}{r+1}$ and $u=r+1$, where $gcd(u,v)=1$ and $u,v\ge 2$. Let $g(x)$ be a generator polynomial of the cyclic BLRC and ${\beta }^{\prime }$ be the uth root of unity. Then, $(uv,uv-deg(g(x)),4,u-1)$ BLRC can be constructed using the generator polynomials given by

(i) 

For $2|r$, $g(x)=(x^v+1)g_1(x)$, where $g_1(x)$ is the minimum polynomial of ${\beta }^{\prime }$ over $F_2$.

(ii) 

For $r=2^m-1$, $g(x)=(x^v+1){(x+1)}^{2^{m-1}}$, where m is a positive integer.

3.4. BLRCs from Random Vectors

A family of high-rate BLRCs with locality two and uneven availabilities was proposed in [42], which requires intermediate procedures. The uneven availability is represented as an availability profile. For its construction, a k-tuple binary column vector $z_k$ with a nonzero element at the random position is required. Let $Z(x)$ be a random function that converts x into a binary vector with the same length by changing a zero element into a nonzero element. From $z_k$, $k\times k$ square matrices $P_{k,l}$ for $1\le l\le k-1$ are constructed individually by increasing l as follows:

$$\begin{array}{c}\hfill P_{k,l}=\left[Z^l(z_k)Z_{(1)}^l(z_k)\cdots Z_{(k-1)}^l(z_k)\right],\end{array}$$

where $Z^l(z_k)$ is generated from $Z^{l-1}(z_k)$ by the lexicographical order of construction, and $Z_{(i)}^l(z_k)$ is the i circularly downward-cyclic-shifted vector of $Z^l(z_k)$. Then, a $k\times k(k-2)$ matrix $P_k$ for the parity part of the generator matrix in a systematic form is generated by concatenating the matrix $P_{k,1},P_{k,2},\cdots ,P_{k,k-2}$ as follows:

$$\begin{array}{c}\hfill P_k=[P_{k,1}{P}_{k,2}\cdots P_{k,k-2}]=\left[Z^1(z_k)Z_{(1)}^1(z_k)\cdots Z_{(k-1)}^1(z_k)\cdots Z^{k-2}(z_k)Z_{(1)}^{k-2}(z_k)\cdots Z_{(k-1)}^{k-2}(z_k)\right].\end{array}$$

Construction (RV) [42]:

Let $G_{(n,k)}$ denote the generator matrix of the proposed $(n,k)$ BLRC $\mathcal{C}$ in a systematic form. Then, a $k\times n$ systematic generator matrix $G_{(n,k)}$ is constructed as

$$\begin{array}{c}\hfill G_{(n,k)}=[I_k{P}_k].\end{array}$$

It should be noted that the $k\times k(k-1)$ generator matrix $G_{(n,k)}$ has a code rate of $R=1/(k-1)$.

An $(n,k)$ BLRC code $\mathcal{C}$ from Construction (RV) has an all-symbol locality equal to $r=2$ and the all-symbol availability profile is given by

$$\begin{array}{c}\hfill t=[k-1,\cdots ,k-1,2,\cdots ,2,1,\cdots ,1],\end{array}$$

where the numbers of $(k-1)$s, 2s, and 1s are k, $k(k-3)$, and k, respectively, and each value denotes the availability for local repair of the ith symbol of a codeword in $\mathcal{C}$.

3.5. BLRCs from Bipartite Graph

In coding theory, a Tanner graph is a bipartite graph with two sets of vertices, a set of n variable nodes and a set of $(n-k)$ check nodes, for the constraint of error correcting codes. Suppose that n variable nodes are partitioned into $l=n/(r+1)$ groups. All variable nodes related to each group are linked to a unique check node called the local check node and the other nodes are called the global check nodes. Then, the constructed BLRC can achieve maximum locality r for all symbols.

Construction (BG) [44]:

Let $H_{BL}=I_{\frac{n}{r+1}}\otimes {\mathbf{1}}_{r+1}\in F_2^{\frac{n}{r+1}\times n}$ and $H_{BG}={\mathbf{1}}_{\frac{n}{r+1}}\otimes H_0^{(r)}\in F_2^{\lceil {log}_2(r+1)\rceil \times n}$, where ⊗ denotes the Kronecker product, ${\mathbf{1}}_{r+1}$ denotes the all-one vector of length $r+1$ and $H_0^{(r)}$ is the parity check matrix of an $(r+1,r+1-\lceil {log}_2(r+1)\rceil )$ Hamming code such as $H_0^{(r)}=(\mathbf{0},\mathbf{1},\dots ,\mathbf{r})\in F_2^{\lceil {log}_2(r+1)\rceil \times (r+1)}$. Then, the parity check matrix of BLRC based on a bipartite graph of parameters $(n,\frac{rn}{r+1}-\lceil {log}_2(r+1)\rceil ,4,r)$ is given as

$$\begin{array}{c}\hfill H=\left(\begin{array}{c}{H}_{BL}\\ H_{BG}\end{array}\right)\in F_2^{(n-k)\times n}.\end{array}$$

The minimum distance of the parity check matrix H in Construction (BG) is 4. This BLRC is optimal in some cases. Even when it is not optimal, it is shown that this code has a near-optimal code rate with a rate gap of $O\left(\frac{logr}{n}\right)$.

In addition, an expander graph based construction of BLRC exists [55,56]. Suppose we have two sets V and C that satisfy the following conditions:

–

$|V|=n$, $|C|=\frac{nt}{r+1}$;

–

the degree of $v\in V$ is t; and

–

the degree of c is $r+1$.

For $0<\alpha ,\gamma \le 1$, the bipartite graph $G=(V\cup C,E)$ is a $(t,r+1,\alpha ,t\gamma )$-expander if for any subset $V^{\prime }\subset V$, $|V^{\prime }|\le \alpha n$ implies the size of the subset of C connected to $V^{\prime }$ is greater than $t\gamma |V^{\prime }|$. In addition, the length of the shortest cycle of the graph G is greater than 4. As such, we can have the following construction:

Construction (EG) [55,56]:

Let $H_E$ be an $m\times n$ parity check matrix $[h_{i,j}]$ where $1\le i\le m$ and $1\le j\le n$, whose columns correspond to the vertices of V and the rows corresponds to the vertices of C. Then, $h_{i,j}$ is equal to one if the corresponding vertices $c_i$ and $v_j$ are connected with an edge. For $t<r+1$, the code ${\mathcal{C}}_E$ constructed from $H_E$ is an $(n,k,\delta ,r,t)$ ${\mathcal{C}}_E$ BLRC.

In Construction (EG), $\gamma$ is chosen from the range $[\frac{1}{1+r},1-\frac{1}{t})$ and $\alpha$ is determined as a solution of the following equation:

$$\begin{array}{c}\hfill (t-1)h(\alpha )/t-h(\alpha \gamma (r+1))/r+1-\delta \gamma (r+1)h(\frac{1}{\gamma (r+1)})=0,\end{array}$$

where $h(x)=-x{log}_{2}x-(1-x){log}_2(1-x)$. The probability that G is a $(t,r+1,{\alpha }^{\prime },t\gamma )$ expander is greater than $1-O(n^{-t(1-\gamma )-1})$ for $0<{\alpha }^{\prime }<\alpha$. In addition, the code rate is bounded by

$$\begin{array}{c}\hfill R\ge 1-\frac{t}{r+1}-o(1),\end{array}$$

where the equality holds for the case whereby $H_E$ is a full rank matrix.

3.6. BLRC from Anticode

An anticode $\mathcal{A}$ of length n is a code that may contain repeated codewords in $F_2^n$ and has an upper bound on the distance between codewords [61]. Contrary to the minimum distance in generic error correcting codes, the maximum distance $\delta$ is defined as the maximum Hamming distance between any pair of codewords in $\mathcal{A}$. This anticode is a core ingredient of the following BLRC.

The generator matrix $G_{\mathcal{A}}$ of the anticode $\mathcal{A}$ is a $k\times n$ matrix, and all codewords in $\mathcal{A}$ can be expressed by a linear combination of k rows of $G_{\mathcal{A}}$. If the rank of $G_{\mathcal{A}}$ is $\gamma$, then each codeword in $\mathcal{A}$ occurs $2^{k-\gamma }$ times. Let ${\mathcal{A}}_{s,2}$ be an anticode of length $n=\left(\genfrac{}{}{0pt}{}{s}{2}\right)$ and Hamming weight of 2 and the columns of its generator matrix $G_{\mathcal{A}}$ are all weight-2 vectors of length s.

Construction (AC1) [57]:

Let ${\mathcal{S}}_m$ be a binary simplex code of length $2^m-1$, dimension m, and minimum Hamming distance $2^{m-1}$. Let $G_m$ be the generator matrix of ${\mathcal{S}}_m$, and let its columns consist of all possible nonzero vectors in $F_2^m$. We prepend $m-s$ zeros to every column of $G_{\mathcal{A}}$ of ${\mathcal{A}}_{s,2}$ to construct an $m\times \left(\genfrac{}{}{0pt}{}{s}{2}\right)$ matrix $G_{\mathcal{A}}^{\prime }$. By deleting the columns in $G_{\mathcal{A}}^{\prime }$ from $G_m$, we can construct a generator matrix G of BLRC, ${\mathcal{C}}_{m,s,2}$, with parameters $(2^m-\left(\genfrac{}{}{0pt}{}{s}{2}\right)-1,m,2^{m-1}-\lfloor \frac{s^2}{4}\rfloor )$ and locality 2.

For $3\le s\le 5$, the code ${\mathcal{C}}_{m,s,2}$ satisfies the C-M bound in Equation (1). Moreover, three instances with locality $r=2$ of Construction (AC1) are listed in [57]:

–

The code ${\mathcal{C}}_{m,3,2}$ from the anticode ${\mathcal{A}}_{3,2}$ is a $(2^m-4,m,2^{m-1}-2)$ LRC.

–

The code ${\mathcal{C}}_{m,4,2}$ from the anticode ${\mathcal{A}}_{4,2}$ is a $(2^m-7,m,2^{m-1}-4)$ LRC.

–

The code ${\mathcal{C}}_{m,5,6}$ from the anticode ${\mathcal{A}}_{5,2}$ is a $(2^m-11,m,2^{m-1}-6)$ LRC.

Construction (AC2) [57]:

Let $A_{t;2,3,\dots ,t-1}$, $3\le t\le m$, be an anticode such that its generator matrix $G_{\mathcal{A}}$ consists of all columns of weight in $\{2,3,\dots ,t-1\}$. Then, $m-t$ zeros are prepended to every column of $G_{\mathcal{A}}$ to form an $m\times {\sum }_{i=2}^{t-1}\left(\genfrac{}{}{0pt}{}{t}{i}\right)$ matrix whose columns will be deleted from $G_m$ to obtain a generator matrix G for the code ${\mathcal{C}}_{m,t}$, which becomes a $(2^m-2^t+t+1,m,2^{m-1}-2^{t-1}+2)$ LRC with locality $r=2$.

This code achieves the Griemer bound [62].

Construction (AC3) [57]:

Let ${\mathcal{A}}_{m-1}$ be an anticode with generator matrix given by

$$\begin{array}{c}\hfill G_{\mathcal{A}}=\left(\begin{array}{cccc}1& 0& \cdots & 0\\ 0& & & \\ ⋮& & G_{m-1}& \\ 0& & & \end{array}\right),\end{array}$$

where $G_{m-1}$ is the generator matrix of the simplex code ${\mathcal{S}}_{m-1}$. Let $\mathcal{C}$ be a code obtained based on the Farrell construction using the simplex code ${\mathcal{S}}_m$ and the anticode ${\mathcal{A}}_{m-1}$. Then, $\mathcal{C}$ is a $(2^{m-1}-1,m,2^{m-2}-1)$ BLRC with locality $r=3$.

It is also shown that this code can satisfy the bound in Equation (1).

3.7. BLRCs from Partial Spread

To introduce BLRCs constructed from partial spread, the definition of partial t-spread is given.

Definition [50]:

A partial t-spread of $F_q^m$ is a collection $S=\{W_1,\dots ,W_l\}$ of t-dimensional subspaces of $F_q^m$ such that $W_i\cap W_j=\{0\}$ for $1\le i<j\le l$. Moreover, S is maximal if it has the largest possible size. In particular, if ${\cup }_{i=1}^n{W}_i=F_q^m$, then S is a t-spread. If $t|n$, a t-spread of $F_q^m$ exists.

Now, we can define a BLRC $\mathcal{C}$ with parity check matrix given by

$$\begin{array}{c}\hfill H=\left(\begin{array}{c}{H}_L\\ H_G\end{array}\right).\end{array}$$

(5)

Then, a BLRC $\mathcal{C}$ of parameters $(n,k\ge \frac{rn}{r+1}-t\lceil {log}_{2}n\rceil ,d\ge 2t+2,r)$ can be constructed in the following way:

Construction (PS1) [50]:

Let ${\mathbf{1}}_n$ be the all-one vector of length n. Let $H_L=I_{\frac{n}{r+1}}\otimes {\mathbf{1}}_{r+1}$ and $H_G$ be a $t\lceil {log}_{2}n\rceil \times n$ matrix that has binary expansions of the vectors $\{{\mathbf{a}}_1,{\mathbf{a}}_2,\dots ,{\mathbf{a}}_n\}$ as its columns, where ${\mathbf{a}}_i={({\beta }_i,{\beta }_i^3,\dots ,{\beta }_i^{2t-1})}^T$ and ${\beta }_1,\dots ,{\beta }_n$ are distinct elements of the finite field $F_{2^{\lceil {log}_{2}n\rceil }}$. Then, the parity check matrix of a BLRC $\mathcal{C}$ is given as in Equation (5).

For the further extension of Construction (PS1), the parity check matrix can be given as

$$\begin{array}{c}\hfill H=\left(\begin{array}{c}{H}_L\\ H_G\end{array}\right)=\left(\begin{array}{cccc}{H}_L^1& H_L^2& \cdots & H_L^l\\ H_G^1& H_G^2& \cdots & H_G^l\end{array}\right),\end{array}$$

(6)

where $l=\frac{n}{r+1}$. For $i\in [1,l]$, $H_L^i$ is an $l\times (r+1)$ matrix, whose ith row is the all-one vector of length $r+1$ and the other rows are all-zero vectors. Moreover, $H_G^i$ is the ith $(n-k-l)\times (r+1)$ submatrix of $H_G=(H_G^1{H}_G^2\dots H_G^l)$. It is well-known that if any $d-1$ columns of the parity check matrix H are linearly independent, the minimum distance of a linear code is greater than or equal to d. Furthermore, for a collection of any $a_i$ columns $\{{\mathbf{c}}_1^i,{\mathbf{c}}_2^i,\dots ,{\mathbf{c}}_{a_i}^i\}$ of $H_G^i$, if ${\sum }_{i=1}^l{\sum }_{j=1}^{a_i}{\mathbf{c}}_j^i\ne \mathbf{0}$, then $d\le 2t+2$, where $a_1,a_2,\dots ,a_l$ satisfy the following two conditions:

(i)

For $1\le i\le l$, $a_i$ is even, where $0\le a_i\le min\{2t,r+1\}$; and

(ii)

$2\le {\sum }_{i=1}^l{a}_i\le 2t$.

Then, we can construct two k-optimal $(n,k,d,r)$ BLRCs with disjoint repair groups as in the following construction.

Construction (PS2) [50]:

Let $r=2^t$ and $\{W_1,\dots ,W_a\}$ be the maximum partial $2t$-spread of $F_2^s$. In addition, let $\{{\mathbf{e}}_1^{(i)},{\mathbf{e}}_2^{(i)},\dots ,{\mathbf{e}}_{2t}^{(i)}\}$ be a basis of $W_i$. For $t\le 3$, there exists a $(2^t,2^t-2t,\ge 5)$ binary linear code with the parity check matrix $H_b$. Let $supp(x)$ be the set of indices corresponding to nonzero coordinates of a vector x. For $i\in [1,a]$, let $T^{(i)}$ be the set $\{0\}\cup \{f_i|1\le i\le n\}$, where $f_i={\sum }_{j\in supp(h_i)}{\mathbf{e}}_j^{(i)}$ and $h_i$ is the ith column of $H_b$. When $t=1,2$, $T^{(i)}=\{\mathbf{0},{\mathbf{e}}_1^{(i)},{\mathbf{e}}_2^{(i)},\dots ,{\mathbf{e}}_{2t}^{(i)}\}$. Let $H_G^i$ be an $s\times (2^t+1)$ matrix whose columns consist of the vectors in $T^{(i)}$. Then, we can define a BLRC with a parity check matrix H as in Equation (6), where $\frac{s}{r}<l\le a$.

A set $T\subseteq F$ is $\tau$-wise weakly independent over $F_2\subseteq F$ if no set $T^{\prime }\subseteq T$, where $2\le |T^{\prime }|\le \tau$, has the sum of its elements equal to zero. Then, we have $d\ge 6$, if the columns of $H_G$ satisfy the following conditions:

(i)

${\mathbf{c}}_1^i+{\mathbf{c}}_2^i\ne 0$ for $1\le i\le l$;

(ii)

${\mathbf{c}}_1^i+{\mathbf{c}}_2^i+{\mathbf{c}}_3^i+{\mathbf{c}}_4^i\ne 0$ for $1\le i\le l$; and

(iii)

${\mathbf{c}}_1^i+{\mathbf{c}}_2^i+{\mathbf{c}}_1^j+{\mathbf{c}}_2^j\ne 0$ for $1\le i\ne j\in l$.

Construction (PS3) [50]:

Let $r=2^t+2^{\lfloor (t+1)/2\rfloor }-1$, and $\{W_1,W_2,\cdots ,W_a\}$ be a maximum partial $(2t+1)$-spread of $F_2^s$ and the basis of $W_i$ is $\{{\mathbf{e}}_1^{(i)},{\mathbf{e}}_2^{(i)},\cdots ,{\mathbf{e}}_{2t+1}^{(i)}\}$. When $t\ge 3$, there is a $(2^t+2^{\lfloor (t+1)/2\rfloor }-1,2^t+2^{\lfloor (t+1)/2\rfloor }-2t-2,5)$ binary linear code. Let $T^{(i)}$ be the same set in Construction (PS2) for $1\le i\le a$. For $t=1,2$, $T^{(i)}$ is defined as $\{\mathbf{0},{\mathbf{e}}_1^{(i)},{\mathbf{e}}_2^{(i)},\cdots ,{\mathbf{e}}_{2t+1}^{(i)}\}$. Let $H_G^i$ be an $s\times (2^t+1)$ matrix whose columns consist of the vectors in $T^{(i)}$. Then, a BLRC $\mathcal{C}$ can be constructed using a parity check matrix H in Equation (6) for $\frac{s}{r}<l\le a$.

Let $A_q(m,k,d)$ be the maximal cardinality of subspace codes over $F_q^m$ with minimum distance d and dimension k. Then, we can construct a BLRC as follows:

Construction (PS4) [50]:

Let $n=3l$ such that $l\ne \frac{2^{2m+1}-2}{3}$ for $m\ge 2$. Then, there exists an $(n,k,6,2)$ BLRC $\mathcal{C}$ with dimension given as

$$\begin{array}{c}\hfill k=\left\{\begin{array}{cc}2l-2m,\hfill & ifl\in [A_2(2m-1,2,4)+2,A_2(2m,2,4)]\hfill \\ 2l-2m-1,\hfill & ifl\in [A_2(2m,2,4)+1,A_2(2m+1,2,4)],\hfill \end{array}\right.\end{array}$$

where it is optimal with respect to the bound in Equation (2). The following construction is nearly optimal with respect to the bound in Equation (2).

Construction (PS5) [50]:

Let $\{W_1,W_2,\dots ,W_a\}$ be a maximum partial two-spread of $F_2^s$. The basis of $W_i$ is given as $\{{\mathbf{e}}_1^{(i)},{\mathbf{e}}_2^{(i)}\}$. Then, a $(4l,\ge 3l-s-1,\ge 6,3)$ BLRC $\mathcal{C}$ with parity check matrix H of the form in Equation (6) for $\frac{s+1}{3}<l\le a$ can be constructed using the submatrices $H_G^i$ for $0\le i\le l$, which is given as

$$\begin{array}{c}\hfill H_G^i=\left(\begin{array}{cccc}\mathbf{0}& {\mathbf{e}}_1^{(i)}& {\mathbf{e}}_2^{(i)}& {\mathbf{e}}_1^{(i)}+{\mathbf{e}}_2^{(i)}\\ 1& 0& 0& 0\end{array}\right).\end{array}$$

Another construction based on the partial t-spread is also proposed in [58]. Let q be a prime power and $V_m(q)$ be the vector space of dimension m over $F_q$.

Construction (PS6) [50]:

Given an integer $r\ge 2$, determine the smallest integer t such that $r+1\le t+\lfloor \frac{t}{2}\rfloor$. An integer m such that $\frac{m+1}{r}\le l$ can be chosen, and there exists a partial t-spread with a size of at least l of $V_m(2)$. Let $B_i=\{b_{i,0},b_{i,1},\dots ,b_{i,t-1}\}$ be a basis of $W_i\in S$ and $C_i=\{c_{i,0},c_{i,1},\dots ,c_{i,\lfloor \frac{t}{2}\rfloor -1}\}$ be a set whose elements are defined as $c_{i,j}=b_{i,2j}+b_{i,2j+1}$ for $i=0,1,\dots ,l-1$ and $j=0,1,\dots ,\lfloor \frac{t}{2}\rfloor -1$. Finally, let $U_i=B_i\cup C_i$ for $i=0,1,\dots ,l-1$. Let s be an integer such that $\frac{m+1}{r}\le s\le l$, and we use any $r+1$ vectors in $U_i$ to fill each submatrix $H_G^i$ as its $r+1$ columns for $i=0,1,\dots ,s-1$. Then, the BLRC ${\mathcal{C}}_{s,m,r}$ has length $n=(r+1)s$, dimension $k=rs-m$, minimum distance $d\ge 6$, and locality r.

Then, the BLRCs ${\mathcal{C}}_{4,4,2}$ and ${\mathcal{C}}_{5,4,2}$ obtained from Construction (PS6) are optimal. In addition, for $s=4,5,\cdots ,9$, the BLRCs ${\mathcal{C}}_{s,5,2}$ from Construction (PS6) are almost optimal in terms of the C-M bound and for $s=3,4,\dots ,9$, the BLRCs ${\mathcal{C}}_{s,6,3}$ from Construction (PS6) are almost optimal with respect to the C-M bound.

3.8. BLRCs from Generalized Hamming Code

Suppose that s and t are two positive integers such that $2t|s$ and $\frac{s}{2t}\ge 2$. Let A be a $2t\times 2^t$ binary parity check matrix such that any four columns of this matrix are linearly independent. For $t\le 2$, A can be chosen as the identity matrix. For $t\ge 3$, A is the parity check matrix of a $(2^t,2^t-2t,5)$ binary linear code that can be built from non-primitive cyclic codes with length $2^t+1$. Let $\beta$ be the primitive root of $x^{2^t+1}-1$, and let $M(x)$ denote the minimum polynomial of $\beta$. The degree of $M(x)$ is $2t$. $A^{\prime }$ is a parity check matrix defining the binary cyclic code with parameters $(2^t+1,2^t-2t,\ge 6)$ that is generated by $(x-1)M(x)$. Then, the set $\{{\beta }^t|i=-2,-1,0,1,2,\dots \}$ forms a subset of the roots of $(x-1)M(x)$. By deleting one coordinate of $A^{\prime }$, we can construct the parity check matrix A of the punctured code with parameters $(2^t,2^t-2t,\ge 5)$. In addition, B is defined as a matrix such that the columns are all nonzero $\frac{s}{2t}$-tuples from $F_{2^{2t}}$, with the first nonzero element equal to 1. Then, B is an $\frac{s}{2t}\times \frac{2^s-1}{2^{2t}-1}$ parity check matrix of a $2^{2t}$-ary Hamming code. Using the matrices A and B, a BLRC construction is provided as follows.

Construction (GH1) [47,48]:

Suppose that $a_1,\dots ,a_{2^t}\in F_{2^{2t}}$ are the $2^t$ elements corresponding to the columns of A, and the ith column of B is denoted by a vector ${\beta }_i$ for $1\le i\le \frac{2^s-1}{2^{2t}-1}$. Let $\mathcal{C}$ be a binary linear code with the parity check matrix given as

$$\begin{array}{c}\hfill H=\left(\begin{array}{cccc}{L}_1& L_2& \dots & L_l\\ H_1& H_2& \dots & H_l\end{array}\right),\end{array}$$

where $l=\frac{2^s-1}{2^{2t}-1}$ and for $1\le i\le l$, $L_i$ is an $l\times (2^t+1)$ matrix whose ith row is an all-one vector, the other rows are all-zero vectors, and $H_i$ is an $s\times (2^t+1)$ matrix over $F_2$ whose columns are binary expansions of the vectors $\{\mathbf{0},a_1{\beta }_i,a_2{\beta }_i,\dots ,a_{2^t}{\beta }_i\}$.

It is shown that this construction can satisfy the bound given in Equation (4).

The shortening for LRCs can also give us another LRC. Let $\mathcal{C}$ be an $(n,k,d)$ BLRC with locality r such that $n\ge 2(r+1)$ and $k\ge 2r$. Then, an $(n^{\prime },k^{\prime },d^{\prime })$ BLRC ${\mathcal{C}}^{\prime }$ with locality r can be obtained by shortening C, where the parameters of $C^{\prime }$ satisfy $n^{\prime }=n-(r+1)$, $k^{\prime }\ge k-r$, and $d^{\prime }\ge d$.

Construction (GH2) [48]:

By applying the shortening of the $(r+1)$ times to C, we have an $(n-(r+1),\ge k-r,\ge d)$ BLRC.

This kind of code modification approach can be extended to the well-known code modification methods such as extending, shorting, expurgating, augmenting, and lengthening [53], as in the following subsection.

3.9. BLRCs from Code Modification

It is well-known that there are various code modification methods for linear codes. For BLRC, we can also use these modification methods to generate codes with new parameters [53]. Let $\mathcal{C}$ be an $(n,k,d)$ binary code with locality r and let $d^{\perp }$ be the minimum distance of its dual code, ${\mathcal{C}}^{\perp }$. By adding a parity bit to each codewords in a $\mathcal{C}$ with parameters $(n,k,d)$, the extended code ${\mathcal{C}}_{ext}$ with parameters $(n+1,k,d_{ext})$ can be obtained. This can be formally presented as

$$\begin{array}{c}\hfill {\mathcal{C}}_{ext}=\left\{(c_1,\dots ,c_n,c_n+1)|(c_1,\dots ,c_n)\in \mathcal{C},c_{n+1}=\sum _{i=1}^n{c}_i\right\},\end{array}$$

where $d_{ext}=d+1$ for odd d and $d_{ext}=d$ for even d [53]. For BLRCs, we are interested in the locality of the derived codes for a give $\mathcal{C}$ with locality r. Let ${\mathcal{C}}_{ext}^{\perp }$ be the dual code of ${\mathcal{C}}_{ext}$. If the maximum Hamming weight among codewords in the code ${\mathcal{C}}^{\perp }$ is $n-r$, then the locality of the extended code ${\mathcal{C}}_{ext}$ is $r_{ext}=r$. If the maximum Hamming weight among codewords in ${\mathcal{C}}^{\perp }$ is $n+1-d^{\perp }$, then the locality of the extended code ${\mathcal{C}}_{ext}$ is $r_{ext}=d^{\perp }-1$. Finally, if $\mathcal{C}$ is an $(n,k,d)$ cyclic code with an odd minimum distance d, then the locality of the dual code $C_{ext}^{\perp }$ in the extended code of $\mathcal{C}$ is $r_{ext}^{\perp }=d$ [53].

The shortening can also be applied to the derivation of new BLRC. By deleting codewords in $\mathcal{C}$ with nonzero values in the last coordinates and removing the last coordinates from the remaining codewords, we can find the shortened code ${\mathcal{C}}_s$ of $\mathcal{C}$. This can be formally represented as

$$\begin{array}{c}\hfill {\mathcal{C}}_s=\{(c_1,\dots ,c_{n-1})|(c_1,\dots ,c_n,0)\in \mathcal{C}\}.\end{array}$$

For an original $(n,k,d)$ binary linear code, it is known that the parameters of the shortened code are given as $(n-1,k-1,d_s\ge d)$. Moreover, if the original code is BLRC with locality $r\ge 2$, then the locality of the shortened code ${\mathcal{C}}_s$ is r or $r-1$. Let ${\mathcal{C}}_s^{\perp }$ be the dual of ${\mathcal{C}}_s$ and let $d^{\perp }\ge 3$ be the minimum distance of the dual code ${\mathcal{C}}^{\perp }$. Then, for an $(n,k,d)$ cyclic code $\mathcal{C}$, the locality of code ${\mathcal{C}}_s$ is either $d^{\perp }-2$ or $d^{\perp }-1$ [53].

Next, the expurgation also can be used to generate new BLRC for an $(n,k,d)$ BLRC $\mathcal{C}$ with odd weight codewords. As such, the expurgated code ${\mathcal{C}}_{exp}$ of $\mathcal{C}$ can be generated as a subcode of $\mathcal{C}$ by selecting only even weight codewords such that

$$\begin{array}{c}\hfill {\mathcal{C}}_{exp}=\{c|c\in \mathcal{C},\mathrm{the}\mathrm{Hamming}\mathrm{weight}w(c)\mathrm{is}\mathrm{even}\}.\end{array}$$

The corresponding parameters of ${\mathcal{C}}_{exp}$ are given as $(n,k-1,w_e)$, where $w_e$ is the minimum Hamming weight of the nonzero codewords in $\mathcal{C}$. Let ${\mathcal{C}}_{exp}^{\perp }$ be the dual code of ${\mathcal{C}}_{exp}$. Then, we have ${\mathcal{C}}_{exp}^{\perp }={\mathcal{C}}^{\perp }\cup \overline{{\mathcal{C}}^{\perp }}$ [53].

As an inverse method of the expurgation as previously described, the augmented code ${\mathcal{C}}_a$ of an $(n,k,d)$ code $\mathcal{C}$ without the all-one codeword $\mathbf{1}$ is defined as the code $\mathcal{C}\cup \{\mathcal{C}+\mathrm{all}-\mathrm{one}\mathrm{codeword}\mathbf{1}\}$ whose parameters are given as $(n,k+1,min\{d,n-w_{max}\})$, where $w_{max}$ is the maximum Hamming weight of codewords in $\mathcal{C}$. If the code $\mathcal{C}$ is cyclic, then the expurgated and augmented codes of $\mathcal{C}$ are also cyclic [53].

Another example of BLRC from the code modification methods is presented in [60] using the shortened expurgated Hamming code.

Construction (SE-Hamming) [60]:

Let β be a primitive element of $F_{2^m}$ and n be a positive integer $\ge 9$ and divisible by 3 such that $\frac{2n}{3}\le 2^m-1$. Let ${\mathcal{C}}_E$ is a $(2^m-1,2^m-m-2,4)$ expurgated Hamming code with the generator polynomial $g(x)=(x+1)g_1(x)$, where $g_1(x)$ is the minimal polynomial of β over $F_2$. Then, a $(\frac{2n}{3},\frac{2n}{3}-m-1,\ge 4)$ shortened expurgated Hamming code ${\mathcal{C}}_S$ can be generated by shortening the first $(2^m-\frac{2n}{3}-1)$ information bits of ${\mathcal{C}}_E$. The concatenation of ${\mathcal{C}}_S$ and an $(n,\frac{2n}{3})$ cyclic code with parity check polynomial $x^{\frac{2n}{3}}+x^{\frac{n}{3}}+1$ as an inner code then yields an $(n,\frac{2n}{3}-\lceil {log}_2(\frac{2n}{3}+1)\rceil -1,d\ge 6,2)$ LRC ${\mathcal{C}}_C$.

3.10. Summary of BLRC Constructions

We summarize the discussed BLRC construction methods in

Table 1. Summary of parameters of various BLRC constructions.

Codes	n	k	d	r	t	S	C-M
CC1	$2^m-1$	$rn/(r+1)$	2	r	1	O	X
CC2	$2^m-1$	$\frac{2}{3}(2^m-1)-m$	$\ge 6$	2	1	X	X
CC3	$2^m-1$	$\le \frac{2}{3}(2^m-1)-2m$	10	2	1	X	X
CC4	$2^m-1$	$3n/7$	4	2	3	X	X
CC5	$2^m+1$	$\frac{2}{3}(2^m+1)-2m$	$\ge 10$	2	1	X	X
CC6	$2^m-1$	$3n/7-m$	$\ge 12$	2	3	X	X
CC7	$2^a-1$	$\frac{a}{2^a-1}(2^m-1)-m$	$\ge 2^{a-1}+2^a$	2	$2^{a-1}-1$	X	X
CC8	n	k	$2^{z-1}$	$\le 2^{z-1}-1$	1	X	X
CC9	n	$n-deg(g(x))$	4	$u-1$	1	X	X
RV	$k^2-k$	k	$2k-2$	2	$\ge 2$ *	O	X
BG	n	$\frac{rn}{r+1}-\lceil {log}_2(r+1)\rceil$	4	r	1	O	X
EG	n	k	d	r	t	O	X
AC1	$2^m-\left(\genfrac{}{}{0pt}{}{s}{2}\right)-1$	m	$2^{m-1}-\lfloor \frac{s^2}{4}\rfloor$	2	1	X	O
AC2	$2^m-2^t+t+1$	m	$2^{m-1}-2^{t-1}+2$	2	1	X	X
AC3	$2^{m-1}-1$	m	$2^{m-2}-1$	3	1	X	O
PS1	n	$\ge \frac{rn}{r+1}-t\lceil {log}_{2}n\rceil$	$\ge 2t+2$	r	1	O	X
PS2	n	k	d	$2^t$	t	O	O
PS3	n	k	d	$2^t+2^{\lfloor \frac{t+1}{2}\rfloor }-1$	t	O	O
PS4	$3l$	$2l-3m$ or $2l-2m-1$	6	2	t	O	O
PS5	$4l$	$\ge 3l-s-1$	$\ge 6$	3	1	O	X
PS6	$(r+1)s$	$rs-m$	$\ge 6$	r	t	O	X
GH1	$2^t+1$	$2^t-l-s-1$	d	r	t	O	X
GH2	$n-r-1$	$\ge k-r$	$\ge d$	r	t	O	X
SE	n	$\frac{2n}{3}-\lceil {log}_2(\frac{2n}{3}+1)\rceil -1$	$\ge 6$	2	1	O	X

* This scheme has an uneven availability represented as an availability profile.

. Generally, in Table 1, X denotes the case that the equality of the bound is not achieved for all parameters. For the case of C-M bound, $k_{opt}$ is assumed to satisfy the Singleton bound for given n and d.

4. Conclusions

This paper summarizes the recently proposed constructions for BLRCs and their features. To achieve efficient hardware implementation, the codes are constructed over the binary field because the need for multiplications is obviated during the encoding, decoding, and repair processes. We explain the various construction methods of BLRCs using cyclic code based, random vector based, bipartite or expander graph based, anticode based, partial spread based, and generalized Hamming code based approaches. In addition, construction methods of the BLRCs using code modification methods for linear codes such as extending, shorting, expurgating, and augmenting are introduced.

We selectively review important achievements on BLRCs from the authors’ perspectives and thus obviously the authors’ bias are reflected. Therefore, not being reviewed here does not mean it is not an important result. Especially, we also apologize in advance for the lack of proper citation or lack of new research results because this area is actively researched and many papers have been introduced in a relatively short period of time.