Multipath Ghost Suppression Based on Generative Adversarial Nets in Through-Wall Radar Imaging

Abstract

In this paper, we propose an approach that uses generative adversarial nets (GAN) to eliminate multipath ghosts with respect to through-wall radar imaging (TWRI). The applied GAN is composed of two adversarial networks, namely generator G and discriminator D. Generator G learns the spatial characteristics of an input radar image to construct a mapping from an input to output image with suppressed ghosts. Discriminator D evaluates the difference (namely, the residual multipath ghosts) between the output image and the ground-truth image without multipath ghosts. On the one hand, by training G, the image difference is gradually diminished. In other words, multipath ghosts are increasingly suppressed in the output image of G. On the other hand, D is trained to improve in evaluating the diminishing difference accompanied with multipath ghosts as much as possible. These two networks, G and D, fight with each other until G eliminates the multipath ghosts. The simulation results demonstrate that GAN can effectively eliminate multipath ghosts in TWRI. A comparison of different methods demonstrates the superiority of the proposed method, such as the exemption of prior wall information, no target images with degradation, and robustness for different scenes.

1. Introduction

For through-wall radar imaging (TWRI), the presence of furniture and walls, floors, and ceilings makes electromagnetic waves have strong reflections between the targets and them, which brings multipath returns to the received radar signal. Based on imaging algorithms, such as the back-projection algorithm [1,2,3], target-like images called multipath ghosts are produced at nontarget locations, which makes the performance of detection and recognition significantly worse.

To solve this problem, a group of methods was designed via the multipath model based on prior information about the walls’ locations and antennas. Specifically, in References [4,5], first-order multipath ghosts were mapped back to the positions of associated targets, while target images that overlapped with multipath ghosts were mistakenly removed from true positions. To preserve the overlapped target images, multipath echoes were removed form the raw radar data in Reference [6]. In addition, in Reference [7], multiple estimated images gained by two different kinds of imaging dictionaries were fused to obtain an image without multipath ghosts.

Nevertheless, prior information of accurate walls’ locations is difficult to gain in an actual detection scene. To achieve multipath-ghost suppression without walls’ locations, the aspect-dependence (AD) feature of multipath ghosts is utilized to develop suppression algorithms. In Reference [8], two aspects of subaperture images were multiplied to an image without multipath ghosts. However, this method has a poor performance in suppressing multipath ghosts of the back wall, as they appear close together in both subaperture images. In Reference [9], multiple images with different array rotation angles were fused to yield an image without multipath ghosts. However, the two methods based on the AD feature both needed complicated parameter deployment. In other words, the subaperture method should find suitable subapertures, and the array rotating method should find appropriate rotating angles.

Depending on the ratio of coherent power to the pixel with the incoherent power, a coherence factor, a phase coherence factor (PCF), and a sign coherence factor were designed to weigh images for suppressing multipath ghosts [10,11,12]. These methods have poor suppression performances for well-focused multipath ghosts in the case of synthetic aperture imaging. Moreover, the methods based on these coherence factors and the aforementioned AD feature enlarge the energy differences between target images, which makes it difficult to identify degraded targets with a low signal-to-multipath-clutter ratio (SMCR).

Considering that generative adversarial nets (GAN) [13,14] is classified as a structured learning network that is applied to construct spatial-structure mapping from input images to output images and multipath-ghost suppression is a typical process of spatial-structure mapping, in this paper, GAN, including a generator G and a discriminator D, is introduced to suppress multipath ghosts in through-wall radar imaging. With regard to an input radar image with multipath ghosts, generator G exploits spatial characteristics to generate an output image with reduced multipath ghosts and adversarial discriminator D recognizes the difference between the output image and the ground truth image. The recognized difference is sent to G to improve the generative ability. Through training, G and D alternate and recur until the end, G generates a desired image without multipath ghosts, and D loses effectiveness. The simulation results verify the feasibility of the proposed method. The comparison of different methods demonstrates the superiorities of the proposed method, which are that the proposed method

• has robustness in finishing multipath-ghost suppression without accurate walls’ locations;
• preserves the target images even if they are overlapped with multipath ghosts;
• finishes multipath ghost suppression without the use of complicated tuning parameters in different detection scenes; and
• prevents the energy difference of target images from enlarging, which is beneficial in identifying all targets.

The remainder of this paper is organized as follows. Section 2 briefly describes the first-order multipath model. Section 3 analyzes the details of the generative adversarial model. Section 4 indicates the detailed structure of the proposed networks. Simulations on different datasets are presented in Section 5. Section 6 concludes this paper.

2. Multipath Model

Assume that a single-channel radar is monitoring an enclosed room with four separate homogeneous walls and a synthesized array centered at the origin is placed against the wall surface at ${\mathrm{R}}_1$, ${\mathrm{R}}_2$, …, ${\mathrm{R}}_{\mathrm{N}}$, as shown in Figure 1. The front-wall surface is located along the x-axis, and the back wall is parallel to the x-axis with a length $D_x$. The left- and right-side walls are symmetric about the y-axis with a length $D_y$. We consider the direct path from target P to antenna ${\mathrm{R}}_{\mathrm{n}}$ as path A and three first-order multipaths as paths B, C, and E. The refraction points of the first-order multipaths on the back wall and the left- and right-side walls are ${\mathrm{B}}_{\mathrm{r}}$, ${\mathrm{C}}_{\mathrm{r}}$, and ${\mathrm{E}}_{\mathrm{r}}$, respectively.

The one-way propagation delays of these four paths are denoted as ${\tau }_p^{\left(n\right)}$, $p\in \left\{A,B,C,E\right\}$ and, of which the numerical solutions were obtained in References [4,7]. Therefore, the radar echo with a direct path and first-order multipaths is given by

$$\begin{array}{c}{r}_n\left(t\right)=T_{An}^{2}s(t-2{\tau }_A^{\left(n\right)})+{\displaystyle \sum _{q\in \left\{B,C,E\right\}}}{T}_{An}^{}{T}_{qn}^{}s(t-{\tau }_A^{\left(n\right)}-{\tau }_q^{\left(n\right)}),\hfill \end{array}$$

(1)

where $s(·)$ is the transmitting signal and $T_{An}$ and $T_{qn}$ are the complex amplitude associated with reflection and transmission coefficients. Based on the back-projection algorithm, multipaths are transformed into multipath ghosts in the formed image.

3. Generative Adversarial Model

GAN is a novel way to train a generative model, which consists of two adversarial nets, namely, a generator G and a discriminator D. In order to make the generator have a wide range of generalization abilities, generator G establishes mapping from a predefined noise distribution $p_z$ to a predefined data distribution $p_{data}$ in the initial GAN [13]. As a result, it can output a high-quality image rather than an image that is full of noise with any input. $p_g$ is defined to represent the output distribution of G. Discriminator D outputs a score to evaluate that x is from $p_{data}$ rather than from $p_g$. G and D are alternately trained to achieve $p_g\approx p_{data}$. Optimizing the parameter of G is to minimize $log(1-D(G\left(z\right)\left)\right)$, where $D\left(G\right(z\left)\right)$ indicates the output of D with the input $G\left(z\right)$ and $G\left(z\right)$ denotes the output of G with input z. The feedback of discriminator D improves the generative ability (to make discriminator D unable to distinguish whether the data are from $p_{data}$ or $p_g$). Optimizing the parameters of D is to increase the correct label of the training sample and generating sample, which means to improve the discriminating ability by trying to make $D\left(x\right)=1$ and $D\left(G\right(z\left)\right)=0$, where $D\left(x\right)$ denotes the output of D with input x. The whole process is just like two players playing a game, where one adjusts G to minimize the objective function $L_{GAN}(D,G)$ and where another adjusts D to maximize it, namely,

$$\underset{G}{min}\underset{D}{max}{L}_{GAN}(D,G)=E_x[logD\left(x\right)]+E_z[log(1-D\left(G\left(z\right)\right))],$$

(2)

where $E[·]$ denotes the mean value. In order to enhance the controllability of G in Equation (2), an additional message y was introduced in Reference [14] that can be accomplished by simultaneously introducing y into G and D. The objective function in Equation (2) can be modified as follows:

$$\begin{array}{c}\underset{G}{min}\underset{D}{max}{L}_{cGAN}(D,G)=E_{x,y}[logD(x,y)]+E_{z,y}[log(1-D(G(z,y),y))],\hfill \end{array}$$

(3)

where $D(x,y)$ indicates the output of D with the inputs of x and y. $G(z,y)$ indicates the output of G with the inputs of z and y. In this paper, a radar image with multipath ghosts is used as a conditional input. The training mechanism is shown in Figure 2. The entire training is an iterative dynamic process of alternately training G and D. First, the parameters of G are fixed, and only D is trained to distinguish the output of G and ground truth as much as possible by labeling the output of G as fake and the ground truth as real. Then, the parameters of D are fixed to train G. By optimizing the parameters of G, a realistic output can be judged as real by D. Eventually, through the process of iterative training, discriminator D is unable to differentiate between the two distributions $p_g$ and $p_{data}$. Theoretically, there exists a unique solution of $D(x,y)=D\left(G\right(z,y),y)=0.5$ that can be used as a sign of the end of training.

For the objective function in Equation (3), a better output can be generated by combining the $L1$ distance [15], expressed as follows:

$$L_{L1}\left(G\right)=E_{x,y,z}\left[{∥x-G(z,y)∥}_1\right].$$

(4)

Therefore, in this paper, we apply the objective function as follows:

$$Loss=\underset{G}{min}\underset{D}{max}{L}_{cGAN}(D,G)+\lambda ·L_{L1}\left(G\right),$$

(5)

where $\lambda$ is a parameter to limit the difference between the output and ground truth.

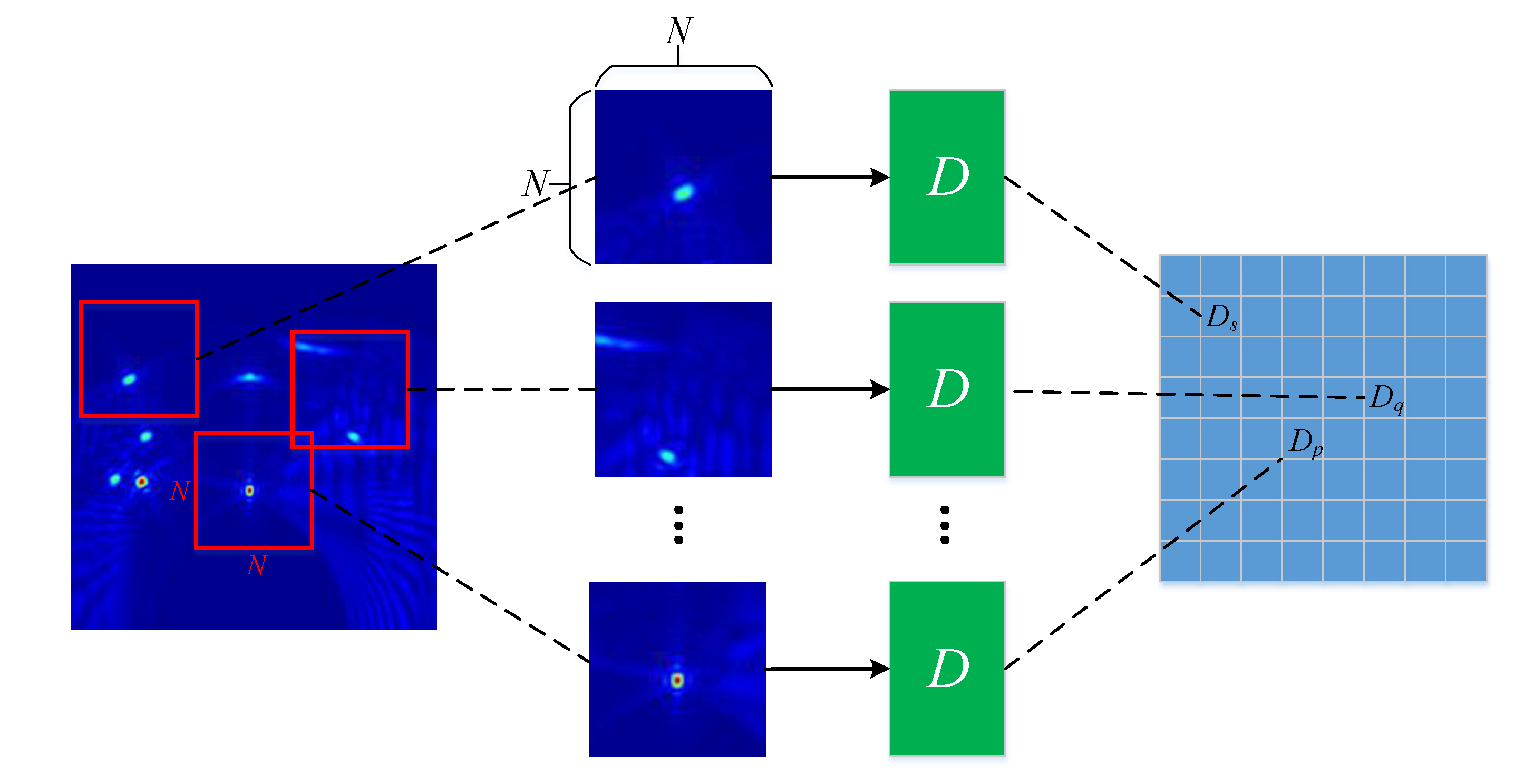
4. Network Architecture

In this section, the structures of generator G and discriminator D are described in detail. In this paper, G makes use of the type of U-net [16] and D adopts the discriminator of PatchGAN [17].

4.1. Generator G

In the original GAN generator [13,18], they mainly adopt a decoder structure to map a vector to an image. Conditional GAN [19,20] almost continues this tradition by an encoder-decoder structure [21], as shown in Figure 3a, which has two drawbacks of information loss and a high training complexity because all information flows through the whole network. However, in the radar image, there is some shared information between the input and output, such as the edges and positions of target images. In order to solve information sharing, in this paper, a skip connection is adopted to enable some information to bypass the middle layer and its specific structure is U-net network. The specific method is to connect the i layer with the $n-i+1$ layer, as shown in Figure 3b.

4.2. Discriminator D

With respect to the applied objective function in Equation (5), $L1$ loss concerns the global information of the input radar image to generate the mean of all possible images. If the effect of $L_{cGAN}(D,G)$ is ignored, the output image is blurred [15]. This means that $L1$ loss determines the low-frequency information of the output image. For this reason, $L_{cGAN}(D,G)$ only needs to generate high-frequency information. In order to force discriminator D to pay more attention to high-frequency information, a superior way is to focus on the locality of the image and to narrow the receptive field. This type of discriminator D is a PatchGAN discriminator [17], which is used to discriminate whether each $N\times N$ block is real or fake. Let D convolve across the entire image to obtain all output values and average them as the final output. The structure of a PatchGAN discriminator is shown in Figure 4.

4.3. Detailed Architectures of G and D

Based on the aforementioned description, generator G adopts the U-net network and discriminator D adopts the full convolution network with a receptive field of $70\times 70$. For simplification, $CB{R}_k$ is used to represent a Convolution–BatchNorm–ReLU layer with k filters, and $CBD{R}_k$ denotes a Convolution–BatchNorm–Dropout–ReLU layer with k filters and a dropout rate of $0.5$. All convolutional layers adopt a filter with a size of $4\times 4$ and a stride of 2. ReLUs are leaky with a slope of $0.2$. In this paper, the detailed architectures of G and D are used as follows.

• Generator architecture
  encoder: $CB{R}_{64}-CB{R}_{128}-CB{R}_{256}-CB{R}_{512}-CB{R}_{512}-CB{R}_{512}-CB{R}_{512}-CB{R}_{512}$
  decoder: $CBD{R}_{512}-CBD{R}_{1024}-CBD{R}_{1024}-CB{R}_{1024}-CB{R}_{1024}-CB{R}_{512}-CB{R}_{256}-CB{R}_{128}-CB{R}_3\left(tanh\right)$
• Discriminator architecture
  $CB{R}_{64}-CB{R}_{128}-CB{R}_{256}-CB{R}_{512}(stride:1)-CB{R}_1(stride:1)\left(sigmoid\right)$

stride: 1 indicates the stride in this layer is 1. tanh and sigmoid denote the activation functions using tanh or sigmoid in this layer, and the others adopt default parameters.

5. Simulation and Discussion

5.1. Data Preparation

Two groups of data are generated with MATLAB to verify the potential of the method, as shown in Figure 1. A synthesized array with 31 single-channel radars monitors an enclosed room. The transmitting signal is a stepped-frequency continuous-wave signal with a carrier frequency of 1.5 GHz and a bandwidth of 1 GHz. The synthesized array is equidistantly placed with a spacing of 0.1 m. The lengths of the back wall and the side walls are both a random number from 5 to 7 m, namely the scenes are changeable. For simplification, the front wall is removed to avoid a penetration effect. The reflection and transmission coefficients $T_{qn}$ and $T_{An}$ are set to 0.5. All point targets are set at random locations inside the enclosed room. Based on Equation (1), echoes with first-order multipaths are obtained to form the input image of generator G. Echoes without first-order multipaths are obtained to form the ground-truth image of discriminator D. Specifically, a back-projection algorithm is used to form these images. The size of the input images and the ground-truth images is set to $256\times 256$.

• Dataset 1
  The number of targets is set to a random number ranging from one to four; 1000 samples and 100 samples of data are respectively used as a training set and a validation set.
• Dataset 2
  The number of targets is increased to a random number ranging from ten to twenty; 2000 samples and 200 samples of data are respectively used as a training set and a validation set.

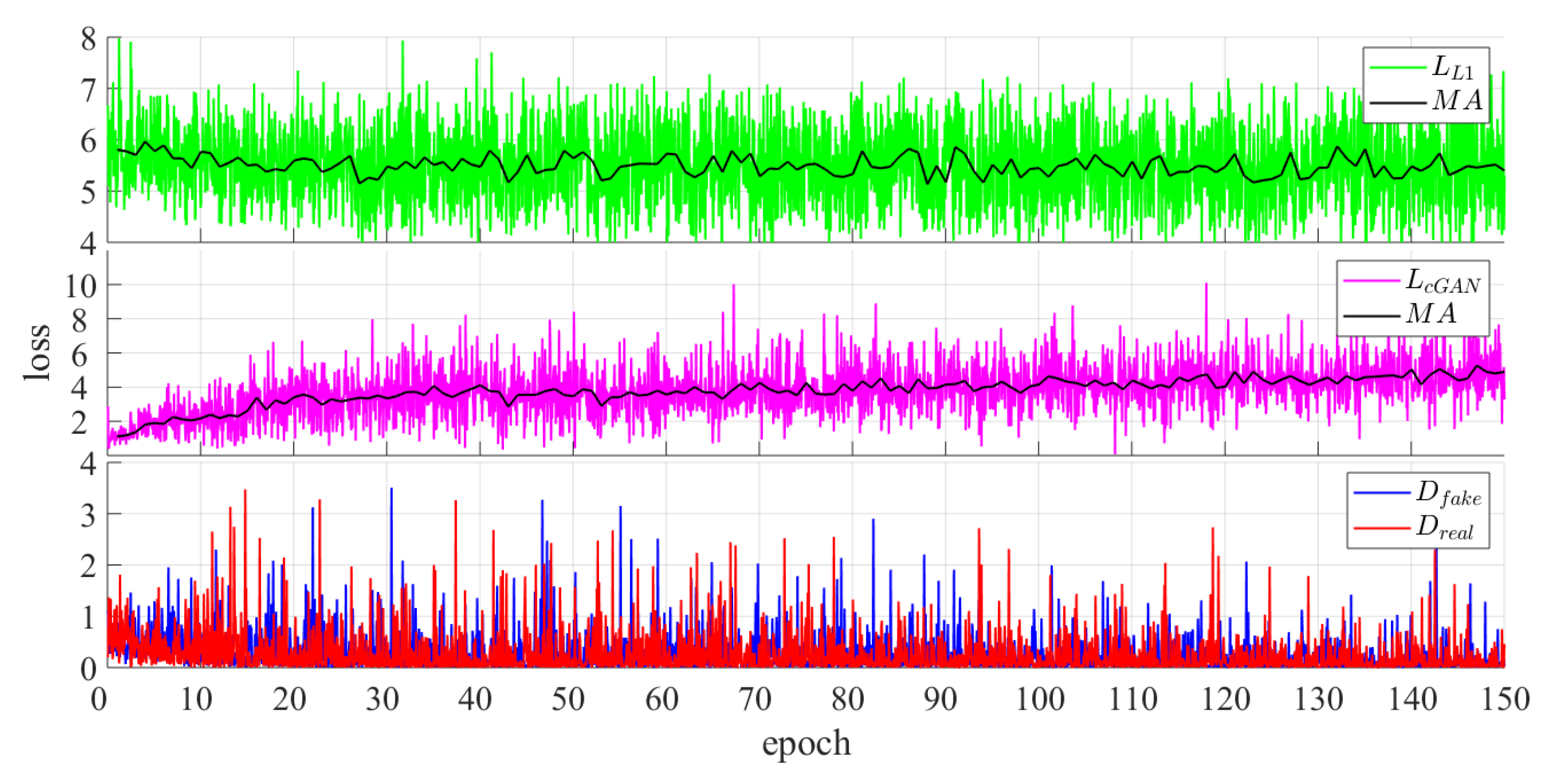
5.2. Training Details

For the convenience of practical training, minimizing $log(1-D(G(z,y),y\left)\right)$ in objective function Equation (5) is replaced by maximizing $logD\left(G\right(z,y),y)$. Minibatch SGD (stochastic gradient descent) and the Adam optimizer are adopted with momentum parameters ${\beta }_1=0.5$ and ${\beta }_2=1.00$. The batch size is set to 1. Moreover, $\lambda$ in Equation (5) is set to 100. All training is run on a single GeForce GTX1080Ti GPU (with 11 GB memory). The loading process of a G network requires 54.414 MB of memory, and the loading process of a D network requires 2.769 MB of memory. As a result, the training of GAN requires at least 57.183 MB of memory, and the testing of GAN requires at least 54.414 MB. The weights of all filters are initialized from a Gaussian distribution with a mean of 0 and a standard deviation of 0.02. In the training of Dataset 1, 50 epochs are trained and each epoch consumes an average of 144 s. In the training of Dataset 2, 150 epochs were trained and each epoch consumes an average of 298 s. The learning rate of the first 100 epochs is 0.0002, and the learning rate of the last 50 epochs is reduced by 0.000002 each time.

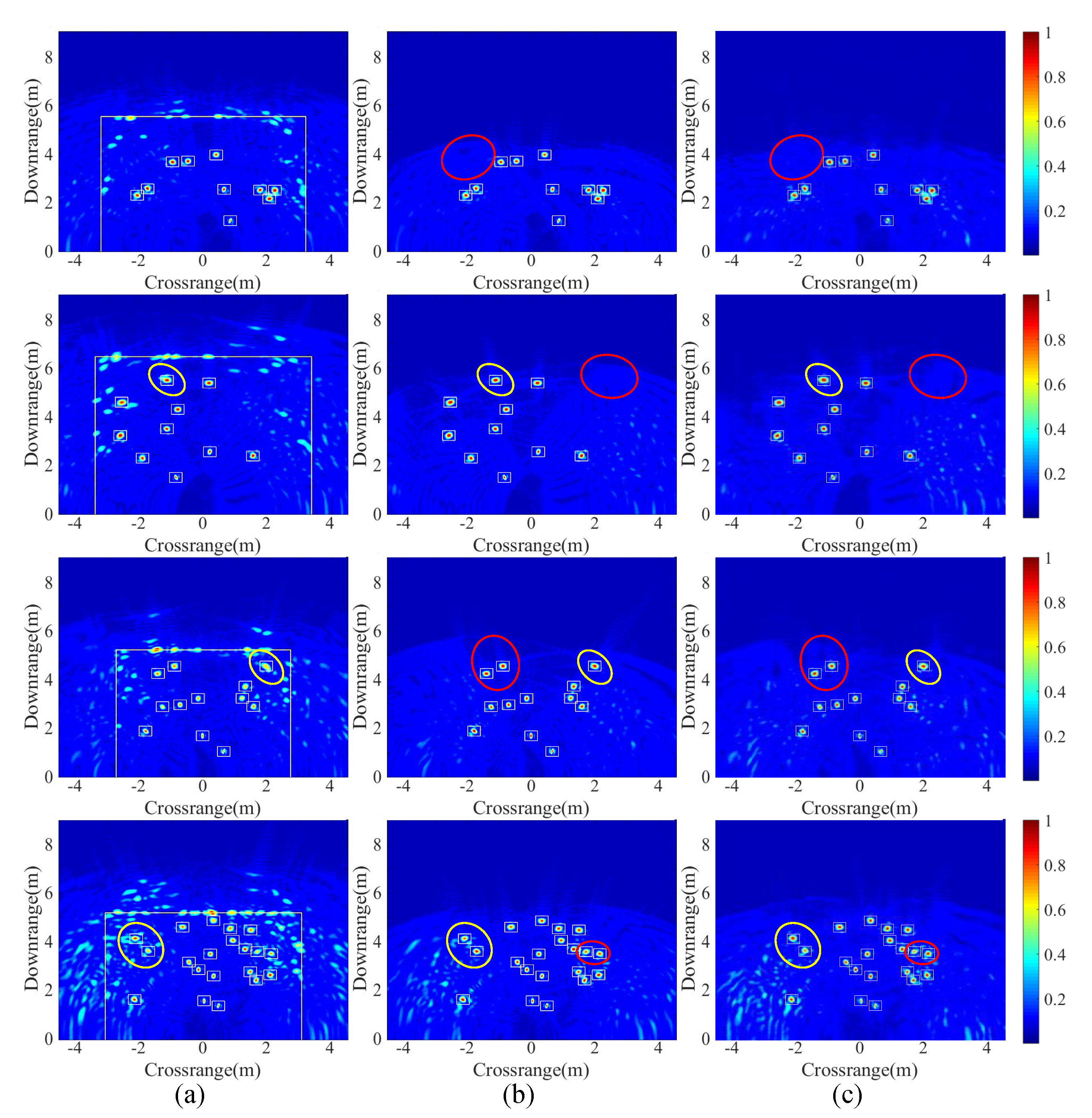
5.3. Result Analysis

After 50 epochs of training of Dataset 1, generator G could correctly eliminate the multipath ghosts. The training-loss curve is shown in Figure 5. Specifically, the curve of $L_{cGAN}(D,G)$ has an undulating trend, since one of generator G and discriminator D is always in a dominant position during the adversarial process. There is a slight downward trend in the curve of $L_{L_1}\left(G\right)$, which indicates that the similarity between the image generated by G and the ground truth is slightly improved. The initial stage of $D_{real}$ is almost greater than $D_{fake}$, which means that generator D can completely distinguish whether the sample is from G or the ground truth. However, both of them later begin to approach each other, which indicates that generator G can correctly eliminate multipath ghosts so that D hardly distinguishes the radar image from G or ground truth. The performance of GAN changing over the iterations is shown in Figure 6, which indicates that multipath ghosts are gradually suppressed but target images are gradually formed.

The results of generator network G are shown in Figure 7, which indicates that multipath ghosts are correctly eliminated. The differences between the output image and the ground truth image are only the grating lobes and side lobes marked with a red oval which can be learned by continuing training. However, as this paper mainly focuses on multipath-ghost suppression, it can be reasonably considered that training is completed. It is worth noting that marks, axis, and color bars are absent in the training samples.

After 150 epochs of training of Dataset 2, the curve of loss is shown in Figure 8. Compared with Figure 5, the $L_{cGAN}$ has a different (ascent) trend due to the mismatch of evolution speed between G and D in the early stages. In a complex situation with a large number of multipath ghosts, the reason for a mismatch could be summarized into two conflict points. On the one hand, complex multipath ghosts bring convenience to D to identify the radar image from G or ground truth. On the other hand, it makes it difficult for G to eliminate multipath ghosts. The mismatch increases the training time, appearing as the ascent trend of $L_{cGAN}$ in Figure 8. The performance of GAN, varying from the iterations, is shown in Figure 9, which indicates that multipath ghosts are gradually suppressed but target images are gradually formed.

The result of the final training is shown in Figure 10. Although the situation is more complicated, multipath ghosts are still correctly eliminated. It is worth noting that true target images can be preserved even if targets are overlapped with multipath ghosts. For example, the overlapped target images marked with red rectangles in the input images are clearly preserved in the output image.

In addition, the performance of elimination is quantitatively measured, and the results are shown in

Table 1. Accuracy.

	One Error	Two Errors or More
GAN trained by Dataset 1	0.5%	0%
GAN trained by Dataset 2	2.5%	0.5%

. The above two networks are separately tested with 200 new test samples. The rate of one error and two or more errors are separately counted, where an error indicates a residual multipath ghost or a lost target image. The statistical results demonstrate the proposed method can effectively eliminate multipath ghosts.

5.4. Comparison of Different Methods

In this section, the proposed method is compared with the PCF method [11], the subaperture-fusion method [8], and the imaging-dictionary-based method [7]. The results are shown in Figure 11. Specifically, the walls’ locations need to be known in advance by the imaging-dictionary-based method.

Table 2. The averaging computation time of 100 trials for four different multipath suppression methods.

Method	Computation Times
PCF	1.09
Subaperture-fusion	0.62
Imaging-dictionary	1.65
The proposed method	0.65

illustrates the averaging computation time of 100 trials for each multipath-suppression method. The PCF method, subaperture-fusion method, and imaging-dictionary-based method run on Matlab 2017a, while the proposed method runs on Python. All methods adopt a workstation including a Intel 2.60 GHz Core(TM) i7-6700HQ CPU processor (with 8 GB of memory) and a NVIDIA GeForce GTX1080Ti GPU (with 11 GB of memory) with CUDA (compute unified device architecture) acceleration. The comparison results in Table 2 demonstrate that the proposed method and subaperture-fusion method have similar time consumptions that are superior to the PCF and imaging-dictionary-based methods.

As shown in Figure 11b, the PCF method is unable to eliminate well-focused multipath ghosts, marked by red ellipses in the case of synthetic aperture imaging (SAI). In Figure 11c, a part of the multipath ghosts, marked by the red ellipses especially about the back wall, still exist with the subaperture-fusion method, as they appear at the close positions in both subaperture images. Figure 11d demonstrates that the imaging-dictionary-based method has an excellent performance in suppressing multipath ghosts while it needs the prior walls’ locations. In Figure 11b,c, the PCF method and the subaperture-fusion method enlarge the energy differences between the target images, which makes it difficult to identify degraded targets such as target images marked by green ellipses with a low SMCR that is a ratio between the peak of the target image and its multipath ghost [10]. As a comparison, as shown in Figure 11e, the proposed method achieves an excellent multipath suppression without walls’ locations. Moreover, the proposed method prevents the difference of target images from enlarging, which is beneficial to identifying all targets.

To strengthen the point of the proposed method being well-suited for the application, the advantages and disadvantages of each method are summarized in

Table 3. The advantages and disadvantages of different methods.

Method	Advantages	Disadvantages
PCF	1. Does not require prior walls’ locations. 2. Does not require complicated tuning parameters.	1. Poor multipath suppression for SAI. 2. A part of target images are degraded with low SMCR.
Subaperture-fusion	Does not require prior walls’ locations.	1. Poor suppression for the multipath ghosts of back wall. 2. A part of target images are degraded with low SMCR. 3. Requires complicated tuning parameters.
Imaging-dictionary	1. Excellent multipath suppression. 2. Does not require complicated tuning parameters.	Requires prior walls’ locations.
The proposed method	1. Excellent multipath suppression. 2. Does not require prior walls’ locations. 3. No target images with degradation. 4. Does not require complicated tuning parameters.	Requires a dataset with labels.

. Furthermore, the SMCR is applied to quantitatively evaluate the performances of multipath-ghost suppression for different methods. Specifically, as shown in Figure 12, the scene with two targets in Figure 11 is chosen as a sample. As shown in

Table 4. Ratios between the peaks of the target images and their multipath ghosts (dB).

Method	${\mathit{P}}_1\mathit{VS}.{\mathit{P}}_{1\_1}$	${\mathit{P}}_1\mathit{VS}.{\mathit{P}}_{1\_2}$	${\mathit{P}}_1\mathit{VS}.{\mathit{P}}_{1\_3}$	${\mathit{P}}_2\mathit{VS}.{\mathit{P}}_{2\_1}$	${\mathit{P}}_2\mathit{VS}.{\mathit{P}}_{2\_2}$	${\mathit{P}}_2\mathit{VS}.{\mathit{P}}_{2\_3}$
Original image	5.89	5.90	8.48	6.37	5.74	6.00
PCF	13.09	6.99	35.11	10.47	12.81	12.53
Subaperture-fusion	17.41	17.15	24.93	20.89	17.41	18.42
Imaging-dictionary	103.56	119.37	172.02	112.93	75.06	123.06
The proposed method	32.45	54.49	56.49	43.49	31.27	27.06

, the proposed method has a much lower SMCR than the PCF method (by about 20–50 dB) and the subaperture-fusion method (by about 15–35 dB). The imaging-dictionary-based method also has the highest SMCR. As a result, both the proposed method and the imaging-dictionary-based method have an excellent multipath suppression while the imaging-dictionary-based method needs prior walls’ locations.

It is worth noting that the side/grating lobes are preserved in ground-truth images and output images. On the one hand, GAN is classified as a structured learning network that is applied to construct spatial structure mapping from input images to output images. The preservation of side/grating lobes is equivalent to preserving the spatial structure, which promotes the elimination of multipath ghosts and the preservation of target images. On the other hand, side/grating lobes in output images could be eliminated by threshold detection thanks to a high signal-to-noise ratio. In other words, side/grating lobes are effective information for multipath suppression and have no effect on the target-detection performance.

6. Conclusions

A GAN-based multipath-ghost suppression algorithm is presented in this paper. Based on Matlab simulation datasets, the generator of GAN is trained to be able to efficiently reduce multipath ghosts, along with fighting with the discriminator. It is demonstrated that GAN has the potential for multipath elimination in TWRI. In a future work, we will research the modification of GAN and use complicated simulation datasets (such as changeable radar parameters) and practical measured datasets to outline the potential of GAN.