High-Density EEG Signal Processing Based on Active-Source Reconstruction for Brain Network Analysis in Alzheimer’s Disease
Abstract
:1. Introduction
2. Materials and Methods
- EEG data were collected from three groups of patients (CNT, MCI, and AD) by a high-density acquisition system. Starting from that, three different electrodes configurations were considered. The signals preprocessing was performed by means of MATLAB (see Section 2.1);
- the preprocessed EEGs were used as input signals for the LORETA-KEY software. In order to quantify the functional connectivity, the Lagged Linear Connectivity (LLC) matrix was computed for each couple of regions of interest (ROIs), for a given frequency range (see Section 2.2);
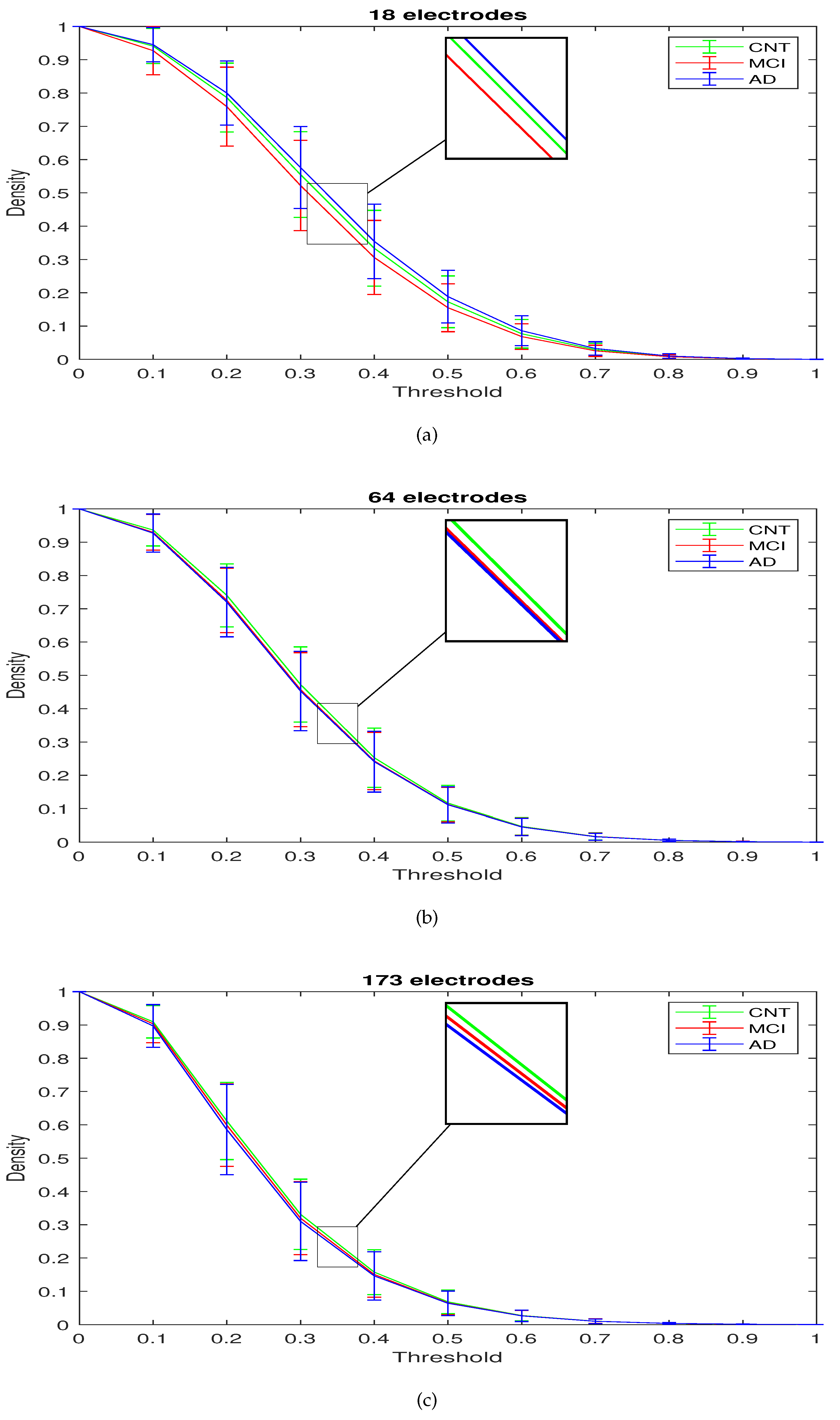
- starting from the LLC, the small-world properties of the brain networks were measured by three parameters: , , and D, estimated through a MATLAB toolbox (see Section 2.3).
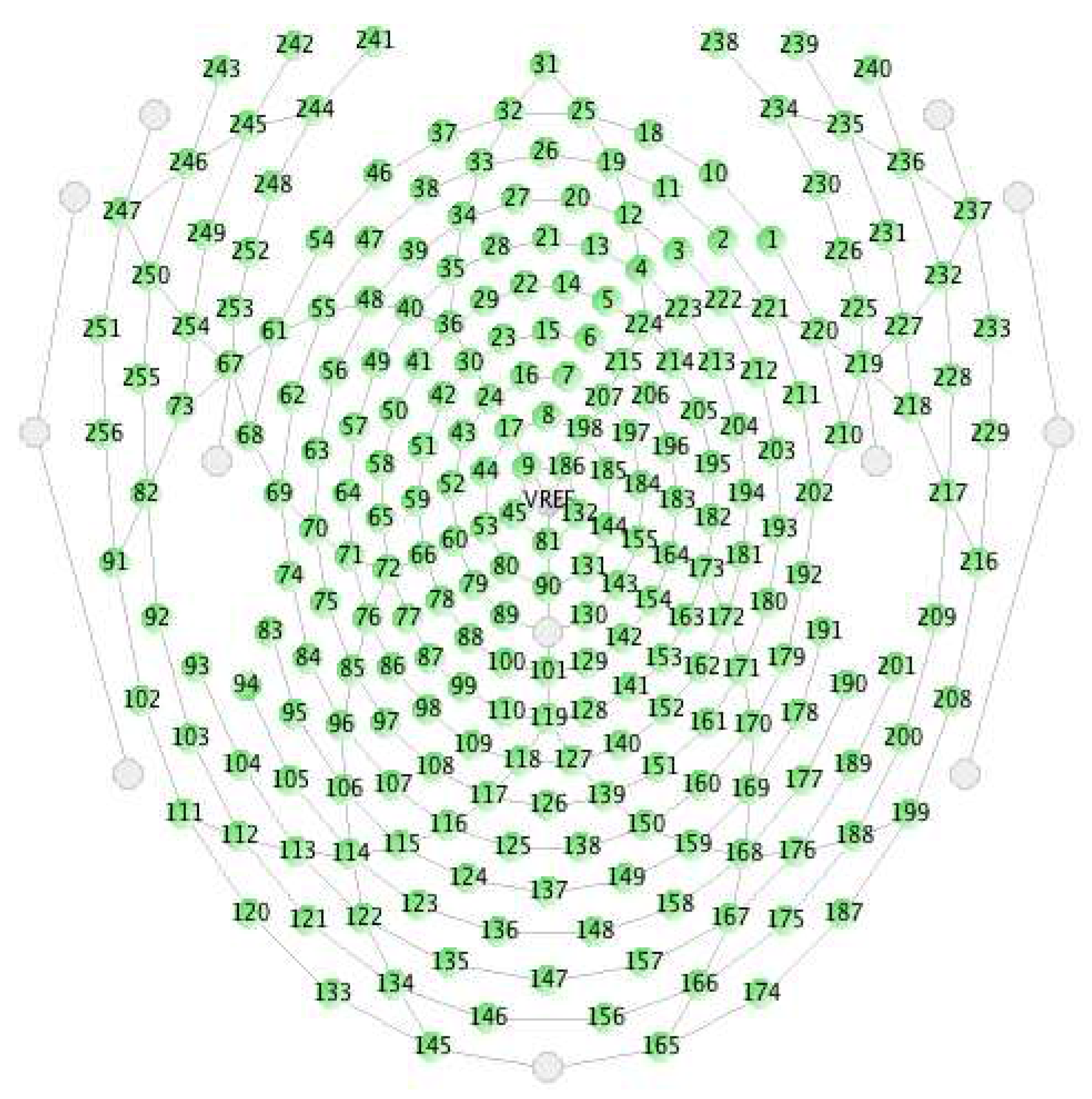
2.1. Data Acquisition System and Preprocessing
2.2. eLORETA and Lagged Linear Connectivity
2.3. Complex Network Analysis
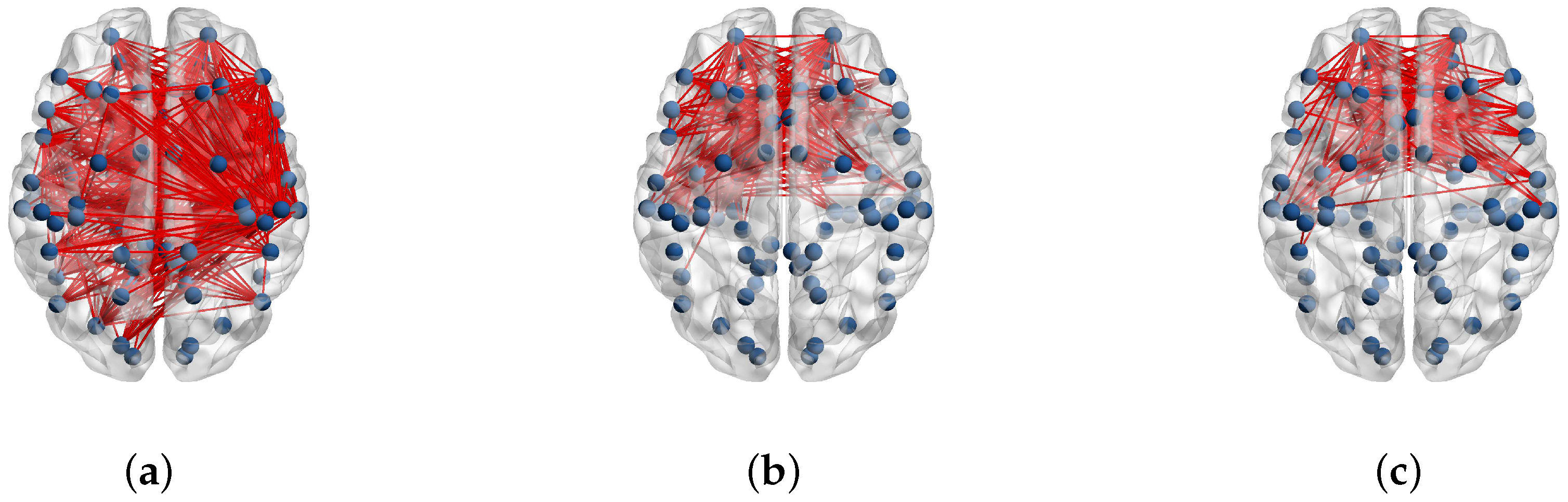
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Labate, D.; La Foresta, F.; Palamara, I.; Morabito, G.; Bramanti, A.; Zhang, Z.; Morabito, F.C. EEG complexity modifications and altered compressibility in mild cognitive impairment and Alzheimer’s disease. In Recent Advances of Neural Network Models and Applications; Springer: Berlin/Heidelberg, Germany, 2014; pp. 163–173. [Google Scholar]
- Morabito, F.C.; Campolo, M.; Ieracitano, C.; Ebadi, J.M.; Bonanno, L.; Bramanti, A.; Desalvo, S.; Mammone, N.; Bramanti, P. Deep convolutional neural networks for classification of mild cognitive impaired and Alzheimer’s disease patients from scalp EEG recordings. In Proceedings of the 2016 IEEE 2nd International Forum on Research and Technologies for Society and Industry Leveraging a Better Tomorrow (RTSI), Bologna, Italy, 7–9 September 2016; pp. 1–6. [Google Scholar]
- Mammone, N.; De Salvo, S.; Bonanno, L.; Ieracitano, C.; Marino, S.; Marra, A.; Bramanti, A.; Morabito, F.C. Brain Network Analysis of Compressive Sensed High-Density EEG Signals in AD and MCI Subjects. IEEE Trans. Ind. Inform. 2019, 15, 527–536. [Google Scholar] [CrossRef]
- Wang, G.; Ren, D. Effect of brain-to-skull conductivity ratio on EEG source localization accuracy. BioMed Res. Int. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Spitzer, A.R.; Cohen, L.G.; Fabrikant, J.; Hallett, M. A method for determining optimal interelectrode spacing for cerebral topographic mapping. Electroencephalogr. Clin. Neurophysiol. 1989, 72, 355–361. [Google Scholar] [CrossRef]
- Tucker, D.M. Spatial sampling of head electrical fields: The geodesic sensor net. Electroencephalogr. Clin. Neurophysiol. 1993, 87, 154–163. [Google Scholar] [CrossRef]
- Freeman, W.J.; Holmes, M.D.; Burke, B.C.; Vanhatalo, S. Spatial spectra of scalp EEG and EMG from awake humans. Clin. Neurophysiol. 2003, 114, 1053–1068. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, R.; Tucker, D.M.; Murias, M. Estimating the spatial Nyquist of the human EEG. Behav. Res. Methods Instrum. Comput. 1998, 30, 8–19. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Worrell, G.; Yang, L.; Wilke, C.; He, B. Interictal spike analysis of high-density EEG in patients with partial epilepsy. Clin. Neurophysiol. 2011, 122, 1098–1105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sohrabpour, A.; Lu, Y.; Kankirawatana, P.; Blount, J.; Kim, H.; He, B. Effect of EEG electrode number on epileptic source localization in pediatric patients. Clin. Neurophysiol. 2015, 126, 472–480. [Google Scholar] [CrossRef]
- Song, J.; Davey, C.; Poulsen, C.; Luu, P.; Turovets, S.; Anderson, E.; Li, K.; Tucker, D. EEG source localization: Sensor density and head surface coverage. J. Neurosci. Methods 2015, 256, 9–21. [Google Scholar] [CrossRef] [Green Version]
- Staljanssens, W.; Strobbe, G.; Van Holen, R.; Birot, G.; Gschwind, M.; Seeck, M.; Vandenberghe, S.; Vulliémoz, S.; van Mierlo, P. Seizure onset zone localization from ictal high-density EEG in refractory focal epilepsy. Brain Topogr. 2017, 30, 257–271. [Google Scholar] [CrossRef]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. Neuroimage 2010, 52, 1059–1069. [Google Scholar] [CrossRef] [PubMed]
- Coito, A.; Genetti, M.; Pittau, F.; Iannotti, G.R.; Thomschewski, A.; Höller, Y.; Trinka, E.; Wiest, R.; Seeck, M.; Michel, C.M.; et al. Altered directed functional connectivity in temporal lobe epilepsy in the absence of interictal spikes: A high density EEG study. Epilepsia 2016, 57, 402–411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Astolfi, L.; De Vico Fallani, F.; Cincotti, F.; Mattia, D.; Marciani, M.; Bufalari, S.; Salinari, S.; Colosimo, A.; Ding, L.; Edgar, J.; et al. Imaging functional brain connectivity patterns from high-resolution EEG and fMRI via graph theory. Psychophysiology 2007, 44, 880–893. [Google Scholar] [CrossRef] [PubMed]
- Bassett, D.S.; Bullmore, E. Small-world brain networks. Neuroscientist 2006, 12, 512–523. [Google Scholar] [CrossRef] [PubMed]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186. [Google Scholar] [CrossRef]
- Jeong, J. EEG dynamics in patients with Alzheimer’s disease. Clin. Neurophysiol. 2004, 115, 1490–1505. [Google Scholar] [CrossRef]
- König, T.; Prichep, L.; Dierks, T.; Hubl, D.; Wahlund, L.; John, E.; Jelic, V. Decreased EEG synchronization in Alzheimer’s disease and mild cognitive impairment. Neurobiol. Aging 2005, 26, 165–171. [Google Scholar] [CrossRef]
- Sankari, Z.; Adeli, H.; Adeli, A. Intrahemispheric, interhemispheric, and distal EEG coherence in Alzheimer’s disease. Clin. Neurophysiol. 2011, 122, 897–906. [Google Scholar] [CrossRef]
- Stam, C.J.; Jones, B.; Nolte, G.; Breakspear, M.; Scheltens, P. Small-world networks and functional connectivity in Alzheimer’s disease. Cereb. Cortex 2006, 17, 92–99. [Google Scholar] [CrossRef]
- He, Y.; Chen, Z.; Gong, G.; Evans, A. Neuronal networks in Alzheimer’s disease. Neuroscientist 2009, 15, 333–350. [Google Scholar]
- Wang, R.; Wang, J.; Yu, H.; Wei, X.; Yang, C.; Deng, B. Decreased coherence and functional connectivity of electroencephalograph in Alzheimer’s disease. Chaos Interdiscip. J. Nonlinear Sci. 2014, 24, 033136. [Google Scholar] [CrossRef] [PubMed]
- Mammone, N.; Ieracitano, C.; Adeli, H.; Bramanti, A.; Morabito, F.C. Permutation Jaccard distance-based hierarchical clustering to estimate EEG network density modifications in MCI subjects. IEEE Trans. Neural Networks Learn. Syst. 2018, 29, 5122–5135. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, M.; Kastner, J.; Wagner, M.; Hawes, S.; Ebersole, J.S. A standardized boundary element method volume conductor model. Clin. Neurophysiol. 2002, 113, 702–712. [Google Scholar] [CrossRef] [Green Version]
- Pascual-Marqui, R.D. Discrete, 3D distributed, linear imaging methods of electric neuronal activity. Part 1: Exact, zero error localization. arXiv 2007, arXiv:0710.3341. [Google Scholar]
- Rossini, P.; Del Percio, C.; Pasqualetti, P.; Cassetta, E.; Binetti, G.; Dal Forno, G.; Ferreri, F.; Frisoni, G.; Chiovenda, P.; Miniussi, C.; et al. Conversion from mild cognitive impairment to Alzheimer’s disease is predicted by sources and coherence of brain electroencephalography rhythms. Neuroscience 2006, 143, 793–803. [Google Scholar] [CrossRef] [PubMed]
- Gianotti, L.R.; Künig, G.; Lehmann, D.; Faber, P.L.; Pascual-Marqui, R.D.; Kochi, K.; Schreiter-Gasser, U. Correlation between disease severity and brain electric LORETA tomography in Alzheimer’s disease. Clin. Neurophysiol. 2007, 118, 186–196. [Google Scholar] [CrossRef] [PubMed]
- Babiloni, C.; Del Percio, C.; Lizio, R.; Noce, G.; Cordone, S.; Lopez, S.; Soricelli, A.; Ferri, R.; Pascarelli, M.T.; Nobili, F.; et al. Abnormalities of cortical neural synchronization mechanisms in subjects with mild cognitive impairment due to Alzheimer’s and Parkinson’s Diseases: An EEG study. J. Alzheimer’s Dis. 2017, 59, 339–358. [Google Scholar] [CrossRef] [PubMed]
- Hata, M.; Kazui, H.; Tanaka, T.; Ishii, R.; Canuet, L.; Pascual-Marqui, R.D.; Aoki, Y.; Ikeda, S.; Kanemoto, H.; Yoshiyama, K.; et al. Functional connectivity assessed by resting state EEG correlates with cognitive decline of Alzheimer’s disease—An eLORETA study. Clin. Neurophysiol. 2016, 127, 1269–1278. [Google Scholar] [CrossRef]
- Babiloni, C.; Del Percio, C.; Lizio, R.; Noce, G.; Lopez, S.; Soricelli, A.; Ferri, R.; Pascarelli, M.T.; Catania, V.; Nobili, F.; et al. Functional cortical source connectivity of resting state electroencephalographic alpha rhythms shows similar abnormalities in patients with mild cognitive impairment due to Alzheimer’s and Parkinson’s diseases. Clin. Neurophysiol. 2018, 129, 766–782. [Google Scholar] [CrossRef]
- Geodesics, E. Geodesic Sensor Net Technical Manual; Electrical Geodesics: Eugene, OR, USA, 2007. [Google Scholar]
- Luu, P.; Ferree, T. Determination of the HydroCel Geodesic Sensor Nets’ Average Electrode Positions and Their 10–10 International Equivalents; Technical Note; Electrical Geodesics, Inc.: Eugene, OR, USA, 2005. [Google Scholar]
- Mammone, N.; Morabito, F.C. Independent component analysis and high-order statistics for automatic artifact rejection. In Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; Volume 4, pp. 2447–2452. [Google Scholar]
- Pascual-Marqui, R.D. Instantaneous and lagged measurements of linear and nonlinear dependence between groups of multivariate time series: Frequency decomposition. arXiv 2007, arXiv:0711.1455. [Google Scholar]
- Pascual-Marqui, R.D.; Lehmann, D.; Koukkou, M.; Kochi, K.; Anderer, P.; Saletu, B.; Tanaka, H.; Hirata, K.; John, E.R.; Prichep, L.; et al. Assessing interactions in the brain with exact low-resolution electromagnetic tomography. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 3768–3784. [Google Scholar] [CrossRef] [PubMed]
- Nunez, P.L.; Srinivasan, R.; Westdorp, A.F.; Wijesinghe, R.S.; Tucker, D.M.; Silberstein, R.B.; Cadusch, P.J. EEG coherency: I: Statistics, reference electrode, volume conduction, Laplacians, cortical imaging, and interpretation at multiple scales. Electroencephalogr. Clin. Neurophysiol. 1997, 103, 499–515. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1998, 393, 440. [Google Scholar] [CrossRef] [PubMed]
- Breslow, N. A generalized Kruskal-Wallis test for comparing K samples subject to unequal patterns of censorship. Biometrika 1970, 57, 579–594. [Google Scholar] [CrossRef]
- Hochberg, J.; TAMHANE, A.C. Multiple Comparison Procedures; Technical Report; John Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- McCarthy, P.; Benuskova, L.; Franz, E.A. The age-related posterior-anterior shift as revealed by voxelwise analysis of functional brain networks. Front. Aging Neurosci. 2014, 6, 301. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.; Gouw, A.A.; Hillebrand, A.; Tijms, B.M.; Stam, C.J.; van Straaten, E.C.; Pijnenburg, Y.A. Different functional connectivity and network topology in behavioral variant of frontotemporal dementia and Alzheimer’s disease: An EEG study. Neurobiol. Aging 2016, 42, 150–162. [Google Scholar] [CrossRef] [PubMed]
- Mammone, N.; Morabito, F.C.; Principe, J.C. Visualization of the short term maximum lyapunov exponent topography in the epileptic brain. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology SocietyE, New York, NY, USA, 30 August–3 September 2006; pp. 4257–4260. [Google Scholar]
- Mammone, N.; Principe, J.C.; Morabito, F.C.; Shiau, D.S.; Sackellares, J.C. Visualization and modelling of STLmax topographic brain activity maps. J. Neurosci. Methods 2010, 189, 281–294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mammone, N.; Inuso, G.; La Foresta, F.; Versaci, M.; Morabito, F.C. Clustering of entropy topography in epileptic electroencephalography. Neural Comput. Appl. 2011, 20, 825–833. [Google Scholar] [CrossRef]
- Mammone, N.; De Salvo, S.; Ieracitano, C.; Marino, S.; Cartella, E.; Bramanti, A.; Giorgianni, R.; Morabito, F. Compressibility of High-Density EEG Signals in Stroke Patients. Sensors 2018, 18, 4107. [Google Scholar] [CrossRef]
- Bastos, A.M.; Schoffelen, J.M. A tutorial review of functional connectivity analysis methods and their interpretational pitfalls. Front. Syst. Neurosci. 2016, 9, 175. [Google Scholar] [CrossRef]
- Rosales, F.; Garcia-Dopico, A.; Bajo, R.; Nevado, A. An efficient implementation of the synchronization likelihood algorithm for functional connectivity. Neuroinformatics 2015, 13, 245–258. [Google Scholar] [CrossRef] [PubMed]
- Lombardi, A.; Tangaro, S.; Bellotti, R.; Bertolino, A.; Blasi, G.; Pergola, G.; Taurisano, P.; Guaragnella, C. A novel synchronization-based approach for functional connectivity analysis. Complexity 2017, 2017. [Google Scholar] [CrossRef]
- Tzimourta, K.D.; Giannakeas, N.; Tzallas, A.T.; Astrakas, L.G.; Afrantou, T.; Ioannidis, P.; Grigoriadis, N.; Angelidis, P.; Tsalikakis, D.G.; Tsipouras, M.G. EEG Window Length Evaluation for the Detection of Alzheimer’s Disease over Different Brain Regions. Brain Sci. 2019, 9, 81. [Google Scholar] [CrossRef] [PubMed]
- Miniussi, C.; Thut, G. Combining TMS and EEG offers new prospects in cognitive neuroscience. Brain Topogr. 2010, 22, 249. [Google Scholar] [CrossRef] [PubMed]
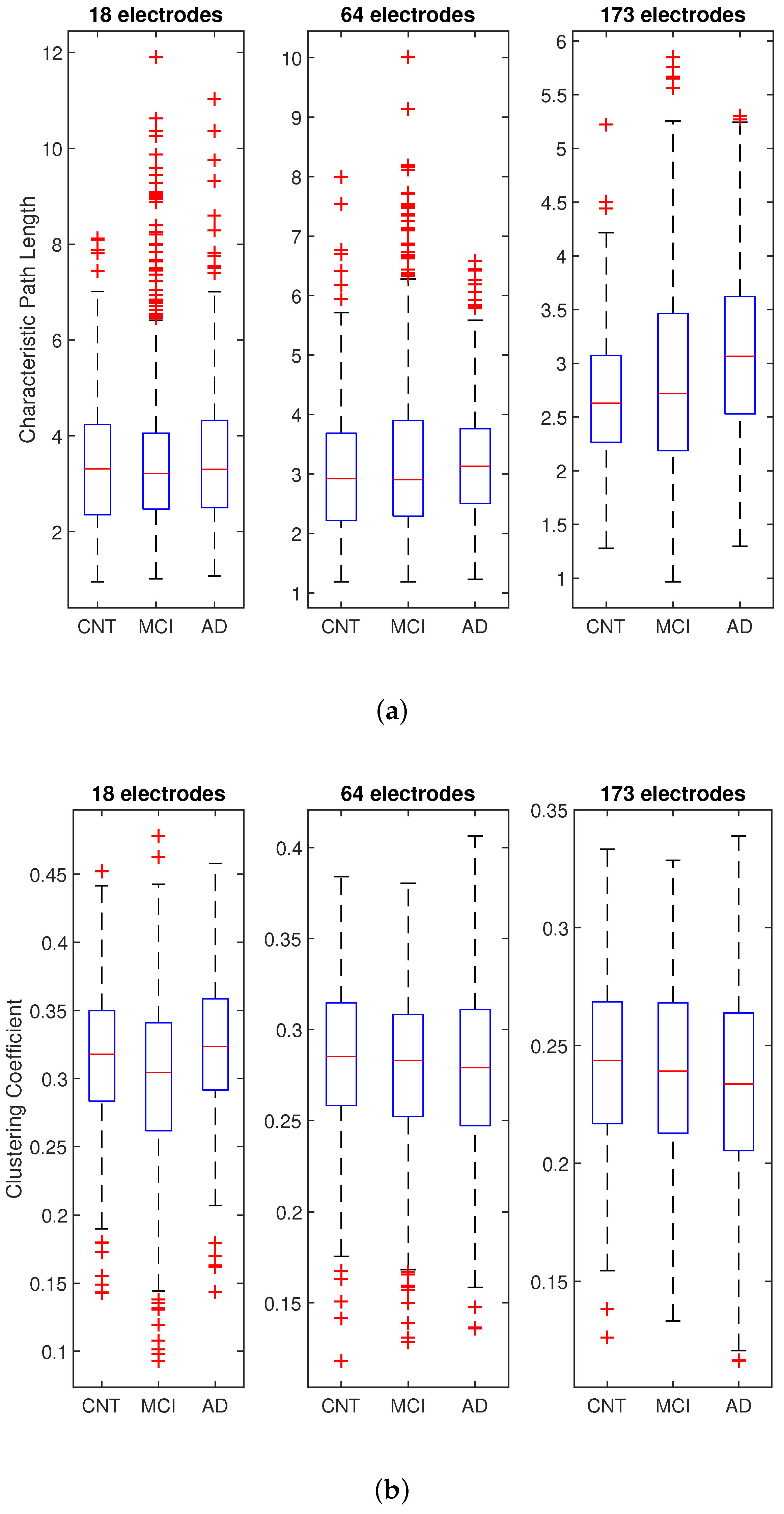


| Characteristic Path Length p-Value | Clustering Coefficient p-Value | Connection Density p-Value | ||||||
|---|---|---|---|---|---|---|---|---|
| 18 | 64 | 173 | 18 | 64 | 173 | 18 | 64 | 173 |
| 0.4345 | 0.0130 | 1.38 × 10 | 6.24 × 10 | 0.0282 | 0.0481 | 0.8780 | 0.9870 | 0.9965 |
| Subjects | Characteristic Path Length p-Value | Clustering Coefficient p-Value | ||||
|---|---|---|---|---|---|---|
| 18 | 64 | 173 | 18 | 64 | 173 | |
| CNT-MCI | 0.9974 | 0.1835 | 0.0101 | 2.8 × 10 | 0.0613 | 0.3000 |
| MCI-AD | 0.4507 | 0.2054 | 8.6 × 10 | 3.0 × 10 | 0.7935 | 0.3353 |
| CNT-AD | 0.5132 | 0.0091 | 9.5 × 10 | 0.0918 | 0.0377 | 0.0368 |
| THRESHOLD | DENSITY | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 18 | 64 | 173 | |||||||
| CNT | MCI | AD | CNT | MCI | AD | CNT | MCI | AD | |
| 0.3 | 0.5549 | 0.5221 | 0.5761 | 0.4725 | 0.4572 | 0.4530 | 0.3312 | 0.3196 | 0.3101 |
| 0.5 | 0.1729 | 0.1551 | 0.1885 | 0.1164 | 0.1123 | 0.1114 | 0.0682 | 0.0651 | 0.0639 |
| 0.7 | 0.0290 | 0.0256 | 0.0327 | 0.0168 | 0.0165 | 0.0161 | 0.0101 | 0.0100 | 0.0099 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
La Foresta, F.; Morabito, F.C.; Marino, S.; Dattola, S. High-Density EEG Signal Processing Based on Active-Source Reconstruction for Brain Network Analysis in Alzheimer’s Disease. Electronics 2019, 8, 1031. https://doi.org/10.3390/electronics8091031
La Foresta F, Morabito FC, Marino S, Dattola S. High-Density EEG Signal Processing Based on Active-Source Reconstruction for Brain Network Analysis in Alzheimer’s Disease. Electronics. 2019; 8(9):1031. https://doi.org/10.3390/electronics8091031
Chicago/Turabian StyleLa Foresta, Fabio, Francesco Carlo Morabito, Silvia Marino, and Serena Dattola. 2019. "High-Density EEG Signal Processing Based on Active-Source Reconstruction for Brain Network Analysis in Alzheimer’s Disease" Electronics 8, no. 9: 1031. https://doi.org/10.3390/electronics8091031
APA StyleLa Foresta, F., Morabito, F. C., Marino, S., & Dattola, S. (2019). High-Density EEG Signal Processing Based on Active-Source Reconstruction for Brain Network Analysis in Alzheimer’s Disease. Electronics, 8(9), 1031. https://doi.org/10.3390/electronics8091031








