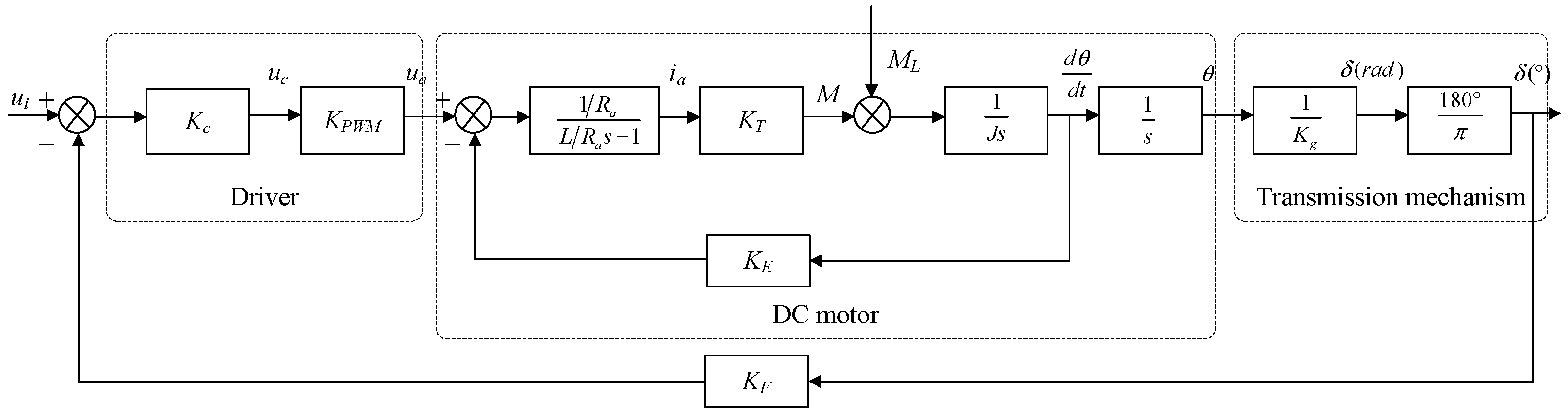
3.2. PID Control System
PID control is a typical negative feedback control method. The input value of the system is subtracted from the output value of the system to obtain the deviation of the system’s output, and then proportional, integral, and derivative control of the output deviation is performed [
13].
In the continuous time domain, the PID control algorithm can be expressed as:
In the above formula, Kp is the proportion coefficient, Ti is the integral time constant, and Td is the differential time constant.
Because the steering gear drive system has a very large overshoot, this article aims to reduce the overshoot of the system. According to the PID parameter setting principle [
14]: the function of the proportional coefficient
Kp is to speed up the response speed of the system and improve the adjustment accuracy of the system, the integral time constant
Ti is to eliminate the steady-state error of the system. The function of the differential time constant
Td is to improve the dynamic performance of the system.
The discrete form of the PID formula can be further derived from Equation (13) as follows:
In the above formula, Kp is the proportion coefficient, Ki is the integral coefficient, and Kd is the differential coefficient.
It is finally determined that when
Kp is within the range of [0.1, 1],
Ki is within the range of [10, 30], and
Kd is within the range of [0.01, 0.03], the system overshoot is less than 15%. When
Kp = 0.1,
Ki = 30, and
Kd = 0.03, PID control of the system uses the unit step signal as the input signal of the model. The simulation result of PID control is shown in
Figure 5, and the simulation data of PID control are shown in
Table 3.
After the preliminary adjustment of PID control, the simulation results show that the system became more stable, accurately reached the predetermined position, and ensured the accuracy of the adjustment by using the original control and PID control. The rise time and the adjustment time of PID control increased slightly, but the overshoot was reduced by 34.25%. The simulation results show that the application of traditional PID control technology increases the rise time and adjustment time of the joint movement but greatly reduces the overshoot and enhances the stability of motion.
3.3. Fuzzy PID Control System
For control objects with large hysteresis, large inertia, and complex signal tracking, PID control is also very limited, but the fuzzy PID control technology can be used to improve PID control defects [
15].
The fuzzy PID controller is implemented on the basis of the conventional PID controller. Generally,
e(
t) and
de(
t)/
dt are used as the input quantity of fuzzy control, and the Δ
Kp, Δ
Ki and Δ
Kd are used as the output quantity of fuzzy control. It is a fuzzy controller with two-input and three-output [
16], as shown in
Figure 6.
The new PID control parameters can be formed by adding the fuzzy parameters in the regular PID parameters:
Use the PID parameters above, Kp = 0.1, Ki = 30, and Kd = 0.03. Add the value of ΔKp, ΔKi and ΔKd of the fuzzy control output to calculate the new PID parameters.
Determine the basic domain of e(t) as [−1,1], the basic domain of de(t)/dt is [−0.014,0.014], the basic domain of ΔKp is [−0.1,0.1], the basic domain of ΔKi is [−20,20], and the basic domain of ΔKd is [−0.02,0.02]. For convenient calculation, we set the fuzzy sets of input and output values as [−2, 2]. The quantization factor of e(t), de(t)/dt, ΔKp, ΔKi and ΔKd respectively, is 2, 0.007, 0.05, 10, and 0.01. Using the e(t) and de(t)/dt as the fuzzy control input, the ΔKp, ΔKi and ΔKd as the fuzzy control output, the fuzzy control of the two inputs and three outputs is performed.
According to actual experience, the values of Δ
Kp, Δ
Ki, and Δ
Kd under different error and rate of error change need to meet the following adjustment principle [
17]:
(1) When the error is large, improve the system’s fast-tracking performance. No matter how much the error varies, it should take a larger value of ΔKp and a smaller value of ΔKd. At the same time, in order to avoid a large overshoot, the integral link should be limited and take a smaller value of ΔKi.
(2) When the error is at a medium size, in order to reduce the overshoot of the system response, the value of ΔKp should be smaller. In order to ensure the response speed of the system, the value of ΔKi and ΔKd should be moderate. The value of ΔKd has a greater impact on the system response.
(3) When the error is small, in order to ensure the system has good steady-state performance, the value of ΔKp and ΔKi should be larger. At the same time, in order to avoid the oscillation of the system near the set value and consider the anti-interference performance of the system, the value of ΔKd can be larger when the rate of error change is small, the value of ΔKd should be smaller when the rate of error change is larger.
Based on experience, the fuzzy control rule table shown in
Table 4 was produced through the simulation experiment.
The simulation is performed according to the fuzzy rules of
Table 5. The simulation result of the fuzzy PID control is shown in
Figure 7.
The simulation results show that compared with the PID control, the rise time and the adjustment time of the fuzzy PID control are further reduced based on the original advantages, and the overshoot is reduced by 7.70%, which enhances the rapidity and stability of the system adjustment.
3.4. Orthogonal-Fuzzy PID Control System
Due to the randomness of the PID parameters selected by experience, the control effect of the fuzzy PID cannot be optimal. In this paper, the orthogonal optimization method is adopted for the setting of PID parameters. The orthogonal optimization method can quickly and accurately select a set of optimal PID parameters. Therefore, the performance of the system can be further improved by the fuzzy control of the PID parameters obtained by orthogonal optimization [
18].
3.4.1. Traditional Orthogonal Test Procedure
(1) Define the purpose of the test and determining the indicator.
The purpose of the test is to select a suitable set of PID parameters to optimize the accuracy and stability of the manipulator control system. The most important indicator in the control system is overshoot and adjustment time. However, the preliminary adjustment of the PID parameters can greatly reduce the overshoot of the system when performing traditional PID control in this paper, so only the adjustment time is determined as an indicator of the test.
(2) Determine the factors and levels, and formulate the factor level table.
Obviously, this experiment is to study the influence of three PID parameters on the control index, so the three parameters determined are
Kp,
Ki and
Kd. The selection of the horizontal range of the orthogonal table is closely related to the theoretical level and practical experience of the operators. The selection of the horizontal range is based on a large amount of practical experience in this paper [
19].
(3) Select the orthogonal table for head design and determine the test plan.
When an orthogonal table is selected, the smallest orthogonal table that satisfies the factors and levels can be selected according to the number of levels and factors. In order to ensure the reliability of the test, this paper selects the orthogonal table
L9(3
4) (four factors and three levels). Single-factor experiments show that although there are interactions among the three parameters, the significance of the impact is relatively small, so the interaction is not considered [
20].
(4) Analysis and comparison of test data.
This test uses visual analysis to analyze data.
(5) Verification of test results.
Substitute the analyzed optimal data into the system to see if it improves the system’s overshoot and adjustment time.
3.4.2. PID Control and Simulation Based on Orthogonal Experiments
After the initial PID adjustment, the system can meet the work demand when the overshoot is less than 15%. Next, aiming at reducing the adjustment time of the system, orthogonal testing was performed to set the PID parameters. An orthogonal table of four factors and three levels was designed. The factor level table is shown in
Table 6.
According to the factor level table, the simulation is carried out sequentially with the goal of adjustment time improvement, and the simulation data are shown in
Table 7.
As can be seen from
Table 7, the range of three parameters
Kp,
Ki and
Kd are
RKp = 0.0751,
RKi = 0.3245, and
RKd = 0.115, respectively. These values satisfy the relationship
RKi >
RKp >
RKd. It shows that
Ki is the factor that has the greatest impact on the settling time, followed by
Kp, and finally
Kd. Combined with horizontal experiments of the mean value analysis of each factor, the effect of PID control is better when
Kp = 0.1,
Ki = 30, and
Kd = 0.02.
The simulation results of the orthogonal-fuzzy PID control are shown in
Figure 8, and the simulation data of the orthogonal-fuzzy PID control are shown in
Table 8.
The simulation results show that the system can be stabilized by separately using original control, PID control, fuzzy PID control, and orthogonal-fuzzy PID control. Compared with the original control, the rise time and adjustment time of the PID control increase slightly, but the overshoot is significantly reduced, which can enhance system’s motion control stability. Compared with the PID control, the rise time, adjustment time, and overshoot of the fuzzy PID control are reduced. The adjustment speed is accelerated while enhancing the stability of the system. Compared with fuzzy PID control, the system of orthogonal-fuzzy PID control with the factor level combination (Kp = 0.1, Ki = 30 and Kd = 0.02) is optimal, and the rise time and the adjustment time are reduced. The oscillation process of the system near the steady state is reduced and the stability of the system control is enhanced. According to the above simulation results, the orthogonal-fuzzy PID control combines the advantages of fuzzy control and orthogonal optimization, which can realize the real-time setting and control of PID parameters, and has good regulation performance for the joint drive of the manipulator.