A Systematic Equalizer Design Technique Using Backward Directional Design
Abstract
:1. Introduction
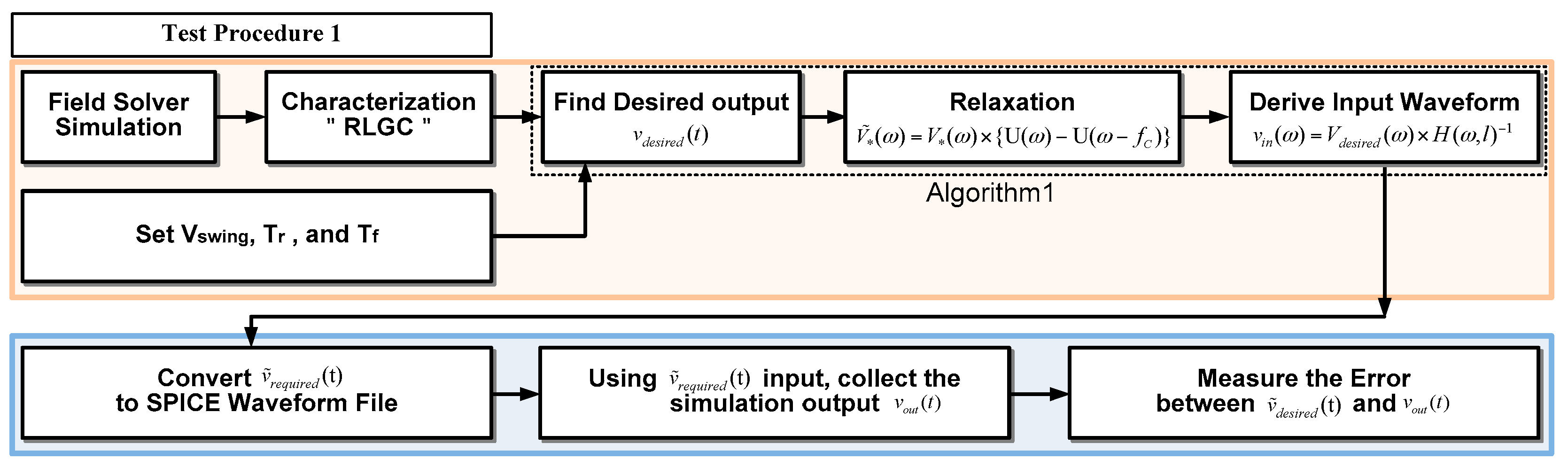
2. Conventional Backward Directional Design Method
3. New DBB Design Technique
| Nomenclature | |
| The piece-wise linear test pulse signal. A lowercase letter represents a time-domain signal and an uppercase letter represents a frequency domain signal. | |
| The voltage difference between low and high on the data link. | |
| The transient rise (fall) time of the output waveform from 0% to 100%. | |
| The total line length. | |
| The line length up to the k-th line segment which is given by , where is the length of one line segment. | |
| vk(t) | The waveform of the k-th line segment. |
| vdesired(t) | The channel output waveform that meets the design criteria. |
| vrequired(t) | The channel input waveform corresponding to vdesired(t). |
| A waveform that applies the relaxation process. | |
| D = [Di(ω)] | The n × 1 digital data input matrix of the channel; the matrix size n is the total number of channels. |
| {↑ 0} | Another expression for D = [1 0]. An arrow indicates that a pulse is excited; its direction indicates the sign of a signal; its position indicates channel number (the left is channel 1). |
| Vin = [Vin_i(ω)] | The n × 1 input waveform matrix of the interconnect. |
| Vout = [Vout_i(ω)] | The n × 1 output waveform matrix of the interconnect. |
| H = [Hi,j(ω)] | The n × n transfer function matrix of the interconnect. |
| The suitable waveform matrix; indicates a required pre-emphasis waveform for the i-th channel; indicates a required crosstalk cancellation waveform; . | |
| Algorithm 1: Equalizer for Single Line |
| Input: |
| Output: |
| Variables: |
| 1: |
| 2:While(True) |
| 3: |
| 4: |
| 5: |
| 6: If |
| 7: Break_while |
| 8: End_if |
| 9: If |
| 10: Break_while |
| 11: End_if |
| 12: |
| 13: End_while |
| 14: |
| 15: |
| 16: |
3.1. Waveform Determination in a Single Line
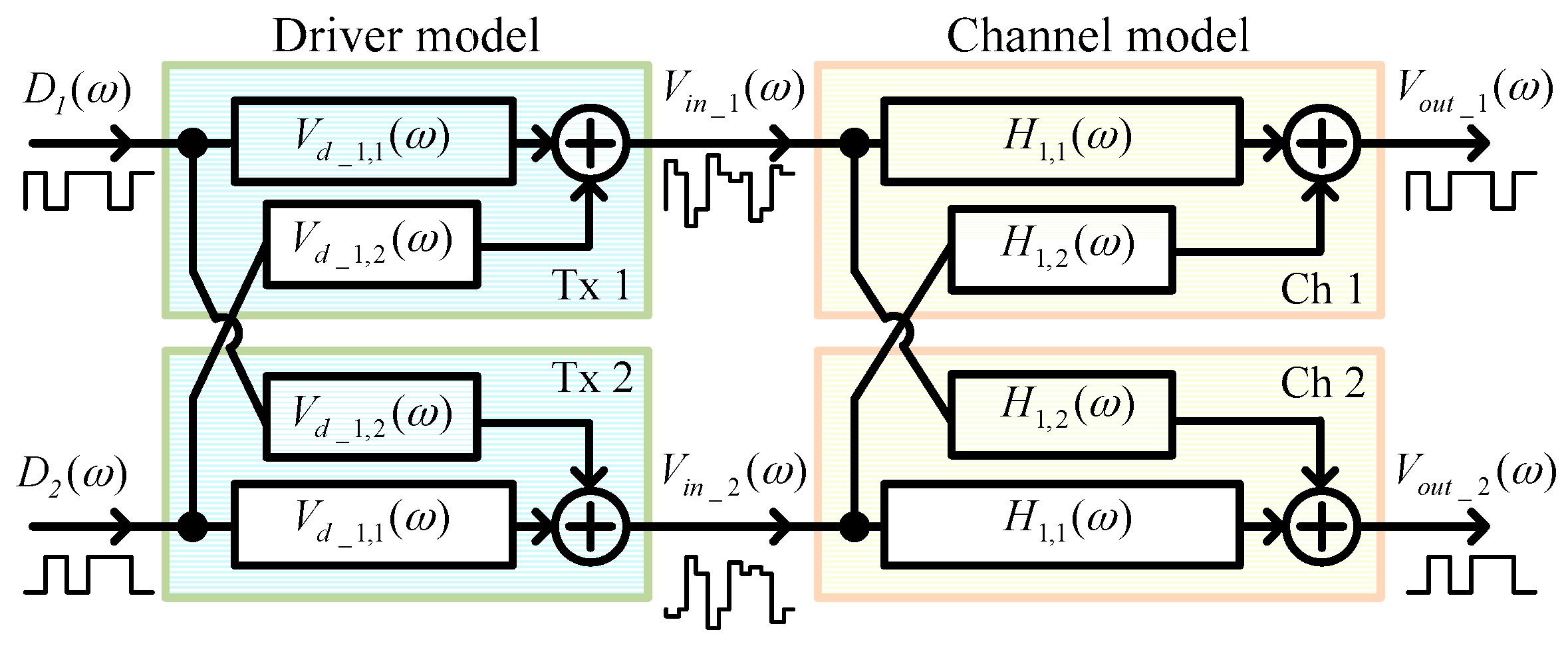
3.2. Waveform Determination in Multi-Line
| Algorithm 2: Equalizer for Multi-Lines |
| Input: Vdesired(ω), H |
| Output: |
| Variables: |
| 1:For |
| 2: |
| 3: |
| 4: |
| 5:End_while |
4. Verification
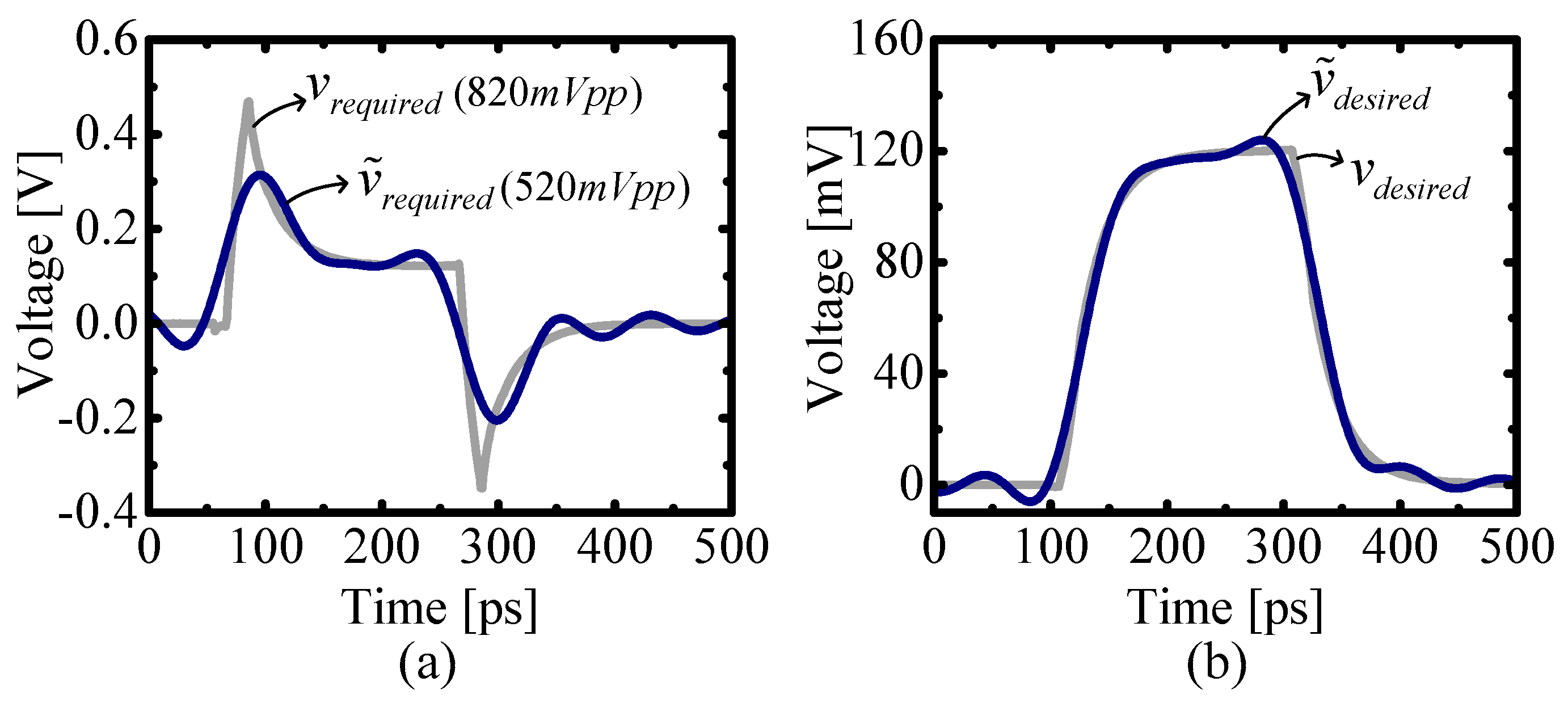
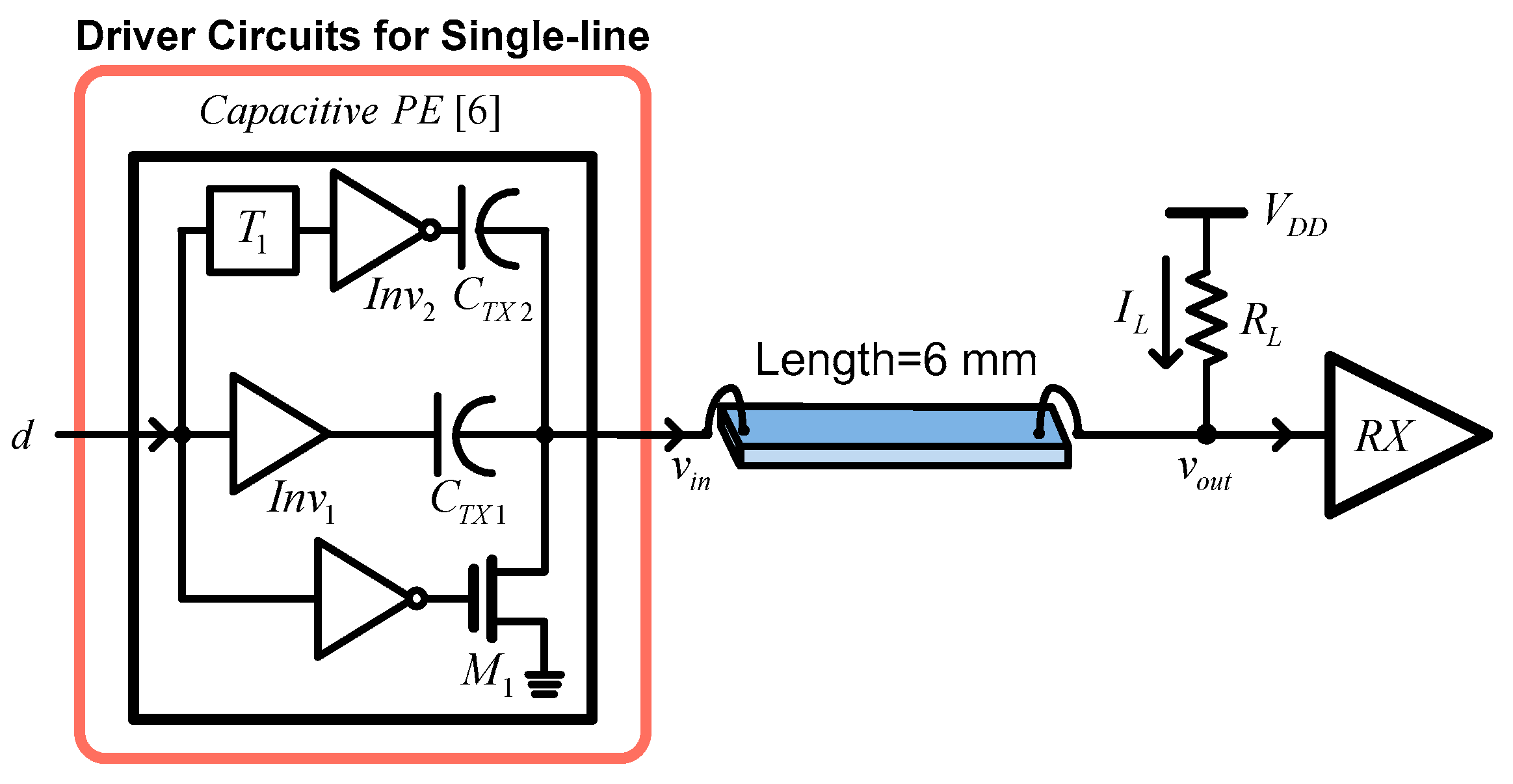
4.1. Equalizer Design for a Single-Line Data Link
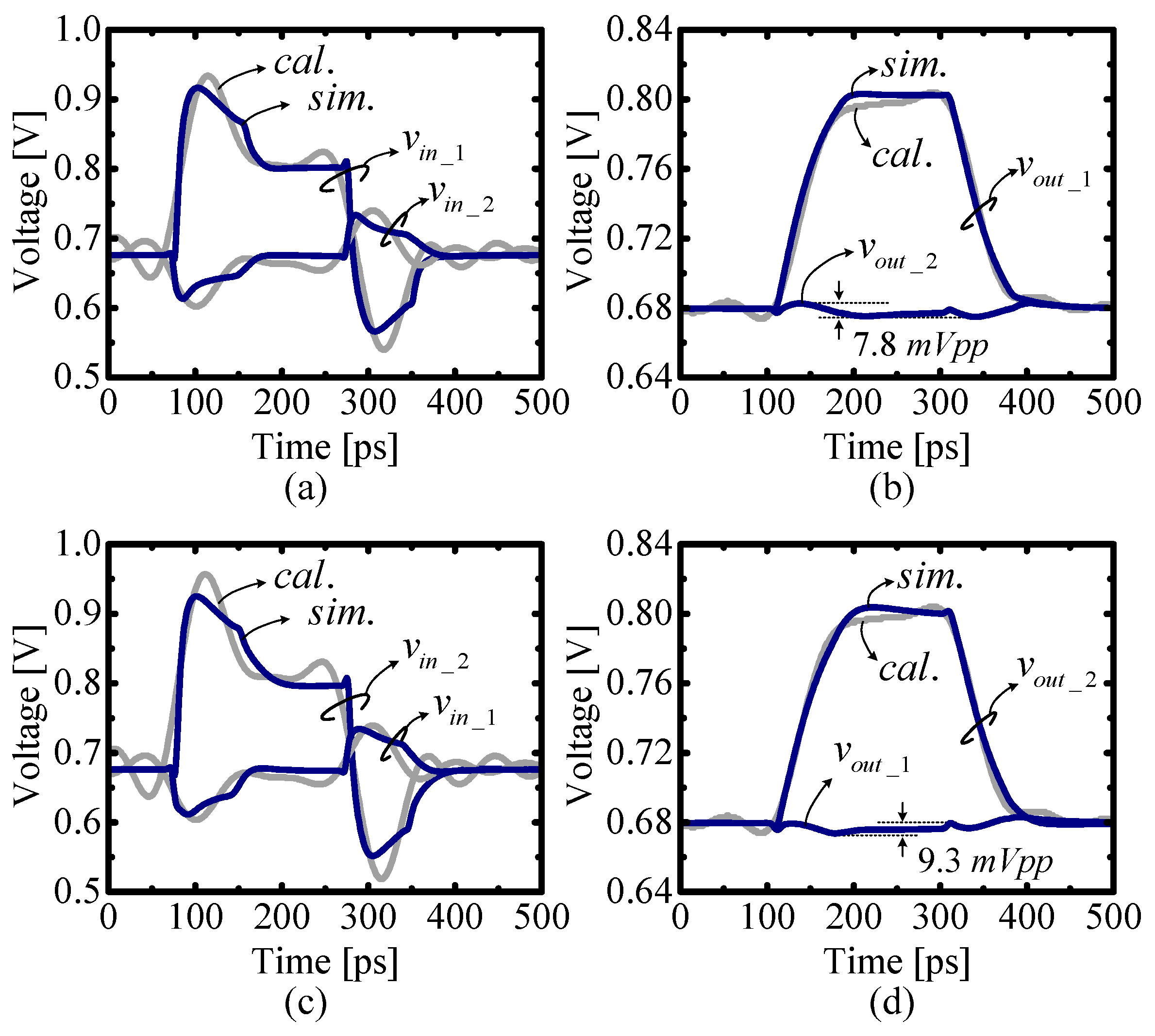
4.2. Equalizer Design for a Multi-Line Data Link
5. Implementation
5.1. Single Line Equalizer Implementation
5.2. Multi-Line Equalizer Implementation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IRTS 2.0: ITRS 2.0_System Integration. Available online: http://www.itrs2.net/ (accessed on 3 September 2019).
- Ho, R.; Ono, T.; Hopkins, R.; Chow, A.; Schauer, J.; Liu, F.; Drost, R. High speed and low energy capacitively driven on-chip wires. IEEE J. Solid-State Circuits 2008, 43, 52–60. [Google Scholar] [CrossRef]
- Kim, B.; Stojanovi´c, V. An energy-efficient equalized transceiver for RC-dominant channels. IEEE J. Solid-State Circuits 2010, 45, 1186–1197. [Google Scholar] [CrossRef]
- Schinkel, D.; Mensink, E.; Klumperink, E.; Tuijl, E.; Nauta, B. A 3-Gb/s/ch transceiver for 10-mm uninterrupted RC-limited global on-chip interconnects. IEEE J. Solid-State Circuits 2006, 41, 297–306. [Google Scholar] [CrossRef]
- Zhang, L.; Wilson, J.; Bashirullah, R.; Luo, L.; Xu, J.; Franzon, P. A 32-Gb/s on-chip bus with driver pre-emphasis signaling. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2009, 17, 1267–1274. [Google Scholar] [CrossRef]
- Mensink, E.; Schinkel, D.; Klumperink, E.; Tuijl, E.; Nauta, B. Power efficient gigabit communication over capacitively driven RC-limited on-chip interconnects. IEEE J. Solid-State Circuits 2010, 45, 447–457. [Google Scholar] [CrossRef]
- Kim, B.; Liu, Y.; Dickson, T.; Bulzacchelli, J.; Friedman, D. A 10-Gb/s compact low-power serial I/O with DFE-IIR equalization in 65-nm CMOS. IEEE J. Solid-State Circuits 2009, 44, 3526–3538. [Google Scholar] [CrossRef]
- Kao, S.; Liu, S. A 7.5-Gb/s one-tap-FFE transmitter with adaptive far-end crosstalk cancellation using duty cycle detection. IEEE J. Solid-State Circuits 2013, 48, 391–404. [Google Scholar] [CrossRef]
- Jung, H.; Yi, I.; Lee, S.; Sim, J.; Park, H. A transmitter to compensate for crosstalk-induced jitter by subtracting a rectangular crosstalk waveform from data signal during the data transition time in coupled microstrip lines. IEEE J. Solid-State Circuits 2012, 47, 2068–2079. [Google Scholar] [CrossRef]
- Wilson, J.; Oh, D. Active crosstalk cancellation for next-generation single-ended memory interface. In Proceedings of the IEEE 61st Electronic Components and Technology Conference (ECTC), Lake Buena Vista, FL, USA, 31 May–3 June 2011; pp. 202–208. [Google Scholar] [CrossRef]
- Bai, Y.; Wong, S. Optimization of driver preemphasis for on-chip interconnects. IEEE Trans. Circuits Syst. I Reg. Pap. 2009, 56, 2033–2041. [Google Scholar] [CrossRef]
- Hall, S.; Heck, H. Advanced Signal Integrity for High-Speed Digital Designs; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 382–386. [Google Scholar]
- Paul, C. Analysis of Multiconductor Transmission Lines, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008; pp. 284–305. [Google Scholar]
- Predictive Technology Model: 22nm PTM HP Model V2.1. Available online: http://ptm.asu.edu/modelcard/HP/22nm_HP.pm (accessed on 3 September 2019).

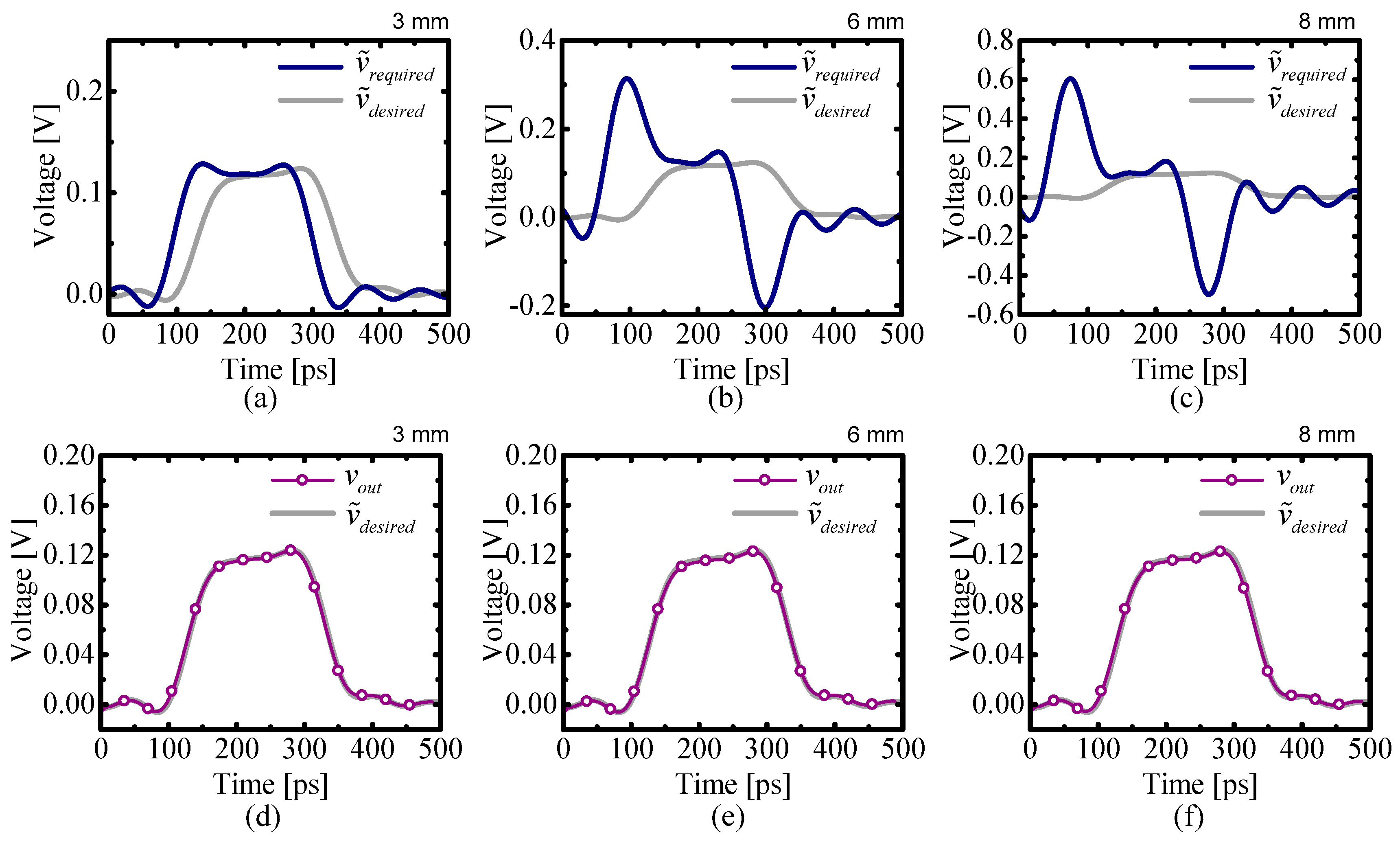
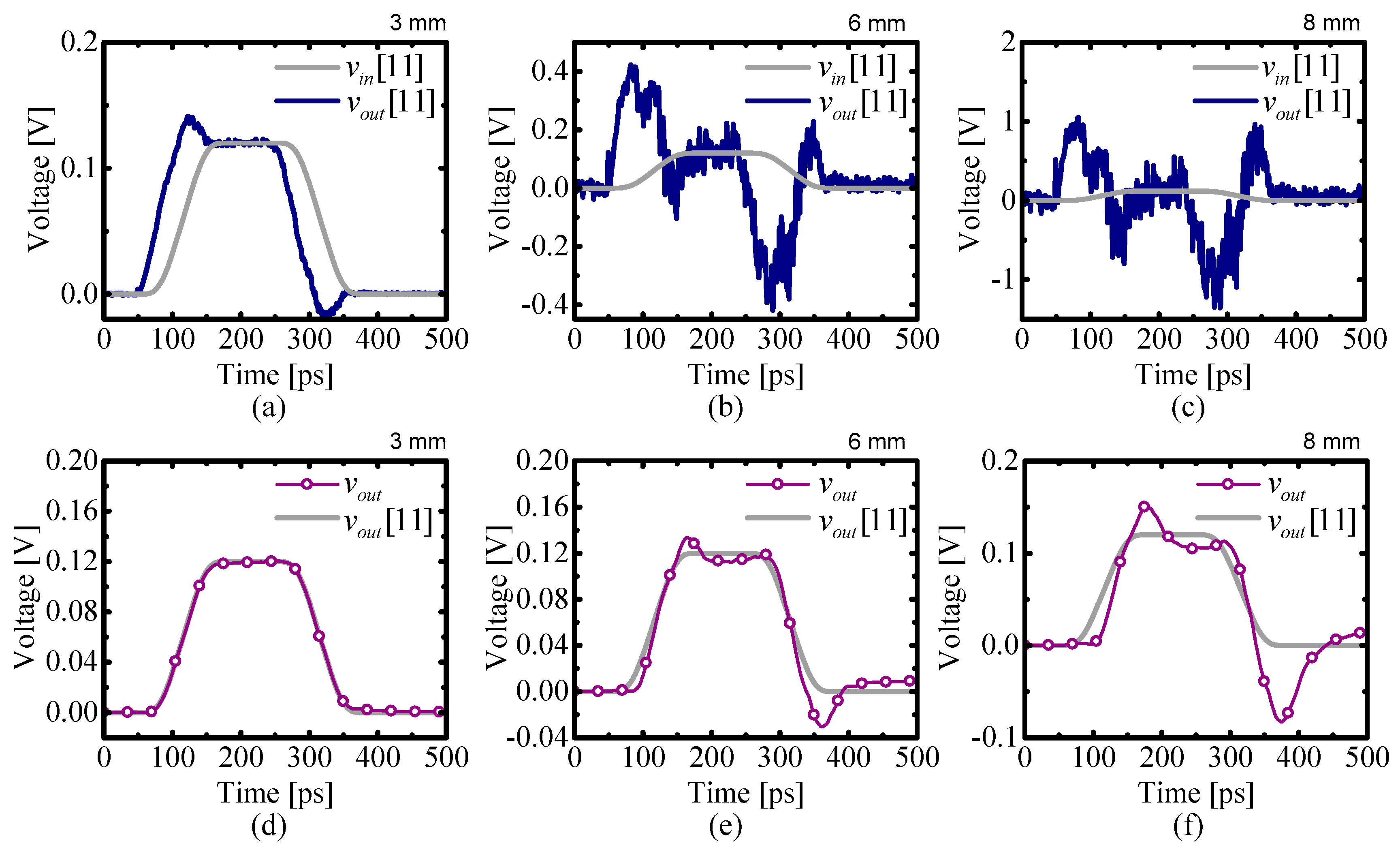



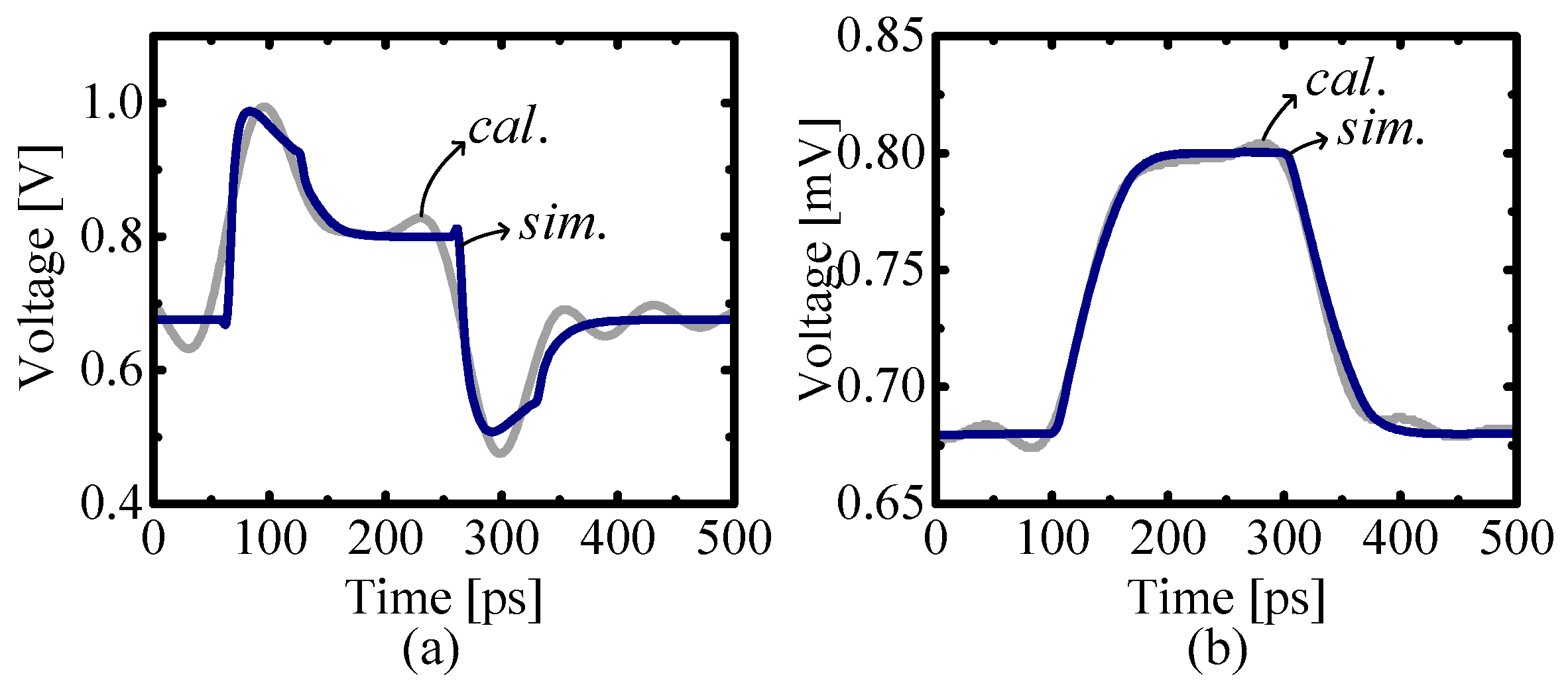



| Dynamic Range 1 | Error 2 | |||||
|---|---|---|---|---|---|---|
| 3 mm | 6 mm | 8 mm | 3 mm | 6 mm | 8 mm | |
| Conventional [11] | 0.16 V | 0.84 V | 2.5 V | 2.5% | 26.6% | 69.2% |
| Proposed | 0.14 V | 0.52 V | 1.1 V | 2.1% | 2.2% | 1.9% |
| Dynamic Range 1 | Error 2 | |||
|---|---|---|---|---|
| Pre-Emphasis | XTC | |||
| {↑0 0} case | 0.39 V | 0.14 V | 2.1% | 2.4% |
| {0↑0} case | 0.14 V | 0.44 V | 2.4% | 2.2% |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, G. A Systematic Equalizer Design Technique Using Backward Directional Design. Electronics 2019, 8, 1053. https://doi.org/10.3390/electronics8091053
Ji G. A Systematic Equalizer Design Technique Using Backward Directional Design. Electronics. 2019; 8(9):1053. https://doi.org/10.3390/electronics8091053
Chicago/Turabian StyleJi, Gihyeon. 2019. "A Systematic Equalizer Design Technique Using Backward Directional Design" Electronics 8, no. 9: 1053. https://doi.org/10.3390/electronics8091053
APA StyleJi, G. (2019). A Systematic Equalizer Design Technique Using Backward Directional Design. Electronics, 8(9), 1053. https://doi.org/10.3390/electronics8091053




