Review of Channel Estimation for Candidate Waveforms of Next Generation Networks
Abstract
:1. Introduction
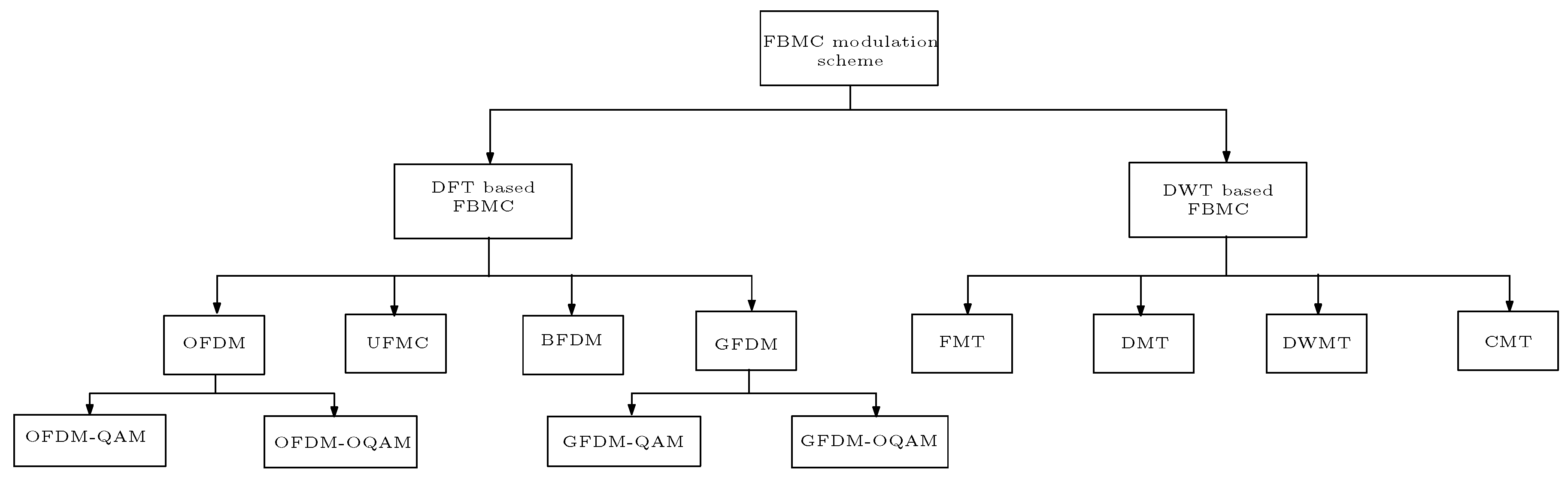
2. Structure of Filter Bank Multi-Carrier Systems
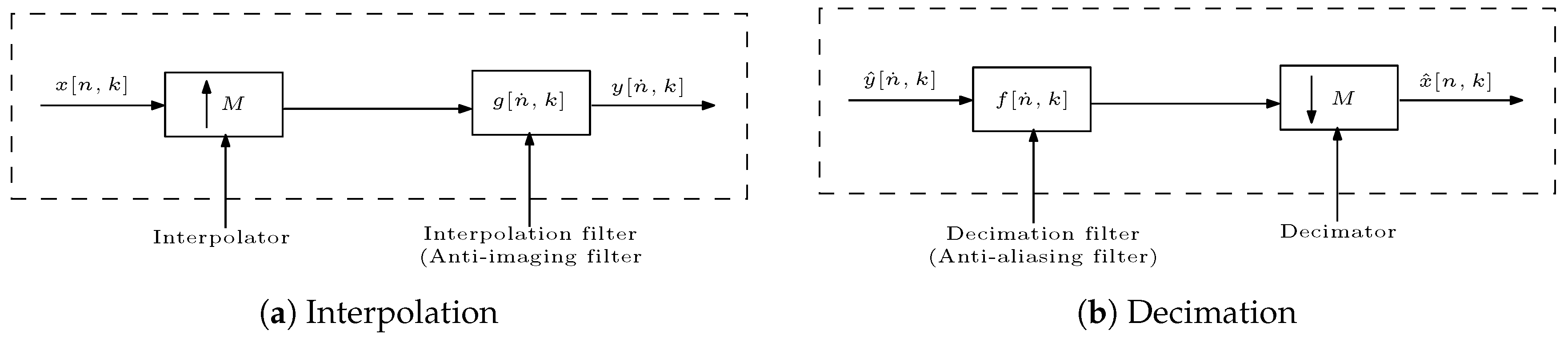
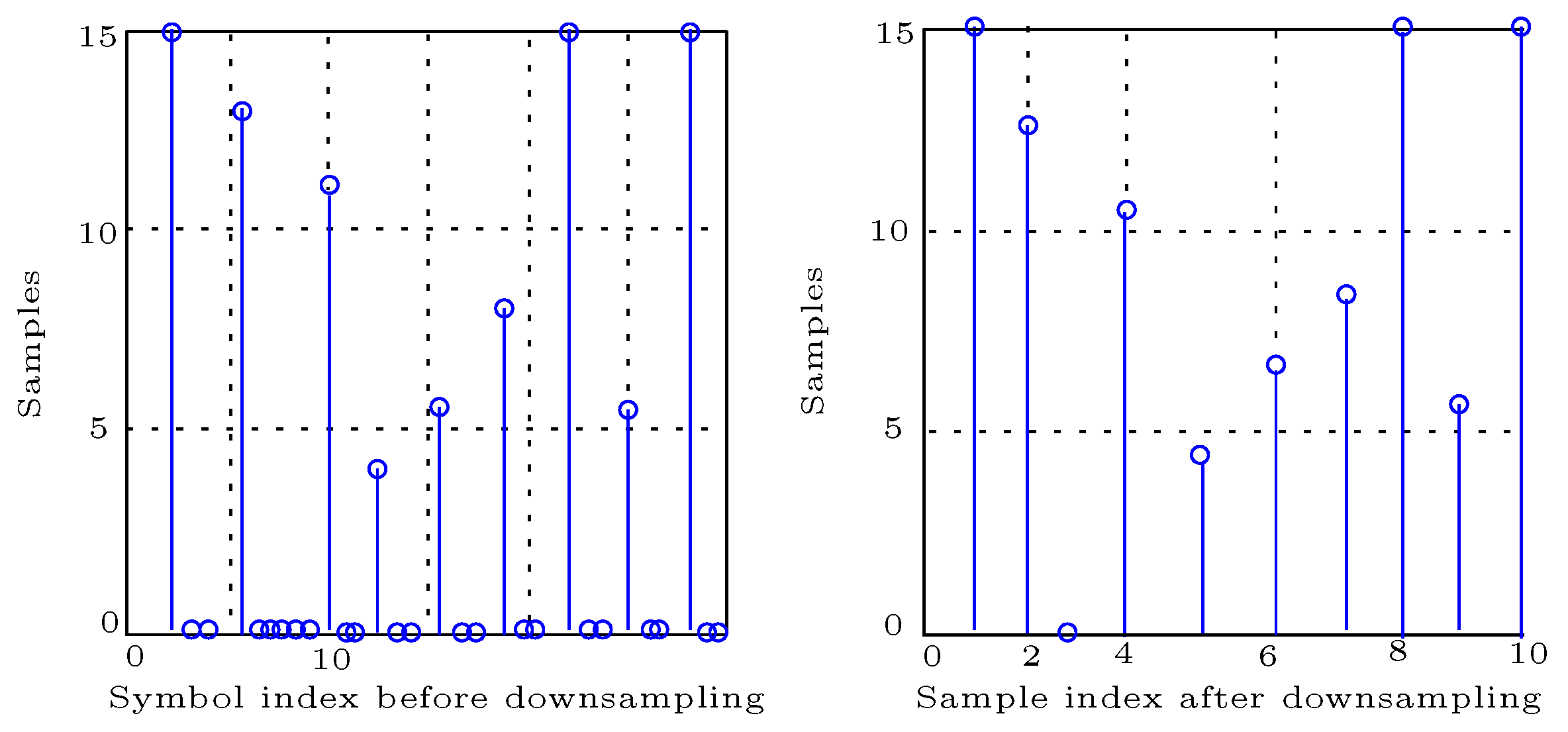
2.1. Multirate Filtering
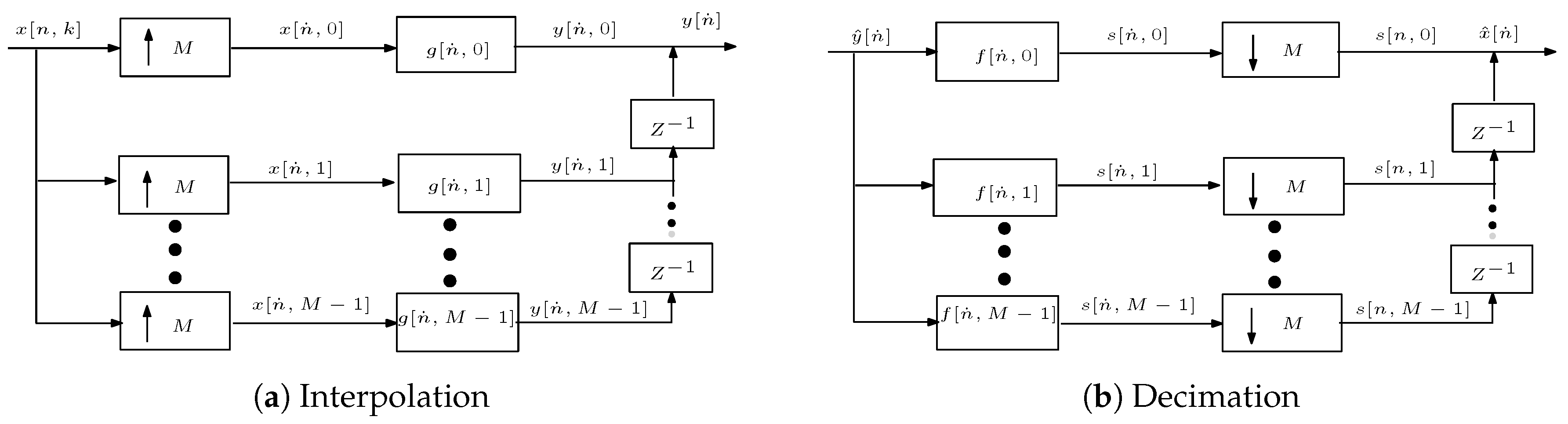
2.2. Design of Multirate Filters: Polyphase Filters
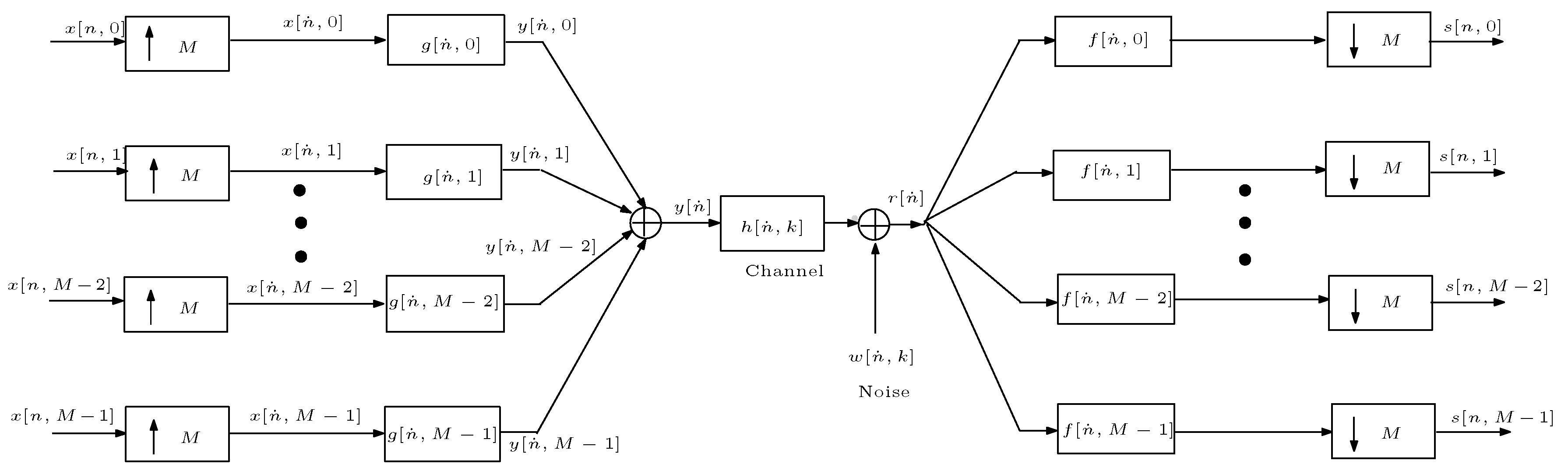
2.3. Basic Structure of FBMC Systems
2.4. Overview of Next Generation Networks (5G)
2.4.1. PHY/MAC Layer Design Considerations for 5G
2.4.2. Candidate Waveforms for 5G Networks
CP-OFDM
SC-FDMA
f-OFDM
Filter Bank OFDM-OQAM
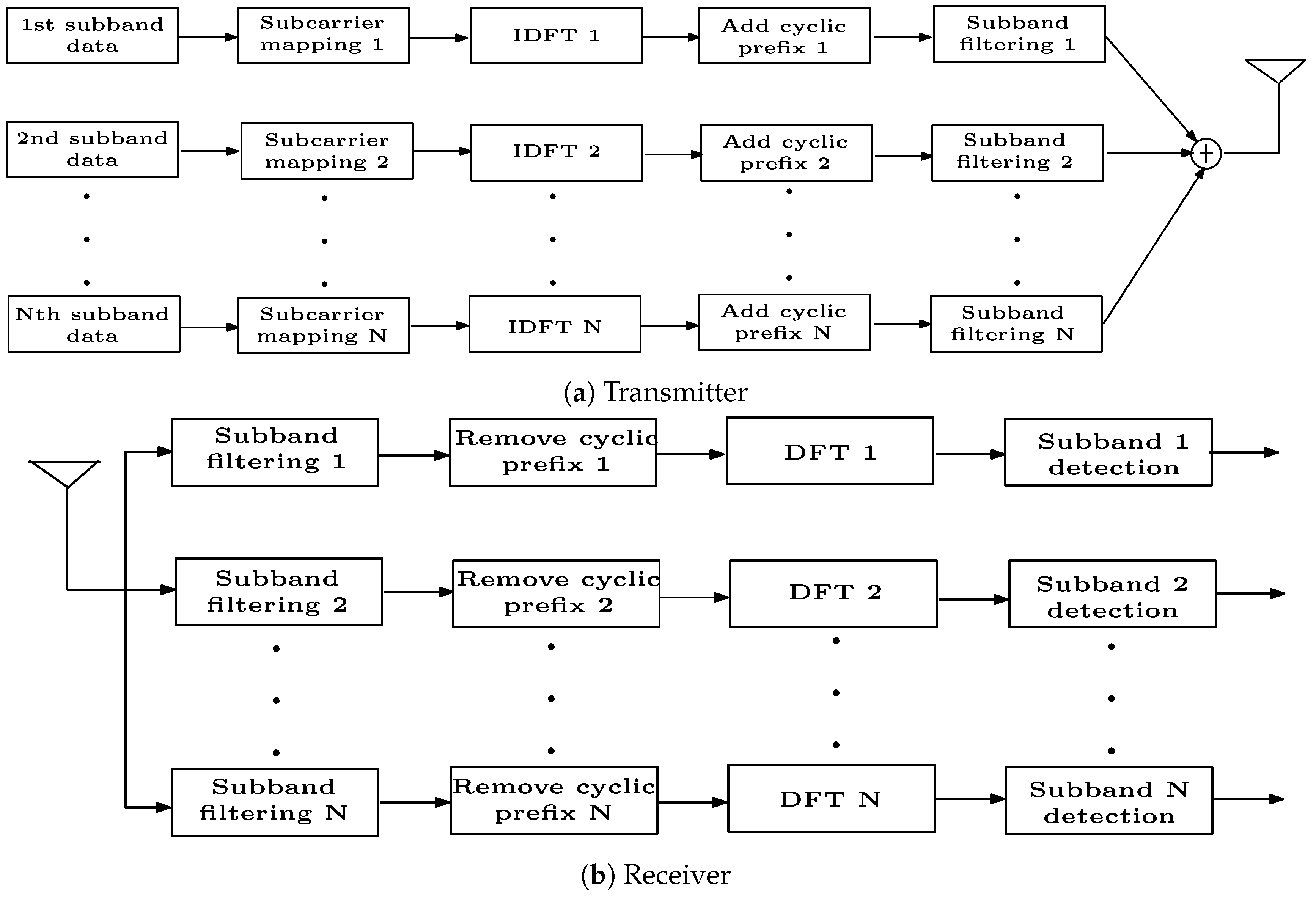
UFMC
GFDM
3. Fundamentals of Channel Estimation
3.1. Classification of Channel Estimation Schemes
3.1.1. Overview of Pilot Based (Non-Blind) CE
3.1.2. Overview of Semi-Blind Channel Estimation
3.1.3. Overview of Blind Channel Estimation
3.2. Channel Estimation for Filter Bank OFDM-OQAM
3.3. Channel Estimation for Filter Bank GFDM
4. System Model Description of FBMC OFDM-OQAM and GFDM-OQAM
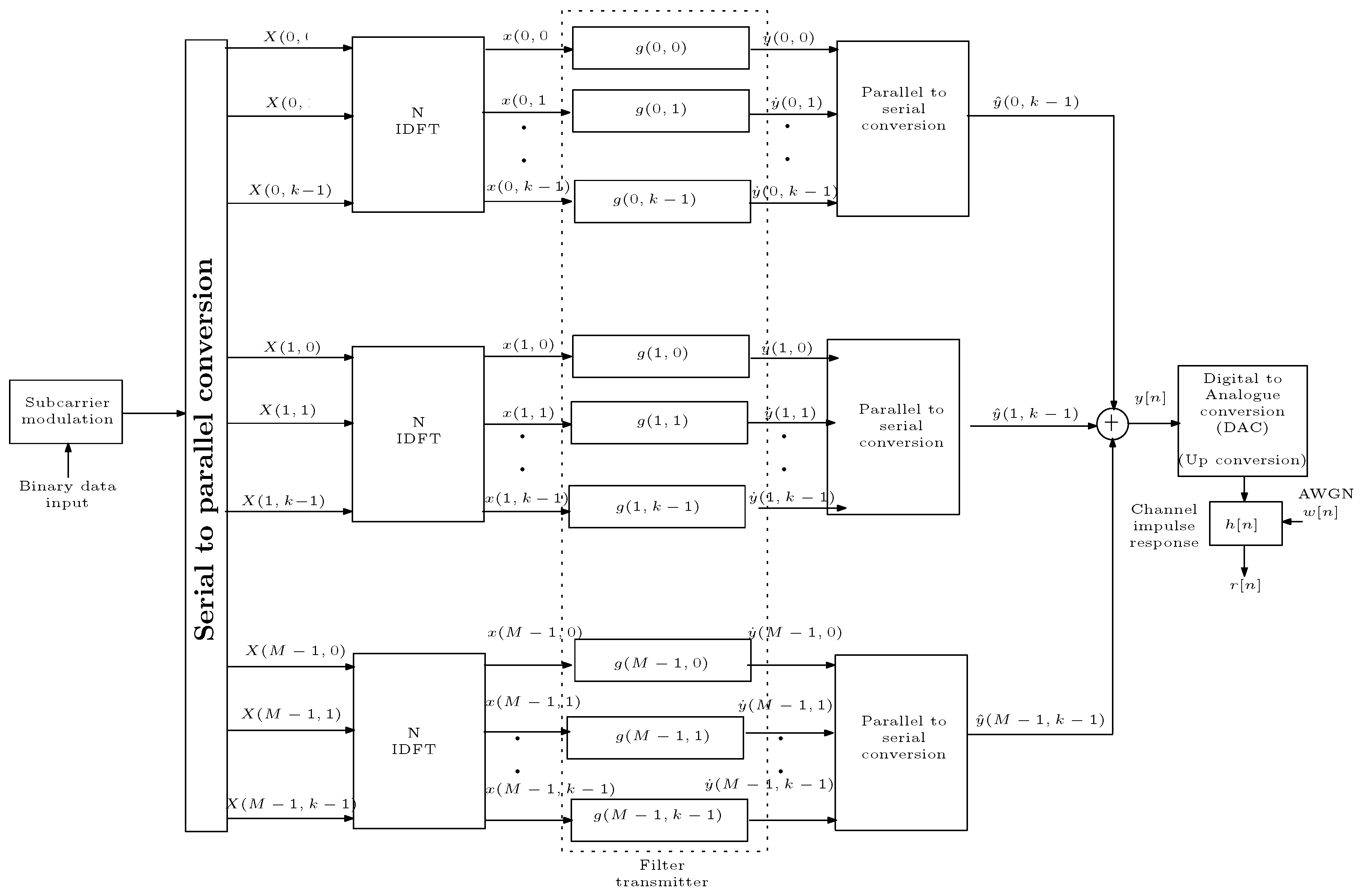
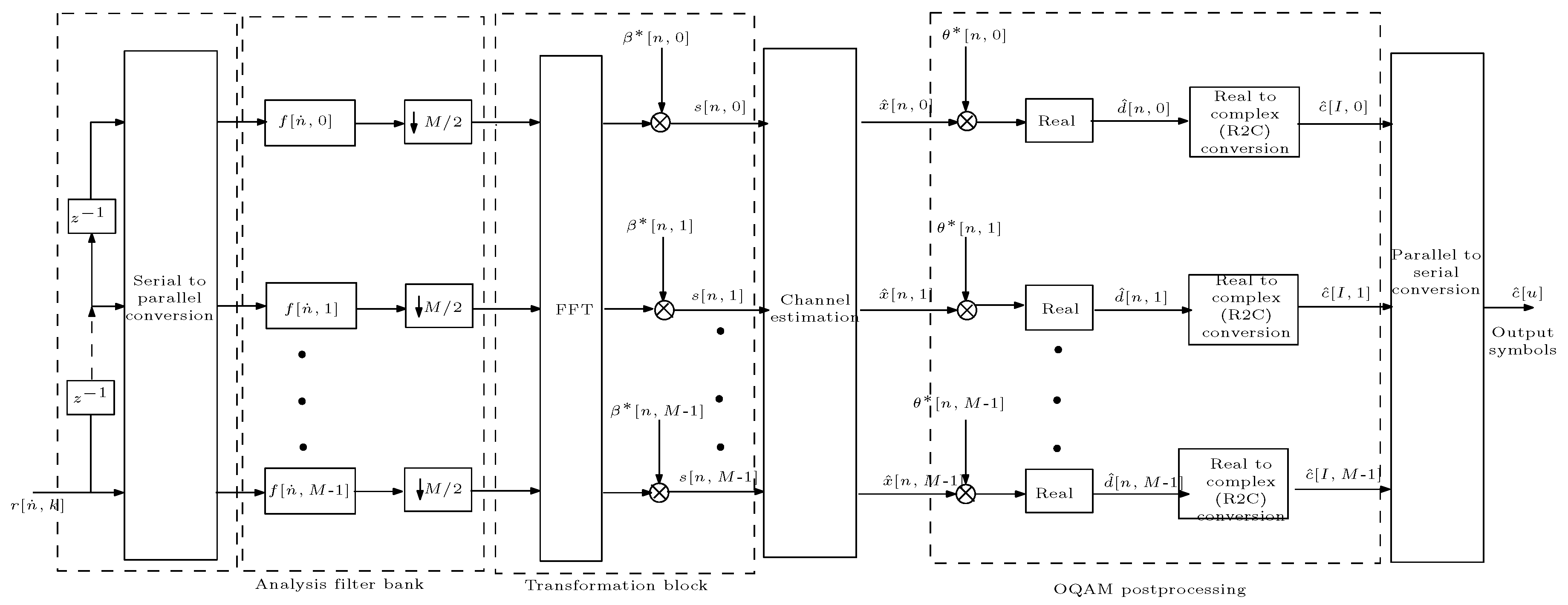
4.1. OFDM-OQAM Transceiver
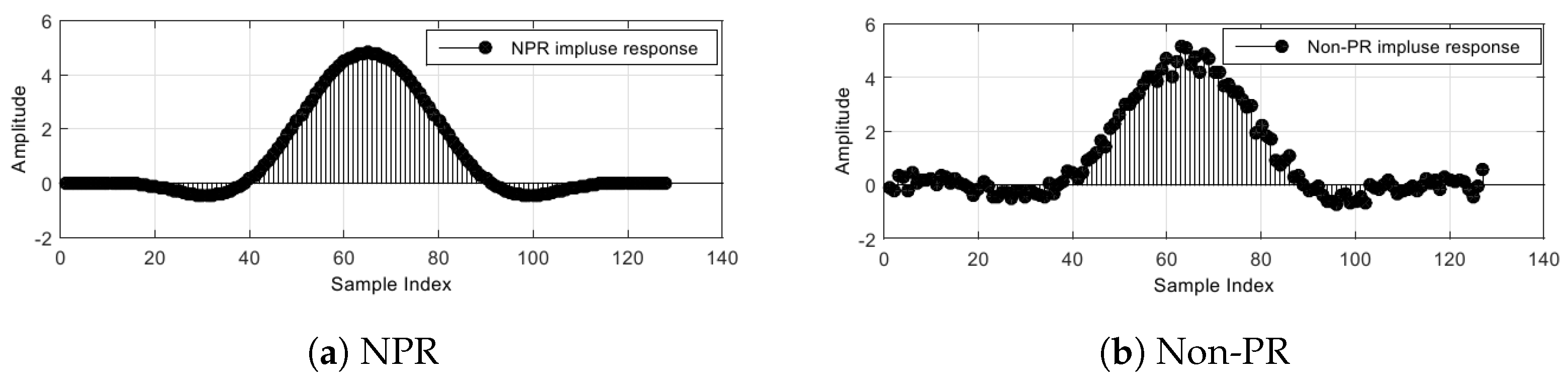
4.1.1. OFDM-OQAM Transceiver: NPR Design
4.1.1.1. Transmitter Description
4.1.1.2. Channel Description
4.1.1.3. Receiver Description
4.1.2. OFDM-OQAM Transceiver: Non-PR design
Transmitter Description
Channel Description
Receiver Description
4.1.3. Channel Estimation for OFDM-OQAM
Least Square
LMMSE
Least Mean Square
Normalised Least Mean Square
Recursive Least Square
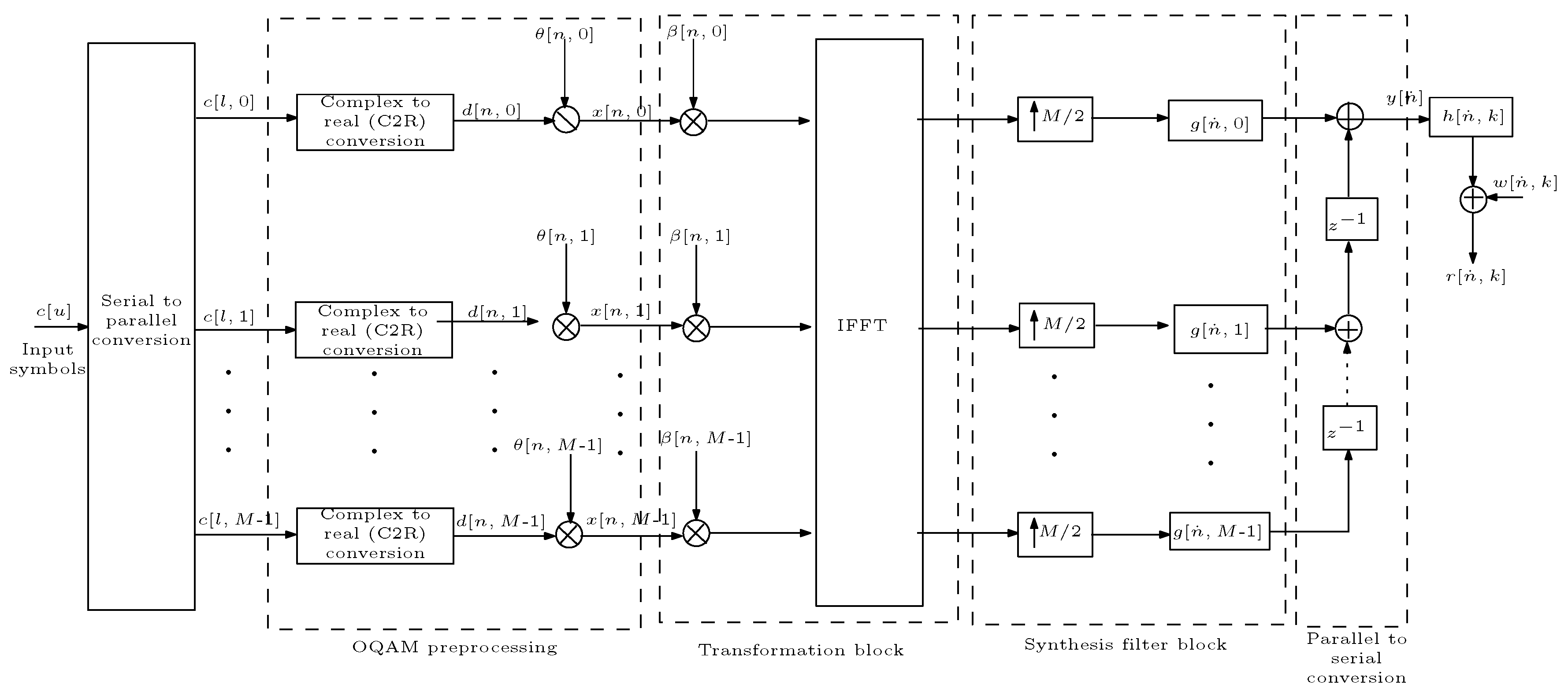
4.2. GFDM-OQAM Transceiver
4.2.1. System Description of GFDM-OQAM Transceiver
4.2.1.1. Transmitter Description
4.2.1.2. Channel Description
4.2.1.3. Receiver Description
| Algorithm 1: Sequential procedure for realising the GFDM-OQAM CCM. |
| Input: {, , , .} |
| Output: . |
| 01 Compute N = ; |
| 02 Generate vector using Equation (12), where length of = ; |
| 03 Compute = ifft() according to Equation (51); |
| 04 Generate = zeros; |
| 05 Compute = ; |
| 06 for ii →; |
| 07 ; |
| 08 ; |
| 09 end for (in line 06); |
| 10 return . |
4.2.2. Channel Estimation for GFDM-OQAM
Least Square
LMMSE
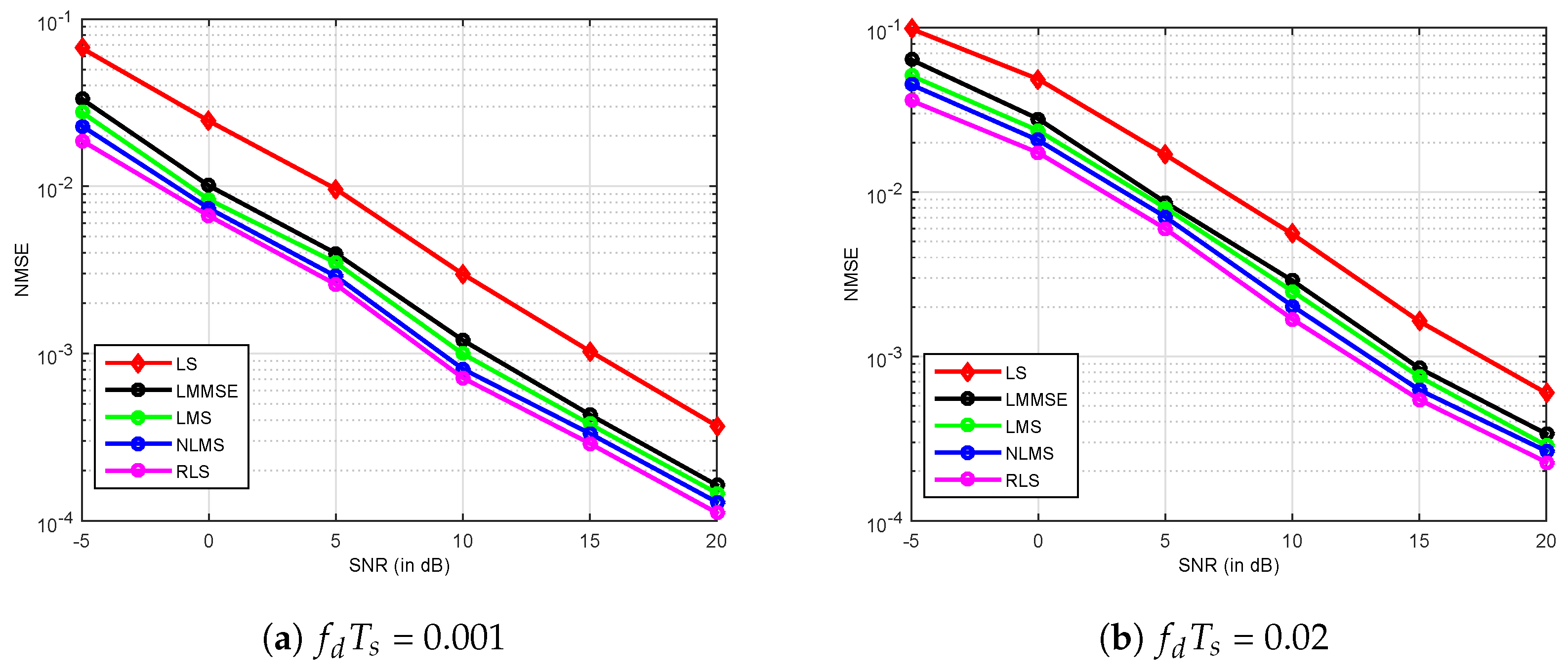
5. Simulations and Discussion of Results
6. Findings and Possible Research Directions
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jain, A.; Nagaria, D. Filter bank spectrum sensing for Cognitive Radio oriented wireless network. In Proceedings of the Conference on Communication, Control and Intelligent Systems (CCIS), Mathura, India, 7–8 November 2015; pp. 133–136. [Google Scholar]
- Farhang-Boroujeny, B. Filter Bank Spectrum Sensing for Cognitive Radios. IEEE Trans. Signal Process. 2008, 56, 1801–1811. [Google Scholar] [CrossRef]
- Lajnef, H.; Dakhli, M.C.; Bouallegue, M.H.R. The Nonlinear Distortion cancellation for the effect of HPA nonlinearities in filter bank based multi-carrier (FBMC) for Cognitive Radio systems. In Proceedings of the Conference on Wireless Communications and Mobile Computing Conference (IWCMC), Paphos, Cyprus, 5–9 September 2016; pp. 638–643. [Google Scholar]
- Akkarajitsakul, K.; Hossain, E.; Niyato, D.; Kim, D.I. Game Theoretic Approaches for Multiple Access in Wireless Networks: A Survey. IEEE Commun. Surv. Tutor. 2011, 13, 372–395. [Google Scholar] [CrossRef]
- Mitra, A. Notes on Mobile Communication; Department of Electronics and Communication Engineering, Indian Institute of Technology: Bangalore, India, 2009. [Google Scholar]
- Hara, S.; Prasad, R. Overview of multicarrier CDMA. IEEE Commun. Mag. 1997, 35, 126–133. [Google Scholar] [CrossRef]
- Sun, S.; Han, S.; Yu, Q.; Meng, W.; Li, C. A survey of two kinds of complementary coded CDMA wireless communications. In Proceedings of the IEEE Global Communications Conference, Austin, TX, USA, 8–10 December 2014; pp. 468–472. [Google Scholar]
- LaSorte, N.; Barnes, W.J.; Refai, H.H. The History of Orthogonal Frequency Division Multiplexing. In Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM), New Orleans, LO, USA, 30 November–4 December 2008; pp. 1–5. [Google Scholar]
- Mirahmadi, M.; Al-Dweik, A.; Shami, A. BER reduction of OFDM based broadband communication systems over multipath channels with impulsive noise. Trans. Commun. 2013, 61, 4602–4615. [Google Scholar] [CrossRef]
- Fang, J.; You, Z.; Lu, I.T.; Li, J.; Yang, R. Comparisons of filter bank multicarrier systems. In Proceedings of the IEEE Long Island Systems, Applications and Technology Conference (LISAT), Farmingdale, NY, USA, 3–3 May 2013; pp. 1–6. [Google Scholar]
- Cui, W.; Qu, D.; Jiang, T.; Farhang-Boroujeny, B. Coded Auxiliary Pilots for Channel Estimation in FBMC-OQAM Systems. Trans. Veh. Technol. 2016, 65, 2936–2946. [Google Scholar] [CrossRef]
- Nam, H.; Choi, M.; Han, S.; Kim, C.; Choi, S.; Hong, D. A New Filter-Bank Multicarrier System with Two Prototype Filters for QAM Symbols Transmission and Reception. IEEE Trans. Wirel. Commun. 2016, 15, 5998–6009. [Google Scholar] [CrossRef]
- Vakilian, V.; Wild, T.; Schaich, F.; ten Brink, S.; Frigon, J.F. Universal-filtered multi-carrier technique for wireless systems beyond LTE. In Proceedings of the IEEE Globecom Workshops (GC Workshops), Atlanta, GA, USA, 9–13 December 2013; pp. 223–228. [Google Scholar]
- Jafri, A.R.; Majid, J.; Shami, M.A.; Imran, M.A.; Najam-Ul-Islam, M. Hardware Complexity Reduction in Universal Filtered Multicarrier Transmitter Implementation. IEEE Access 2017, 5, 13401–13408. [Google Scholar] [CrossRef]
- Ayadi, R.; Siala, M.; Kammoun, I. Transmit/receive pulse-shaping design in BFDM systems over time-frequency dispersive AWGN channel. In Proceedings of the IEEE Conference on Signal Processing and Communications (ICSPC), Dubai, UAE, 24–27 November 2007; pp. 772–775. [Google Scholar]
- Siclet, C.; Siohan, P. Design of BFDM/OQAM systems based on biorthogonal modulated filter banks. In Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM), San Francisco, CA, USA, 27 November–1 December 2000; pp. 701–705. [Google Scholar]
- Gaspar, D.; Mendes, L.; Pimenta, T. GFDM BER Under Synchronization Errors. Commun. Lett. 2017, 21, 1743–1746. [Google Scholar] [CrossRef]
- Lim, B.; Ko, Y.C. SIR Analysis of OFDM and GFDM Waveforms with Timing Offset, CFO and Phase Noise. Trans. Wirel. Commun. 2017, 16, 6979–6990. [Google Scholar] [CrossRef]
- Rana, M.M. An adaptive channel estimation technique for OFDM based cognitive radio systems. In Proceedings of the Conference on Computer and Information Technology (ICCIT), Dhaka, Bangladesh, 22–24 December 2011; pp. 315–320. [Google Scholar]
- Zhao, Z.; Cheng, X.; Wen, M.; Jiao, B.; Wang, C. Channel Estimation Schemes for IEEE 802.11p Standard. IEEE Intell. Transp. Syst. Mag. 2013, 5, 38–49. [Google Scholar] [CrossRef]
- Ogundile, O.O.; Versfeld, D.J.J. Iterative Channel Estimation and Symbol Level Reed-Solomon Decoding Receivers for OFDM Systems. IEICE Trans. Commun. 2017, E100-B, 500–508. [Google Scholar] [CrossRef]
- Velamala, H. Filter Bank Multicarrier Modulation for Spectrally Agile Waveform Design. Ph.D. Thesis, Department Electrical & Computer Engineering, Worcester Polytechnic Institute, Worcester, MA, USA, 2013. [Google Scholar]
- Kuc, R. Introduction to Digital Signal Processing; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Crochiere, R.E.; Rabiner, L.R. Interpolation and decimation of digital signals—A tutorial review. Proc. IEEE 1981, 69, 300–331. [Google Scholar] [CrossRef]
- Proakis, J.G.; Manolakis, D.G. Digital Signal Processing; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Kumar, R.; Kumar, A.; Singh, S.P. A review on decade of multi-rate filters. In Proceedings of the Conference on Electronics and Communication Systems (ICECS), Coimbatore, India, 26–27 February 2015; pp. 1615–1620. [Google Scholar]
- Vaidyanathan, P.P. Multirate digital filters, filter banks, polyphase networks, and applications: A tutorial. Proc. IEEE 1990, 78, 56–93. [Google Scholar] [CrossRef]
- Shynk, J.J. Frequency-domain and multirate adaptive filtering. IEEE Signal Process. Mag. 1992, 9, 14–37. [Google Scholar] [CrossRef]
- Meyer, R.; Burrus, C. Design and implementation of multirate digital filters. IEEE Trans. Acoust. Speech Signal Process. 1976, 24, 53–58. [Google Scholar] [CrossRef]
- Shenoy, R.G.; Burnside, D.; Parks, T.W. Linear periodic systems and multirate filter design. IEEE Trans. Signal Process. 1994, 42, 2242–2256. [Google Scholar] [CrossRef]
- Farhang-Boroujeny, B. Filter Bank Multicarrier Modulation: A Waveform Candidate for 5G and Beyond. Hindawi Adv. Electr. Eng. 2014, 2014, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Martin, K.W. Small side-lobe filter design for multitone data-communication applications. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1998, 45, 1155–1161. [Google Scholar] [CrossRef]
- Zhou, D. A Review of Polyphase Filter Banks and Their Application; In-House final technical report—Air Force Research Laboratory: New York, NY, USA, 2006; pp. 1–29. [Google Scholar]
- Zahradnik, P.; Vlcek, M. Perfect decomposition narrow-band FIR filter banks. IEEE Trans. Circuits Syst. II Express Briefs 2012, 59, 805–809. [Google Scholar] [CrossRef]
- Vetterli, M. A theory of multirate filter banks. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 356–372. [Google Scholar] [CrossRef] [Green Version]
- Diniz, L.R.; Netto, S.L. Design of high-resolution cosine-modulated transmultiplexers with sharp transition band. IEEE Trans. Signal Process. 2004, 52, 1278–1288. [Google Scholar] [CrossRef]
- Michailow, N.; Matthé, M.; Gaspar, I.S.; Caldevilla, A.N.; Mendes, L.L.; Festag, A.; Fettweis, G. Generalized frequency division multiplexing for 5th generation cellular networks. IEEE Trans. Commun. 2014, 62, 3045–3061. [Google Scholar] [CrossRef]
- Farhang-Boroujeny, B.; Lin, L. Cosine modulated multitone for very high-speed digital subscriber lines. In Proceedings of the IEEE Conference on Acoustics, Speech, and Signal Processing Proceedings (ICASSP), Philadelphia, PA, USA, 23–23 March 2005; pp. 345–348. [Google Scholar]
- Lakshmanan, M.K.; Nikookar, H. A Review of Wavelets for Digital Wireless Communication. Int. J. Wirel. Pers. Commun. 2006, 37, 387–420. [Google Scholar] [CrossRef]
- Sandberg, S.D.; Tzannes, M.A. Overlapped discrete multitone modulation for high speed copper wire communications. IEEE J. Sel. Areas Commun. 1995, 13, 1571–1585. [Google Scholar] [CrossRef] [Green Version]
- Alhava, J.; Renfors, M. Exponentially-modulated filter bank transmultiplexer with fine-coarse adaptive filtering. In Proceedings of the International Symposium on Communications, Control and Signal Processing (ISCCSP), St Julians, Malta, 12–14 March 2008; pp. 68–72. [Google Scholar]
- Lin, L.; Farhang-Boroujeny, B. Convergence analysis of blind equalizer in a filter-bank-based multicarrier communication system. IEEE Trans. Signal Process. 2006, 54, 4061–4067. [Google Scholar] [CrossRef]
- Farhang-Boroujeny, B.; Lin, L. Analysis of post-combiner equalizers in cosine-modulated filterbank-based transmultiplexer systems. IEEE Trans. Signal Process. 2003, 51, 3249–3262. [Google Scholar] [CrossRef]
- Mirabbasi, S.; Martin, K. Overlapped complex-modulated transmultiplexer filters with simplified design and superior stopbands. IEEE Trans. Circuits Syst. II Analog Digital Signal Process. 2003, 50, 456–469. [Google Scholar] [CrossRef]
- Alhava, J.; Viholainen, A.; Renfors, M. Efficient implementation of complex exponentially-modulated filter banks. In Proceedings of the International Symposium on Circuits and Systems (ISCAS), Bangkok, Thailand, 25–28 May 2003; pp. 157–160. [Google Scholar]
- Evans, D. The Internet of Things: How the Next Evolution of the Internet is Changing Everything; Cisco White Paper; Cisco Internet Business Solutions Group (IBSG): San Jose, CA, USA, 2011; p. 1. [Google Scholar]
- Roessler, A. 5G Waveform Candidates. Available online: https://scdn.rohde-schwarz.com/ur/pws/dl_downloads/dl_application/application_notes/1ma271/1MA271_0e_5G_waveform_candidates.pdf (accessed on 14 January 2019).
- Sahni, V.D.; Kumar, N.; Saxena, V.N. Novel hybrid technique(s) for PAPR reduction in OFDM systems. In Proceedings of the Conference on Signal Processing and Communication (ICSC), Noida, India, 26–28 Decemebr 2016; pp. 512–515. [Google Scholar]
- Lim, D.W.; Heo, S.J.; No, J.S. An overview of peak-to-average power ratio reduction schemes for OFDM signals. J. Commun. Netw. 2009, 11, 229–239. [Google Scholar] [CrossRef]
- Ehsanfar, S.; Matthe, M.; Zhang, D.; Fettweis, G. Theoretical Analysis and CRLB Evaluation for Pilot-Aided Channel Estimation in GFDM. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–7. [Google Scholar]
- Ehsanfar, S.; Matthe, M.; Zhang, D.; Fettweis, G. Interference-Free Pilots Insertion for MIMO-GFDM Channel Estimation. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Ehsanfar, S.; Matthe, M.; Zhang, D.; Fettweis, G. A Study of Pilot-Aided Channel Estimation in MIMO-GFDM Systems. In Proceedings of the International ITG Workshop on Smart Antennas (WSA), Munich, Germany, 9–11 March 2016; pp. 1–8. [Google Scholar]
- Chang, H.L.; Tsai, M.H. Optimistic DRX for Machine-Type Communications in LTE-A Network. IEEE Access 2018, 6, 9887–9897. [Google Scholar] [CrossRef]
- Li, Y.; Sun, K.; Cai, L. Cooperative Device-to-Device Communication With Network Coding for Machine Type Communication Devices. IEEE Trans. Wirel. Commun. 2018, 17, 296–309. [Google Scholar] [CrossRef]
- Cheng, R.G.; Becvar, Z.; Yang, P.H. Modeling of Distributed Queueing-Based Random Access for Machine Type Communications in Mobile Networks. IEEE Commun. Lett. 2018, 22, 129–132. [Google Scholar] [CrossRef]
- Akpakwu, G.A.; Silva, B.J.; Hancke, G.P.; Abu-Mahfouz, A.M. A Survey on 5G Networks for the Internet of Things: Communication Technologies and Challenges. IEEE Access 2018, 6, 3619–3647. [Google Scholar] [CrossRef]
- Ji, H.; Park, S.; Yeo, J.; Kim, Y.; Lee, J.; Shim, B. Ultra-Reliable and Low-Latency Communications in 5G Downlink: Physical Layer Aspects. IEEE Wirel. Commun. 2018, 25, 124–130. [Google Scholar] [CrossRef]
- Liu, C.F.; Bennis, M. Ultra-Reliable and Low-Latency Vehicular Transmission: An Extreme Value Theory Approach. IEEE Commun. Lett. 2018, 22, 1292–1295. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Leng, S.; He, Y.; Maharjan, S.; Zhang, Y. Mobile Edge Computing and Networking for Green and Low-Latency Internet of Things. IEEE Commun. Mag. 2018, 56, 39–45. [Google Scholar] [CrossRef]
- Abu-Lebdeh, M.; Sahoo, J.; Glitho, R.; Tchouati, C.W. Cloudifying the 3GPP IP multimedia subsystem for 4G and beyond: A survey. IEEE Commun. Mag. 2016, 54, 91–97. [Google Scholar] [CrossRef]
- Ijaz, A.; Zhang, L.; Xiao, P.; Tafazolli, R. Analysis of Candidate Waveforms for 5G Cellular Systems. Towards 5G Wireless Networks: Chapter 1; Intech Open: London, UK, 2016; pp. 1–25. [Google Scholar]
- Nguyen, T.M.; Ajib, W.; Assi, C. A Novel Cooperative Non-Orthogonal Multiple Access (NOMA) in Wireless Backhaul Two-Tier HetNets. IEEE Trans. Wirel. Commun. 2018, 17, 4873–4887. [Google Scholar] [CrossRef]
- Ni, D.; Hao, L.; Tran, Q.T.; Qian, X. Power Allocation for Downlink NOMA Heterogeneous Networks. IEEE Access 2018, 6, 26742–26752. [Google Scholar] [CrossRef]
- Fu, Y.; Hong, Y.; Chen, L.K.; Sung, C.W. Enhanced Power Allocation for Sum Rate Maximization in OFDM-NOMA VLC Systems. IEEE Photonics Technol. Lett. 2018, 30, 1218–1221. [Google Scholar] [CrossRef]
- Zhang, H.; Qiu, Y.; Long, K.; Karagiannidis, G.K.; Wang, X.; Nallanathan, A. Resource Allocation in NOMA-Based Fog Radio Access Networks. IEEE Wirel. Commun. 2018, 25, 110–115. [Google Scholar] [CrossRef]
- Richardson, T.; Kudekar, S. Design of Low-Density Parity Check Codes for 5G New Radio. IEEE Commun. Mag. 2018, 56, 28–34. [Google Scholar] [CrossRef]
- Wu, X.; Jiang, M.; Zhao, C.; Ma, L.; Wei, Y. Low-Rate PBRL-LDPC Codes for URLLC in 5G. IEEE Wirel. Commun. Lett. 2017, 21, 1–4. [Google Scholar] [CrossRef]
- Bellili, F.; Methenni, A.; Amor, S.B.; Affes, S.; Stèphenne, A. Time Synchronization of Turbo-Coded Square-QAM-Modulated Transmissions: Code-Aided ML Estimator and Closed-Form Cramér–Rao Lower Bounds. IEEE Trans. Veh. Technol. 2017, 66, 10776–10792. [Google Scholar] [CrossRef]
- Ahn, B.; Yoon, S.; Heo, J. Low Complexity Syndrome-Based Decoding Algorithm Applied to Block Turbo Codes. IEEE Access 2018, 6, 26693–26706. [Google Scholar] [CrossRef]
- İşcan, O.; Xu, W. Window-Interleaved Turbo Codes. IEEE Commun. Lett. 2018, 22, 676–679. [Google Scholar] [CrossRef]
- Dai, J.; Niu, K.; Si, Z.; Dong, C.; Lin, J. Polar-Coded Non-Orthogonal Multiple Access. IEEE Trans. Signal Process. 2018, 66, 1374–1389. [Google Scholar] [CrossRef]
- Gerzaguet, R.; Kténas, D.; Cassiau, N.; Doré, J.B. Comparative study of 5G waveform candidates for below 6 GHz air interface. In Proceedings of the ETSI Workshop on Future Radio Technologies-Air Interface, Sophia Antipolis, France, 27–28 January 2016; pp. 1–9. [Google Scholar]
- Coleri, S.; Ergen, M.; Puri, A.; Bahai, A. Channel estimation techniques based on pilot arrangement in OFDM systems. IEEE Trans. Broadcast. 2002, 48, 223–229. [Google Scholar] [CrossRef]
- Almoneer, M.; Rohde, C.; Hassan, K.; Gerstacker, W.H. Intercarrier Interference-Aware Pilot-Aided Channel Estimation in OFDM Systems. IEEE Trans. Broadcast. 2017, 63, 449–462. [Google Scholar] [CrossRef]
- Idris, A.; Farhana, A.N.; Adiba, H.; Kassim, M. BER and PAPR analysis of MIMO OFDMA and SCFDMA system using different diversity techniques. In Proceedings of the IEEE Conference on Control System, Computing and Engineering (ICCSCE), Penang, Malaysia, 24–26 November 2017; pp. 293–298. [Google Scholar]
- Zhang, X.; Jia, M.; Chen, L.; Ma, J.; Qiu, J. Filtered-OFDM–Enabler for Flexible Waveform in the 5th Generation Cellular Networks. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar]
- Wu, D.; Zhang, X.; Qiu, J.; Gu, L.; Saito, Y.; Benjebbour, A.; Kishiyama, Y. A Field Trial of f-OFDM toward 5G. In Proceedings of the IEEE Globecom Workshops (GC Wkshps), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Zhang, L.; Ijaz, A.; Xiao, P.; Molu, M.M.; Tafazolli, R. Filtered OFDM Systems, Algorithms, and Performance Analysis for 5G and Beyond. IEEE Trans. Commun. 2018, 66, 1205–1218. [Google Scholar] [CrossRef]
- Zhang, X. Design of FIR Halfband Filters for Orthonormal Wavelets Using Remez Exchange Algorithm. IEEE Signal Process. Lett. 2009, 16, 814–817. [Google Scholar] [CrossRef]
- Chen, L.; Yu, J.G. Interference cancelation scheme with variable bandwidth allocation for universal filtered multicarrier systems in 5G networks. EURASIP J. Wirel. Commun. Netw. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Poornima, T.; Dhinesh, K.; Sudhakar, R. Waveform candidates for 5G mobile communications. In Proceedings of the IEEE Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bangalore, India, 19–20 May 2017; pp. 856–860. [Google Scholar]
- Desta, Y.T.; Tao, J.; Zhang, W. Review on Selected Channel Estimation Algorithms for Orthogonal Frequency Division Multiplexing System. Inf. Technol. J. 2011, 10, 914–926. [Google Scholar] [CrossRef] [Green Version]
- Balogun, B.M. Frequency Synchronization in Multiuser OFDM-IDMA Systems. Ph.D. Thesis, Department of Electrical Engineering, & Computer Engineering, University of Kwazulu-Natal, Durban, South Africa, 2013. [Google Scholar]
- Ijiga, O.E. Channel Estimation Techniques for Filter Bank Multicarrier Based Transceivers for Next Generation of Wireless Networks. Ph.D. Thesis, School of Election & Information Engineering, University of the Witwatersrand, Johannesburg, South Africa, 2017. [Google Scholar]
- Ogundile, O.O.; Oyerinde, O.O.; Versfeld, D.J.J. Decision directed iterative channel estimation and Reed Solomon decoding over flat fading channels. IET Commun. 2015, 9, 2077–2084. [Google Scholar] [CrossRef]
- Van de Beek, J.-J.; Edfors, O.; Sandell, M.; Wilson, S.K.; Borjesson, P.O. On channel estimation in OFDM systems. In Proceedings of the IEEE Vehicular Technology Conference, Chicago, IL, USA, 25–28 July 1995; pp. 815–819. [Google Scholar]
- James, A.R.; Benjamin, R.S.; John, S.; Joseph, T.M.; Mathai, V.; Pillai, S.S. Channel estimation for OFDM systems. In Proceedings of the Conference on Signal Processing, Communication, Computing and Networking Technologies, Thuckafay, India, 21–22 July 2011; pp. 587–591. [Google Scholar]
- Morelli, M.; Mengali, U. A comparison of pilot-aided channel estimation methods for OFDM systems. IEEE Trans. Signal Process. 2001, 49, 3065–3073. [Google Scholar] [CrossRef]
- Kong, D.; Xia, X.G.; Jiang, T.; Gao, X. Channel Estimation in CP-OQAM-OFDM Systems. IEEE Trans. Signal Process. 2014, 62, 5775–5786. [Google Scholar] [CrossRef]
- Ogundile, O.O.; Versfeld, D.J.J. A Low Complexity Iterative Channel Estimation and Decoding Receiver Based on Reed-Solomon PTA. IEEE Access 2016, 4, 8805–8813. [Google Scholar] [CrossRef] [Green Version]
- Park, S.; Shim, B.; Choi, J.W. Iterative Channel Estimation Using Virtual Pilot Signals for MIMO-OFDM Systems. IEEE Trans. Signal Process 2015, 63, 3032–3045. [Google Scholar] [CrossRef]
- Ozdemir, M.K.; Arslan, H. Channel estimation for wireless ofdm systems. IEEE Commun. Surv. Tutor. 2007, 9, 18–48. [Google Scholar] [CrossRef]
- Yoo, D.S.; Lim, J. MSE expression for transform-based decision-directed channel estimation schemes in M-PSK OFDM systems. Electron. Lett. 2016, 52, 363–365. [Google Scholar] [CrossRef]
- Park, S.; Choi, J.W.; Lee, K.; Shim, B. Soft decision-directed channel estimation for multiuser MIMO systems. In Proceedings of the IEEE Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Hong Kong, China, 30 August–2 September 2015; pp. 95–99. [Google Scholar]
- Tseng, C.H.; Cheng, Y.C.; Chung, C.D. Subspace-Based Blind Channel Estimation for OFDM by Exploiting Cyclic Prefix. IEEE Wirel. Commun. Lett. 2013, 2, 691–694. [Google Scholar] [CrossRef]
- Mawatwal, K.; Sen, D.; Roy, R. A Semi-Blind Channel Estimation Algorithm for Massive MIMO Systems. IEEE Wirel. Commun. Lett. 2017, 6, 70–73. [Google Scholar] [CrossRef]
- Chang, T.H.; Ma, W.K.; Chi, C.Y. Maximum-Likelihood Detection of Orthogonal Space-Time Block Coded OFDM in Unknown Block Fading Channels. IEEE Trans. Signal Process. 2008, 56, 1637–1649. [Google Scholar] [CrossRef]
- Wang, M.L.; Li, C.P.; Huang, W.J. Semi-Blind Channel Estimation and Precoding Scheme in Two-Way Multi-Relay Networks. IEEE Trans. Signal Process. 2017, 65, 2576–2587. [Google Scholar] [CrossRef]
- Ban, Y.; Hu, Q.; Mao, Z.; Zhao, Z. Semi-blind pilot-aided channel estimation in uplink cloud radio access networks. China Commun. 2016, 13, 72–79. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, J.; Li, S. A channel estimation method for NC-OFDM systems in cognitive radio context. In Proceedings of the IEEE Singapore International Conference on Communication Systems (ICCS), Guangzhou, China, 19–21 Novemebr 2008; pp. 208–212. [Google Scholar]
- Min, J.; Xue-mai, G.; Qun, W. An improved channel estimation method for NC-OFDM systems in Cognitive Radio context. In Proceedings of the Conference on Communications and Networking in China (CHINACOM), Harbin, China, 17–19 August 2011; pp. 147–150. [Google Scholar]
- Zhu, C.; Yang, S. The Interference Constrained Pilot Design for NC-OFDM Systems in Cognitive Radios. In Proceedings of the Conference on Wireless Communications, Networking and Mobile Computing (WiCOM), Shanghai, China, 21–23 September 2012; pp. 1–4. [Google Scholar]
- Liu, J.; Feng, S.; Wang, H. Comb-Type Pilot Aided Channel Estimation in Non-Contiguous OFDM Systems for Cognitive Radio. In Proceedings of the Conference on Wireless Communications, Networking and Mobile Computing (WiCom), Beijing, China, 24–26 September 2009; pp. 1–4. [Google Scholar]
- Zhang, Y.; Xu, X.; Chen, B.; Dai, X. A suboptimal pilot design for NC-OFDM systems. In Proceedings of the IEEE Conference on Communication Technology (ICCT), Nanjing, China, 11–14 November 2010; pp. 801–804. [Google Scholar]
- Manasseh, E.; Ohno, S.; Nakamoto, M. Pilot design for non-contiguous spectrum usage in OFDM-based cognitive radio networks. In Proceedings of the European Signal Processing Conference (EUSIPCO), Bucharest, Romania, 27–31 August 2012; pp. 465–469. [Google Scholar]
- Berger, C.R.; Wang, Z.; Huang, J.; Zhou, S. Application of compressive sensing to sparse channel estimation. IEEE Commun. Mag. 2010, 48, 164–174. [Google Scholar] [CrossRef]
- Jia, M.; Liu, X.; Gu, X. Channel estimation algorithm based on compressive sensing for NC-OFDM systems in cognitive radio context. Int. J. Adv. Comput. Technol. (IJACT) 2013, 5, 343–351. [Google Scholar]
- Chen, E.; Chu, C. Channel estimation for NC-OFDM systems based on subspace pursuit algorithm. In Proceedings of the IEEE Conference on Signal Processing (ICSP), Beijing, China, 21–25 October 2012; pp. 88–91. [Google Scholar]
- Huang, S.; Lin, J.; Chou, K. Novel Channel Estimation Techniques on SC-FDMA Uplink Transmission. In Proceedings of the IEEE Vehicular Technology Conference, Taipei, Taiwan, 16–19 May 2010; pp. 1–5. [Google Scholar]
- Luan, Y.; Kan, C.; Du, H.; Zhao, Q. An improved LS channel estimation algorithm of SC-FDMA. In Proceedings of the IEEE Conference on Anti-counterfeiting, Security, and Identification (ASID), Xiamen, China, 25–27 September 2015; pp. 128–131. [Google Scholar]
- Jin, X. Channel Estimation Techniques of SC-FDMA. Ph.D. Thesis, Karlstad University, Karlstad, Sweden, 2007. [Google Scholar]
- Mongol, B.; Yamazato, T.; Okada, H.; Katayama, M. Channel Estimation for BFDM/OQAM System in Dispersive Time-Varying Channels. In Proceedings of the International Symposium on Wireless Communication Systems, Valencia, Spain, 6–8 September 2006; pp. 159–163. [Google Scholar]
- Wang, X.; Wild, T.; Schaich, F.; ten Brink, S. Pilot-Aided Channel Estimation for Universal Filtered Multi-Carrier. In Proceedings of the IEEE Vehicular Technology Conference (VTC2015-Fall), Boston, MA, USA, 6–9 September 2015; pp. 1–5. [Google Scholar]
- Qi, C.; Wu, L. A hybrid compressed sensing algorithm for sparse channel estimation in MIMO OFDM systems. In Proceedings of the IEEE Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 3488–3491. [Google Scholar]
- Baltar, L.G.; Mezghani, A.; Nossek, J.A. Spectral efficient channel estimation algorithms for FBMC/OQAM systems: A comparison. In Proceedings of the International Symposium on Wireless Communications Systems (ISWCS), Barcelona, Spain, 26–29 August 2014; pp. 707–711. [Google Scholar]
- Kwon, B.; Kim, S.; Jeon, D.; Lee, S. Iterative Interference Cancellation and Channel Estimation in Evolved Multimedia Broadcast Multicast System Using Filter-Bank Multicarrier-Quadrature Amplitude Modulation. IEEE Trans. Broadcast. 2016, 62, 864–875. [Google Scholar] [CrossRef]
- Fuhrwerk, M.; Moghaddamnia, S.; Peissig, J. Scattered Pilot-Based Channel Estimation for Channel Adaptive FBMC-OQAM Systems. IEEE Trans. Wirel. Commun. 2017, 16, 1687–1702. [Google Scholar] [CrossRef] [Green Version]
- Lélé, C.; Javaudin, J.P.; Legouable, R.; Skrzypczak, A.; Siohan, P. Channel estimation methods for preamble-based OFDM/OQAM modulations. Eur. Trans. Telecommun. 2008, 19, 741–750. [Google Scholar] [CrossRef]
- Kofidis, E.; Katselis, D. Improved interference approximation method for preamble-based channel estimation in FBMC/OQAM. In Proceedings of the European Signal Processing Conference, Barcelona, Spain, 29 August–2 September 2011; pp. 1603–1607. [Google Scholar]
- Kofidis, E. Short preamble-based estimation of highly frequency selective channels in FBMC/OQAM. In Proceedings of the Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 8058–8062. [Google Scholar]
- Zhao, Z.; Vucic, N.; Schellmann, M. A simplified scattered pilot for FBMC/OQAM in highly frequency selective channels. In Proceedings of the International Symposium on Wireless Communications Systems (ISWCS), Barcelona, Spain, 26–29 August 2014; pp. 819–823. [Google Scholar]
- Baltar, L.G.; Mezghani, A.; Nossek, J.A. EM based per-subcarrier ML channel estimation for filter bank multicarrier systems. In Proceedings of the International Symposium on Wireless Communication Systems (ISWCS), Ilmenau, Germany, 27–30 August 2013; pp. 1–5. [Google Scholar]
- Aldababseh, M.; Jamoos, A. Estimation of FBMC/OQAM fading channels using dual Kalman filters. Sci. World J. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Tang, N.; He, S.; Wang, H.; Huang, Y.; Yang, L. Training sequence design for channel estimation and IQ imbalance compensation in GFDM systems. In Proceedings of the International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 11–13 October 2017; pp. 1–6. [Google Scholar]
- Zhang, J.; Li, Y.; Niu, K. Iterative channel estimation algorithm based on compressive sensing for GFDM. In Proceedings of the IEEE Conference on Network Infrastructure and Digital Content (IC-NIDC), Beijing, China, 23–25 September 2016; pp. 244–248. [Google Scholar]
- Vilaipornsawai, U.; Jia, M. Scattered-pilot channel estimation for GFDM. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Istanbul, Turkey, 6–9 April 2014; pp. 1053–1058. [Google Scholar]
- Niazadeh, R.; Babaie-Zadeh, M.; Jutten, C. On the Achievability of Cramér–Rao Bound in Noisy Compressed Sensing. IEEE Trans. Signal Process. 2012, 60, 518–526. [Google Scholar] [CrossRef]
- Zakaria, R.; Le Ruyet, D. A novel filter-bank multicarrier scheme to mitigate the intrinsic interference: application to MIMO systems. IEEE Trans. Wirel. Commun. 2012, 11, 1112–1123. [Google Scholar] [CrossRef]
- Tensubam, B.D.; Singh, S. A review on FBMC: An efficient multicarrier modulation system. Int. J. Comput. Appl. 2014, 98, 6–9. [Google Scholar]
- Danneberg, M.; Michailow, N.; Gaspar, I.; Zhang, D.; Fettweis, G. Flexible GFDM Implementation in FPGA with Support to Run-Time Reconfiguration. In Proceedings of the IEEE Vehicular Technology Conference, VTC Fall 2015, Boston, MA, USA, 6–9 September 2015; pp. 1–2. [Google Scholar]
- Viholainen, A.; Ihalainen, T.; Stitz, T.H.; Renfors, M.; Bellanger, M. Prototype filter design for filter bank based multicarrier transmission. In Proceedings of the European Signal Processing Conference, Glasgow, UK, 24–28 August 2009; pp. 1359–1363. [Google Scholar]
- Masson, J.; Picel, Z. Flexible design of computationally efficient nearly perfect QMF filter banks. In Proceedings of the IEEE Conference on Acoustics, Speech, and Signal Processing (ICASSP), Tampa, FL, USA, 26–29 April 1985; pp. 541–544. [Google Scholar]
- Saideh, M.; Berbineau, M.; Dayoub, I. On the Performance of Sliding Window TD-LMMSE Channel Estimation for 5G Waveforms in High Mobility Scenario. IEEE Trans. Veh. Technol. 2018, 67, 8974–8977. [Google Scholar] [CrossRef]
- Ihalainen, T.; Viholainen, A.; Stitz, T.H.; Renfors, M. Generation of filter bank-based multicarrier waveform using partial synthesis and time domain interpolation. IEEE Trans. Circuits Syst. I Regul. Papers 2010, 57, 1767–1778. [Google Scholar] [CrossRef]
- Baddour, K.E.; Beaulieu, N.C. Autoregressive modeling for fading channel simulation. Trans. Wirel. Commun. 2005, 4, 1650–1662. [Google Scholar] [CrossRef]
- Haykin, S. Adaptive Filter Theory; Prentice Hall: Upper Saddle River, NJ, USA, 1986. [Google Scholar]
- Scharf, L.L. Statistical Signal Processing: Detection, Estimation and Time Series Analysis; Addison-Wesley: Boston, MA, USA, 1991. [Google Scholar]
- Ghosh, M.; Srinivasarao, C.; Sahoo, H.K. Adaptive channel estimation in MIMO-OFDM for indoor and outdoor environments. In Proceedings of the Conference on Wireless Communications, Signal Processing and Networking (WiSPNET), Chennai, India, 22–24 March 2017; pp. 2743–2747. [Google Scholar]
- Rana, M.M.; Kim, J. LMS based blind channel estimation of SC-FDMA systems using variable step size and phase information. Electron. Lett. 2011, 47, 346–348. [Google Scholar] [CrossRef]
- Beena, A.O.; Pillai, S.S.; Vijayakumar, N. An Adaptive Sparse Channel Estimation algorithm with fast convergence for broad band MIMO-OFDM systems. In Proceedings of the IEEE Conference on Circuits and Systems (ICCS), Thiruvananthapuram, India, 20–21 December 2017; pp. 151–156. [Google Scholar]
- Rana, M.M. Performance comparison of LMS and RLS channel estimation algorithms for 4G MIMO OFDM systems. In Proceedings of the International Conference on Computer and Information Technology (ICCIT), Dhaka, Bangladesh, 22–24 December 2011; pp. 635–639. [Google Scholar]
- Chang, L.; Li, G.Y.; Li, J.; Li, R. Blind parameter estimation of GFDM signals over frequency-selective fading channels. IEEE Trans. Commun. 2016, 64, 1120–1131. [Google Scholar] [CrossRef]
- Michailow, N.; Mendes, L.; Matthé, M.; Gaspar, I.; Festag, A.; Fettweis, G. Robust WHT-GFDM for the Next Generation of Wireless Networks. IEEE Commun. Lett. 2015, 19, 106–109. [Google Scholar] [CrossRef]
- Farhang, A.; Marchetti, N.; Doyle, L.E. Low-Complexity Modem Design for GFDM. IEEE Trans. Signal Process. 2016, 64, 1507–1518. [Google Scholar] [CrossRef]
- Farhang, A.; Marchetti, N.; Doyle, L.E. Low complexity GFDM receiver design: A new approach. In Proceedings of the IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 4775–4780. [Google Scholar]
- Farhang-Boroujeny, B.; Moradi, H. Derivation of GFDM based on OFDM principles. In Proceedings of the IEEE Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 2680–2685. [Google Scholar]
- Wang, P.S.; Lin, D.W. Maximum-likelihood blind synchronization for GFDM systems. IEEE Signal Process. Lett. 2016, 23, 790–794. [Google Scholar] [CrossRef]
- Matthe, M.; Gaspar, I.; Zhang, D.; Fettweis, G. Reduced complexity calculation of LMMSE filter coefficients for GFDM. In Proceedings of the IEEE Vehicular Technology Conference, VTC F, Boston, MA, USA, 6–9 September 2015; pp. 1–2. [Google Scholar]
- Minn, H.; Al-Dhahir, N. Optimal training signals for MIMO OFDM channel estimation. IEEE Trans. Wirel. Commun. 2006, 5, 1158–1168. [Google Scholar] [CrossRef]
- Bandari, S.K.; Mani, V.V.; Drosopoulos, A. OQAM implementation of GFDM. In Proceedings of the International Conference on Telecommunications (ICT), Thessaloniki, Greece, 16–18 May 2016; pp. 1–5. [Google Scholar]
- Akyildiz, I.F.; Lee, W.-Y.; Vuran, M.C.; Mohanty, S. NeXt generation/dynamic spectrum access/cognitive radio wireless networks: A survey. J. Comput. Netw. 2006, 50, 2127–2159. [Google Scholar] [CrossRef]
- Schafhuber, D.; Matz, G. MMSE and adaptive prediction of time-varying channels for OFDM systems. IEEE Trans. Wirel. Commun. 2005, 4, 593–602. [Google Scholar] [CrossRef] [Green Version]
- Motade, S.N.; Kulkarni, A.V. Channel Estimation and Data Detection Using Machine Learning for MIMO 5G Communication Systems in Fading Channel. MDPI Technol. 2018, 6, 72. [Google Scholar] [CrossRef]














| Specifications | CP-OFDM | f-OFDM |
|---|---|---|
| Band structure | Single band | Multiple (sub) band |
| Filtering | Wideband filtering | Subband filtering required |
| Filter length | Less than length of CP | No longer than half of symbol duration |
| Sub-carrier spacing | Uniform | Different |
| Spectral efficiency | Poor | Better (from bandwidth splitting) |
| Computational Complexity | Low | Higher |
| Transmission Time Interval (TTI)/Latency | Long | Shorter |
| OOB leakages | High | Lower (due to subband filtering) |
| Time domain orthogonality | Orthogonal | Non-orthogonal |
| Frequency domain orthogonality | Orthogonal | Partly (quasi) Orthogonal |
| Throughput gain | Low | Higher |
| Specifications | CP-OFDM | SC-FDMA | f-OFDM | FBMC | UFMC | GFDM |
|---|---|---|---|---|---|---|
| Spectral efficiency | Low | Low | Low | High | High | High |
| Computational Complexity | Low | Low | Medium | High | High | High |
| OOB Emission | High | High | Low | Low | Low | Low |
| PAPR | High | Low | High | Medium | High | Medium |
| Latency | Medium | Medium | High | High | High | High |
| Flexibility | High | High | Medium | Medium | Medium | High |
| Robustness to CFO | Low | Low | Medium | High | High | High |
| Reference | Aim of Research | CE Schemes Applied | Applicable Technique or Waveform | Approach | Obtained Results |
|---|---|---|---|---|---|
| [86] | Time domain channel statistics pilot based CE over AWGN | LS and MMSE | Pilot-based CE for SISO-CP-OFDM | CE modifications assuming finite length impulse response | MMSE CE demonstrated superior performance over LS CE in terms of MSE and BER |
| [87] | Time domain channel statistics pilot based CE over AWGN | LS, MMSE and DFT based CE | Pilot-based CE for SISO-CP-OFDM | Time domain estimation of noise variance and channel autocorrelation estimation using denoise CIR | The MMSE estimator demonstrated superior performance to DFT based CE with LS offering the worst CE performance |
| [88] | Performance investigation of MLE and Bayesian MMSEE estimators over multipath fading channel | MLE and Bayesian MMSEE | Pilot-aided CE for SISO-CP-OFDM | Bayesian MMSEE Exploitation of prior channel information |
|
| [89] | To design optimal CE schemes for CP-OQAM-OFDM system in comparison to OQAM-OFDM system | WLS and PoP estimators | Pilot-aided CE for SISO-CP-OQAM-OFDM |
|
|
| [93] | Development of an analytic MSE formula for DDCE schemes in M-ary PSK modulated OFDM | Two dimensional DFT based DDCE | Pilot-based CE for SISO-CP-OFDM based on LTE/LTE-A | Dependent and identically distributed coded bit error | Simulated MSE performance obtained using the developed formula matches practical values for downlink LTE-A systems |
| [94] | Design of a novel CE technique for MU-MIMO OFDM systems | Virtual pilot based CE using iterative detection and decoding (IDD) | Pilot-assisted DDCE for MIMO -OFDM |
| Proposed estimator achieves substantial block error rate (BLER) performance gain over conventional single user CE schemes such as MMSE with SUD and MUD |
| [95] | Development of an inverse channel based blind CE (ICBCE) scheme for CP-OFDM to improve the CE performance with limited number of received blocks | ICBCE for CP-OFDM | Blind CE for SISO-CP- OFDM |
|
|
| [96] | Design of a novel semi-blind iterative space alternating generalised expectation (SAGE) based CE for massive MIMO systems | Semi-blind iterative SAGE CE | Pilot/data-assisted SAGE based CE for Massive MIMO | Iterative update of pilot based MMSE using SAGE algorithm |
|
| [97] | Design of blind ML detection with single orthogonal space time block codes OFDM (OSTBC-OFDM) blocks | Semi-blind/blind CE based on use of minimal training sequence | Semi-blind/blind CE for OSTBC-OFDM |
|
|
| [98] | Design of a low complexity semi-blind CE technique and recording scheme for two-way relay networks | Semi-blind CE based on MSE | Second order statistics based semi-blind CE for two-way relay networks |
|
|
| [99] | Derivation of a quasi-Newton based procedure for semi-blind CE in uplink cloud radio access networks (C-RANs) | Semi-blind CE based on quasi-Newton method | data symbols CE method |
|
|
| Reference | Aim of Research | CE Schemes Applied | Applicable Technique or Waveform | Approach | Obtained Results |
|---|---|---|---|---|---|
| [51] | Modification of GFDM systems for CE using orthogonal pilot insertion method for interference free CE | Interference free pilot insertion (IFPI) based CE | Pilot-assisted CE for GFDM transceivers | Insertion of pilot subsymbols such that received symbol frequency domain at pilot frequencies have no influence from the data subsymbols for IFPI CE |
|
| [112] | Reduced complexity CE for BFDM-OQAM transceivers in dispersive time-varying channels | Training-based CE for BFDM-OQAM | ML based CE for BFDM-OQAM based transceivers | ML CE based on use of correlation matrix | Proposed estimator offers significant robustness against Doppler spread |
| [113] | CE for UFMC based transceivers using FIR pre-compensation and SW approach | Pilot-aided CE for UFMC based transceivers | LS and LMMSE based approach for UFMC systems |
| UFMC achieves the same or slightly better SER performance under AWGN and frequency/flat fading vehicular-A channels in comparison to CP-OFDM systems using SW approach |
| [115] | Development of a novel narrowband per-subcarrier ML CE scheme for FBMC systems | EM based CE | Preamble-based CE for FBMC based transceivers |
| The EM-ML estimator offers improvement in spectral efficiency using few sub-carriers that are filled with training symbols |
| [119] | Performance analysis of Extended-IAM preamble-based CE scheme in comparison to IAM scheme | E-IAM preamble based CE | Preamble-based CE for Filter bank OFDM-OQAM | Design of a preamble structure which exploits the symmetry of the interference weights for generating pseudo-pilots of higher magnitude than IAM-C | The E-IAM-C algorithm demonstrates superiority over IAM-R and IAM-C techniques in terms of NMSE at various SNR values over mildly and highly frequency selective fading channels |
| [118] | Development of two novel CE schemes for filter bank OFDM-OQAM based transceivers | Pair of real Pilots (PoP) and IAM preamble based CE | Pilot-based CE for OFDM-OQAM |
| OQAM-IAM method demonstrated superior performance in comparison to OQAM-PoP in both CP-OFDM and OFDM-OQAM based transceivers |
| [122] | Performance comparison of three variants of interference embedded CE |
| Preamble-based CE for FBMC-OQAM based transceivers |
|
|
| [124] | Design of training sequence for IQ imbalance and CE in GFDM systems with low complexity receiver | Training sequence design for IQ imbalance estimation | Preamble-based CE for GFDM transceivers | Sparse frequency domain based training sequence design over low complexity GFDM systems | The proposed technique improves the BER performance of GFDM systems in comparison to uncompensated case |
| [125] |
| CS based OMP CE | Pilot-based CE for GFDM transceivers | Adoption of OMP technology for accurate CE to yield precise reconstruction of ICI |
|
| Overlapping Factor (K) | 4 | 3 | 2 | 1 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Filter impulse () | ||||||||||
| 1 | 0.9720 | 0.2351 | 1 | 0.9114 | 0.4114 | 1 | 1 | |||
| Parameters | Specification | |
|---|---|---|
| OFDM-OQAM | GFDM-OQAM | |
| No. of Sub-carriers | 512 | 512 |
| Signal Constellation | 16-QAM-OQAM | 16-QAM-OQAM |
| Sampling Frequency | 10,000 Hz | 10,000 Hz |
| Doppler Frequency | 10 and 200 (Hz) | 10 and 200 (Hz) |
| Sampling Rate | ||
| Doppler Rate(s) | 0.001 and 0.02 | 0.001 and 0.02 |
| Overlapping Factor | 4 | 4 |
| Filter Coefficient | 0.97195983 | 0.97195983 |
| Channel Type | Rayleigh fading | Rayleigh fading |
| Cyclic Prefix Overhead | − | 25% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ijiga, O.E.; Ogundile, O.O.; Familua, A.D.; Versfeld, D.J.J. Review of Channel Estimation for Candidate Waveforms of Next Generation Networks. Electronics 2019, 8, 956. https://doi.org/10.3390/electronics8090956
Ijiga OE, Ogundile OO, Familua AD, Versfeld DJJ. Review of Channel Estimation for Candidate Waveforms of Next Generation Networks. Electronics. 2019; 8(9):956. https://doi.org/10.3390/electronics8090956
Chicago/Turabian StyleIjiga, Owoicho E., Olayinka O. Ogundile, Ayokunle D. Familua, and Daniel J. J. Versfeld. 2019. "Review of Channel Estimation for Candidate Waveforms of Next Generation Networks" Electronics 8, no. 9: 956. https://doi.org/10.3390/electronics8090956
APA StyleIjiga, O. E., Ogundile, O. O., Familua, A. D., & Versfeld, D. J. J. (2019). Review of Channel Estimation for Candidate Waveforms of Next Generation Networks. Electronics, 8(9), 956. https://doi.org/10.3390/electronics8090956





