A Novel 3D Encapsulation Structure Based on Subwavelength Structure and Inserted Pyrex Glass for RF MEMS Infrared Detectors
Abstract
:1. Introduction
2. Structure Design and Discussion
2.1. Optical Transmission of the 3D Encapsulation Structure
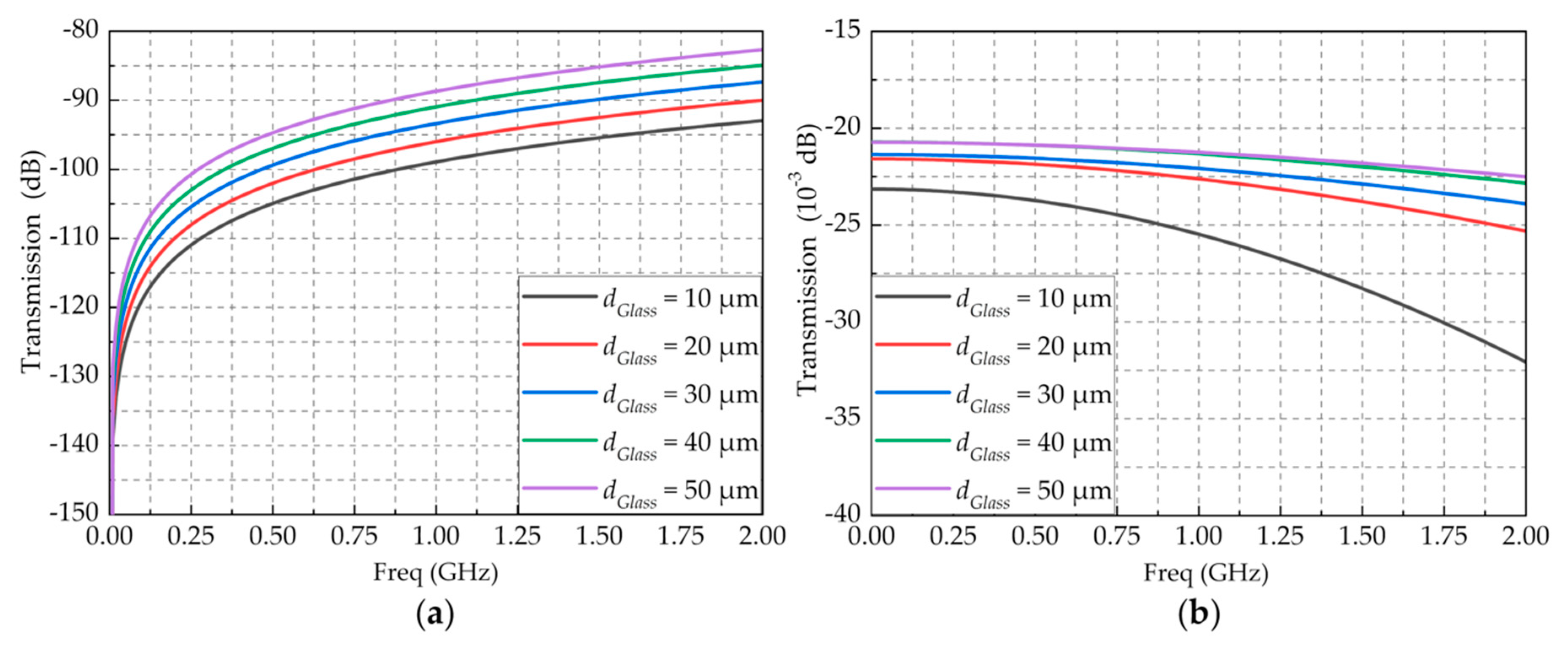
2.2. Electrical Transmission of the 3D Encapsulation Structure
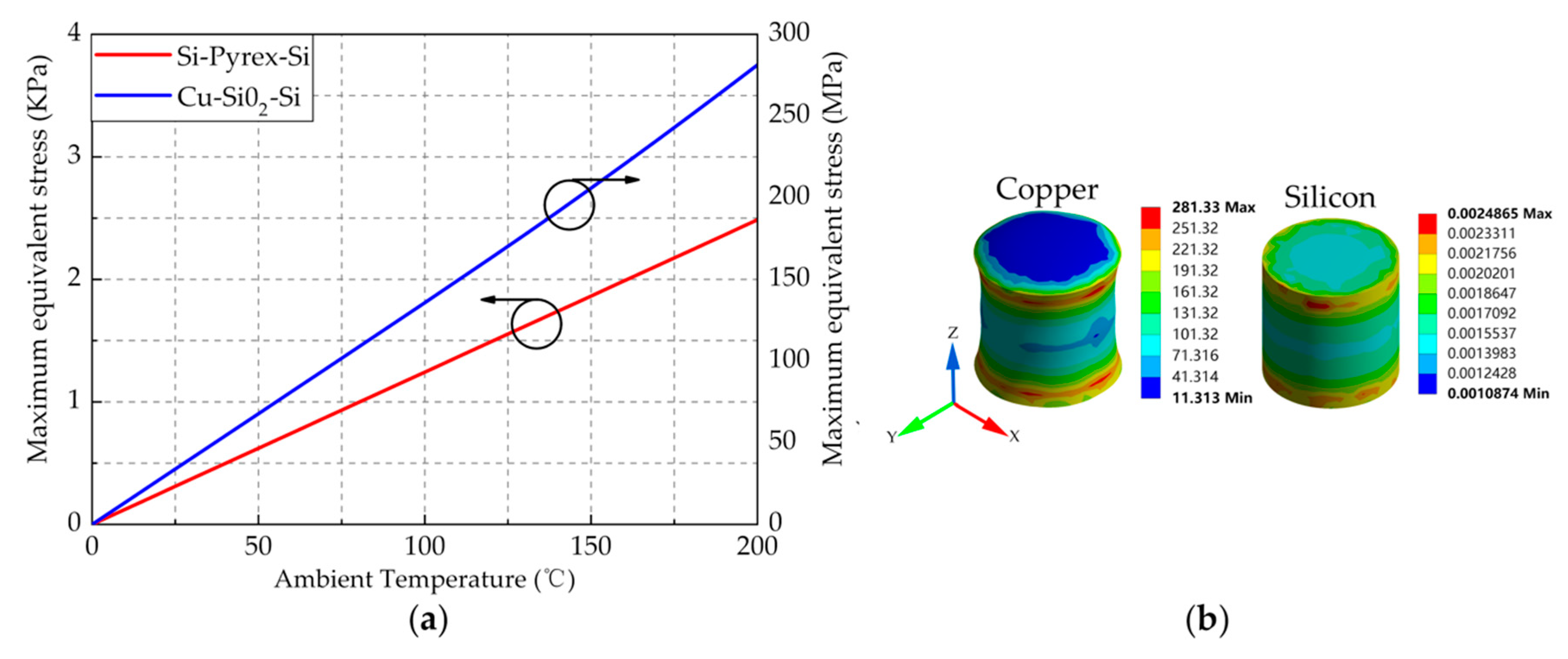
2.3. Thermal Stress of the 3D Encapsulation Structure
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hui, Y.; Gomez-Diaz, J.S.; Qian, Z.Y.; Alu, A.; Rinaldi, M. Plasmonic piezoelectric nanomechanical resonator for spectrally selective infrared sensing. Nat. Commun. 2016, 7, 11249. [Google Scholar] [CrossRef] [PubMed]
- Qian, Z.; Hui, Y.; Liu, F.; Kai, S.; Rinaldi, M. 1.27 GHz Graphene-Aluminum Nitride nano plate resonant infrared detector. In Proceedings of the 18th International Conference on Solid-State Sensors, Actuators and Microsystems, Anchorage, AK, USA, 21–25 June 2015; pp. 1429–1432. [Google Scholar]
- Kozlowski, L.J.; Arias, J.M.; Williams, G.M.; Vural, K.; Cooper, D.E.; Cabelli, S.A.; Bruce, C.F., Jr. Recent advances in staring hybrid focal plane arrays: Comparison of HgCdTe, InGaAs, and GaAs/AlGaAs detector technologies. Proc. SPIE 1994, 2274, 93–116. [Google Scholar]
- Rogalski, A. Infrared detectors: Status and trends. Prog. Quantum Electron. 2003, 27, 59–210. [Google Scholar] [CrossRef]
- Hotel, O.; Poli, J.P.; Mer-Calfati, C.; Scorsone, E.; Saada, S. A review of algorithms for SAW sensors e-nose based volatile compound identification. Sens. Actuat. B-Chem. 2018, 255, 2472–2482. [Google Scholar] [CrossRef]
- Candler, R.N.; Hopcroft, M.A.; Kim, B.; Park, W.-T.; Melamud, R.; Agarwal, M.; Yama, G.; Partridge, A.; Lutz, M.; Kenny, T.W. Long-Term and Accelerated Life Testing of a Novel Single-Wafer Vacuum Encapsulation for MEMS Resonators. J. Microelectromech. Syst. 2006, 15, 1446–1456. [Google Scholar] [CrossRef]
- Chen, K.-L.; Wang, S.S.; Salvia, J.C.; Melamud, R.; Howe, R.T.; Kenny, T.W. Wafer-Level Epitaxial Silicon Packaging for Out-of-Plane RF MEMS Resonators with Integrated Actuation Electrodes. IEEE Trans. Compon. Packag. Manuf. Technol. 2011, 1, 310–317. [Google Scholar] [CrossRef]
- Lim, Y.Y.; Chen, B.T.; Yu, A.B.; Shi, J.L. A broadband 3D package for RF MEMS devices utilizing through silicon vias (TSV). In Proceedings of the 16th International Conference on Solid-State Sensors, Actuators and Microsystems, Beijing, China, 5–9 June 2011; pp. 406–409. [Google Scholar]
- Wang, Z.Y. 3-D Integration and Through-Silicon Vias in MEMS and Microsensors. J. Microelectromech. Syst. 2015, 24, 1211–1244. [Google Scholar] [CrossRef]
- Arab, J.; Mishra, D.K.; Kannojia, H.K.; Adhale, P.; Dixit, P. Fabrication of multiple through-holes in non-conductive materials by Electrochemical Discharge Machining for RF MEMS Packaging. J. Mater. Process. Tech. 2019, 271, 542–553. [Google Scholar] [CrossRef]
- Zoschke, K.; Manier, C.-A.; Wilke, M.; Oppermann, H.; Ruffieux, D.; Dekker, J.; Jaakkola, A.; Pizza, S.D.; Allegato, G.; Lang, K.-D. Application of TSV integration and wafer bonding technologies for hermetic wafer level packaging of MEMS components for miniaturized timing devices. In Proceedings of the 65th International Conference on Electronic Components and Technology, San Diego, CA, USA, 26–29 May 2015; pp. 1343–1350. [Google Scholar]
- Marauska, S.; Claus, M.; Lisec, T.; Wagner, B. Low temperature transient liquid phase bonding of Au/Sn and Cu/Sn electroplated material systems for MEMS wafer-level packaging. Microsyst. Technol. 2013, 19, 1119–1130. [Google Scholar] [CrossRef]
- Jin, J.Y.; Yoo, S.; Yoo, B.W.; Kim, Y.K. Characterisation of silicon through-vias for wafer-level interconnection with glass reflows. Electron. Lett. 2012, 48, 1354–1355. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, J.; He, Y.R.; Yang, F.; Yang, F.H.; Han, G.W.; Si, C.W.; Ning, J. Research on a 3D Encapsulation Technique for Capacitive MEMS Sensors Based on Through Silicon Via. Sensors 2019, 19, 93. [Google Scholar] [CrossRef] [PubMed]
- Haque, R.M.; Wise, K.D. A Glass-in-Silicon Reflow Process for Three-Dimensional Microsystems. J. Microelectromech. Syst. 2013, 22, 1470–1477. [Google Scholar] [CrossRef]
- Yu, H.; Rinaldi, M. Fast and high resolution thermal detector based on an aluminum nitride piezoelectric microelectromechanical resonator with an integrated suspended heat absorbing element. Appl. Phys. Lett. 2013, 102, 093501. [Google Scholar]
- Su, W.T.; Li, B.; Liu, D.Q.; Zhang, F.S. Characterization and application of cerium fluoride film in infrared antireflection coating. Infrared Phys. Technol. 2009, 52, 204–207. [Google Scholar] [CrossRef]
- Wu, H. Cost-effective double-layer antireflection coatings in mid-wavelength infrared band. Infrared Phys. Technol. 2014, 67, 473–476. [Google Scholar] [CrossRef]
- Wang, Y.K.; Hong, X.R.; Yang, G.F.; Sang, T. Filtering characteristics of a graphene ribbon with a rectangle ring in infrared region. AIP Adv. 2016, 6, 115311. [Google Scholar] [CrossRef] [Green Version]
- Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Planar Photonics with Metasurfaces. Science 2013, 339, 1232009. [Google Scholar] [CrossRef] [Green Version]
- Jaksic, Z.; Smiljanic, M.M.; Vasiljevic-Radovic, D.; Obradov, M.; Radulovic, K.; Tanaskovic, D.; Krstajic, P.M. Field localization control in aperture-based plasmonics by Boolean superposition of primitive forms at deep subwavelength scale. Opt. Quant. Electron. 2016, 48, 225. [Google Scholar] [CrossRef]
- Niu, K.K.; Huang, Z.X.; Fang, M.; Li, M.Q.; Li, X.H.; Wu, X.L. Coupling of Gain Medium and Extraordinary Optical Transmission for Effective Loss Compensation. IEEE Access 2018, 6, 14820–14826. [Google Scholar] [CrossRef]
- Gao, H.; Zheng, Z.Y.; Chen, S.J.; Hao, H.Y. Achieving enhanced mid-infrared transmission through subwavelength periodic structures via redshift effect of the extraordinary optical transmission. J. Mod. Opt. 2014, 61, 766–772. [Google Scholar] [CrossRef]
- Ruan, H.X.; Shuang, Y.; Wang, L.G.; Li, L.L. Calculation of the Transmission Through a Rectangular Hole Filled with an Extreme Uniaxial Metamaterial. IEEE Trans. Antenn. Propag. 2018, 66, 6414–6419. [Google Scholar] [CrossRef]
- Tanaka, S.J. Wafer-level hermetic MEMS packaging by anodic bonding and its reliability issues. Microelectron. Reliab. 2014, 54, 875–881. [Google Scholar] [CrossRef]
- Lei, C.X.; Chen, L.Y.; Tang, Z.X.; Li, D.Y.; Cheng, Z.Z.; Tang, S.L.; Du, Y.W. Enhancement of magneto-optical Faraday effects and extraordinary optical transmission in a tri-layer structure with rectangular annular arrays. Opt. Lett. 2016, 41, 729–732. [Google Scholar] [CrossRef] [PubMed]
- Behera, G.; Ramakrishna, S.A. Enhanced broadband transmission through structured plasmonic thin films for transparent electrodes. J. Nanophotonics 2014, 8, 083889. [Google Scholar] [CrossRef]
- Ordal, M.A.; Bell, R.J.; Alexander, R.W.; Long, L.L.; Querry, M.R. Optical properties of Au, Ni, and Pb at submillimeter wavelengths. Appl. Opt. 1987, 26, 744–752. [Google Scholar] [CrossRef]
- Lynch, D.W.; Hunter, W.R. Handbook of Optical Constants of Solids, An Introduction to the Data for Several Metals; Academic Press: Salt Lake, UT, USA, 1997; Volume 2, pp. 341–419. [Google Scholar]
- Xiao, S.S.; Peng, L.; Mortensen, N.A. Enhanced transmission of transverse electric waves through periodic arrays of structured subwavelength apertures. Opt. Express 2010, 18, 6040–6047. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zayats, A.V.; Smolyaninov, I.I.; Maradudin, A.A. Nano-optics of surface plasmon polaritons. Phys. Rep. 2005, 408, 131–314. [Google Scholar] [CrossRef]
- Zhang, M.; Huang, C.P.; Wang, G.D.; Zhu, Y.Y. Theory of extraordinary light transmission through sub-wavelength circular hole arrays. J. Opt. 2010, 12, 015004. [Google Scholar] [CrossRef]
- Krishnan, A.; Thio, T.; Kim, T.J.; Lezec, H.J.; Ebbesen, T.W.; Wolff, P.A.; Pendry, J.; Martin-Moreno, L.; Garcia-Vidal, F.J. Evanescently coupled resonance in surface plasmon enhanced transmission. Opt. Commun. 2001, 200, 1–7. [Google Scholar] [CrossRef]
- Degiron, A.; Ebbesen, T.W. The role of localized surface plasmon modes in the enhanced transmission of periodic subwavelength apertures. J. Opt. A Pure Appl. Opt. 2005, 7, S90–S96. [Google Scholar] [CrossRef]


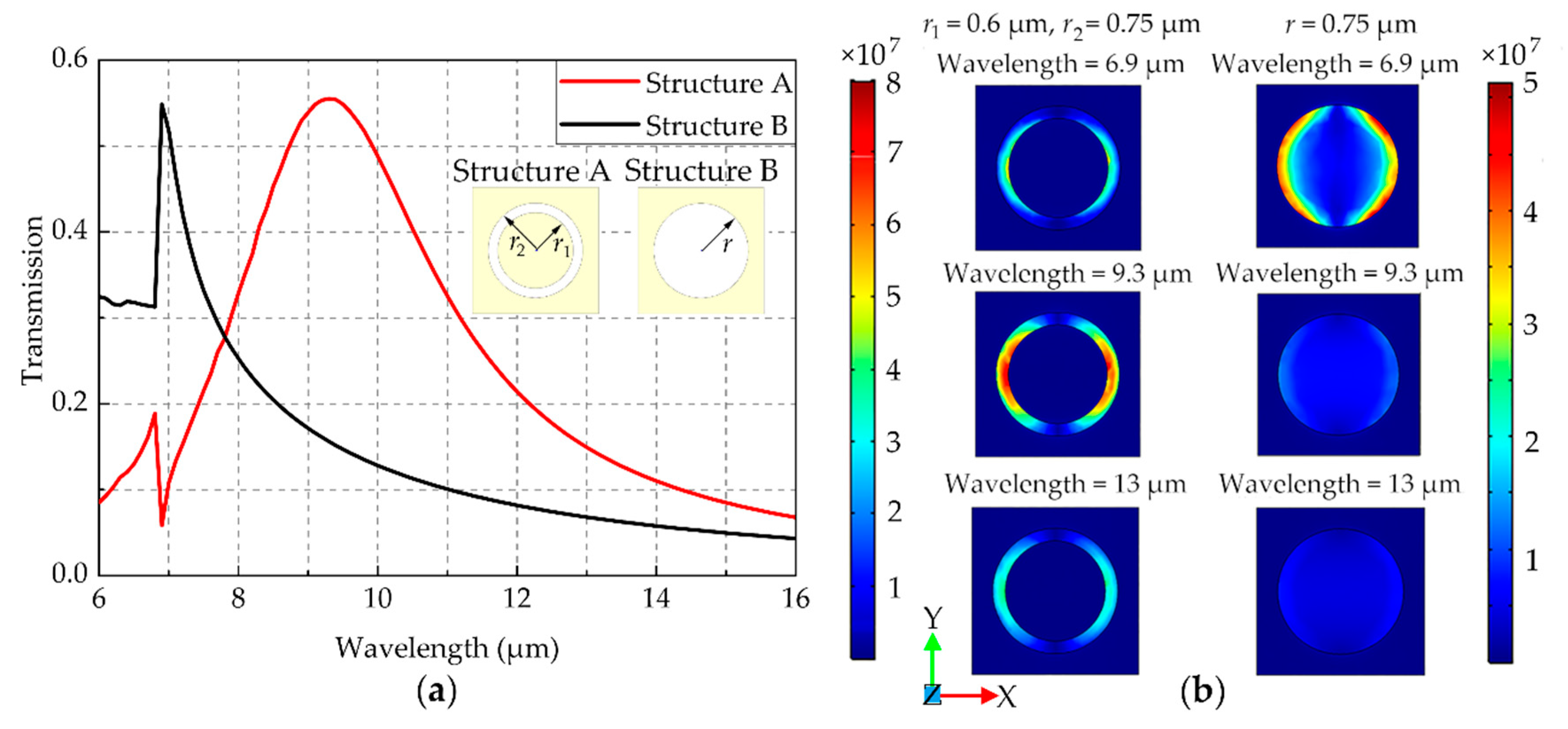
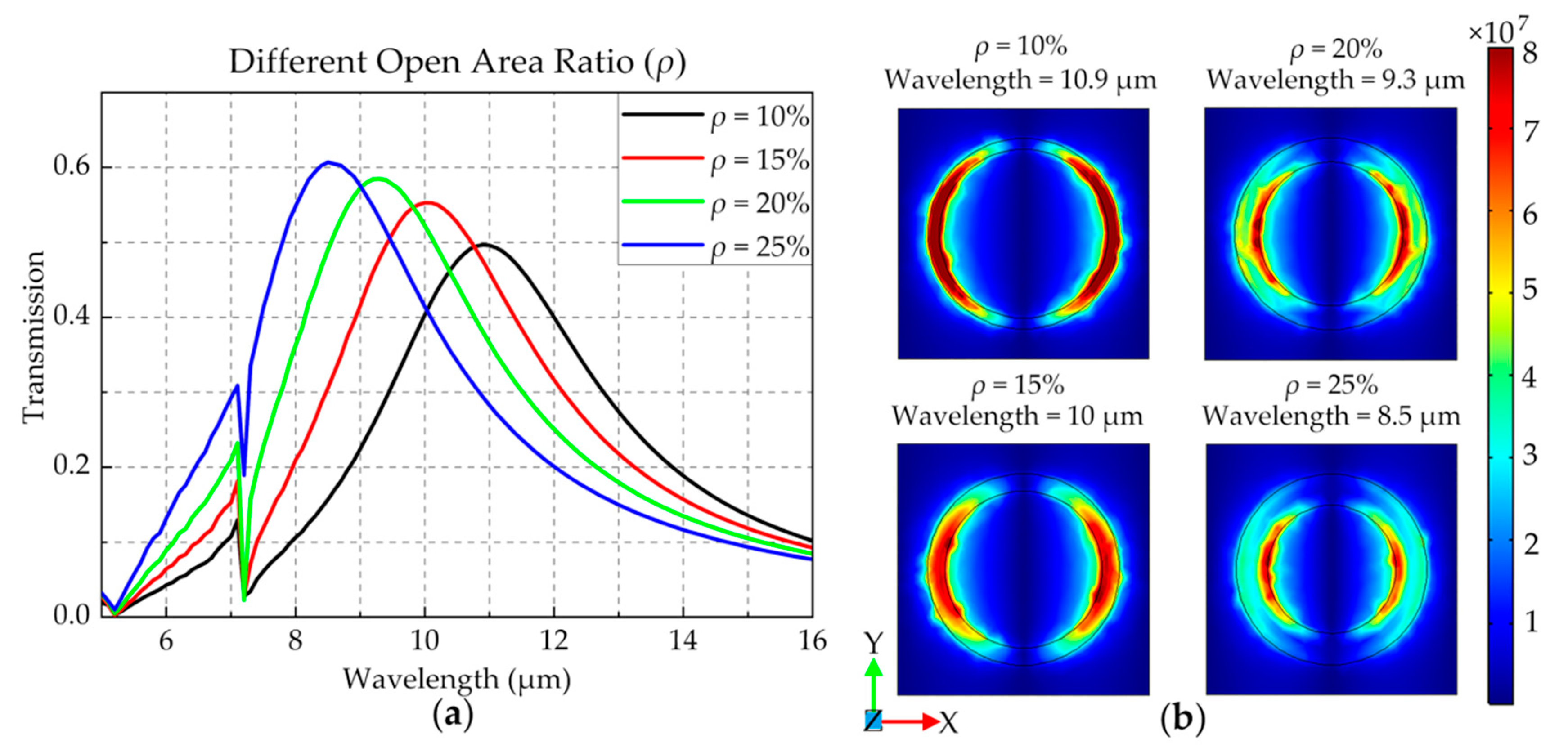
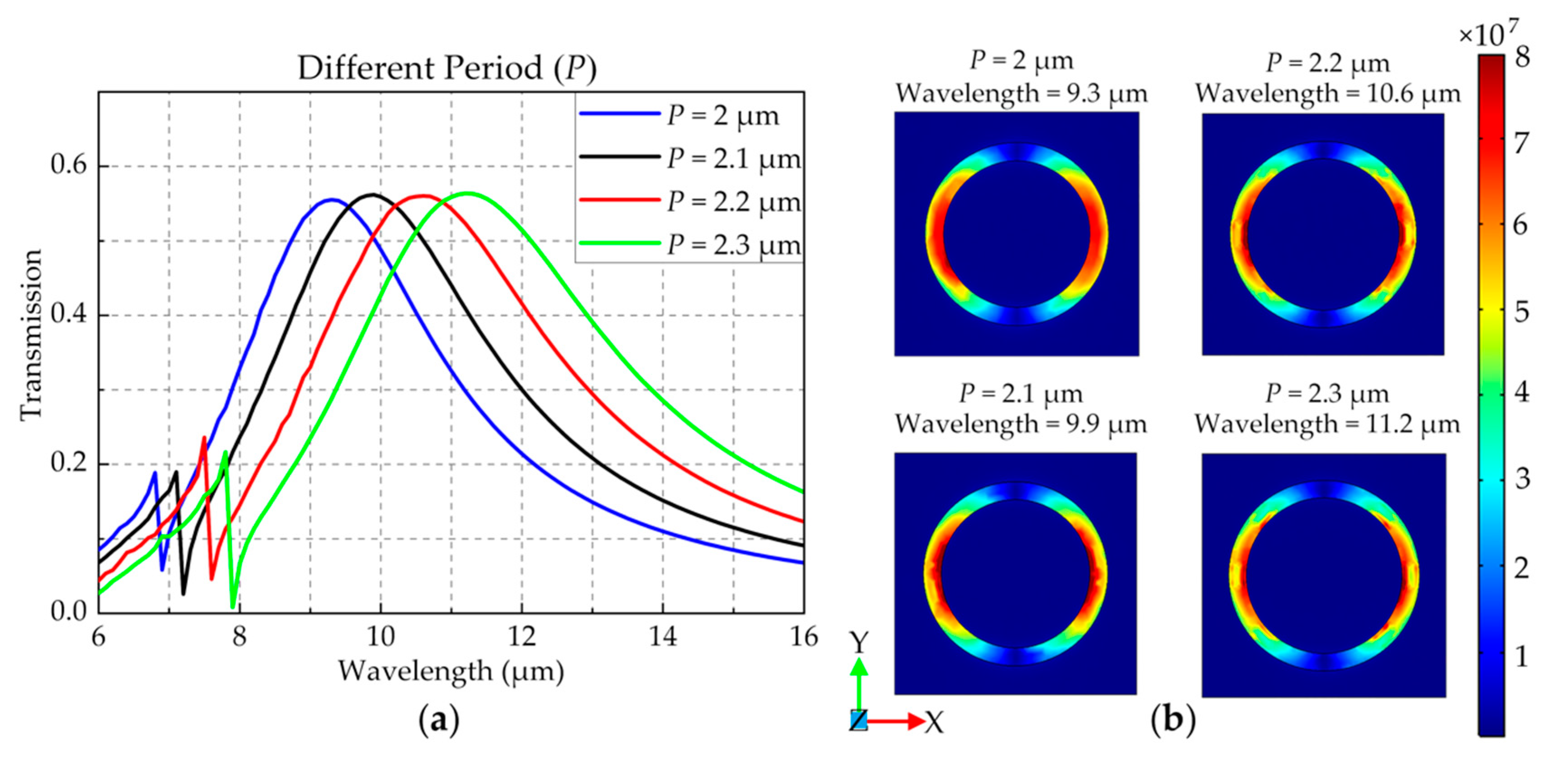
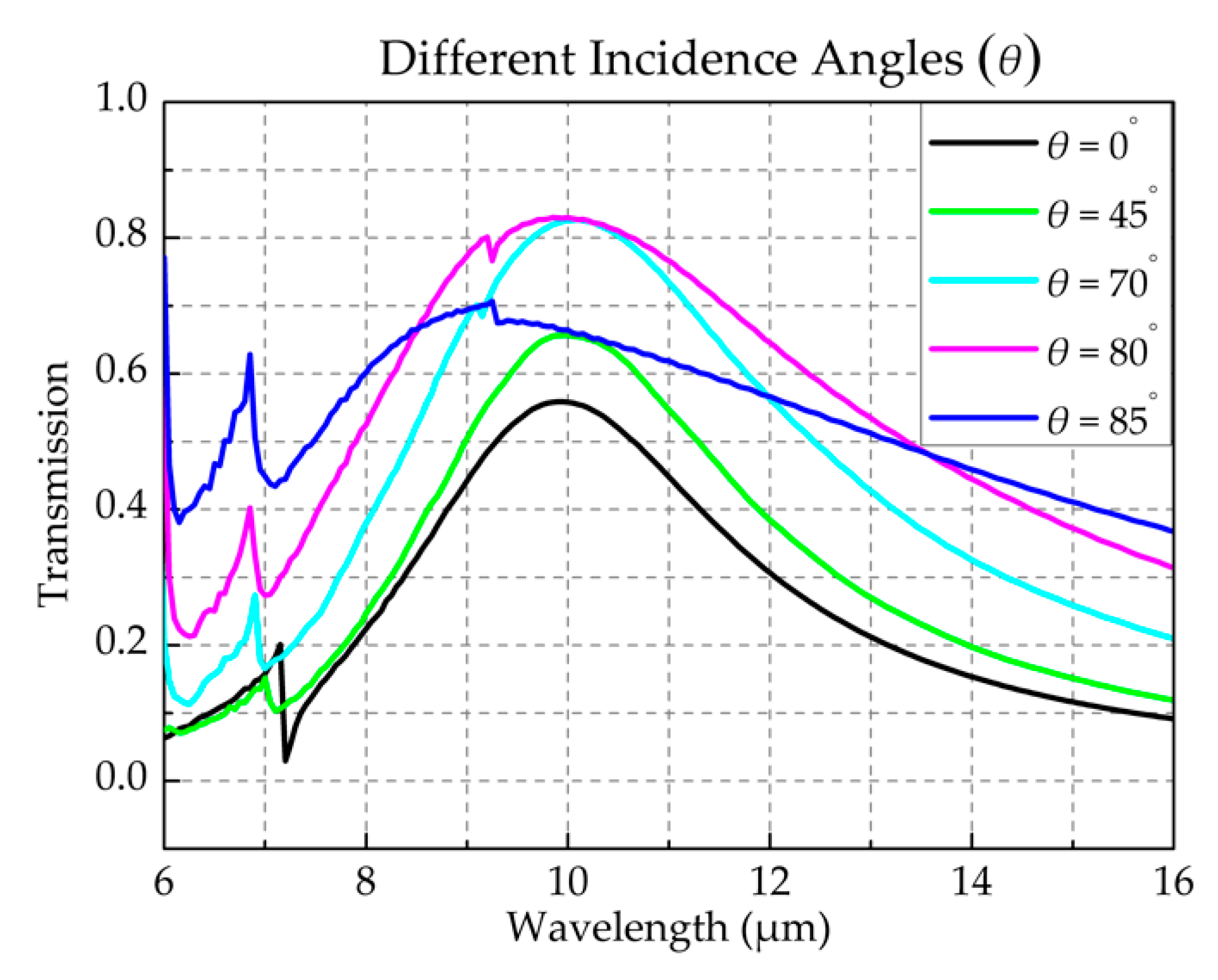


| Structure | Feedthrough Conductivity | Feedthrough Radius | Substrate Conductivity | Insulation Thickness |
|---|---|---|---|---|
| This work | 1 × 105 S/m | 50 μm | 1 × 105 S/m | 50 μm |
| TSV A | 5.8 × 107 S/m | 50 μm | 1 × 105 S/m | 1 μm |
| TSV B | 5.8 × 107 S/m | 50 μm | 0 S/m | 1 μm |
| Material | Si | Cu | Pyrex Glass | SiO2 |
|---|---|---|---|---|
| Density (kg/m3) | 5050 | 8300 | 2230 | 2220 |
| TEC (1/°C) | 2.81 × 10−6 | 1.80 × 10−5 | 3.25 × 10−6 | 0.5 × 10−6 |
| Young’s Modulus (Pa) | 1.30 × 1011 | 1.10 × 1011 | 9.10 × 106 | 7.31 × 106 |
| Poisson’s ratio | 0.28 | 0.34 | 0.2 | 0.17 |
| Thermal Conductivity (W/(m∙°C)) | 125 | 401 | 1.13 | 1.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Ge, M.; Song, C.; Sun, L.; Sun, H. A Novel 3D Encapsulation Structure Based on Subwavelength Structure and Inserted Pyrex Glass for RF MEMS Infrared Detectors. Electronics 2019, 8, 974. https://doi.org/10.3390/electronics8090974
Zhao J, Ge M, Song C, Sun L, Sun H. A Novel 3D Encapsulation Structure Based on Subwavelength Structure and Inserted Pyrex Glass for RF MEMS Infrared Detectors. Electronics. 2019; 8(9):974. https://doi.org/10.3390/electronics8090974
Chicago/Turabian StyleZhao, Jicong, Mingmin Ge, Chenguang Song, Ling Sun, and Haiyan Sun. 2019. "A Novel 3D Encapsulation Structure Based on Subwavelength Structure and Inserted Pyrex Glass for RF MEMS Infrared Detectors" Electronics 8, no. 9: 974. https://doi.org/10.3390/electronics8090974
APA StyleZhao, J., Ge, M., Song, C., Sun, L., & Sun, H. (2019). A Novel 3D Encapsulation Structure Based on Subwavelength Structure and Inserted Pyrex Glass for RF MEMS Infrared Detectors. Electronics, 8(9), 974. https://doi.org/10.3390/electronics8090974





