Single-Phase Inverter Deadbeat Control with One-Carrier-Period Lag
Abstract
:1. Introduction
2. Deadbeat Control Design of Multi-Loop Inverter Control Structure
2.1. Multi-Loop Inverter Control Structure
2.2. Deadbeat Control Theory
2.2.1. Design of the Deadbeat Controller of the Inner Current Loop
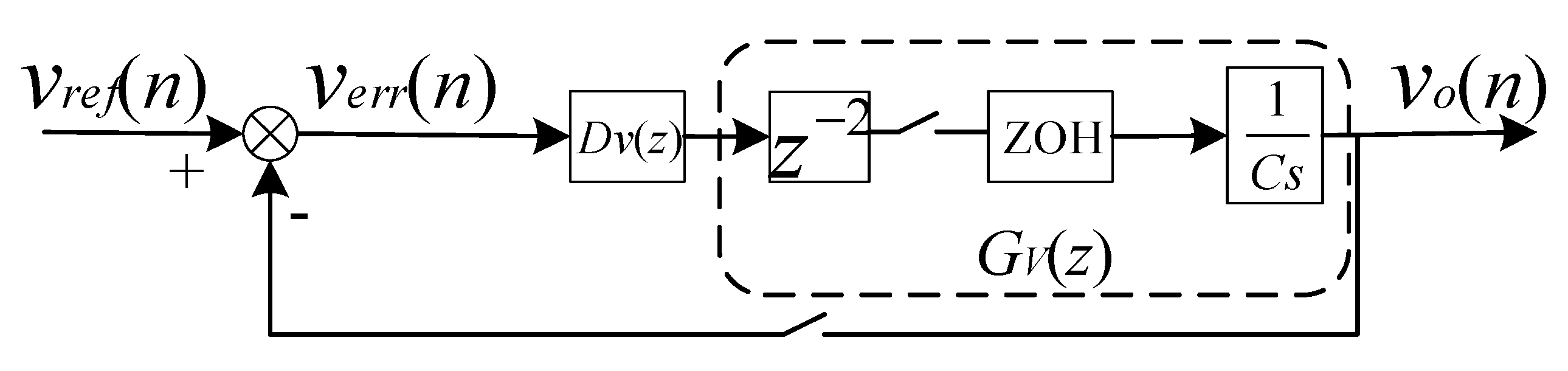
2.2.2. Design of the Deadbeat Controller of the Outer Voltage Loop
3. Simulation and Experiment
3.1. Robustness of the Proposed Control Scheme
3.2. Simulation Results
3.3. Experiment Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| DC bus voltage | |
| reference voltage | |
| load current | |
| capacitance voltage | |
| inductance current | |
| output voltage of the full bridge | |
| R | equivalent resistance of the inductor |
| L | filter inductor |
| C | filter capacitor |
| closed-loop z-transfer function of the deadbeat control | |
| deadbeat controller z-transfer function | |
| z-transfer function of the discrete controlled object in the current loop | |
| z-transfer function of the unit step | |
| current-loop error sequence | |
| z-transfer function of the current closed loop | |
| undetermined polynomial of | |
| deadbeat controller z-transfer function of the current loop | |
| z-transfer function of the discrete controlled object in the voltage loop | |
| voltage error sequence | |
| z-transfer function of the voltage closed loop | |
| deadbeat controller z-transfer function of the voltage loop |
References
- Shan, H.; Peng, L.; Kong, X.; Ouyang, H.; Liu, Z.; Wang, S. Effect of Digital Process on the Performance of Pulse Width Modulation Inverter. Proc. CSEE 2009, 29, 29–35. [Google Scholar]
- Peng, L.; Zhang, K.; Kang, Y.; Chen, J. Performance analysis and improvement of digital controlled PWM inverter. Proc. CSEE 2006, 26, 65–70. [Google Scholar]
- Deng, H.; Oruganti, R.; Srinivasan, D. PWM methods to Handle time delay in digital control of a UPS inverter. IEEE Power Electron. Lett. 2005, 3, 1–6. [Google Scholar] [CrossRef]
- Kai, Z.; Yong, K.; Jian, X.; Jian, C. Direct repetitive control of SPWM inverter for UPS purpose. IEEE Trans. Power Electron. 2003, 18, 784–792. [Google Scholar]
- Sintanavevong, W.; Boonto, S.; Naetiladdanon, S. Robust repetitive control with feedforward scheme for stand-alone inverter. In Proceedings of the 2016 16th International Conference on Control, Automation and Systems (ICCAS), Gyeongju, Korea, 16–19 October 2016; pp. 359–364. [Google Scholar]
- 519-2014-IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE: Piscataway, NJ, USA, 2014. [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Liserre, M.; Loh, P.C. Proportional-resonant controllers and filters for grid-connected voltage-source converters. IEE Proc.-Electr. Power Appl. 2006, 153, 750–762. [Google Scholar] [CrossRef] [Green Version]
- Castilla, M.; Miret, J.; Matas, J.; Vicuna, L.G.; Guerrero, J.M. Linear current control scheme with series resonant harmonic compensator for single-phase grid-connected photovoltaic inverters. IEEE Trans. Ind. Electron. 2008, 55, 2724–2733. [Google Scholar] [CrossRef]
- Biricik, S.; Komurcugil, H. Proportional-Integral and Proportional-Resonant Based Control Strategy for PUC Inverters. In Proceedings of the IECON 2018 44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 3369–3373. [Google Scholar]
- Gokhale, K.P.; Kawamura, A.; Hoft, R.G. Deadbeat microprocessor Control of PWM Inverter for Sinusoidal Output Waveform Synthesis. IEEE Trans. Ind. Appl. 1987, 5, 901–910. [Google Scholar] [CrossRef]
- Kawamura, A.; Chuarayapratio, R.; Haneyoshi, T. Deadbeat control of PWM inverter with modified pulse pattern for uninterruptible power supply. IEEE Trans. Ind. Electron. 1988, 35, 295–300. [Google Scholar] [CrossRef]
- Jung, S.; Huang, H.; Chang, M. DSP-Based Multiple-loop control strategy for single-phase inverters used in AC power sources. In Proceedings of the 28th IEEE Power Electronics Specialists Conference, Saint Louis, MO, USA, 27–27 June 1997; pp. 22–27. [Google Scholar]
- Abdel-Rahim, N.M.; Quaicoe, J.E. Analysis and design of a multiple feedback loop control strategy for single-phase voltage-source UPS inverters. IEEE Trans. PE 1996, 11, 532–541. [Google Scholar] [CrossRef]
- Buso, S.; Fasolo, S.; Mattavelli, P. Uninterruptible Power Supply Multi-Loop Control Employing Digital Predictive Voltage and Current Regulator. IEEE Trans. Ind. Appl. 2001, 37, 1846–1854. [Google Scholar] [CrossRef]
- Mattavelli, P. An improved deadbeat control for UPS using disturbance observers. IEEE Trans. Ind. Electron. 2005, 52, 206–212. [Google Scholar] [CrossRef]
- Ueta, H.; Yokoyama, T. 1MHz Multisampling Deadbeat Control with Disturbance Compensation Method for Three Phase PWM Inverter. In Proceedings of the 2018 International Power Electronics Conference, Niigata, Japan, 20–24 May 2018; pp. 1883–1889. [Google Scholar]
- Mohamed, Y.A.I.; El-Saadany, E.F. An Improved Deadbeat Current Control Scheme with a Novel Adaptive Self-Tuning Load Model for a Three-Phase PWM Voltage-Source Inverter. IEEE Trans. Ind. Electron. 2007, 54, 747–759. [Google Scholar] [CrossRef]
- Monfared, M.; Golestan, S.; Guerrero, J.M. Analysis Design and Experimental Verification of a Synchronous Reference Frame Voltage Control for Single-Phase Inverters. Ind. Electron. IEEE Trans. 2014, 61, 258–269. [Google Scholar] [CrossRef]
- Lazzarin, T.B.; Bauer, G.A.T.; Barbi, I. A Control Strategy for Parallel Operation of Single-Phase Voltage Source Inverters: Analysis Design and Experimental Results. Ind. Electron. IEEE Trans. 2013, 60, 2194–2204. [Google Scholar] [CrossRef]









| Rated power | 2.4 kW |
| Rated output voltage | 220 V |
| DC bus voltage | 400 V |
| Filter inductance | 1.2 mH |
| Inductance resistance | 0.68 Ω |
| Filter capacitance | 30 uF |
| PWM frequency | 16 kHz |
| Sampling frequency | 16 kHz |
| Resistive Load | Rectifier Load | |||||
|---|---|---|---|---|---|---|
| Full Load | Half Load | Empty Load | Full Load | Half Load | Empty Load | |
| The PI scheme | 2.02 | 1.83 | 0.87 | 2.63 | 2.37 | 1.52 |
| The proposed | 1.62 | 1.39 | 0.38 | 2.34 | 2.11 | 1.27 |
| Resistive Load | Rectifier Load | |||||
|---|---|---|---|---|---|---|
| Full Load | Half Load | Empty Load | Full Load | Half Load | Empty Load | |
| THD (%) | 1.90 | 1.84 | 0.98 | 2.96 | 2.61 | 1.87 |
| RMS (V) | 216 | 212 | 214 | 215 | 215 | 213 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, W.; Cui, J.; Yao, W. Single-Phase Inverter Deadbeat Control with One-Carrier-Period Lag. Electronics 2020, 9, 154. https://doi.org/10.3390/electronics9010154
Yao W, Cui J, Yao W. Single-Phase Inverter Deadbeat Control with One-Carrier-Period Lag. Electronics. 2020; 9(1):154. https://doi.org/10.3390/electronics9010154
Chicago/Turabian StyleYao, Wei, Jiamin Cui, and Wenxi Yao. 2020. "Single-Phase Inverter Deadbeat Control with One-Carrier-Period Lag" Electronics 9, no. 1: 154. https://doi.org/10.3390/electronics9010154
APA StyleYao, W., Cui, J., & Yao, W. (2020). Single-Phase Inverter Deadbeat Control with One-Carrier-Period Lag. Electronics, 9(1), 154. https://doi.org/10.3390/electronics9010154





