Maximized Privacy-Preserving Outsourcing on Support Vector Clustering
Abstract
:1. Introduction
- (1)
- A reformative SVC with elementary operations (RSVC-EO) is proposed with an updated dual coordinate descent (DCD) solver for the dual problem. In the training phase, it prefers a linear method to approach the objective without losing validity. Furthermore, it easily trades time for space by calculating kernel values on demand.
- (2)
- A fresh convex decomposition clustering labeling (FCDCL) method is presented, by which iterations are not required for convex decomposition. In connectivity analysis, the traditional segmer sampling checks in feature space are also avoided. Consequently, to complete calculations in each step of the outsourcing scene, a single interaction is sufficient for prototype finding and connectivity analysis. Without a mass of essential iterations, the labeling phase will not hurt the outsourcing.
- (3)
- Towards privacy-preserving, MPPSVC is proposed by introducing homomorphic encryption, two-party computation, and linear transformation to reconstruct RSVC-EO. Although these protocols limit the calculation types, MPPSVC works well with maximized outsourcing capability. In the field of SVC, to the best of our knowledge, it is the first known client–server privacy-preserving clustering framework solving the dual problem without interaction. Furthermore, it can securely outsource the cluster number analysis and cluster assignment on demand.
2. Preliminaries
2.1. Support Vector Clustering
2.1.1. Estimation of a Trained Support Function
2.1.2. Cluster Assignments
2.2. Homomorphic Encryption
- (1)
- Encryption: Ciphertext .
- (2)
- Decryption: Plaintext .
- (3)
- Additive homomorphism: , . Here, and are two numeric features in PD and is an integer constant. In practical situations, if , its equivalence class value can be a substitution.
2.3. Privacy Violation and Limited Operations of SVC Outsourcing
2.3.1. Privacy Violation of SVC
2.3.2. Limited Operations of Homomorphic Encryption
3. Reformative Support Vector Clustering with Elementary Operations
3.1. DCD Solver for SVC’s Dual Problem
| Algorithm 1 DCD solver for SVC’s dual problem in Equation (2). |
| Require: Dataset , kernel width q, and penalty C Ensure: Coefficient vector
|
3.2. Convex Decomposition without Iterative Analysis
- (1)
- If the division position is not in the SVs subset in which each one links up two nearest neighboring convexity and concavity, for instance, is replaced by , then the corresponding convex hull has to be further split into two convex hulls enclosed by and , respectively, even though all these SVs converge to . Here, is an imaginary sample that is extremely similar to . Because no overlapping region or intersection of vertices of convex hulls is allowed, unfortunately, this result conflicts with the definition that SVs in a convex hull will converge to the same SEV.
- (2)
- From the other perspective, if is not in the division position which only includes , we have to find a substitute to construct the convex hull . might locate between and or between and . For the prior case, it means is not the closest SV to that violates the premise of linking up two nearest neighboring convex hulls. For the latter case, no matter is a new arrival SV or is just , the concavity will be formed along or . However, it becomes true only when is no longer on the cluster boundary or converging to . Unfortunately, this violates the hypothesis of being a SV and converging to .
| Algorithm 2 Non-iterative convex decomposition. |
| Require: SVs set , decomposition threshold Ensure: Convex hulls , set of triples
|
3.3. Connectivity Analysis Irrespective of Sampling
3.4. Implementation of RSVC-EO
| Algorithm 3 RSVC-EO. |
| Require: Dataset , kernel width q, penalty C, and thresholds or the cluster number K Ensure: Clustering labels for all the data samples
|
3.5. Time Complexity of RSVC-EO
4. Maximized Privacy-Preserving Outsourcing on SVC
4.1. Privacy-Preserving Primitives
4.1.1. Secure Multiplication
4.1.2. Secure Comparison
4.1.3. Secure Vector Distance Measurement
| Algorithm 4 Secure comparison protocol. |
| Require: Server: , , ; Client: Ensure: Server output or
|
4.1.4. Secure 1-NN Query
| Algorithm 5 Secure 1-NN query protocol. |
| Require: Encrypted data and dataset SVs set Ensure: the nearest neighbor in
|
4.2. The Proposed MPPSVC Model
4.2.1. Preventing Data Recovery from Kernel Matrix
4.2.2. Privacy-Preserving DCD Solver
4.2.3. Privacy-Preserving Convex Decomposition
4.2.4. Privacy-Preserving Connectivity Analysis
| Algorithm 6 Connectivity analysis in ED with K. |
| Require: Server: , , , K; Client: Ensure: Server output encrypted array of labels
|
| Algorithm 7 Connectivity analysis in ED with . |
| Require: Server: , , , ; Client: Ensure: Server output encrypted array of labels
|
4.2.5. Privacy-Preserving Remaining Samples Labeling
4.3. Work Mode of MPPSVC
4.4. Analysis of MPPSVC
4.4.1. Time Complexity of MPPSVC
- (1)
- For step 1, “Pre-computed Q” and “Instance ” denote doing Algorithm 1 of RSVC-EO with the pre-computed kernel matrix or calculating the row of kernel values on demand, respectively. Although seems time-consuming, in practice, it is frequently much lower than of the classical SVC, which consumes space . For MPPSVC, the client is recommended to outsource a pre-computation in for the orthogonal matrix M following [27,28] before Step 1. Then, nothing has to be done by the client except decrypting by in . The major workload of is moved to the server, which may afford the space complexity of .
- (2)
- Step 2 is not in the classical SVC. The most recent convex decomposition based method [22] takes and the SEVs based methods [12,29] require . Here, is the number of iterations. For RSVC-EO, the difference brought by the “Instance ” is calculating with d-dimensional input before getting the gradient in Equation (12). For MPPSVC, upon using the kernel matrix of SVs or not, the client’s complexity is where . Meanwhile, the server is designated by a polling program in . Notice that the essential tasks of Algorithm 2 for the client in ED have been cut down even though they have similar time complexity with that of in PD.
- (3)
- In Step 3, connectivity analysis of the classical SVC is m times sampling checks for each SVs-pair. However, calculating Equation (3) requires SVs, the whole consumption is up to . On the contrary, RSVC-EO only requires due to the direct use of the convergence directions. is because Algorithms 6 and 7 are provided for choice. Similarly, the client responses SMP, SVDMP, and SCP in Algorithm 6 or SCP in Algorithm 7 with .
- (4)
- Step 4 is particular for the classical SVC while the prior leaves an adjacency matrix. Its complexity is .
- (5)
- Similar to classification, the traversal of the whole set in Step 5 cannot be avoided for every method. Its complexity is or except for the server in MPPSVC. Using S1NNQ, the major operations are carried out with the client under protocols of SVDMP and SCP.
4.4.2. Communication Complexity of MPPSVC
4.4.3. Security of MPPSVC under the Semi-Honest Model
- (1)
- According to Section 4.2.1 and Section 4.2.2, the execution image of the server is given by and C. is a diagonal matrix protected by the matrix M secretly held by the client and C is a single-use parameter without strict limitation. Notice that from to the kernel matrix is a one-to-many mapping. No one can recover an N-dimensional vector by only one number. Without any plain item of , the server cannot infer any data sample even though it occasionally gets several data samples. When the server finishes Algorithm 1, the output is naturally protected by M.
- (2)
- For the second step, the major works are carried out on the client side as a response to the server. As marked in Figure 3, the accessible sensitive data are , , , and . However, all of them are encrypted by .
- (3)
- Step 3 depends on the output of Step 2. It includes SMP, SCP, and SVDMP whose prototypes are proved by [20]. The server can only get the number of clusters, but cannot infer any relationship between data samples in PD. Furthermore, the client can easily hide the real number by tuning the predefined parameters K or . Then, an uncertain cluster number is meaningless for the server.
- (4)
- Step 5 employs S1NNQ. The server cannot infer the actual label for a plain data sample, even if it occasionally has several samples.
4.4.4. Security of MPPSVC under the Malicious Model
5. Experimental Results
5.1. Experimental Setup
5.2. Experimental Dataset
5.3. Experiments in the Plain-Domain
5.3.1. Analysis of Parameter Sensitivity
5.3.2. Analysis of Iteration Sensitivity
5.3.3. Performance Related to Kernel Utilization
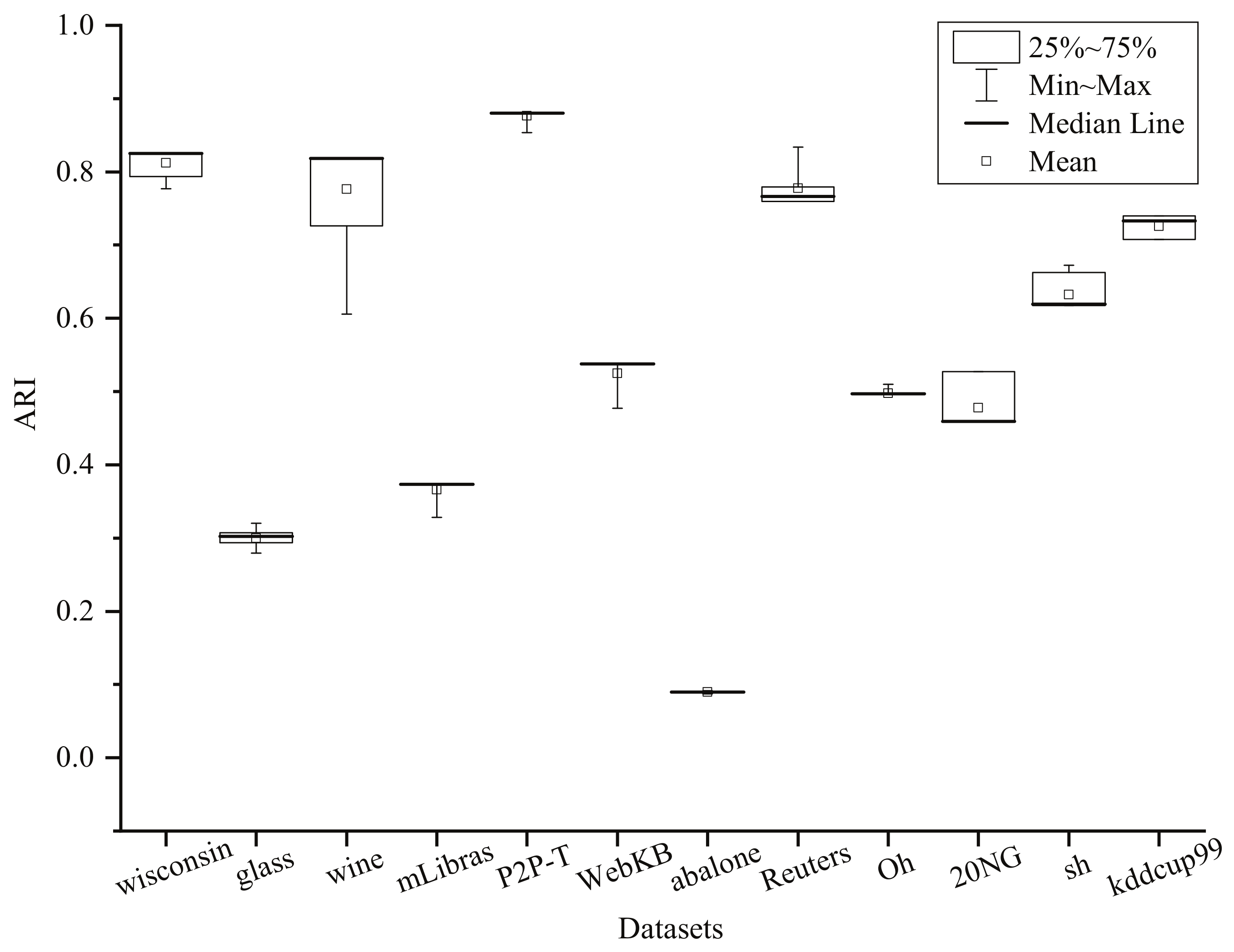
5.3.4. Benchmark Results for Accuracy Comparison
5.3.5. Effectiveness of Capturing Data Distribution
5.4. Experiments in the Encrypted-Domain
5.4.1. Performance in the Encrypted-Domain
5.4.2. Computational Complexity
6. Related Work
- (1)
- For model training, the core is solving the dual problem in Equation (2). Major studies prefer generic optimization algorithms, e.g., gradient descent, sequential minimal optimization [4], and evolutionary strategies [46]. Later, studies rewrote the dual problem by introducing the Jaynes maximum entropy [47], the position-based weight [44], and the relationship amongst SVs [26]. However, conducting a solver with the full dataset suffers from huge consumption of kernel matrix. Thus, FSSVC [26] steadily selects the boundaries while VCC [8] samples a predefined ratio of data. Other methods related to reducing the working set and divide-and-conquer strategy were surveyed in [4]. However, bottlenecks still easily appear due to the nonlinear strategy and the pre-computed kernel matrix. Thus, FRSVC [22] employs a linear method to seek a balance between efficiency and memory cost.
- (2)
- For the labeling phase, connectivity analysis adopts a sampling check strategy for a long time. Reducing the number of sample pairs thus becomes the first consideration, for instance, using the full dataset by CG [1], the SVs by PSVC [44], the SEVs by RCG [24], and the transition points by E-SVC [29,42]. Although the number of sample pairs is gradually reduced, they have a side-effect of additional iterations in seeking SEVs or TS. Thus, CDCL [23] suggests a compromise way of using SVs to construct convex hulls, which are employed as substitutes of SEVs. For efficiency, CDCL reduces the average sample rate by a nonlinear sampling strategy. Later, FSSVC [26] and FRSVC [22] made further improvements by reducing the average sample m close to 1. Besides, Chiang and Hao [48] introduced a cell growth strategy, which starts at any data sphere, expands by absorbing fresh neighboring spheres, and splits if its density is reduced to a certain degree. Later, CCL [43] created a new way by checking the connectivity of two SVs according to a single distance calculation. However, too strict constraints emphasized on the solver degrade its performance. In fact, for these methods, the other pricey consumption is the adjacent matrix, which usually ranges from to .
7. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ben-Hur, A.; Horn, D.; Siegelmann, H.T.; Vapnik, V.N. Support Vector Clustering. J. Mach. Learn. Res. 2001, 2, 125–137. [Google Scholar] [CrossRef]
- Saltos, R.; Weber, R.; Maldonado, S. Dynamic Rough-Fuzzy Support Vector Clustering. IEEE Trans. Fuzzy Syst. 2017, 25, 1508–1521. [Google Scholar] [CrossRef]
- Ye, Q.; Zhao, H.; Li, Z.; Yang, X.; Gao, S.; Yin, T.; Ye, N. L1-Norm Distance Minimization-Based Fast Robust Twin Support Vector k-Plane Clustering. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 4494–4503. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Ping, Y. Recent Advances in Support Vector Clustering: Theory and Applications. Int. J. Pattern Recogn. Artif. Intell. 2015, 29, 1550002. [Google Scholar] [CrossRef]
- Sheng, Y.; Hou, C.; Si, W. Extract Pulse Clustering in Radar Signal Sorting. In Proceedings of the 2017 International Applied Computational Electromagnetics Society Symposium–Italy (ACES), Florence, Italy, 26–30 March 2017; pp. 1–2. [Google Scholar]
- Lawal, I.A.; Poiesi, F.; Anguita, D.; Cavallaro, A. Support Vector Motion Clustering. IEEE Trans. Circuits Syst. Video Technol. 2017, 27, 2395–2408. [Google Scholar] [CrossRef]
- Pham, T.; Le, T.; Dang, H. Scalable Support Vector Clustering Using Budget. arXiv 2017, arXiv:1709.06444v1. [Google Scholar]
- Kim, K.; Son, Y.; Lee, J. Voronoi Cell-Based Clustering Using a Kernel Support. IEEE Trans. Knowl. Data Eng. 2015, 27, 1146–1156. [Google Scholar] [CrossRef]
- Yu, Y.; Li, H.; Chen, R.; Zhao, Y.; Yang, H.; Du, X. Enabling Secure Intelligent Network with Cloud-Assisted Privacy-Preserving Machine Learning. IEEE Netw. 2019, 33, 82–87. [Google Scholar] [CrossRef]
- Song, C.; Ristenpart, T.; Shmatikov, V. Machine Learning Models that Remember Too Much. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, CCS’ 2017, Dallas, TX, USA, 30 October–3 November 2017; ACM: New York, NY, USA, 2017; pp. 587–601. [Google Scholar]
- Dritsas, E.; Kanavos, A.; Trigka, M.; Sioutas, S.; Tsakalidis, A. Storage Efficient Trajectory Clustering and k-NN for Robust Privacy Preserving Spatio-Temporal Databases. Algorithms 2019, 12, 266. [Google Scholar] [CrossRef] [Green Version]
- Jung, K.H.; Lee, D.; Lee, J. Fast support-based clustering method for large-scale problems. Pattern Recogn. 2010, 43, 1975–1983. [Google Scholar] [CrossRef]
- Paillier, P. Public-Key Cryptosystems Based on Composite Degree Residuosity Classes. In Proceedings of the 17th International Conference on Theory and Application of Cryptographic Techniques (EUROCRYPT’ 99), Prague, Czech Republic, 2–6 May 1999; pp. 223–238. [Google Scholar]
- Shan, Z.; Ren, K.; Blanton, M.; Wang, C. Practical Secure Computation Outsourcing: A Survey. ACM Comput. Surv. 2018, 51, 31:1–31:40. [Google Scholar] [CrossRef]
- Liu, X.; Deng, R.; Choo, K.R.; Yang, Y. Privacy-Preserving Outsourced Support Vector Machine Design for Secure Drug Discovery. IEEE Trans. Cloud Comput. 2019, 1–14. [Google Scholar] [CrossRef]
- Rahulamathavan, Y.; Veluru, S.; Phan, R.C.W.; Chambers, J.A.; Rajarajan, M. Privacy-Preserving Clinical Decision Support System using Gaussian Kernel based Classification. IEEE J. Biomed. Health Inform. 2014, 18, 56–66. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rahulamathavan, Y.; Phan, R.C.W.; Veluru, S.; Cumanan, K.; Rajarajan, M. Privacy-Preserving Multi-Class Support Vector Machine for Outsourcing the Data Classification in Cloud. IEEE Trans. Dependable Secure Comput. 2014, 11, 467–479. [Google Scholar] [CrossRef] [Green Version]
- Karapiperis, D.; Verykios, V.S. An LSH-based Blocking Approach with A Homomorphic Matching Technique for Privacy-preserving Record Linkage. IEEE Trans. Knowl. Data Eng. 2015, 27, 909–921. [Google Scholar] [CrossRef]
- Lin, K.P.; Chang, Y.W.; Chen, M.S. Secure Support Vector Machines Outsourcing with Random Linear Transformation. Knowl. Inf. Syst. 2015, 44, 147–176. [Google Scholar] [CrossRef]
- Samanthula, B.; Elmehdwi, Y.; Jiang, W. k-Nearest Neighbor Classification over Semantically Secure Encrypted Relational Data. IEEE Trans. Knowl. Data Eng. 2015, 27, 1261–1273. [Google Scholar] [CrossRef] [Green Version]
- Lin, K.P.; Chen, M.S. On the Design and Analysis of the Privacy-Preserving SVM Classifier. IEEE Trans. Knowl. Data Eng. 2011, 23, 1704–1717. [Google Scholar] [CrossRef]
- Ping, Y.; Tian, Y.; Guo, C.; Wang, B.; Yang, Y. FRSVC: Towards making support vector clustering consume less. Pattern Recogn. 2017, 69, 286–298. [Google Scholar] [CrossRef]
- Ping, Y.; Tian, Y.; Zhou, Y.; Yang, Y. Convex Decomposition Based Cluster Labeling Method for Support Vector Clustering. J. Comput. Sci. Technol. 2012, 27, 428–442. [Google Scholar] [CrossRef]
- Lee, J.; Lee, D. An Improved Cluster Labeling Method for Support Vector Clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 461–464. [Google Scholar] [PubMed]
- Ping, Y.; Zhou, Y.; Yang, Y. A Novel Scheme for Accelerating Support Vector Clustering. Comput. Inform. 2011, 31, 1001–1026. [Google Scholar]
- Ping, Y.; Chang, Y.; Zhou, Y.; Tian, Y.; Yang, Y.; Zhang, Z. Fast and Scalable Support Vector Clustering for Large-scale Data Analysis. Knowl. Inf. Syst. 2015, 43, 281–310. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, K.; Salinas, S.; Li, P. SecFact: Secure Large-scale QR and LU Factorizations. IEEE Trans. Big Data 2019, 1–13. [Google Scholar] [CrossRef]
- Zhou, L.; Li, C. Outsourcing Eigen-Decomposition and Singular Value Decomposition of Large Matrix to a Public Cloud. IEEE Access 2016, 4, 869–879. [Google Scholar] [CrossRef]
- Lee, J.; Lee, D. Dynamic Characterization of Cluster Structures for Robust and Inductive Support Vector Clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1869–1874. [Google Scholar]
- Xu, R.; Wunsch, D.C. Clustering; A John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Frank, A.; Asuncion, A. UCI Machine Learning Repository. 2010. Available online: http://archive.ics.uci.edu/ml (accessed on 23 July 2018).
- Ping, Y.; Zhou, Y.; Xue, C.; Yang, Y. Efficient representation of text with multiple perspectives. J. China Univ. Posts Telecommun. 2012, 19, 101–111. [Google Scholar] [CrossRef]
- Graven, M.; DiPasquo, D.; Freitag, D.; McCallum, A.; Mitchell, T.; Nigam, K.; Slattery, S. Learning to Extract Symbolic Knowledge form The World Wide Web. In Proceedings of the 15th National Conference for Artificial Intelligence (AAAI’98), Madison, WI, USA, 26–30 July 1998; pp. 509–516. [Google Scholar]
- Lang, K. NewsWeeder: Learning to filter netnews. In Proceedings of the Twelfth International Conference on Machine Learning, Tahoe City, CA, USA, 9–12 July 1995; pp. 331–339. [Google Scholar]
- Lewis, D.D. Reuters-21578 Text Categorization Collection. 1997. Available online: http://kdd.ics.uci.edu/databases/reuters21578/ (accessed on 19 March 2012).
- Hersh, W.R.; Buckley, C.; Leone, T.J.; Hickam, D.H. Ohsumed: An Interactive Retrieval Evaluation and New Large Test Collection for Research. In Proceedings of the 17th Annual ACM SIGIR Conference, Dublin, Ireland, 3–6 July 1994; pp. 192–201. [Google Scholar]
- UNIBS. The UNIBS Anonymized 2009 Internet Traces. 18 March 2010. Available online: http://www.ing.unibs.it/ntw/tools/traces (accessed on 12 May 2011).
- Peng, J.; Zhou, Y.; Wang, C.; Yang, Y.; Ping, Y. Early TCP Traffic Classification. J. Appl. Sci.-Electron. Inf. Eng. 2011, 29, 73–77. [Google Scholar]
- Guo, C.; Zhou, Y.; Ping, Y.; Zhang, Z.; Liu, G.; Yang, Y. A Distance Sum-based Hybrid Method for Intrusion Detection. Appl. Intell. 2014, 40, 178–188. [Google Scholar] [CrossRef]
- UCI. Kdd Cup 99 Intrusion Detection Dataset. 1999. Available online: http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html (accessed on 10 February 2016).
- Hsieh, C.J.; Chang, K.W.; Lin, C.J.; Keerthi, S.S.; Sundararajan, S. A Dual Coordinate Descent Method for Large-scale Linear SVM. In Proceedings of the 25th International Conference on Machine Learning (ICML ’08), Helsinki, Finland, 5–9 July 2008; ACM: New York, NY, USA, 2008; pp. 408–415. [Google Scholar]
- Lee, D.; Jung, K.H.; Lee, J. Constructing Sparse Kernel Machines Using Attractors. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 20, 721–729. [Google Scholar]
- Lee, S.H.; Daniels, K.M. Cone Cluster Labeling for Support Vector Clustering. In Proceedings of the 6th SIAM Conference on Data Mining, Bethesda, MD, USA, 20–22 April 2006; pp. 484–488. [Google Scholar]
- Wang, C.D.; Lai, J.H. Position Regularized Support Vector Domain Description. Pattern Recogn. 2013, 46, 875–884. [Google Scholar] [CrossRef]
- Garcia, S.; Herrera, F. An Extension on “Statistical Comparisons of Classifiers over Multiple Datasets” for all Pairwise Comparisons. J. Mach. Learn. Res. 2008, 9, 2677–2694. [Google Scholar]
- Jun, S.H. Improvement of Support Vector Clustering using Evolutionary Programming and Bootstrap. Int. J. Fuzzy Logic Intell. Syst. 2008, 8, 196–201. [Google Scholar] [CrossRef] [Green Version]
- Guo, C.; Li, F. An Improved Algorithm for Support Vector Clustering based on Maximum Entropy Principle and Kernel Matrix. Expert Syst. Appl. 2011, 38, 8138–8143. [Google Scholar] [CrossRef]
- Chiang, J.H.; Hao, P.Y. A New Kernel-based Fuzzy Clustering Approach: Support Vector Clustering with Cell Growing. IEEE Trans. Fuzzy Syst. 2003, 11, 518–527. [Google Scholar] [CrossRef]
- Hua, J.; Shi, G.; Zhu, H.; Wang, F.; Liu, X.; Li, H. CAMPS: Efficient and Privacy-Preserving Medical Primary Diagnosis over Outsourced Cloud. Inf. Sci. 2019. [Google Scholar] [CrossRef]
- Sumana, M.; Hareesha, K. Modelling A Secure Support Vector Machine Classifier for Private Data. Int. J. Inf. Comput. Secur. 2018, 10, 25–41. [Google Scholar] [CrossRef]
- Jia, Q.; Guo, L.; Jin, Z.; Fang, Y. Preserving Model Privacy for Machine Learning in Distributed Systems. IEEE Trans. Parallel Distrib. Syst. 2018, 29, 1808–1822. [Google Scholar] [CrossRef]
- Liu, X.; Choo, K.R.; Deng, R.H.; Lu, R.; Weng, J. Efficient and Privacy-Preserving Outsourced Calculation of Rational Numbers. IEEE Trans. Dependable Secure Comput. 2018, 15, 27–39. [Google Scholar] [CrossRef]
- Salinas, S.; Luo, C.; Liao, W.; Li, P. Efficient Secure Outsourcing of Large-scale Quadratic Programs. In Proceedings of the ASIA CCS ’16: 11th ACM on Asia Conference on Computer and Communications Security, Xi’an, China, 31 May–3 June 2016; ACM: New York, NY, USA, 2016; pp. 281–292. [Google Scholar]
- Gonzalez-Serrano, F.J.; Navia-Vazquez, A.; Amor-Martin, A. Training Support Vector Machines with privacy-protected data. Pattern Recogn. 2017, 72, 93–107. [Google Scholar] [CrossRef]







| Classical SVC [1] | RSVC-EO | MPPSVC | ||||
|---|---|---|---|---|---|---|
| Pre-Computed | Instance | Client | Server | |||
| Step 1. | DCD Solver for coefficient indicating SVs* | |||||
| Step 2. | Convex decomposition in one iter. using SVs | — | ||||
| Step 3. | Connectivity analysis withprior knowledge | |||||
| Step 4. | Find the connected comp-onents by DFS | — | — | — | ||
| Step 5. | Labeling the remaining data samples | or | or | or | ||
| Datasets | Dataset Description | ||
|---|---|---|---|
| Dims | Size | # of Classes | |
| wisconsin | 9 | 683 | 2 |
| glass | 9 | 214 | 7 |
| wine | 13 | 178 | 3 |
| movement_libras (mLibras) | 90 | 360 | 15 |
| P2P traffic (P2P-T) | 4 | 9206 | 4 |
| WebKB | 4 | 4199 | 4 |
| abalone | 7 | 4177 | 29 |
| Reuters-21578(Reuters) | 10 | 9990 | 10 |
| Ohsumed (Oh) | 23 | 13,929 | 23 |
| 20Newsgroups (20NG) | 20 | 13,998 | 20 |
| shuttle (sh) | 9 | 43,500 | 7 |
| kddcup99 | 9 | 494,021 | 5 |
| Dataset | CG | RCG | E-SVC | CCL | FSVC | PSVC | CDCL | VCC | FSSVC | FRSVC | RSVC-EO |
|---|---|---|---|---|---|---|---|---|---|---|---|
| wisconsin | 0.7793 | 0.8035 | 0.1344 | 0.9076 | 0.6687 | 0.2574 | 0.8685 | 0.8029 ± 0.0514 | 0.9248 | 0.8798 | 0.8632 |
| glass | 0.2771 | 0.2823 | 0.2743 | 0.2201 | 0.2458 | 0.2801 | 0.2911 | 0.2771 ± 0.0031 | 0.2998 | 0.2582 | 0.3540 |
| wine | 0.5912 | 0.7928 | 0.4159 | 0.8190 | 0.8042 | 0.3809 | 0.8961 | 0.8088 ± 0.0563 | 0.8992 | 0.8483 | 0.8185 |
| mLibras | 0.2422 | 0.2356 | — | 0.0899 | 0.1421 | 0.2541 | 0.3320 | 0.3065 ± 0.0181 | 0.3703 | 0.3366 | 0.3732 |
| P2P-T | — | 0.8815 | — | — | 0.8367 | — | 0.8917 | 0.7389 ± 0.0066 | 0.8815 | 0.8678 | 0.8807 |
| WebKB | — | 0.3072 | — | — | 0.5144 | — | 0.4645 | 0.4434 ± 0.0156 | 0.5670 | 0.6395 | 0.5381 |
| abalone | — | 0.0332 | — | — | 0.0515 | — | 0.0603 | 0.0710 ± 0.0011 | 0.0587 | 0.0657 | 0.0996 |
| Reuters | — | 0.0148 | — | — | 0.4775 | — | 0.8064 | 0.4908 ± 0.0616 | 0.5831 | 0.7295 | 0.8338 |
| Oh | — | — | — | — | — | — | — | 0.4280 ± 0.0292 | 0.4514 | 0.4840 | 0.5019 |
| 20NG | — | — | — | — | — | — | — | 0.4397 ± 0.0461 | 0.3628 | 0.4927 | 0.6084 |
| sh | — | — | 0.59 [12] | — | 0.58 [12] | — | — | 0.5898 ± 0.0198 | 0.6857 | 0.8050 | 0.7337 |
| kddcup99 | — | — | — | — | — | — | — | — | — | — | 0.7621 |
| Methods | Average Ranks | Unadjusted p | |
|---|---|---|---|
| Control Method: RSVC-EO, Average Rank = 2.1667 | |||
| CG | 8.3333 | 5.2539 | 4.2031 |
| RCG | 6.7500 | 7.1174 | 0.0036 |
| E-SVC | 8.7083 | 1.3562 | 1.3562 |
| CCL | 8.0417 | 1.4315 | 1.0020 |
| FSVC | 7.1250 | 2.5028 | 0.0015 |
| PSVC | 8.4583 | 3.3728 | 2.6982 |
| CDCL | 4.6250 | 0.0694 | 0.2083 |
| VCC | 5.5000 | 0.0138 | 0.0553 |
| FSSVC | 2.9167 | 0.5796 | 0.5796 |
| FRSVC | 3.3749 | 0.3722 | 0.5796 |
| Dataset | Scaling Factor | ||||
|---|---|---|---|---|---|
| wisconsin | 0.8254 | 0.8519 | 0.8519 | 0.8519 | 0.8519 |
| glass | 0.1817 | 0.3197 | 0.3540 | 0.3540 | 0.3540 |
| wine | 0.4272 | 0.8185 | 0.8185 | 0.8185 | 0.8185 |
| mLibras | 0.3281 | 0.3264 | 0.3415 | 0.3415 | 0.3415 |
| P2P-T | 0.7757 | 0.7938 | 0.8048 | 0.8048 | 0.8048 |
| WebKB | 0.4824 | 0.5235 | 0.4428 | 0.4795 | 0.4795 |
| abalone | 0.0870 | 0.0915 | 0.0917 | 0.0917 | 0.0917 |
| Reuters | 0.7860 | 0.7284 | 0.7063 | 0.7062 | 0.7062 |
| Oh | 0.4851 | 0.4954 | 0.4898 | 0.4898 | 0.4898 |
| 20NG | 0.4752 | 0.5120 | 0.5171 | 0.5169 | 0.5169 |
| sh | 0.6586 | 0.6346 | 0.6346 | 0.6596 | 0.6596 |
| kddcup99 | 0.6799 | 0.7629 | 0.7714 | 0.7620 | 0.7620 |
| Dataset | Step 1 | Step 2 | Step 3 | Step 5 | #SVs | #Convex Hulls | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| C | S | C | S | C | S | C | S | |||
| wisconsin | 1.2524 | 0.0194 | 21.6361 | 43.4891 | 1.3200 | 9.4463 | 0.0200 | 1.4403 | 64 | 30 |
| glass | 0.7072 | 0.0059 | 14.4307 | 22.4403 | 1.2900 | 9.4809 | 0.0164 | 1.3288 | 44 | 31 |
| wine | 1.1567 | 0.0567 | 24.8310 | 40.4476 | 1.8900 | 21.4400 | 0.0244 | 3.0628 | 51 | 43 |
| mLibras | 4.3020 | 0.0186 | 195.1682 | 305.3468 | 0.8100 | 67.2533 | 0.0713 | 12.9299 | 62 | 23 |
| P2P-T | 4.6369 | 0.0805 | 103.4480 | 1577.1325 | 21.1350 | 356.6295 | 0.0112 | 8.0530 | 661 | 471 |
| WebKB | 0.7981 | 0.0057 | 41.7010 | 267.3922 | 6.1050 | 37.9054 | 0.0031 | 2.7794 | 266 | 137 |
| abalone | 0.9594 | 0.0131 | 49.0764 | 225.5012 | 2.6700 | 17.8104 | 0.0052 | 2.9876 | 189 | 69 |
| Reuters | 0.5403 | 0.0148 | 27.2192 | 59.0562 | 0.5250 | 4.5836 | 0.0081 | 1.4473 | 75 | 15 |
| Oh | 1.9096 | 0.0171 | 93.8732 | 255.4895 | 1.1250 | 18.1687 | 0.0175 | 4.8598 | 113 | 25 |
| 20NG | 0.8993 | 0.0140 | 45.5341 | 77.9957 | 0.8250 | 16.2751 | 0.0152 | 2.8590 | 63 | 25 |
| sh | 1.4285 | 0.0259 | 45.9365 | 166.4430 | 0.8550 | 6.2177 | 0.0103 | 2.3485 | 141 | 22 |
| kddcup99 | 0.4751 | 1.3404 | 24.8795 | 54.2872 | 0.6900 | 4.7367 | 0.0068 | 1.3015 | 74 | 17 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ping, Y.; Hao, B.; Hei, X.; Wu, J.; Wang, B. Maximized Privacy-Preserving Outsourcing on Support Vector Clustering. Electronics 2020, 9, 178. https://doi.org/10.3390/electronics9010178
Ping Y, Hao B, Hei X, Wu J, Wang B. Maximized Privacy-Preserving Outsourcing on Support Vector Clustering. Electronics. 2020; 9(1):178. https://doi.org/10.3390/electronics9010178
Chicago/Turabian StylePing, Yuan, Bin Hao, Xiali Hei, Jie Wu, and Baocang Wang. 2020. "Maximized Privacy-Preserving Outsourcing on Support Vector Clustering" Electronics 9, no. 1: 178. https://doi.org/10.3390/electronics9010178
APA StylePing, Y., Hao, B., Hei, X., Wu, J., & Wang, B. (2020). Maximized Privacy-Preserving Outsourcing on Support Vector Clustering. Electronics, 9(1), 178. https://doi.org/10.3390/electronics9010178





