1. Introduction
The exoskeleton robot could be a revolutionary technology in human limb rehabilitation [
1] and power enhancement [
2]. However, the motion intention of its wearer has limited the development of this technology, because traditional sensors for the exoskeleton are unable to detect motion tendency ahead of time. Since the surface electromyography (sEMG) signal is noninvasive, and has the potential to predict people’s movement intentions 30–100 ms in advance [
1], the sEMG has been favored by many researchers, and with the help of sEMG sensors, the performance of wearable devices would be improved [
1,
3,
4,
5]. Thus, in addition to the exoskeleton technology, there are a wide range of applications for using sEMG, such as wearable devices [
6], prosthetic limbs [
7], and other such myoelectric control systems [
8]. The existing studies focus on how the sEMG signals relate to human movement for better control of the wearable devices and similar products.
Some of the existing research has investigated the relationship between sEMG and human biomechanics. Chen et al. [
9] proposed a musculoskeletal biomechanical model connecting sEMG and knee joint torque, based on the underlying physiological mechanism facilitating the study of neural control. Tagliapietra et al. [
10] used a subject-specific EMG-driven Neuro MusculoSkeletal (NMS) model to estimate ankle torque and muscle forces expressed by the subject. Zhuang et al. [
11] proposed an sEMG-based admittance controller that could enable a more synchronized human–robot interaction, as compared to the torque-sensing-based admittance controller.
However, to avoid building a complicated biomechanical model, some researchers have tried to use a data training method to do the job. Anwar et al. [
12] proposed an adaptive neuro fuzzy inference system (ANFIS), such as a neuro-fuzzy type knowledge-based adaptive network that contained a non-parametric model, with an EMG signal of two muscles used as the input to estimate torque. Gui et al. [
13] used radial basis function (RBF) neural networks to approximate the active joint torque of subjects during the swing phase.
Besides the biomechanical method, there is a new intuitive myoelectric control strategy for assistive devices, which relies on the sEMG-based intention estimation of human motion. These predictions can be broadly categorized as classification and regression models [
14]. For the classification, Toledo-Pérez et al. [
15] used a support vector machine (SVM) based on sEMG to classify the intention of right lower limb movement. Morbidoni et al. [
16] proposed a deep learning (DL) approach for sEMG-based classification of stance/swing phases and the prediction of the foot–floor-contact signal in more natural walking conditions. Nazmi et al. [
17] proposed a classification system for both stance and swing phases, by extracting the patterns of electromyography signals from time domain features and feeding them into an artificial neural network (ANN) classifier.
For the continuous estimation of the joint angle, there are various methods. Bao et al. [
18] presented a single stream convolutional neural network (CNN) for mapping sEMG to wrist angles within three degrees-of-freedoms. Xiao et al. [
19] used the mean absolute value, waveform length, zero crossing, slope signs changes, and the difference in absolute standard deviation value of sEMG, in order to estimate continuous elbow motion by random forest (RF). Lei Z. [
20] used the back propagation (BP) neural network to establish a model of the relationship between elbow angles and sEMG signals features, through which they estimated the angles of the elbow joint and achieved continuous motion control of the exoskeleton. Huang et al. [
21] presented deep-recurrent neural networks (RNNs) for predicting the knee joint angle in real-time, based on a fusion of sEMG and kinematics signals.
It can be concluded that most of the existing studies are model-free approaches for the estimation of joint angles from sEMG, based on machine learning (ML). Furthermore, the majority of the existing research used a single method of ML, and most of them seldom considered the influence of the previous sEMG as the input on the accuracy of their methods, even though both the joint movement and sEMG signals are in a continuous time-sequence. Also, the size of the training sample for ML is also a debatable issue in terms of the accuracy of estimation, since a large training sample would lead to overfitting and be time consuming.
Thus, a novel double-ML-method, based on random forest combined with principal component analysis (RFPCA) has been proposed in this work to estimate the movement of the knee joint from sEMG, with the expectation of achieving high accuracy and efficiency. This method was also utilized to analyze how the input of the previous sEMG and the sample size for model validation affect the estimation of the knee joint movement. Moreover, a BPPCA was constructed to compare with the RFPCA, and the RFPCA presented a better performance in this work.
The remainder of the paper is organized as follows.
Section 2 introduces the experiment and proposes the knee angle estimation method.
Section 3 presents the estimation results using RFPCA and BPPCA, followed by the discussion in
Section 4. Finally, the conclusions are drawn in
Section 5.
2. Materials and Methods
2.1. Subjects
A total of six healthy subjects, who have never suffered from muscular atrophy or disorders, participated in this study, with an average height, age and weight of 181 ± 3.8 cm, 72.5 ± 6.9 kg and 24.2 ± 1.6 yrs, respectively. All of the subjects enrolled in this study knew the procedure of the experiment, and signed and agreed to participate in the experimental study as the test subjects. The experiment was approved by Nanjing University of Science and Technology (Date granted: June 12, 2019) and performed in accordance with the Declaration of Helsinki.
2.2. Experimental Preparation and Protocol
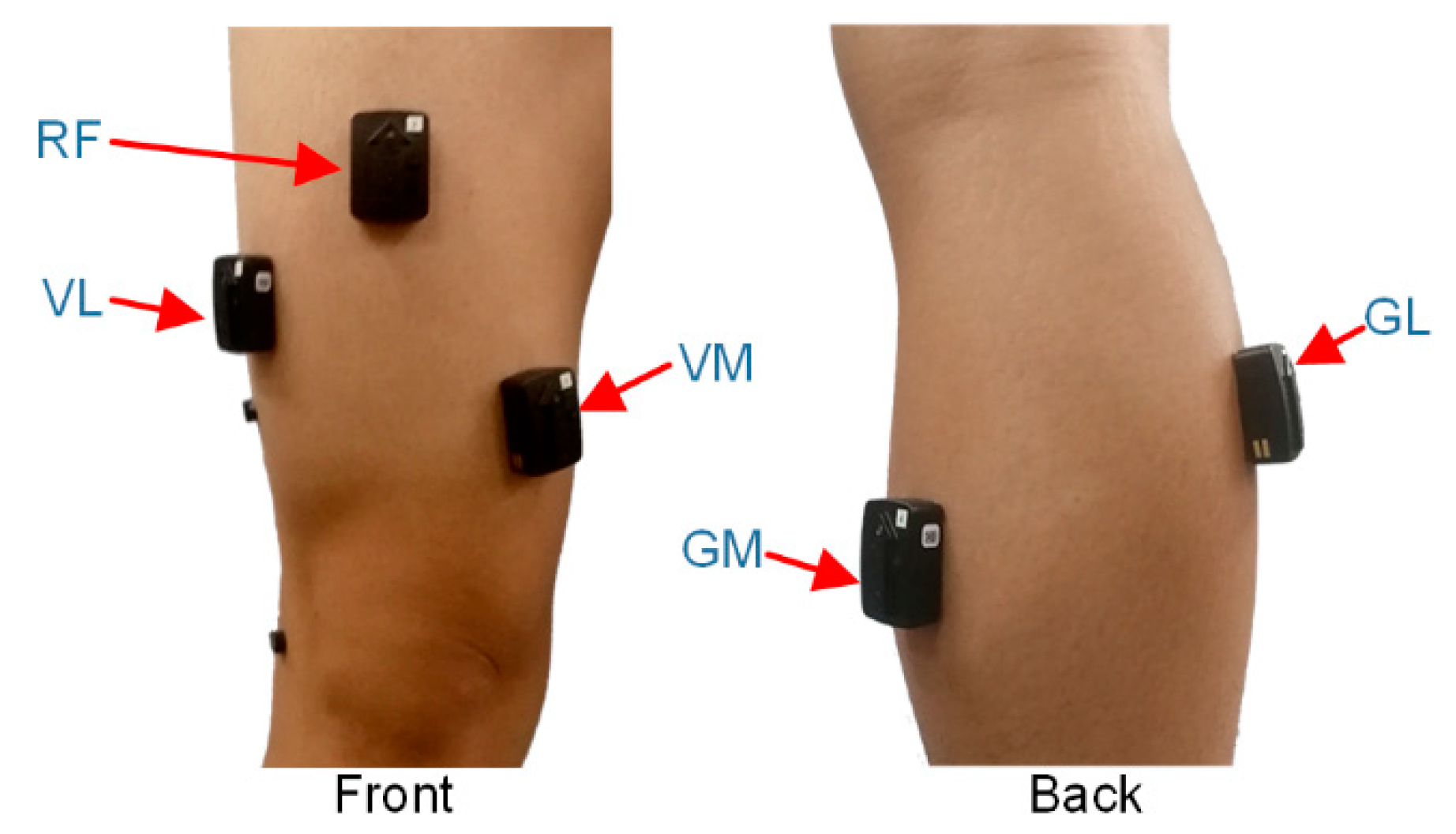
The unilateral lower limb of the human body contains at least 30 muscles that drive 7 degrees of freedom of the lower limb. Since the knee is a vital joint in the lower limb, we have chosen it as the key aspect in our research. The sEMG signals related to the knee of the unilateral leg were obtained by Trigno wireless sEMG instrument. To obtain better sEMG signals, several muscles that are easily detected were selected, including the vastus lateralis (VL), rectus femoris (RF), vastus medialis (VM), gastrocnemius medialis (GM) and gastrocnemius lateralis (GL). The adhesive positions (shown in
Figure 1) of the surface electrodes are the positions recommended by SENIAM [
22]. Before the experiment, the skin surfaces, where the electrodes had to be placed, were shaved and then cleaned with alcohol. This was done to reduce the impedance between the measured skin and electrodes and also to improve the sensor–skin contact.
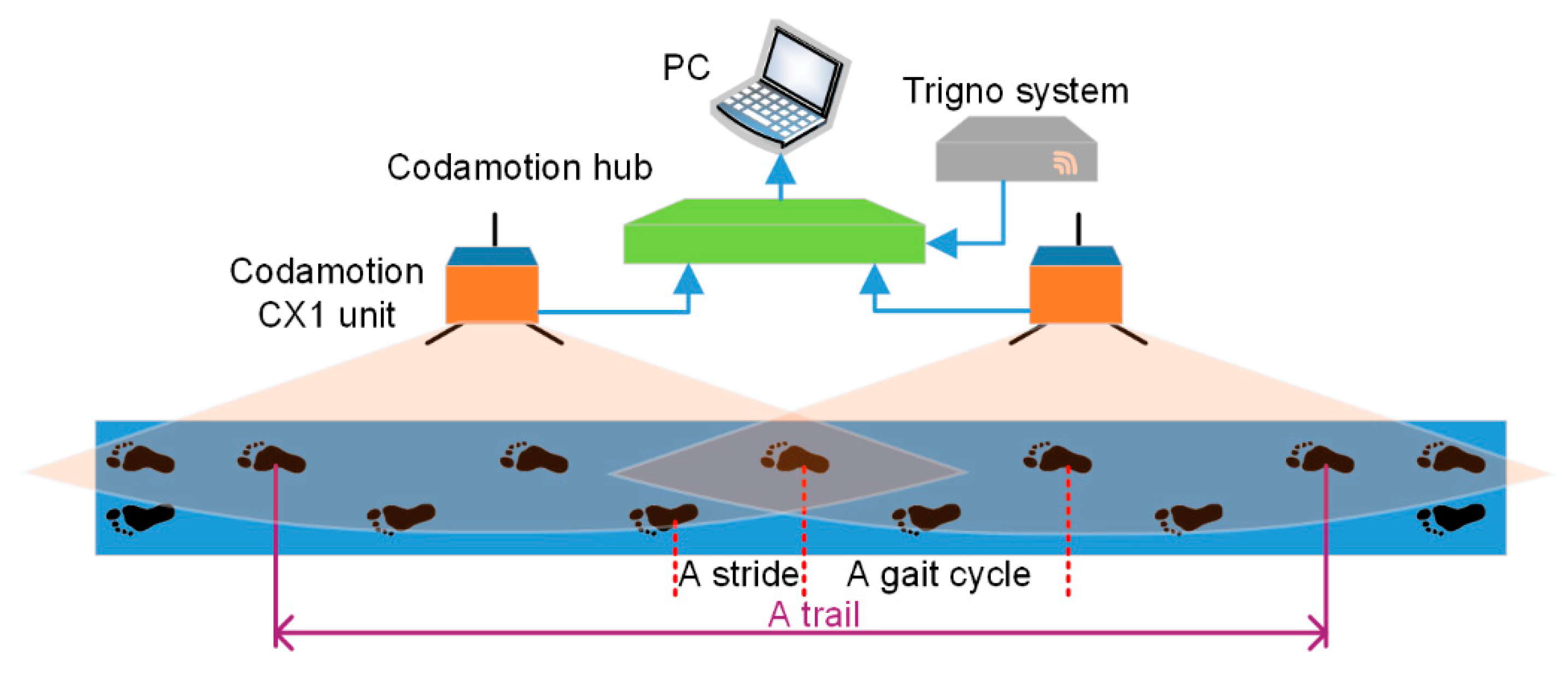
On the lateral side of the leg with sEMG sensors, three markers were placed to obtained the kinematic data of the knee, through a 3D motion capture system called Codamotion. As shown in
Figure 2, Marker B was placed at the approximate center of the knee joint, on the sagittal skin of the subject, while Marker A and Marker C were respectively placed on the projection line of the thigh femur and calf tibia on the sagittal skin of the subject. The approximate flexion–extension motion angle of the knee joint was obtained by collecting the spatial motion trajectory of Markers A, B and C.
During the experiment, the subject was asked to walk back and forth nearly 20 times along a straight line about 5 m in length, at his natural or free cadence, as shown in
Figure 3. The two Codamotion CX1 units on the right of the subject collected the kinematic data of the markers at a sampling frequency of 100 Hz, while the wireless Trigno system picked up the raw sEMG signals from the five muscles at a frequency of 2000 Hz. The data were then synchronized and transferred to the Codamotion hub, and finally, transmitted to the PC and stored. If the subject felt uncomfortable while the experiment was in progress, he would rest for 10 minutes to reduce the effects of such factors as fatigue. If he felt better after the rest, the experiment would continue. Otherwise, the experiment would be stopped. In this way, the data of one trail from as many as 8 strides could be collected, which was more than adequate to obtain 4 representative sEMG profiles for each muscle and gait cycle (GC) of the leg. Approximately 80 full GCs and their corresponding sEMG signals were recorded in all for each subject. Since each subject needed to be properly equipped with the sensors, and it required approximately one hour for each subject to undergo the experiment process, including preparation (15 min), resting (30 min) and walking (15 min), the entire experiment lasted 2 days, with one person in the morning and two in the afternoon.
2.3. Signal Processing
The sEMG signals were focused on the time domain because of the time-sequence. The amplitude extracted from the raw sEMG signals was used for the training of the RFPCA, similar to the work done by the authors of [
16], who directly used the envelopes of the EMG signal to train the network. This feature was carried out from digital filtering and using simple math. A Butterworth band-pass filter (band length of 10–500 Hz, 4th order) was used to filter interference signals and extract effective signals. After that, a full-wave rectification of the sEMG signal was conducted, and the signal was then filtered through a low-pass filter (Butterworth at 6 Hz, 2nd order) [
23]. One of the representative examples of the sEMG signal processing of one trial is shown in
Figure 4.
For processing the kinematic data of the knee, the vector
consisting of Markers A and B represents the direction of the thigh, while vector
consisting of Markers B and C represents the direction of the shank. The motion angle of knee could then be calculated approximatively as:
In order to keep the data synchronized with the knee and facilitate subsequent knee movement prediction, the sEMG signal, after the original processing, was resampled at 100 Hz. Thus, a set of data at time t was obtained, where Ei,t represents the envelope of i sEMG signal after processing, and yknee,t represents the knee angle θknee at time t.
For the study of the sEMG historical influence, the data from one trail of each subject was chosen for training, in order to establish the estimation models. The influence of previous sEMG signals was studied by the number of previous sEMG signals used as a feature vector in the learning course. A typical sample is a combination of sEMG and knee angle [
Xt,
Yt], where the sEMG
Xt is the input, while the knee angle
Yt =
yknee,t is the output. In this work, the sEMG input
Xt at time
t is defined as follows:
where,
xt is the vector of sEMG at time
t after processing, namely
;
n is the number of previous sEMG signals used as the input, Δ
t is the sample interval which is 1/100 Hz. The input dimension of
Xt increases as
n increases.
For the sample size,
n was zero, and all of the processed data of each subject was segmented into groups according to the GC. One group contains different sampling numbers for different subjects, which are listed in
Table 1. For each subject, 61 complete groups of data (GDs, approximately 7808 samples) were selected for the following work.
2.4. Estimation Model
Because of the complexity of the sEMG signal and the differences between subjects, it is hard to establish a general mathematical model to represent the mapping relationship from sEMG to the knee angle. Furthermore, the biomechanical model describing the relationship between the sEMG and joint angle is also complicated and difficult to construct for practical application. Therefore, to establish a universal sEMG–angle model of a human joint, with a learning function, this study adopted a novel model-free method using random forest (RF) in combination with principal component analysis (PCA), in order to set up the estimation model between sEMG signal and knee movement. It is expected that this coupled ML method will be able to handle the estimation issue for different participants with a parametric adaptive approach. The input of the model is the processed sEMG, and the output is the knee angle.
2.4.1. Random Forest
Random forest (RF), based on the theory of decision trees, was first proposed by Breiman [
24]. RF is an effective tool in prediction, because with the right input, RF produces accurate classifiers and regressors [
24]. In standard trees, each node is split using the best split among all variables. In a RF, each node is split using the best among a subset of predictors randomly chosen at that node. This somewhat counterintuitive strategy performs very well in comparison to other classifiers, including discriminant analysis, SVM and neural networks, and is robust against overfitting [
25]. Additionally, the execution time of RF is far less than RBF and SVM when used to process high dimensional data, because the RF algorithm itself can select the important features automatically [
19]. It is also relatively robust to outliers and noise. Due to these advantages, RF was chosen for application to the relationship between the sEMG and knee joint in this study.
As an ensemble learning method, RF achieves better generalization performance by establishing multiple decision trees. If RF has
N decision trees, it is necessary to generate
N sample sets to train each tree. Each tree is grown as follows [
26]:
If the number of cases in the training set is Tr, then Tr cases at random are sampled—but with replacement, from the original data. This sample will be the training set for growing the tree.
If there are Iv input variables, a number Nf << Iv is specified, such that at each node, Nf variables are selected at random out of the Iv and the best split on these, m, is used to split the node. The value of Nf is held constant during the forest growing.
Each tree is grown to the largest extent possible. There is no pruning.
2.4.2. Principal Component Analysis
Principal component analysis (PCA) is a statistical technique that performs a linear transformation from an original set of values into a smaller one of uncorrelated variables [
15]. The idea was conceived of by K. Pearson [
27] and later developed by Hotelling [
28].
PCA needs to find some encoding function that produces the code for an input, and a decoding function that produces the reconstructed input, given its code [
29]. In general, PCA uses a covariance matrix to reduce the data dimension. By calculating the eigenvalue eigenvector of the covariance matrix of the data, and selecting the matrix composed of eigenvectors corresponding to
k features with the largest eigenvalue (i.e., the largest variance), the data matrix can be converted into a new space to achieve dimensional reduction of data features. However, in our study, PCA is used to improve the estimation performance, rather than dimension reduction, which is the same PCA application described in [
15].
2.4.3. Random Forest with Principal Component Analysis
The structural diagram of the RFPCA method used for the knee estimation from the sEMG is shown in
Figure 5. In this figure, the blue lines represent the training process and the red lines describe the studying course. The time-domain amplitudes were extracted from 5 sEMG channels. After the process and PCA, one part of the data would be used for training to build the estimation model and the rest would be used for testing.
In our work, the processed sEMG
Xt forms the original data set
Xemg, and
Xemg which is then transformed through a matrix
P by PCA. Next, the input
X of the following RF is obtained, which is described as follows:
with the combination of
X and the knee angle
yknee, the data set after PCA is derived as (
X,
yknee). These data are divided into training set and testing set.
When the training sample
Tr = (
Xtr,Ytr) is given, the goal is to use the
Tr to establish a estimation model
E(
X) and apply it to estimate the new knee angle from sEMG. The RF consists of a collection of
N randomized regression trees
r(
X,
vi), where
vi (
i = 1, 2, …,
N) are the independent random variables. They are used to resample the training set and select the successive direction for splitting [
19]. The estimation model
E(
X) is an average of the regression trees in the RF, expressed as:
When the testing data set
Xtest is used to validate the estimation performance, the estimated knee angle can be calculated as follows:
2.5. Arguments Selection
For comparison with RFPCA in this study, another method, namely BPPCA, was also presented. This method is similar to RFPCA in
Section 2.4.3, with a substitution of a conventional BP for RF. For different methods, there are different arguments regarding the effect they have on the performance of the estimation. In a model of RF, there are three main parameters to be determined, namely the number of trees in the forest (
N), the number of features of the input (
Nf) and the minimum size of the terminal nodes (
Nm). The parameters for the BP are the number of epochs (
Ne), the number of hidden layer nodes (
Nh), the learning rate (
Lr) and the learning goal (
Lg).
During the test of the ML methods, the results showed that the performance of motion estimation was not sensitive to the difference of individuals using the same parameters, which was similar to the results found in [
19]. Thus, it meant that universal values could be chosen from these parameters. Referring to the parameter settings in [
19], and to reach a compromise between estimation accuracy and computational time, the parameters for our methods were set as recorded in
Table 2.
To study the historic effect of previous sEMG, the data from one trail with 4 GCs from each subject would be introduced. A total of 75% of the data was used for training and the rest was used for the testing set.
For the study of the sample size, as noted, 61 GDs were utilized for the estimation work of one subject, and the last GD, with approximately 128 samples, was always the testing set. Hereby, parameter Ss in the interval of [1, 60] was defined to represent the sample size. For example, when Ss = 1, the 60th GD would be the training set, when Ss = 2, the 60th and the 59th GDs were the training set, and by that logic, when Ss was 60, all of the 60 GDs would be used for training. The sample size was nearly proportional to the Ss.
2.6. Evaluation Metric
The performance of the estimation model was mainly evaluated by comparing the root mean square error (
R) between the estimated value
and the experiment value (EV)
defined as follows:
where
S is the number of test samples. In this work,
R is an indicator for the judgement of the estimation models, and the accuracy of the estimation model increases with a decrease of
R.
4. Discussion
In this paper, a novel estimation method of RFPCA was proposed to study the relationship between sEMG and knee movement. Compared with the results of BPPCA, the RFPCA performs better, both in terms of the root mean square error and the execution time. All of the estimation results using RFPCA are also generally in line with the EV. These results may be due to the strong regression ability of RF, which generates an internal unbiased estimate of the generalization error as the forest building progresses. PCA is able to generate a better input for RF from the original data, which also promotes the accuracy of the results of estimation.
As seen in
Figure 7, with the increasing of input samples,
R starts to decrease and eventually stabilizes, which means that the prediction accuracy increases at first, and then does not change significantly for both methods. As known, walking is a regular movement, the kinematic parameter of the gait is a cyclic process and the sEMG also appears as a periodic signal in different GCs. Thus, we believe that when the sample size increases to a certain value, the differences between the samples decrease, so that the prediction results show little change. However, the larger the data, the longer the time. With acceptable accuracy, choosing a better sample size can effectively reduce the time consumption caused by large samples,, and this would contribute to the efficiency of online control using sEMG.
The historic effect of the input has a positive influence on motion estimation, according to the authors of [
19]. In this work, as the input size increases, there is a tendency for the
R of both RFPCA and BPPCA to increase, as shown in
Figure 8, and the previous signals seem to have little to no effect on the estimation after more dimensional data is involved in the calculation. Generally, in the high-dimensional input case, the problem of sparse data samples and the difficulty of distance calculation are a common and serious obstacle for all machine learning methods, which is called the "curse of dimensionality". Thus, except for the PCA used in our work, further study of the input dimension of sEMG needs to be considered. Multichannel sensors of sEMG detecting are also worthy of research.
As seen in
Figure 9, in terms of the physical and mental quality of the test subjects, the prediction results of different subjects also vary. In addition, the skin preparations of the subjects vary from one subject to another, which can also contribute to detection errors of in the raw sEMG. Moreover, different times for the experiment and other environmental factors will also cause diversity in the outcome when the raw sEMG is being collected. However, both
Figure 9 and
Figure 10 show that the results of the BPPCA are more unstable for all participants, relatively, and that the results of the RFPCA have estimations similar to the EV. That is, RFPCA has a better error tolerance and is not adversely affected by variations in test subjects.
The root mean square error of RFPCA was small (
R ≈ 5°) in the previous sEMG study when
n = 2, as shown in
Figure 10, and this result seems to be large in comparison to the motion angle of the knee. However, we believe that this is acceptable for the exoskeleton control, since the control precision of the exoskeleton joint is not in high demand as a machine tool, and the pilot of the exoskeleton is able to tolerate the small differences of several degrees due to the flexibility of the human body. Also, the estimation model using RFPCA has some hyperparameters in the structure of the forest. Therefore, a better parameter selection may lead to a more accurate estimation model of RFPCA, and this would also help the application of RFPCA for estimation of joint movement in myoelectric control. Furthermore, while the RFPCA performed better in our study, the BPPCA may have advantages over the RFPCA with a better parameter choice.
Since the aim of this work is using ML to build an estimation model which can be adjusted to suit the subject himself, the training and testing data are from the same subject for each validation, and a similar method can be found in [
30]. The results of the subjects in this work using RFPCA was acceptable. However, sEMG is unstable, as mentioned above, and the RFPCA method may be unfeasible for subjects who are middle-aged and elderly, since the subjects in our study were under 30 years of age, and the data from different people for training and testing may be an issue through the method of RFPCA. Thus, more people will be invited to participate in the study to further validate the proposed method.
5. Conclusions
In this study, a new method of combining RF and PCA was utilized to establish an estimation model from sEMG to the knee. Better than BPPCA, the RFPCA method is able to predict the knee angle at a low root mean square error about 5° and the execution time is several times smaller, and these results indicate that RFPCA is suitable for knee movement estimation with high accuracy and requiring minimal time. Both the sample size and the input dimension of the RFPCA were investigated. RFPCA is insensitive to the estimation accuracy when the sample size increases to a certain value, but requires more time. Also, as the previous sEMG increases, the accuracy of the RFPCA first increases and then decreases, and the work would be beneficial to the estimation model construction using ML methods. Moreover, the results of the RFPCA are more stable in comparison to the BPPCA in terms of sample size and previous sEMG input, and RFPCA is also robust in terms of differences among test subjects. All in all, the estimation of RFPCA performs well in the estimation from sEMG to knee movement in this work, which is conductive to motion analysis and exoskeleton control.
Future work of improving the estimation accuracy will be done by extracting more signal features or fusing other physical sensors, as well as testing more people and other daily activities such as different speeds of walking, and ascending or descending stairs. Furthermore, a wider application for RFPCA may be utilized for estimation using different sEMG data from various people to find a general relationship between sEMG and joint motion. Finally, the RFPCA method will be applied to estimate human motion for exoskeleton control.