1. Introduction
Wireless sensor networks (WSNs) comprise a number of tiny sensor nodes for sensing and computation, transmission and reception for smart applications [
1]. In WSNs, sensor nodes collect data about some targets and transmit sensed data to the sink node (or base station) via multiple hops [
2]. Due to the ease of deployment, WSNs are utilized in many smart applications, such as security surveillance [
3], disaster relief [
4], IoT use cases [
5], medical care [
6], E-mobility [
7], traffic management [
8] and precision agriculture [
9]. Enhancing the network lifetime and minimizing the packet delivery delays are some of the challenging tasks for WSNs based smart applications [
10]. The size of the sensor nodes is small, and need regular power from a tiny size battery. However, it is unfeasible to recharge or alter the battery in case of hostile environments centric applications. In wireless sensor networks, we can extend the operating lifetime of nodes by energy harvesting mechanism and therefore enhancing the network lifetime [
11]. Furthermore, this technology decreases the operation cost of WSNs, thus making it very essential for a sustainable “near-perpetual” WSNs operability. Therefore, energy harvesting in WSNs (EH-WSNs) is crucial for the sustainable operations of WSNs [
12].
Various challenges exist in improving the environment of EH-WSNs. Further, there is a need for enhancing the performance of various applications for uplifting the ecosystem and human life by using EH-WSNs [
13]. Efficient energy regulating schemes are required to make the nodes working proficiently without hurdles and thereby making the network more efficient [
14]. Some mechanism is needed to address the issue of energy scarcity in EH-WSNs [
15].
There are still various unresolved problems and to effectively manage the harvested energy, EH-WSNs should use a customized packet forwarding scheme. This minimizes the energy consumption and maximizes the lifetime of the network [
16]. Opportunistic packet forwarding schemes (OPEH) are broadly used in WSNs, and usually yield high packet delivery ratio (PDR) and low end-to-end delay (EED). In EH-WSNs, the packet-transmission method acknowledges multistage relay set optimization mechanisms and renders an exact estimation to the cost of transmission. The relay nodes can be optimally chosen either by prioritization of the relay nodes or clustering the relay nodes in WSNs [
17]. Likewise, in WSNs, nodes are generally duty-cycled to prolong the network lifetime. According to the duty cycle method, the nodes periodically switches among active and sleep mode and it is a most commonly applied scheme for energy saving. A node can transmit or receive packets while in active mode, but cannot communicate while in sleep mode. Thus, raising the duty cycle results in higher energy consumption and lower delay, while it produces the opposite effect by reducing the duty cycle.
Furthermore, sensor nodes usually work with sleep-wake up schedules to save power by using the duty cycle scheme. [
18,
19] discusses the duty cycle adjustment scheme that is based on residual energy aware and changing the wake-up interval as per the harvested energy.
In EH-WSNs, the concept of dynamic and heterogeneous duty cycle (DC) of nodes helps in improving the energy acquisition. This approach would make the nodes working proficiently for a longer time. The reason belongs to the fact that the energy acquisition is typically insufficient, time-shifted and uneven in static duty cycle centric EH-WSNs. The opportunistic packet forwarding methods do not acknowledge the effect of the dynamic and heterogeneous DC. Zhang et al. [
20] have improved the dynamic and heterogeneous DC methods with the assistance of the energy consumption calculation and utilized ESN [
21] for predicting energy acquisition for next time slot, however only the traditional ESN model was used. In conventional ESN, the weight choice methodology is time-consuming making it non-scalable for WSNs. This research article overcomes the limitations of ESN and proposes an improved echo state network which have been named modified echo state network (MESN).
Further, in MESN, the interconnection weights are optimally chosen by utilizing a whale optimization algorithm (WOA) [
22]. We will describe the MESN model in
Section 3. For further improvement, this article proposes the MESN based dynamic DC with optimal opportunistic routing (OOR) for EH-WSNs. This MESN model predicts the expected energy acquisition value for the next time slot. The principal goal of the proposed OOR method is to select the relay set by using multiple energy centric parameters and alter DC by using energy consumption, energy acquisition, and energy threshold.
The key contributions of this article are listed as follows:
This article proposes the modified echo state network (MESN) which is used as a predictor for finding the expected energy acquisition of the next time slot. The proposed scheme is a novel research in this article and stops the unstable output of ESN due to the random weight selection in the reservoir layer. This model utilizes the whale optimization algorithm (WOA) for optimally selecting the weights of the neurons in the reservoir layer of the echo state network.
In the optimal opportunistic routing (OOR) scheme, the relay set is selected using multiple parameters such as energy consumption, congestion rate and estimated duty-cycled wakeups (EDW). The relay set selection scheme selects appropriate forwarding paths for each forwarder node.
The proposed scheme achieves an optimized style to update duty cycle since it is updated based on energy consumption, energy acquisition of the next slot and energy threshold as the optimal energy is acquired from the prediction of the next slot with the help of the MESN model.
Finally, the comparison of the proposed technique with existing methods such as ESN, AOR, and Max-SNR in terms of performance parameters such as delay, packet delivery ratio and throughput is done. This reveals that the average percentage improvement of the proposed approach outperforms the existing techniques.
The organization of the article is as follows:
Section 2 provides related work.
Section 3 provides complete detail of the proposed MESN technique.
Section 4 discusses the working structure of the MESN based OOR scheme.
Section 5 describes the results of simulation and performance comparisons. Finally,
Section 6 presents the conclusion of the paper.
3. Proposed Modified Echo State Network (MESN) Model
In EH-WSNs, nodes can consistently harvest energy from the surroundings. However, the energy acquisition in EH-WSNs is usually deficient, time varied and unstable. The dynamic and heterogeneous duty cycle (DC) of nodes can be used to improve energy acquisition and hence, would keep the nodes operational for a longer time. It is noticeable that the traditional opportunistic packet-forwarding schemes in EH-WSNs do not consider the concept of dynamic DC while building, the relay set and selecting the forwarding paths. Thus, the performance is lower than expected by using conventional OPEH in EH-WSNs when dynamic DC is not used. Zhang et al. [
20] have improved dynamic and heterogeneous DC methods but used the traditional ESN model utilizing random weight selection for neurons in the reservoir layer which may produce an unstable output. Therefore, in this article, MESN is utilized for the same purpose and the method is described next.
The proposed modification in ESN enhances the efficiency of predicting the expected energy acquisition precisely for enabling better duty cycle calculation. In traditional ESN, every cycle of the training phase consists of refreshing the weights of the neurons; until the error amongst output and input is within tolerance. The weights generated during the training phase will be used to test on the newer data. However, the weight selection procedure is time-consuming. This article overcomes this limitation by using WOA with ESN for optimally selecting the weights in the reservoir layer of ESN, named as MESN. MESN is an enhancement over the ESN. ESN is a neural network algorithm that has high correctness in guessing time-series data, regardless of whether the data fluctuate rapidly. Hence, ESN can be utilized to assess the time-sensitive fluctuating energy acquisition estimations of the next slot. ESN provides more accuracy in predicting expected energy acquisition compare to pure mathematical model-based algorithms, especially for a rapidly changing environment. ESN comprises three layers, namely the input layer, dynamic layer and the output layer, respectively. Also, ESN has the training and analyzing phases similar to the machine learning algorithm. During training, the weights of the neurons are refreshed in every cycle until the training error between output and input is within acceptable limits. However, the training of traditional ESN is time-consuming. We have proposed modified ESN for acquiring the optimal set of weights to be applied in the interconnection links of ESN for improving the trained prediction model. In modified ESN, the WOA is applied to choose the interconnection weights optimally.
Figure 1 shows the proposed MESN and depicts the various layers.
Here, the input data is the expected active transmission cost (EATC) [
20] of the active relay set, and the corresponding target is the expected energy acquisition value of the next time slot. Likewise, the training data is generated and trained with MESN. Here, input(
t) represents input data,
internal(
t) represents neurons and
output(
t) represents output data.
Winput represents the weight matrix for input,
Winternal represents the weight matrix for neurons, and
Woutput represents the weight matrix for output. During training, the training error is reduced depicted by Equation (1) below:
Until the training error is reduced, the weights of the neurons are modified to generate the prediction model. Equation (2) represents the weights update mechanism for the neurons in the dynamic layer:
where
represents the activation function of the dynamic layer. Moreover, the following Equation (3) demonstrates the update in weight at the output layer:
where
represents the linear activation function at the output layer.
3.1. Role of Whale Optimization Algorithm in the Modified Echo State Network (MESN) Model
The general acts of whales influence the working of the WOA. The WOA is used to raise the speed of the training process using optimally calculating the interconnection weights and is a metaheuristic algorithm. The following section shows the various steps of the WOA.
• Initialization
The algorithm is formed by randomly developing the initial solution (i.e., the interconnection weights of the ESN). The random value in the search space is as:
where
signifies the initial population of the whales at ‘
’ i.e., number of interconnection links.
• Fitness Calculation
The fitness value of the solution is computed by:
The fitness value is essential for becoming the best network structure. If the training error is minimum, it means that the network has been sufficiently trained to predict the energy acquisition values of the next time slot. Later, the best solution will be one having minimum training error.
3.2. Update the Position of the Current Solution
• Encircling prey
Consider the below equations:
where ‘
’ demonstrates a current iteration,
represent a coefficient vector,
demonstrate best solution,
refers a current state. Also:
where,
is reducing from 2 to 0,
.
• Exploitation phase
Two mechanisms are:
1) Shrinking encircling mechanism
The Equation (8) shows this act, where the value of is reduced.
2) Spiral updating position.
The equation is as follows:
where
It means the distance between the
whale to the prey (which is the best set of weights attained so far),
takes value from
,
signifies the logarithmic spiral shape. During optimization, supposing a probability of 50%. Consider the below Equation (11).
where,
.
• Exploration phase
The following equation demonstrates the exploration phase:
where the current population random position vector is
. Throughout every solution updating process, the fitness function is evaluated to find the best solution among them. Based on the best solution, a set of novel solutions will be generated, and the fitness is again evaluated to continue the above solution updating steps.
• Termination criteria
The termination criteria of WOA include the best interconnection weights. As a result of finding the optimal interconnection weights, the prediction model is qualified. Since the objective is to become the weights for which the training error is minimum, the prediction model, achieved for the best weights, is well qualified to predict for unknown data. When the training procedure is stable, the proposed modified ESN(MESN) can be used to predict the energy acquisition values of the next time slot, on giving the EATC values of the previous time slot.
Figure 2 shows the flow diagram of the WOA algorithm.
4. The Working Structure of the Proposed Modified Echo State Network (MESN) Based Dynamic Duty Cycle (DC) with Optimal Opportunistic Routing (OOR)
In the OOR scheme, the relay set is initially selected using multiple parameters such as energy consumption, congestion rate, and estimated duty-cycled wakeups (EDW) [
23]. Further, appropriate forwarding path is selected from the relay sets of each of the direct neighbor nodes. In
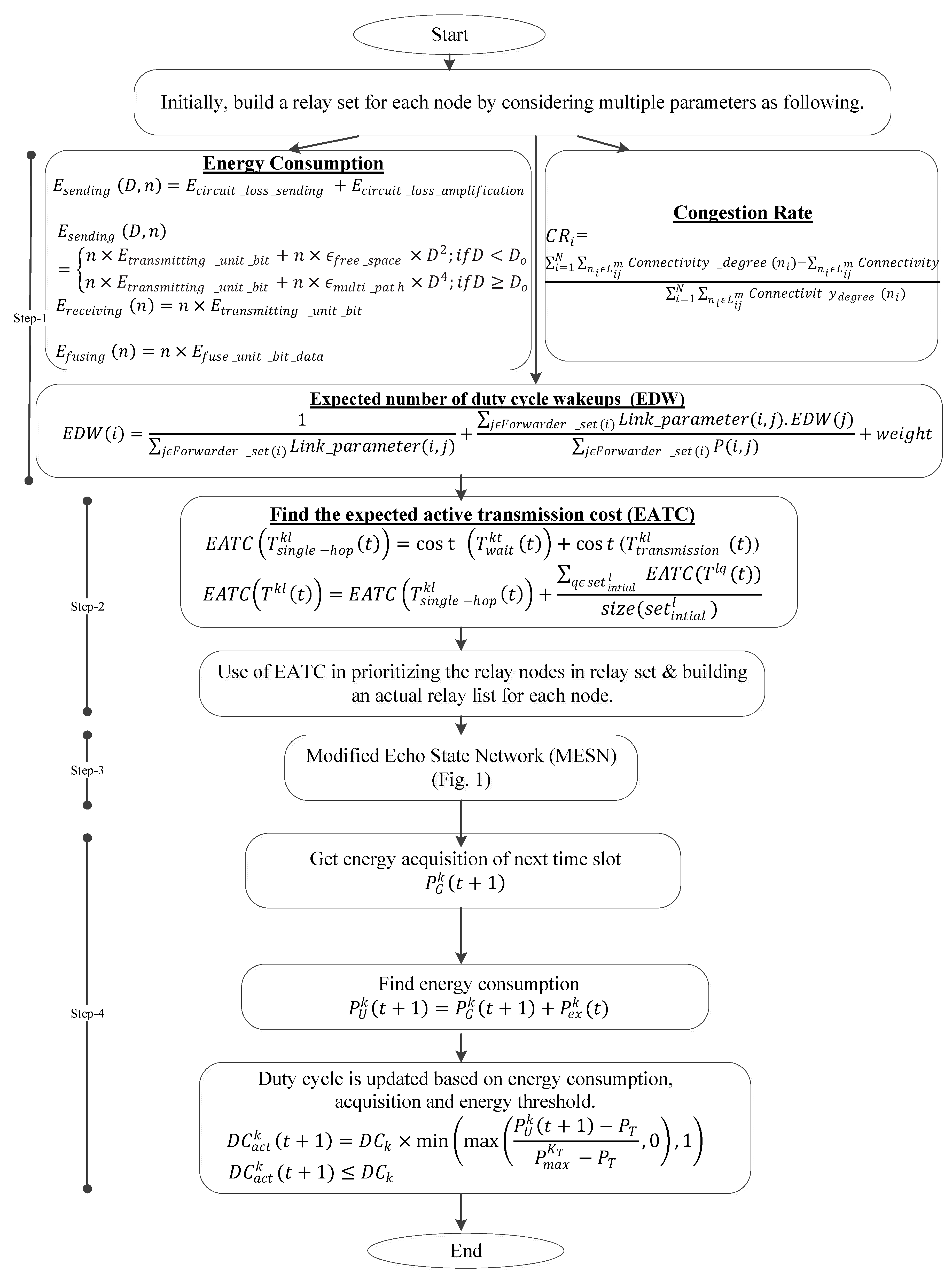
Figure 3, a complete working structure of MESN enabled OOR is detailed.
The formation of the initial relay set
Setinitial for all nodes utilizes multiple parameters such as energy consumption [
31], congestion rate [
32], and the EDW. In the first step, we use multiple parameters for relay selection. Therefore, we have named this approach a hybrid relay selection mechanism.
Now we are explaining the various parameters used for relay selection as follows:
The energy consumption in the data transmission mechanism consists of three parts, such as energy consumption in sending data, energy consumption in receiving data and energy consumption for the fusion of data [
31]. The energy consumption in sending data can be expressed as given in Equation (14):
Here,
D is the distance for sending n bits data,
represents energy consumption due to the circuit loss and
shows the energy consumption due to the amplification circuit loss. Similarly, the energy consumption in sending into two different transmission environments, namely, free space and multipath can be expressed as given in Equation (15):
represent energy consumption in sending unit bit data,
shows energy consumption of unit bit in free space and
demonstrates energy consumption of unit bit in multi-path, and
. Similarly, the energy consumption in receiving n bit data can be expressed as given in Equation (16):
Similarly, the energy consumption in n bit data fusion can be expressed as given in Equation (17):
where,
shows energy consumption in unit bit data fusion. The congestion rate (CR) [
24] is used to evaluate the load of relay nodes. Here, each intermediate node can adaptively detect the occurrence of congestion and then notify the parent node to reduce the packet delivery rate according to the congestion level. The CR at each neighbor node can be expressed as given in Equation (18):
Here
Connectivity_degree(
ni) represents degree of connectivity, and
Lij is the route. The relay set formation from the neighborhoods of the sensor nodes utilizes the concept of the EDW required to transmit packets from source to destination efficiently [
23]. The EDW of particular node
i can be expressed as given in Equation (19):
here
is the expected number of duty cycle wakeups in single-hop transmission, and
is the expected number of duty cycle wakeups in multi hop transmission, and weight represent the forwarding cost in terms of energy. Also, Link_Parameter (
i,
j) represents success probabilities and Forwarder_set(
i) denotes the set of candidate forwarders.
Next, we collect the current duty cycle of relay nodes from the initial relay set
Setinitial generated in step-1 (
Figure 3). The relay set is updated based on the current duty cycle of relay nodes, and
Setactual is the updated relay set. The step-2 (
Figure 3) consists of two primary functions, namely; calculation of expected active transmission cost (EATC) and prioritization of relay nodes by using EATC. Therefore, the actual relay list L
actual is built for each node in step-2 itself. For each sender node ‘
,’ the relay nodes set
are generated for further steps. The EATC of single-hop data forwarding,
at particular slot
t is derived from the sum of transmission cost and the wait cost as given in Equation (20):
The expected time interval between receiving a packet and beginning to send that packet to other nodes is known as wait cost. EATC of multi-hop data forwarding uses EATC of the single-hop and average EATC of subsequent relay nodes. It can be expressed as given in Equation (21):
where
is the size of the relay set, and
is the expected active transmission cost for a single hop of receiver node
in the relay node-set
. Moreover,
represents the average dynamic transmission cost of the relay node-set,
.
Next, we are explaining the prioritization of relay nodes. The relay nodes are prioritized primarily by applying the EATC. From the previously found relay set
Setactual, we construct the actual relay list
Lactual for each node based on EATC. The higher priority is assigned to relay nodes which are having lower EATC value. The step-3 (
Figure 3) consists of the formation of the proposed MESN model. Here, we use the WOA for optimally selecting the weights of neurons in the reservoir layer of MESN. After successful training the model, the MESN predicts the expected energy acquisition of the next slot in the dynamic duty cycle scenario. In step-4 (
Figure 3), updating of the dynamic duty cycle is performed. Here, the energy utilization of
time slot is nothing but the sum of the expected energy acquisition of the next time slot and the excess energy of the current time slot. It can be expressed as given in Equation (22):
where,
denotes the expected energy gain of next time slot and
represents the excess energy in the current time slot. Similarly, the duty cycle updating can be expressed as given in Equation (23):
where, for node
k,
represents the active time at slot
and
represents the duty cycle slot length. Also,
refers to the energy utilization of
time slot,
represents maximum consumption of energy for a slot, and
represent the energy threshold. The active-duty cycle is referred as
and,
represents that the node is entirely inactive for
time slot.
5. Results and Discussion
In this section, the MESN based dynamic DC with OOR for EH-WSNs is analyzed using network simulator (NS2), the performance analysis uses two simulation scenarios. In the first simulation scenario, the sensor nodes vary from 100 to 500 in the network region 1000 m × 1000 m. In the second simulation scenario, the average energy harvesting rate ranges from 20, 40, 60, 80, and 100 mW with a fixed number of nodes as 500. Each sensor node is having initial energy of 0.5 J in the region. For sending a single packet of size 512 bytes per node, the transmission energy per node is , also receiving energy per node is . The transmission range of each sensor node is 150 m. Here, every node uses the AODV routing protocol for packet transmission. This scenario also uses MAC protocol 802_11. Each sensor node uses an omnidirectional antenna. Also, this scenario uses the two-ray ground radio propagation model. The simulation time is 100 s, and the transmission rate is 500 kbps. Also, this section consists of a comparison of the proposed scheme with the existing state-of-art techniques such as ESN-based, AOR and Max-SNR in terms of parameters such as delay, packet delivery ratio and throughput.
5.1. Impact of Varying the Number of Sensor Nodes
Considering this scenario, we vary the node numbers as 100, 200, 300, 400, and 500 in the experiments.
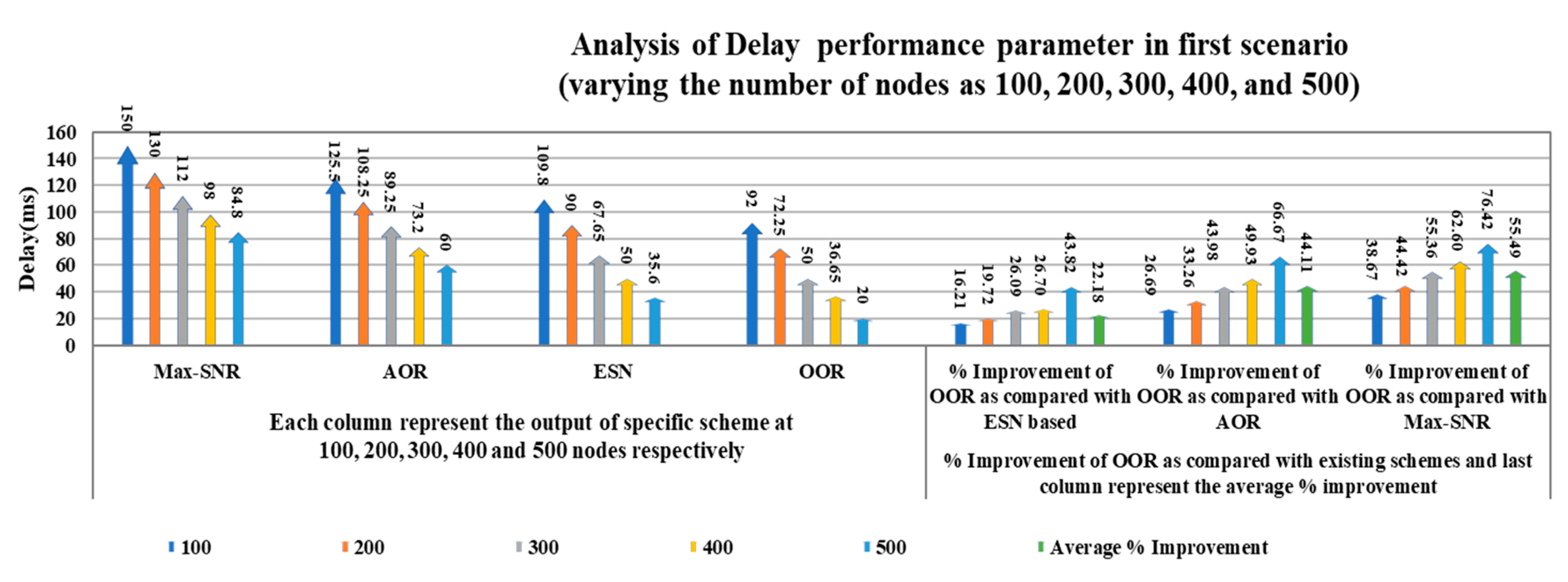
Figure 4 displays the comparison of the proposed OOR scheme with the existing schemes in terms of delay. The graph demonstrates that the delay of our proposed OOR scheme is lower than the existing ESN based, AOR, and Max-SNR schemes respectively.
From the above
Figure 4 it can be observed that delay reduces as the number of nodes increases. In OOR, the possibility of selecting the sleeping node as the relay node is less; therefore, the packet is transmitted from source to destination without much delay. Next,
Table 1 depicts the performance measurement of the OOR scheme with variation in the number of nodes. Also,
Table 1 shows the percentage improvement and average percentage improvement.
In case of delay, the average percentage improvement of OOR is 22.18, 44.11, and 55.49 as compared to ESN based, AOR, and Max-SNR, respectively. We can show the performance comparison of OOR in a more detailed way in the following
Figure 5.
In
Figure 5 the five different columns in the first part of the figure show the outcomes of the delay parameter with variation in the number of nodes for each scheme, respectively. For example, consider different columns of the OOR scheme in the first part of the figure; the first column represents the value of delay parameter as 92 ms at 100 nodes, whereas the fifth column depicts the value of 20 ms at 500 nodes. In the second part of the figure, the five different columns show the percentage improvement, and the sixth column represents the average percentage improvement.
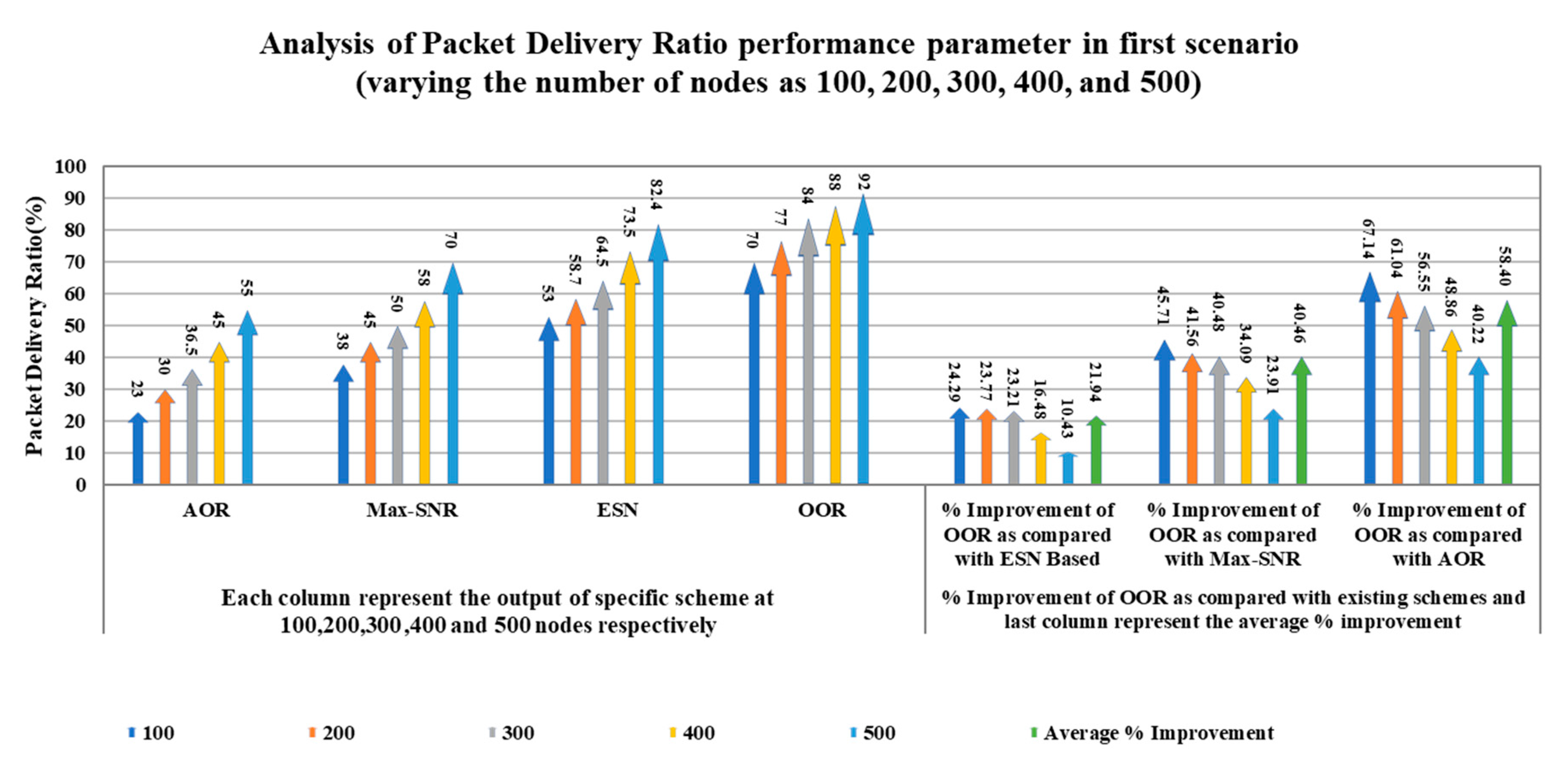
Figure 6 demonstrates the comparison of the packet delivery ratio of the proposed OOR scheme and existing schemes. The result indicates that the packet delivery ratio of the proposed OOR scheme is higher than the existing ESN based, Max-SNR, and AOR schemes, respectively.
Concerning the above graph, increasing the number of nodes, packet delivery ratio (PDR) increases; this shows the perfect agreement with the theoretical background. In our proposed scheme, the possibility of selecting the sleeping forwarder node is very less because we have applied the multistage relay set optimization mechanism, which results in a higher packet delivery ratio. Hence, we can say that the proposed OOR is the best solution out of various algorithms available in the literature. Further,
Table 2 depicts the performance of the OOR scheme with variation in the number of nodes. Also,
Table 2 shows the percentage improvement and average percentage improvements both.
Next for the packet delivery ratio, the average percentage improvement of OOR is 21.94, 40.46, and 58.40 as compared to ESN based, Max-SNR, and AOR, respectively.
We can show the performance comparison of OOR in a more presentable way in the following
Figure 7.
In
Figure 7, again, the five different columns in the first part of the figure show the outcomes of the packet delivery ratio parameter with variation in the number of nodes for each scheme, respectively. For example, consider different columns of the OOR scheme in the first part of the figure; the second column represents the value of the packet delivery ratio parameter as 77 at 200 nodes, whereas the fifth column depicts the value 92 at 500 nodes. In the second part of the figure, the five different columns show the percentage improvement, and the sixth column describes the average percentage improvement.
Figure 8 depicts the comparison of the proposed OOR scheme with the existing schemes in terms of throughput. The graph demonstrates that the throughput of the proposed OOR scheme is higher than the existing ESN-based, Max-SNR, and AOR schemes, respectively.
From the above
Figure 8, it is noticeable that as the number of nodes increases, throughput decreases, and the reason behind it is that the probability of packet error is proportional to the number of nodes. Therefore, the number of nodes increases, the packet error also increases, results in decreasing throughput. Moreover,
Table 3 depicts the performance of the OOR scheme with variation in the number of nodes. Furthermore,
Table 3 shows the percentage improvement and average percentage improvements both.
From the above table, the average percentage improvement of OOR is 17.02, 33.01, and 47.72 as compared to ESN based, Max-SNR, and AOR respectively. Further, we can show the performance comparison of OOR in a more descriptive way in the following
Figure 9.
In
Figure 9 the five different columns in the first part of the figure show the outcomes of the throughput parameter in 100 scale with variation in the number of nodes for each scheme, respectively. For example, consider different columns of OOR scheme in the first part of the figure, the third column represents the value of throughput parameter as 88.1 (packets/s) at 300 nodes in 100 scale whereas the fifth column depicts the value of 69.5 (packets/s) at 500 nodes in 100 scale. The values can be verified in
Table 3. We use the 100 scale for better representation of columns in the figure. In the second part of the figure, the five different columns show the percentage improvement, and the sixth column depicts the average percentage improvement.
5.2. Impact of Varying Average Energy Harvesting Rate
In this scenario, we vary the average energy-harvesting rate as 20, 40, 60, 80, and 100 mW with a fixed number of nodes as 500.
Figure 10 demonstrates the comparison of the proposed OOR scheme with existing schemes. In terms of delay. The analysis demonstrates that the delay of the proposed OOR scheme is lower than the existing ESN-based, AOR, and Max-SNR schemes, respectively.
From the above
Figure 10 it can find out that delay decreases with an increase in average energy harvesting rate, and the reason behind is that the number of nodes is 500, and the average energy harvesting rate is increasing gradually from 20, 40, 60, 80 and 100 mW. Now active relay nodes will be high as compared with sleeping relay nodes, and consequently, the delay will decrease. Next,
Table 4 depicts the performance of the OOR scheme with variation in the average energy harvesting rates. Also,
Table 4 shows the percentage improvement and average percentage improvements both.
In case of delay, the average percentage improvement of OOR is 38.17, 59.03, and 67.03 as compared to ESN-based, AOR, and Max-SNR respectively. Further, we can show the performance comparison of OOR in a more illustrative way in the following
Figure 11.
In
Figure 11, the five different columns in the first part of the figure show the outcomes of the delay parameter with variation in average energy harvesting rates for each scheme, respectively. For example, consider different columns of the OOR scheme in the first part of the figure; the first column represents the value of delay parameter as 80 ms at 20 mW average energy harvesting rate whereas the fifth column depicts the value of 7.85 ms at 100 mW average energy harvesting rate. In the second part of the figure, the five different columns show the percentage improvement, and the sixth column depicts the average percentage improvement.
Figure 12 demonstrates the comparison of the packet delivery ratio of the proposed OOR scheme and existing schemes. The graph clearly shows that the packet delivery ratio of the proposed OOR scheme is higher than the existing ESN-based, Max-SNR, and AOR schemes, respectively.
Here also, it may be observed that increasing the average harvesting rate, packet delivery ratio (PDR) increases, in this case, we have fixed the number of nodes as 500, and the average energy-harvesting rate is increasing gradually. Due to the multistage relay set optimization mechanism, the possibility of selecting the sleeping forwarder node is very less in our approach. Next,
Table 5 depicts the performance of the OOR scheme with variation in the average energy harvesting rates. Also,
Table 5 shows the percentage improvement and average percentage improvements both.
Next for the packet delivery ratio, the average percentage improvement of OOR is 14.70, 36.80, and 51.43 as compared to ESN-based, Max-SNR, and AOR, respectively. Further, we can show the performance comparison of OOR in a more detailed way in the following
Figure 13.
In
Figure 13, the five different columns in the first part of the figure show the outcomes of the packet delivery ratio parameter with variation in average energy harvesting rates for each scheme, respectively. For example, consider different columns of the OOR scheme in the first part of the figure; the second column represents the value of the packet delivery ratio parameter as 66.25 at 40 mW average energy harvesting rate whereas the fifth column depicts the value of 90 at 100 mW average energy harvesting rate. In the second part of the figure, the five different columns show the percentage improvement, and the sixth column depicts the average percentage improvement.
Figure 14 illustrates the comparison of throughput of the proposed OOR scheme and existing schemes. The analysis demonstrates that the throughput of the proposed OOR scheme is higher than the existing ESN-based, Max-SNR and AOR schemes respectively.
Here also from
Figure 14, it is noticeable that as average energy harvesting rate increases, throughput decreases, and this is because the probability of packet error is proportional to the increase in the number of nodes. Though in this scenario, the number of nodes is fixed as 500 when 500 nodes start communication, then the probability of packet error start increasing and result in decreasing throughput. Next,
Table 6 depicts the performance of the OOR scheme with variation in the average energy harvesting rates. Also,
Table 6 shows the percentage improvement and average percentage improvements both.
Last for throughput, the above table reveals that the average percentage improvement of OOR is 30.35, 48.76, and 63.15 as compared to ESN-based, Max-SNR, and AOR, respectively. Further, we can show the performance comparison of OOR in a more detailed way in the following
Figure 15.
In
Figure 15, the five different columns in the first part of the figure show the outcomes of the throughput parameter in 100 scale with variation in average energy-harvesting rates for each scheme, respectively. For example, consider different columns of OOR scheme in first part of figure, the third column represents the value of throughput parameter as 76.2 (packets/s) at 60 mW average energy harvesting rate in 100 scale whereas the fifth column depicts the value 57.25 (packets/s) at 100 mW average energy harvesting rate in 100 scale. We use the 100 scale for better representation of columns in the figure. The values can be verified from above
Table 6 In the second part of the figure, the five different columns show the percentage improvement, and the sixth column depicts the average percentage improvement.