A Robust Double Active Control System Design for Disturbance Suppression of a Two-Axis Gimbal System
Abstract
:1. Introduction
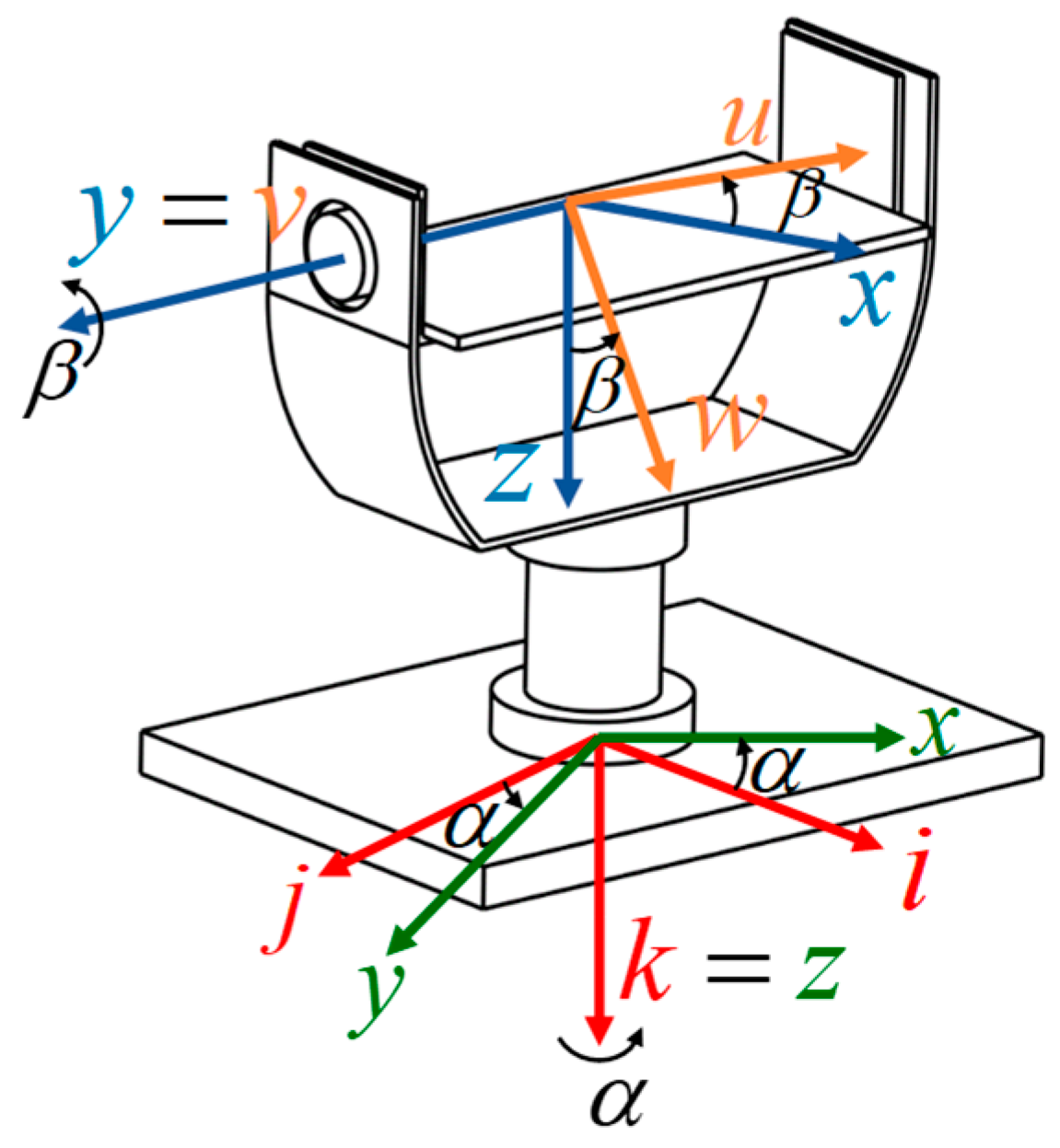
2. Dynamic Model of 2-DOF Gimbal System
3. Control System Design
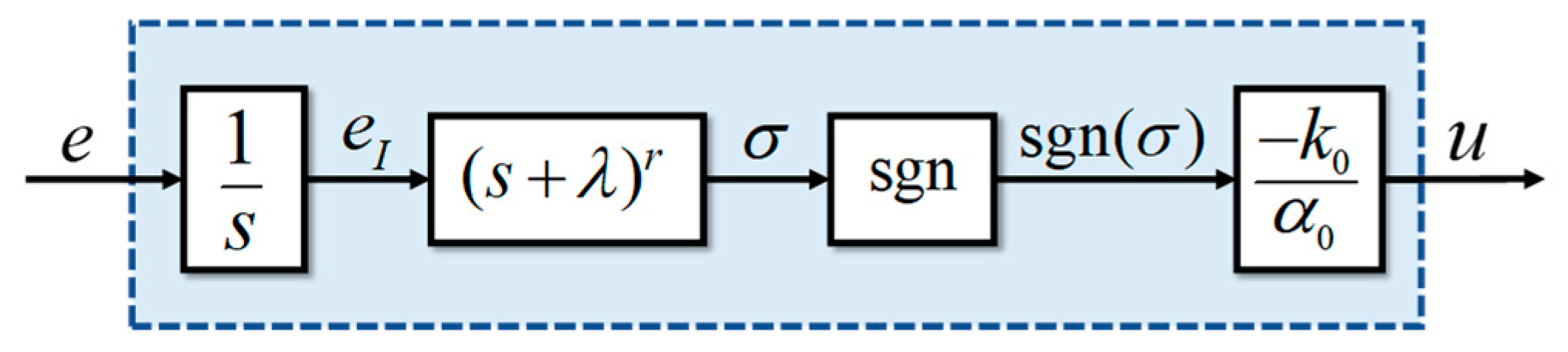
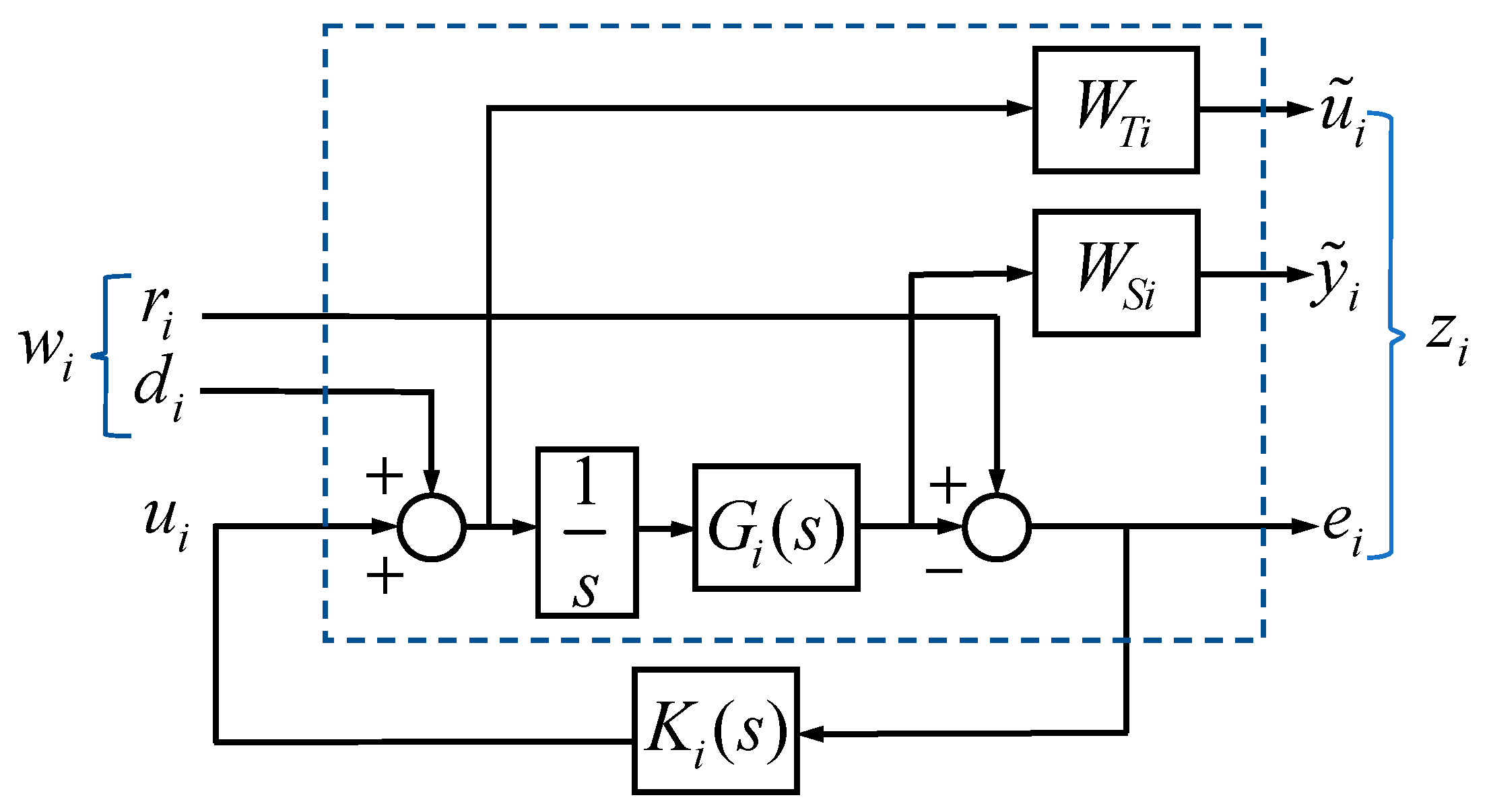
3.1. Design of the Integral Sliding-Mode Controller (ISMC)
3.2. Design Procedure of the Controller with an Integral Action
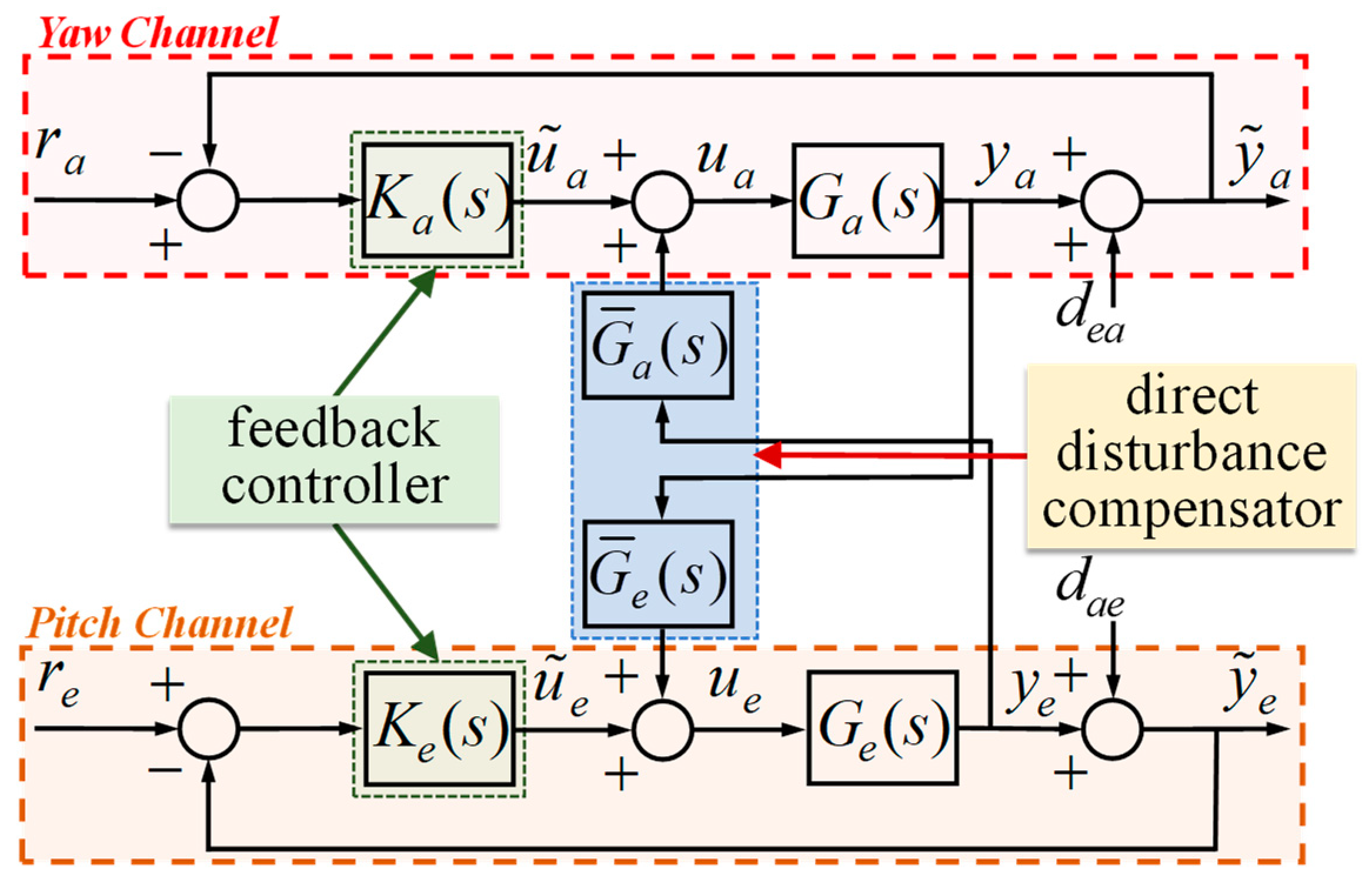
3.2.1. Disturbance Suppression Compensator
- The transfer function of the azimuth gimbal;
- The transfer function of the elevation gimbal;
- The transfer function of the direct disturbance on the elevation gimbal;
- The transfer function of the direct disturbance on the azimuth gimbal.
3.2.2. Feedback Controller Design
- Introducing poles at the origin in the weighting filters related to the system error; an integrator is expected to appear in the controller to account for the error requirement.
- Adding integrators in series with the plant; the controller is calculated for the augmented plant.
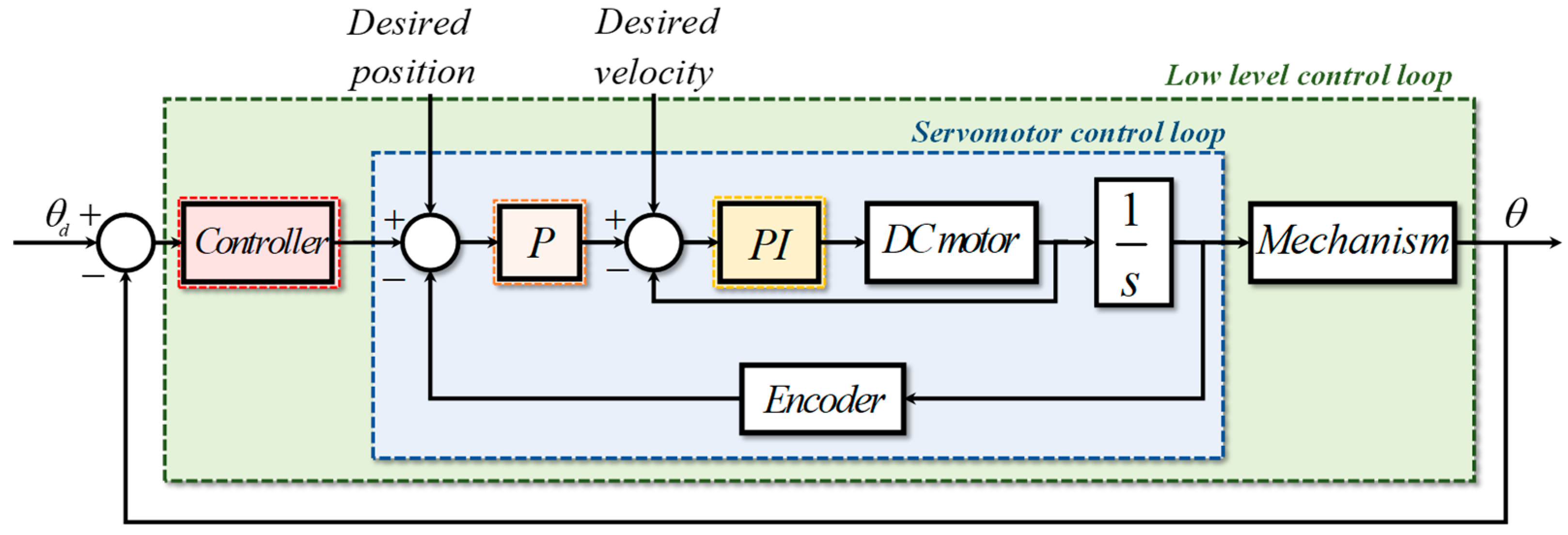
3.3. The Proposed Control Algorithm Implementation
- The dynamics of the two-axis gimbal are identified experimentally. The channels of the gimbal system are powered on separate occasions, and when the yaw gimbal is active its transfer function is obtained. The effect of the yaw channel on the non-powered pitch channel is recorded. Then, the mathematical representation is calculated using the System Identification toolbox of MATLAB software, and vice versa for the pitch channel.
- The inner loop controllers of the azimuth and elevation gimbals are calculated using Equations (20) and (21).
- The mixed sensitivity configuration of the control framework requires the definition of weighting functions. The mutual disturbances are chosen as the weighting function since they interfere with the overall output.
- On the other hand, even though the inner loop controller helps suppress the mutual disturbances, it is considered as a disturbance to the control input. Therefore, the weighting function is simply chosen as the inner loop compensator, with minor modification during the calculation of the controller.
- The computation of the -based controller is done using the MATLAB software; the function ‘hinfsyn’ is used.
- The order reduction algorithm is not necessary after determining the feedback controller. The balanced truncation reduces the order of high-order representation (Hankel singular values).
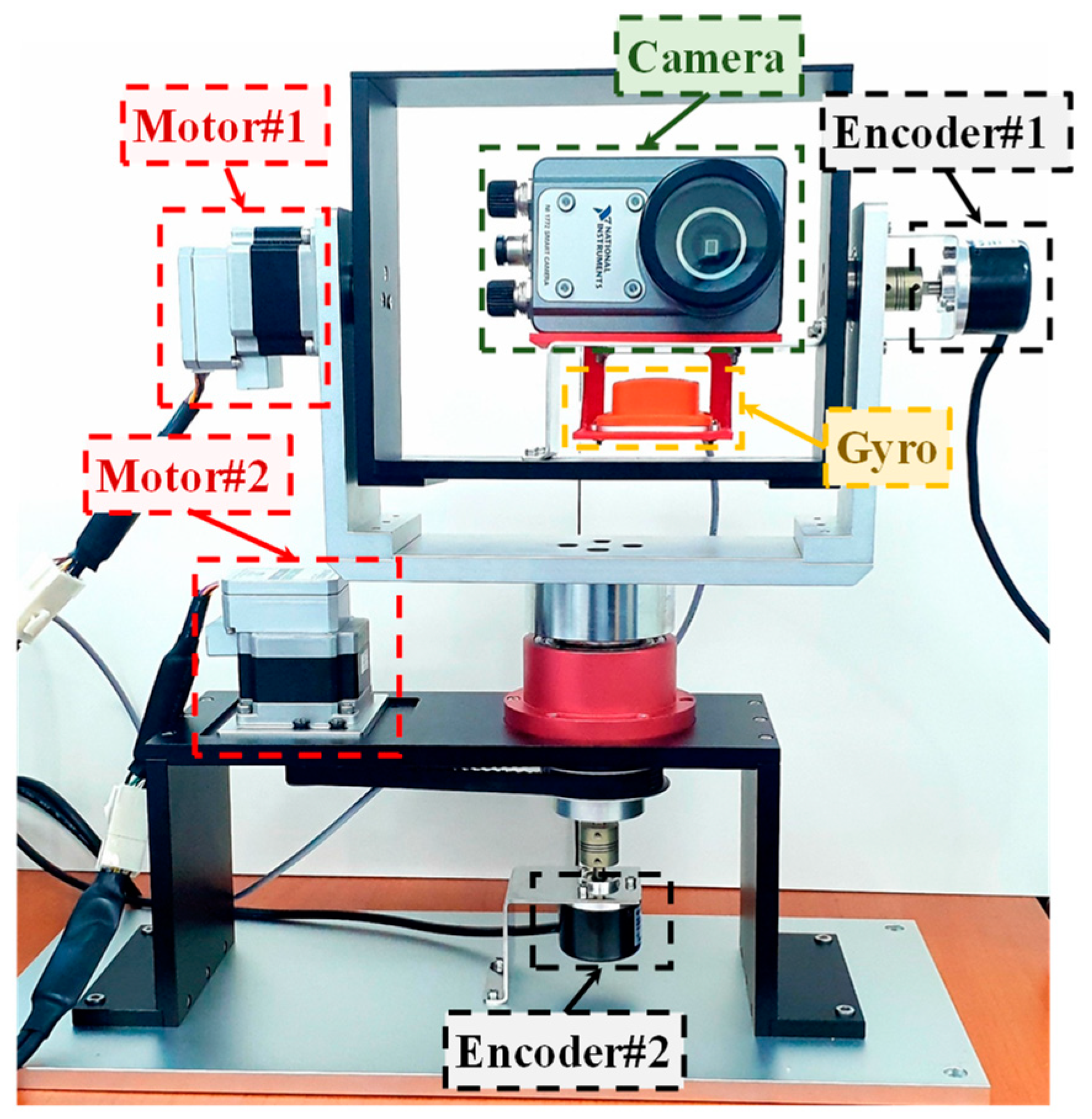
4. Experiment and Results: Control of the High-Precision Gimbal System
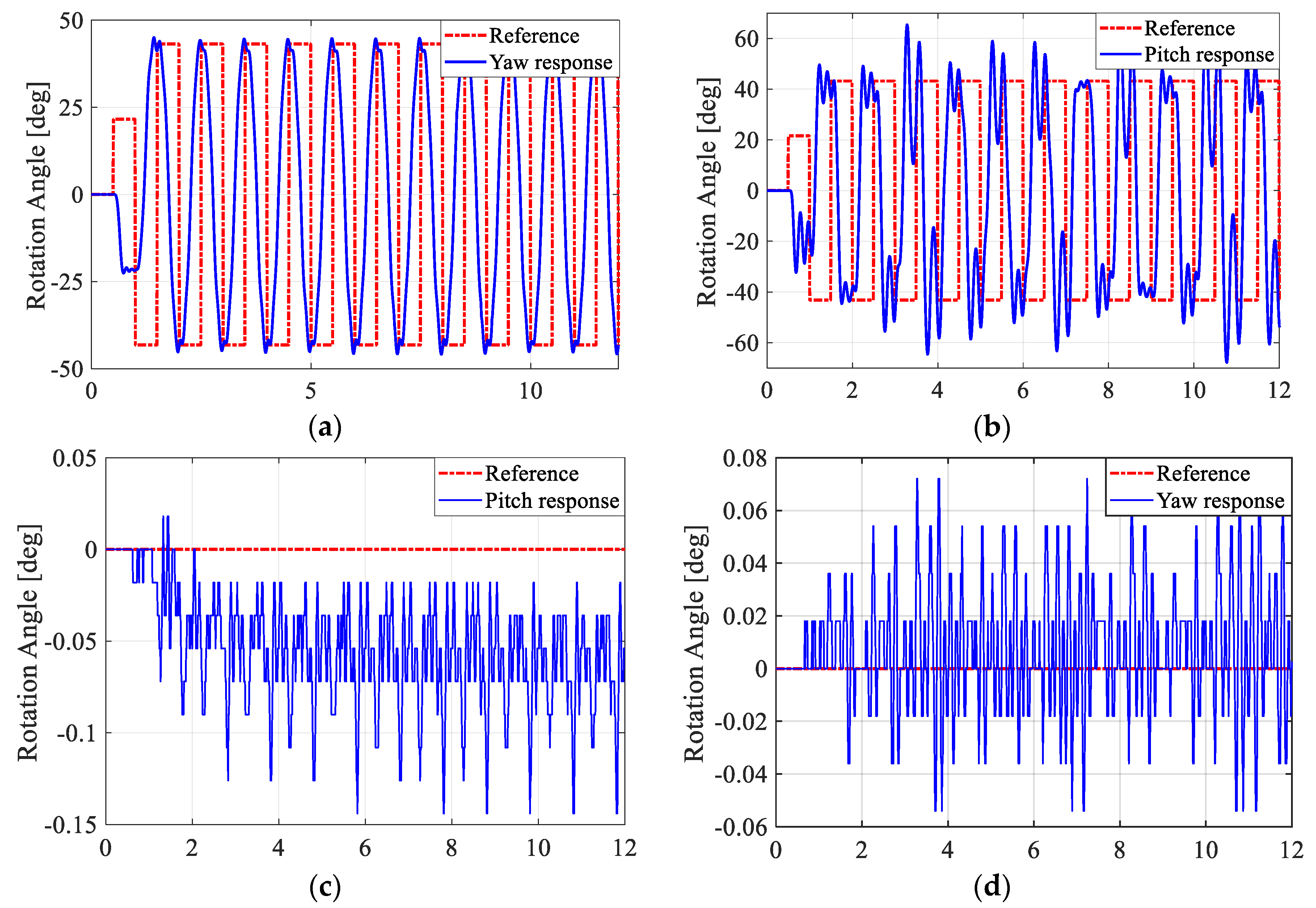
4.1. Mutual Disturbances Effect
4.2. Experiment Methodology
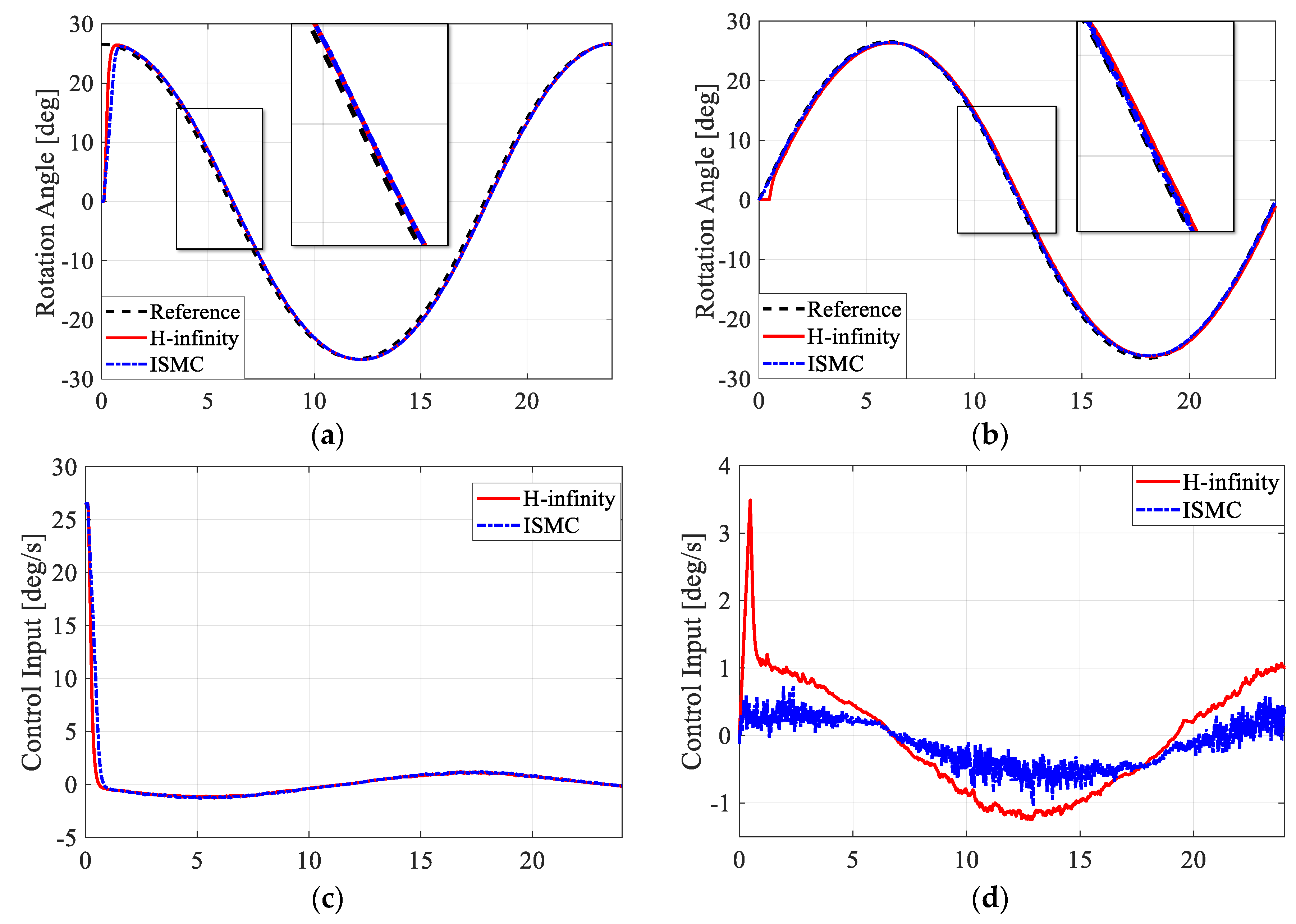
4.3. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Masten, M.K. Inertially Stabilized Platforms for Optical Imaging Systems. IEEE Control Syst. 2008, 28, 47–64. [Google Scholar] [CrossRef]
- Kennedy, P.J.; Kennedy, R.L. Direct versus indirect line of sight (LOS) stabilization. IEEE Trans. on Control Syst. Technol. 2003, 11, 3–15. [Google Scholar] [CrossRef]
- Smith, B.J.; Schrenk, W.J.; Gass, W.B.; Shtessel, Y.B. Sliding mode control in a two-axis gimbal system. IEEE Aerosp. App. Conf. Proc. 1999, 5, 457–470. [Google Scholar] [CrossRef] [Green Version]
- Seong, K.J.; Kang, H.G.; Yeou, B.Y.; Lee, H.P. The Stabilization Loop Design for a Two-Axis Gimbal System Using LQG/LTR Controller. In Proceedings of the 2006 SICE-ICASE International Joint Conference, Busan, Korea, 18–21 October 2006; pp. 755–759. [Google Scholar] [CrossRef]
- Seong, K.J.; Kang, H.G.; Yeou, B.Y.; Lee, H.P. The digital anti-windup LQG/LTR controller design for a two-axis gimbal system. In Proceedings of the 2007 International Conference on Control, Automation and Systems, Seoul, Korea, 17–20 October 2007; pp. 1717–1720. [Google Scholar] [CrossRef]
- Hastürk, Ö.; Erkmen, A.M.; Erkmen, İ. Proxy-Based Sliding Mode Stabilization of a Two-Axis Gimbaled Platform. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 19–21 October 2011. [Google Scholar]
- Naderolasli, A.; Tabatabaei, M. Stabilization of the Two-Axis Gimbal System Based on an Adaptive Fractional-Order Sliding-Mode Controller. IETE J. Res. 2017, 63, 124–133. [Google Scholar] [CrossRef]
- Mao, J.; Yang, J.; Li, S.; Li, Q. Output Feedback Stabilization of Inertial Stabilized Platform with Unmatched Disturbances Using Sliding Mode Approach. IFAC-PapersOnLine 2017, 50, 5149–5154. [Google Scholar] [CrossRef]
- Kürkçü, B.; Kasnakoǧlu, C.; Efe, M.Ö. Disturbance/Uncertainty Estimator Based Integral Sliding-Mode Control. IEEE Trans. Automat. Contr. 2018, 63, 3940–3947. [Google Scholar] [CrossRef]
- Kürkçü, B.; Kasnakoǧlu, C.; Efe, M.Ö. Disturbance/Uncertainty Estimator Based Robust Control of Nonminimum Phase Systems. IEEE/ASME Trans. Mechatronics 2018, 23, 1941–1951. [Google Scholar] [CrossRef]
- Sangveraphunsiri, V.; Malithong, K. Control of Inertial Stabilization Systems Using Robust Inverse Dynamics Control and Sliding Mode Control. In Proceedings of the 6th International Conference on Automotive Engineering (ICAE-6) BITEC, Bangkok, Thailand, 29 March–2 April 2010; Volume 1, pp. 1–10. [Google Scholar]
- Wongkamchang, P.; Sangveraphunsiri, V. Control of Inertial Stabilization Systems Using Robust Inverse Dynamics Control and Adaptive Control. Thammasat Int. J. Sc. Tech. 2008, 13, 20–32. [Google Scholar]
- Mao, J.; Li, S.; Li, Q.; Yang, J. Design and implementation of continuous finite-time sliding mode control for 2-DOF inertially stabilized platform subject to multiple disturbances. ISA Trans. 2019, 84, 214–224. [Google Scholar] [CrossRef]
- Abdo, M.; Vali, A.R.; Toloei, A.R.; Arvan, M.R. Modeling control and simulation of two axes gimbal seeker using fuzzy PID controller. In Proceedings of the 2014 22nd Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 20–22 May 2014; pp. 1342–1347. [Google Scholar] [CrossRef]
- Königseder, F.; Kemmetmüller, W.; Kugi, A. Attitude control strategy for a camera stabilization platform. Mechatronics 2017, 46, 60–69. [Google Scholar] [CrossRef]
- Li, H.; Ning, X.; Han, B. Composite decoupling control of Gimbal Servo System in double-gimbaled variable speed CMG Via disturbance observer. IEEE/ASME Trans. Mechatronics 2017, 22, 312–320. [Google Scholar] [CrossRef]
- Khodadadi, H.; Motlagh, M.R.J.; Gorji, M. Robust control and modeling a 2-DOF inertial stabilized platform. In Proceedings of the International Conference on Electrical, Control and Computer Engineering 2011 (InECCE), Pahang, Malaysia, 21–22 June 2011; pp. 223–228. [Google Scholar] [CrossRef]
- Khayatian, M.; Aghaee, P.K. Adaptive control of a two-axis gimbal system using modified error. In Proceedings of the 3rd International Conference on Control, Instrumentation, and Automation, Tehran, Iran, 28–30 December 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, H.; Yu, R. Decoupling control for two-axis inertially stabilized platform based on an inverse system and internal model control. Mechatronics 2014, 24, 1203–1213. [Google Scholar] [CrossRef]
- Krishnamoorthy, J.A.R.; Marathe, R.; Sule, V.R. H∞ control law for line-of-sight stabilization for mobile land vehicles. Opt. Eng. 2002, 41. [Google Scholar] [CrossRef]
- Kodhanda, A.; Kolhe, J.P.; Kuber, M.M.; Parlikar, V.V. Uncertainty and Disturbance Estimation based Control of Three-axis Stabilized Platform. Int. J. Latest Trends Eng. Technol. (IJLTET) 2014, 3, 289–297. [Google Scholar]
- Li, H.; Zheng, S.; Ning, X. Precise Control for Gimbal System of Double Gimbal Control Moment Gyro Based on Cascade Extended State Observer. IEEE Trans. Ind. Electron. 2017, 64, 4653–4661. [Google Scholar] [CrossRef]
- Kürkçü, B.; Kasnakoğlu, C. Estimation of Unknown Disturbances in Gimbal Systems. Appl. Mech. Mater. 2015, 789–790, 951–956. [Google Scholar] [CrossRef]
- Chakir, S.; Suh, J.H.; Ji, S.W.; Kim, Y.B. A composite control design for suppressing mutual interference of interconnected systems. J. Mech. Sc. Technol. 2020, 34, 867–875. [Google Scholar] [CrossRef]
- Ekstrand, B. Equations of motion for a two-axis gimbal system. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 1083–1091. [Google Scholar] [CrossRef]
- Abdo, M.; Vali, A.R.; Toloei, A.; Arvan, M.R. Research on the cross-coupling of a two axes gimbal system with dynamic unbalance. Int. J. Adv. Robot. Syst. 2013, 10. [Google Scholar] [CrossRef] [Green Version]
- Gu, D.W.; Petkov, P.H.; Konstantinov, M.M. H∞ Design. In Advanced Textbooks in Control and Signal Processing: Robust Control Design with MATLAB, 2nd ed.; Springer: London, UK, 2013; pp. 31–48. [Google Scholar]
- Doyle, J.C.; Glover, K.; Khargonekar, P.P.; FRANCIS, B.A. State-Space Solutions to Standard H2 and H∞ Control Problems. IEEE Trans. Automat. Contr. 1989, 34, 831–847. [Google Scholar] [CrossRef]
- Zhou, K.; Doyle, J.C. Essentials of Robust Control, 1st ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1998; pp. 81–128. [Google Scholar]
- Miranda, M.F.; Takahashi, R.H.C.; Jota, F.G. H∞ controllers with integral action: An experimental evaluation. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2010, 224, 21–29. [Google Scholar] [CrossRef]
- Miranda, M.F.; Jota, F.G.; Takahashi, R.H.C. On H∞ controllers with integral action: An experimental evaluation. IFAC Proc. Vol. 2002, 15, 419–424. [Google Scholar] [CrossRef]



| Parameters | Pitch Channel | Yaw Channel |
|---|---|---|
| 100 | 200 | |
| 15.5 | 25.5 | |
| 2.6 | 2.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.-H.; Tran, D.-Q.; Kim, Y.-B.; Chakir, S. A Robust Double Active Control System Design for Disturbance Suppression of a Two-Axis Gimbal System. Electronics 2020, 9, 1638. https://doi.org/10.3390/electronics9101638
Lee D-H, Tran D-Q, Kim Y-B, Chakir S. A Robust Double Active Control System Design for Disturbance Suppression of a Two-Axis Gimbal System. Electronics. 2020; 9(10):1638. https://doi.org/10.3390/electronics9101638
Chicago/Turabian StyleLee, Dong-Hun, Duc-Quan Tran, Young-Bok Kim, and Soumayya Chakir. 2020. "A Robust Double Active Control System Design for Disturbance Suppression of a Two-Axis Gimbal System" Electronics 9, no. 10: 1638. https://doi.org/10.3390/electronics9101638
APA StyleLee, D.-H., Tran, D.-Q., Kim, Y.-B., & Chakir, S. (2020). A Robust Double Active Control System Design for Disturbance Suppression of a Two-Axis Gimbal System. Electronics, 9(10), 1638. https://doi.org/10.3390/electronics9101638






