An Efficient Hardware Architecture with Adjustable Precision and Extensible Range to Implement Sigmoid and Tanh Functions
Abstract
:1. Introduction
- For the first time, we propose a hardware architecture with adjustable precision and extensible input range to implement and functions, which is based on the RHC-VLC method. In addition, we propose another architecture with unlimited input range and adjustable accuracy, which is based on CSM-VLC method.
- Of the two proposed methods, the accuracy magnitude based on the CSM-VLC method can reach best, while the magnitude of the accuracy based on the RHC-VLC method can be much better, such as or . At the same time, the proposed methods can change the accuracy by adjusting the iterations of CORDIC without changing the current computing architecture. The lower the accuracy requirement, the lower the overall latency. Other methods of adjusting the precision require architectural changes, which are extremely unfriendly in hardware implementation.
- In hardware implementation, the RHC-VLC-based method only requires shift-and-add (or subtract) operations. Another method based on CSM-VLC requires a constant multiplier, we also optimize it to achieve shorter delay and smaller area. Compared with other existing methods to implement a hardware architecture with adjustable precision, our hardware implementation is more efficient. The proposed architecture has dual computing capabilities ( and ), which can be determined by the input selection bit.
- Under TSMC 40 nm CMOS technology, the hardware architecture based on our proposed methods can work at 1.5 GHz frequency or even higher. Except for the high frequency, our methods are also compatible with other advantages: efficient hardware, adjustable precision, and extensible input range. With the same adjustable range of precision, our architecture has lower area and power consumption compared with other methods.
2. Proposed Architecture Based on RHC-VLC Method
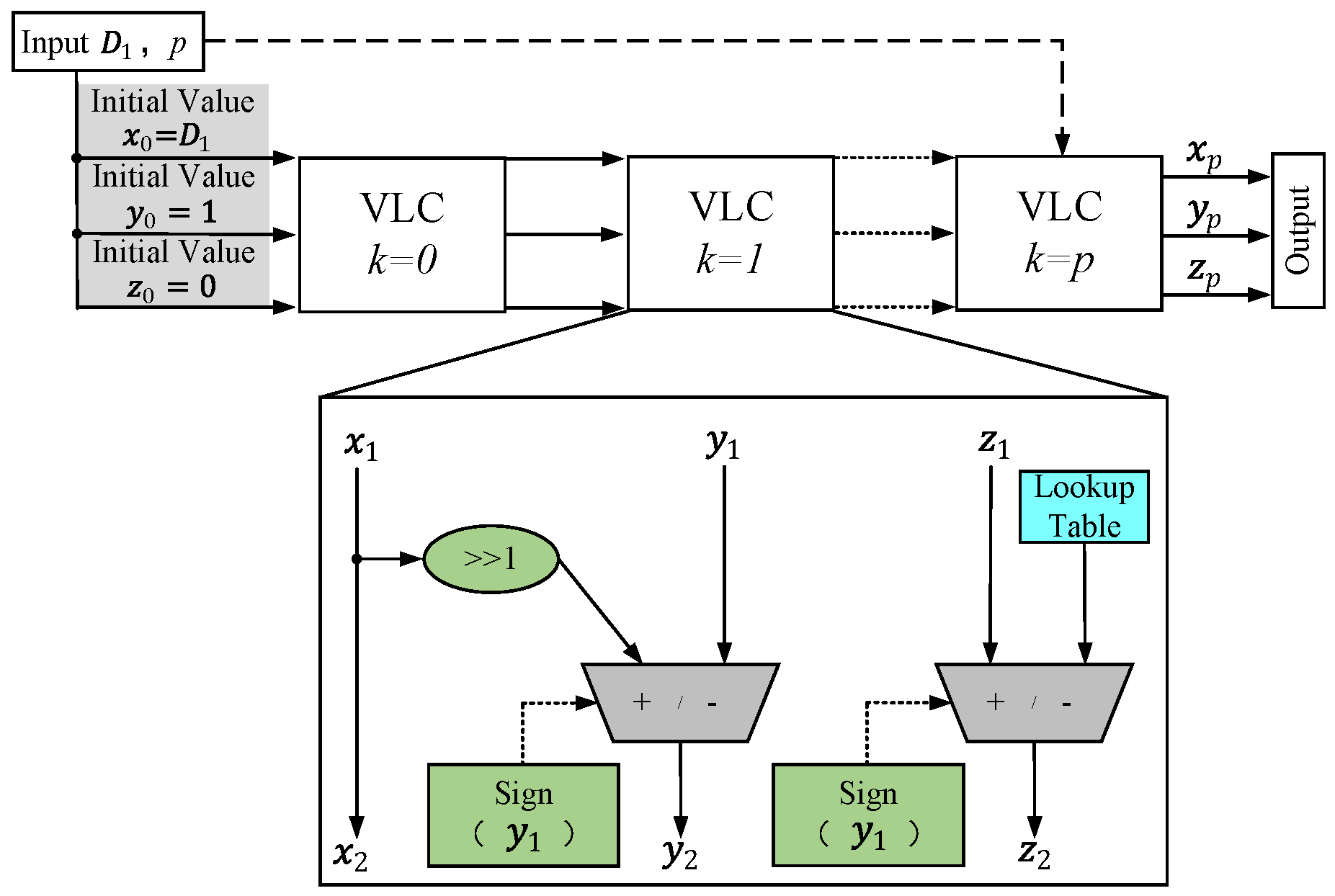
2.1. Overview of RHC and VLC
2.2. The RHC-VLC-Based Method
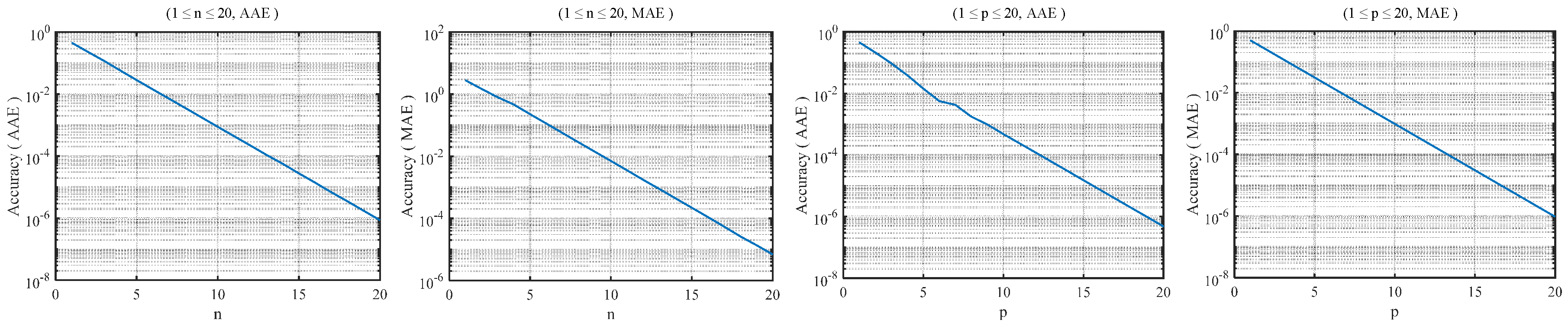
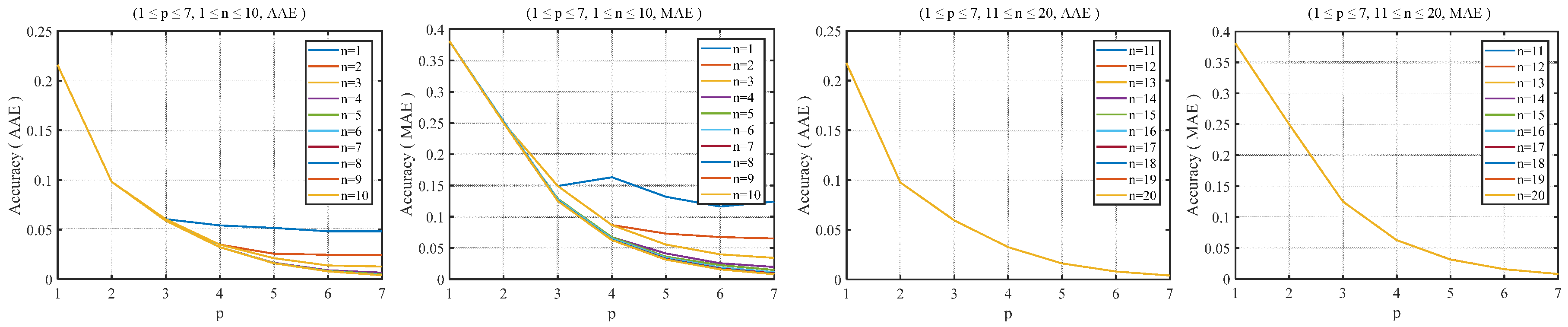
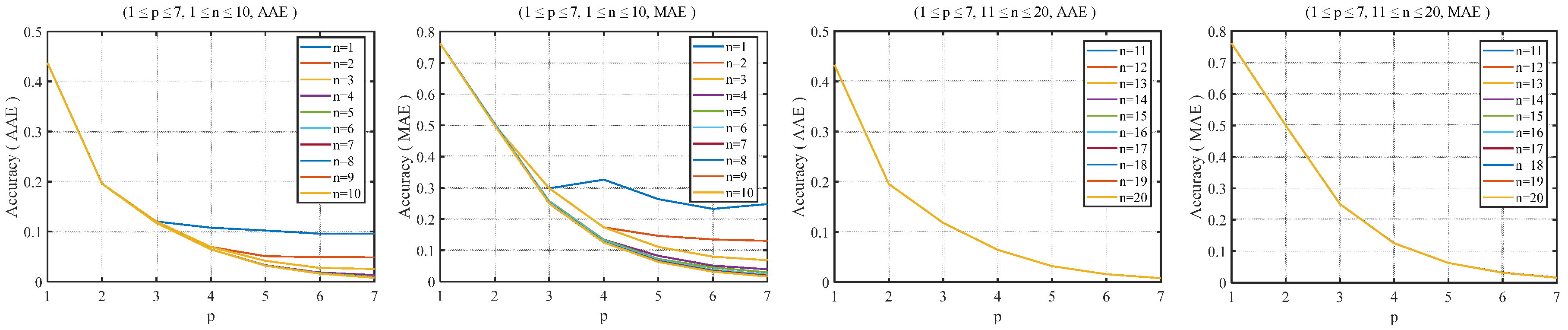
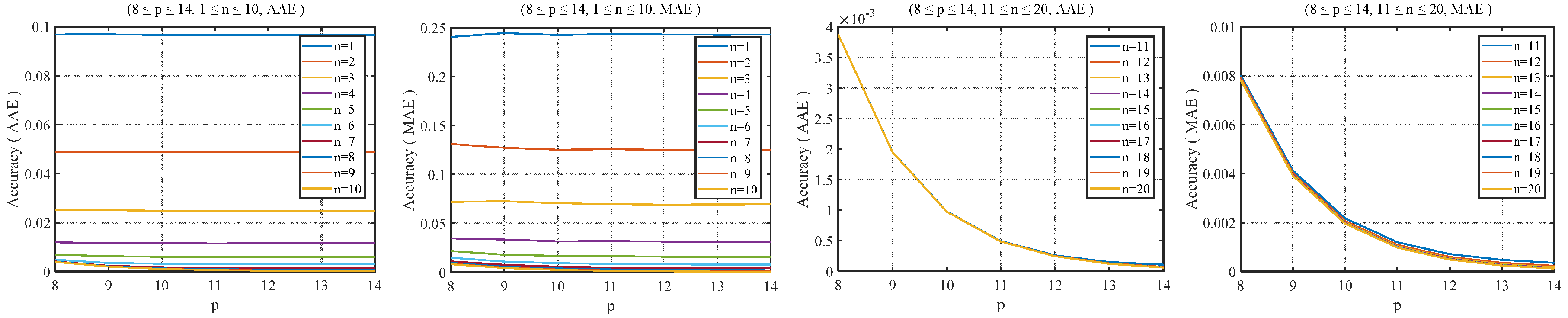
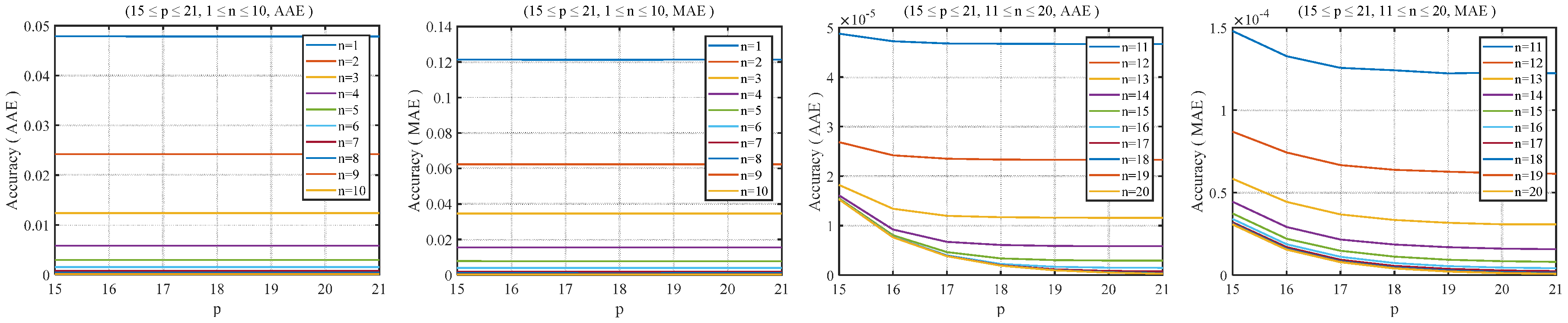
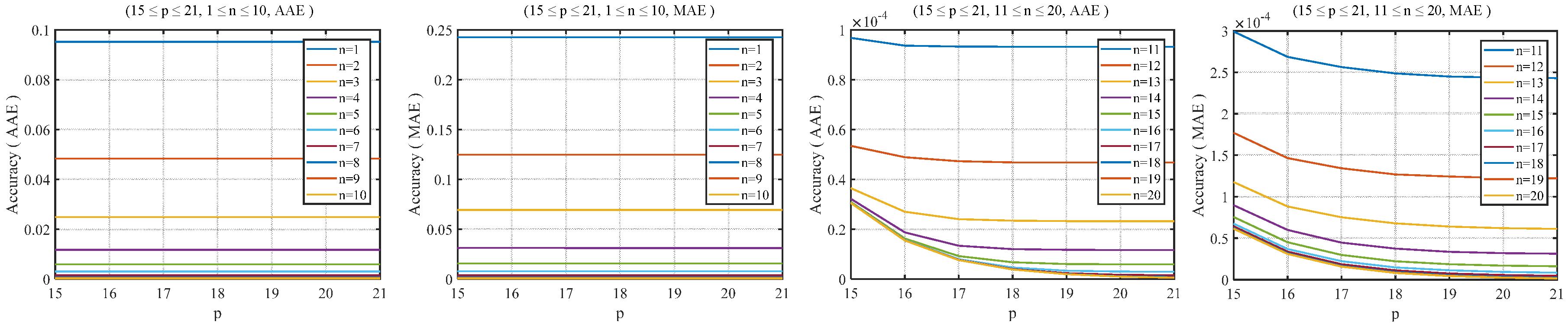
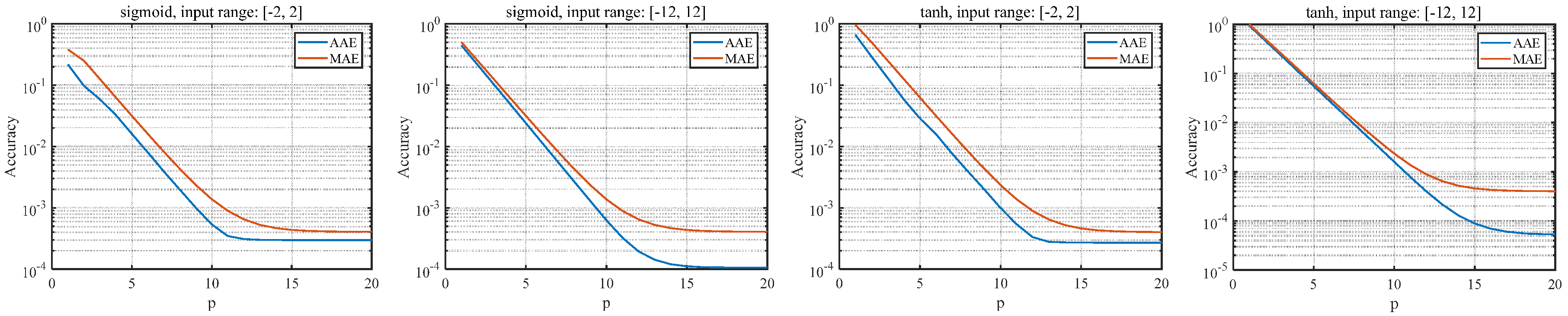
2.3. Software Test for the RHC-VLC-Based Method
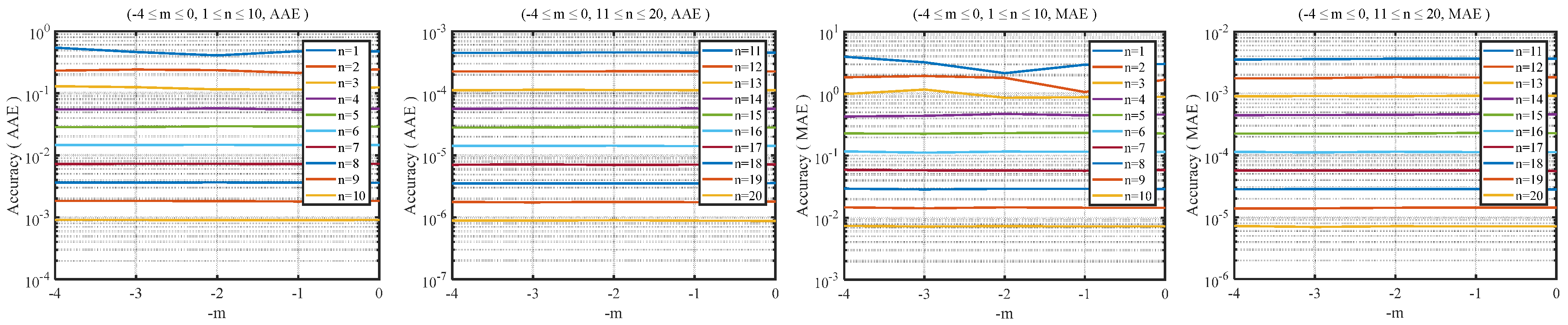
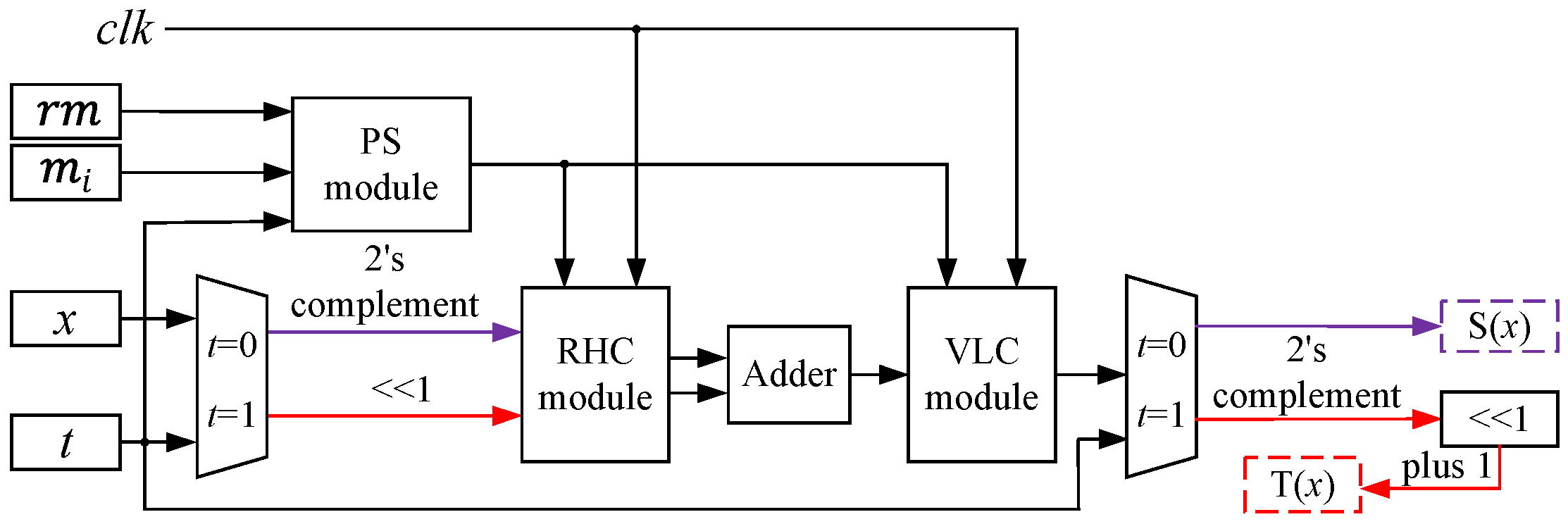
2.4. Proposed Algorithm with Adjustable Precision
| Algorithm 1 algorithm. |
| Input: The parameter x that needs to be calculated; the calculated type t ( and ); the required order of magnitude () of (all are positive numbers, for example, 2 actually represents “”); determines the input range of x |
Output: Final result
|
| Algorithm 2S algorithm. |
|
Input: The parameter x that needs to be calculated; m, n, and p correspond to the iterations of RHC and VLC, respectively |
Output: result
|
| Algorithm 3T algorithm. |
Input: They are the same as S algorithm Output: result
|
3. Proposed Architecture Based on CSM-VLC Method
3.1. Compute and
3.2. Software Test for the CSM-VLC-Based Method
3.3. Proposed Algorithm with Adjustable Precision
| Algorithm 4 algorithm. |
Input: They are the same as algorithm Output: Final result
|
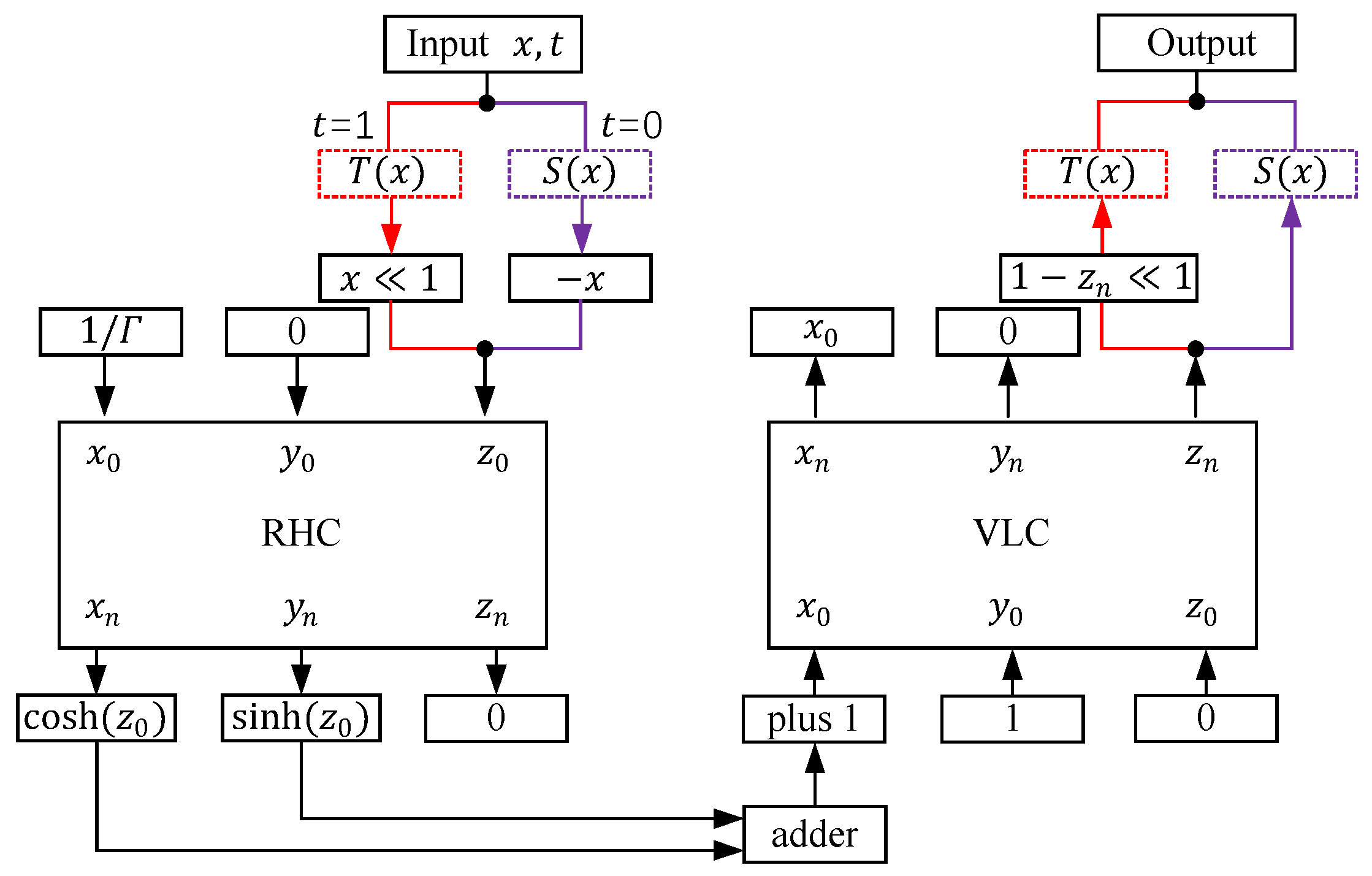
4. Hardware Implementation
4.1. General Architecture Based on RHC-VLC Method
4.2. General Architecture Based on CSM-VLC Method
4.3. Implementation of a Specific Case
4.4. Comparison with Existing Methods
4.4.1. Comparison with LUT-Based Method
4.4.2. Comparison with PWL-Based Method
4.4.3. Comparison with Other Related Methods
- Efficient hardware: Our RHC-VLC-based method only requires shift-and-add (or subtract) operations, which can avoid the direct use of inefficient multiplication and division. For the constant multiplier used in the CSM-VLC-based method, we also made specific optimization and design to improve the hardware efficiency.
- Adjustable precision: Both of our methods can easily adjust the accuracy of calculation results by increasing or decreasing the number of CORDIC iterations.
- Extensible range: According to the application requirements, the method based on RHC-VLC can adjust the negative iterations of RHC freely to expand or narrow the input range. In theory, the method based on CSM-VLC even has no limitation of input range.
- High speed: The hardware architecture based on our proposed methods can work at the frequency of 1.5 GHz, or even higher, such as 2 GHz.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Namin, A.H.; Leboeuf, K.; Muscedere, R.; Wu, H.; Ahmadi, M. Efficient Hardware Implementation of the Hyperbolic Tangent Sigmoid Function. In Proceedings of the IEEE International Symposium on Circuits and Systems, Taipei, Taiwan, 24–27 May 2009; pp. 2117–2120. [Google Scholar]
- Sartin, M.A.; da Silva, A.C.R. Approximation of Hyperbolic Tangent Activation Function Using Hybrid Methods. In Proceedings of the International Workshop on Reconfigurable and Communication-Centric Systems-on-Chip (ReCoSoC), Darmstadt, Germany, 10–12 July 2013. [Google Scholar]
- Gomar, S.; Mirhassani, M.; Ahmadi, M. Precise Digital Implementations of Hyperbolic Tanh and Sigmoid Function. In Proceedings of the Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 6–9 November 2016; pp. 1586–1589. [Google Scholar]
- Piazza, F.; Uncini, A.; Zenobi, M. Neural Networks with Digital LUT Activation Functions. In Proceedings of the International Conference on Neural Networks, Nagoya, Japan, 25–29 October 1993; Volume 2, pp. 1401–1404. [Google Scholar]
- Leboeuf, K.; Namin, A.H.; Muscedere, R.; Wu, H.; Ahmadi, M. High Speed VLSI Implementation of the Hyperbolic Tangent Sigmoid Function. In Proceedings of the International Conference on Convergence and Hybrid Information Technology, Busan, Korea, 11–13 November 2008; Volume 1, pp. 1070–1073. [Google Scholar]
- Meher, P.K. An Optimized Lookup-Table for the Evaluation of Sigmoid Function for Artificial Neural Networks. In Proceedings of the IEEE/IFIP International Conference on VLSI and System-on-Chip, Madrid, Spain, 27–29 September 2010; pp. 91–95. [Google Scholar]
- Low, J.Y.L.; Jong, C.C. A Memory-Efficient Tables-and-Additions Method for Accurate Computation of Elementary Functions. IEEE Trans. Comput. 2013, 62, 858–872. [Google Scholar] [CrossRef]
- Myers, D.J.; Hutchinson, R.A. Efficient Implementation of Piecewise Linear Activation Function for Digital VLSI Neural Networks. Electron. Lett. 1989, 25, 1662–1663. [Google Scholar] [CrossRef]
- Basterretxea, K.; Tarela, J.M.; del Campo, I. Approximation of Sigmoid Function and the Derivative for Hardware Implementation of Artificial Neurons. IEE Proc. Circuits Devices Syst. 2004, 151, 18–24. [Google Scholar] [CrossRef]
- Armato, A.; Fanucci, L.; Scilingo, E.; Rossi, D.D. Low-Error Digital Hardware Implementation of Artificial Neuron Activation Functions and Their Derivative. Microprocess. Microsyst. 2011, 35, 557–567. [Google Scholar] [CrossRef]
- Nguyen, V.; Luong, T.; Le Duc, H.; Hoang, V. An Efficient Hardware Implementation of Activation Functions Using Stochastic Computing for Deep Neural Networks. In Proceedings of the IEEE International Symposium on Embedded Multicore/Many-Core Systems-on-Chip (MCSoC), Hanoi, Vietnam, 12–14 September 2018; pp. 233–236. [Google Scholar]
- Zhang, M.; Vassiliadis, S.; Delgado-Frias, J.G. Sigmoid Generators for Neural Computing Using Piecewise Approximations. IEEE Trans. Comput. 1996, 45, 1045–1049. [Google Scholar] [CrossRef]
- Xie, Z. A Non-Linear Approximation of the Sigmoid Function Based on FPGA. In Proceedings of the IEEE Fifth International Conference on Advanced Computational Intelligence (ICACI), Nanjing, China, 18–20 October 2012; pp. 221–223. [Google Scholar]
- Zamanlooy, B.; Mirhassani, M. Efficient VLSI Implementation of Neural Networks with Hyperbolic Tangent Activation Function. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2014, 22, 39–48. [Google Scholar] [CrossRef]
- Feng, F.; Li, L.; Wang, K.; Fu, Y.X.; Pan, H.B. Design and Application Space Exploration of a Domain-Specific Accelerator System. Electronics 2018, 7, 45. [Google Scholar] [CrossRef] [Green Version]
- Volder, J.E. The CORDIC Trigonometric Computing Technique. IRE Trans. Electron. Comput. 1959, EC-8, 330–334. [Google Scholar] [CrossRef]
- Walther, J.S. The Story of Unified CORDIC. J. VlSI Signal Process. Syst. Signal Image Video Technol. 2000, 25, 107–112. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, L.; Luo, Y.Y.; Lu, Z.H.; Fu, Y.X.; Li, L.; Yu, Z.Z. A CORDIC-Based Architecture with Adjustable Precision and Flexible Scalability to Implement Sigmoid and Tanh Functions. In Proceedings of the IEEE International Symposium on Circuits & Systems, Sevilla, Spain, 10–21 October 2020. [Google Scholar]
- Hu, X.; Harber, R.G.; Bass, S.C. Expanding the Range of Convergence of the CORDIC Algorithm. IEEE Trans. Comput. 1991, 40, 13–21. [Google Scholar] [CrossRef]
- Bedrij, O.J. Carry-Select Adder. IRE Trans. Electron. Comput. 1962, EC-11, 340–346. [Google Scholar] [CrossRef]
- Ramkumar, B.; Kittur, H.M. Low-Power and Area-Efficient Carry Select Adder. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2012, 20, 371–375. [Google Scholar] [CrossRef]
- Kesava, R.B.S.; Rao, B.L.; Sindhuri, K.B.; Kumar, N.U. Low Power and Area Efficient Wallace Tree Multiplier Using Carry Select Adder with Binary to Excess-1 Converter. In Proceedings of the Conference on Advances in Signal Processing (CASP), Pune, India, 9–11 June 2016; pp. 248–253. [Google Scholar]
- Mopuri, S.; Acharyya, A. Low-Complexity Methodology for Complex Square-Root Computation. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2017, 25, 3255–3259. [Google Scholar] [CrossRef]
- Sun, H.Q.; Luo, Y.Y.; Ha, Y.J.; Shi, Y.H.; Gao, Y.; Shen, Q.H.; Pan, H.B. A Universal Method of Linear Approximation With Controllable Error for the Efficient Implementation of Transcendental Functions. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 177–188. [Google Scholar] [CrossRef]
- Parhi, K.K.; Liu, Y. Computing Arithmetic Functions Using Stochastic Logic by Series Expansion. IEEE Trans. Emerg. Top. Comput. 2019, 7, 44–59. [Google Scholar] [CrossRef]



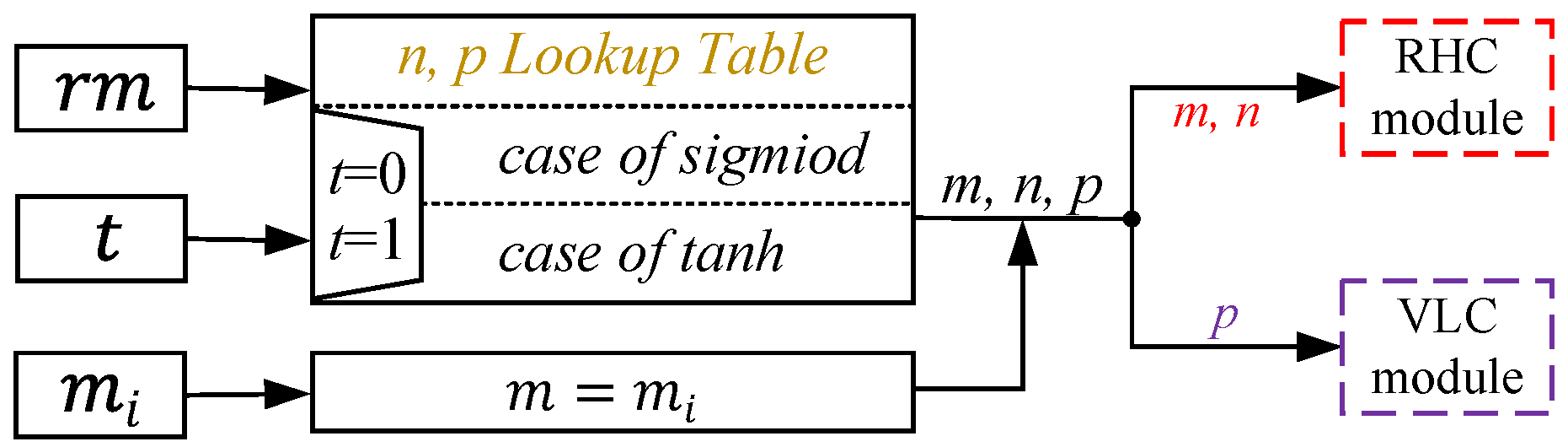
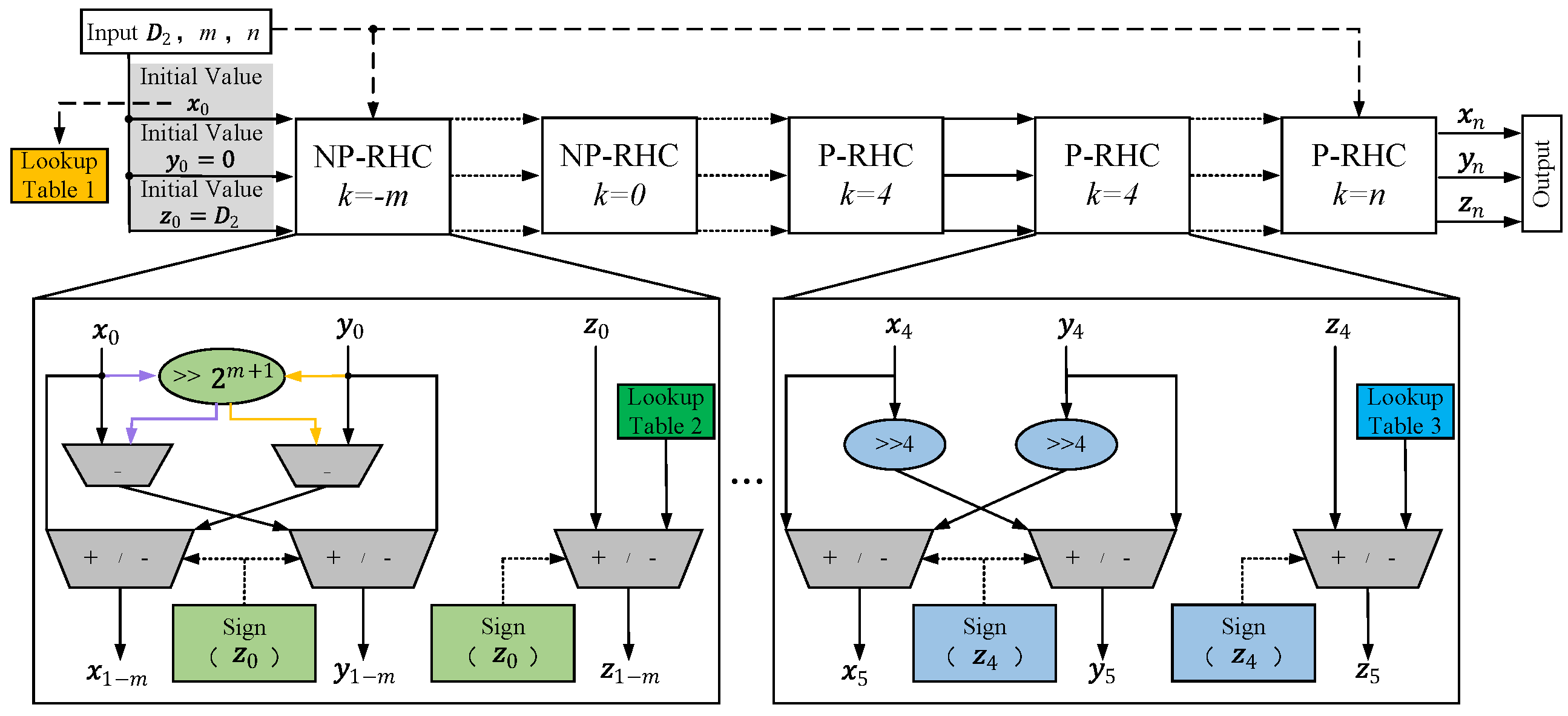
| Mode of CORDIC | Outputs |
|---|---|
| RHC | |
| VLC | |
| m | x for | x for | |
|---|---|---|---|
| 0 | 2.028 | [−2.028, 2.028] | [−1.014, 1.014] |
| 1 | 3.745 | [−3.745, 3.745] | [−1.872, 1.872] |
| 2 | 6.863 | [−6.863, 6.863] | [−3.431, 3.431] |
| 3 | 12.755 | [−12.755, 12.755] | [−6.377, 6.377] |
| 4 | 24.192 | [−24.192, 24.192] | [−12.096, 12.096] |
| 5 |
| Accuracy Magnitude | Accuracy Type | RHC&VLC | K | MTI |
|---|---|---|---|---|
| AAE | (0,2,4) | 3.49 | 6 | |
| MAE | (0,3,6) | 3.99 | 9 | |
| (0,4,5) | 4.13 | |||
| AAE | (0,5,7) | 4.84 | 12 | |
| MAE | (0,8,8) | 4.77 | 16 | |
| (0,9,7) | 3.78 | |||
| (0,10,6) | 4.53 | |||
| AAE | (0,8,11) | 4.33 | 19 | |
| MAE | (0,10,12) | 4.72 | 22 | |
| AAE | (0,11,15) | 4.77 | 26 | |
| (0,12,14) | 3.59 | |||
| MAE | (0,14,15) | 4.51 | 29 |
| Accuracy Magnitude | Accuracy Type | RHC&VLC | K | MTI |
|---|---|---|---|---|
| AAE | (0,2,6) | 4.95 | 8 | |
| (0,3,5) | 4.18 | |||
| MAE | (0,4,7) | 3.39 | 11 | |
| (0,5,6) | 4.49 | |||
| AAE | (0,6,8) | 4.75 | 14 | |
| MAE | (0,8,10) | 3.84 | 18 | |
| (0,9,9) | 4.72 | |||
| AAE | (0,9,12) | 4.35 | 21 | |
| MAE | (0,11,13) | 4.78 | 24 | |
| AAE | (0,12,16) | 4.77 | 28 | |
| (0,13,15) | 3.63 | |||
| MAE | (0,15,16) | 4.48 | 31 |
| 1 | (0,3) | 0.55028235384 | |
| 2 | (0,4) | 0.54920653198 | |
| 3 | (0,8) | 0.54885034814 | |
| 4 | (0,10) | 0.54884903958 | |
| 5 | (0,11) | 0.54884897415 | |
| 6 | (0,14) | 0.54884895268 | |
| 7 | (0,15) | 0.54884895243 |
| Accuracy Magnitude | Accuracy Type | Function Type | K | MIV p |
|---|---|---|---|---|
| E = −2 | AAE | Sigmoid | 3.24 | 4 |
| Tanh | 2.84 | 5 | ||
| MAE | Sigmoid | 3.16 | 5 | |
| Tanh | 3.16 | 6 | ||
| E = −3 | AAE | Sigmoid | 3.96 | 7 |
| Tanh | 3.89 | 8 | ||
| MAE | Sigmoid | 4.31 | 8 | |
| Tanh | 3.29 | 9 | ||
| E = −4 | AAE | Sigmoid | 3.52 | 11 |
| Tanh | 3.26 | 12 | ||
| MAE | Sigmoid | 4.66 | 14 | |
| Tanh | 4.61 | 15 |
| Module | Data | Sign bit | Integral bit | Fractional bit | Total bit |
|---|---|---|---|---|---|
| top-level | Input | 1 | 2 | 9 | 12 |
| Output | 1 | 0 | 9 | 10 | |
| RHC | Input | 1 | 2 | 6 | 9 |
| Output | 1 | 3 | 6 | 10 | |
| CEC | Input | 1 | 2 | 7 | 10 |
| Output | 0 | 3 | 7 | 10 | |
| Adder | Input | 1 | 3 | 9 | 13 |
| Output | 0 | 3 | 9 | 12 | |
| VLC | Input | 0 | 3 | 11 | 14 |
| Output | 0 | 1 | 11 | 12 |
| Purpose: To Build a Hardware Architecture with Adjustable Precision and Extensible Input Range. | |||||
|---|---|---|---|---|---|
| Method | LUT [6] | PWL [10] | MSC-PWL [11] | RHC-VLC (Proposed) | CSM-VLC (Proposed) |
| Area | 62,376.21 m | 11,521.68 m | 8638.49 m | 4364.57 m | 4048.64 m |
| Power | 7.75 mW | 5.14 mW | 3.29 mW | 1.89 mW | 1.75 mW |
| Frequency | 1 GHz | 700 MHz | 800 MHz | 1.5 GHz | 1.5 GHz |
| Input Range | [−2, 2] | [−1, 1] | [−1, 1] | [−2, 2] | |
| Range of MAE | |||||
| Range of AAE | |||||
| Has multipliers or dividers? | No | Multipliers and Dividers | Multipliers and Dividers | An optimized constant multiplier | No |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Jiang, L.; Yang, H.; Lu, Z.; Fu, Y.; Li, L.; Yu, Z. An Efficient Hardware Architecture with Adjustable Precision and Extensible Range to Implement Sigmoid and Tanh Functions. Electronics 2020, 9, 1739. https://doi.org/10.3390/electronics9101739
Chen H, Jiang L, Yang H, Lu Z, Fu Y, Li L, Yu Z. An Efficient Hardware Architecture with Adjustable Precision and Extensible Range to Implement Sigmoid and Tanh Functions. Electronics. 2020; 9(10):1739. https://doi.org/10.3390/electronics9101739
Chicago/Turabian StyleChen, Hui, Lin Jiang, Heping Yang, Zhonghai Lu, Yuxiang Fu, Li Li, and Zongguang Yu. 2020. "An Efficient Hardware Architecture with Adjustable Precision and Extensible Range to Implement Sigmoid and Tanh Functions" Electronics 9, no. 10: 1739. https://doi.org/10.3390/electronics9101739
APA StyleChen, H., Jiang, L., Yang, H., Lu, Z., Fu, Y., Li, L., & Yu, Z. (2020). An Efficient Hardware Architecture with Adjustable Precision and Extensible Range to Implement Sigmoid and Tanh Functions. Electronics, 9(10), 1739. https://doi.org/10.3390/electronics9101739







