Abstract
Nowadays, Biclustering is one of the most widely used machine learning techniques to discover local patterns in datasets from different areas such as energy consumption, marketing, social networks or bioinformatics, among them. Particularly in bioinformatics, Biclustering techniques have become extremely time-consuming, also being huge the number of results generated, due to the continuous increase in the size of the databases over the last few years. For this reason, validation techniques must be adapted to this new environment in order to help researchers focus their efforts on a specific subset of results in an efficient, fast and reliable way. The aforementioned situation may well be considered as Big Data context. In this sense, multiple machine learning techniques have been implemented by the application of Graphic Processing Units (GPU) technology and CUDA architecture to accelerate the processing of large databases. However, as far as we know, this technology has not yet been applied to any bicluster validation technique. In this work, a multi-GPU version of one of the most used bicluster validation measure, Mean Squared Residue (MSR), is presented. It takes advantage of all the hardware and memory resources offered by GPU devices. Because of to this, gMSR is able to validate a massive number of biclusters in any Biclustering-based study within a Big Data context.
1. Introduction
Because of the technological advances in the field of computational biology, the huge amount of gene expression data collected represent a great opportunity to learn about the complex biological mechanisms of living organisms [1]. In this context, machine learning (ML) techniques have been successfully applied to gene expression data in order to discover significant, non-trivial, and useful knowledge about how genes interact in a specific biological process [2,3]. Among the different ML techniques, Biclustering stands out as one of the most important approaches in this field, being applied to the discovery of functional annotations, co-regulation of metabolic pathways and gene networks, modularity analysis, biological networks elucidation, or disease sub-type identification of gene-drug association, among others [4,5,6,7,8,9].
The main objective of Biclustering is to extract local patterns from input datasets, which is known to be a NP-hard problem. In particular, Biclustering techniques find groups of genes that share a common behaviour under a certain group of experimental conditions (biclusters) [10]. However, nowadays, they present two main issues: the computational performance when processing large input gene expression datasets and the need to validate the huge number of generated biclusters [11].
In the last years, Biclustering-based studies have focused their efforts on overcoming the processing of large datasets in a reasonable time and scalable way [12,13]. This new situation may well be considered as Big Data context. To do so, High Performance Computing (HPC) computational technologies have been used in the literature [14]. HPC technology provides hardware and software resources to create parallel and distributed computing strategies, such as Apache Hadoop, Apache Spark and Graphic Processing Units (GPU), among others. Apache Hadoop [15] uses its distributed file system (HDFS) and the Map Reduce [16] paradigm to process huge amounts of data. For example, in the work of Liao et al. [17], the authors developed a Hadoop version of the Non-Negative Factorization Biclustering algorithm, able to process matrices with a size of up to millions of rows per a million of columns. Regarding Apache Spark [18], the difference between it and Hadoop is that the former does not distribute data, only operates on distributed data collections. Apache Spark is used in the work of Sarazin et al. [19], in which a cluster of 10 machines is used in order to obtain biclusters from four synthetic datasets with a dimension of up to two-million rows and columns. Finally, Graphics Processing Units (GPUs) and the CUDA [20] environment are also used by the last Biclustering research works to accelerate their computational performance [21,22,23,24]. As an example, in the work of Liu et al. [25], the Geometric Biclustering Algorithm (GBC) is adapted to GPU technology. During experimentation, GBC was able to process five large gene expression datasets, generating a maximum of 8280536 biclusters.
All of the aforementioned efforts to process large gene expression datasets have a direct consequence: the number of biclusters generated becomes huge [25,26]. Additionally, the application of a Biclustering technique to this kind of datasets does not imply that all its results are biologically relevant, since their goodness is subject to a subsequent validation process. Biclusters are usually validated by statistical methods or biological knowledge stored in public databases [27]. For example, one of the most used statistical measure to evaluate biclusters is the Mean Squared Residue (MSR) [28], while gene enrichment analysis based on the knowledge stored in Gene Ontology Database (GO) [29], is the most used biological validation method. During the last years, Biclustering evaluation measures and tools have focused their efforts on improving the accuracy of the results and on developing intuitive and accessible web user interfaces. Thus, they did not consider massively evaluating more than one bicluster. The following tools, like gProfiler [30], Enrichr [31], UBiT2 [32], or WebGestalt [33], are some examples. The only exception is BiGO [34], that is able to analyze and compare more than one gene list at a time, although it has not been designed to scale against a very high number of results. The lack of validation methods to massively process a large number of biclusters makes some of the latest Biclustering approaches have to limit their results. For example, in the work of Orzechowski et al. [35], the number of biclusters generated by EBIC, an evolutionary multi-GPU Biclustering algorithm, was limited to 100. Thus, authors were able to use the R package GOStats [36], which works with a single gene list, in order to validate the biclusters in a biological way.
This work presents gMSR, a multi-GPU version of the MSR bicluster validation measure. This version offers the possibility of validating a huge number of biclusters in a reasonable time. Consequently, a short and ordered list of the best validated biclusters is shown. The high level of parallelization of the calculation of MSR measure and the use of the GPU devices in current Biclustering techniques are the main reasons that gMSR also uses this technology as acceleration method. As long as we know, gMSR is the first method that exploits all of the computational capabilities of GPU devices to accelerate the validation of a large number of biclusters. Only the work of Gomez-Pulido et al. [37] implemented before the MSR value in a parallel way. The main difference is that authors used a hardware implementation by means of Field Programmable Gate Array (FPGA) technology. Additionally, gMSR is able to equally distribute the processing tasks between multiple GPU devices (multi-GPU), improving its performance and scalability. The results show that gMSR achieves the validation task in a very optimal way when the number of biclusters and their size increase. gMSR source code is publicly available at https://github.com/aureliolfdez/gmsr.
In summary, this work provides some novelty features, such as the ability to validate a huge number of biclusters in a very fast way and without memory issues, due to the the use of all available GPU resources. Additionally, gMSR has been designed to use more than one GPU device, thus multiplying its processing capacity. Besides, gMSR is independent of the Biclustering algorithm that generated the results. Due to this, it can easily be used as an evaluation module in Biclustering algorithms that are implemented in CUDA C/C++.
2. Materials and Methods
The main objective of gMSR implementation is to take advantage of the computational resources of the GPU devices to accelerate the evaluation of a large number of biclusters. In this section, the MSR measure is analyzed from the parallelization point of view. Subsequently, the implementation of the novel gMSR based on the different levels of the MSR parallelization is detailed. Finally, the datasets and the experimental design used in the present work are described.
2.1. Parallelization of the MSR Measure
In the MSR measure [28], the residue, R, is used in order to evaluate the coherence of an element of a bicluster regarding the rest of elements of the bicluster. A residue R of an element of the bicluster =, composed by a set of rows I and a set of columns J, is:
where is the expression level of the gene i under the experimental condition j, the mean of the i-th row of a bicluster, the mean of the j-th column, and is the mean of all elements in the bicluster. The means are calculated by:
Finally, the MSR value of a bicluster = is the sum of the square residues of all the elements that a bicluster contains:
A bicluster is -bicluster if MSR ≤ for some given threshold ≥ 0. The coherence of a -bicluster improves as its MSR value is closer to 0. The Equation (3) can also be used to measure cluster error in general systems [38].
The mean square residue (MSR) is suitable to be parallelized in several levels:
- High level: the calculation of the MSR value, , of every bicluster =, is an independent task (see Equation (3)).
- Medium level: for each bicluster, , the residue, , of every element , can be processed independently (see Equation (1)).
- Low level: for each residue , every mean (see Equation (2)) can be calculated in an independent way.
As can be observed, the degree of parallelization of the MSR measure makes it very suitable to be implemented using GPU technology. In the next section, the way these independent tasks are distributed among the GPU resources in an efficient way will be explained.
2.2. The gMSR Algorithm
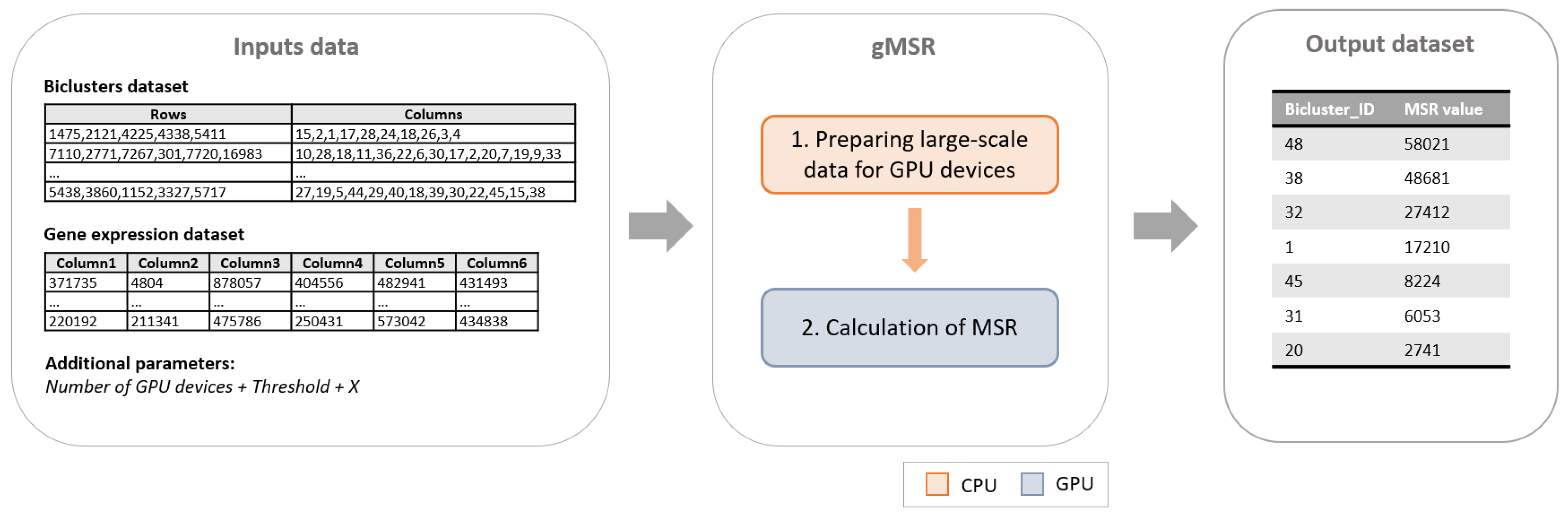
gMSR is a CUDA implementation of the MSR measure organized in two main phases (see Figure 1). The first phase, which is executed in CPU, is the responsible for the input data distribution. The second phase calculates in GPU the MSR value of each biclusters.
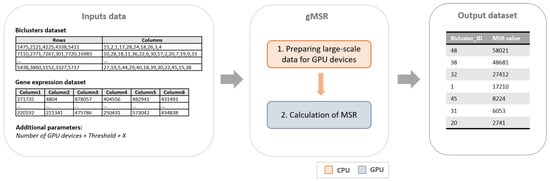
Figure 1.
The general gMSR scheme is shown. As it can be observed, the input data is composed by the gene expression dataset, the set of biclusters extracted from it, the number of Graphic Processing Units (GPU) devices to use, the number of the best biclusters to be returned by gMSR, X, and the Mean Squared Residue (MSR) value threshold. Then, the gMSR algorithm is composed by two phases, the first one is executed in CPU, while the second one is executed in GPU. Finally, the output is a ranking of the X first biclusters based on their MSR value.
The input of this implementation is composed by a gene expression dataset, a set of biclusters extracted from it, the number of the best biclusters to be returned by gMSR, the number of GPU devices to use, and a MSR value threshold. As an output, gMSR generates an ordered list with the best biclusters according to their MSR value. The following subsections will address the characteristics of each phase of gMSR.
2.2.1. Phase 1: Preparing Large-Scale Data for GPU Devices
Implementing an algorithm using CUDA architecture implies important challenges. One of them is related with the proper use of the GPU’s memory storage. In a GPU device, there are two types of memories: the shared memory (lower latency and lower storage capacity) and the global memory (higher latency and higher storage capacity). To process large input datasets without memory issues, it is necessary to select the appropriate type of memory in each case. In this work, the GPU global memory will storage the input data, while the GPU shared memory will be used to storage partial results.
Because the input data are initially stored in CPU memory, this first phase handles the transfer of data from CPU to GPU. For this reason, this is the only phase executed on the CPU. Thus, the input data are distributed, as follows:
- The gene expression dataset is stored completely in the global memory of each GPU device. Because this dataset is used to calculate the MSR of each bicluster, the number of the necessary data transfers between the GPU and the CPU is minimized.
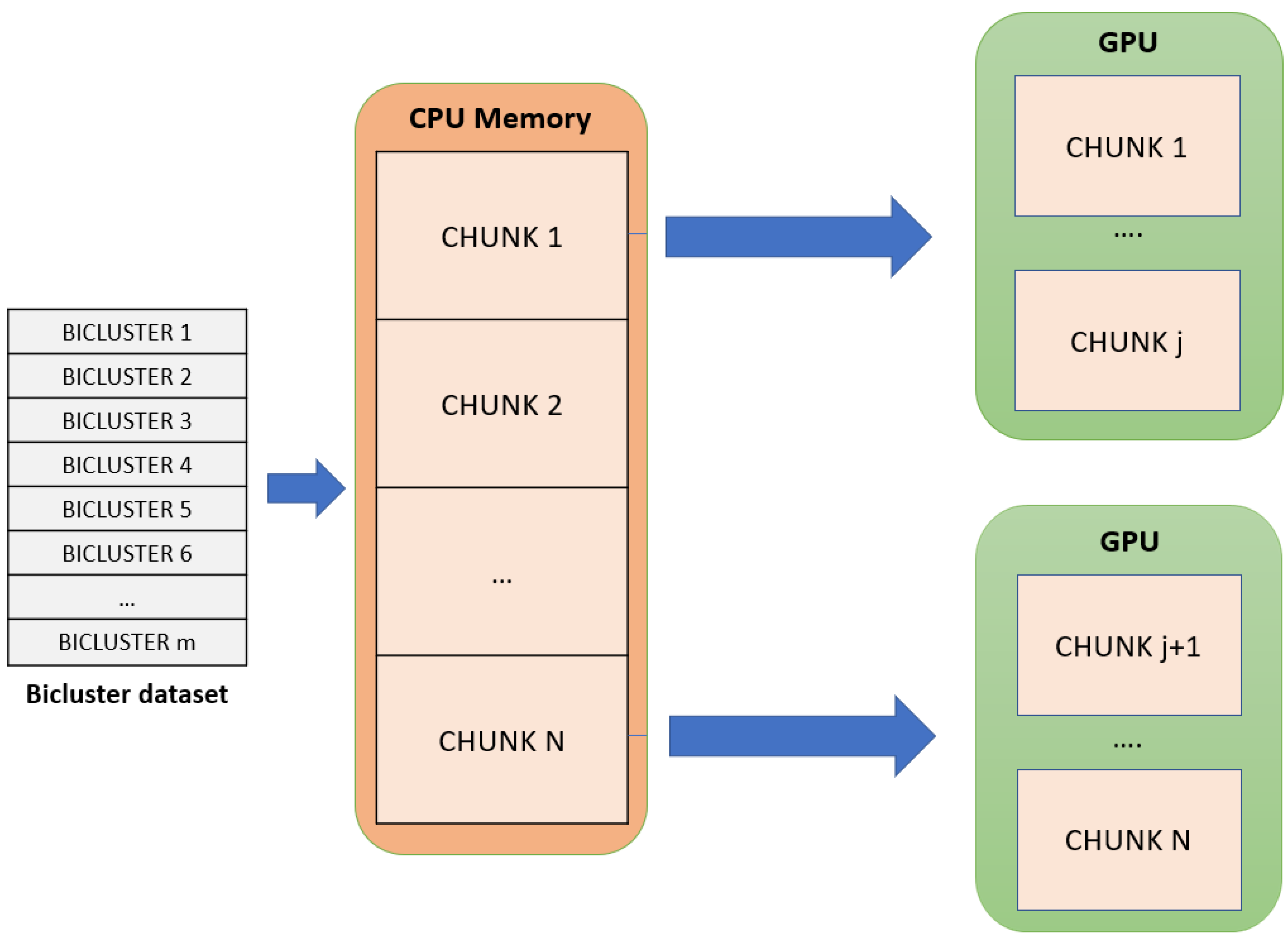
- The set of biclusters is distributed in the remaining part of the global memory of each GPU device. As it can be observed in Figure 2, the set of biclusters stored in the CPU memory is divided into different parts, called chunks, that are distributed in a balanced way between all GPU devices. Every chunk adjusts to the space that is still available in every GPU global memory. That way, the GPU storage capacity is maximized.
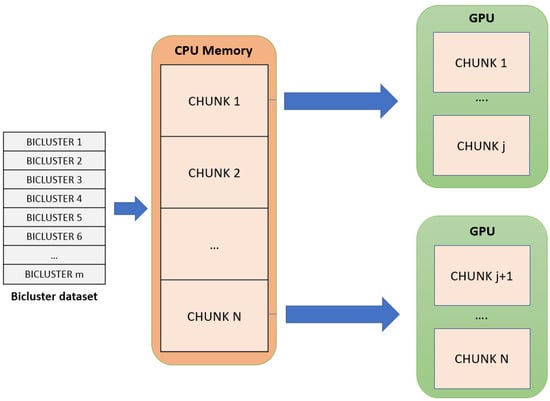 Figure 2. The distribution of the input biclusters dataset is shown. It is divided into multiple chunks that will be distributed equally depending on the available global memory in the GPU devices.
Figure 2. The distribution of the input biclusters dataset is shown. It is divided into multiple chunks that will be distributed equally depending on the available global memory in the GPU devices.
This input data distribution allows for gMSR to process large input datasets without suffering any type of memory overflow in the GPU devices, minimizing the number of data transfers with the CPU memory.
2.2.2. Phase 2: Calculation of MSR on GPU Devices
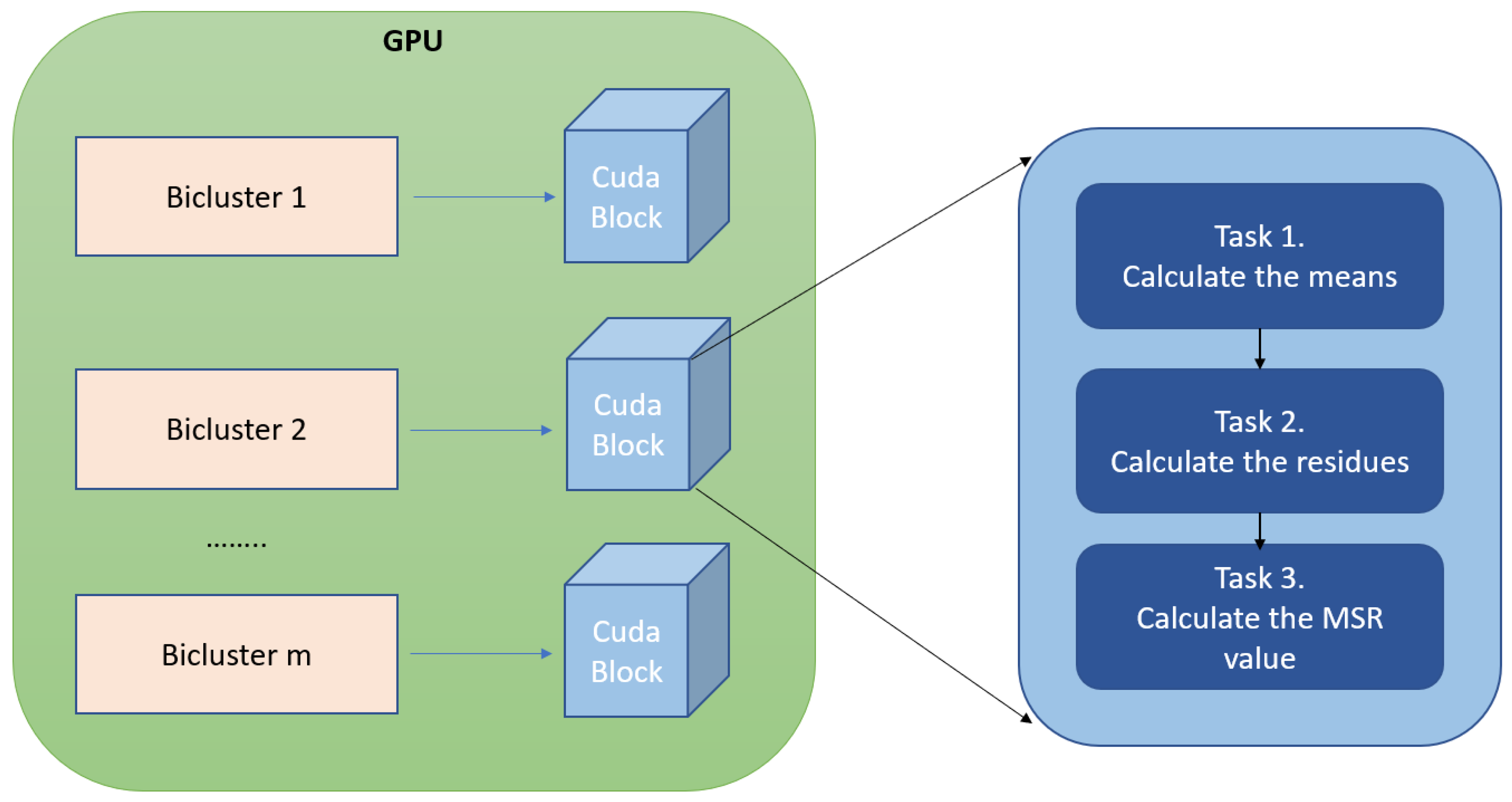
The MSR measure is suitable to be parallelized in several levels, as was commented in Section 2.1. A GPU device is composed by a lot of threads that are distributed in several CUDA blocks. Every CUDA block is responsible for processing the MSR of a single bicluster. Figure 3 shows how the execution threads of a CUDA block process three independent tasks during the MSR calculation:
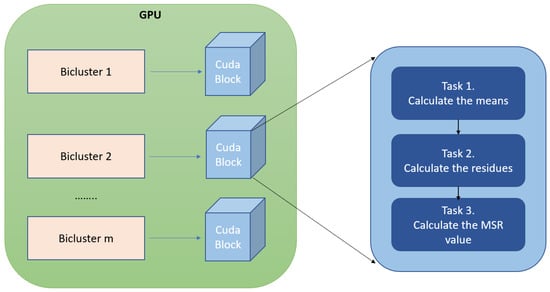
Figure 3.
This figure shows how the MSR values of the input biclusters are calculated by gMSR. Each bicluster stored in global memory is associated with a CUDA block. A block is responsible for performing three tasks. First, the means of the rows, columns, and total mean of the bicluster are calculated. These means are used to calculate the residues of each element of each bicluster in the second task. Finally, the residues are use for calculating the MSR value in the third task.
- Calculation of the means of a bicluster.
- Calculation of the residues of each element of a bicluster.
- Calculation of the MSR value of a bicluster.
The first task corresponds to the low level of parallelization of the MSR (see Section 2.1). Thus, a CUDA block is responsible of calculating all of the means associated to a bicluster. Each thread of a CUDA block calculates the average of a row and a column of a bicluster. However, a bicluster can have more rows and/or columns than threads (generally 1024 threads for each block). In these cases, gMSR distributes groups of rows and columns between each thread in a CUDA block in a balanced way. The number of rows and columns and the results of the means calculation are stored in the GPU shared memory. Thus, these values are used by all of the CUDA threads in a block during the whole MSR calculation process.
The medium level of parallelization of the MSR (see Section 2.1) corresponds to the second task, which is, the calculation of the residue of each element in a bicluster. All the elements are distributed equally between the threads of the block and each thread calculates the residue of an element at a time. The sum of all the residues of a bicluster is being stored in the shared memory, since this value is used by the next task.
Finally, the last task corresponds to the highest level of parallelization of the MSR value (see Section 2.1). The final MSR value of a bicluster is calculated in a CUDA block simultaneously with the processing of the residues. Once this process is finished, one of the threads of the CUDA block stores the MSR value of the bicluster in the GPU global memory. When all of the biclusters are processed in the GPU devices, the MSR values are stored in CPU memory in form of an ordered list. In this list, the biclusters with a MSR value greater than the threshold that was provided as an input parameter are eliminated.
In summary, during this implementation, the global and shared memory of GPU devices have been used by all tasks. The global memory has been used to store the input datasets and other data structures, such as arrays. On the other hand, the shared memory has been used for storing the partial results of each CUDA block, allowing for improving of the computational performance. Finally, gMSR makes the most of all the resources of the GPU devices, since in every task the processing is distributed equally between all of the threads.
2.3. Datasets Description
There are two different types of biclusters datasets used in the experimentation part of this work: those that are composed by synthetic biclusters and those composed by real biclusters. The synthetic biclusters are generated by randomly combining the rows and columns from a gene expression matrix. The real ones are those obtained by applying a Biclustering algorithm to a gene expression matrix. In this work, the BiBit Biclustering algorithm [39] has been used to generate real biclusters. This algorithm has been selected, because it can generate a great number of results in a short time.
For each experiment, gMSR needs a gene expression dataset to calculate the MSR value of the biclusters generated from it. Hence, for the tests carried out with synthetic biclusters, the small cell lung cancer (SCLC) gene expression dataset is used. This dataset, provided by Sato et al. [40], is available on the NCBI database (accession number GDS4794). It comprises 65 samples and 54,675 genes, including 23 clinical SCLC samples and 42 normal tissue samples. Additionally, the human GTEX gene expression dataset obtained from [41] has been used in the test based on real biclusters. This dataset, a float number matrix of 8555 × 5177, contains analysis of RNA sequencing data from 1641 postmortem samples across 43 tissues from 175 individuals.
The BiBit algorithm has been designed in order to process binary data, so the binarization of the input gene expression dataset is a mandatory step to generate the real biclusters datasets. Then, binary values 1 and 0 mean that a gene r is expressed or not under an experimental condition c, respectively [24]. Although there are many strategies to create a binary version of a gene expression dataset [42], in this work one of the simplest statistical methods to transform the data into binary values has been used: the mean of all expression values from every gene r has been considered as a threshold. If a concrete expression value of a gene r is under the threshold, it is considered as a 0 (1 in any other case).
Once the gene expression matrix has been binarized, some input parameters are required to apply the BiBit algorithm. The input parameters mnr (minimum number of rows allowed in final biclusters) and mnc (minimum number of columns allowed in final biclusters) are set to 2, in order to generate the maximum number of biclusters and test the implementations under the least favorable conditions.
3. Results and Discussion
In this section, the study of the computational performance and the scalability behavior of the gMSR implementation is presented. A sequential version of the original MSR algorithm has been used in order to complete this study with a performance comparison. Only the process of calculating the MSR for all biclusters has been took into account in order to measure the execution times, so the time required for storing the results in external files is not considered. The GPU and the sequential versions of the MSR algorithm receive the same gene expression and bicluster datasets. The output of both versions is the same for all experiments of this work.
The analysis of two different types of biclusters datasets has been included in this experimentation: synthetic biclusters datasets and real biclusters datasets. The synthetic biclusters have been randomly generated from a gene expression dataset in order to control the number of biclusters and their size. The real biclusters datasets are obtained by the application of gBiBit [43], a multi-GPU implementation of BiBit [39] biclustering algorithm. The objective of both analysis is to compare the performance and the scalability of gMSR in its single-GPU and multi-GPU version.
All of the experiments have been carried out on an Intel Xeon E5-2686 v4 (18 cores at 2.30 GHz) with 32 GB RAM and 8 NVIDIA K80 12 GB graphics cards, with a total of 2496 CUDA cores each. CUDA 11 version and compute capability (CC) 3.7 version have been used to compile gMSR. These versions depend on the type of NVIDIA graphics card installed in the system. The two implementations of the MSR under study are implemented in C/C++. Finally, single-GPU and multi-GPU versions of gMSR has been applied to all the datasets.
3.1. Synthetic Biclusters Analysis
In this experimentation, synthetic biclusters randomly generated from the small cell lung cancer (SCLC) gene expression dataset are used. The objective is to analyze how the performance and scalability of gMSR is affected by the number of biclusters processed and their size. To do so, 27 synthetic bicluster datasets have been created. In twenty of them, the size of the biclusters is fixed (30 × 30), while the number of biclusters generated are between 50,000 and 1,000,000, with an increase of 50,000 for each dataset. In the other 7 datasets, the number of biclusters is fixed to 500,000, while the size of every bicluster varies from 5 × 5 to 50 × 50, with an increase of 5 × 5 for each dataset.
Following, the results of the two evaluations are presented: a performance comparison between gMSR and its sequential version and a scalability study for multi-GPU environments.
3.1.1. Performance Evaluation
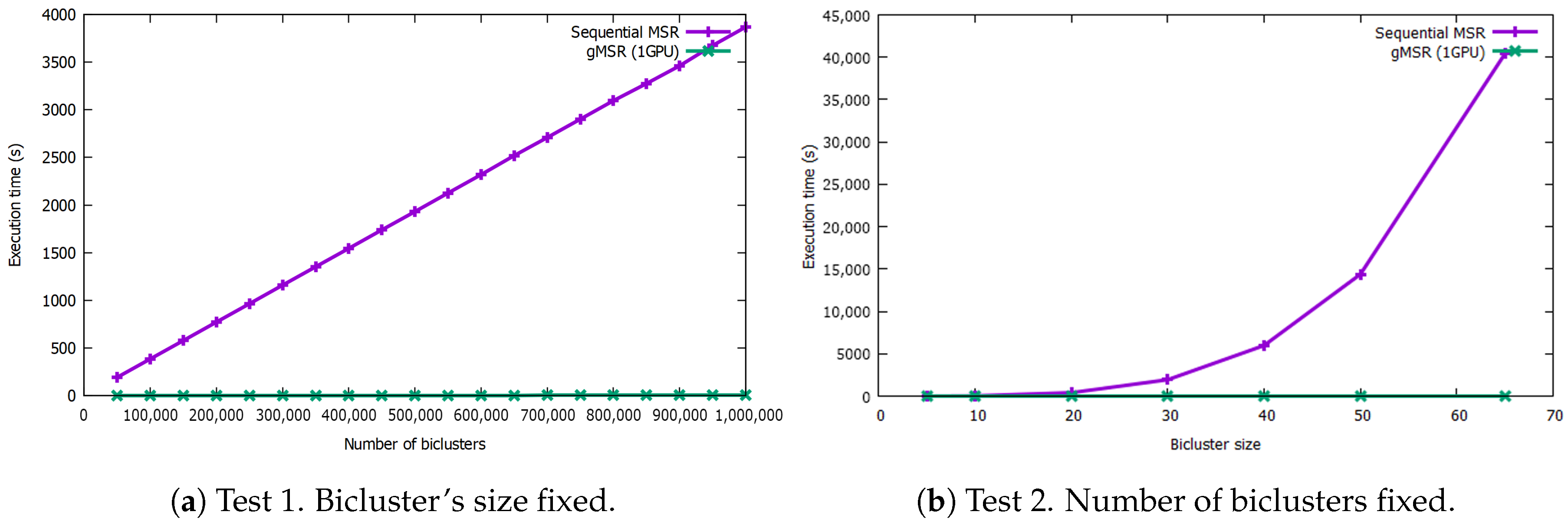
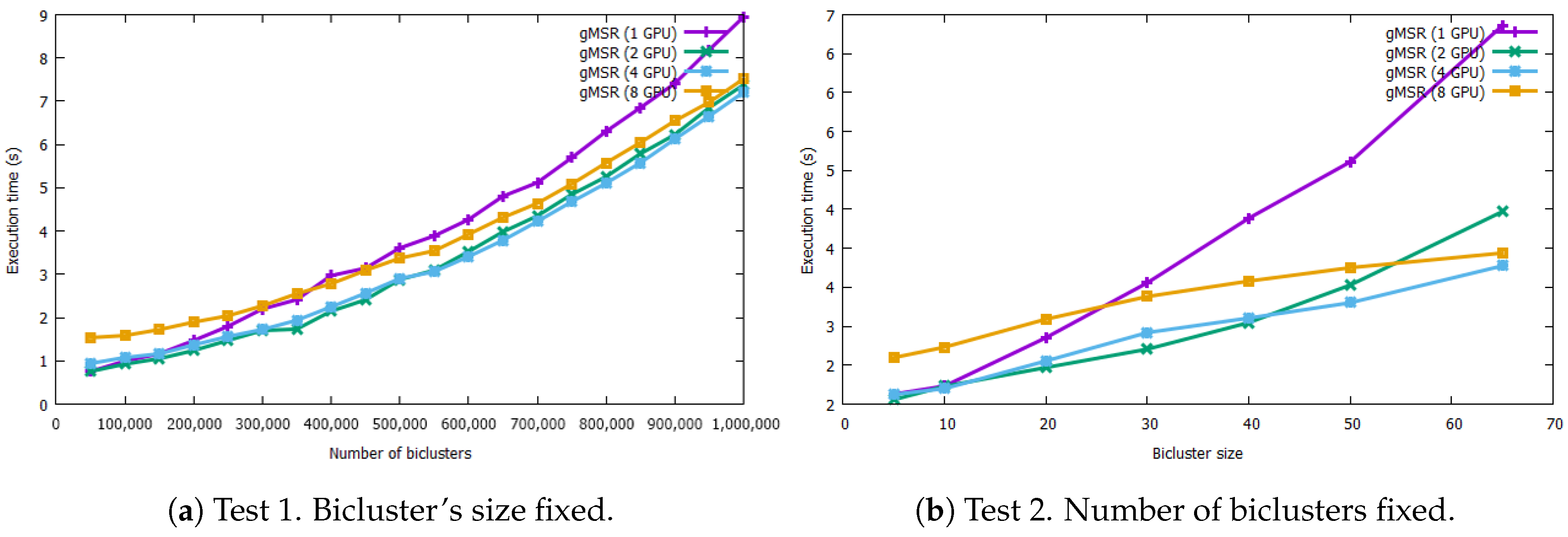
Figure 4 shows the results of the comparison between the sequential version of MSR and single-GPU mode of gMSR. The graph on the left shows the behavior of gMSR when the number of biclusters increases. As it can be seen, the trend of the computational performance of the sequential version is linear, while gMSR presents a constant behavior. As it can be observed in the execution times Table A1 (see the Appendix A), for the datasets with 50,000 and 1,000,000 biclusters, the sequential version takes 93.34 s and 3869.25 s, respectively, in order to evaluate the biclusters. However, for the gMSR version, the times registered are 0.75 s and 8.94 s, for the same datasets.
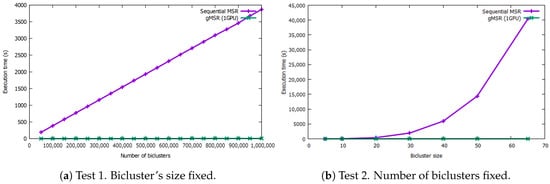
Figure 4.
This figure includes two graphs that measure the execution rates in seconds for the sequential version and single-GPU mode when processing synthetic bicluster datasets. The graph on the left shows the results when the number of biclusters increase but its size is fixed. The graph on the right shows the execution times when the size of the biclusters increases. In both test, the single-GPU version behaves nearly in a constant way.
In Figure 4, the graph on the right shows the execution times when the size of the biclusters increases. In this case, the sequential version shows an exponential behavior, reaching 40395.9 s in order to process 500,000 biclusters with size 65 × 65. However, the trend of the gMSR behavior is constant again, like in the first test, being able to process the same dataset in 6.85 s. The execution times can be consulted in the Table A2 in the Appendix A.
It can be concluded that, for the sequential version of MSR, its execution time increases with the two variables tested: the number of biclusters and their size. Particularly, its performance is worse when the size of each bicluster increases. However, gMSR is not affected by the increase of any of the two aforementioned variables. Thus, gMSR is 493.89 times faster, on average, than the sequential version of MSR when the number of biclusters varies, with a standard deviation value of 69.67. Additioanlly, gMSR is 1538.03 faster, on average, when the size of the biclusters varies, with a standard deviation value of 2007.78.
3.1.2. Scalability Evaluation
gMSR scalability has been analyzed using 1, 2, 4, and 8 GPU devices for each synthetic bicluster dataset. All of the execution times of gMSR are presented in Table A1 and Table A2 in the Appendix A. Figure 5 presents the behaviour of the scalability of gMSR, in which a comparison between the execution times of the multi-GPU mode of gMSR is depicted.
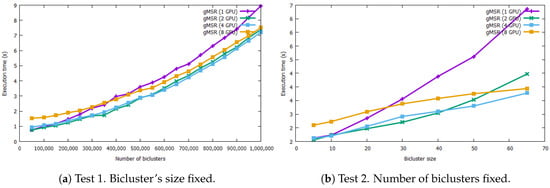
Figure 5.
This figure includes two graphs that measure the execution rates in seconds for the single-GPU and multi-GPU modes when processing synthetic bicluster datasets. The graph on the left shows the result when the number of biclusters increases while their size is fixed. The graph on the right shows the execution times when the size of the biclusters increases. In both cases, the multi-GPU version presents an optimal scalability.
In Figure 5, the graph on the left shows the evolution in the scalability when the number of biclusters increases. It can be observed that, with a lower number of biclusters, the best execution times are registered when using a single GPU device. In this case, for a dataset with 50,000 biclusters, the results were obtained in 0.75 s in single-GPU mode, while the 8 GPUs execution (multi-GPU mode) took 1.53 s. As the number of biclusters grows, the execution times of the single-GPU version increases, while the execution time with multiple GPUs tends to stabilize. For example, for 500,000 biclusters, the gMSR execution is 3.60 s with single-GPU and 2.87 s with 2 GPU devices. It is also worth to mention that when the number of biclusters is high, there is a greater difference in the execution times between multi-GPU and single-GPU modes. For example, gMSR took 8.94 s in its single-GPU mode and 7.20 s with 4 GPU devices. Therefore, the scalability study resumes that the use of multiple GPU devices is proportionally related to the number of biclusters contained in a data set.
The scalability behavior when the size of each bicluster increases is shown in the graph on the right of Figure 5. In this case, gMSR presents a similar behaviour than in the graph on the left. That is, if a dataset contains biclusters with a small size, then a single-GPU presents a better performance. However, as the size of the bicluster increases, using more than one GPU device is worthy. For example, when processing a dataset with 500,000 biclusters of size 65 × 65, gMSR needs 6.85 s in its single-GPU mode and 3.77 s with 4 GPU devices. That is, the use of several GPU devices reduces the execution times by 55%, compared to using a single device.
It has been verified that the computational performance and the scalability of gMSR have a very good behaviour when the number of biclusters or their size increase due to the tests carried out using synthetic biclusters datasets. Regarding the performance evaluation, it has been shown that gMSR is not negatively affected by these two variables due to the suitable use of GPU device resources, obtaining the validation results in a reasonable time. In the scalability evaluation, the tests determine that, when the amount of data is not big enough, the data partition and the transfer of data between multiple GPU devices penalise the overall performance. However, as the volume of datasets increases, the use of multiple GPU devices significantly improves the computational performance.
3.2. Real Biclusters Analysis
In this case, the objective of this experimentation is to test the usefulness of gMSR in a real case. To do so, 25 real biclusters datasets, generated from the GTEx gene expression dataset by the gBiBit biclustering algorithm, are used. For the first 24 datasets, the number of biclusters varies from 50,000 to 1,000,000, with an increase of 50,000 for each dataset. The latest dataset contains a total of 17,331,328 biclusters, which represent all the possible biclusters that the gBiBit algorithm is able to generate. In this experimentation, the size of the biclustes generated by gBiBit cannot be controlled, due to the algorithm’s own methodology.
In the previous experimentation (see Section 3.1), the maximum size of a bicluster was 65 × 65. However, in this case, the mean of the number of the rows and the columns of the biclusters are 1712 and 1726, respectively. This significant increase in the number of rows and columns caused the execution times of the sequential version of MSR to exceed four days, also registering continuous memory overflow problems. For this reason, the sequential version of MSR has not been included in this experimentation.
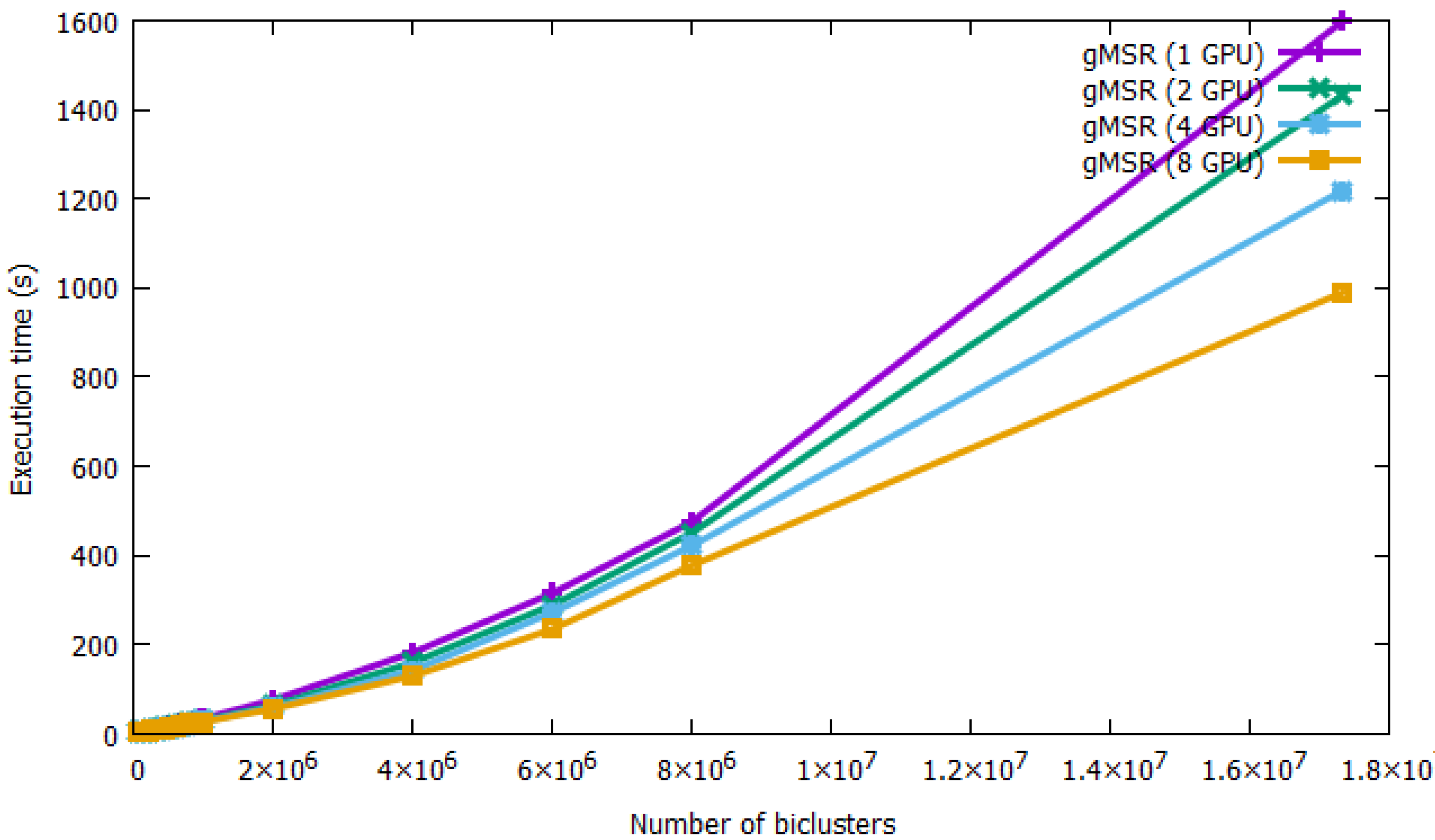
The performance and scalability of the single-GPU and multi-GPU modes is presented in Figure 6. All of the execution times of gMSR have been collected in Table A3 in the Appendix A. As it can observed, gMSR is able to process all datasets regardless of the number of biclusters. For the smallest dataset, 50,000 biclusters, gMSR took 6.55 s in its single-GPU version and 2.45 s with 2 GPU devices. That is, multi-GPU systems improve computing performance by 37% over the single-GPU version. For the maximum number of biclusters generated, 17,331,328, gMSR took 1597.68 s in its single-GPU version, while the use of 8 GPU devices reduced the execution time to 989.87 s. Therefore, in this case, using multiple GPU devices improved the run-time by 61.95%. This fact implies that the multi-GPU version of gMSR is a useful tool for validating a large number of biclusters in a real experimentation.
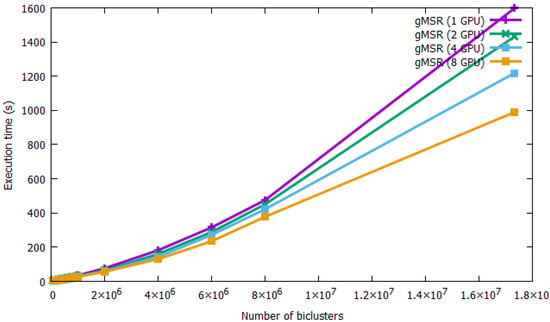
Figure 6.
The performance of single-GPU and multi-GPU mode of gMSR is presented. The graph shows that gMSR is capable of processing large datasets with a very good performance. Additionally, gMSR scales very well, showing better results in multi-GPU mode as the number of biclusters increases.
Besides, in order to help researchers to focus in the best biclusters, gMSR includes the possibility to generate a final ranking of the best N biclusters acoording their MSR value, as it can be seen in Table 1.

Table 1.
This table shows an example of the output that gMSR generates: a ranking with the N best biclusters accoding their MSR val ues, being 10 in this case. Additionally, an MSR value threshold of 150 is used.
In conclusion, there are two characteristics that negatively affect, to a greater or lesser extent, the performance of the MSR measure: the size and number of biclusters in a dataset. Despite changing the execution conditions on these two variables, gMSR is able to process the validation of the biclusters in a reasonable time in all cases. To do this, it incorporates an architecture that is able to evenly distribute the input biclusters among the GPU devices in order sto improve performance, scalability, and avoid memory overhead problems. In addition, the proper use of shared and global memory on GPU devices has helped to further minimize the time that is spent on data transfers.
4. Conclusions
Bicluster validation is currently facing new challenges, due to the generation of large amounts of biological data. As genetic expression databases are getting bigger, Biclustering algorithms generate a huge amount of biclusters. This implies that validating this massive number of biclusters is a great challenge. GPU technology and CUDA architecture are one of the most used options for obtaining results in a reasonable time of any type of computational algorithm in an parallelizable environment. In the case of bicluster validation, as far as we know, there is not an implementation of a bicluster validation measure that uses the computational resources of GPU devices to be able to face the aforementioned challenge.
In this work, a new implementation of the MSR measure, called gMSR, is presented. gMSR is implemented in C/C++ in order to run in an environment with only one GPU device or in a multi-GPU system. gMSR is able to process a huge number of biclusters in a very short time and without memory overflow problems. To do this, it incorporates a methodology that takes full advantage of all the computational resources offered by GPU devices, allowing the distribution of processing tasks equally among multiple devices when it is executed in a multi-GPU system.
Two experiments have been carried out to test the goodness of gMSR. The first experiment, in which synthetic biclusters datasets are used, showed that the increase in the number of biclusters and their size does not negatively affect the computational performance of gMSR. Besides, in a multi-GPU environment, gMSR also improves computational performance as the number of biclusters increases, showing a very good scalability. The second experimentation proves that gMSR is suitable to be used in a real Biclustering-based study, being able to validate millions of biclusters very fast and without problems of lack of resources.
Finally, future works will aim to develop, using GPU technology, news methodologies in order to validate biclusters with biological information stored in public databases. To do so, all of the available resources of the Cloud will be used to access to these databases and validate the biclusters in a parallel way.
Author Contributions
Conceptualization, A.L.-F. and D.S.R.-B.; methodology, A.L.-F. and D.S.R.-B.; software, A.L.-F.; validation, A.L.-F.; formal analysis, A.L.-F; investigation, A.L.-F., D.S.R.-B. and F.G.-V.; resources, A.L.-F.; data curation, A.L.-F.; writing–original draft preparation, A.L.-F., D.S.R.-B. and F.G.-V.; writing–review and editing, A.L.-F., D.S.R.-B. and F.G.-V.; visualization, A.L.-F., D.S.R.-B. and F.G.-V.; supervision, D.S.R.-B. and F.G.-V.; project administration, A.L.-F. and D.S.R.-B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Figures and Tables
In this appendix, the results obtained in Section 3 are collected in tables in order to clarify the data represented in Figure 4, Figure 5 and Figure 6.
All the tables that are presented below are referenced in the main text.

Table A1.
This table shows the execution times in seconds for the processing of synthetic biclusters datasets when the number of biclusters increases from 50,000 to 1,000,000 (first column). The second column corresponds to the sequential implementation of the MSR measure. The other four columns represents the gMSR executions using 1, 2, 4 and 8 GPU devices, respectively. As it can be observed, gMSR outperforms the sequential version and scales optimally.
Table A1.
This table shows the execution times in seconds for the processing of synthetic biclusters datasets when the number of biclusters increases from 50,000 to 1,000,000 (first column). The second column corresponds to the sequential implementation of the MSR measure. The other four columns represents the gMSR executions using 1, 2, 4 and 8 GPU devices, respectively. As it can be observed, gMSR outperforms the sequential version and scales optimally.
| Biclusters | MSR Sequential | gMSR(1) | gMSR(2) | gMSR(4) | gMSR(8) |
|---|---|---|---|---|---|
| 50,000 | 193.34 s | 0.75 s | 0.75 s | 0.94 s | 1.53 s |
| 100,000 | 386.565 s | 0.99 s | 0.92 s | 1.07 s | 1.58 s |
| 150,000 | 579.779 s | 1.16 s | 1.04 s | 1.16 s | 1.72 s |
| 200,000 | 773.741 s | 1.46 s | 1.23 s | 1.36 s | 1.89 s |
| 250,000 | 966.482 s | 1.79 s | 1.47 s | 1.56 s | 2.04 s |
| 300,000 | 1160.55 s | 2.19 s | 1.70 s | 1.72 s | 2.27 s |
| 350,000 | 1353.08 s | 2.41 s | 1.73 s | 1.93 s | 2.55 s |
| 400,000 | 1546.94 s | 2.97 s | 2.14 s | 2.24 s | 2.78 s |
| 450,000 | 1740.07 s | 3.14 s | 2.41 s | 2.56 s | 3.09 s |
| 500,000 | 1932.82 s | 3.60 s | 2.87 s | 2.90 s | 3.37 s |
| 550,000 | 2127.71 s | 3.88 s | 3.09 s | 3.06 s | 3.54 s |
| 600,000 | 2320.18 s | 4.26 s | 3.52 s | 3.41 s | 3.92 s |
| 650,000 | 2520.62 s | 4.80 s | 3.98 s | 3.78 s | 4.31 s |
| 700,000 | 2709.06 s | 5.11 s | 4.35 s | 4.22 s | 4.64 s |
| 750,000 | 2902.9 s | 5.69 s | 4.84 s | 4.67 s | 5.08 s |
| 800,000 | 3096.84 s | 6.30 s | 5.25 s | 5.10 s | 5.57 s |
| 850,000 | 3276.43 s | 6.85 s | 5.78 s | 5.57 s | 6.04 s |
| 900,000 | 3462.87 s | 7.40 s | 6.22 s | 6.12 s | 6.54 s |
| 950,000 | 3675.22 s | 8.18 s | 6.85 s | 6.65 s | 6.97 s |
| 1,000,000 | 3869.25 s | 8.94 s | 7.37 s | 7.20 s | 7.51 s |

Table A2.
This table shows the execution times in seconds for the processing of synthetic biclusters datasets when the size of each bicluster increases from 5 × 5 to 65 × 65 (first column). The second column corresponds to The second column corresponds to the sequential implementation of the MSR measure. The other four columns represents to the gMSR executions using 1, 2, 4 and 8 GPU devices, respectively. As it can be observed, gMSR outperforms the sequential version and scales optimally.
Table A2.
This table shows the execution times in seconds for the processing of synthetic biclusters datasets when the size of each bicluster increases from 5 × 5 to 65 × 65 (first column). The second column corresponds to The second column corresponds to the sequential implementation of the MSR measure. The other four columns represents to the gMSR executions using 1, 2, 4 and 8 GPU devices, respectively. As it can be observed, gMSR outperforms the sequential version and scales optimally.
| Sizes | MSR Sequential | gMSR(1) | gMSR(2) | gMSR(4) | gMSR(8) |
|---|---|---|---|---|---|
| 5 × 5 | 2.76 s | 2.12 s | 2.05 s | 2.12 s | 2.59 s |
| 10 × 10 | 27.83 s | 2.23 s | 2.21 s | 2.19 s | 2.73 s |
| 20 × 20 | 406.84 s | 2.85 s | 2.46 s | 2.55 s | 3.09 s |
| 30 × 30 | 1934.68 s | 3.55 s | 2.70 s | 2.91 s | 3.38 s |
| 40 × 40 | 5977.15 s | 4.38 s | 3.04 s | 3.10 s | 3.57 s |
| 50 × 50 | 14,378.5 s | 5.10 s | 3.52 s | 3.30 s | 3.75 s |
| 65 × 65 | 40,395.9 s | 6.85 s | 4.47 s | 3.77 s | 3.93 s |

Table A3.
This table shows the execution times in seconds for the real biclusters datasets. The first column represents to the number of biclusters generated by gBiBit, from 50,000 to 17,331,328. The other four columns represent the gMSR executions using 1, 2, 4 and 8 GPU devices, respectively. As it can be observed, multi-GPU mode improves runtimes as the volume of the bicluster dataset increases. Despite the large volume of data to be processed, gMSR execution times are small.
Table A3.
This table shows the execution times in seconds for the real biclusters datasets. The first column represents to the number of biclusters generated by gBiBit, from 50,000 to 17,331,328. The other four columns represent the gMSR executions using 1, 2, 4 and 8 GPU devices, respectively. As it can be observed, multi-GPU mode improves runtimes as the volume of the bicluster dataset increases. Despite the large volume of data to be processed, gMSR execution times are small.
| Biclusters | gMSR(1) | gMSR(2) | gMSR(4) | gMSR(8) |
|---|---|---|---|---|
| 50,000 | 6.55 s | 2.45 s | 2.46 s | 2.95 s |
| 100,000 | 7.40 s | 3.71 s | 3.72 s | 4.19 s |
| 150,000 | 8.52 s | 5.34 s | 5.10 s | 5.58 s |
| 200,000 | 9.44 s | 7.08 s | 6.42 s | 6.76 s |
| 250,000 | 10.78 s | 8.52 s | 7.78 s | 8.11 s |
| 300,000 | 11.94 s | 10.29 s | 9.40 s | 9.51 s |
| 350,000 | 14.11 s | 11.76 s | 10.76 s | 10.76 s |
| 400,000 | 15.69 s | 13.49 s | 12.26 s | 12.11 s |
| 450,000 | 17.01 s | 14.51 s | 12.82 s | 12.47 s |
| 500,000 | 18.31 s | 15.58 s | 14.66 s | 14.13 s |
| 550,000 | 20.26 s | 16.94 s | 15.93 s | 15.23 s |
| 600,000 | 21.57 s | 18.44 s | 17.45 s | 16.89 s |
| 650,000 | 22.93 s | 19.84 s | 18.89 s | 18.34 s |
| 700,000 | 24.60 s | 21.53 s | 20.25 s | 19.99 s |
| 750,000 | 26.23 s | 22.86 s | 21.74 s | 20.98 s |
| 800,000 | 27.88 s | 24.34 s | 23.31 s | 22.78 s |
| 850,000 | 29.83 s | 25.92 s | 25.07 s | 24.46 s |
| 900,000 | 31.50 s | 27.41 s | 25.98 s | 24.96 s |
| 950,000 | 33.48 s | 29.11 s | 28.18 s | 26.71 s |
| 1,000,000 | 35.52 s | 30.72 s | 28.85 s | 27.28 s |
| 2,000,000 | 76.80 s | 64.01 s | 59.90 s | 56.76 s |
| 4,000,000 | 182.60 s | 160.59 s | 143.11 s | 130.55 s |
| 6,000,000 | 316.01 s | 289.01 s | 272.39 s | 235.22 s |
| 8,000,000 | 475.89 s | 451.27 s | 422.36 s | 378.34 s |
| 17,331,328 | 1597.68 s | 1431.62 s | 1218.39 s | 989.87 s |
References
- Gauthier, J.; Vincent, A.T.; Charette, S.J.; Derome, N. A brief history of bioinformatics. Brief. Bioinform. 2019, 20, 1981–1996. [Google Scholar] [CrossRef] [PubMed]
- Libbrecht, M.W.; Noble, W.S. Machine learning applications in genetics and genomics. Nat. Rev. Genet. 2015, 16, 321–332. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, H.A.; Bhattacharyya, D.K.; Kalita, J.K. (Differential) Co-Expression Analysis of Gene Expression: A Survey of Best Practices. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 17, 1154–1173. [Google Scholar] [CrossRef]
- Su, L.; Liu, G.; Wang, J.; Xu, D. A rectified factor network based biclustering method for detecting cancer-related coding genes and miRNAs, and their interactions. Methods 2019, 166, 22–30. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Bhanot, G.; Khiabanian, H. TuBA: Tunable biclustering algorithm reveals clinically relevant tumor transcriptional profiles in breast cancer. GigaScience 2019, 8, giz064. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.; Chen, Y.; Liu, L.; Tao, D.; Li, X. On Combining Biclustering Mining and AdaBoost for Breast Tumor Classification. IEEE Trans. Knowl. Data Eng. 2020, 32, 728–738. [Google Scholar] [CrossRef]
- Gao, C.; McDowell, I.C.; Zhao, S.; Brown, C.D.; Engelhardt, B.E. Context specific and differential gene co-expression networks via Bayesian biclustering. PLoS Comput. Biol. 2016, 12, e1004791. [Google Scholar] [CrossRef] [PubMed]
- Bentham, R.B.; Bryson, K.; Szabadkai, G. Biclustering Analysis of Co-regulation Patterns in Nuclear-Encoded Mitochondrial Genes and Metabolic Pathways. In Cancer Metabolism; Humana Press: New York, NY, USA, 2019; pp. 469–478. [Google Scholar]
- Xie, J.; Ma, A.; Fennell, A.; Ma, Q.; Zhao, J. It is time to apply biclustering: A comprehensive review of biclustering applications in biological and biomedical data. Brief. Bioinform. 2018, 20, 1450–1465. [Google Scholar] [CrossRef]
- Li, J.; Reisner, J.; Pham, H.; Olafsson, S.; Vardeman, S. Biclustering with missing data. Inf. Sci. 2020, 510, 304–316. [Google Scholar] [CrossRef]
- Gomez-Vela, F.; López, A.; Lagares, J.A.; Baena, D.S.; Barranco, C.D.; García-Torres, M.; Divina, F. Bioinformatics from a Big Data Perspective: Meeting the Challenge. In Lecture Notes in Computer Science, Proceedings of the Bioinformatics and Biomedical Engineering, Granada, Spain, 26–28 April 2017; Springer: Cham, Switzerland, 2017; pp. 349–359. [Google Scholar]
- Vandromme, M.; Jacques, J.; Taillard, J.; Jourdan, L.; Dhaenens, C. A Biclustering Method for Heterogeneous and Temporal Medical Data. IEEE Trans. Knowl. Data Eng. 2020, 1, 1. [Google Scholar] [CrossRef]
- Orzechowski, P.; Moore, J.H. EBIC: A scalable biclustering method for large scale data analysis. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Prague, Czech Republic, 13–17 July 2019; pp. 31–32. [Google Scholar]
- Orzechowski, P.; Boryczko, K. Effective biclustering on GPU-capabilities and constraints. Prz Elektrotech. 2015, 1, 133–136. [Google Scholar] [CrossRef]
- White, T. Hadoop: The Definitive Guide; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2009. [Google Scholar]
- Dean, J.; Ghemawat, S. MapReduce: Simplified data processing on large clusters. Commun. ACM 2008, 51, 107–113. [Google Scholar] [CrossRef]
- Liao, R.; Zhang, Y.; Guan, J.; Zhou, S. CloudNMF: A MapReduce implementation of nonnegative matrix factorization for large-scale biological datasets. Genom. Proteom. Bioinform. 2014, 12, 48–51. [Google Scholar] [CrossRef]
- Zaharia, M.; Xin, R.S.; Wendell, P.; Das, T.; Armbrust, M.; Dave, A.; Meng, X.; Rosen, J.; Venkataraman, S.; Franklin, M.J.; et al. Apache spark: A unified engine for big data processing. Commun. ACM 2016, 59, 56–65. [Google Scholar] [CrossRef]
- Sarazin, T.; Lebbah, M.; Azzag, H. Biclustering using Spark-MapReduce. In Proceedings of the 2014 IEEE International Conference on Big Data (Big Data), Washington, DC, USA, 27–30 October 2014; pp. 58–60. [Google Scholar]
- NVIDIA. NVIDIA CUDA Programming Guide 2.0; NVIDIA Corporation: Santa Clara, CA, USA, 2008. [Google Scholar]
- Orzechowski, P.; Boryczko, K. Rough assessment of GPU capabilities for parallel PCC-based biclustering method applied to microarray data sets. Bio-Algorithms Med-Syst. 2015, 11, 243–248. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Cui, Y. A GPU-accelerated algorithm for biclustering analysis and detection of condition- dependent coexpression network modules. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Clevert, D.A.; Unterthiner, T.; Povysil, G.; Hochreiter, S. Rectified factor networks for biclustering of omics data. Bioinformatics 2017, 33, i59–i66. [Google Scholar] [CrossRef] [PubMed][Green Version]
- González-Domínguez, J.; Expósito, R.R. Accelerating binary biclustering on platforms with CUDA-enabled GPUs. Inf. Sci. 2019, 496, 317–325. [Google Scholar] [CrossRef]
- Liu, B.; Yu, C.; Wang, D.Z.; Cheung, R.C.; Yan, H. Design exploration of geometric biclustering for microarray data analysis in data mining. IEEE Trans. Parallel Distrib. Syst. 2013, 25, 2540–2550. [Google Scholar] [CrossRef]
- Orzechowski, P.; Boryczko, K.; Moore, J.H. Scalable biclustering—the future of big data exploration? GigaScience 2019, 8, giz078. [Google Scholar] [CrossRef] [PubMed]
- Saber, H.; Elloumi, M. A new study on biclustering tools, bicluster validation and evaluation functions. Int. J. Comput. Sci. Eng. Surv. 2015, 6, 1. [Google Scholar] [CrossRef]
- Cheng, Y.; Church, G.M. Biclustering of expression data. Ismb 2000, 8, 93–103. [Google Scholar]
- Consortium, T.G.O. Expansion of the Gene Ontology knowledgebase and resources. Nucleic Acids Res. 2016, 45, 331–338. [Google Scholar]
- Raudvere, U.; Kolberg, L.; Kuzmin, I.; Arak, T.; Adler, P.; Peterson, H.; Vilo, J. g: Profiler: A web server for functional enrichment analysis and conversions of gene lists (2019 update). Nucleic Acids Res. 2019, 47, W191–W198. [Google Scholar] [CrossRef]
- Kuleshov, M.V.; Jones, M.R.; Rouillard, A.D.; Fernandez, N.F.; Duan, Q.; Wang, Z.; Koplev, S.; Jenkins, S.L.; Jagodnik, K.M.; Lachmann, A.; et al. Enrichr: A comprehensive gene set enrichment analysis web server 2016 update. Nucleic Acids Res. 2016, 44, W90–W97. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Fan, D.; Slowikowski, K.; Gehlenborg, N.; Kharchenko, P. UBiT2: A client-side web-application for gene expression data analysis. bioRxiv 2017, 118992. [Google Scholar] [CrossRef]
- Liao, Y.; Wang, J.; Jaehnig, E.J.; Shi, Z.; Zhang, B. WebGestalt 2019: Gene set analysis toolkit with revamped UIs and APIs. Nucleic Acids Res. 2019, 47, W199–W205. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Fernandez, A.; Rodriguez-Baena, D.; Gomez-Vela, F.; Diaz-Diaz, N. BIGO: A web application to analyse gene enrichment analysis results. Comput. Biol. Chem. 2018, 76, 169–178. [Google Scholar] [CrossRef]
- Orzechowski, P.; Moore, J.H. EBIC: An open source software for high-dimensional and big data analyses. Bioinformatics 2019, 35, 3181–3183. [Google Scholar] [CrossRef]
- Falcon, S.; Gentleman, R. Using GOstats to test gene lists for GO term association. Bioinformatics 2007, 23, 257–258. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Pulido, J.A.; Cerrada-Barrios, J.L.; Trinidad-Amado, S.; Lanza-Gutierrez, J.M.; Fernandez-Diaz, R.A.; Crawford, B.; Soto, R. Fine-grained parallelization of fitness functions in bioinformatics optimization problems: Gene selection for cancer classification and biclustering of gene expression data. BMC Bioinform. 2016, 17, 330. [Google Scholar] [CrossRef]
- Li, Y.; Shang, Y.; Yang, Y. Clustering coefficients of large networks. Inf. Sci. 2017, 382, 350–358. [Google Scholar] [CrossRef]
- Rodriguez-Baena, D.S.; Perez-Pulido, A.J.; Aguilar-Ruiz, J.S. A biclustering algorithm for extracting bit-patterns from binary datasets. Bioinformatics 2011, 27, 2738–2745. [Google Scholar] [CrossRef]
- Sato, T.; Kaneda, A.; Tsuji, S.; Isagawa, T.; Yamamoto, S.; Fujita, T.; Yamanaka, R.; Tanaka, Y.; Nukiwa, T.; Marquez, V.E.; et al. PRC2 overexpression and PRC2-target gene repression relating to poorer prognosis in small cell lung cancer. Sci. Rep. 2013, 3, 1911. [Google Scholar] [CrossRef]
- Saelens, W.; Cannoodt, R.; Saeys, Y. A comprehensive evaluation of module detection methods for gene expression data. Nat. Commun. 2018, 9, 1090. [Google Scholar] [CrossRef]
- Müssel, C.; Schmid, F.; Blätte, T.J.; Hopfensitz, M.; Lausser, L.; Kestler, H.A. BiTrinA—multiscale binarization and trinarization with quality analysis. Bioinformatics 2016, 32, 465–468. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Fernandez, A.; Rodriguez-Baena, D.; Gomez-Vela, F.; Divina, F.; Garcia-Torres, M. A multi-GPU biclustering algorithm for binary datasets. J. Parallel Distrib. Comput. 2021, 147, 209–219. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).