Lipofuscin-Type Pigment as a Marker of Colorectal Cancer
Abstract
:1. Introduction
2. Materials and Methods
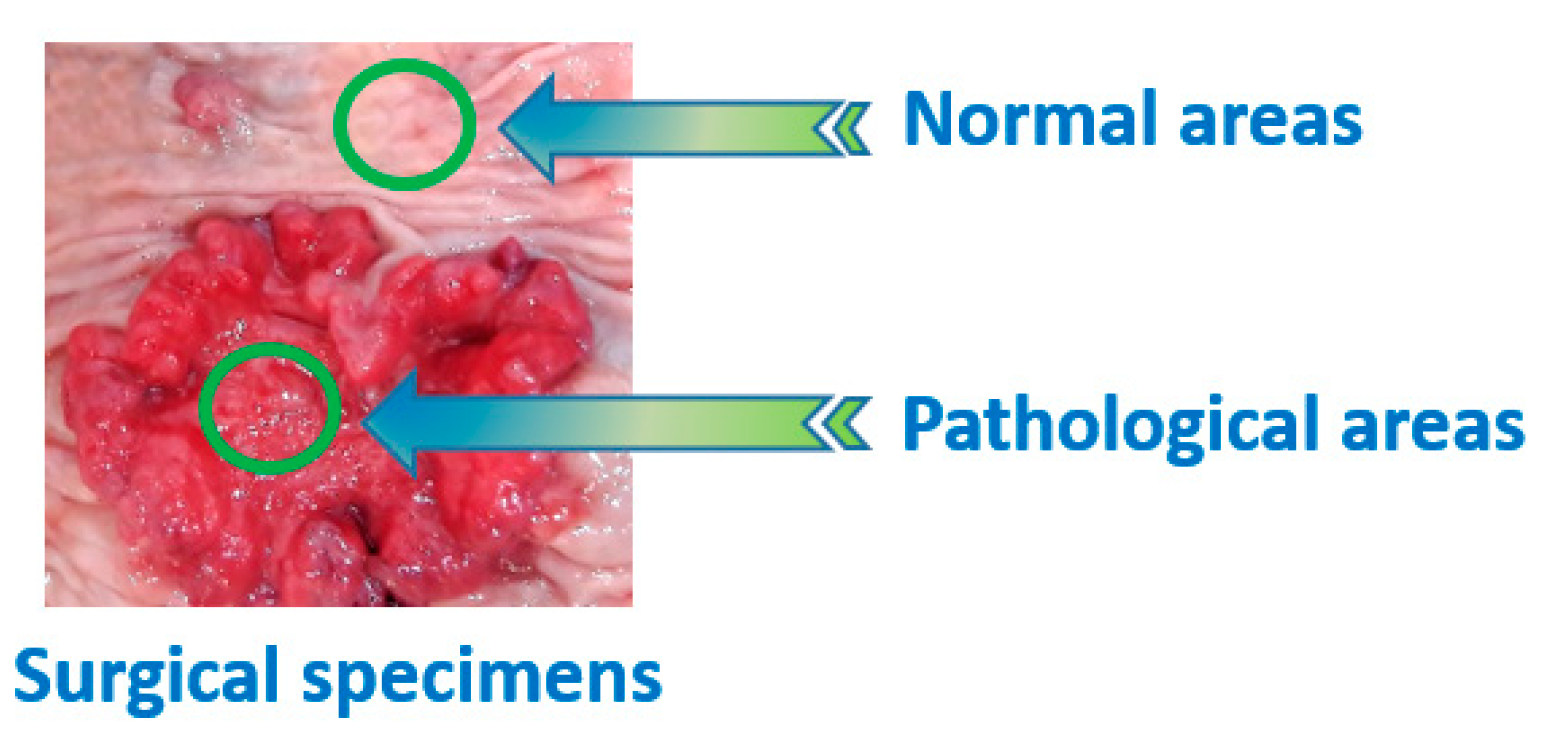
2.1. Tissue Samples
2.2. Spectral Measurements
2.3. Calculations
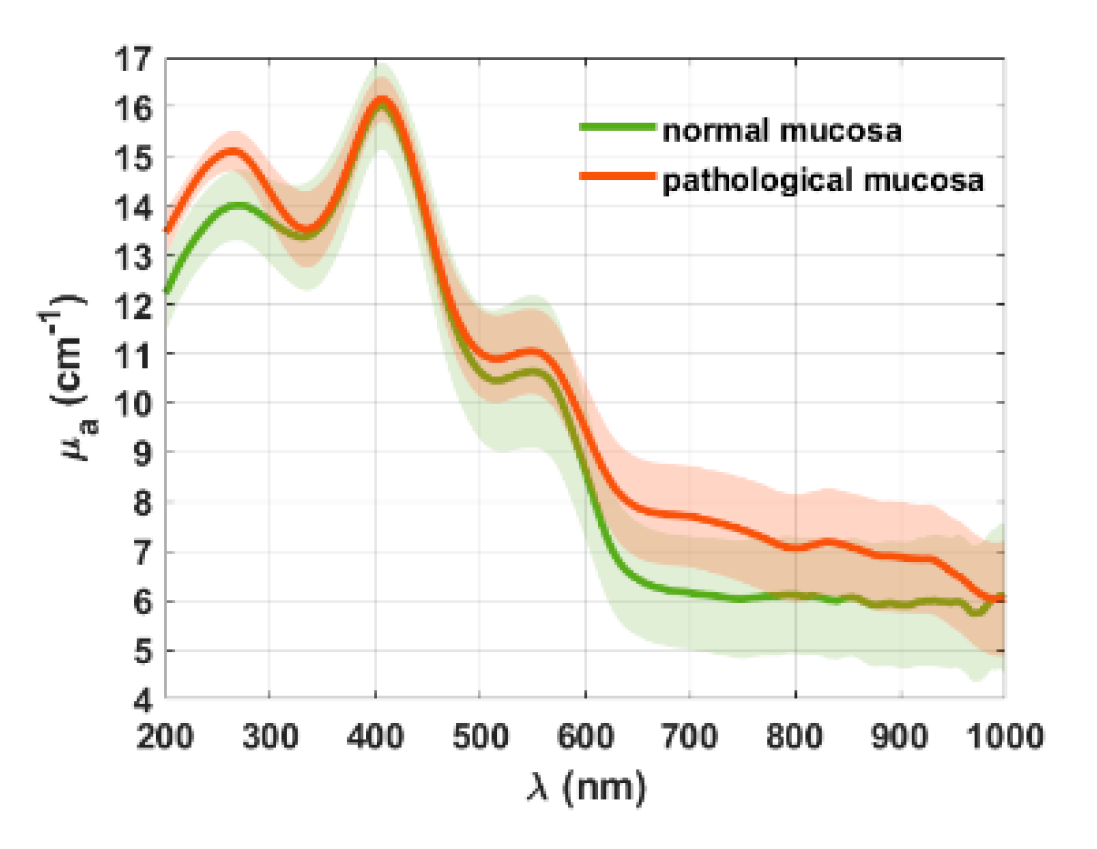
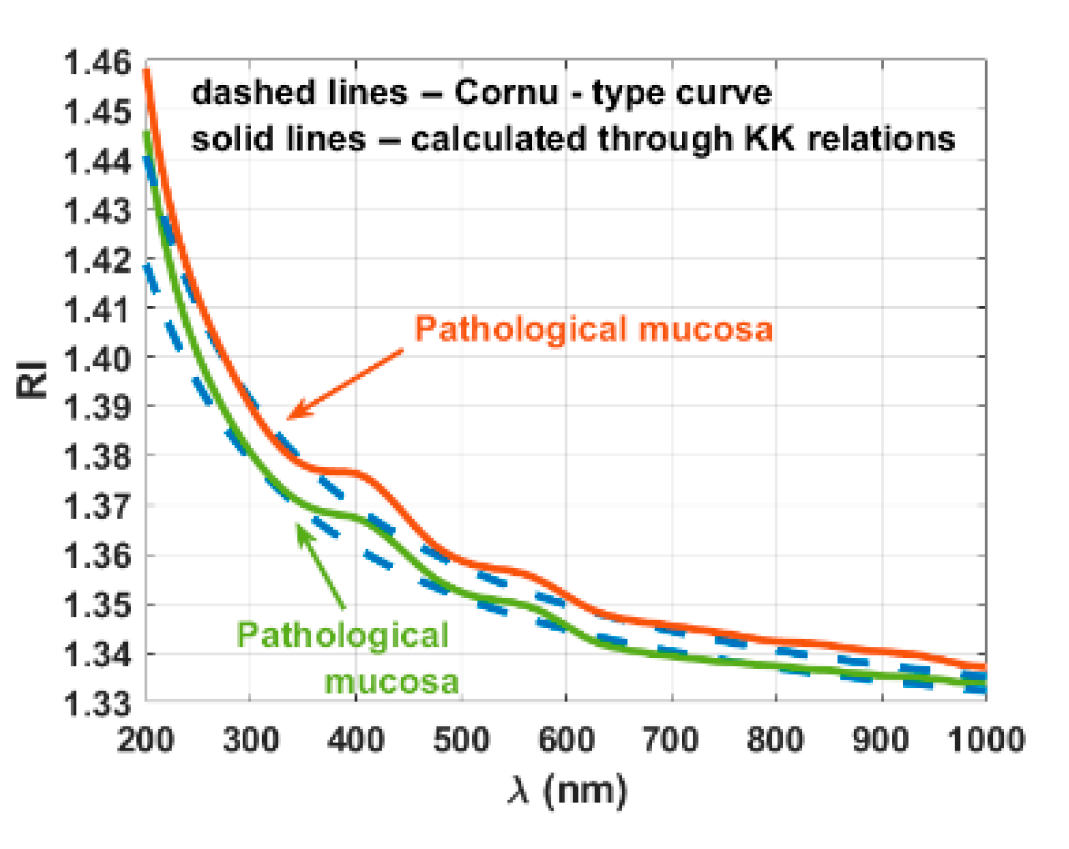
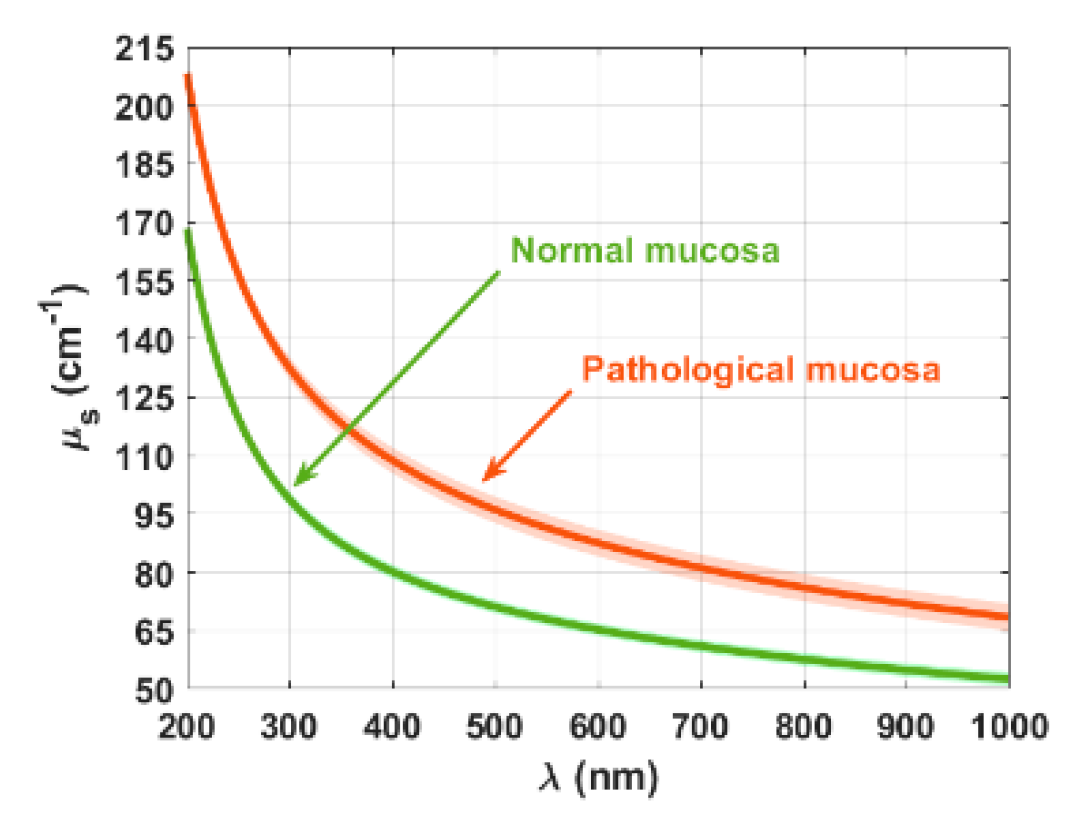
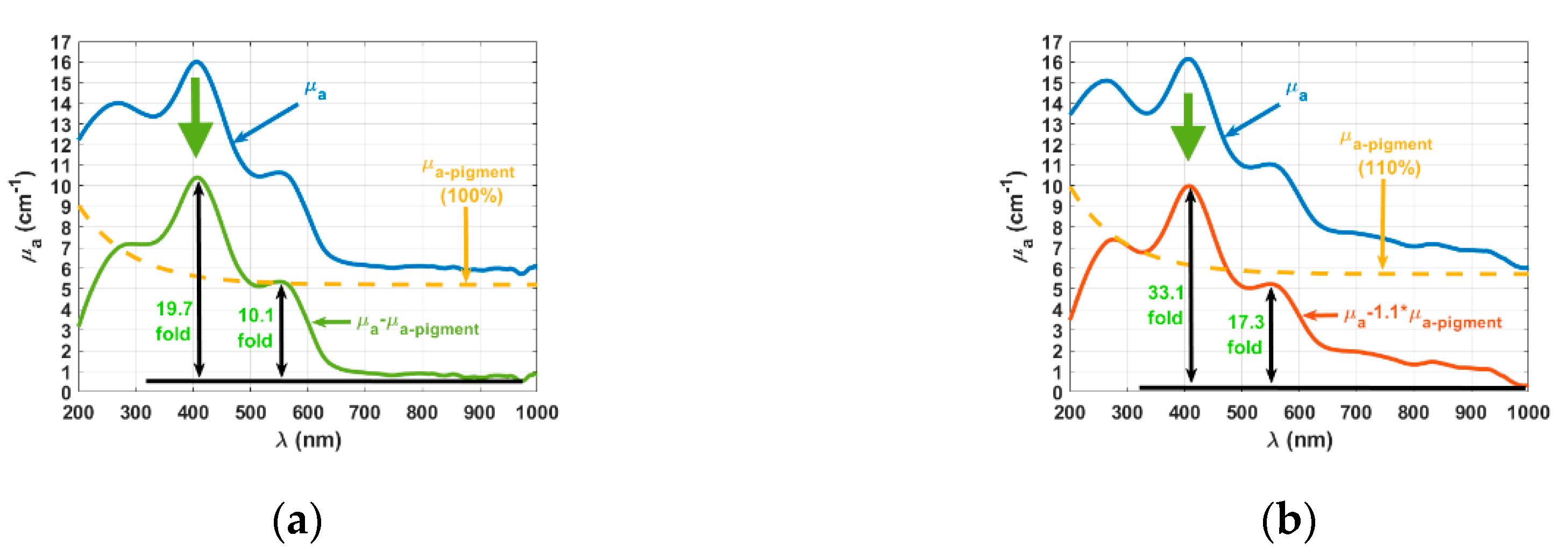
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Brenner, H.; Kloor, M.; Pox, C.P. Colorectal cancer. Lancet 2014, 383, 1490–1502. [Google Scholar] [CrossRef]
- Oliveira, L.M.; Tuchin, V.V. The Optical Clearing Method—A New Tool for Clinical Practice and Biomedical Engineering; SPRINGER: Cham, Switzerland, 2019; pp. 1–106. [Google Scholar]
- Sordillo, D.C.; Sordillo, L.A.; Sordillo, P.P.; Shi, L.; Alfano, R.R. Short wavelength infrared optical windows for evaluation of benign and malignant tissues. J. Biomed. Opt. 2017, 22. [Google Scholar] [CrossRef]
- Shi, L.; Sordillo, L.A.; Rodríguez-Contreras, A.; Alfano, R. Transmission in near-infrared optical windows for deep brain imaging. J. Biophotonics 2016, 9, 38–43. [Google Scholar] [CrossRef] [PubMed]
- Bashkatov, A.N.; Genina, E.A.; Kozintseva, M.D.; Kochubei, V.I.; Gorodkov, S.Y.; Tuchin, V.V. Optical properties of peritoneal biological tissues in the spectral range of 350-2500 nm. Opt. Spectrosc. 2016, 120, 6–14. [Google Scholar] [CrossRef]
- Carneiro, I.; Carvalho, S.; Henrique, R.; Oliveira, L.; Tuchin, V. Moving tissue spectral window to the deep-ultraviolet via optical clearing. J. Biophotonics 2019, 12. [Google Scholar] [CrossRef] [PubMed]
- Carneiro, I.; Carvalho, S.; Henrique, R.; Selifonov, S.; Oliveira, L.; Tuchin, V.V. Enhanced ultraviolet spectroscopy by optical clearing for biomedical applications. IEEE J. Sel. Top. Quant. Elect. 2021, 27. [Google Scholar] [CrossRef]
- Oliveira, L.M.; Zaytsev, K.I.; Tuchin, V.V. Improved biomedical imaging over a wide spectral range from UV to THz towards multimodality. In SPIE Proceedings of the Third International Conference on Biophotonics Riga 2020, Riga, Latvia, 24–25 August 2020; Spigulis, J., Ed.; SPIE: Bellingham, WA, USA, 2020; Volume 11585, p. 11585. [Google Scholar]
- Bashkatov, A.N.; Genina, E.A.; Kochubey, V.I.; Rubtsov, V.S.; Kolesnikova, E.A.; Tuchin, V.V. Optical properties of human colon tissues in the 350-2500 spectral range. Quant. Elect. 2014, 44, 779–784. [Google Scholar] [CrossRef] [Green Version]
- Tuchin, V.V. Tissue Optics: Light Scattering Methods and Instruments for Medical Diagnosis, 3rd ed.; SPIE Press: Bellingham, WA, USA, 2015; pp. 245–358. [Google Scholar]
- Vo-Dinh, T. Biomedical Photonics Handbook, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2014; Volume 1, pp. 23–168. [Google Scholar]
- Bashkatov, A.N.; Genina, E.A.; Kochubey, V.I.; Tuchin, V.V. Optical properties of human skin, subcutaneous and mucous tissues in the wavelength range from 400 to 2000 nm. J. Phys. D Appl. Phys. 2005, 38, 2543. [Google Scholar] [CrossRef]
- Bashkatov, A.N.; Genina, E.A.; Kochubey, V.I.; Tuchin, V.V. Optical properties of the subcutaneous adipose tissue in the spectral range 400–2500 nm. Opt. Spectrosc. 2005, 99, 836–842. [Google Scholar] [CrossRef]
- Bashkatov, A.N.; Genina, E.A.; Kochubey, V.I.; Tuchin, V.V. Optical properties of human cranial bone in the spectral range from 800 to 2000 nm. In SPIE Proceedings of the Saratov Fall Meeting 2005: Optical Technologies in Biophysics and Medicine VII, Saratov, Russian, 27–30 September 2005; Tuchin, V.V., Ed.; SPIE: Bellingham, WA, USA, 2006; Volume 6163, p. 6163. [Google Scholar]
- Bashkatov, A.N.; Genina, E.A.; Kochubey, V.I.; Gavrilova, A.A.; Kapralov, S.V.; Grishaev, V.A.; Tuchin, V.V. Optical properties of human stomach mucosa in the spectral range from 400 to 2000 nm: Prognosis for gastroenterology. Med. Las. Appl. 2007, 22, 95–104. [Google Scholar] [CrossRef]
- Bashkatov, A.N.; Genina, E.A.; Kochubey, V.I.; Tuchin, V.V. Optical properties of human sclera in spectral range 370–2500 nm. Opt. Spectrosc. 2010, 109, 197–204. [Google Scholar] [CrossRef]
- Carvalho, S.; Gueiral, N.; Nogueira, E.; Henrique, R.; Oliveira, L.; Tuchin, V. Comparative study of the optical properties of colon mucosa and colon precancerous polyps between 400 and 1000 nm. In SPIE Proceedings of BIOS-Photonics West 2017: Dynamics and Fluctuations in Biomedical Photonics, San Francisco, CA, USA, 28 January–2 February 2017; Tuchin, V.V., Larin, K.V., Leahy, M.J., Wang, R.K., Eds.; SPIE: Bellingham, WA, USA, 2017; Volume 10063, p. 10063. [Google Scholar]
- Carneiro, I.; Carvalho, S.; Henrique, R.; Oliveira, L.; Tuchin, V.V. Optical properties of colorectal muscle in visible/NIR range. In SPIE Proceedings of Photonics Europe: Biophotonics—Photonic Solutions for Better Health Care VI, Strasbourg, France, 22–26 April 2018; Popp, J., Tuchin, V.V., Pavone, F.S., Eds.; SPIE: Bellingham, WA, USA, 2018; Volume 10685, p. 10685. [Google Scholar]
- Carneiro, I.; Carvalho, S.; Henrique, R.; Oliveira, L.; Tuchin, V.V. Measuring optical properties of human liver between 400 and 1000 nm. Quant. Electr. 2019, 49, 13–19. [Google Scholar] [CrossRef]
- Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Biol. 2013, 58, R37–R61. [Google Scholar] [CrossRef] [PubMed]
- Carneiro, I.; Carvalho, S.; Silva, V.; Henrique, R.; Oliveira, L.; Tuchin, V.V. Kinetics of optical properties of human colorectal tissues during optical clearing: A comparative study between normal and pathological tissues. J. Biomed. Opt. 2018, 23. [Google Scholar] [CrossRef] [Green Version]
- Carneiro, I.; Carvalho, S.; Henrique, R.; Oliveira, L.; Tuchin, V.V. Kinetics of Optical Properties of Colorectal Muscle During Optical Clearing. IEEE J. Sel. Top. Quant. Elect. 2019, 25. [Google Scholar] [CrossRef]
- Prahl, S.A.; van Gemert, M.J.C.; Welch, A.J. Determining the optical properties of turbid media by using the adding-doubling method. Appl. Opt. 1993, 32, 559–568. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML-Monte Carlo modeling of light transport in multi-layered tissues. Comp. Method Prog. Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Ianina, I.Y.; Lazareva, E.N.; Tuchin, V.V. Refractive index of adipose tissue and lipid droplet measured in wide spectral and temperature ranges. Appl. Opt. 2018, 57, 4839–4848. [Google Scholar] [CrossRef]
- Lazareva, E.N.; Tuchin, V.V. Measurement of refractive index of hemoglobin in the visible/NIR spectral range. J. Biomed. Opt. 2018, 23. [Google Scholar] [CrossRef] [Green Version]
- Lazareva, E.N.; Tuchin, V.V. Blood refractive index modelling in the visible and near infrared spectral regions. J. Biomed. Photonics Eng. 2018, 4. [Google Scholar] [CrossRef] [Green Version]
- Carneiro, I.; Carvalho, S.; Henrique, R.; Oliveira, L.; Tuchin, V.V. Water content and scatterers dispersion evaluation in colorectal tissues. J. Biomed. Photonics Eng. 2017, 3, 40301. [Google Scholar] [CrossRef] [Green Version]
- Carneiro, I.; Carvalho, S.; Henrique, R.; Oliveira, L.; Tuchin, V.V. Simple multimodal technique for evaluation of free/bound water and dispersion of human liver tissue. J. Biomed. Opt. 2017, 22. [Google Scholar] [CrossRef]
- Sydoruk, O.; Zhernovaya, O.; Tuchin, V.V.; Douplik, A. Refractive index of solutions of human hemoglobin from the near-infrared to the ultraviolet range: Kramers-Kronig analysis. J. Biomed. Opt. 2012, 17. [Google Scholar] [CrossRef] [PubMed]
- Gienger, J.; Groβ, H.; Neukammer, J.; Bär, M. Determining the refractive index of human hemoglobin solutions by Kramers-Kronig relations with an improved absorption model. Appl. Opt. 2016, 55, 8951–8961. [Google Scholar] [CrossRef] [PubMed]
- Gomes, N.; Tuchin, V.V.; Oliveira, L.M. UV-NIR efficiency of the refractive index matching mechanism on colorectal muscle during treatment with different glycerol osmolarities. J. Biomed. Photonics Eng. 2020, 6, 20307. [Google Scholar] [CrossRef]
- Zhou, Y.; Yao, J.; Wang, L. Tutorial on photoacoustic tomography. J. Biomed. Opt. 2006, 6, 61007. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, S.; Gueiral, N.; Nogueira, E.; Henrique, R.; Oliveira, L.; Tuchin, V.V. Wavelength dependence of the refractive index of human colorectal tissues: Comparison between healthy mucosa and cancer. J. Biomed. Photonics Eng. 2016, 2. [Google Scholar] [CrossRef] [Green Version]
- Peña-Llopis, S.; Brugarolas, J. Simultaneous isolation of high-quality DNA, RNA, miRNA and proteins from tissues for genomic applications. Nat. Protoc. 2017, 8, 2240–2255. [Google Scholar] [CrossRef] [Green Version]
- Bashkatov, A.N.; Genina, E.A.; Kochubey, V.I.; Tuchin, V.V.; Chikina, E.E.; Knyazev, A.B.; Mareev, O.V. Optical properties of mucous membrane in the spectral range 350–2000 nm. Opt. Spect. 2004, 97, 1043–1048. [Google Scholar] [CrossRef]
- Johansson, J.D. Spectroscopic method for determination of the absorption coefficient in brain tissue. J. Biomed. Opt. 2010, 15. [Google Scholar] [CrossRef] [Green Version]
- Johansson, J.D.; Wårdell, K. Intracerebral quantitative chromophore estimation from reflectance spectra captured during deep brain stimulation implantation. J. Biophotonics 2013, 6, 435–445. [Google Scholar] [CrossRef] [PubMed] [Green Version]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvalho, S.; Carneiro, I.; Henrique, R.; Tuchin, V.; Oliveira, L. Lipofuscin-Type Pigment as a Marker of Colorectal Cancer. Electronics 2020, 9, 1805. https://doi.org/10.3390/electronics9111805
Carvalho S, Carneiro I, Henrique R, Tuchin V, Oliveira L. Lipofuscin-Type Pigment as a Marker of Colorectal Cancer. Electronics. 2020; 9(11):1805. https://doi.org/10.3390/electronics9111805
Chicago/Turabian StyleCarvalho, Sónia, Isa Carneiro, Rui Henrique, Valery Tuchin, and Luís Oliveira. 2020. "Lipofuscin-Type Pigment as a Marker of Colorectal Cancer" Electronics 9, no. 11: 1805. https://doi.org/10.3390/electronics9111805
APA StyleCarvalho, S., Carneiro, I., Henrique, R., Tuchin, V., & Oliveira, L. (2020). Lipofuscin-Type Pigment as a Marker of Colorectal Cancer. Electronics, 9(11), 1805. https://doi.org/10.3390/electronics9111805







