Optimal Transient Search Algorithm-Based PI Controllers for Enhancing Low Voltage Ride-Through Ability of Grid-Linked PMSG-Based Wind Turbine
Abstract
:1. Introduction
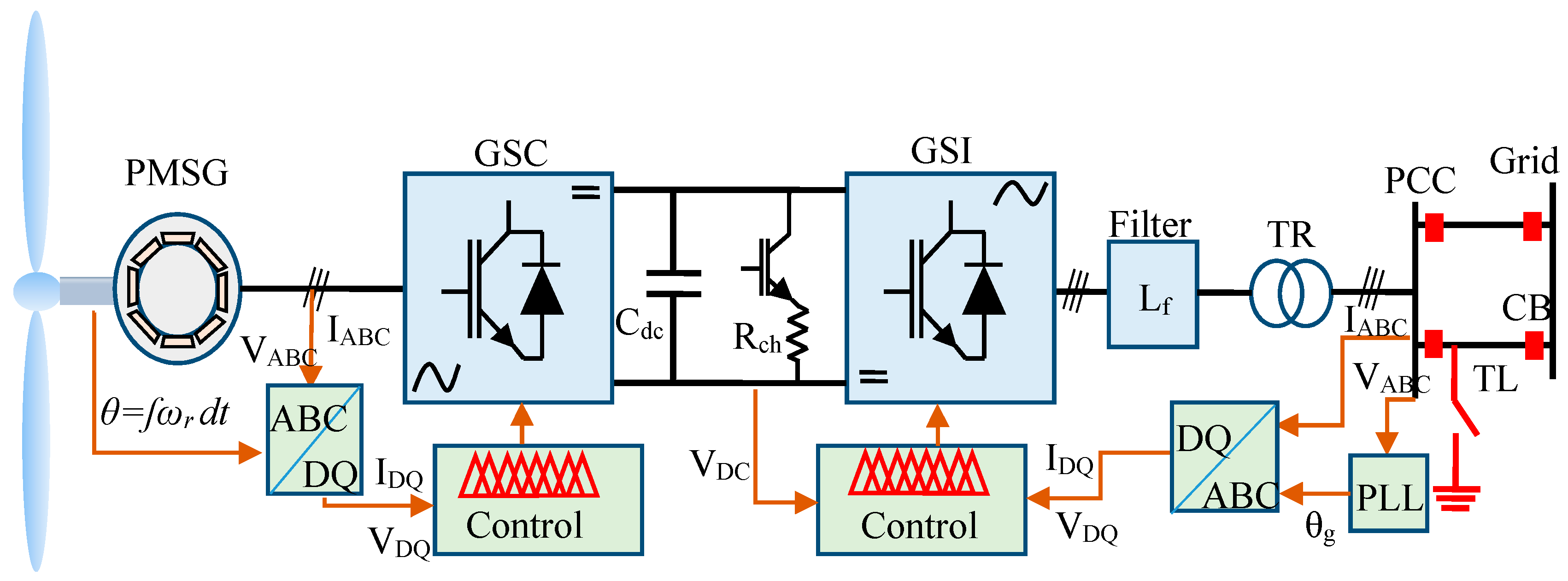
2. Power System Modeling
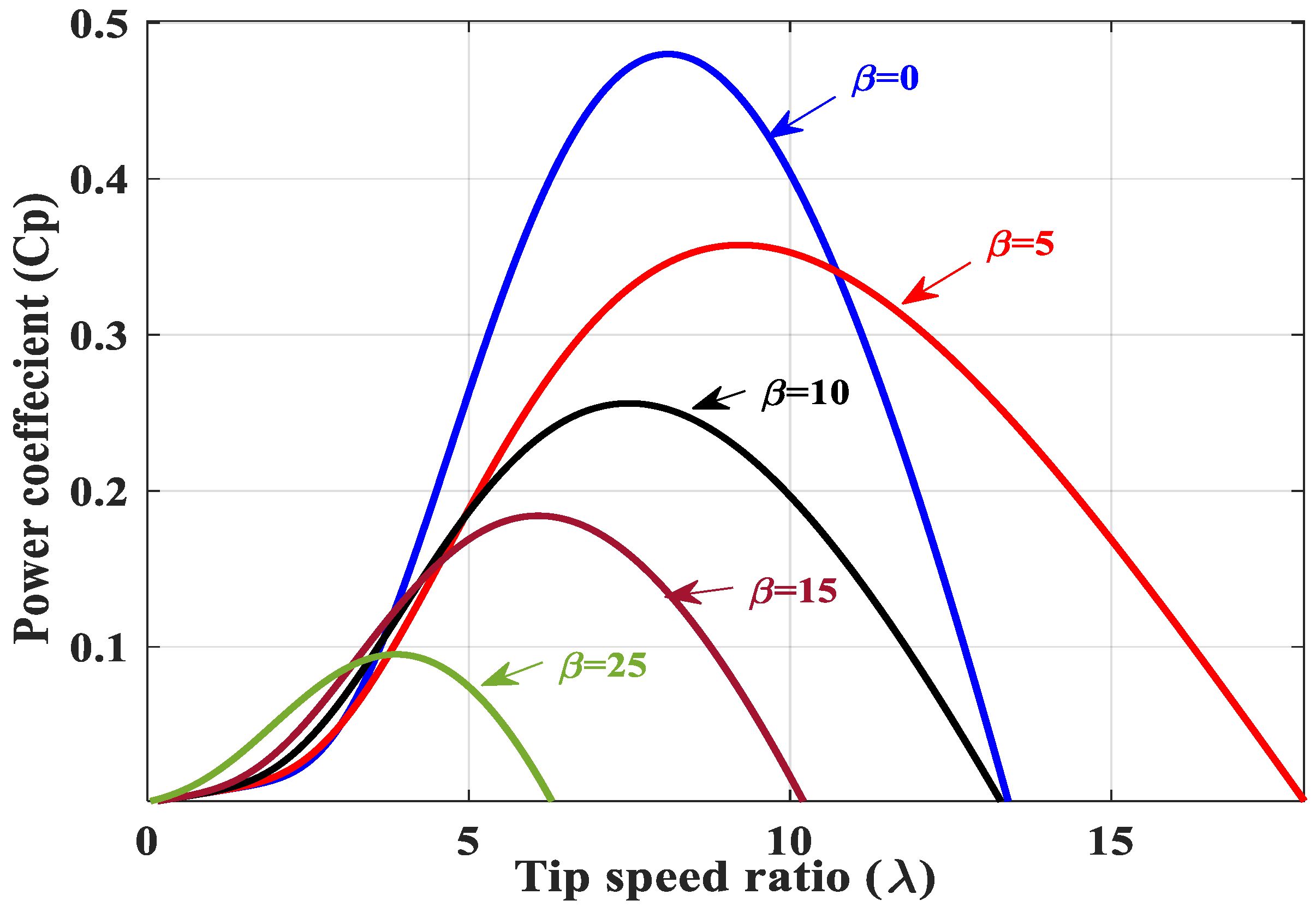
2.1. Horizontal-Axis WT Modeling
2.2. Gearless Shaft Modeling
2.3. Generator-Side Modeling
2.4. Grid Side Modeling
3. Frequency Converter Modeling
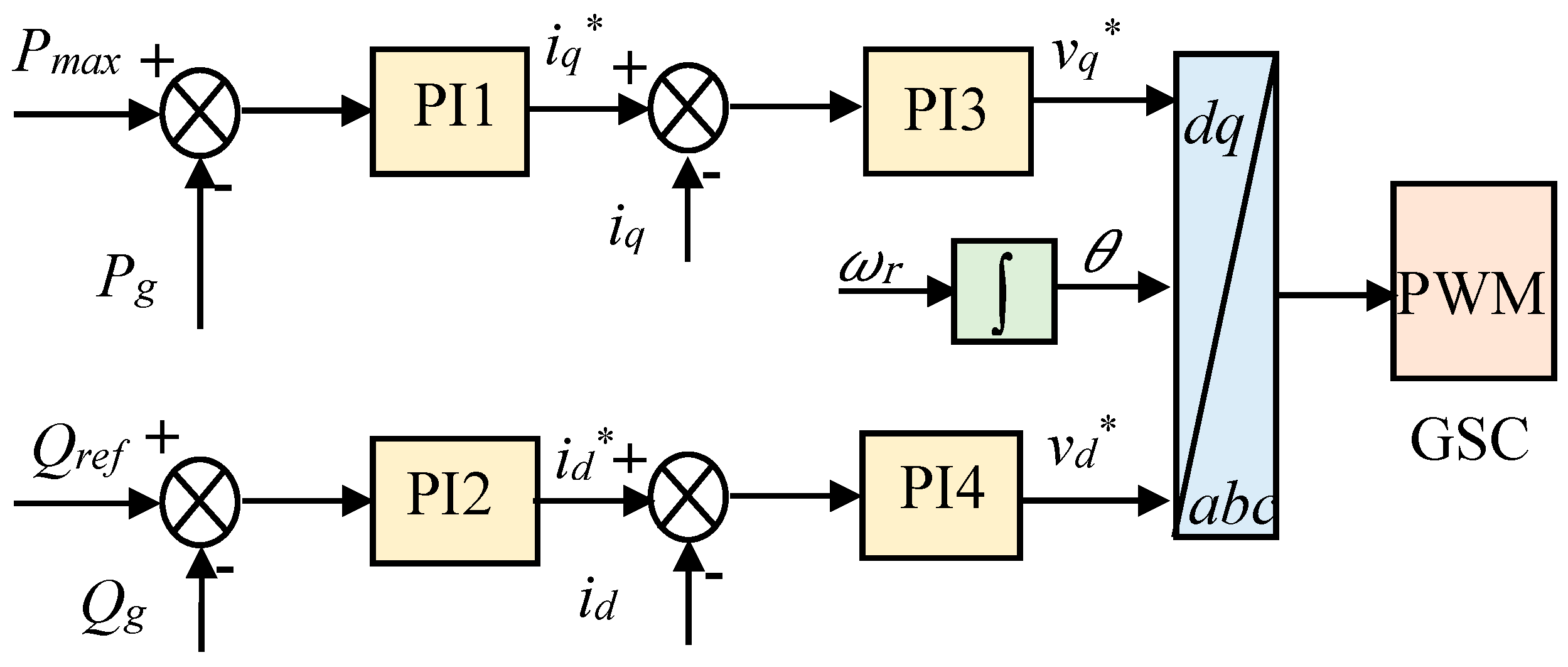
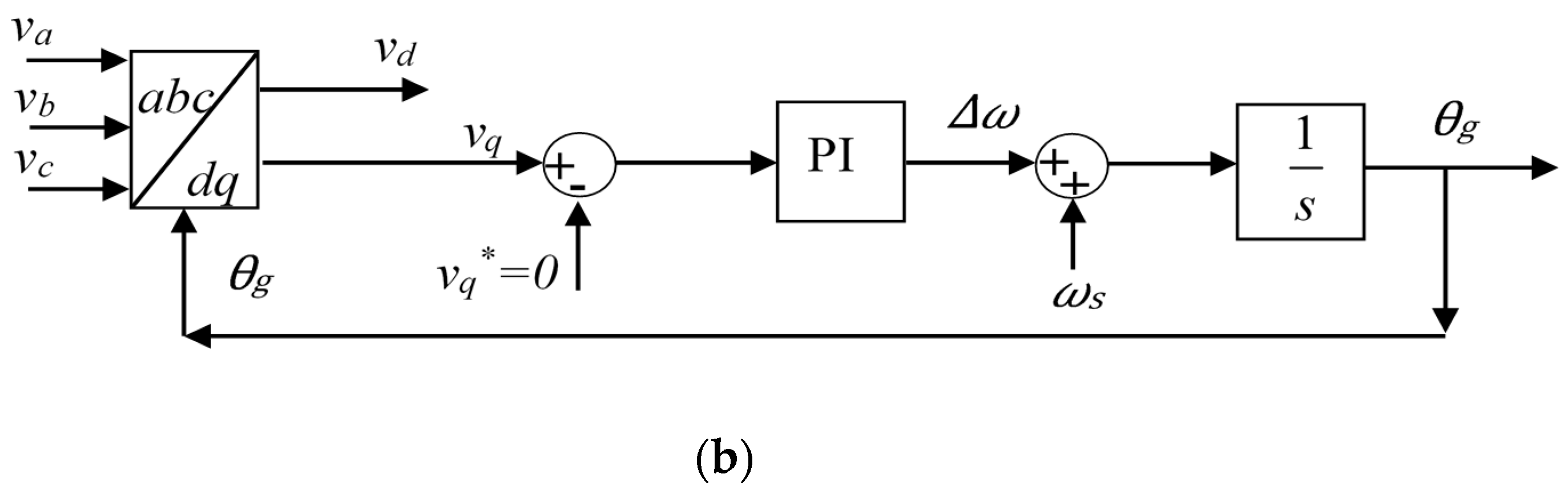
3.1. GSC Control Modeling
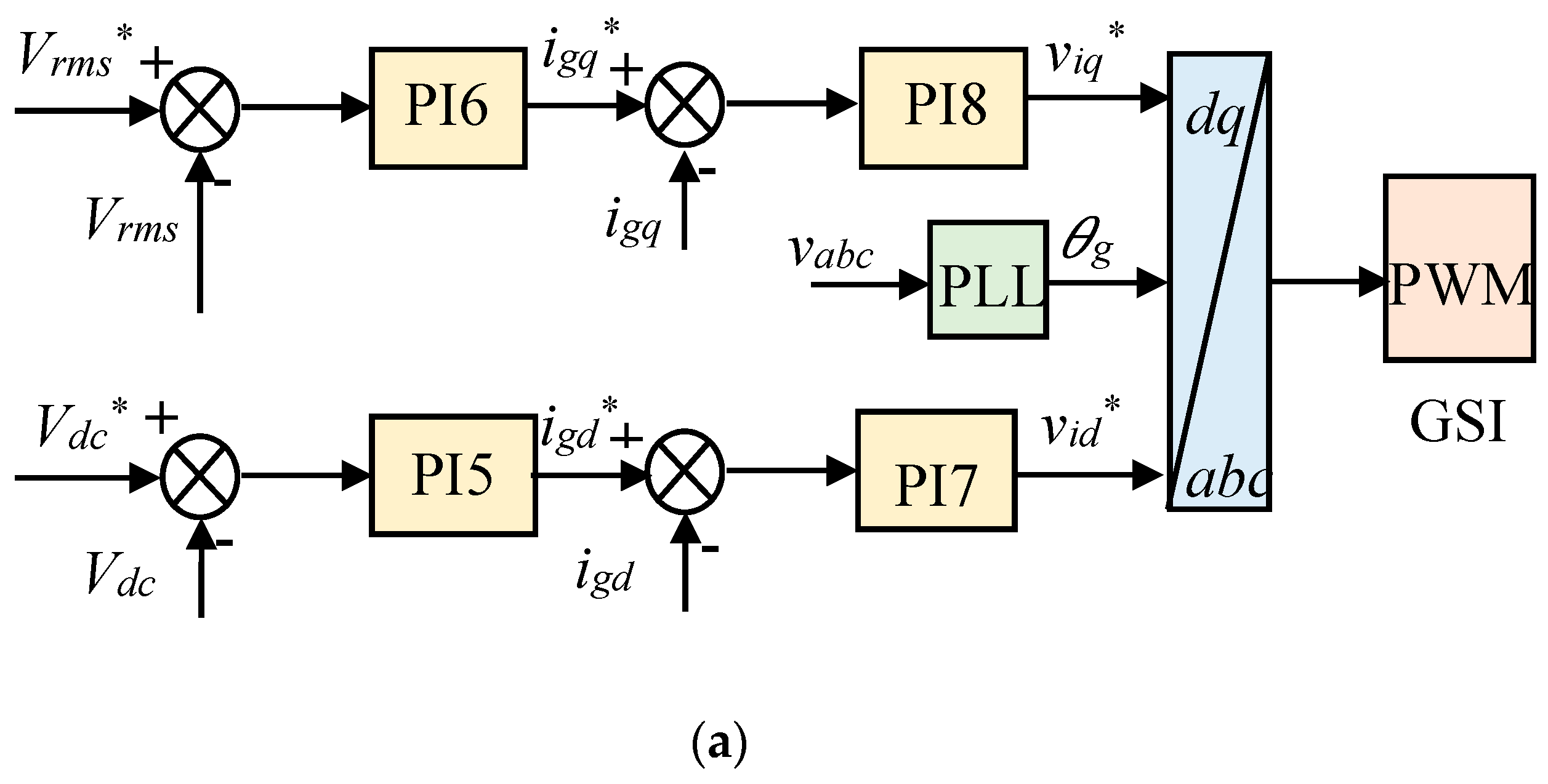
3.2. GSI Control Modeling
4. Optimization Methodology
4.1. Transient Search Optimization (TSO)
| Algorithm 1 Transient search optimization (TSO) |
| Input the random initial values of search agents Xl = {kp1, kp2, …, kp8, Ti1, Ti2…., Ti8} between 0.01 ≤ kp ≤ 10 and 0.001 ≤ Ti ≤ 1 Calculate the ISE(Xl) while l < Lmax Modify A and W do all search agents Xl Update the search agents by Equation (26) end do Compute the ISE(Xl+1) Compare the ISE(Xl) with ISE(Xl+1) and find the new best search agents X* l = l + 1 end while return the best search agents X* |
4.2. Grey Wolf Optimizer (GWO)
| Algorithm 2 Grey wolf optimizer (GWO) |
| Input the random initial values of search agents Xl = {kp1, kp2, …, kp8, Ti1, Ti2 …, Ti8} between 0.01 ≤ kp ≤ 10 and 0.001 ≤ Ti ≤ 1 Compute the ISE(Xl) while l < Lmax Modify a, A, and C for All search agents Update the search agent (Xl+1) by Equation (31) end for Compute the ISE(Xl+1) Compare ISE(Xl+1) with ISE(Xl)and update Xα, Xβ, and Xδ l = l + 1 end while Output best search agent Xα |
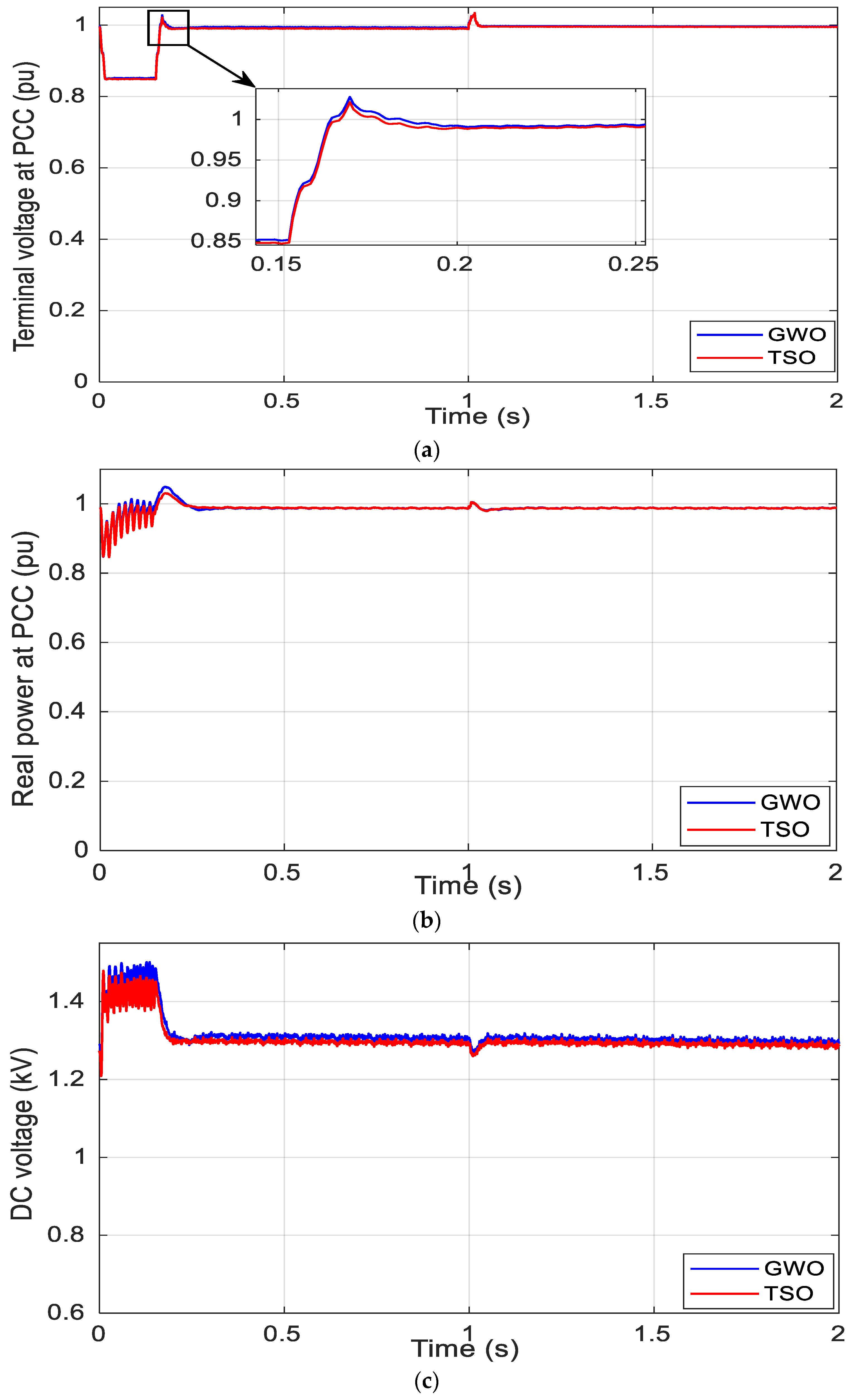
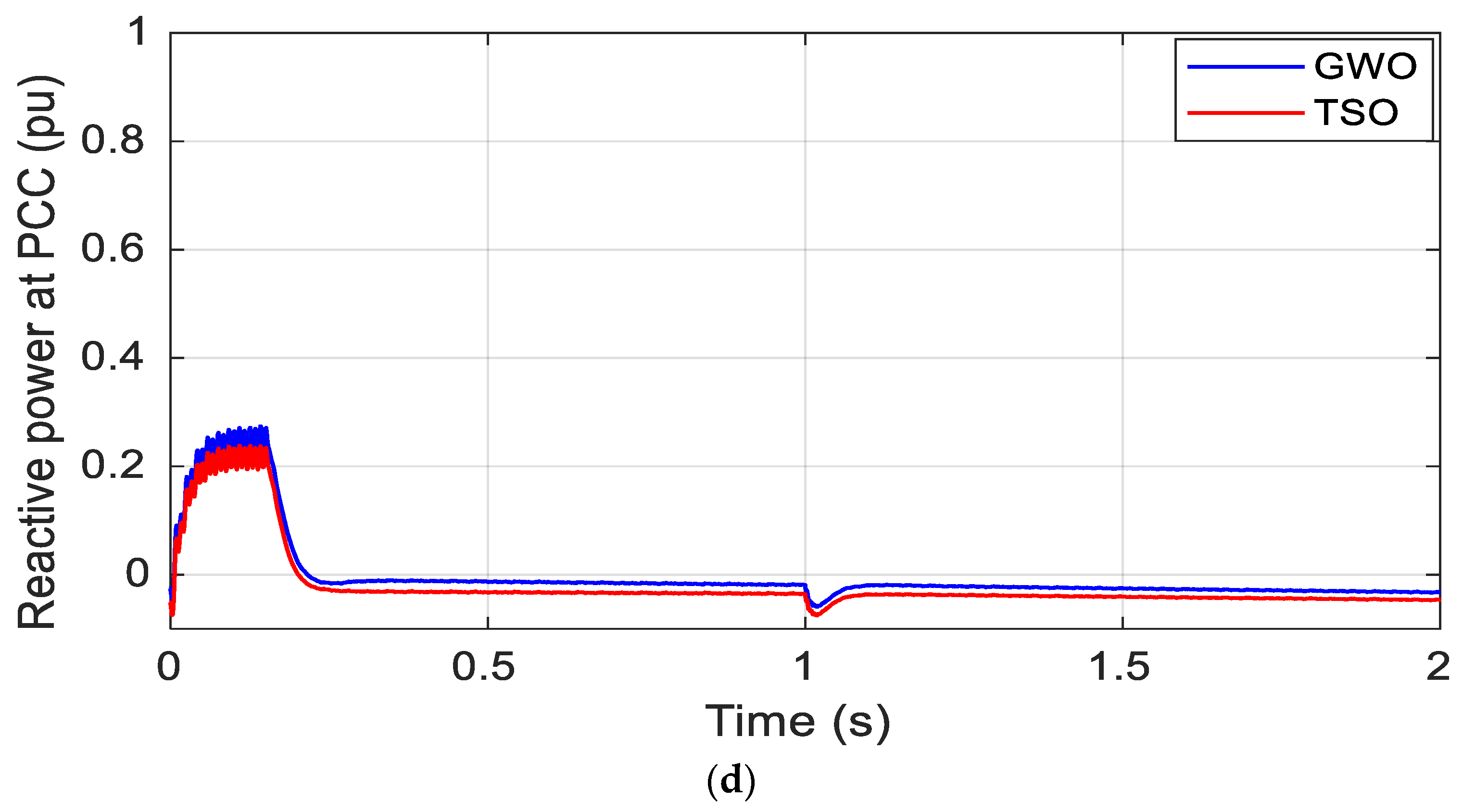
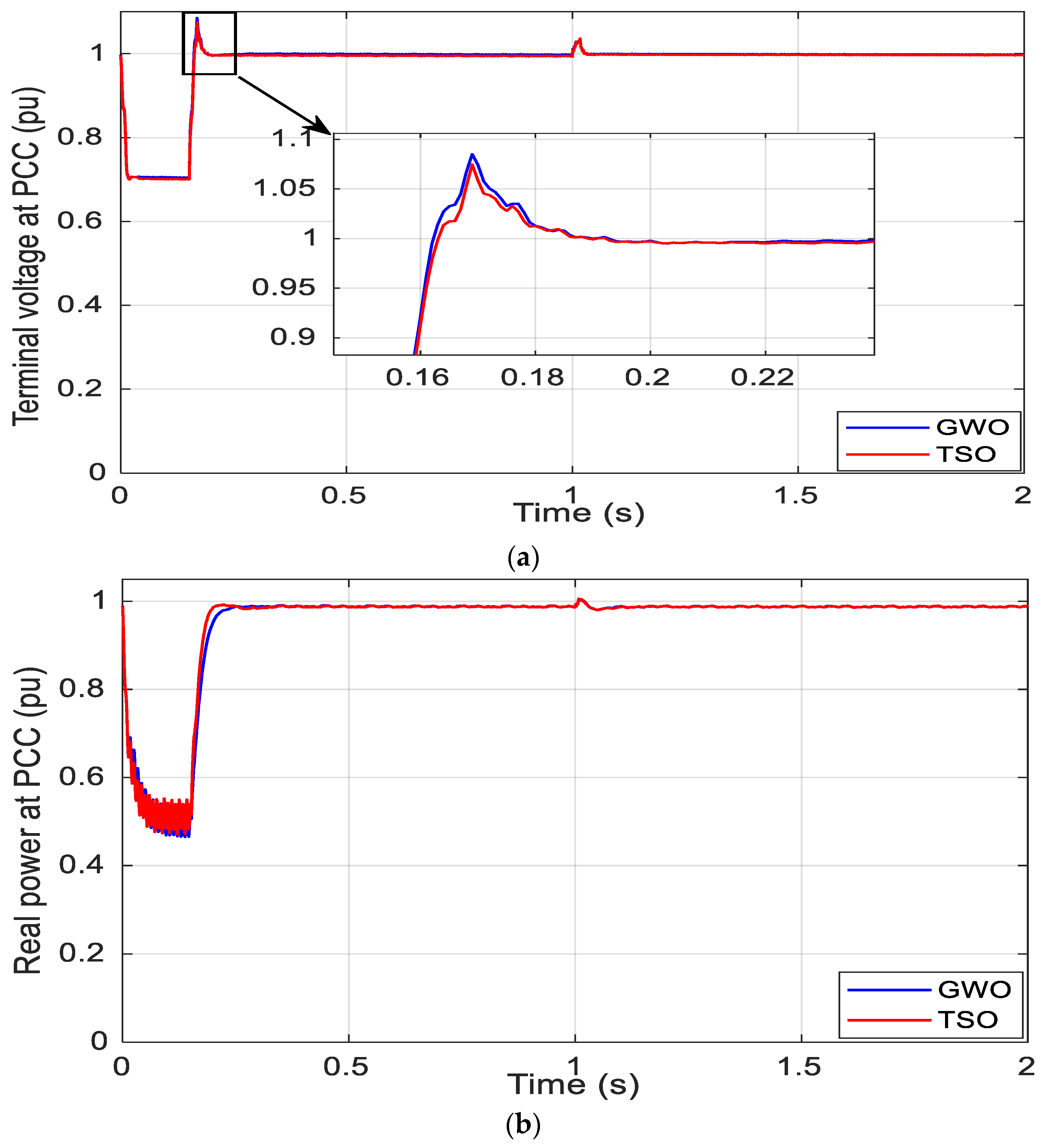
5. Results and Discussion
5.1. Optimization Results
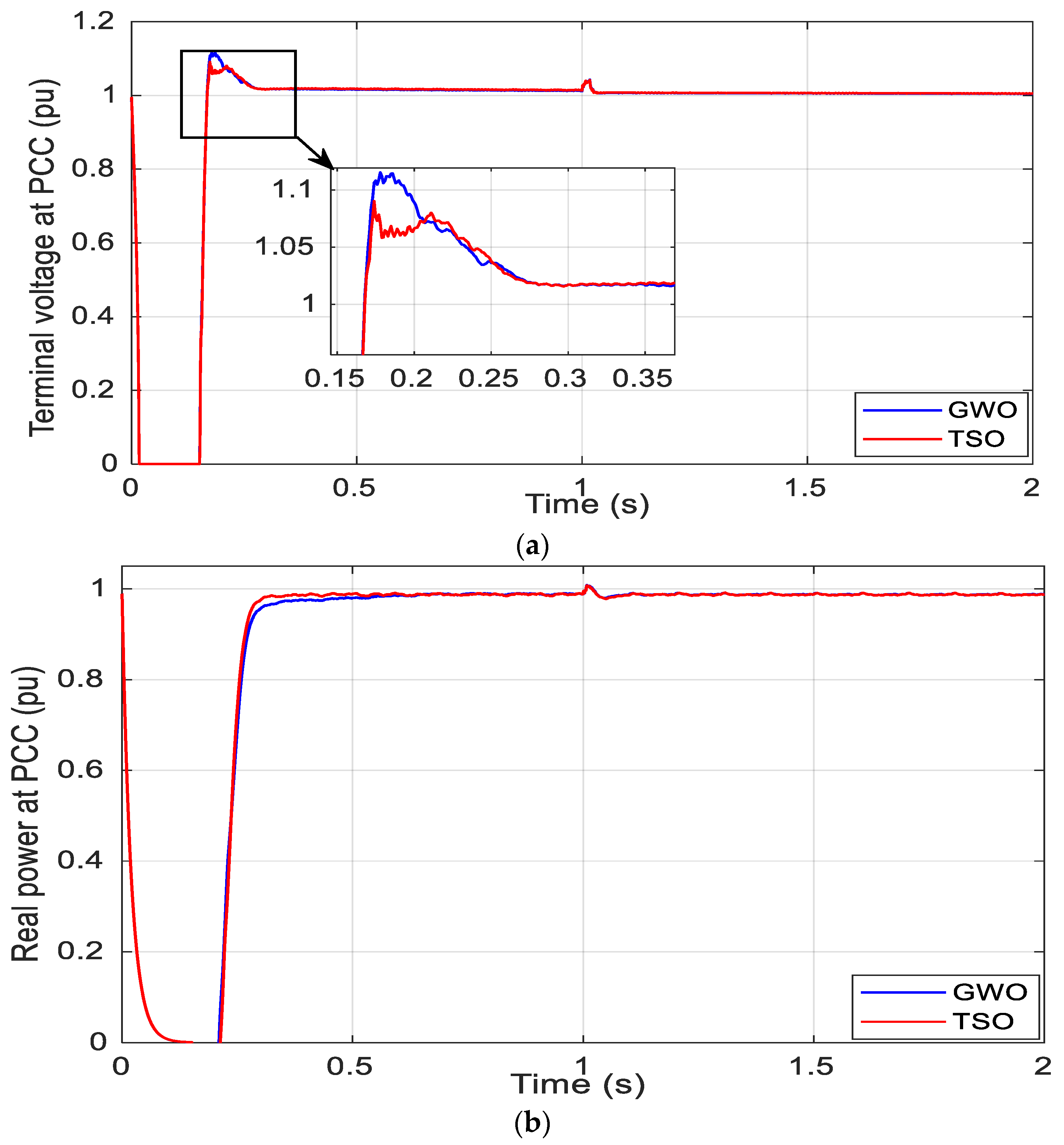
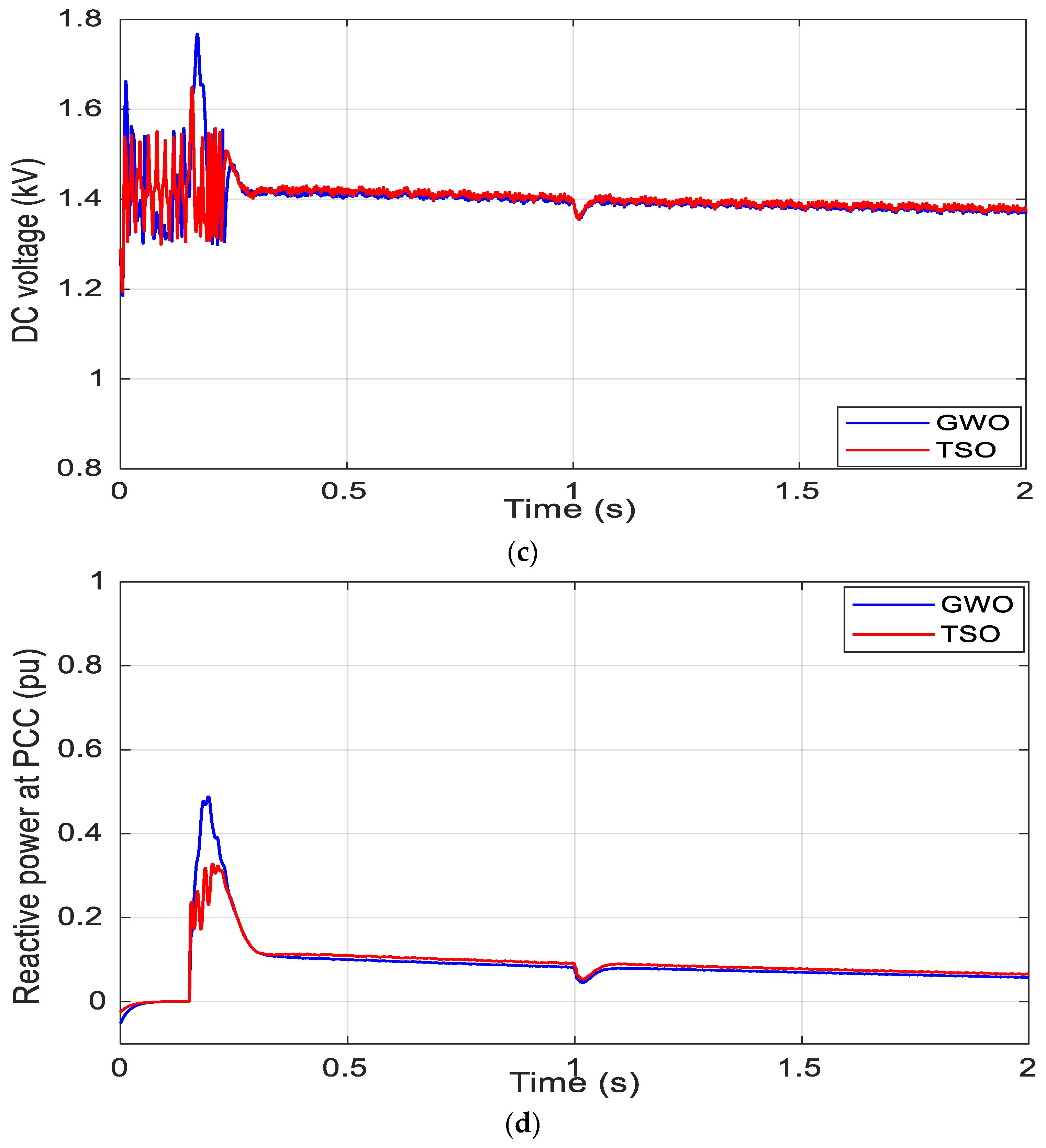
5.2. Simulation Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| WT | |||
| Diameter | 92 m | ||
| PMSG ratings | |||
| Power | 5 MVA | Rotor poles | 150 |
| Voltage (line to line) | 690 V | Inertia time | 3 s |
| Frequency | 30 Hz | resistor | 0.01 pu |
| Xd | 0.28 pu | Xq | 0.28 pu |
| Magnetic flux | 1.04 pu | ||
| Filter | |||
| Inductor | 0.2 mH | ||
| Transformer | |||
| Low voltage | 0.69 kV | High voltage | 33 kV |
| Reactance | 0.08 pu | Frequency | 60 Hz |
References
- Kusch-Brandt, S. Urban Renewable Energy on the Upswing: A Spotlight on Renewable Energy in Cities in REN21’s “Renewables 2019 Global Status Report”. Resources 2019, 8, 139. [Google Scholar] [CrossRef] [Green Version]
- IRENA. Renewable Power Generation Costs in 2017. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2018/Jan/IRENA_2017_Power_Costs_2018.pdf (accessed on 11 November 2018).
- Global Wind Energy Council (GWEC). Global Wind Report Annual Market Update 2019. Available online: https://gwec.net/global-wind-report-2019 (accessed on 12 September 2020).
- Atherton, J.; Sharma, R.; Salgado, J. Techno-economic analysis of energy storage systems for application in wind farms. Energy 2017, 135, 540–552. [Google Scholar] [CrossRef] [Green Version]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Hur, S.-H. Modelling and control of a wind turbine and farm. Energy 2018, 156, 360–370. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Output power smoothing of grid-connected permanent-magnet synchronous generator driven directly by variable speed wind turbine: A review. J. Eng. 2017, 2017, 1755–1759. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Low voltage ride-through capability enhancement of grid-connected permanent magnet synchronous generator driven directly by variable speed wind turbine: A review. J. Eng. 2017, 2017, 1750–1754. [Google Scholar] [CrossRef]
- Mohseni, M.; Islam, S.M. Review of international grid codes for wind power integration: Diversity, technology and a case for global standard. Renew. Sustain. Energy Rev. 2012, 16, 3876–3890. [Google Scholar] [CrossRef]
- Hasanien, H.M. An Adaptive Control Strategy for Low Voltage Ride Through Capability Enhancement of Grid-Connected Photovoltaic Power Plants. IEEE Trans. Power Syst. 2015, 31, 3230–3237. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Output power smoothing of wind power plants using self-tuned controlled SMES units. Electr. Power Syst. Res. 2020, 178, 106056. [Google Scholar] [CrossRef]
- Kayk, M.; Milanovic, J.V. Reactive Power Control Strategies for DFIG-Based Plants. IEEE Trans. Energy Convers. 2007, 22, 389–396. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. A novel LMSRE-based adaptive PI control scheme for grid-integrated PMSG-based variable-speed wind turbine. Int. J. Electr. Power Energy Syst. 2021, 125, 106505. [Google Scholar] [CrossRef]
- Soliman, M.A.; Hasanien, H.M.; Al-Durra, A.; Alsaidan, I. A Novel Adaptive Control Method for Performance Enhancement of Grid-Connected Variable-Speed Wind Generators. IEEE Access 2020, 8, 82617–82629. [Google Scholar] [CrossRef]
- Qais, M.; Hasanien, H.M.; Alghuwainem, S. Salp swarm algorithm-based TS-FLCs for MPPT and fault ride-through capability enhancement of wind generators. ISA Trans. 2020, 101, 211–224. [Google Scholar] [CrossRef] [PubMed]
- Hasanien, H.M.; Muyeen, S. Speed control of grid-connected switched reluctance generator driven by variable speed wind turbine using adaptive neural network controller. Electr. Power Syst. Res. 2012, 84, 206–213. [Google Scholar] [CrossRef] [Green Version]
- Ribrant, J.; Bertling, L. Survey of failures in wind power systems with focus on Swedish wind power plants during 1997–2005. 2007 IEEE Power Eng. Soc. Gen. Meet. 2007, 22, 1–8. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Augmented grey wolf optimizer for grid-connected PMSG-based wind energy conversion systems. Appl. Soft Comput. 2018, 69, 504–515. [Google Scholar] [CrossRef]
- Soliman, M.; Hasanien, H.; Al-Durra, A.; Debouza, M. High Performance Frequency Converter Controlled Variable-Speed Wind Generator Using Linear-Quadratic Regulator Controller. IEEE Trans. Ind. Appl. 2020, 56, 1. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Whale optimization algorithm-based Sugeno fuzzy logic controller for fault ride-through improvement of grid-connected variable speed wind generators. Eng. Appl. Artif. Intell. 2020, 87, 103328. [Google Scholar] [CrossRef]
- Soliman, M.A.; Hasanien, H.M.; Azazi, H.Z.; El-Kholy, E.E.; Mahmoud, S.A. Hybrid ANFIS-GA-based control scheme for performance enhancement of a grid-connected wind generator. IET Renew. Power Gener. 2018, 12, 832–843. [Google Scholar] [CrossRef]
- Hasanien, H.M.; Muyeen, S.M. Design Optimization of Controller Parameters Used in Variable Speed Wind Energy Conversion System by Genetic Algorithms. IEEE Trans. Sustain. Energy 2012, 3, 200–208. [Google Scholar] [CrossRef]
- Hasanien, H.M.; Muyeen, S.M. A Taguchi Approach for Optimum Design of Proportional-Integral Controllers in Cascaded Control Scheme. IEEE Trans. Power Syst. 2012, 28, 1636–1644. [Google Scholar] [CrossRef] [Green Version]
- Hasanien, H.M.; Matar, M. Water cycle algorithm-based optimal control strategy for efficient operation of an autonomous microgrid. IET Gener. Transm. Distrib. 2018, 12, 5739–5746. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. A Grey Wolf Optimizer for Optimum Parameters of Multiple PI Controllers of a Grid-Connected PMSG Driven by Variable Speed Wind Turbine. IEEE Access 2018, 6, 44120–44128. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Enhanced whale optimization algorithm for maximum power point tracking of variable-speed wind generators. Appl. Soft Comput. 2020, 86, 105937. [Google Scholar] [CrossRef]
- Soliman, M.A.; Hasanien, H.M.; Alghuwainem, S.; Al-Durra, A. Symbiotic organisms search algorithm-based optimal control strategy for efficient operation of variable-speed wind generators. IET Renew. Power Gener. 2019, 13, 2684–2692. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Enhanced salp swarm algorithm: Application to variable speed wind generators. Eng. Appl. Artif. Intell. 2019, 80, 82–96. [Google Scholar] [CrossRef]
- Mahmoud, H.Y.; Hasanien, H.M.; Besheer, A.H.; Abdelaziz, A.Y. Hybrid cuckoo search algorithm and grey wolf optimiser-based optimal control strategy for performance enhancement of HVDC-based offshore wind farms. IET Gener. Transm. Distrib. 2020, 14, 1902–1911. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Transient search optimization: A new meta-heuristic optimization algorithm. Appl. Intell. 2020, 50, 3926–3941. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Transient search optimization for electrical parameters estimation of photovoltaic module based on datasheet values. Energy Convers. Manag. 2020, 214, 112904. [Google Scholar] [CrossRef]
- M. H. R. Center, “PSCAD/EMTDC Software.” Manitoba, Canada. Available online: https://www.pscad.com/software/pscad/overview (accessed on 24 June 2020).
- Hazari, R.; Mannan, M.A.; Muyeen, S.; Umemura, A.; Takahashi, R.; Tamura, J. Stability Augmentation of a Grid-Connected Wind Farm by Fuzzy-Logic-Controlled DFIG-Based Wind Turbines. Appl. Sci. 2017, 8, 20. [Google Scholar] [CrossRef] [Green Version]
- Yaramasu, V.; Kouro, S.; Dekka, A.; Alepuz, S.; Rodriguez, J.; Duran, M. Power Conversion and Predictive Control of Wind Energy Conversion Systems; Springer: Singapore, Singapore, 2019; pp. 113–139. [Google Scholar]
- Vittal, V.; Ayyanar, R. Grid Integration and Dynamic Impact of Wind Energy; Springer: New York, NY, USA, 2013; pp. 115–144. [Google Scholar]
- Wu, B.; Lang, Y.; Zargari, N.; Kouro, S. Power conversion and control of wind energy systems, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]






| Algorithm | Parameters of Algorithms |
|---|---|
| TSO | Lmax = 1000, k = 1, a ϵ [2, 0], dimensions = 16, no. of population = 10 |
| GWO | Lmax = 1000, a ϵ [2, 0], dimensions = 16, no. of population = 10 |
| PI1 | PI2 | PI3 | PI4 | |||||
|---|---|---|---|---|---|---|---|---|
| kp | Ti | kp | Ti | kp | Ti | kp | Ti | |
| TSO | 2.014644 | 0.017984 | 1.011208 | 0.017122 | 5.038511 | 0.998511 | 1.012340 | 0.020618 |
| GWO | 2.028126 | 0.020285 | 1.109651 | 0.214817 | 1.624001 | 0.416161 | 0.667845 | 0.186149 |
| PI5 | PI6 | PI7 | PI8 | |||||
|---|---|---|---|---|---|---|---|---|
| kp | Ti | kp | Ti | kp | Ti | kp | Ti | |
| TSO | 3.312642 | 0.064859863 | 1.032979 | 0.862991 | 6.006839 | 0.001015 | 3.755012 | 0.008518 |
| GWO | 1.188707 | 0.993525 | 0.065729 | 0.877969 | 3.181436 | 0.140109 | 2.468010 | 0.001349 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Optimal Transient Search Algorithm-Based PI Controllers for Enhancing Low Voltage Ride-Through Ability of Grid-Linked PMSG-Based Wind Turbine. Electronics 2020, 9, 1807. https://doi.org/10.3390/electronics9111807
Qais MH, Hasanien HM, Alghuwainem S. Optimal Transient Search Algorithm-Based PI Controllers for Enhancing Low Voltage Ride-Through Ability of Grid-Linked PMSG-Based Wind Turbine. Electronics. 2020; 9(11):1807. https://doi.org/10.3390/electronics9111807
Chicago/Turabian StyleQais, Mohammed H., Hany M. Hasanien, and Saad Alghuwainem. 2020. "Optimal Transient Search Algorithm-Based PI Controllers for Enhancing Low Voltage Ride-Through Ability of Grid-Linked PMSG-Based Wind Turbine" Electronics 9, no. 11: 1807. https://doi.org/10.3390/electronics9111807






