Median Filtering Using First-Order and Second-Order Neighborhood Pixels to Reduce Fixed Value Impulse Noise from Grayscale Digital Images

Abstract

It is essential to restore digital images corrupted by noise to make them more useful. Many approaches have been proposed to restore images affected by fixed value impulse noise, but they still do not perform well at high noise density. This paper presents a new method to improve the detection and removal of fixed value impulse noise from digital images. The proposed method consists of two stages. The first stage is the noise detection stage, where the difference values between the pixels and their surrounding pixels are computed to decide whether they are noisy pixels or not. The second stage is the image denoising stage. In this stage, the original intensity value of the noisy pixels is estimated using only their first-order and second-order neighborhood pixels. These neighboring orders are based on the Euclidean distance between the noisy pixel and its neighboring pixels. The proposed method was evaluated by comparing it with some of the recent methods using 50 images at 18 noise densities. The experimental results confirm that the proposed method outperforms the existing filters, excelling in noise removal capability with structure and edge information preservation.

1. Introduction

Digital images have an important role in our life [1]. Digital imaging has a wide range of applications in many research areas, such as medical sciences, biology, particle physics, geology, the science of materials, photography and remote sensing [1,2,3]. For some medical practices, digital imaging plays an important role, especially for studying physiology abnormalities and anatomy of the internal organs [4]. Countless images are made, translated and edited daily [5].

However, many images that are created have some imperfections called noise [6]. Such imperfections may be caused by the incapacity and instability of imaging systems or sensors to obtain ideal images [1], or natural disruptions in the surroundings during image processing [1,7], inadequate illumination, or sensor temperature resulting in noise, or during compression and transmission [1,7,8]. Data obtained with these noises can make the data unusable or lose confidence in them [1,9].

Noise is simply an unnecessary detail, impacting the consistency of the signals and data [10,11]. This is because noise results in alterations in images where the original values of some pixels are changed to different values [5]. One of the common types of noise is impulse noise [12]. Impulse noise frequently distorts the image during the phase of image processing and transmission [11,13]. Impulse noise can be divided into two categories, which are random value impulse noise and fixed value impulse noise [13,14,15]. Random value impulse noise is usually caused by errors in timing or synchronization of analog to digital converter [15,16], malfunctioning pixel elements in the camera sensors or faulty transmission [3,15,16,17]. The intensity values of the damaged pixels in the image by random value impulse noise ranged from the minimum value to the maximum value in the dynamic range [13,15,18,19]. On the other hand, fixed value impulse noise is usually caused by malfunctioning pixel elements in the camera sensors, faulty memory locations or errors in the digitization process [15]. The damaged pixels in the image by fixed value impulse noise take only the maximum or the minimum values in the dynamic range [12,13,15,19]. Therefore, the damaged pixels appear as black and white pixels [20,21].

Impulse noise significantly impacts the processing and analysis of digital images, such as image segmentation, object recognition, object tracking and edge detection [22,23]. Thus, it is important to eliminate the impulse noise from the image before proceeding with any subsequent processing [11,23,24]. Effective impulse noise removal is therefore highly needed.

Median filter and mean filter have initially been proposed to eliminate the impulse noise [22]. Both filters have a simple process, but the mean filter was found not able to maintain image structure and edge details, while the median filter gave better results. Other classic filters are Kuwahara and Nagao filters; unlike mean and median filters, these filters are more complicated because they divide the window into groups, and the mean value of the most homogeneous group, based on the lowest standard deviation, is the new value of the pixel to be restored [25,26,27,28]. Besides the complexity, they have two main drawbacks. One is the block structure of the output, particularly evident in textured areas. The second one is that every time the minimum value of the standard deviation is reached by more than one subregion, the output of the filter operators cannot be uniquely determined [29].

However, the median filter still has several limitations, especially for removing high noise density. This is because it filters all pixels in the image, even those pixels that are not corrupted by noise [22,24]. Researchers have proposed several changes or enhancements to the Standard Median Filter (SMF) due to the limitations of the SMF filter [24,30,31]. Various advanced filters have been proposed by integrating various techniques [8]. However, the SMF drawback is that the filter is applied to all pixels in the image evenly, to the noisy pixels and noise-free pixels, which leads to original details lost. The switching median filter (SwMF) came to solve this drawback [32].

SwMF and its enhancement filters consist of two stages. The first stage is noise detection. In this stage, each pixel in the image is denoted as a noisy pixel or noise-free pixel [33]. This stage is very important, as the second stage depends on it to maintain the original details of the image and not to miss any noisy pixel for restoration. The existing impulse noise detectors may miss many noisy pixels from being detected, especially for high noise density or on white and black regions. Also, they still detect many of the noise-free pixels with extreme intensity as noisy pixels, which leads to a loss in the original details of the image [1]. From that, an enhancement of impulse noise detectors is required.

The second stage of the SwMF and its enhancement filters is the restoration of the corrupted pixels in the image. The restoration of corrupted pixels is done by estimating the original intensity value using the pixels around it. The existing restoration filters still cannot achieve high-quality restored images from corrupted images at high noise density as observed in the recent works by Chen et al. [22], Samantaray et al. [34], Chen et al. [35] and Sangave and Jain [12]. From that, an enhancement of impulse noise restoration is required.

In this paper, an enhanced SwMF method is proposed. The proposed method has two stages. The first stage is the fixed value impulse noise detection, wherein the pixels having extreme intensities in the corrupted image will be denoted as noisy pixels or noise-free pixels depending on the difference values between their intensities and the intensities of the surrounding pixels. In the second stage, the original intensity value of the noisy pixels will be estimated using the median value of the non-extreme intensity pixels of the first-order neighborhood pixels. In case all the pixels in the first-order neighborhood are having extreme intensity pixels, the median value of the non-extreme intensity pixels in the second-order neighborhood pixels will be used to estimate the original intensity of the noisy pixel.

2. Related Works

Many methods were proposed to enhance SwMF. For example, in work by Samantaray et al. [34], a variable threshold detector (VTD) was used, where the threshold value was dependent on the estimated noise density. The noise density was estimated by sliding an 11 × 11 mask over all the image regions. For each mask having a non-extreme intensity pixel at its center, the method counts the number of pixels with extreme intensity within this area. Then, the noise density was estimated by dividing this number of extreme intensity pixels by the number of the mask’s positioning over the entire image. To restore the noisy pixels, Samantaray et al. [34] proposed a neighborhood-based decision filter (NBDF), where only the first-order neighborhood (FON) pixels were used to estimate the original intensity value of the noisy pixel.

In work by Chen et al. [22], the 3σ and local statistics principal (D3PLS) distinguish the noisy pixels and the noise-free pixels in the corrupted image. For the restoration of the noisy pixels, Chen et al. [22] proposed an adaptive sequentially weighted median filter (ASWMF). The median value of the weighted noise-free pixels in a small window is used as the new value of the noisy pixels. If all the pixels in the window are noisy pixels, the window is enlarged until there is at least one noise-free pixel, or it reaches its maximum size.

In work by Chen et al. [35], a fixed threshold detector (FTD) was used, where the number of pixels having the same intensity value as the pixel to be checked in a window of size 5 × 5 determines whether the pixel is noisy or not. In the work by Chen et al. [35], iterative grouping median filter (IGMF) was proposed to restore the noisy pixels. The uncorrupted pixels within a window of size 5 × 5 pixels were arranged in ascending or descending order. They are then divided into groups as the number of edges is found by applying a threshold value between each pixel and its adjacent pixel.

In work by Sangave and Jain [12], a boundary discriminative noise detector (BDND) is used to discriminate the noisy pixels in the corrupted image. The pixels in a window of size 21 × 21 pixels were divided into two groups of equal number, after ascending sort. The two boundaries determined by the pixel intensity value had the largest difference in value with the intensity value of the next pixel to it in each group. After that, to restore the noisy pixels, Euclidean distance filter (EDF) was used, where the original intensity value of a noisy pixel was estimated by the mean value of the noise-free pixels in a window of size w × w pixels after being weighted by the Euclidean distance.

3. The Proposed Method

In this work, we aim to generate a restored image R from the image C corrupted by fixed value impulse noise. The proposed method is based on SwMF. Therefore, the proposed method consists of two stages, with the first stage being the noise detection stage, and the second stage being the image denoising stage. This is shown in Figure 1. In the noise detection stage, each pixel in the corrupted image C will be denoted as either a noisy pixel or noise-free pixel. This information will be stored in a noise mask N. Then, in the image denoising stage, those pixels denoted as noisy pixels in noise mask N will undergo the process to estimate their original intensity value. The result is the restored image R.

3.1. Noise Detection Stage

This method aims to remove fixed value impulse noise only. For this type of impulse noise, all corrupted pixels in image C have extreme intensity values (i.e., 0 or L-1), where L is the number of intensity levels of the image (e.g., for an eight-bit-per-pixel grayscale image, L is equal to 256 levels). Therefore, all pixels in image C that have non-extreme intensity values will be denoted as noise-free pixels. On the other hand, initially, all pixels in image C having extreme intensity value will be denoted as noise candidate pixels. However, some of the pixels with the extreme intensity value are not noisy pixels. As a consequence, in this work, noise candidate pixels will be further undergoing the detection stage to distinguish which of them are noisy pixels, and which ones are noise-free pixels.

As mentioned in work by Chen et al. [22], it is assumed that the intensity distribution of the uncorrupted pixels within a local window usually follows a normal distribution. This means that the intensities in the local window have a small difference in value between each other. Hence, the noise-free pixels with extreme values are normally surrounded by pixels that have the same or similar intensity values (i.e., with a small difference in value) to them. From these assumptions, the proposed detector considers that the noise candidate pixel’s intensity is significantly different from the neighboring pixels as a noisy pixel. On the other hand, if the intensity value of the noise candidate pixel is similar to its neighboring pixels, this pixel is considered as a noise-free pixel.

Based on that, two threshold values will be used to evaluate the intensity differences between the noise candidate pixel with its neighboring pixels. The first threshold value is the highest difference value (HDV), and the second threshold value is the highest mean value (HMV) of the difference values. Both HDV and HMV will be determined from a set of training images. The training image T_r is considered a clean image without noise.

HDV will be calculated by taking the intensity differences between normal extreme intensity (NEI) pixels, which are the pixels having extreme intensity value in image T_r, with all of their surrounding pixels, within a window of size 3 × 3 pixels. These difference values will be obtained from all training images that will be used in this work. As the dynamic range is from 0 to 255, the difference values will be grouped and each group will be of 10 difference values. The groups having less than 6% repetitive rate will be denoted as infrequent difference values and will be excluded. Then, the largest intensity difference that is obtained after excluding the infrequent values will be the HDV.

On the other hand, HMV will be calculated by taking the mean values of the difference values between each NEI in image T_r and its surrounding pixels within a window of size 3 × 3 for all original images. The infrequent mean values will be excluded. The mean values having less than 2% will be denoted as infrequent mean values and will be excluded. The highest mean value after excluding the infrequent values will be the HMV.

Based on that, the proposed detector denotes noise candidate pixels on an image as noisy pixels or noise-free pixels depending on either of those two threshold values. First, the difference value between the intensity value of the pixel will be checked with the intensity values of the pixels surrounding that pixel, as these difference values will be compared with HDV. Second, the mean value of all the difference values between the noise candidate pixel and its surrounding pixels, as this value, will be compared with HMV.

After that, each noise candidate pixel will be compared with all non-extreme intensity pixels surrounding it in a window of size 3 × 3 pixels. If any difference value is bigger than HDV, the noise candidate pixel will be denoted as a noisy pixel. Otherwise, the mean value of all the difference values will be computed. The difference value between noise candidate pixels and extreme intensity pixels will be constant. For the opposite extreme intensity pixels than the noise candidate pixel, the difference will be equal to the HDV value. For the pixels having the same extreme intensity value as the noise candidate pixel, the difference will equal to 0. If the mean value of the difference values is bigger than HMV, the noise candidate pixel will be denoted as a noisy pixel, otherwise as a noise-free pixel.

If all the pixels surrounding the noise candidate pixel have extreme-intensity values, the fixed threshold detector will be used. For the fixed threshold detector, a window of size 5 × 5 pixels and a threshold of 21 will be used, as recommended in the work by Chen et al. [22]. The number of pixels having the same intensity as the noise candidate pixel will be counted in a window of size 5 × 5 pixels. If the number counted is bigger than the threshold, the noise candidate pixel will be denoted as a noise-free pixel, otherwise as a noisy pixel.

The following eight steps are presented to summarize the procedure:

Step 1:

Initialize all pixels as noise-free pixels by making all elements in matrix N equal to 0.

Step 2:

Denote all pixels having extreme intensity value as noise candidate pixel P_NC.

$$P_{NC}(x,y)=\{\begin{array}{cc}1& C(x,y)=0\mathrm{or}C(x,y)=255\\ 0& \mathrm{otherwise}\end{array}$$

(1)

where (x,y) are the spatial coordinates, and C(x,y) is the intensity value of the corrupted image at coordinates (x,y). P_NC(x,y) equal to 1 is used to indicate that the pixel is a noise candidate pixel, whereas P_NC(x,y) equal to 0 is used to indicate that the pixel is noise-free.

Step 3:

For each P_NC(x,y) equal to 1, compute the intensity difference values between this pixel with each of its neighboring pixels within a 3 × 3 window, with coordinates (x,y) at the center of that window. These difference values are stored in vector D.

$$D(i)=|C(x,y)-C(x+a_i,y+b_i)|\begin{array}{cc}& \end{array}0\le i\le 7$$

(2)

with vector a = {−1,0,1,1,1,0,−1,−1} and vector b = {−1,−1,−1,0,1,1,1,0}.

Step 4:

If all the neighboring pixels have the same intensity with the center pixel, which is ${\displaystyle \sum _{i}D(i)=0}$, go to Step 6. Otherwise, compare all values in D with HDV value. If any value in D is bigger than HDV, the pixel at these coordinates is denoted as a noisy pixel. Thus, N(x,y) is given the value 1 and go to Step 8. Otherwise, go to Step 5.

Step 5:

Replace any element in D which is equal to 255 with HDV value. Then, compute the mean value of the elements in the updated D. If the mean value is greater than HMV, P_NC is denoted as a noisy pixel (i.e., N(x,y) = 1), otherwise as a noise-free pixel (i.e, N(x,y) = 0), then go to Step 8.

Step 6:

Count the number of pixels that have the same intensity as P_NC(x,y) within a window of size 5 × 5 pixels, with coordinates (x,y) at the center of the window. Save this count as Cs.

Step 7:

If Cs > 21, P_NC is denoted as a noise-free pixel (i.e., N(x,y) = 0), otherwise as a noisy pixel (i.e., N(x,y) = 1), then go to Step 8.

Step 8:

Repeat the steps from Step 3 to Step 8 for all P_NC.

3.2. Image Denoising Stage

The proposed image denoising stage is based on the work by Samantaray et al. [34], where only FON pixels are used to estimate the original intensity value of the noisy pixel, as they are more correlated to the noisy pixel than the others. In the work by Samantaray et al. [34], as some pixels left with an extreme intensity value in case of all FON pixels have extreme intensity values, the process of restoration needed to be repeated to ensure that all noisy pixels have been restored. Some pixels have extreme intensity values that remain in the second round to be restored. In the second round, the FON pixels may already be restored depending on the second-order neighborhood (SON) and third-order neighborhood (TON) pixels. This means, in the second round, the process depends on SON and TON to estimate the original intensity value of the noisy pixel. Figure 2 shows the positions of FON, SON and TON pixels in relation to the noisy pixel P_N (i.e., the pixel with N(x,y) = 1). These neighboring orders are based on the Euclidean distance between the noisy pixel and its neighboring pixels.

However, the SON pixels are more correlated to the central pixel than the TON pixels [22]. Based on that, an enhancement is proposed to the work by Samantaray et al. [34], where the SON pixels are used to estimate the original intensity value of the noisy pixels in the case of all the FON pixels having extreme intensity values. Thereafter, if all FON and SON pixels have extreme intensities, the pixel to be restored will either have an extreme intensity as the new intensity value or it should be left unchanged.

The proposed method replaces the intensity value of the noisy pixel by the median value of the non-extreme intensity FON pixel intensities. The intensity value of the noisy pixel is replaced by the median value of the non-extreme intensity SON pixel intensities if all the FON pixels have extreme intensities. If all the FON and SON pixels have extreme intensities and the number of the opposite extreme intensity value pixels is bigger than 6, the new value of the corrupted pixel will be the opposite extreme intensity; otherwise, it will be left with no change.

To summarize, the steps are as follows:

Step 1:

Locate the noisy pixel P_N (i.e., the pixel with N(x,y) = 1).

Step 2:

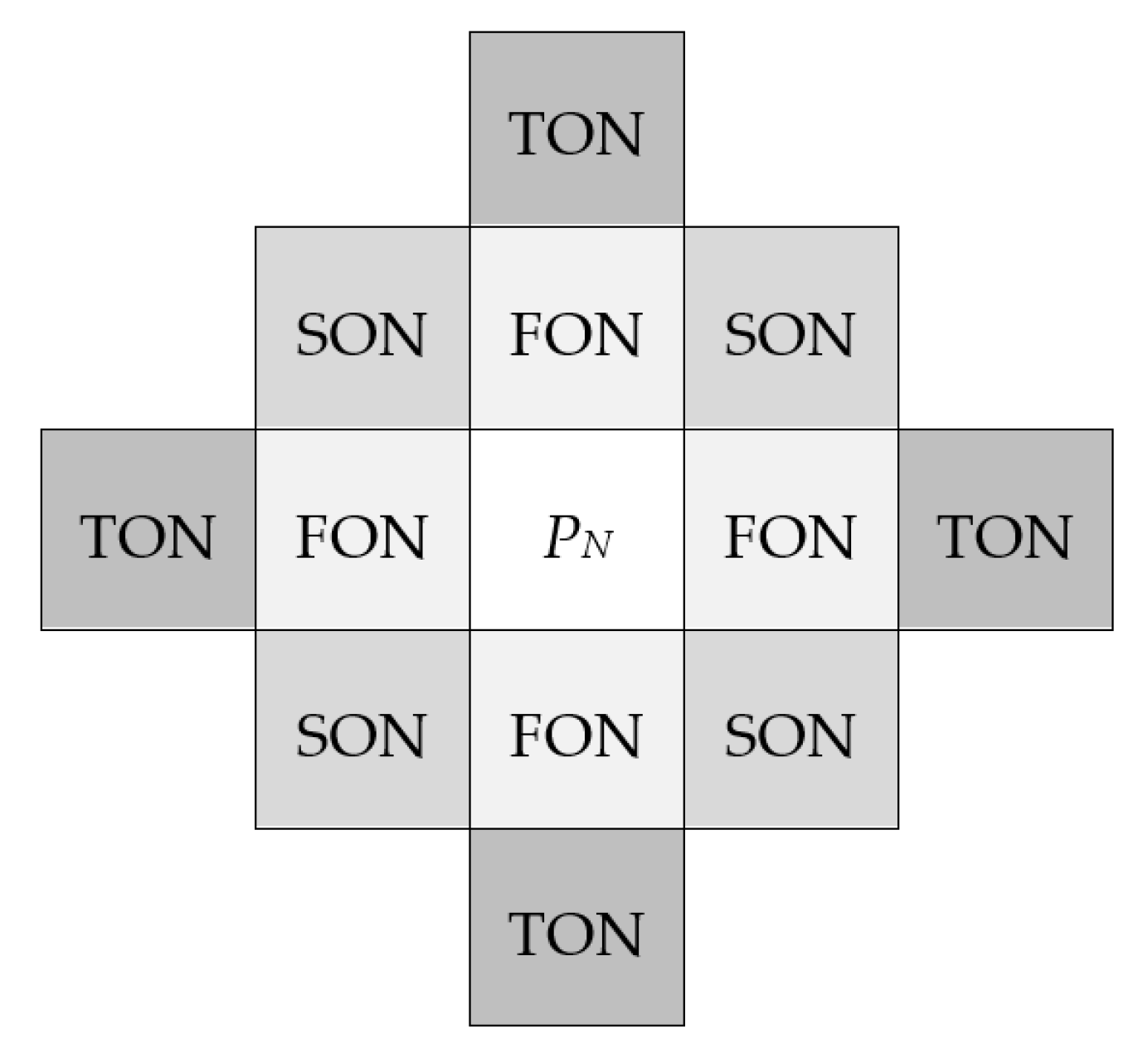
Check the pixels surrounding P_N in a window of size 3 × 3 with P_N at the center of the window. If all pixels in the window have extreme intensities go to Step 4. Otherwise, go to Step 3.

Step 3:

If all FON pixels have extreme intensities, the median value of SON pixels will be the new intensity value of P_N. Otherwise, the median value of FON will be the new value of P_N. Then go to Step 6.

Step 4:

Count the number of the pixels having the opposite extreme intensity of P_N, which is C_o. Then go to Step 5.

Step 5:

If C_o greater than 6, the new value of P_N will be the opposite extreme value of it. Otherwise, leave it with no change. Then move to Step 6.

Step 6:

Repeat all steps for all noisy pixels in the image (i.e., the pixels with N(x,y) = 1).

4. Results and Discussions

To evaluate the results of the proposed noise detector and the mentioned detectors above, the missing detection rate (MDR), and the false detection rate (FDR) were used. Equations (3) and (4) show the mathematical expression for the MDR and the FDR, respectively [22].

$$\mathrm{MDR}=\frac{{\displaystyle {\sum }_{p\in f}\left(R_r(p)=0\wedge R_d(p)=1\right)}}{{\displaystyle {\sum }_{p\in f}{R}_r(p)}}\times 100\%$$

(3)

$$\mathrm{FDR}=\frac{{\displaystyle {\sum }_{p\in f}\left(R_r(p)=1\wedge R_d(p)=0\right)}}{{\displaystyle {\sum }_{p\in f}{R}_r(p)}}\times 100\%$$

(4)

where f is the image matrix, R_r is the matrix for indicating noises added by Matlab 2018a, which indicates a noisy pixel with R_r(p) = 0, or noise-free with R_r(p) = 1; R_d is the matrix for indicating the detected noises, which indicates a noisy pixel with R_d(p) = 0, or noise-free with R_d(p) = 1; symbol ˄ refer to logical AND.

MDR calculates the ratio of noisy pixels that the detector did not detect to the total number of noisy pixels in the corrupted image. Therefore, the lower the MDR ratio the better detecting capability. FDR calculates the ratio of noise-free pixels that the detector detects as noisy pixels to the total number of noisy pixels in the corrupted image. Therefore, the lower the FDR ratio, the better at not detecting false pixels.

However, to evaluate the image denoising stage of the proposed method and the methods mentioned above, the peak signal to noise ratio (PSNR) and structural similarity index (SSIM) are used. Equations (5) and (6) show the PSNR and SSIM mathematical expressions [22].

$$\mathrm{PSNR}=10{\log }_{10}\frac{m\times n\times {255}^2}{{\displaystyle {\sum }_{i=1}^m{\displaystyle {\sum }_{j=1}^n{\left(f(i,j)-g(i,j)\right)}^2}}}$$

(5)

$$\mathrm{SSIM}=\frac{(2{\mu }_f{\mu }_g+C_1)\left(2{\sigma }_{fg}+C_2\right)}{\left({\mu }_f^2+{\mu }_g^2+C_1\right)\left({\sigma }_f^2+{\sigma }_g^2+C_2\right)},\begin{array}{cc}& \end{array}{C}_1={(K_{1}L)}^2,C_2={(K_{2}L)}^2$$

(6)

where, f is the original image and g is the restored image; m is the height of the image and n is the width of the image, σ_f is the standard deviation of f and µ_f is the mean value of f, σ_g is the standard deviation of g and µ_g is the mean value of g, σ_fg is the covariance of f and g, C₁ and C₂ are the stabilizing constants, L is the number of intensities levels in the image, K₁ and K₂ are selected by default as 0.01 and 0.03, respectively.

PSNR measures the resemblance between the original image and the restored image. Therefore, the higher the PSNR the better the restored image, which means the better the image denoiser restoring capability. SSIM measures the preservation capability of the structural information. Therefore, the higher the SSIM the better the preservation capability, which means better image denoiser structure information preservation capability.

4.1. Data Preparation

In this paper, 83 standard images will be used. These images are taken from the internet. All images are gray-scale images, with different size (i.e., 480 × 480 pixels, 512 × 512 pixels, 640 × 480 pixels, 720 × 576 pixels, and 720 × 580 pixels). These images have been selected because they are normally used in digital image processing research. Furthermore, most of them have large black or white regions on the image.

These images are divided into two groups. The first group consists of 33 images and is used as the training images T_r. These images are used to determine the values of HDV and HMV. The remaining 50 images are used as the testing images T_s. Because all images are considered noise-free images, to evaluate the performance of the methods in noise detection and image denoising, image T_s will be synthetically corrupted by fixed value impulse noise using Matlab 2018a, from noise density 5% to 90%, with increment step of 5%. Therefore, 18 noise density levels are evaluated in this work.

4.2. Calculations to Determine HDV and HMV

To calculate the value of HDV, a procedure was conducted on the 33 original uncorrupted T_r images. The procedure calculated the difference values between the NEI pixels and their surrounding pixels in a window of size 3 × 3 pixels. The results of this procedure are based on 59,122 NEI pixels found in the 33 T_r images, which means 472,976 surrounding pixels. The results of the procedure are shown in

Table 1. The ratio of the difference values NEI pixels and their surrounded pixels in window of size 3 × 3.

The Difference Values	0	1–10	11–20	21–30	31–40	41–50	51–100	101–150	151–200	201–255
Repetition rate	58.0%	14.7%	5.7%	5.9%	3.7%	2.5%	6.2%	2.2%	0.9%	0.3%

.

It can be analyzed from the results of Table 1 that NEI pixels are correlated to their surroundings. Of the surrounding pixels, 58.01% have the same intensity level as their NEI pixel and 14.7% have a difference in intensity level with their NEI between 1 to 10 intensity levels. However, it can be observed that the differences in intensity level ratio become less as the difference in intensity levels becomes higher.

The ratio of the difference value of less than 11 intensity levels between NEI pixels and their surrounding pixels in a window of size 3 × 3 pixels is equal to 72.7%. Therefore, the ratio of the difference value higher than 10 intensity levels between NEI pixels and their surrounding pixels in a window of size 3 × 3 pixels is equal to 27.3%. From this observation, the recommended HDV for the proposed method is 10 intensity levels.

To calculate the recommended value for HMV, another procedure has been conducted. The procedure was applied to these pixels surrounding NEI pixels in a window of size 3 × 3 pixels. As the recommended value for HDV is 10 intensity levels, the procedure was applied only on those pixels that had differences in intensity value from their NEI pixels that were less than 11 intensity levels.

The procedure to determine the value of HMV calculates the ratio of the mean values of the difference values between the intensity level of NEI pixels and their surrounding pixels within a window of size 3 × 3 pixels. The procedure was conducted on the same 33 images used to calculate the HDV value.

Table 2. The ratio of the mean values of the difference values between the intensity level of NEI pixels and their surrounding pixels.

Mean Value of the Differences	<1	<2	<3	<4	<5	<6	<7	<8
The ratio	83.4%	91.9%	95.5%	96.9%	98.1%	99.3%	99.9%	100%

shows the results of the procedure.

As shown in Table 2, it can be observed that most of the pixels surrounding the NEI pixels have a small difference in intensity level. The other differences may exist as they are on the border of an edge. The ratio for mean values less than three is equal to 95.5%. The ratio for mean values greater than three is increased slightly. Based on that, the recommended HMV value is 3.

4.3. Noise Detection Stage Evaluation

The proposed fixed value impulse noise detector and some of the recent detectors were applied to the 50 images from testing set T_s, after adding noise to them. The detectors applied to images at each noise density from 5% to 90% with a gap difference of 5%. The MDR and FDR have been taken for each detector at each noise density. The average of MDR and FDR have been taken for all images at each noise density.

Table 3. The results of the noise detection stage.

ND	VTD [33]		FTD [34]		BDND [12]		D3PLS [22]		Proposed
	MDR	FDR	MDR	FDR	MDR	FDR	MDR	FDR	MDR	FDR
5	0.00	3.69	0.00	3.67	0.00	3.80	0.39	3.23	0.13	2.65
10	0.00	1.84	0.00	1.81	0.00	1.89	0.41	1.57	0.13	1.30
15	0.00	1.23	0.00	1.19	0.00	1.21	0.40	1.01	0.13	0.85
20	0.00	0.81	0.00	0.88	0.00	0.88	0.39	0.75	0.13	0.63
25	0.00	0.63	0.00	0.69	0.00	0.69	0.40	0.58	0.14	0.50
30	0.00	0.53	0.00	0.57	0.00	0.56	0.39	0.47	0.14	0.42
35	0.01	0.44	0.00	0.48	0.00	0.46	0.39	0.39	0.14	0.36
40	0.14	0.31	0.00	0.41	0.00	0.39	0.39	0.33	0.15	0.31
45	0.27	0.28	0.00	0.36	0.00	0.34	0.39	0.28	0.16	0.27
50	0.47	0.25	0.00	0.32	0.00	0.29	0.39	0.25	0.16	0.24
55	2.41	0.16	0.00	0.28	0.00	0.26	0.39	0.22	0.17	0.22
60	5.91	0.14	0.00	0.25	0.00	0.23	0.39	0.19	0.17	0.19
65	8.15	0.13	0.00	0.23	0.00	0.20	0.38	0.17	0.18	0.17
70	10.74	0.11	0.00	0.20	0.00	0.18	0.37	0.15	0.18	0.16
75	35.03	0.06	0.00	0.18	0.00	0.16	0.37	0.14	0.19	0.15
80	40.76	0.06	0.00	0.16	0.01	0.14	0.45	0.12	0.19	0.14
85	46.55	0.05	0.00	0.15	0.15	0.13	1.24	0.10	0.18	0.13
90	52.45	0.05	0.02	0.13	2.36	0.11	6.50	0.08	0.16	0.12
AVG	11.30	0.60	0.00	0.67	0.14	0.66	0.78	0.56	0.16	0.49
AVG MDR + FDR	11.87		0.67		0.81		1.34		0.65

shows the results of the noise detection stage, where ND refers to noise density and AVG refers to the average.

From Table 3, it can be observed that FTD has the best results for MDR, which means its miss-detection of noisy pixels is the lowest. Yet, FTD has the highest FDR, which means it detects noise-free pixels as noisy pixels more than the other methods.

The proposed method has the best result for FDR. This means that the proposed method has the lowest false noise detection ratio. Besides, the proposed method also performs well in terms of MDR, where the average MDR is still less than 1%. Furthermore, the proposed method also gives the lowest value when we add the average MDR with the average FDR, showing that the proposed method is the best noise detector amongst the evaluated methods in this work.

4.4. Image Denoising Stage Evaluation

To evaluate the noise cancelation stage, the proposed method and the recent methods we applied to the 50 T_s images, after adding noise to them. The methods applied to images at each noise density from 5% to 90% with a gap difference of 5%. The PSNR and SSIM are used to evaluate each method at each noise density for all images. The average PSNR and the average SSIM have been taken for all images at each noise density for each method. The same fixed value impulse noise detector is used for methods. The detector used is FTD with threshold of 21.

Table 4. The results of the noise cancelation stage.

ND	IGMF [34]		EDF [12]		ASWMF [22]		NBMF [33]		Proposed
	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
5	39.67	0.990	34.86	0.954	42.90	0.993	43.41	0.994	43.76	0.994
10	37.02	0.980	30.21	0.854	39.96	0.987	40.43	0.988	40.66	0.988
15	35.30	0.971	26.71	0.732	38.07	0.980	38.53	0.982	38.66	0.982
20	34.06	0.961	23.95	0.617	36.59	0.973	37.04	0.975	37.12	0.975
25	32.99	0.950	21.67	0.520	35.36	0.965	35.77	0.967	35.87	0.968
30	32.11	0.940	19.72	0.438	34.28	0.956	34.70	0.959	34.75	0.959
35	31.35	0.927	18.06	0.371	33.33	0.947	33.78	0.950	33.76	0.950
40	30.63	0.915	16.59	0.316	32.50	0.936	32.90	0.940	32.89	0.939
45	29.98	0.902	15.31	0.271	31.71	0.924	32.09	0.928	32.03	0.928
50	29.33	0.888	14.13	0.232	30.96	0.911	31.31	0.916	31.27	0.915
55	28.71	0.872	13.08	0.200	30.24	0.897	30.57	0.902	30.51	0.901
60	28.11	0.855	12.15	0.172	29.56	0.882	29.85	0.887	29.80	0.886
65	27.52	0.836	11.29	0.148	28.86	0.864	29.10	0.869	29.07	0.868
70	26.90	0.815	10.52	0.126	28.16	0.845	28.33	0.849	28.32	0.848
75	26.21	0.791	9.74	0.105	27.38	0.821	27.51	0.824	27.57	0.825
80	25.50	0.762	9.02	0.085	26.55	0.793	26.63	0.795	26.72	0.797
85	24.71	0.726	8.35	0.067	25.57	0.756	25.60	0.757	25.75	0.760
90	23.77	0.682	7.76	0.051	24.36	0.705	24.37	0.705	24.50	0.709
AVG	30.22	0.876	16.84	0.348	32.02	0.896	32.33	0.899	32.39	0.700

shows the results of the experiment, where, ND refers to noise density and AVG refers to the average.

It can be observed from Table 4, that the EDF method has the worst results in this experiment for both PSNR and SSIM. On the other hand, the proposed method has the best PSNR and SSIM results in the average of all densities in this experiment. This means that the proposed method has the best restoring and structure information preservation capability.

4.5. State-of-Art Evaluation

To evaluate the state-of-art of the proposed method, an experiment was conducted. The proposed method is evaluated by comparing it with some of the recent state-of-art methods. PSNR and SSIM will be used to evaluate the output images for each state-of-art at each noise density from 5% to 90% with 5% as a gap difference between those noise densities, using 50 T_s images.

Table 5. The results of the state-of-art experiment.

ND	IGMF + FTD		EDF + BDND		ASWMF + D3PLS		NBMF + VTD		Proposed
	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
5	39.67	0.990	34.91	0.954	42.83	0.993	43.64	0.994	43.85	0.994
10	37.02	0.980	30.21	0.855	39.95	0.987	40.61	0.989	40.86	0.989
15	35.30	0.971	26.70	0.731	38.05	0.980	38.73	0.983	38.86	0.983
20	34.06	0.961	23.93	0.617	36.56	0.973	37.22	0.976	37.29	0.976
25	32.99	0.950	21.67	0.519	35.34	0.965	36.00	0.969	36.05	0.969
30	32.11	0.940	19.73	0.438	34.30	0.956	34.91	0.960	34.98	0.960
35	31.35	0.928	18.06	0.371	33.33	0.946	33.97	0.951	33.96	0.951
40	30.63	0.915	16.60	0.316	32.47	0.936	33.10	0.941	33.09	0.941
45	29.98	0.902	15.31	0.271	31.68	0.924	32.28	0.930	32.23	0.930
50	29.33	0.888	14.14	0.233	30.95	0.911	31.53	0.918	31.47	0.918
55	28.71	0.872	13.10	0.200	30.22	0.898	30.76	0.905	30.72	0.904
60	28.11	0.856	12.16	0.172	29.53	0.882	30.03	0.890	29.99	0.889
65	27.52	0.837	11.28	0.147	28.87	0.864	29.27	0.872	29.25	0.872
70	26.90	0.815	10.50	0.126	28.13	0.844	28.48	0.851	28.48	0.852
75	26.21	0.791	9.74	0.105	27.37	0.821	27.62	0.826	27.73	0.829
80	25.50	0.762	9.03	0.086	26.56	0.793	26.76	0.797	26.89	0.801
85	24.71	0.726	8.36	0.067	25.57	0.756	25.73	0.758	25.91	0.765
90	23.77	0.682	7.77	0.051	24.34	0.704	24.42	0.705	24.63	0.714
AVG	30.22	0.876	16.84	0.348	32.00	0.896	32.50	0.901	32.57	0.902

shows the average results for all images at each noise density, where, ND refers to noise density and AVG refers to the average.

From Table 5, it can be observed that the state-of-art consists of EDF as a denoiser, and BDND as a noise detector has the worst results in both PSNR and SSIM. On the other hand, the state-of-art consists of the proposed detector, and the proposed denoiser has the best results in both PSNR and SSIM. This means, the proposed method is better than the other methods mentioned in this work.

Figure 3, Figure 4 and Figure 5 show noisy images and their restored images. The noisy images are affected by fixed value impulse noise at 10%, 50% and 90% noise density, respectively. Each noisy image is restored by the proposed method and some of the recent methods.

Figure 3 shows a noisy “Girl face” image by fixed value impulse noise at 10% density and its restored images by the proposed method and some of the recent methods that have been mentioned in this work. This figure presents the performance of the methods for a low corruption level. It can be observed that EDF+BDND has the worst restored image. On the other hand, the proposed method and the others have better results and they look similar. However, the PSNR of the proposed method is the highest.

Noisy “Girl” image at 50% noise density and its restored images are shown in Figure 4. This figure presents the performance of the methods for a medium corruption level. From the appearance of the restored images, it can be observed that EDF+BDND has the worst restored image. On the other hand, the other methods have a better appearance on their restored images, but the PSNR of the restored image by the proposed method is the highest.

Figure 5. presents noisy “Tulips” image along with its restored images. In this figure, the noise density added is at 90%, to present a high corruption level. It can be observed from the appearance of the restored images that EDF+BDND has a less similar output image to the original image. On the other hand, the other methods have more similarity to the original image, but the restored image by the proposed method has the highest PSNR, which means that it has the most similarity to the original image.

5. Conclusions

In this paper, a method has been proposed to restore corrupted images by fixed value impulse noise. The proposed method has two stages, the noise detection stage and the image denoising stage. In the noise detection stage, the pixels with extreme intensities are denoted as noisy or noise-free pixels depending on the difference between their intensities and the intensities of the pixels surrounding them. An experiment was conducted to evaluate the proposed detector by comparing it with some of the recent detectors used to detect the fixed value impulse noise. The results of the experiment showed that the proposed detector has the best result in the average of all outputs.

In the image denoising stage, the noisy pixels are restored by estimating their original intensities based on the first-order and second-order neighborhood pixel intensities. An experiment has been conducted to evaluate the proposed image denoiser by comparing its output images with the output of some of the recent methods used to restore the images corrupted by fixed value impulse noise. The results of the experiments show that the proposed method has better restoring and structure information preservation capability. In future works, to further improve the method’s performance, the authors will explore the possibilities of using inpainting approaches in the image-denoising stage. The inpainting methods have been used in noise reduction works, such as Zhou et al. [36] and Zhou et al. [37].