High-Throughput Measurement of the Contact Resistance of Metal Electrode Materials and Uncertainty Estimation

Abstract

Low and stable contact resistance of metal electrode materials is mainly demanded for reliable and long lifetime electrical engineering. A novel test rig is developed in order to realize the high-throughput measurement of the contact resistance with the adjustable mechanical load force and load current. The contact potential drop is extracted accurately based on the proposed periodical current chopping (PCC) method in addition to the sliding window average filtering algorithm. The instrument is calibrated by standard resistors of 1 mΩ, 10 mΩ, and 100 mΩ with the accuracy of 0.01% and the associated measurement uncertainty is evaluated systematically. Furthermore, the contact resistance between standard indenter and rivet specimen is measured by the commercial DMM-based instruments and our designed test rig for comparison. The variations in relative expanded uncertainty of the measured contact resistance as a function of various mechanical load force and load current are presented.

1. Introduction

Metal electrode materials are widely used in the electrical and electronic engineering for conducting and/or switching current, such as connectors [1], electromechanical devices [2], thin-film devices [3], microelectromechanical system [4], and switchgear [5], etc. The roughness of the material surfaces causes only small peaks or asperities within the apparent surface to be in contact. The induced constriction resistance and film resistance together make up the contact resistance.

Today, ‘High performance and high reliability’ of electromechanical devices and electronic components that are used in the high-end equipment manufacturing industry is always required. Therefore, the optimal selection method for supporting electrode material and contact resistance measuring method are needed to make them perfect. For example, the contact resistance measurement has been successfully used to evaluate the conditions of main contacts and arcing contacts without dismantling the high voltage SF₆ circuit breaker [6]. Additionally, it could be used to estimate the contact a-spot temperature, and further judge the contact welding situation by classical Voltage–Temperature theory [5,7]. Particularly, the contact resistance results could be selected as the criteria of contact material surface quality, including roughness, hardness, or contamination situation [8,9].

The value of contact resistance is normally very small, ranging from microohms to a few milliohms in cases of practical interest. However, for contacts with worn surface or corroded or contaminated surface, the contact resistance dramatically increases into the scale of ohms or higher [10,11,12]. The general described contact resistance test methods are characterized as four-terminal Kelvin configuration.

The challenge of measuring microohm scales of contact resistance is that the value is so low level that overwhelmed by the diverse noise easily. Particularly, the thermal potentials are the main source of influencing the measured voltage signals. Either AC or DC test currents may be used, but the most general method of eliminating the effects of thermal potentials is to make forward-and-reverse-current readings and calculating resistance. The measurement accuracy of contact resistance could reach up to 0.1 μΩ by using the innovative methods [13,14,15,16,17].

The scientific instruments for single pair contact material are developed by many researchers in order to investigate and evaluate the electrical contact characteristics. Some instruments also include fretting mode and corrosion film current-voltage (I-V) characteristics and environmental atmosphere application [13]. Particularly, the nano-scale electrical contact resistance tool (nanoECR, BRUKER, Minneapolis, MN, USA), provide a powerful solution for simultaneous, in-situ electrical and mechanical measurements [17]. Unfortunately, the mentioned contact resistance measurement apparatus are always based on the commercial digital multimeter for the research work in the laboratory. Additionally, only one contact pair could be tested in one experiment so that the test efficiency is very low. Nevertheless, the loading range of the contact force is too large (up to 1 ton) and the loading accuracy (±1 kg) is too low. These could not meet the contact resistance measurement requirements within 500 g contact force for batches of rivet contacts in engineering. Consequently, the main goal of the present work is to fill this gap by developing an apparatus which allow simultaneous automated measurements of contact force and contact resistance with the variable contact current and open voltage. This apparatus should also provide motion mechanism for precise positioning among samples and associated control programme which satisfy the high-throughput measurement.

In this paper, we design a novel test rig (including the circuit and associated programme for measuring the low value contact resistance, the electrical actuators combinations and the auxiliary optical observation unit) that could meet the mentioned requirement. A suit of DC standard resistors are selected as the calibration source for minimizing the measurement error. Further, the contact resistance results of electrode materials are measured and compared with the use of our designed test rig and commercial Digital Multimeter instruments simultaneously. Finally, the uncertainty of measured contact resistance is estimated and analysed in detail.

2. Description of the New Designed Test Rig

In general, the new designed test rig allows studying the high-throughput measurement of contact resistance between two electrode materials under the selectable load force and load current. It was designed to fulfill the goals mentioned in the introduction:

• Variable load forces to achieve pure elastic or elastic–plastic contact mode.
• Different electrical current levels to discriminate the roles of electrical loads and mechanical loads in contact resistance.
• Highly efficient test for batches of rivet contacts: 10 s for single contact pair and 2 min for maximum 12 contact pairs automatically.
• Measurement principle conforming to the regulation of Standard Test Methods ASTM B539-2013 and ASTM B667-2014.

2.1. Mechanical Structures

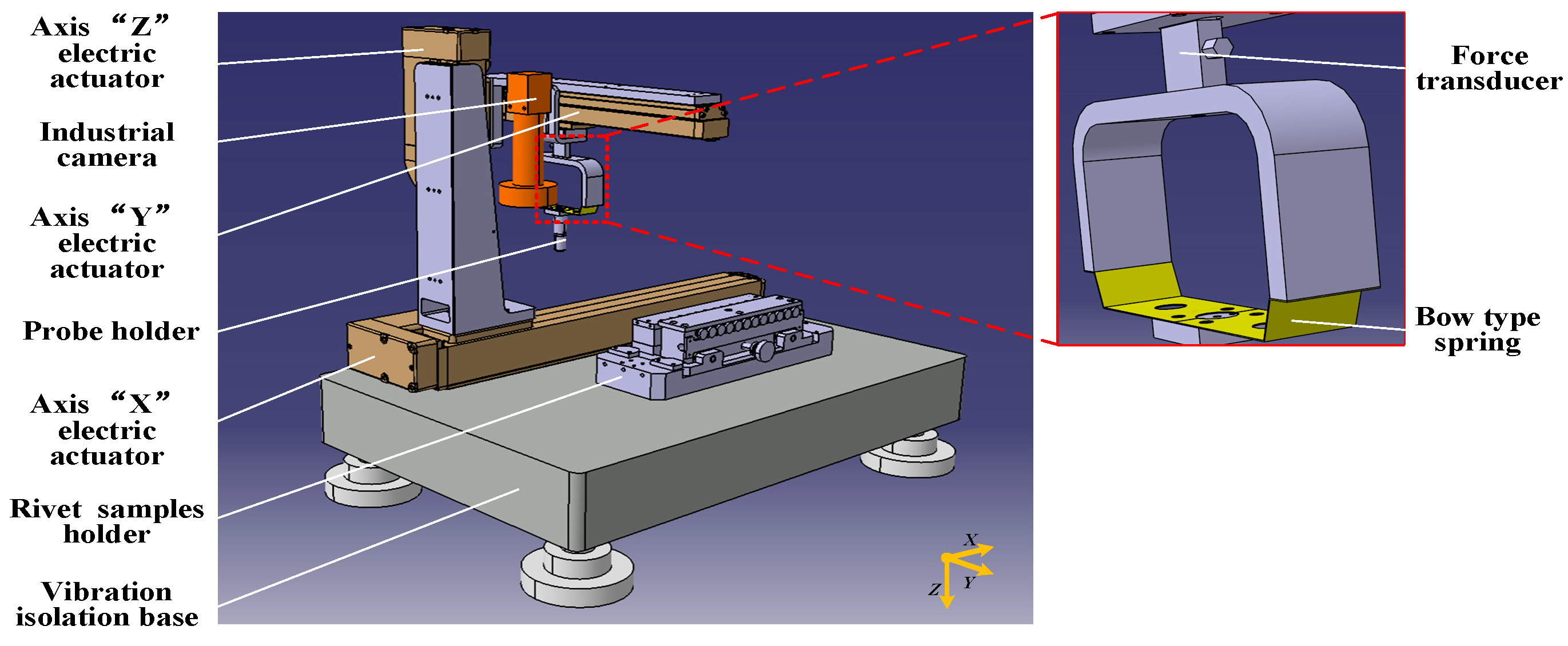
The designed mechanical structure (shown in Figure 1) is placed in a dust-tight transparent Plexiglas housing which is secured on a vibration isolation base to ensure the stability of the measurement. The rivet samples holder is fixed on the base. Furthermore, there are multiple workstations in the holder which could clamp maximum 12 rivets simultaneously in one row. The clamping structure is designed suitable for different contact dimensions. The minimum shank diameter of rivet samples should be no less than 1 mm. The counterpart probe could be a silver palladium AgPd alloy indenter with 10 μm gold coating (hemispherical shape, 0.5 mm diameter) or a mated rivet. The roughness of the indenter tip is measured by a con-focal optical microscope (LEXT 3000, Olympus, Tokyo, Japan) and the surface roughness (SRa) is 0.4 μm, calculated from a scan size of 50 μm × 50 μm. Figure 2 schematically shows the four-wire measurement setup, including the probe holder structure and the rivet clamping structure of one measurement workstation. It is noted that the surfaces of components within the applied current and test voltage circuits are electroplated with gold to reduce the connection resistance. Furthermore, the coaxial shielded lines are selected to reduce the interference from external signals. The probe is attached to a “bow” type Beryllium bronze belt (stiffness is about 0.4 N/mm) to achieve the flexible contact with low load force. A force transducer is connected vertically with it for the measurement of contact force. The probe could move accurately among each workstations in “X” axis direction and makeup mechanical contact with test sample in “Z” axis direction using two electric actuators (the step position is 0.15 μm). The maximum contact force could be set as 5 N with a resolution of 0.5 mN. Additionally, an auxiliary observation unit, which includes a color CCD camera (MV-SUB1600C-T, Mindvision, Shenzhen, China) connected with the zoom lens with the pixel of 1.34 μm × 1.34 μm, is placed parallel to the indenter in “X” axis direction. The capture pictures could be read from USB3.0 interface of camera connected with PC. The appearance of designed instrument is shown in Figure 3.

2.2. Electrical Control and Measurement System

Figure 4 shows the schematic diagram of the electrical control and measurement system. The core unit is the high-performance microcontroller (STM32F103, STMicroelectronics, Geneve, Switzerland), which is used to achieve the movement control of electrical actuators and the measurement of electrical signals. The open circuit voltage and the load current used in the measurement of contact resistance is provided by the 16-bit D/A Converter AD5541.The open circuit voltage could be set from 10 mV to 6 V with steps of 1 mV and the constant current source is capable to provide 1 mA to 1 A with 1 mA step and the accuracy of ±2.5%. The original sampled contact force signal U_F and applied current signal U_v (converted by a 2 Ω precise resistor) both are processed by the low pass filter and unity gain amplifier to eliminate the high frequency noise. Furthermore, the special designed weak signal processing circuit is used for accurate restoring the passing contact voltage drop signal. Next, the processed signals of contact force U_F, contact voltage drop U_c, open circuit voltage U_o and contact current U_v are transmitted into the 24-bit Σ—Δ A/D Converter AD7193, which has the advantage of ultra-low noise and adjustable gain. Finally, above conditioned and converted digital signals are uniformly collected by the microcontroller for the next data processing stage.

In order to guarantee the accurate and stable measurement for the contact potential drop signal in the microvolt range, two important highlights that is the periodical current chopping (PCC) method and the sliding window average filtering algorithm are proposed.

2.2.1. Periodical Current Chopping (PCC)

When the excitation current I is loaded, the contact voltage drop U_c could be expressed by

$$U_{\mathrm{c}}=I{R}_{\mathrm{c}}+U_{\mathrm{r}}+U_{\mathrm{h}}$$

(1)

where R_c is the true value of contact resistance, U_r is the existed thermal potential, and U_h is the chemical potential on the contact interface.

When the excitation current is broken, the contact voltage U_c^* could be written as

$$U_{\mathrm{c}}^{\ast }=0+U_{\mathrm{r}}+U_{\mathrm{h}}$$

(2)

Thus, according to the Equations (1) and (2), the expression of the difference of U_c and U_c^* could be expressed as

$$U_{\mathrm{c}}-U_{\mathrm{c}}^{\ast }=I{R}_{\mathrm{c}}$$

(3)

Therefore, if the used current chopping frequency is far higher than the variation rate of the thermal potential U_r and the chemical potential U_h, thus these two additional potentials are almost constant, and then their influence on the measurement results could be neglected.

Considering the voltage value of ${\widehat{U}}_{\mathrm{c}}$ and ${\widehat{U}}_{\mathrm{c}}^{\ast }$ output by the amplified analog circuits always contains the offset voltage U_s and the noise U_z, thus ${\widehat{U}}_{\mathrm{c}}$ and ${\widehat{U}}_{\mathrm{c}}^{\ast }$ are written by

$${\widehat{U}}_{\mathrm{c}}=A\left(U_{\mathrm{c}}+U_{\mathrm{s}}+U_{\mathrm{z}}\right)$$

(4)

$${\widehat{U}}_{\mathrm{c}}^{\ast }=A\left(U_{\mathrm{c}}^{\ast }+U_{\mathrm{s}}+U_{\mathrm{z}}\right)$$

(5)

where A is the magnification factor, U_c and U_c^* represent the expected true voltage value.

The optimal period of current chopping is 1 s with the help of trial and error, and then the contact resistance R_c could be calculated by

$$R_{\mathrm{c}}=\frac{{\widehat{U}}_{\mathrm{c}}-{\widehat{U}}_{\mathrm{c}}^{\ast }}{AI}$$

(6)

In order to filter the offset voltage U_s efficiently, based on AC coupling amplifier principle a low noise low drift amplifying circuit is presented. The amplifying circuit mainly includes DC-AC modulator, variable gain operational amplifier 8221, and synchronous demodulation filter.

Meanwhile, the introduced 1 kHz square wave excitation source results into the amplifier frequency deviating from 0.1 Hz~10 Hz frequency band. The direct consequence of such modulation operation is the obvious suppression of flickering noise. The selected modulation frequency of 1 kHz is an exact multiple of power frequency of 50 Hz, and then the considerable disturbance from the power frequency is eliminated. Moreover, the introduced RC low-pass filter with the cutoff frequency of 10 Hz at the end of amplifier, could further filter the weak white noise in ${\widehat{U}}_{\mathrm{c}}$ and ${\widehat{U}}_{\mathrm{c}}^{\ast }$.

2.2.2. Sliding Window Average Filtering Algorithm

In order to further improve the measurement accuracy and stability of contact resistance, the sliding window average filtering algorithm is used to filter the contact voltage and contact current signals digitally. The amplitude-frequency response function of the sliding window average filter with width N could be written as

$$H\left(e^{j\omega }\right)=\left(\frac{\sin (\frac{\omega N}{2})}{N\sin (\frac{\omega }{2})}\right)e^{\frac{-j\omega \left(N-1\right)}{2}}$$

(7)

When the window width N is 20 and the sampling frequency f_s is 10 Hz, the variations in amplitude response of the filter as a function of frequency is shown in Figure 5. The essence of the proposed filtering algorithm is a low–pass digital filter. Thus, the amplitude response that is the ratio of the output signal to the input signal decreases with the increasing frequency of input signal. When the cutoff frequency f_co of digital filter is 0.22 Hz, the signal amplitude decreases to 0.707 times the maximum value and the gain reaches −3 dB. Thus, the signal sampling period is set as 4 s to obtain the stable measurement results.

3. Standard Resistance Calibration and Uncertainty Estimation

According to the above mentioned test principle, the measurement results of contact resistance is written by

$$R_{\mathrm{c}}=\frac{U_{\mathrm{c}}-U_0}{I}$$

(8)

where U₀, U_c and I are the arithmetic means of drift voltage when no current is applied, the measured contact voltage drop and the applied test current for one sampling period (4 s).

To further validate the accuracy and stability of designed circuits, the DC standard resistors (BZ3, Shanghai Precision Instrument, China) with the rated value of 1 mΩ, 10 mΩ, and 100 mΩ and the accuracy of 0.01% are selected as the test sample. The applied current is set from 1 mA to 100 mA and the test current interval is 1 mA and 10 mA corresponding to the current ranges from 1 mA to 10 mA and 10 mA to 100 mA. Furthermore, 20 series of tests are conducted under each current value.

The measured values of U₀, U_c, and I could be considered as the independent quantities. Thus, the combined standard uncertainty for the measured resistance could be calculated as [18]

$$U\left(R_c\right)=\sqrt{{(\frac{\partial R_{\mathrm{c}}}{\partial U_{\mathrm{c}}})}^{2}u{(U_{\mathrm{c}})}^2+{(\frac{\partial R_{\mathrm{c}}}{\partial U_0})}^{2}u{(U_0)}^2+{(\frac{\partial R_c}{\partial I})}^{2}u{(I)}^2}$$

(9)

where the sensitivity coefficients ∂R/∂U_c = 1/I, ∂R/∂U₀ = −1/I and ∂R/∂I = −(U_c − U₀)/I² could be obtained from Equation (8) and u(U_c), u(U₀) and u(I) are the type A evaluation of standard uncertainty for the variables U_c, U_0, and I to reflect the deviation of repeated measurement. Thus, the combined standard uncertainty could be further written as

$$U\left(R_{\mathrm{c}}\right)=\sqrt{{(\frac{1}{I})}^{2}u{(U_{\mathrm{c}})}^2+{(-\frac{1}{I})}^{2}u{(U_0)}^2+{(-\frac{U_{\mathrm{c}}-U_0}{I})}^{2}u{(I)}^2}$$

(10)

The expanded uncertainty of measurement stated as the combined standard uncertainty of measurement multiplied by a coverage factor k = 2, corresponding to a coverage probability of approximately 95%. Taking the standard resistance with rated value of 1 mΩ measured by 10 mA as an example, the measurement results and corresponding measurement uncertainty are shown in

Table 1. Measured results and corresponding uncertainty. (standard resistance of 1 mΩ and load current of 10 mA).

Parameter	Value	Type	Uncertainty
Uc/μV	7.3877	A	0.0035
U0/μV	−2.6853	A	0.0033
I/mA	10.0246	A	0.0002

. The available estimate of the measured resistance is 1.004 mΩ and the expanded uncertainty is 0.00096 mΩ corresponding to a coverage probability of approximately 95%. It is noted that the drift voltage U₀ is about 26.6% of the total contact voltage drop (10.073 μV), which is the sum of the absolute value of the measured U_c and U₀, and is almost constant for various load current. The proposed periodical current chopping method could solve this problem readily to realize the precise measurement of the low value resistance. Similarly, the test results and uncertainty estimation for standard resistors of 1 mΩ, 10 mΩ, and 100 mΩ under load currents of 1 mA, 10 mA, 50 mA, and 100 mA are listed in

Table 2. Measurement results and corresponding expanded uncertainty. (standard resistance of 1 mΩ, 10 mΩ and 100 mΩ).

Load Current (mA)	Rs (mΩ)	Rc (mΩ)	Error (mΩ)	Combined Standard Uncertainty	Expanded Uncertainty (k = 2)
1	1	1.002	0.002	0.00619	0.01239
1	10	9.962	−0.038	0.00537	0.00974
1	100	99.75	−0.25	0.002916	0.05832
10	1	1.004	0.004	0.00048	0.00096
10	10	10.002	0.002	0.00057	0.00115
10	100	99.93	−0.07	0.0032	0.0064
50	1	1.005	0.005	0.00008	0.00016
50	10	10.021	0.021	0.00016	0.00032
50	100	99.95	−0.05	0.00186	0.00372
100	1	1.005	0.005	0.00005	0.0001
100	10	10.021	0.021	0.00015	0.0003
100	100	99.97	−0.03	0.00176	0.00352

. Furthermore, the variations in contact resistance as a function of the applied current from 1 mA to 100 mA logarithmically are plotted in Figure 6.

The measured contact resistance decreases and the fluctuation range enlarges with the test current decreasing for the standard resistance of 1 mΩ, 10 mΩ and 100 mΩ. This could be attributed to the fact that the voltage drop would be interfered by the noise signal easily under the lower test current from 1 mA to 10 mA. Thus, the contact resistance would fluctuate locally. After that, the measurement resistance is close to the nominal value and would be stable. The results show that the error between the measured resistance and rated values of standard resistors under different current load is smaller than 1%, even including the low level measurement under dry circuit conditions where the contact current is limited to 1 mA and the contact potential drop on resistor of 1 mΩ is below 1 μV. As expected, the deviation of measured resistance apparently increases with the smaller load current. Particularly, the highest deviation of each standard resistance appears when the load current is 1 mA. The test uncertainty ratio between the required error limit and expanded measurement uncertainty is higher than 10 for three scales of standard resistors, except for the case of 1 mΩ with current of 1 mA. This results indicate that the presented method is directly applicable for measurements of the low resistance value. Furthermore, the maximum combined standard uncertainty u = 0.00619 mΩ is taken as the type B evaluation of standard uncertainty to further estimate the deviation of the test results.

4. Electrical Contact Resistance and Uncertainty Estimation

4.1. Experimental Details

Two representative metal electrical electrode materials, which are the copper alloy electroplated with gold (thickness of 1 μm) and the silver cadmium oxide (AgCdO), are selected as experimental specimens. Samples are all flat type and the dimension parameters are explained in Figure 7. The specimens were degreased using alcohol and distilled water in an ultrasonic cleaner, dried, and carefully mounted in the instrument. The movable indenter with curvature radius of r = 0.5 mm is made of silver palladium alloy (AgPd) electroplated with gold (thickness of 10 μm). The experiments are carried out in ambient lab air.

For direct comparison with the presented measurement method, the commercial calibrated DC current source (6221, Keithley, Cleveland, OH, USA) and programmable nano-volt meter (2182 A, Keithley, USA) are introduced to measure the contact resistance between the indenter and rivet samples. The setup of experimental circuits is also consistent with four-wire configuration. As shown in Figure 8, the commercial current source is interfaced to a PC using Ethernet to transmit the control instructions and measurement results. Four groups of SPDT switches controlled by PC are used to switch the signal measurement channels and associated measurement instruments. The data acquisition and measurement process are controlled with the help of LabVIEW software specifically programmed for this purpose. Figure 9 illustrates the testing procedure. Initially, the open circuit voltage 20 mV is applied between two contact members. That is sufficient for the dry circuit experiment. Next, the indenter is driven to approaching the rivet specimen until the contact force reaches the given value. After that, the load current is applied and then the contact potential drop is recorded by the proposed PCC method. Keeping the mechanical contact status, and the four test probes are shift to the digital multimeter side automatically. The contact resistance is measured again by the commercial instruments with the same load current. In order to compare the measurement accuracy for varied contact resistance values, the mechanical load force is set to 0.01 N, 0.08 N, 0.15 N, 0.2 N, 0.3 N, 0.4 N, and 0.5 N to change the contact area, and the applied current is set from 1 mA to 100 mA.

4.2. Experimental Results and Discussion

Figure 10 shows the variations of measured contact resistance R_c versus the current load I with varied load force from 0.01 N to 0.5 N by the PCC method and DMM-based method for gold-plated copper alloy samples and AgCdO samples. As shown, the measured resistance of the PCC method agree well with that of DMM-based method under different combinations of current and force. It is noted that the proposed PCC method is simpler compared to the conventional DMM-based method due to two sampling points in one period. Furthermore, the maximum sampling frequency of the proposed PCC method is 45 Hz, which is almost twice of the 24 Hz of the DMM method. This indicates that PCC method is more effective and sufficiently convincing in the measurement. For the case of 0.01 N load force, the contact resistance of gold-plated sample decreases from 18.11 mΩ to 14.65 mΩ with the test current from 1 mA to 100 mA and the major drop of contact resistance concentrates on the current load from 6 mA to 20 mA, which demonstrate similar trends known as Branly effect [19,20]. For the load force higher than 0.01 N, the contact resistance decreases slightly in the whole test process. Such behavior is indicative of change of conduction area or conduction path, and the possible reason is surface film breakdown mechanisms induced by microscope thermal effects [21]. The contact resistance nonlinearly decreases with the ever-increasing mechanical load, which correlates well with those of the other researchers [22,23]. However, when the applied force increases from 0.01 N to 0.08 N, the contact resistance of AgCdO sample is almost constant. This suggests the occurrence of oxidation film in the samples, which are exposed in the air for a long time. Therefore, the film resistance is the majority of electrical contact resistance relative to the constriction resistance. The resistance decreases greatly from 38.09 mΩ to 10.7 mΩ when the contact load changes from 0.15 N to 0.5 N.

Figure 11 and Figure 12 show the variations of the relative expanded uncertainty of the measured contact resistance versus the load current and load force for the gold-plated contacts and AgCdO contacts, respectively. Furthermore, the expanded uncertainty corresponding to a coverage probability of approximately 95% consists of the type A evaluation of standard uncertainty of the uncorrelated repeatability and the type B evaluation of standard uncertainty for the PCC method mentioned in Section 3 for each measurement condition. As shown, the maximum relative expanded uncertainty of the gold-plated contact and AgCdO contact are 3.29% and 1.01% with current load of 2 mA, respectively. Furthermore, the relative expanded uncertainty of the gold-plated contacts is always higher than that of the AgCdO contacts for the same load force and current due to the lower contact resistance for the gold-plated contacts. The measurement uncertainty of contact resistance decreases from 3.29% to 0.76% sharply in the range of 1~10 mA with the contact force of 0.2 N. This could be attributed to the fact that the increasing current load makes the contact voltage drop larger and stable, and thus the type A evaluation of standard uncertainty decreases. After that, the measurement uncertainty of contact resistance is almost a constant, which means that the measurement results tends to be stable.

As shown in Figure 12, the relative expanded uncertainty of the measured contact resistance fluctuates greatly from 0.02% to 3.29% for gold-plated samples and the maximum uncertainty always corresponds to the contact load of 0.2 N. For AgCdO samples, the relative expanded uncertainty increases with the applied force loading when the test current is smaller than 20 mA. After that, the maximum uncertainty always corresponds to load force of 0.3 N. This means that the reasonable determination of the contact force and applied current is important to evaluate the surface condition of materials with the help of contact resistance. Furthermore, the measurement uncertainty could also be taken as an auxiliary reference to determine if the surface condition is stable under the load current and load force. Meanwhile, for the metal material and its oxidation film with higher softening voltage, the larger test current would produce a larger and stable contact voltage drop across contacts, which is beneficial to being measured and evaluating the surface condition of material. For the metal material with larger hardness and denser film, the larger contact force between contacts would not destroy the surface of test material and the measurement results is also more stable.

5. Conclusions

A novel high-throughput test rig, which could realize the accurate and in situ automated contact resistance measurement based on the precise motion control and circuit design, is described. A special mechanical structure allows multiple workstations clamping various rivets and four wires circuit configuration. The μV scales of contact voltage drop is measured accurately with the proposed periodical current chopping method and the sliding window average filtering algorithm, differently from other existing techniques. It is found that the measurement uncertainty of standard resistor is 0.00619 mΩ. The preliminary results showed good resolution of contact resistance measurement with the test rig with the various mechanical load force and current. The variations in contact resistance as a function of load force and current, as measured by the test rig, correlates well with existing theoretical results. The instrument is found capable of evaluating the surface features of metal materials directly and in real time.