SRMM: A Social Relationship-Aware Human Mobility Model †
Abstract
:1. Introduction
- First, most of existing mobility models do not consider human movement characteristics. Even though a few mobility models take into account human movement characteristics, they lack consideration for social relationships on human movements. Therefore, realistic human movement patterns cannot be presented. To address this problem, SRMM reflects both human movement characteristics and social relationships on human movements. Specifically, we take into account the characteristics of human movements in terms of flights, ICTs, the radius of gyration, and pause-time distributions. Moreover, social contexts in human movement (e.g., people in the same community usually visit similar places; people prefer to visit places where many of their friends are staying) are also considered.
- Second, to better approximate realistic environments when validating mobility models, mobility models are simulated not only on a synthetic map but also on a real road map (i.e., a real road map of Helsinki downtown [12]). Various experiments are conducted to validate mobility models.
- Third, various metrics are used to validate human movement characteristics. Specifically, Kullback—Leibler divergence [13], Kolmogorov—Smirnov test [14], and weighted mean relative difference [15] are used to show how well the human movement characteristic generated by mobility models match a real trace. Then, Akaike information criterion and Bayesian information criterion [16] are used to validate the fitting of the human movement characteristics with truncated power-law distributions. To evaluate the reflection of social relationships, a new performance metric, called the same social group ratio (SSGR), is proposed. The obtained results indicate that human movement characteristics from SRMM are close to the real trace and SRMM is the best to reflect social relationships.
2. Background
2.1. Preliminaries
2.1.1. Kullback–Leibler Divergence
2.1.2. Kolmogorov-Smirnov Test
2.1.3. Weighted Mean Relative Difference
2.1.4. Model Selection Criteria
- AIC is the model selection criterion established by a relationship between KL divergence and MLE. The quality of the models is estimated by AIC values. A lower AIC value indicates that the model is a better fit to the given data. Let us define the number of estimated parameters to be . The AIC is calculated as:
- BIC is another model selection criterion based on information theory but set within Bayesian context. The model with the lowest BIC is preferred. Let be the number of data samples in . BIC is defined as:
2.2. Related Work
3. Social Relationship–aware Human Mobility Model
3.1. Model
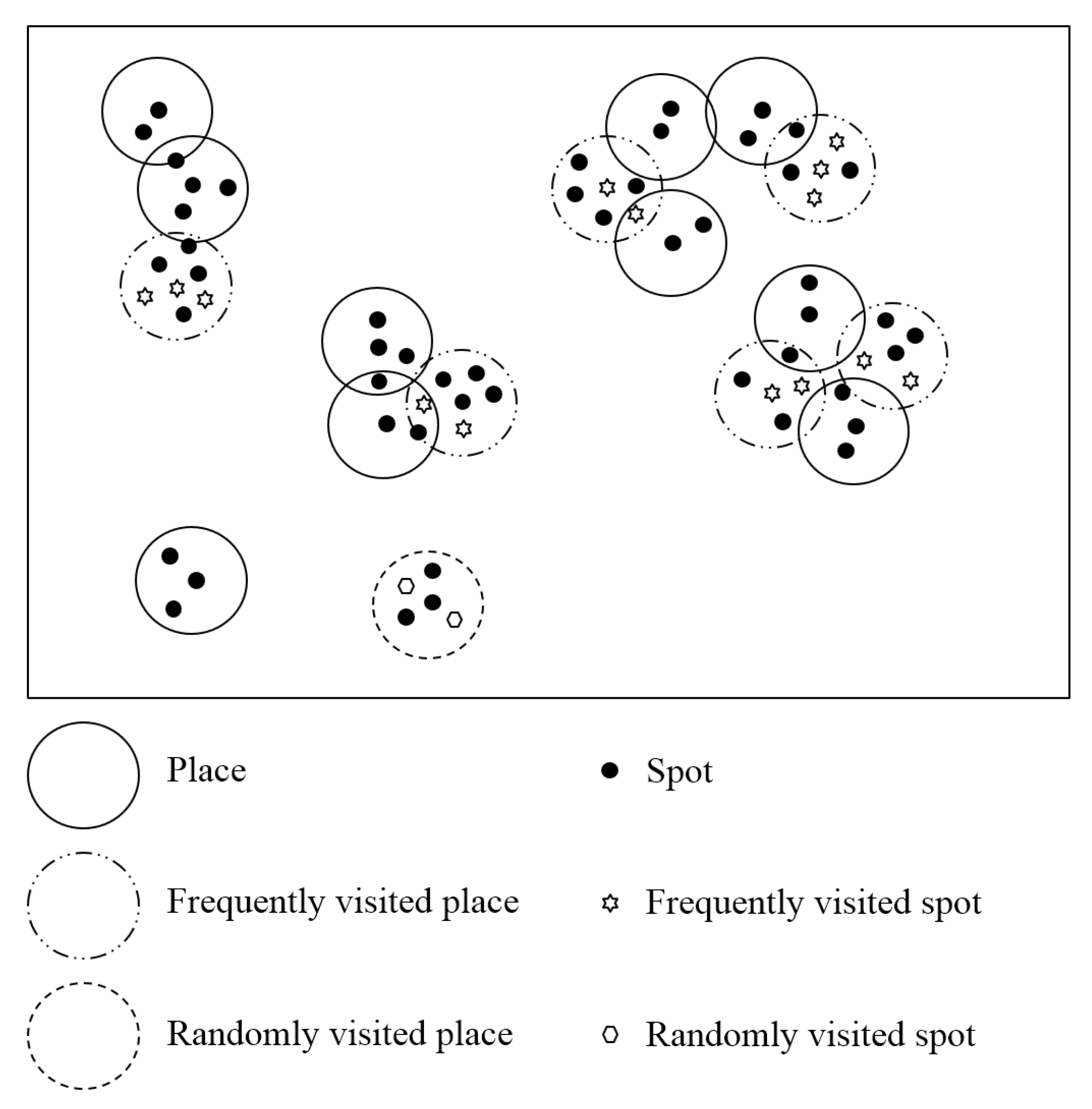
3.2. Phase 1: Human Grouping
3.3. Phase 2: Generation of Spots
3.4. Phase 3: Selection of Candidate Places and Candidate Spots
- Step 1: Selecting frequently visited placesPeople in a social group often visit the same places. That is a common context in real life. For example, a group of friends usually visits the same mall, park, and restaurant. In SRMM, each social group is associated with several places called frequently visited places. Accordingly, people in the same social group have the same frequently visited places. We define random variable x as the number of frequently visited places selected for a social group. Let A be a place in , and denotes the number of spots in place A. Let be the probability that social group G selects place A as a frequently visited place. is calculated as:where () is a parameter that adjusts the effect of the number of spots in selecting frequently visited places. Equation (7) indicates that a place with more spots has a higher probability of being selected. That agrees with the context in real life whereby most people prefer visiting popular places with more popularly visited points, rather than unpopular places. A higher also implies that several places with more spots will be frequently selected by social groups. In contrast, a lower value will reduce the possibility that different social groups will select the same frequently visited places.
- Step 2: Selecting frequently visited spotsWe define random variable y y as a percentage value. After obtaining the set of frequently visited places (), person u randomly picks y percent of the spots from each place in as frequently visited spots (where person u usually visits during day trips).
- Step 3: Selecting a randomly visited place and randomly visited spots on a day tripTo match the context of real life (on a day trip, a person visits not only frequently visited spots but additional spots, on occasion), this step randomly selects a new place and new spots at the beginning of each day.First, social group G randomly selects several new places. The number of new places is denoted as z. Then, person u randomly chooses a place from the z newly selected places as the randomly visited place (), and picks y percent of the spots in to obtain randomly visited spots.
3.5. Phase 4: Selection of the Destination Spots
- Step 1: Person u selects place from set to visitBased on the assumption that people usually prefer visiting nearby places rather than faraway places, and they are also attracted to places where many of their friends are visiting, SRMM considers two components (the distances from the places to person u’s current location, and the social relationships of person u) while selecting place from set .Let i be an arbitrary place in . To obtain the probability that person u visits place i, two probability components are used.First, we consider the probability related to distance. Let denote the distance from person u to place i. denotes the probability of selection related to distance. This probability is calculated as:where an adjustment parameter, , modifies the effect of the distance. To avoid situations where the distance from person u to a place is 0, we use a small constant, . Equation (8) implies that a place within a shorter distance has a higher value for .Secondly, we consider the probability of selection related to social relationships. Recall that person u belongs to group G. Let be the number of people, who are currently visiting place i and belong to group G. We define as the probability of selection related to social relationships. is calculated as:where parameter adjusts the effect of social relationships, and a small constant, , is used to avoid a result where . Equation (9) indicates that a place with many friends of person u has a higher value for .Finally, we define as the probability that person u chooses to visit place i. is calculated by combining two components, and , as follows:where a tunable parameter, , modifies the balance between distance and social relationship.
- Step 2: Person u selects a destination spot inLet denote the set of candidate spots that are in place for person u. In this step, person u selects a spot in as the destination spot. Let s be a spot in , and let be the distance from person u to spot s. denotes the probability that person u selects spot s as the destination spot. This probability is calculated as:where adjustment parameter is used to adjust the effect of the distance. Equation (11) indicates that spots near person u have higher probability values, which also agrees with the real-life context.
3.6. Complexity Analysis
4. Evaluation Results
4.1. Simulation Setup
4.2. Synthetic Map
4.2.1. Verifying the Human Movement Characteristics
Flight
The Radius of Gyration
Inter-Contact Time
4.2.2. Verifying Social Relationships
The Same Social Group Ratio
- First, we find the social group set, . Set is extracted from the social matrix during phase 1 in SRMM. For a fair comparison in SRMM, SLAW, CMM, and ORBIT, the same social group set is used.
- Secondly, to determine set , we analyze the synthetic trace of each model to obtain a matrix of encounter rates (). The values in the matrix are the number of times people encounter each other over the total simulation time. Suppose m and n denote two arbitrary people. denotes the number of encounters between m and n during simulation time T. Let be the encounter rate between m and n. Then, is calculated as:In reality, people who have strong relationships tend to meet each other frequently [36,37]. Thus, a higher value in the matrix can represent a stronger relationship between people. Then, the matrix is used by the spectral clustering algorithm to obtain social group set . The values in the matrix are normalized to within the range [0,1] before the matrix is used in spectral clustering.
- Finally, we compare and to obtain the SSGR value.
The Results of the Same Social Group Ratio
4.3. Real Road Map
4.3.1. Verifying the Human Movement Characteristics
Flight
The Radius of Gyration
Inter-Contact Time
4.3.2. Verifying Social Relationships
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hyytia, E.; Lassila, P.; Virtamo, J. A markovian waypoint mobility model with application to hotspot modeling. In Proceedings of the IEEE International Conference on Communications, 2006, ICC’06, Istanbul, Turkey, 11–15 June 2006; Volume 3, pp. 979–986. [Google Scholar]
- Royer, E.M.; Melliar-Smith, P.M.; Moser, L.E. An analysis of the optimum node density for ad hoc mobile networks. In Proceedings of the ICC 2001. IEEE International Conference on Communications. Conference Record (Cat. No.01CH37240), Helsinki, Finland, 11–14 June 2001; Volume 3, pp. 857–861. [Google Scholar]
- Gonzalez, M.C.; Hidalgo, C.A.; Barabasi, A.L. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef]
- Rhee, I.; Shin, M.; Hong, S.; Lee, K.; Kim, S.J.; Chong, S. On the Levy-Walk Nature of Human Mobility. IEEE/ACM Trans. Netw. 2011, 19, 630–643. [Google Scholar] [CrossRef]
- Lee, K.; Hong, S.; Kim, S.J.; Rhee, I.; Chong, S. SLAW: A New Mobility Model for Human Walks. In Proceedings of the IEEE INFOCOM 2009, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 855–863. [Google Scholar]
- Ekman, F.; Keränen, A.; Karvo, J.; Ott, J. Working Day Movement Model. In Proceedings of the 1st ACM SIGMOBILE Workshop on Mobility Models; ACM: New York, NY, USA, 2008; MobilityModels ’08; pp. 33–40. [Google Scholar]
- Musolesi, M.; Mascolo, C. Designing Mobility Models Based on Social Network Theory. SIGMOBILE Mob. Comput. Commun. Rev. 2007, 11, 59–70. [Google Scholar] [CrossRef]
- Boldrini, C.; Passarella, A. HCMM: Modelling spatial and temporal properties of human mobility driven by users’ social relationships. Comput. Commun. 2010, 33, 1056–1074. [Google Scholar] [CrossRef]
- Chaintreau, A.; Hui, P.; Crowcroft, J.; Diot, C.; Gass, R.; Scott, J. Impact of Human Mobility on Opportunistic Forwarding Algorithms. IEEE Trans. Mobile Comput. 2007, 6, 606–620. [Google Scholar] [CrossRef]
- Kim, M.; Kotz, D.; Kim, S. Extracting a Mobility Model from Real User Traces. In Proceedings of the IEEE INFOCOM 2006. 25TH IEEE International Conference on Computer Communications, Barcelona, Spain, 23–29 April 2006; pp. 1–13. [Google Scholar]
- Rhee, I.; Shin, M.; Hong, S.; Lee, K.; Kim, S.; Chong, S. CRAWDAD Dataset ncsu/mobilitymodels (v. 2009-07-23). 2009. Available online: http://crawdad.org/ncsu/mobilitymodels/20090723 (accessed on 27 January 2020).
- Maanmittauslaitos. The National Land Survey of Finland Topographic Database 03/2019. 2019. Available online: https://www.maanmittauslaitos.fi (accessed on 27 January 2020).
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Massey, F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Duffield, N.; Lund, C.; Thorup, M. Estimating flow distributions from sampled flow statistics. IEEE/ACM Trans. Netw. 2005, 13, 933–946. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel Inference: Understanding AIC and BIC in Model Selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- MacKay, D.J. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Pfanzagl, J. Parametric Statistical Theory; Walter de Gruyter: Berlin, Germany, 1994. [Google Scholar]
- McNett, M.; Voelker, G.M. Access and Mobility of Wireless PDA Users. SIGMOBILE Mob. Comput. Commun. Rev. 2005, 9, 40–55. [Google Scholar] [CrossRef]
- Scott, J.; Gass, R.; Crowcroft, J.; Hui, P.; Diot, C.; Chaintreau, A. CRAWDAD Dataset Cambridge/Haggle (v. 2009-05-29). 2009. Available online: https://crawdad.org/cambridge/haggle/20090529 (accessed on 27 January 2020).
- Stopczynski, A.; Sekara, V.; Sapiezynski, P.; Cuttone, A.; Madsen, M.M.; Larsen, J.E.; Lehmann, S. Measuring large-scale social networks with high resolution. PLoS ONE 2014, 9, e95978. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Munjal, A.; Camp, T.; Navidi, W.C. SMOOTH: A Simple Way to Model Human Mobility. In Proceedings of the 14th ACM International Conference on Modeling, Analysis and Simulation of Wireless and Mobile Systems; MSWiM ’11; Association for Computing Machinery: New York, NY, USA, 2011; pp. 351–360. [Google Scholar] [CrossRef]
- Solmaz, G.; Akbaş, M.; Turgut, D. A Mobility Model of Theme Park Visitors. IEEE Trans. Mobile Comput. 2015, 14, 2406–2418. [Google Scholar] [CrossRef]
- Kang, X.; Liu, L.; Ma, H.; Zhao, D. Urban context aware human mobility model based on temporal correlation. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Mei, A.; Stefa, J. SWIM: A Simple Model to Generate Small Mobile Worlds. In Proceedings of the IEEE INFOCOM 2009, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 2106–2113. [Google Scholar]
- Zheng, Q.; Hong, X.; Liu, J.; Cordes, D.; Huang, W. Agenda Driven Mobility Modelling. Int. J. Ad Hoc Ubiquitous Comput. 2010, 5, 22–36. [Google Scholar] [CrossRef] [Green Version]
- US Department of Transportation. 2001 National Household Travel Survey. 2007. Available online: http://nhts.ornl.gov (accessed on 27 January 2020).
- Ghosh, J.; Philip, S.J.; Qiao, C. Sociological orbit aware location approximation and routing (SOLAR) in MANET. Ad Hoc Netw. 2007, 5, 189–209. [Google Scholar] [CrossRef]
- Borrel, V.; Legendre, F.; de Amorim, M.D.; Fdida, S. SIMPS: Using Sociology for Personal Mobility. IEEE/ACM Trans. Netw. 2009, 17, 831–842. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Yang, X.; Zhang, C.; Spyrou, E. Using social network theory for modeling human mobility. IEEE Netw. 2010, 24, 6–13. [Google Scholar] [CrossRef]
- Von Luxburg, U. A Tutorial on Spectral Clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Oakland, CA, USA, 21 June 1967; Volume 1, pp. 281–297. [Google Scholar]
- Ng, A.Y.; Jordan, M.I.; Weiss, Y. On spectral clustering: Analysis and an algorithm. In Proceedings of the 14th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 3–8 December 2001; pp. 849–856. [Google Scholar]
- Lee, K.; Hong, S.; Kim, S.J.; Rhee, I.; Chong, S. Demystifying Levy Walk Patterns in Human Walks. NCSU, Technical Report. 2008. Available online: http://netsrv.csc.ncsu.edu/export/Demystifying_Levy_Walk_Patterns.pdf (accessed on 27 January 2020).
- Bohannon, R.W.; Andrews, A.W. Normal walking speed: A descriptive meta-analysis. Physiotherapy 2011, 97, 182–189. [Google Scholar] [CrossRef] [PubMed]
- Bulut, E.; Szymanski, B.K. Exploiting Friendship Relations for Efficient Routing in Mobile Social Networks. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 2254–2265. [Google Scholar] [CrossRef]
- Li, F.; Wu, J. LocalCom: A Community-based Epidemic Forwarding Scheme in Disruption-tolerant Networks. In Proceedings of the 2009 6th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, Rome, Italy, 22–26 June 2009; pp. 1–9. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef] [Green Version]










| The set of places | |
| The set of spots | |
| The set of people | |
| The set of social groups | |
| The set of frequently visited places for person u | |
| The set of frequently visited spots for person u | |
| The set of randomly visited places for person u | |
| The set of randomly visited spots for person u | |
| The set of candidate places for person u | |
| The set of candidate spots for person u |
| Parameter | Value |
|---|---|
| Radius of places (r) | 100 m |
| Number of people () | 100 |
| Simulation time (T) | 200 h |
| Speed of people | km/h |
| Transmission range | 100 m |
| Social matrix | |
| Number of social groups () | 10 |
| Number of frequently visited places (x) | |
| Percentage value of spots picked from candidate places (y) | |
| Number of new places selected by a group at the beginning of each day (z) | |
| Homecoming time () |
| SRMM | SLAW | CMM | ORBIT | |||||
|---|---|---|---|---|---|---|---|---|
| Flight | Radius of Gyration | Flight | Radius of Gyration | Flight | Radius of Gyration | Flight | Radius of Gyration | |
| KL divergence with real trace | 0.0325 | 0.5211 | 0.0625 | 0.6627 | 0.3205 | 0.6921 | 0.2985 | 0.7223 |
| WMRD | 0.7716 | 1.9260 | 0.9868 | 1.9900 | 1.8420 | 2.0000 | 1.6658 | 2.0000 |
| P value of K-S test | 0.5180 | 0 | 0 | |||||
| SRMM | SLAW | CMM | ORBIT | NYC | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Flight | RoG | ICT | Flight | RoG | ICT | Flight | RoG | ICT | Flight | RoG | ICT | Flight | RoG | ICT | |
| Selected model by AIC | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Exp | Pow | Pow | N/A |
| Selected model by BIC | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Exp | Pow | Pow | N/A |
| SRMM | SLAW | CMM | ORBIT | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Flight | RoG | ICT | Flight | RoG | ICT | Flight | RoG | ICT | Flight | RoG | ICT | |
| Selected model by AIC | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Exp | Pow | Pow |
| Selected model by BIC | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Pow | Exp | Pow | Pow |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Anh Duong, D.; Yoon, S. SRMM: A Social Relationship-Aware Human Mobility Model. Electronics 2020, 9, 221. https://doi.org/10.3390/electronics9020221
Van Anh Duong D, Yoon S. SRMM: A Social Relationship-Aware Human Mobility Model. Electronics. 2020; 9(2):221. https://doi.org/10.3390/electronics9020221
Chicago/Turabian StyleVan Anh Duong, Dat, and Seokhoon Yoon. 2020. "SRMM: A Social Relationship-Aware Human Mobility Model" Electronics 9, no. 2: 221. https://doi.org/10.3390/electronics9020221
APA StyleVan Anh Duong, D., & Yoon, S. (2020). SRMM: A Social Relationship-Aware Human Mobility Model. Electronics, 9(2), 221. https://doi.org/10.3390/electronics9020221






