1. Introduction
The 4th Industrial Revolution is the convergence of information and communications. Data resulting from the 3rd Industrial Revolution are shared among devices through wireless communication and then used and processed for various purposes. A representative technology of the 4th Industrial Revolution is the Internet of Things (IoT). IoT is an infrastructure that enables the communication of objects by information exchange. It can control home devices in certain areas and display all information pertaining to the present situation in real time through a video device such as a camera. As such, human life has become more convenient; however, IoT devices do not guarantee personal privacy when exchanging data through wireless communication. Therefore, data encryption is required during data exchange.
Generally, the data encryption method is divided into symmetric and asymmetric key encryptions. The symmetric key encryption method uses the same secret key for encryption and decryption between the transmitting and receiving sides. To prevent the secret key from being leaked in advance, it must be transmitted through a secure transmission method such as a secret communication network or a direct transmission. The Advanced Encryption Standard (AES) [
1] and Data Encryption Standard (DES) [
2] are typical symmetric key encryption methods. The symmetric key cryptosystem affords fast encryption and decryption rates, but the data cannot be safely protected even if one of the two sides of the transmitter side is leaked. In addition, the symmetric key cryptosystem is inefficient in many-to-many communication methods such as IoT because the key of each device must be separately generated when a large number of devices is connected [
3].
Asymmetric key cryptography or public key cryptography uses different keys for encryption and decryption. The key for encryption is called the public key, and it can be easily used by anyone. The secret key for decryption is kept in a safe place, accessible only by the receiving end that receives the encrypted data. Even if encrypted data are acquired, it is extremely difficult to decrypt them if the private key is not known. Typical asymmetric key cryptosystems are RSA [
4] and ECC [
5]. In an embedded system such as IoT, power must be used efficiently. The RSA encryption method used in conventional PCs cannot cope with the memory space and power consumption for calculation, as it uses an extremely large key. Therefore, although the ECC encryption method has been developed, the computation process is highly complicated, and it is limited to algorithm expansion because it is developed to use only elliptic curves.
Generally, IoT primarily uses the ZigBee [
6] or WiFi [
7] communication method; similar to most wireless communication methods, security problems exist in ZigBee communication. High-performance wireless communication methods such as WiFi solve this problem through a high-level encryption process; however, it is difficult to apply high-level encryption technology to ZigBee because of the lack of performance of the terminal itself. The existing ZigBee communication uses the AES-CCM [
8] method for data encryption; however, the AES-CCM method does not guarantee confidentiality if the key is leaked even if by only one device through the key transmission process or various methods.
In the one-to-one communication method, the asymmetric key encryption method is primarily used, and in the one-to-many or many-to-many communication method, the symmetric key encryption method is effective. Therefore, the asymmetric key encryption method is effective in IoT equipment, which is a communication method. However, it is difficult to apply RSA encryption to wireless communication or small devices because it requires an extremely large encryption key for security.
Hence, the existing encryption methods used in PCs are not suitable to be used in devices that exchange data in real time. Further, because information regarding temperature, time, etc., does not require high security, it is inefficient to use the existing encryption method as it is. To secure the security of the existing RSA encryption, a key size of 2048 bits is generally required. Transmission of 2048 bits through wireless communication such as ZigBee consumes considerable power, and arithmetic computation with such a large bit number is expensive. Therefore, it is impossible to use the existing RSA’s 2048 bit key. In addition, memory is required to store the 2048 bit private key, and preparation for various side attacks is required because it has a memory to save the key.
We herein propose a feasible cryptosystem for situations where extremely high security is not required but real-time encrypted data must be exchanged. It introduces a new encryption mechanism based on the RSA algorithm with a small key and a true prime random number generator for discarding and regenerating keys in real time.
2. RSA Overview
The RSA algorithm was first used to implement the concept of public key cryptography and has been widely used because it is easier to understand and implement than other public key algorithms. However, the RSA algorithm is computationally intensive with very large integer numbers. Strong primes are required for RSA security. Thus, additional cost is indispensable for generating strong primes in RSA [
9]. The RSA key generation formula is defined as follows:
For encryption,
e is made available to anyone. Furthermore,
d for decryption is disclosed only to users requiring decryption. Therefore,
e may be leaked, but
d should not be leaked.
P is the original message, and
C is the encrypted message. The process of encrypting and decrypting data is defined as follows:
The first step of the RSA algorithm is to generate two prime numbers, p and q, through a random number generator. The values of p and q should be generated as unpredictable random numbers of different values. The generated p and q are used to calculate and n, respectively. Furthermore, is used to calculate e. e is used for text encryption, and d can be obtained via e. d is used to decrypt the encrypted text and must be kept secure such that only the user can view it. If d is leaked, the RSA algorithm is completely broken.
3. True Prime Random Number Generator
A prime number generator using a pseudo random number generator (PRNG) causes a fatal defect in RSA security. Recently, a method for quickly obtaining the private key of the RSA algorithm using PRNG has been reported [
10]. Therefore, to maintain RSA security, an unpredictable true random prime number generator (TRPNG) is required. A TRNG with high entropy is required to generate random numbers that cannot be predicted. In this study, we use TRNG based on Linear-feedback shift register (LFSR) using bio-signals [
11]. Photoplethysmogram (PPG) sensors [
12], which are built into most wearable devices, measure values by capturing changes in the arterial perfusion rate of light as the arterial blood flow varies with each heartbeat. The PPG sensor suffers from noise due to physical and environmental factors such as light entering from the outside when moving a finger or arm. However, this disadvantage is an advantage when implementing the TRNG. This is because the value is changed every time according to the fine movement of the person or the surrounding environment, which cannot be predicted.
We use the most representative 16 bit LFSR of the PRNG because PPG data alone cannot generate the same ratio of zero and one, which are the most important factors in generating random numbers. The fact that zero and one are equal implies that the maximum length sequence of the generated bits is output, and the polynomial is set to
[
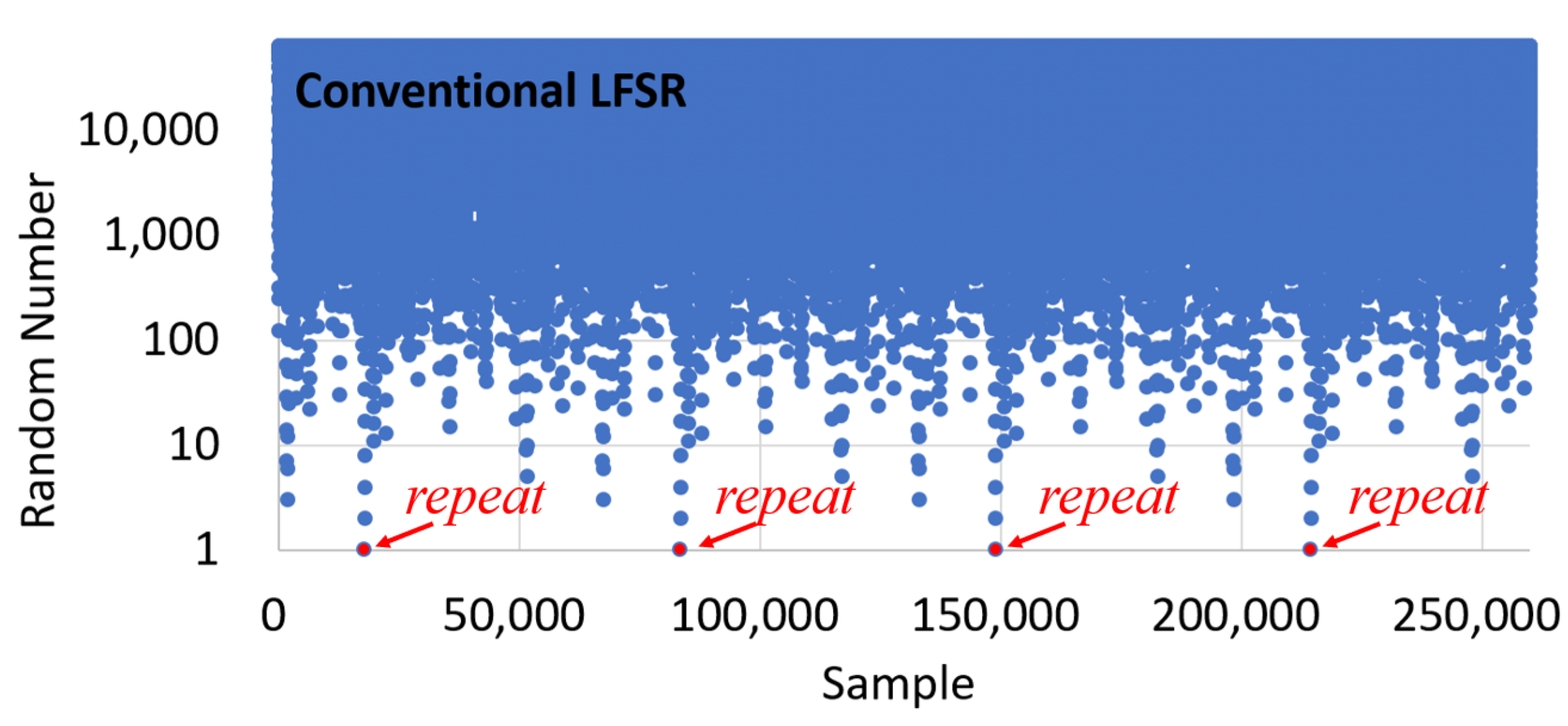
13]. In this study, we use the initial seed value as a physical source obtained from the PPG sensor because the LFSR requires an initial seed value for random number generation. Because the physical sources that can be obtained from PPG sensors are generally processed in wearable devices, no additional processing is required. When the 16 bit LFSR outputs the initial seed value and 65,535 random numbers, which is the maximum length sequence of 16 bits, a problem arises in that the random number of the same pattern is repeated, as shown in
Figure 1. Hence, a new polynomial is added. An XOR gate is added, as shown in
Figure 2, to perform the XOR operation with the physical source value of the PPG sensor, in which the random number generated in the LFSR cannot be predicted.
To use the random numbers generated by the TRNG as the
p and
q values of the RSA algorithm, a discriminator is required to determine the prime number. Because a discriminator through the factorial decomposition requires considerable time and hardware area to discriminate the prime numbers, the random numbers generated from the TRNG are compared with the decimal values stored as the parameter values to be determined as a prime number. If the random number generated by the TRNG is equal to the decimal value stored in the parameter, it is determined to be a prime number, and the output random prime is
p,
q in the RSA algorithm. The reason for using unpredictable prime numbers as
p and
q values is that the prime factorization algorithm from a recently published paper [
10] cannot be applied.
4. Proposed RSA
The RSA algorithm requires a key of 2048 bits or more to guarantee security. The encryption algorithm using such a large key size is not suitable for use in wireless communication devices, small devices, or places requiring fast data processing. Therefore, the RSA algorithm is not used in IoT devices or cell phones, which constantly exchange data and are being miniaturized increasingly. AES encryption, a symmetric key encryption method, affords an extremely fast processing speed and a small hardware area for encrypting and decrypting data; however, it is inefficient in one-to-many or many-to-many communications. Further, even if one device key is leaked, the security of all devices cannot be maintained. The use of symmetric keys is risky because IoT devices communicate with many other devices. ECC exploits the idea that it takes a long time to find a discrete log of a random elliptic curve for a particular known point [
5]. As shown in
Table 1 [
14], ECC encryption can provide a similar level of security while using a key with a much shorter length than that of the RSA. However, the elliptic curve is complicated and expensive to operate.
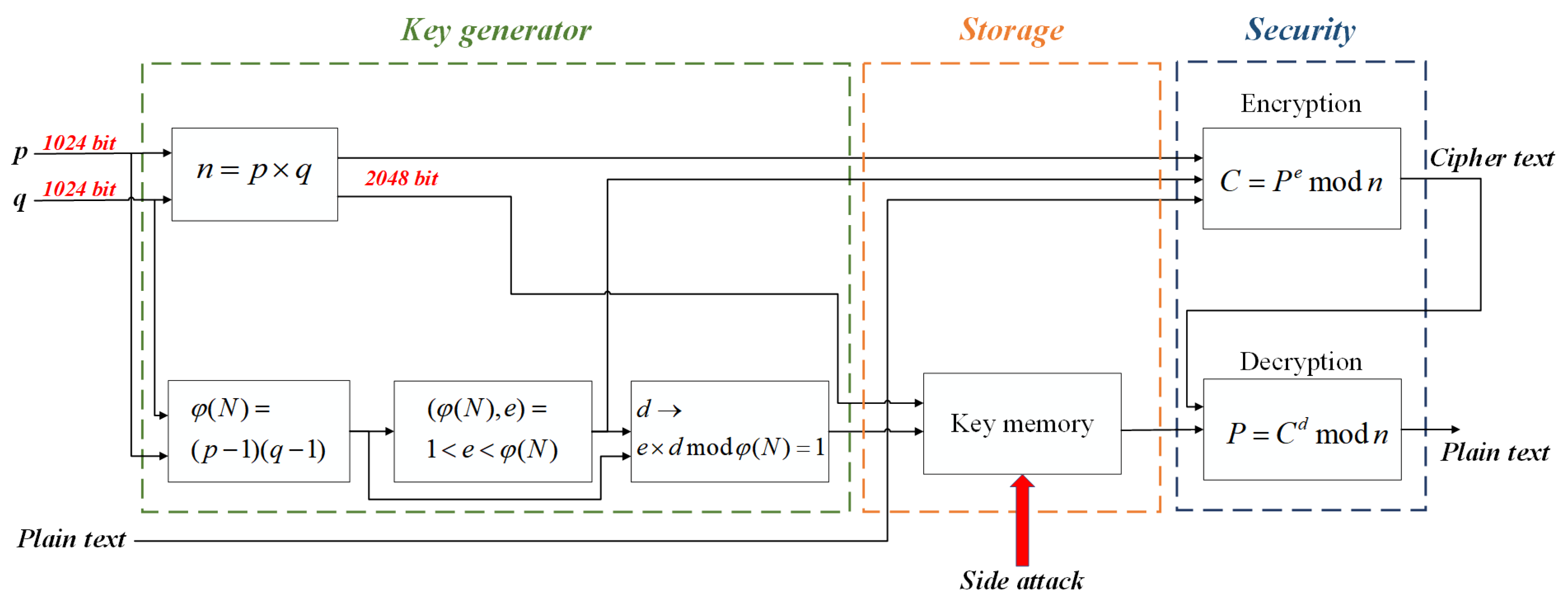
As shown in
Figure 3, the existing RSA encryption is primarily classified into three processing modules. First, the key generator module receives a 1024 bit pseudo-random number and generates both a private and public key. The second storage module is a memory that holds a 2048 bit private key. It is highly vulnerable to side attacks because it stores a 2048 bit key in memory continuously. If the side attack is successful, the security of the RSA encryption algorithm is lost regardless of the encryption key size. Next, the security module uses 2048 bit private and public keys to encrypt data. The algorithm for encrypting and decrypting through the 2048 bit key requires extremely large hardware, which is virtually impossible to implement. In addition, it is difficult to exchange 2048 bit private and public keys through wireless communication.
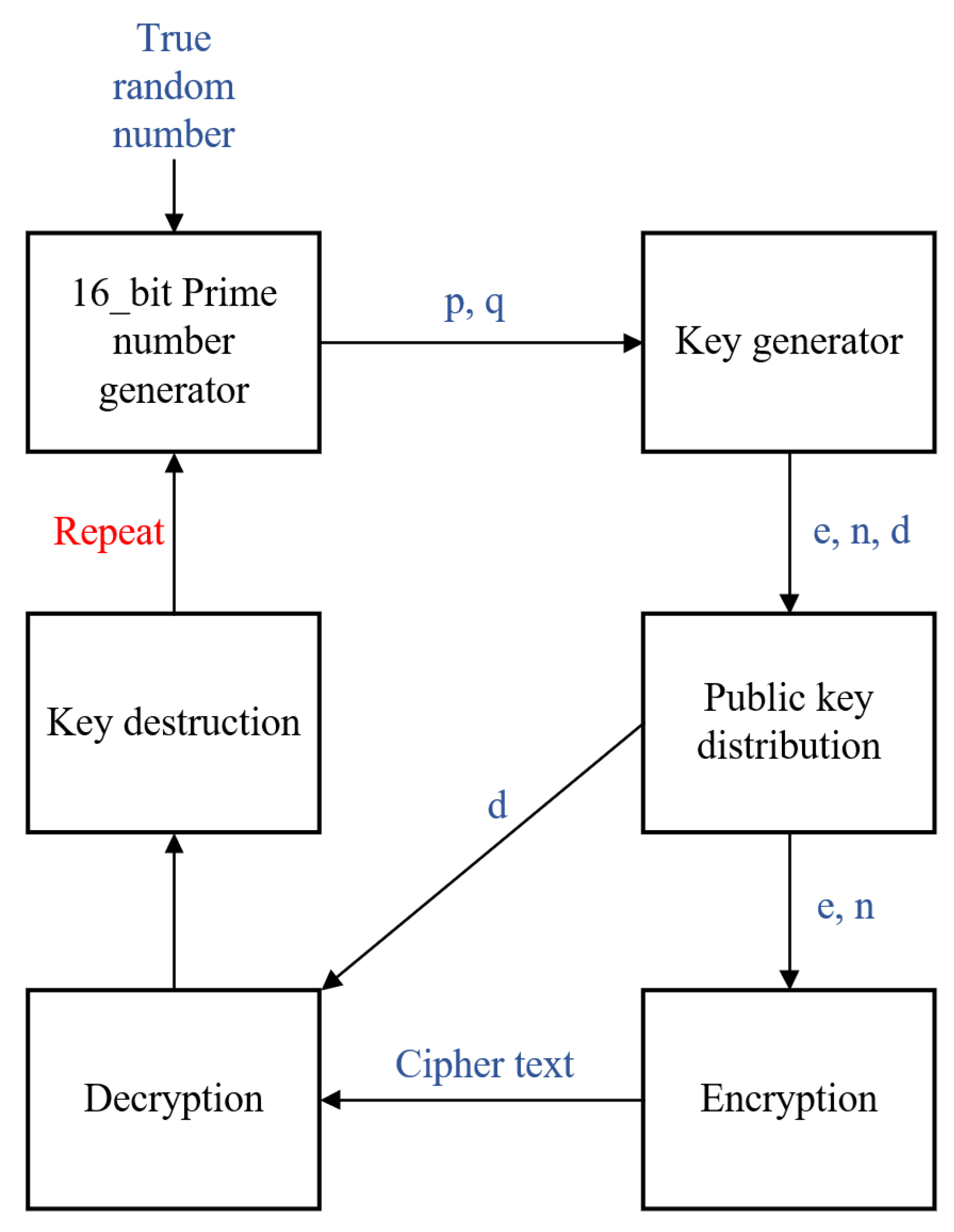
To solve the problem of the conventional RSA, we herein propose a new RSA mechanism, as shown in
Figure 4. The proposed RSA mechanism obtains two 16 bit random prime numbers in the TPRNG using unpredictable PPG data. The next two 16 bit prime numbers
p and
q are used to generate 32 bit public and private keys. When both a public and private key are generated, the public key (
e,
n) is distributed to the device requiring encryption and the plain text is encrypted. Encrypted cipher text is sent where data are required and decrypted via private key (
d). When all the steps from key generation to decryption are completed, the prime number, public key, and private key are immediately destroyed and then regenerated. The RSA contains a key that is much smaller than the key used by the RSA, which can be deciphered at a much faster rate than the existing 2048 bit key; however, it can be estimated by constantly regenerating the key. In addition, real-time transmission is possible when transmitting key and encrypted data through wireless communication because it has extremely small keys. In terms of hardware design for encryption and decryption, the side attack does not apply because of the destruction and regeneration through the process, rather than maintaining the key in memory constantly.
5. Implementation
For the proposed hardware design, we used the Verilog HDL, FPGA in Zynq UltraScale , xczu6cg-ffvb1156-2 device. This design was synthesized and implemented using the Vivado design suite provided by Xilinx. NIST SP 800-22 was used to evaluate the randomness of the implemented TRNG.
5.1. TPRNG
An unpredictable random number can be generated as shown in
Figure 5 by performing an XOR operation with the random number generated in the conventional LFSR and the physical source value of the PPG sensor, as shown in
Figure 1. The proposed random number generator is verified by all passing the NIST test suite [
15], as shown in
Table 2. As explained in
Section 3, to implement TPRNG, the random numbers generated through the TRNG are compared with the numbers stored in the parameters and then output as a decimal number. If the number of decimals stored as the parameter value is extremely small, the decimal number is assessed whether it is real time. Thus, a decimal value of 1000 or less is not stored as the parameter value. The TPRNG has an extremely small hardware area, as shown in
Table 3.
5.2. RSA
We herein propose an RSA system architecture, as shown in
Figure 4. The two prime numbers generated by the TPRNG are
p,
q with the RSA. The private key (
d) and public key (
e) are computed using the
p and
q values, respectively. Data are encrypted and decrypted through the generated
e and
d, respectively. Once all the encryption and decryption processes have been completed through
e and
d, the TPRNG is used to regenerate the key by inputting new
p and
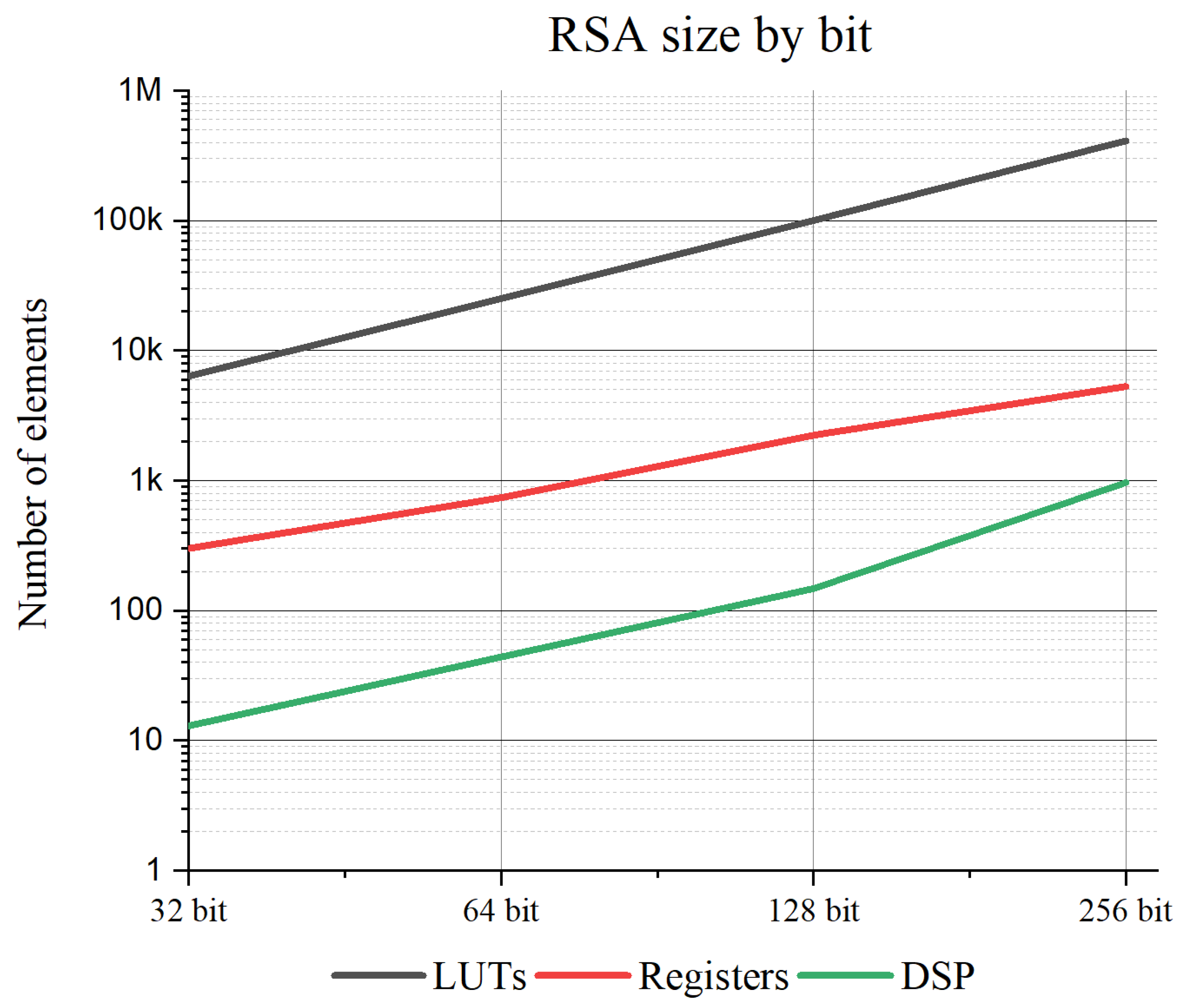
q values. When the RSA algorithm is implemented in hardware, the hardware area increases exponentially, as shown in
Figure 6, as the number of bits increases. The elements used for each bit are as shown in
Table 4. Therefore, a 32 bit RSA encryption is suitable for IoT devices requiring small hardware area and low power. The RSA encryption module implemented in hardware is shown in
Figure 7 [
16,
17,
18]. The
p,
q values and plain text are input in the decryption module, and the keys (
n,
e,
d) are generated according to the RSA algorithm. The 1542 value of the plain text according to the RSA encryption formula
is encrypted to the 8,135,351 value cipher text. The decryption module implemented in hardware is shown in
Figure 8. Cipher text is transmitted to the input of the decryption module and decrypted to the 1542 value plain text through the 3,849,029 value private key (
d) according to the RSA decryption formula
. Once the decryption is completed, the encryption and decryption keys are discarded.
6. Conclusions
We herein proposed a new RSA mechanism applicable to small wireless communications devices such as IoT. Conventional RSA algorithms use a very large key size, which requires large hardware areas and expensive arithmetic calculations. For this reason, a traditional RSA encryption is not suitable for devices used in IoT environments. The proposed RSA encryption mechanism has an extremely small key, but compensates for the problem of small encryption keys by continuously changing the key using an unexpected random number. Furthermore, side attack problems do not occur because the key does not remain in memory continuously. The proposed method is highly suitable for IoT devices that use many-to-many communications, as it does not suffer from problems in existing public key encryptions, which hinder data encryption. Further, as the information exchanged between IoT devices does not require high security, this method is feasible in that data are decrypted quickly with little hardware. The RSA mechanism proposed in this paper exploits the randomness of the bio-signals with a very small number of keys (e.g., 16 bits) for power and area efficiency in RSA encryption. For this reason, the proposed method may not be sufficient for environments that require an extremely high level of encryption. Future work will evolve into research that increases area and power efficiency even with greater key size. This method is applicable to cases where data must be transmitted and received quickly in real time, e.g., an unmanned vehicle.
Author Contributions
Conceptualization, H.Y. and Y.K.; methodology, H.Y.; software, H.Y.; validation, H.Y. and Y.K.; investigation, H.Y.; resources, H.Y. and Y.K.; writing, original draft preparation, H.Y.; writing, review and editing, Y.K.; supervision, Y.K.; project administration, Y.K.; funding acquisition, Y.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by MIST under Grant NRF-2019M3F3A1A02072093.
Acknowledgments
This work was supported by the NRF of Korea funded by the MSIT under Grant NRF-2019M3F3A1A02072093 (Intelligent Semiconductor Technology Development Program).
Conflicts of Interest
The authors declare no conflict of interest.
References
- NIST. Advanced Encryption Standard; FIPS Publication 197; NIST: Gaithersburg, MD, USA, 2001. [Google Scholar]
- Eli, B.; Shamir, A. Differential cryptanalysis of DES-like cryptosystems. J. Cryptol. 1991, 4, 3–72. [Google Scholar]
- INFOSEC. Available online: https://resources.infosecinstitute.com/review-asymmetric-cryptography/#gref/ (accessed on 6 November 2019).
- Rivers, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar]
- Singh, L.D.; Singh, K.M. Implementation of text encryption using elliptic curve cryptography. Procedia Comput. Sci. 2015, 54, 73–82. [Google Scholar] [CrossRef] [Green Version]
- ZigBee, A. Available online: https://www.eena.org/ (accessed on 6 November 2019).
- Beal, V. Available online: www.webopedia.com/TERM/W/Wi_Fi.html (accessed on 6 November 2019).
- Vidgren, N.; Hataja, K.; Patiño-Andres, J.L.; Ramírez-Sanchis, J.J.; Toivanen, P. Security Threats in ZigBee-Enabled Systems: Vulnerability Evaluation, Practical Experiments, Countermeasures, and Lessons Learned. In Proceedings of the 2013 46th Hawaii International Conference on System Sciences, Maui, HI, USA, 7–10 January 2013. [Google Scholar]
- Rivest, R.; Silverman, R. Are ‘Strong’ Primes Needed for RSA. In Cryptology ePrint Archive, Report 2001/007; Available online: https://eprint.iacr.org/2001/007 (accessed on 6 November 2019).
- Nemec, M.; Sys, M.; Svenda, P.; Klinec, D.; Matyas, V. The Return of Coppersmith’s Attack: Practical Factorization of Widely Used RSA Moduli. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 1631–1648. [Google Scholar]
- Yu, H.; Kim, Y. True Random Number Generator Using Bio-related Signals in Wearable Devices. In Proceedings of the 2018 Conference on International SoC Design Conference, Daegu, Korea, 12–15 November 2018. [Google Scholar]
- Wood, P.T.; Wood, L.B.; Asada, H.H. Active motion artifact cancellation for wearable health monitoring sensors using collocated MEMS accelerometers. In Smart Structures and Materials 2005: Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, International Society for Optics and Photonics; International Society for Optics and Photonics: San Diego, CA, USA, 2005; Volume 5765, pp. 811–820. [Google Scholar]
- Hellebrand, S. Built-in test for circuits with scan based on reseeding of multiple-polynomial linear feedback shift registers. IEEE Trans. Comput. 1995, 44, 223–233. [Google Scholar] [CrossRef]
- Yu, Z. A High Performance Pseudo-Multi-Core Elliptic Curve Cryptographic Processor over GF (2163). Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2010. [Google Scholar]
- Rukhin, A. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; NIST: Gaithersburg, MD, USA, 2010. [Google Scholar]
- Shams, R.; Khan, F.H.; Umair, M. Cryptosystem an Implementation of RSA Using Verilog. Int. J. Comput. Netw. Commun. Security 2013, 1, 102–109. [Google Scholar]
- Rahman, M.; Rokon, I.R.; Rahman, M. Efficient Hardware Implementation of RSA Cryptography. In Proceedings of the 3rd International Conference on Anti-Counterfeiting, Security, and Identification in Communication, Hong Kong, China, 20–22 August 2009; pp. 316–319. [Google Scholar]
- Leelavathi, G.; Shaila, K.; Venugopal, K.R. Design and Implementation of Montgomery Multipliers in RSA Cryptography for Wireless Sensor Networks. In Proceedings of First International Conference on Smart System, Innovations and Computing; Springer: Singapore, 2018; pp. 565–574. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).