Feasibility Study of Interleaving Approach for Quasi-Z-Source Inverter
Abstract
:1. Introduction
2. Description of a Case Study System with a Quasi-Z-Source Inverter
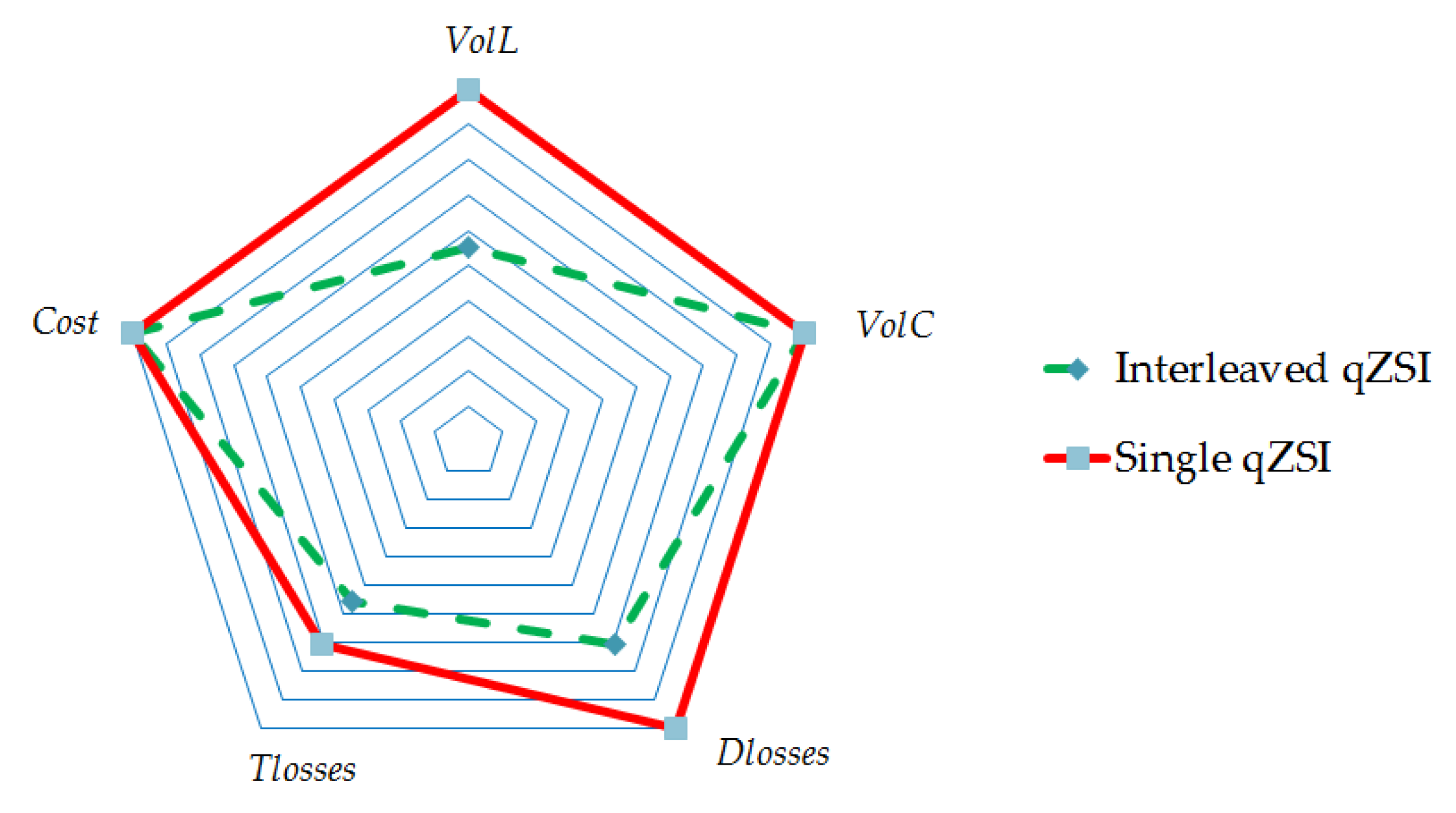
3. Component Selection and Comparison
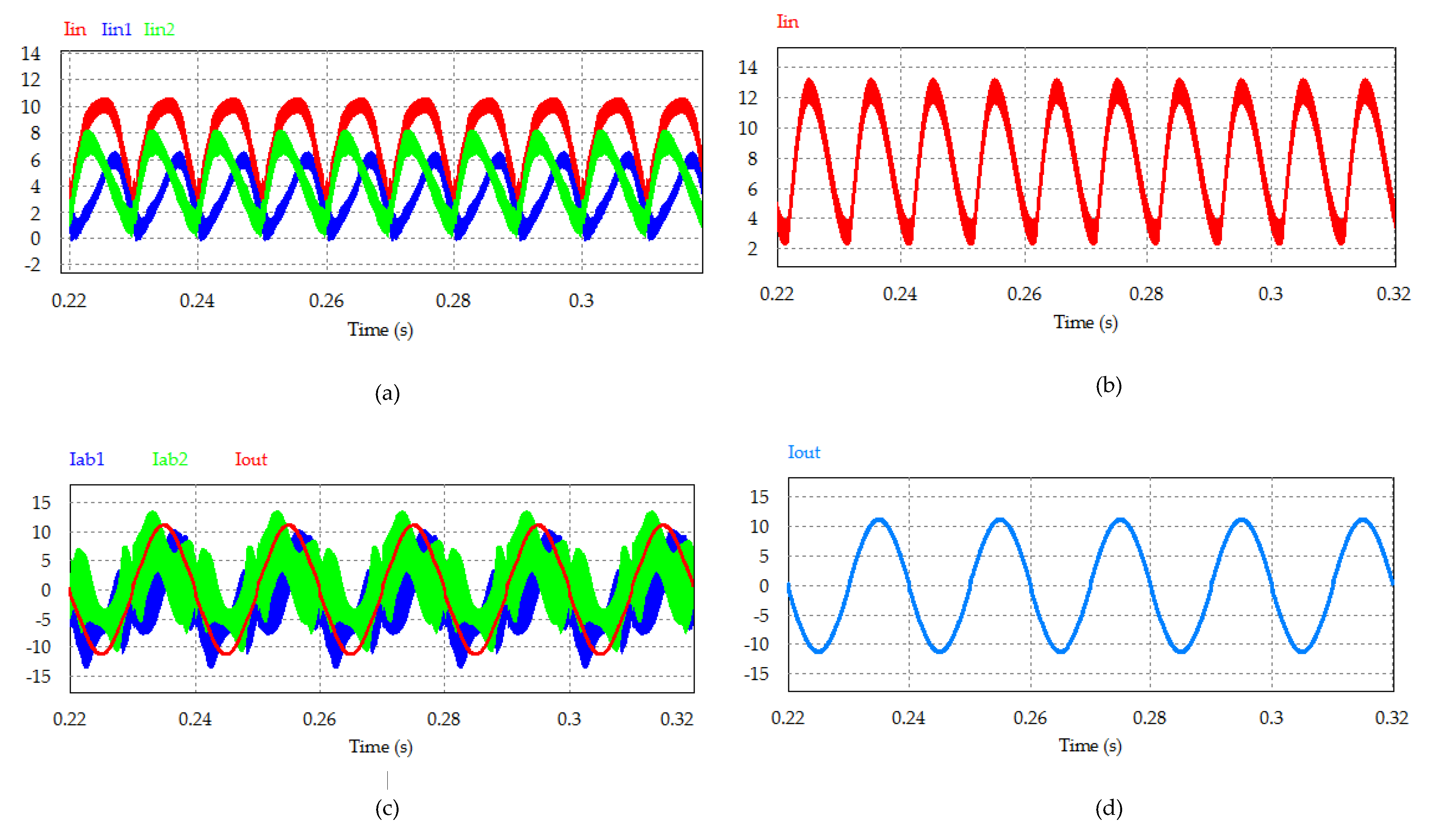
4. Simulation and Experimental Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bortis, D.; Neumayr, D.; Kolar, J.W. ηρ-Pareto optimization and comparative evaluation of inverter concepts considered for the GOOGLE Little Box Challenge. In Proceedings of the IEEE 17th Workshop on Control and Modeling for Power Electronics (COMPEL), Trondheim, Norway, 27–30 June 2016; pp. 1–5. [Google Scholar]
- Morsy, A.; Enjeti, P. Comparison of Active Power Decoupling Methods for High-Power-Density Single-Phase Inverters Using Wide-Bandgap FETs for Google Little Box Challenge. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 790–798. [Google Scholar] [CrossRef]
- Kaminski, N.; Hilt, O. SiC and GaN Devices—Competition or Coexistence. In Proceedings of the 2012 7th International Conference on Integrated Power Electronics Systems (CIPS), Nuremberg, Germany, 6–8 March 2012; pp. 1–11. [Google Scholar]
- Kroics, K.; Zakis, J.; Suzdalenko, A.; Husev, O. Design Considerations for Gan-Based Microinverter for Energy Storage Integration Into Ac Grid. Latv. J. Phys. Tech. Sci. 2017, 54, 14–25. [Google Scholar] [CrossRef] [Green Version]
- Hoene, E.; Ostmann, A.; Marczok, C. Packaging Very Fast Switching Semiconductors. In Proceedings of the 8th International Conference on Integrated Power Electronics Systems, Nuremberg, Germany, 25–27 February 2014; pp. 1–7. [Google Scholar]
- Singh, R.; Asif, A.A. Ultra Large Scale Manufacturing Challenges of Silicon Carbide and Gallium Nitride Based Power Devices and Systems. ECS Trans. 2016, 75, 11. [Google Scholar] [CrossRef] [Green Version]
- Peng, F.Z. Z-Source Inverter. IEEE Trans. Ind. Appl. 2003, 39, 504–510. [Google Scholar] [CrossRef]
- Chub, A.; Vinnikov, D.; Blaabjerg, F.; Peng, F.Z. A Review of Galvanically Isolated Impedance-Source DC–DC Converters. IEEE Trans. Power Electron. 2016, 31, 2808–2828. [Google Scholar] [CrossRef]
- Husev, O.; Strzelecki, R.; Blaabjerg, F.; Chopyk, V.; Vinnikov, D. Novel family of single-phase modified impedance-source buck-boost multilevel inverters with reduced switch count. IEEE Trans. Power Electron. 2016, 31, 7580–7591. [Google Scholar] [CrossRef]
- Siwakoti, Y.P.; Peng, F.; Blaabjerg, F.; Loh, P.; Town, G.E. Impedance Source Networks for Electric Power Conversion Part-II: Review of Control Method and Modulation Techniques. IEEE Trans. Power Electron. 2015, 30, 1887–1906. [Google Scholar] [CrossRef]
- Liu, Y.; Abu-Rub, H.; Ge, B. Z-source/quasi-Z-source inverters: Derived networks, modulations, controls, and emerging applications to photovoltaic conversion. IEEE Ind. Electron. Mag. 2014, 8, 32–44. [Google Scholar] [CrossRef]
- Husev, O.; Roncero-Clemente, C.; Romero-Cadaval, E.; Vinnikov, D.; Stepenko, S. Single phase three-level neutral-point-clamped quasi-Z-source inverter. IET Power Electron. 2015, 8, 1–10. [Google Scholar] [CrossRef]
- Samadian, A.; Hosseini, S.H.; Sabahi, M.; Maalandish, M. A New Coupled Inductor Non-isolated High step up Quasi Z-Source DC-DC Converter. IEEE Trans. Ind. Electron. 2019. [Google Scholar] [CrossRef]
- Nguyen, M.-K.; Tran, T.-T.; Zare, F. An Active Impedance-Source Three-Level T-Type Inverter with Reduced Device Count. IEEE J. Emerg. Sel. Top. Power Electron. 2019. [Google Scholar] [CrossRef]
- Vinnikov, D.; Roasto, I. Quasi-Z-Source-Based Isolated DC/DC Converters for Distributed Power Generation. IEEE Trans. Ind. Electron. 2011, 58, 192–201. [Google Scholar] [CrossRef] [Green Version]
- Bayhan, S.; Trabelsi, M.; Abu-Rub, H.; Malinowski, M. Finite-Control-Set Model-Predictive Control for a Quasi-Z-Source Four-Leg Inverter under Unbalanced Load Condition. IEEE Trans. Ind. Electron. 2017, 64, 2560–2569. [Google Scholar] [CrossRef]
- Komurcugil, H.; Bayhan, S.; Bagheri, F.; Kukrer, O.; Abu-Rub, H. Model-Based Current Control for Single-Phase Grid-Tied Quasi-Z-Source Inverters with Virtual Time Constant. IEEE Trans. Ind. Electron. 2018, 65, 8277–8286. [Google Scholar] [CrossRef]
- Husev, O.; Blaabjerg, F.; Roncero-Clemente, C.; Romero-Cadaval, E.; Vinnikov, D.; Siwakoti, Y.P.; Strzelecki, R. Comparison of Impedance-Source Networks for Two and Multilevel Buck-Boost Inverter Applications. IEEE Trans. Power Electron. 2016, 31, 7564–7579. [Google Scholar] [CrossRef]
- Burkart, R.; Kolar, J.W.; Griepentrog, G. Comprehensive comparative evaluation of single- and multi-stage three-phase power converters for photovoltaic applications. In Proceedings of the 2012 IEEE International Telecommunications Energy Conference, Scottsdale, AZ, USA, 30 September–4 October 2012; pp. 1–8. [Google Scholar]
- Panfilov, D.; Husev, O.; Blaabjerg, F.; Zakis, J.; Khandakji, K. Comparison of three-phase three-level voltage source inverter with intermediate dc-dc boost converter and quasi-Z-source inverter. IET Power Electron. 2016, 9, 1238–1248. [Google Scholar] [CrossRef]
- Husev, O.; Shults, T.; Vinnikov, D.; Roncero-Clemente, C.; Romero-Cadaval, E.; Chub, A. Comprehensive Comparative Analysis of Impedance-Source Networks for DC and AC Application. Electronics 2019, 8, 405. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Anderson, J.; Peng, F.Z.; Liu, D. Quasi-Z-Source Inverter for Photovoltaic Power Generation Systems. In Proceedings of the 2009 Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; pp. 918–924. [Google Scholar] [CrossRef]
- Stepenko, S.; Husev, O.; Vinnikov, D.; Roncero-Clemente, C.; Pires Pimentel, S.; Santasheva, E. Experimental Comparison of Two-Level Full-SiC and Three-Level Si–SiC Quasi-Z-Source Inverters for PV Applications. Energies 2019, 12, 2509. [Google Scholar] [CrossRef] [Green Version]
- Stepenko, S.; Roncero-Clemente, C.; Husev, O.; Makovenko, E.; Pimentel, S.P.; Vinnikov, D. New interleaved single-phase quasi-Z-source inverter with active power decoupling. In Proceedings of the 2018 IEEE 12th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG 2018), Doha, Qatar, 10–12 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Stepenko, S.; Husev, O.; Pimentel, S.P.; Makovenko, E.; Vinnikov, D. Small Signal Modeling of Interleaved Quasi-Z-Source Inverter with Active Power Decoupling Circuit. In Proceedings of the 2018 IEEE 59th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 12–13 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Roncero-Clemente, C.; Husev, O.; Stepenko, S.; Romero-Cadaval, E.; Vinnikov, D. Interleaved single-phase quasi-Z-source inverter with special modulation technique. In Proceedings of the 2017 IEEE First Ukraine Conference on Electrical and Computer Engineering (UKRCON), Kiev, Ukraine, 29 May–2 June 2017; pp. 593–598. [Google Scholar] [CrossRef]
- Roncero-Clemente, C.; Stepenko, S.; Husev, O.; Romero-Cadaval, E.; Vinnikov, D. Maximum boost control for interleaved single-phase Quasi-Z-Source inverter. In Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 7698–7703. [Google Scholar] [CrossRef]
- Zhang, L.; Ruan, X. Control Schemes for Reducing Second Harmonic Current in Two-Stage Single-Phase Converter: An Overview from DC-Bus Port-Impedance Characteristics. IEEE Trans. Power Electron. 2019, 34, 10341–10358. [Google Scholar] [CrossRef]
- Nguyen, M.K.; Tran, T.T.; Lim, Y.C. A Family of PWM Control Strategies for Single-Phase Quasi-Switched-Boost Inverter. IEEE Trans. Power Electron. 2019, 34, 1458–1469. [Google Scholar] [CrossRef]
- Zhang, L.; Ruan, X.; Ren, X. Second-harmonic current reduction for two-stage inverter with boost-derived front-end converter: Control schemes and design considerations. IEEE Trans. Power Electron. 2018, 33, 1458–1469. [Google Scholar] [CrossRef]
- Zhang, L.; Ruan, X.; Ren, X. One-cycle control for electrolytic capacitor-less second harmonic current compensator. IEEE Trans. Power Electron. 2018, 33, 1724–1739. [Google Scholar] [CrossRef]
- Gambhir, A.; Mishra, S.K.; Joshi, A. Power Frequency Harmonic Reduction and its Redistribution for Improved Filter Design in Current-Fed Switched Inverter. IEEE Trans. Ind. Electron. 2019, 66, 4319–4333. [Google Scholar] [CrossRef]
- Sullivan, C.R.; Awerbuch, J.; Latham, A.M. Decrease in photovoltaic power output from ripple: Simple general calculation and effect of partial shading. IEEE Trans. Power Electron. 2013, 28, 740–744. [Google Scholar] [CrossRef]
- Schrittwieser, L.; Leibl, M.; Haider, M.; Thöny, F.; Kolar, J.W.; Soeiro, T.B. 99.3% Efficient Three-Phase Buck-Type All-SiC SWISS Rectifier for DC Distribution Systems. IEEE Trans. Power Electron. 2019, 34, 126–140. [Google Scholar] [CrossRef]
- Kasper, M.; Antivachis, M.; Bortis, D.; Kolar, J.W.; Deboy, G. 4D-Interleaving of Isolated ISOP Multi-Cell Converter Systems for Single Phase AC/DC Conversion. In Proceedings of the PCIM Europe 2016: International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 10–12 May 2016; pp. 7698–7703. [Google Scholar] [CrossRef]
- Ren, Y.; Xu, M.; Zhou, J.; Lee, F.C. Analytical loss model of power MOSFET. IEEE Trans. Power Electron. 2006, 21, 310–319. [Google Scholar]
- Application Note. Available online: http://application-notes.digchip.com/070/70-41484.pdf (accessed on 5 February 2020).
- Ma, C.L.; Lauritzen, P.O. A Simple Power Diode Model with Forward and Reverse Recovery. IEEE Trans. Power Electron. 1993, 8, 342–346. [Google Scholar] [CrossRef]





| System Parameters | Values |
|---|---|
| Nominal power Pnom, W | 1800 |
| Nominal input voltage Vnom, V | 200–600 |
| Nominal input current Inom, A | 5 |
| Output RMS voltage Vload, V | 230 |
| Output current THD, % | <3 |
| Input current ripple ΔI, % | <10 |
| Interleaved qZSI | Single qZSI | |
|---|---|---|
| HF current ripple, % | 70 | 35 |
| qZS inductance L1, L2, mH | 0.9 | 0.9 |
| Maximum current across inductance, A | 3.4 | 5.9 |
| Voltage ripple across C1, % | <1 | <1 |
| qZS capacitor C1, mF | 0.68 | 1.36 |
| Maximum voltage across capacitor C1, V | 500 | |
| Voltage ripple across C2, % | <1 | <1 |
| qZS capacitor C2, mF | 1.5 | 3 |
| Maximum voltage across capacitor C2, V | 250 | |
| Switching frequency, kHz | 60 | |
| Interleaved qZSI | Single qZSI | |
|---|---|---|
| Transistors | ||
| Type | C2M0160120D | C2M0080120D |
| Blocking voltage, V | 1200 | |
| Total Gate Charge, nC | 34 | 62 |
| Diode reverse recovery charge, nC | 192 | 105 |
| Turn-on delay time, ns | 9 | 11 |
| Rise time, ns | 11 | 20 |
| Turn-off time delay, ns | 16 | 23 |
| Fall time, ns | 10 | 19 |
| Rds, mOhms | 160 | 80 |
| Cost, Euro | 7.5 | 15 |
| Diodes | ||
| Type | C4D05120A | C4D10120A |
| Blocking voltage, V | 1200 | |
| Forward voltage drop, V | 1.9 | 2.2 |
| Reverse recovery charge, nC | 23 | 45 |
| Diode reverse recovery time | - | - |
| Current, A | 5 | 10 |
| Cost, Euro | 5.04 | 10.13 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stepenko, S.; Husev, O.; Vinnikov, D.; Fesenko, A.; Matiushkin, O. Feasibility Study of Interleaving Approach for Quasi-Z-Source Inverter. Electronics 2020, 9, 277. https://doi.org/10.3390/electronics9020277
Stepenko S, Husev O, Vinnikov D, Fesenko A, Matiushkin O. Feasibility Study of Interleaving Approach for Quasi-Z-Source Inverter. Electronics. 2020; 9(2):277. https://doi.org/10.3390/electronics9020277
Chicago/Turabian StyleStepenko, Serhii, Oleksandr Husev, Dmitri Vinnikov, Artem Fesenko, and Oleksandr Matiushkin. 2020. "Feasibility Study of Interleaving Approach for Quasi-Z-Source Inverter" Electronics 9, no. 2: 277. https://doi.org/10.3390/electronics9020277
APA StyleStepenko, S., Husev, O., Vinnikov, D., Fesenko, A., & Matiushkin, O. (2020). Feasibility Study of Interleaving Approach for Quasi-Z-Source Inverter. Electronics, 9(2), 277. https://doi.org/10.3390/electronics9020277








