Bidirectional Short-Circuit Current Blocker for DC Microgrid Based on Solid-State Circuit Breaker
Abstract
:1. Introduction
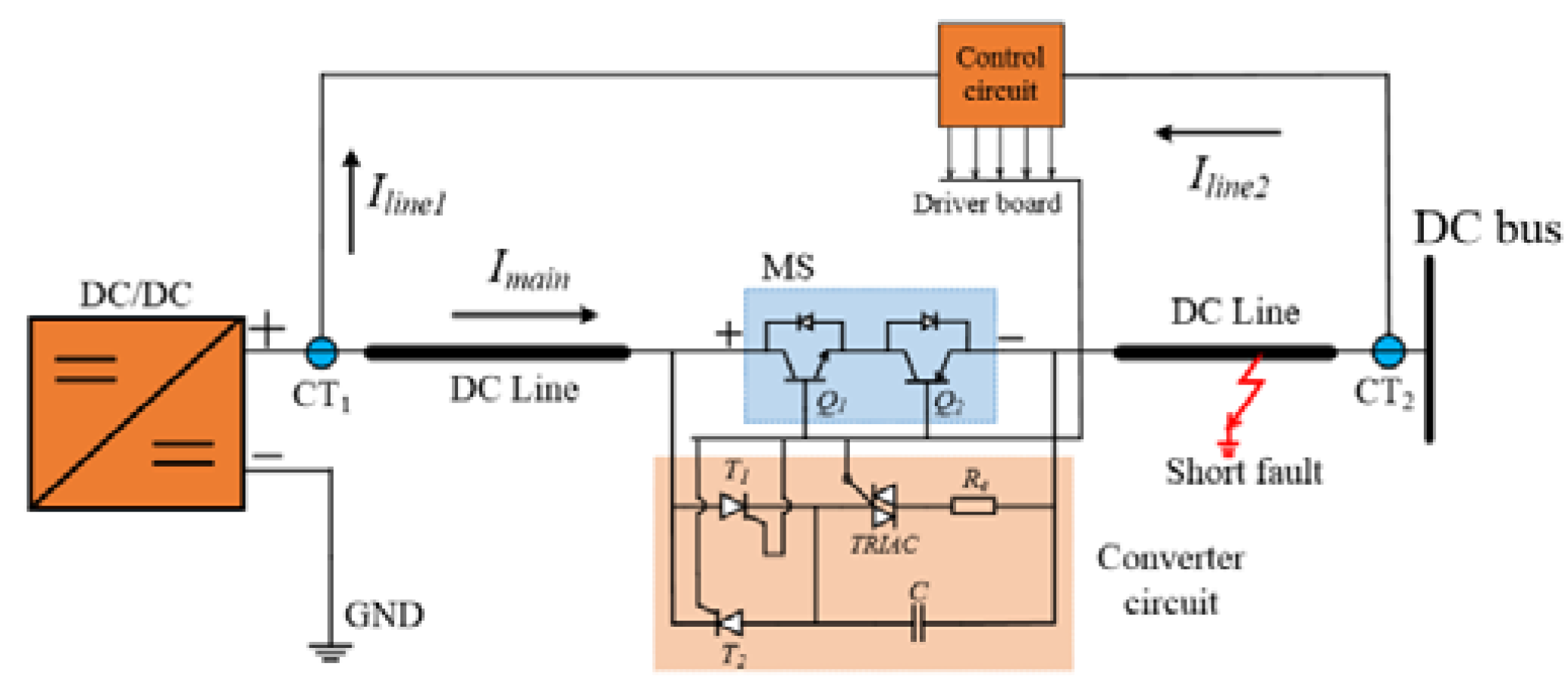
2. Working Principle of the Bidirectional DC Solid-State Circuit Breaker
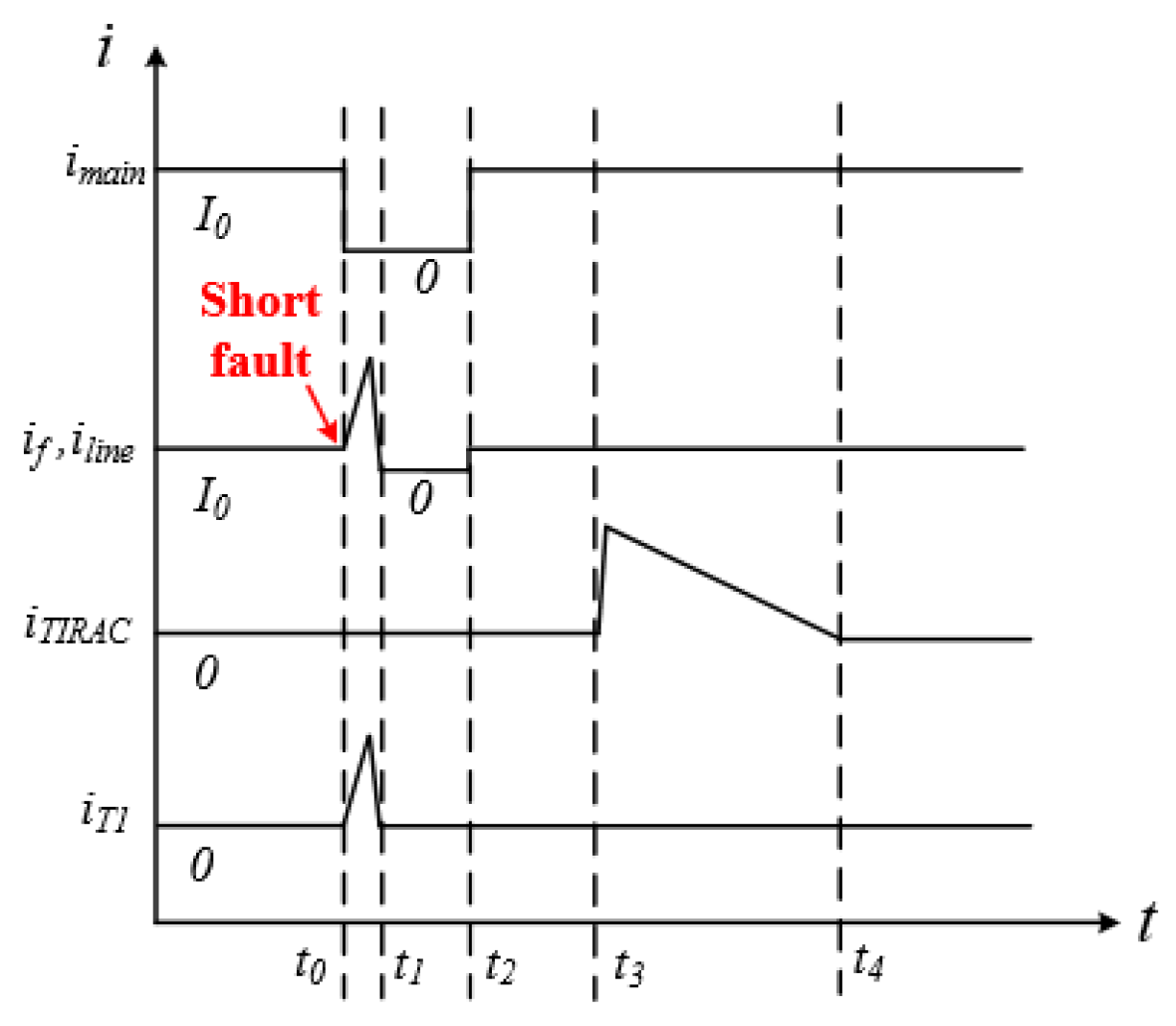
2.1. Normal Operating Mode (t < t0)
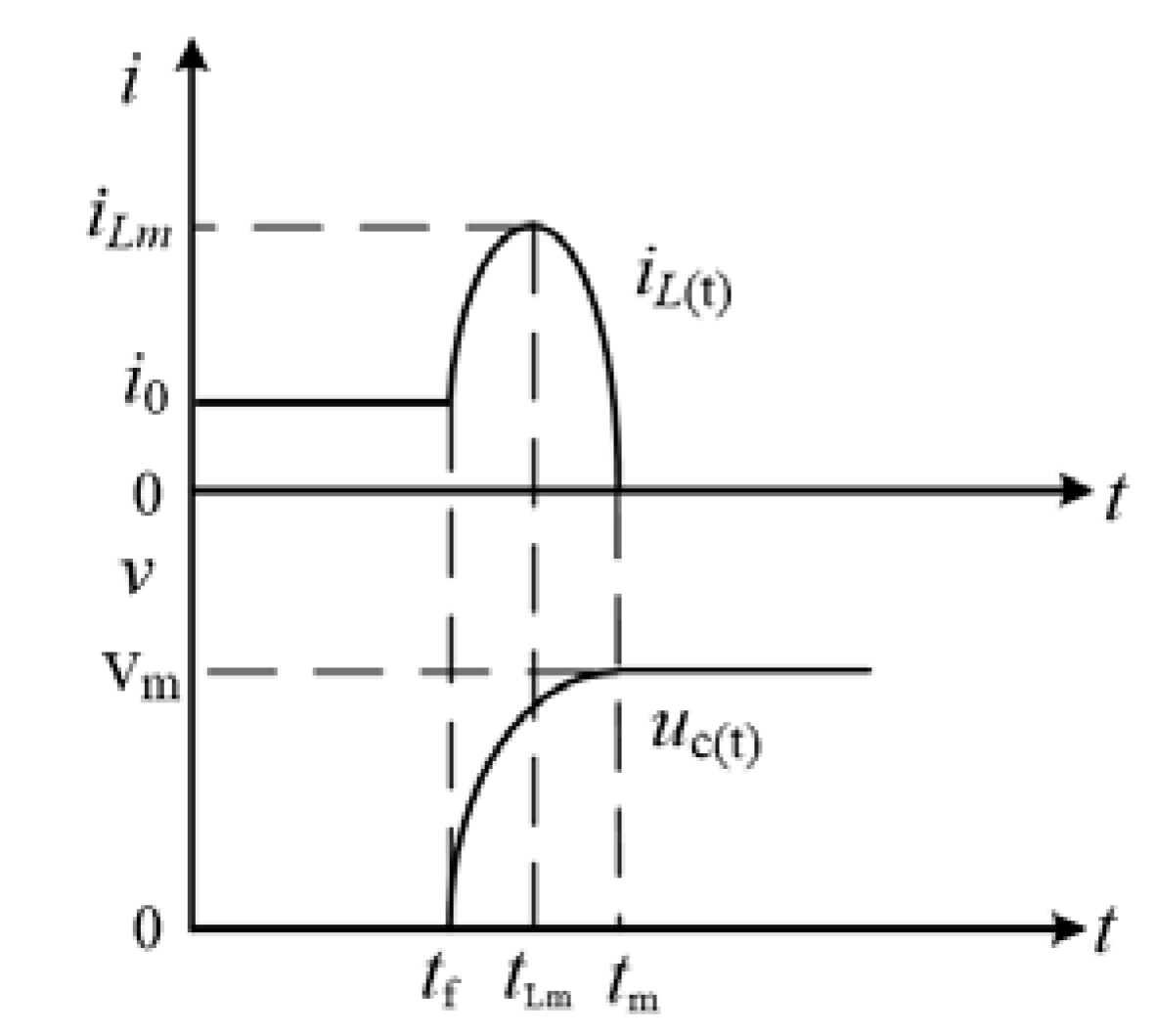
2.2. Blocking Capacitor Charging Stage (t0 ≤ t < t1)
2.3. Fault-Current-Blocked Stage (t1 ≤ t < t2)
2.4. Reclosing Stage (t2 ≤ t < t3)
2.5. Dump Energy Releasing Stage (t3 ≤ t < t4)
3. Control Strategy of Proposed BSCCB
3.1. Differential Protection Strategy
3.2. Switch Timing Sequence Setting
4. Parameter Design
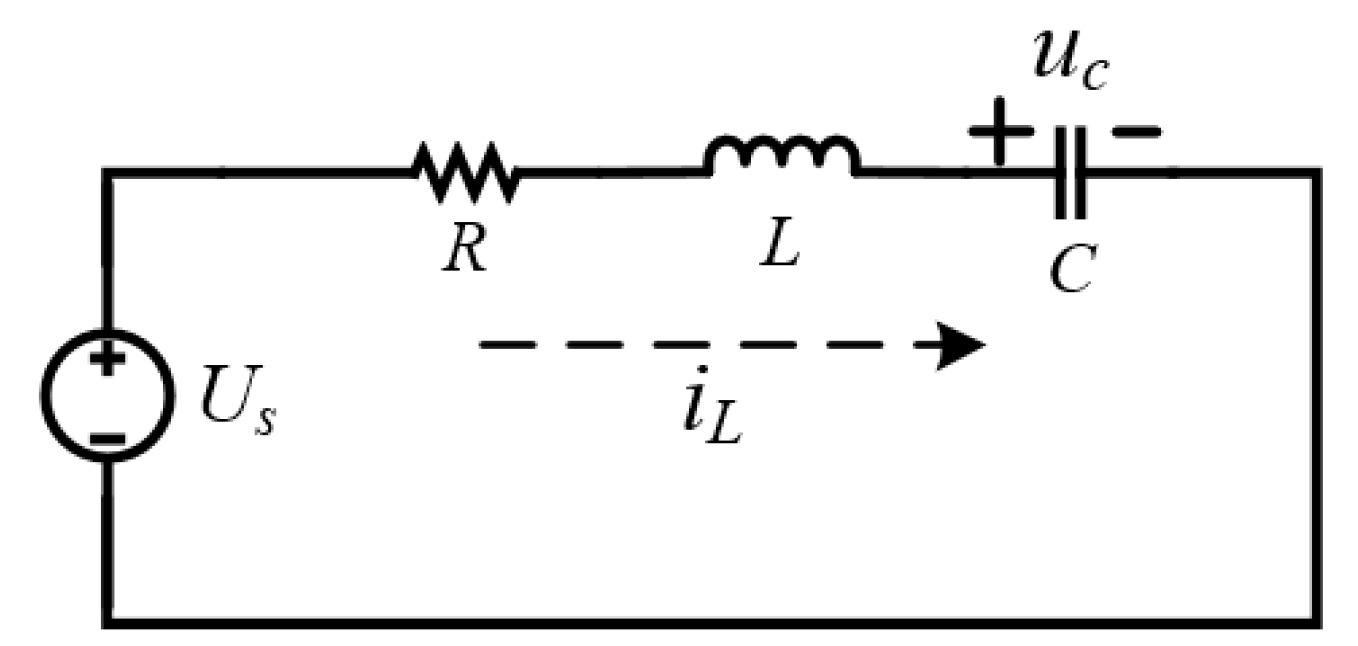
4.1. Capacitor Charging Stage
4.2. Energy Release Phase
4.3. Energy Loss Analysis
4.4. Analysis of Parameters
4.4.1. The Selection of Blocking Capacitor C
4.4.2. The Selection of Re
5. Performance Evaluation and Analysis
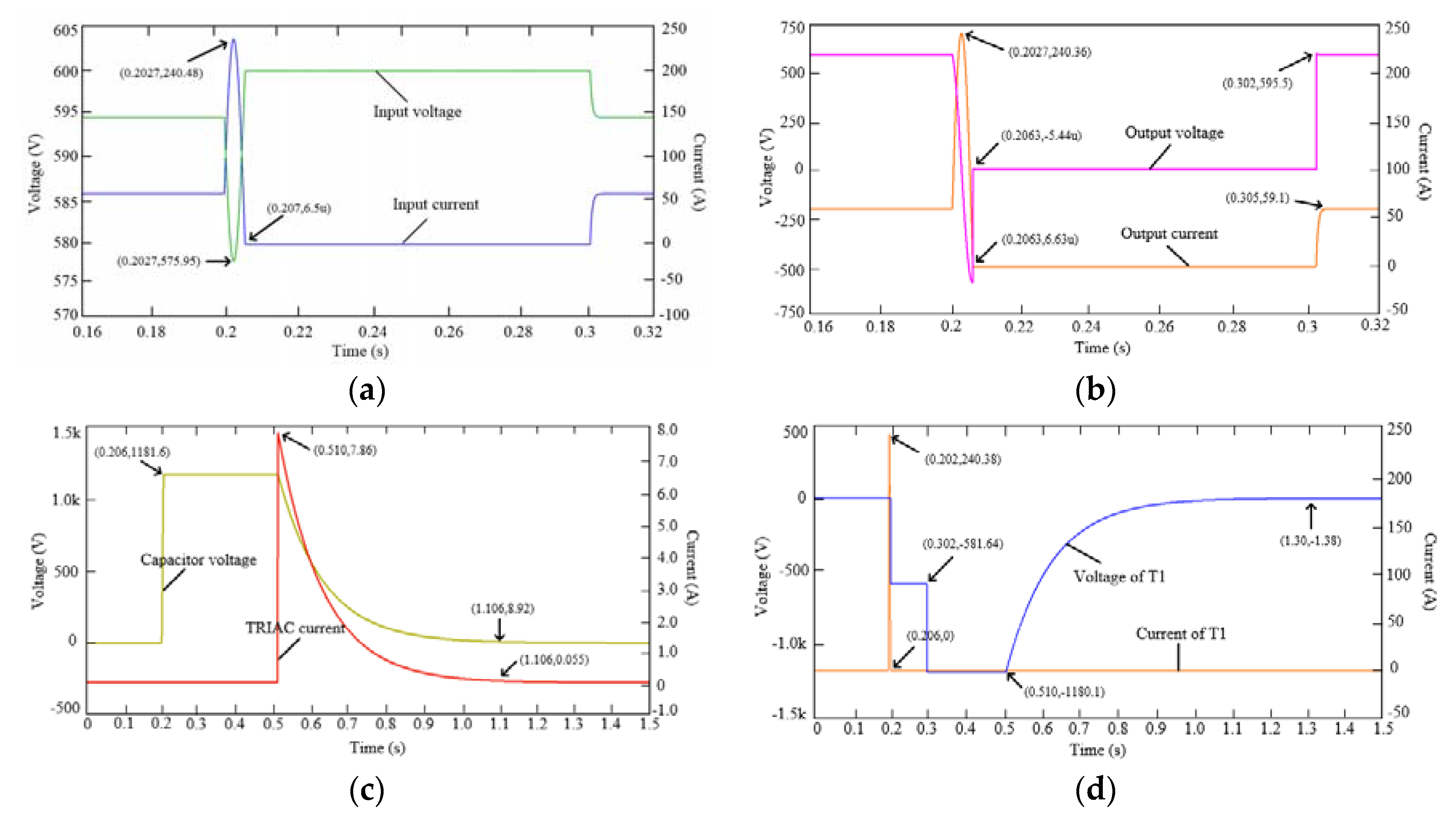
5.1. Simulation Results
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rouzbehi, K.; Miranian, A.; Escano, J.M.; Rakhshani, E.; Shariati, N.; Pouresmaeil, E. A Data-Driven Based Voltage Control Strategy for DC-DC Converters: Application to DC Microgrid. Electronics 2019, 8, 493. [Google Scholar] [CrossRef] [Green Version]
- Silva, P.; Claudio, M.D.S.M. A Promising Future to DC Power System: A Review. IEEE Lat. Am. Trans. 2017, 15, 1639–1642. [Google Scholar] [CrossRef]
- Salomonsson, D.; Soder, L.; Sannino, A. Protection of Low-Voltage DC Microgrids. IEEE Trans. Power Deliv. 2009, 24, 1045–1053. [Google Scholar] [CrossRef]
- Virdag, A.; Hager, T.; Doncker, R.W.D. Estimation of short-circuit currents in future LVDC microgrids. Cired Open Access Proc. J. 2017, 2017, 1098–1101. [Google Scholar] [CrossRef] [Green Version]
- Abramovitz, A.; Smedley, K.M. Survey of Solid-State Fault Current Limiters. IEEE Trans. Power Electron. 2012, 27, 2770–2782. [Google Scholar] [CrossRef]
- Qi, L.; Antoniazzi, A.; Raciti, L. Design of Solid-State Circuit Breaker Based Protection for DC Shipboard Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 260–268. [Google Scholar] [CrossRef]
- Amir Khan, U.; Lee, J.G.; Amir, F. A Novel Model of HVDC Hybrid-Type Superconducting Circuit Breaker and Its Performance Analysis for Limiting and Breaking DC Fault Currents. IEEE Trans. Appl. Supercond. 2015, 25, 1–9. [Google Scholar] [CrossRef]
- Song, S.M.; Kim, J.Y.; Choi, S.S. New Simple-Structured AC Solid-State Circuit Breaker. IEEE Trans. Ind. Electron. 2018, 65, 8455–8463. [Google Scholar] [CrossRef]
- Magnusson, J.; Saers, R.; Liljestrand, L.; Engdahl, G. Separation of the energy absorption and overvoltage protection in solid-state breakers by the use of parallel varistors. IEEE Trans. Power Electron. 2014, 29, 2715–2722. [Google Scholar] [CrossRef]
- Martin, W.A.; Deng, C.; Fiddiansyah, D. Investigation of low-voltage solid-state DC breaker configurations for DC microgrid applications. IEEE Int. Telecommun. Energy Conf. 2016. [Google Scholar]
- Liu, F.; Liu, W.; Zha, X. Solid-State Circuit Breaker Snubber Design for Transient Overvoltage Suppression at Bus Fault Interruption in Low-Voltage DC Microgrid. IEEE Trans. Power Electron. 2017, 32, 3007–3021. [Google Scholar] [CrossRef]
- Liu, W.; Yang, H.; Liu, F. An improved RCD snubber for solid-state circuit breaker protection against bus fault in low-voltage DC microgrid. IEEE Future Energy Electron. Conf. 2015.
- Meyer, C.; Doncker, R.W.D. LCC analysis of different resonant circuits and solid-state circuit breakers for medium-voltage grids. IEEE Trans. Power Deliv. 2006, 21, 1414–1420. [Google Scholar] [CrossRef]
- Radmanesh, H.; Fathi, S.H.; Gharehpetian, G.B. A Novel Solid-State Fault Current-Limiting Circuit Breaker for Medium-Voltage Network Applications. IEEE Trans. Power Deliv. 2016, 31, 236–244. [Google Scholar] [CrossRef]
- Ghanbari, T.; Farjah, E. Development of an Efficient Solid-State Fault Current Limiter for Microgrid. IEEE Trans. Power Deliv. 2013, 28, 361–369. [Google Scholar] [CrossRef]
- Hagh, M.T.; Abapour, M. DC reactor type transformer inrush current limiter. Iet Elect. Power Appl. 2007, 1, 808–814. [Google Scholar] [CrossRef]
- Radmanesh, H.; Fathi, S.H.; Gharehpetian, G.B. Series Transformer-Based Solid-State Fault Current Limiter. IEEE Trans. Smart Grid 2015, 6, 1983–1991. [Google Scholar] [CrossRef]
- Hassanpoor, A.; Hafner, J.; Jacobson, B. Technical Assessment of Load Commutation Switch in Hybrid HVDC Breaker. IEEE Trans. Power Electron. 2015, 35, 5393–5400. [Google Scholar] [CrossRef]
- Hafner, J.; Jacobson, B. Proactive hybrid HVDC breakers—A key innovation for reliable HVDC grids. In Proceedings of the CIGRE International Symposium on The Electric Power System of the Future, Italy, Bologna, 13–15 September 2011; pp. 1–9. [Google Scholar]
- Dujic, D.; Steinke, G.K.; Bellini, M.; Rahimo, M.; Storasta, L.; Steinke, J.K. Characterization of 6.5 kV IGBTs for high-power medium frequency soft-switched applications. IEEE Trans. Power Electron. 2014, 29, 906–919. [Google Scholar] [CrossRef]
- Li, S.; Zhao, C.; Xu, J. A new topology for current-limiting solid-state HVDC circuit breaker. In Proceedings of the 2016 IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5–8 December 2016. [Google Scholar]

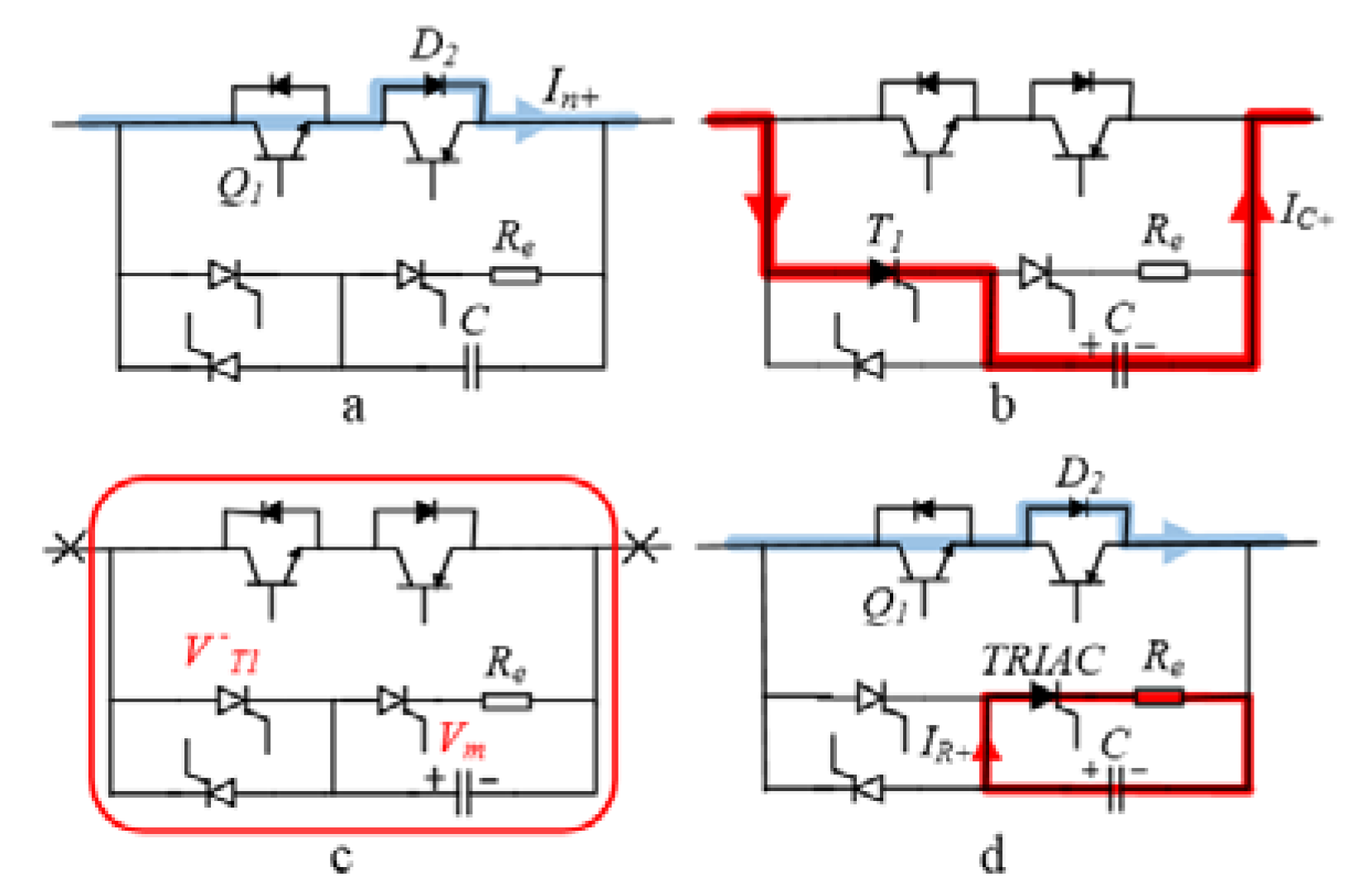





| Switch | Q1/Q2 | T1/T2 | TRIAC | |
|---|---|---|---|---|
| Mode | ||||
| Normal mode | ON | OFF | OFF | |
| Capacitor charging | OFF | ON | OFF | |
| Circuit blocking | OFF | OFF | OFF | |
| Reclosing | ON | OFF | OFF | |
| Energy release | ON | OFF | ON | |
| C (mF) | Vm (V) | iLm (A) | tm (ms) |
|---|---|---|---|
| 0.1 | 1333 | 104 | 2.0 |
| 0.2 | 1256 | 133 | 2.7 |
| 0.4 | 1212 | 177 | 4.0 |
| 0.6 | 1191 | 210 | 5.0 |
| 0.8 | 1179 | 239 | 6.0 |
| 1.0 | 1171 | 265 | 7.0 |
| 1.2 | 1165 | 288 | 7.3 |
| 1.4 | 1159 | 309 | 7.9 |
| 1.6 | 1151 | 347 | 8.5 |
| R (Ω) | ic(0+) (A) | tr (s) |
|---|---|---|
| 50 | 24.0 | 0.2 |
| 100 | 11.8 | 0.4 |
| 150 | 7.8 | 0.6 |
| 200 | 5.9 | 0.8 |
| 250 | 4.7 | 1.0 |
| Parameter | Value | Instructions |
|---|---|---|
| Rs | 0.1 Ω | Input resistance |
| Ls | 1 uH | Input inductance |
| Rload | 10 Ω | Load resistance |
| Lload | 5 mH | Load inductance |
| C | 0.8 mF | Blocking capacitor |
| Re | 150 Ω | Release resistance |
| VDC | 600 V | DC bus voltage |
| Parameters | Vm | |||||
|---|---|---|---|---|---|---|
| RC Circuit | ||||||
| 0.1 mF, 50 Ω | 1335 V | 105 A | 26.6 A | 2 ms | 30 ms | |
| 0.1 mF, 150 Ω | 1335 V | 105A | 8.9 A | 2 ms | 90 ms | |
| 0.8 mF, 50 Ω | 1181 V | 240 A | 23.6 A | 6 ms | 380 ms | |
| 0.8 mF, 150 Ω | 1181 V | 240 A | 7.8 A | 6 ms | 800 ms | |
| 1.6 mF, 50 Ω | 1156 V | 330 A | 23 A | 9 ms | 1500 ms | |
| 1.6 mF, 150 Ω | 1156 V | 330 A | 7.7 A | 9 ms | 1600 ms | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Feng, B.; Wang, Y.; Wu, T.; Lin, H. Bidirectional Short-Circuit Current Blocker for DC Microgrid Based on Solid-State Circuit Breaker. Electronics 2020, 9, 306. https://doi.org/10.3390/electronics9020306
Wang L, Feng B, Wang Y, Wu T, Lin H. Bidirectional Short-Circuit Current Blocker for DC Microgrid Based on Solid-State Circuit Breaker. Electronics. 2020; 9(2):306. https://doi.org/10.3390/electronics9020306
Chicago/Turabian StyleWang, Lujun, Boyu Feng, Yu Wang, Tiezhou Wu, and Huipin Lin. 2020. "Bidirectional Short-Circuit Current Blocker for DC Microgrid Based on Solid-State Circuit Breaker" Electronics 9, no. 2: 306. https://doi.org/10.3390/electronics9020306
APA StyleWang, L., Feng, B., Wang, Y., Wu, T., & Lin, H. (2020). Bidirectional Short-Circuit Current Blocker for DC Microgrid Based on Solid-State Circuit Breaker. Electronics, 9(2), 306. https://doi.org/10.3390/electronics9020306




