Nonlinear Dynamics, Switching Kinetics and Physical Realization of the Family of Chua Corsage Memristors

Abstract

This article reviews the nonlinear dynamical attributes, switching kinetics, bifurcation analysis, and physical realization of a family of generic memristors, namely, Chua corsage memristors (CCM). CCM family contains three 1-st order generic memristor dubbed as 2-lobe, 4-lobe, and 6-lobe Chua corsage memristors and can be distinguished in accordance with their asymptotic stable states. The 2-lobe CCM has two asymptotically stable equilibrium states and regarded as a binary memory device. In contrast, the versatile 4-lobe CCM and 6-lobe CCM are regarded as a multi-bit-per-cell memory device as they exhibit three and four asymptotic stable states, respectively, on their complex and diversified dynamic routes. Due to the diversified dynamic routes, the CC memristors exhibit a highly nonlinear DC V-I curve. Unlike most published highly-nonlinear DC V-I curves with several disconnected branches, the DC V-I curves of CCMs are contiguous along with a locally active negative slope region. Moreover, the DC V-I curves and parametric representations of the CCMs are explicitly analytical. Switching kinetics of the CCM family can be demonstrated with universal formulas of exponential state trajectories x_n(t), time period t_fn, and applied minimum pulse amplitude V_A and width Δw. These formulas are regarded universal as they can be applied to any piecewise linear dynamic routes for any DC or pulse input and with any number of segments. When local activity, and bifurcation and chaos theorems are employed, CMMs exhibit unique stable limit cycles spawn from a supercritical Hopf bifurcation along with static attractors. In addition, the nonlinear circuit and system theoretic approach is applied to explain the asymptotic stability behavior of CCMs and to design real memristor emulators using off-the-shelf circuit components.

1. Introduction

Memristor is a nonlinear two-terminal electrical component that completes a theoretical quartet of fundamental electrical components by relating electric charge and magnetic flux linkage. It was postulated by Leon Chua [1] and later generalized to a broader class of dynamical circuit-theoretic concept to a memristive system [2]. Memristor creates immense attention after the seminal paper published by hp in 2008, which reveals that the electrical resistance of the device is not constant, but depends on the history of previous inputs [3]. It is considered as one of the most promising element in emerging memory sector [4,5,6] and neural applications [7,8], due to its propitious attributes under DC or AC excitation and miniature nanoscale physical dimension along with synapse alike operation. Recently, numerous research activities are ongoing on binary and multistate phenomena in generic and extended memristors [9,10,11,12,13,14,15,16] which could lead to another stage of technical innovation in the memristor area. Nonlinear dynamics theory, and circuit and system theoretic concepts can be devoted to explaining the principle of the multistate memristors [9].

This review paper presents an in-depth and rigorous nonlinear and bifurcation analysis, switching kinetics, and physical realization of the three members of Chua corsage memristor (CCM) family. The CC memristors exhibit a highly nonlinear DC V-I curves, due to the presence of a higher degree of versatility in its dynamic route map (DRM) which has multiple stable equilibrium points. The DC V-I curves of CCMs are contiguous compared to most published highly-nonlinear DC V-I curves which have several disconnected branches. The DC V-I curves of CCMs have an explicit analytical equation with its parametric representation that rarely happens. In addition, each member of CCM family exhibits a negative slope region on its DC V-I curve which give rise to complexity by exploiting local activity; and complex phenomenon and information processing might emerge over the parameter ranges of CCMs either operating on or near the neighborhood of its edge of chaos domain [12,13,14,15,16].

The locally active CCM family exhibit asymptotical stability via the supercritical Hopf bifurcation [13,14,15,16]. The state altering of CCMs follows the nonlinear dynamic route of a chosen initial state x_n(0) and repeats until the state reaches in a particularly stable state which is termed as an “attractor”. The state space of CCMs contain various attractors, and each attractor has its own basin of attraction [13,14,15,16]. The equilibrium state of these type of memristors moves by the amount of time integral of applied inputs or noises that are applied at a stable equilibrium state. However, the state of CCMs returns back to its original equilibrium state (attractor), unless the state moves beyond the boundary of the current basin of attraction [13,14,15,16]. Therefore, it can be utilized as a robust bistable or multistate memory device. However, the CC memristors lost a part of previous programming history in this procedure, where such a phenomenon is known as “local fading memory” in bistable and multistate memory devices [10,11].

Another feature of the multistate CCMs is the alteration of stable equilibria which requires an input pulse, either a sufficiently large amplitude with a short pulse width or a minimum pulse amplitude with lengthy pulse width. When input pulse is applied, the corsage memristors switch from one stable equilibrium state to another stable state by converging into the basin of the new stable attractor. The resistances or conductances of each attractor, i.e., stable equilibrium states, are distinguishably different from each other [12,13,14,15,16]. The successful alteration of the stable equilibria of CCMs is dependent on applied input pulse amplitude and width along with the initial condition. Trajectory movement of the altering equilibria can be demonstrated by computing the time-dependent exponential state trajectories x_n(t) for an individual straight-line segment of PWL DRM where time t = t_fn is required for the trajectory of x_n(t) to move from any initial point to the end point of that particular segment.

In spite of theoretical insights, concepts from circuit and system theory, and techniques from nonlinear dynamics theory are devoted in this review to investigate the physical realization of the real emulator circuits for CCM family. To design a physical emulator circuit for CCMs, at least a passive nonlinear-resistive two-port along with a dynamic first-order one-port is required [10,11,12]. The passive nonlinear-resistive two-port is designed with two parallel connected Graetz bridges [17]. In contrast, the dynamic first-order one-port is designed with a capacitor in parallel with an active and locally active resistor where the resistor must exhibit the behavioral attributes of piecewise linear CCMs.

Rest of the article is organized as follows: Introduction of CCM family and their nonlinear dynamical attributes are presented in Section 2, followed by memory state switching kinetics in Section 3. Local activity and Hopf bifurcation are analyzed in Section 4, and the physical realization of CCM emulator is demonstrated in Section 5. Section 6 contains the concluding remarks.

2. CCM Family and their Nonlinear Dynamical Attributes

The versatile CCM family has three types of generic memristors, namely, 2-lobe CCM, 4-lobe CCM, and 6-lobe CCM. The state-dependent Ohm’s law and the piecewise linear state equations of the CCMs are defined as

State–Dependent Ohm’s Law:

$$i=G\left(x\right)v,$$

(1)

where

$$G\left(x\right)=G_0{x}^2,$$

(2)

and

State Equation:

$$\raisebox{1ex}{$dx$}\!\left/ \!\raisebox{-1ex}{$dt$}\right.=f_m\left(x\right)+v,$$

(3)

where x, v, and I denote the memristor state, voltage, and current, respectively. The intrinsic memductance scale of the memristor is fitted with scaling constant G₀ and choose such a way so that the parameters of small-signal equivalent circuit or the current of CCMs will not be excessive. For simplicity in this review article, we choose G₀ = 1. The state function f_m(x) (“m = {2, 4, 6}” in Equation (3) represents the lobe number of the CCMs and determines one of the member of CCM family.) of the three types of CCM are different from each other and defined as

$$\mathbf{2}-\mathbf{lobe}\mathit{CCM}:f_2\left(x\right)=30-x+\left|x-20\right|-\left|x-40\right|,$$

(4)

$$\mathbf{4}-\mathbf{lobe}\mathit{CCM}:f_4\left(x\right)=59-x+\left|x-20\right|-\left|x-40\right|+\left|x-65\right|-\left|x-95\right|,$$

(5)

and

$$\mathbf{6}-\mathbf{lobe}\mathit{CCM}:f_6\left(x\right)=33-x+\left|x-6\right|-\left|x-12\right|+\left|x-20\right|-\left|x-30\right|+\left|x-42\right|-\left|x-56\right|.$$

(6)

The CCM family exhibits several interesting nonlinear dynamical attributes. Among them, this section analyzes the dynamic route map (DRM), power-off plot (POP), multivalued DC V-I curves and its explicit parametric representation.

2.1. Dynamic Route Map (DRM) and Power-off Plot (POP)

Any curve f(x, v) plotted in the phase plane, dx/dt vs. x plane, along with the direction of motion from the representative points is called a dynamic route in nonlinear circuit theory. It prescribes the dynamics of defining scalar nonlinear differential equation [18,19]. The dynamic route map (DRM) is the most powerful tool for analyzing the dynamics of any first-order differential equation dx/dt = f(x, v) despite its simplicity. It predicts the evolution of any initial state with increasing time [20]. However, the short-circuited (v = 0) dynamic route is known as the Power-off-Plot (POP) and defined as

$$\raisebox{1ex}{$dx$}\!\left/ \!\raisebox{-1ex}{$dt$}\right.{|}_{v=0}=\widehat{f_m}\left(x, \mathbf{0}\right),$$

(7)

where

$$\widehat{f_m}\left(x,\mathbf{0}\right)=f_m\left(x\right).$$

(8)

The power-off plot of CCM family is shown in Figure 1a–c. Observe from Figure 1a–c that any initial state x(0) on the upper half of the POP, where dx/dt > 0, the state variable x(t) must move to the right as x(t) increases with time. Contrarily, any initial state x(0) on the lower half of the POP, where dx/dt < 0, the state variable x(t) decreases with time and must move to the left. The stationary points, where dx/dt = 0 (i.e., $\widehat{f_m}\left(x\right)$ intersects the x-axis), are known as equilibrium points in the theory of nonlinear dynamics [21]. According to nonlinear dynamics theory, the 2-lobe CCM has three equilibrium points (shown in Figure 1a), whereas, 4-lobe and 6-lobe CCMs contains five (shown in Figure 1b) and seven (shown in Figure 1c) equilibrium points, respectively. Equilibrium points Q₁ (x = X_Q1 = 3), Q₃ (x = X_Q3 = 15), Q₅ (x = X_Q5 = 35), and Q₇ (x = X_Q7 = 63), in Figure 1c, are stable, whereas, Q₂ (x = X_Q2 = 9), Q₄ (x = X_Q4 = 25), and Q₆ (x = X_Q6 = 49) are unstable equilibrium points because the state variable x(t) diverges away from Q₂, Q₄, and Q₆. Similarly, equilibrium point Q₂ (x = X_Q2 = 30) in 2-lobe CCM, and the equilibrium points Q₁ (x = X_Q1 = 31) and Q₃ (x = X_Q3 = 81) in 4-lobe CCM are unstable equilibrium points, as shown in Figure 1a and b, respectively. Moreover, the equilibrium points Q₁, Q₃, Q₅, and Q₇ of 6-lobe CCM (in Figure 1c), Q₀, Q₂, Q₄ of 4-lobe CCM (in Figure 1b), and Q₀, Q₁ of 2-lobe CCM (in Figure 1a) are stable as the corresponding eigenvalues of those equilibrium points of the CCMs are negative real numbers. In contrast, the unstable equilibrium points have positive real eigenvalues [22].

The dynamic route map of the 6-lobe CCM is shown in Figure 1d for input voltages v = V = {−9 V, −7 V, −5 V, −3 V, 0 V, 3 V, 5 V, 7 V, 9 V}. Figure 1d shows that for any applied non-zero positive voltage (v = +V_A), the red curve f(x, 0) is translated upward by V_A units. For example, for v = +3 V, the corresponding DRM f(x, 3) (blue curve) is obtained by translating the red curve (parametrized by v = 0) upwards by 3 units. In contrast, for any non-zero negative voltage (v = −V_A), the red curve f(x, 0) is translated downwards by V_A units, as the DRM for f(x, −7) (burgundy curve) is obtained by translating the red curve (f(x, 0)) downward by 7 units for an input voltage v = −7 V, as shown in Figure 1d.

2.2. DC V-I Curve of CCM

DC V-I loci of the voltage-controlled CCMs are determined through circuit theoretic approach. For each value of voltage V, all equilibria (“k” represents the number of equilibrium points of a CCM.) $x=X_k$ of the CCMs are calculated using state equation (3) where dx/dt = 0 and defined as

$$f_m\left(x\right)=-V.$$

(9)

Then, the DC current i = I of the CCMs are determined at each corresponding equilibrium points as

$$I=G\left(x\right) V=-G_0{X}^2{f}_m\left(x\right)$$

(10)

The DC V-I curves of CCM family are drawn in Figure 2 by plotting the coordinates (V, I) computed from Equations (9) and (10) for each value of X. The solid curves, in Figure 2, correspond to stable equilibrium states, and the dash curves correspond to unstable equilibrium states. Since the DC V-I curve, in Figure 2a, contains two contiguous lobes; hence, the V-I curve is called “two lobes corsage V-I curve” and the generic memristor is named as 2-lobe CCM. Similarly, the DC V-I curves in Figure 2b,c contain four and six contiguous lobes and known as “four lobes corsage V-I curve” and “six lobes corsage V-I curve”, respectively, and the generic memristors are named as 4-lobe CCM and 6-lobe CCM.

The five different colored DC V-I branches in Figure 2b represent the equilibrium points of corresponding colors in Figure 1b. The state variables at v = 0 V are x = 9 (red DC V-I curve Q₀), x = 31 (green DC V-I curve Q₁), x = 49 (blue DC V-I curve Q₂), x = 81 (magenta DC V-I curve Q₃), and x = 109 (purple DC V-I curve Q₄) which reveals that the slopes (i.e., conductances G(x) = G₀ x²) at origin are different and eventually indicates the presence of multiple states. The tabulated upper left inset of Figure 2b shows that the red DC V-I curve represents the lowest conductance state (resp., highest resistance state), whereas, the purple DC V-I curve represents the highest conductance state (resp., lowest resistance state). Similar to 4-lobe CCM, 6-lobe and 2-lobe CCM also exhibit the presence of multistate as shown in Figure 2c, and Figure 2a, respectively. However, the unstable dotted V-I curves correspond to unstable equilibrium points are going to converge either to the upper stable solid V-I curves (for any disturbance δx > X_Qn or δv > V_Qn) or lowering stable V-I curves (for δx < X_Qn or δv < V_Qn), where n determines the number of unstable equilibrium points. This affirms that the 2-lobe CCM has two stable states, whereas, 4-lobe and 6-lobe CCMs have three and four stable states. These stable equilibrium states can be utilized as memory states in a binary or multi-bit-per-cell memory device [12,13,14,15,16].

Moreover, Figure 2a and the lower right inset of Figure 2b and c show that each member of CCM family contain a negative-slope region on its DC V-I curves which reveals that the CC memristors are locally-active over its corresponding negative slope region as Re Z(iω) < 0 for DC input voltage (ω = 0) [14]. The locally-active negative slope region of Chua corsage memristors are significant in circuit theory as they might give rise to complexity through which complex phenomenon and information processing might emerge [23,24].

2.3. Explicit Parametric Representation of CCM

In contrast to DC V-I analysis, the parametric representation of CCMs can be derived for each DC voltage v = V at the DC equilibrium state x = X, namely, ${\raisebox{1ex}{$dx$}\!\left/ \!\raisebox{-1ex}{$dt$}\right.|}_{\left(v=V, x=X\right)}=f_m\left(x\right)+v=0$. In particular, substituting v = V, x = X, and $dx/dt=0$ in (3), and solving for V, one can obtain

$$V=-f_m\left(x\right)\triangleq \widehat{v}\left(X\right).$$

(11)

The parametric representation of the DC curreIt i = I of the CCMs can be derived by substituting V given by (11) for v = V in (1); namely,

$$I=G\left(x\right) V=-G_0{X}^2{f}_m\left(x\right)\triangleq \widehat{i}\left(X\right).$$

(12)

The parametric representations of 6-lobe CCM (Due to the page limit we only analyze the parameter representation of the 6-lobe CCM.) are shown in Figure 3. Figure 3a, and b show the loci of parametric representation of $V =\widehat{v}\left(x\right) vs. X$, and $I =\widehat{i}\left(x\right) vs. X$, respectively, and the loci of parametrically represented $V =\widehat{v}\left(x\right) vs. I =\widehat{i}\left(x\right)$ is shown in Figure 3c.

Observe from Figure 3a,b that the equilibrium state X spans the entire horizontal axis, namely, −∞ < X < ∞. For any value X ∈ (−∞, ∞), one can calculate the corresponding DC voltage V, and DC current I using the exact formulas in Equations (11) and (12), respectively. Each point on the DC V-I curve, shown in Figure 3c, corresponds to an equilibrium state X, which may be stable (solid line), or unstable (dotted line). Since, for voltage −7 V ≤ V ≤ 7 V, the DC V-I curve exhibits multiple values, due to corresponding equilibrium states, hence, known as multivalued DC V-I curve.

It is important to note that the DC V-I curve in Figure 3c is obtained without solving any algebraic, or differential equations. Indeed, it is obtained by substituting any desired value of X, where −∞ < X < ∞, into the explicit analytical equations (11) for $V=\widehat{v}\left(x\right)$ and (12) for $I=\widehat{i}\left(x\right)$. This derivation of CCMs DC V-I curve by direct substitution into the explicit state-dependent Ohm’s law, and state equation is a truly remarkable example for future researchers.

In addition, one of the most important features of CCMs is that the DC V-I curve is contiguous, which is different from many other published nonlinear DC V-I curves which exhibit several disconnected branches [18]. Another impressive feature is that the parametric representation and DC V-I curve of the CCMs have an explicit analytical equation, which rarely happens.

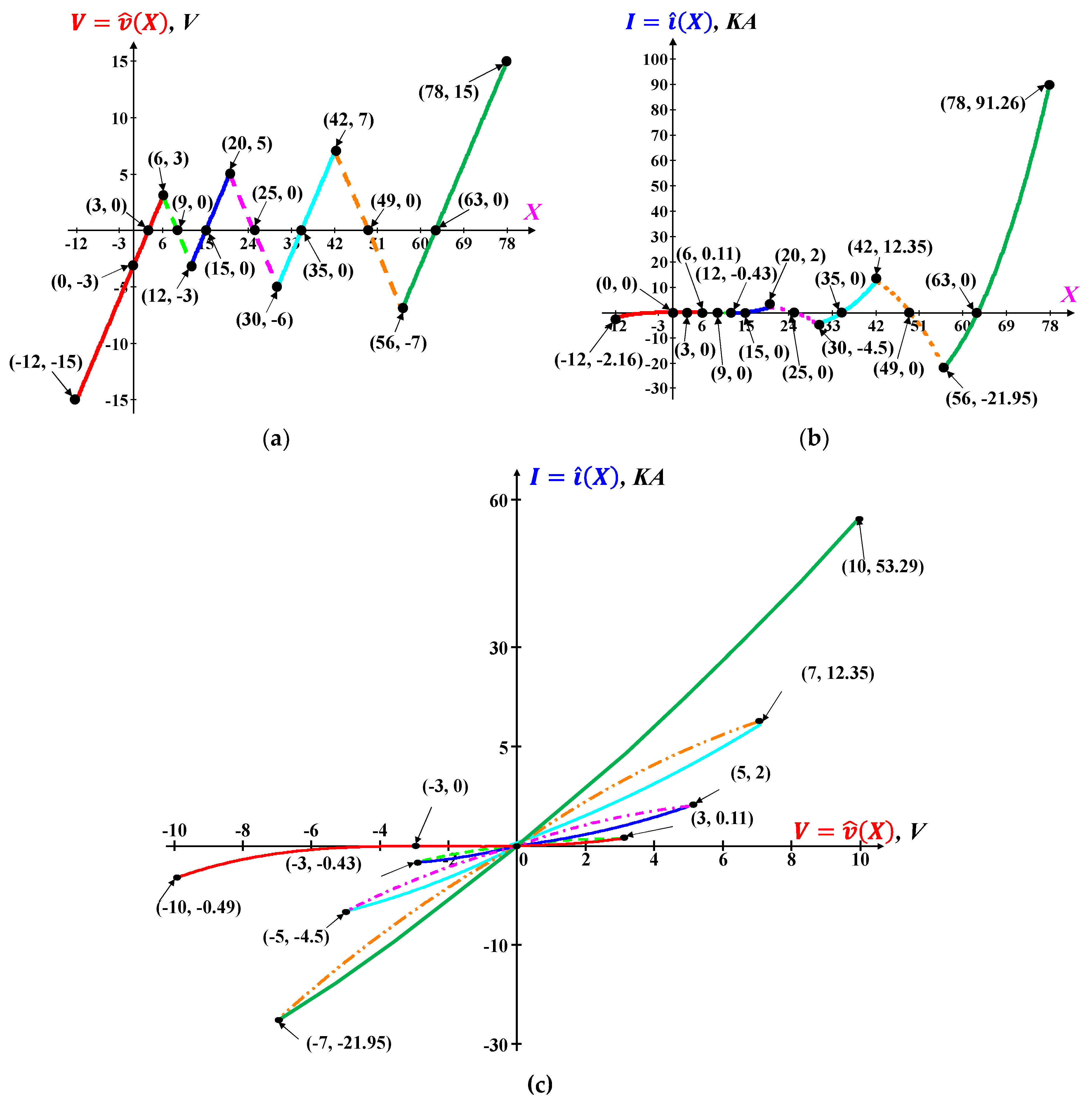
3. Switching Kinetics of CCM Family

DC V-I analysis, in Figure 3, and power-off-plot, in Figure 2, explicitly indicate that the Chua corsage memristors can be used as a binary and multistate memory device at v = 0 V. Conceptually, the simplest way to switch the memory states of a memory device is to apply a pulse input with an appropriate pulse amplitude V_A, and pulse width Δw. For successful switching between the memory states of CCM, the square pulse should have a minimum pulse width Δw for appropriate pulse amplitude, V_A. Any square pulse with less than the minimum pulse width results in switching failure. The switching kinetics of CCMs can be represented through its dynamic route map where the solution of each straight-line segments of DRM is an exponential function of state variable x_n(t). The complete solution of time-dependent x(t) is made of a sequence of the exponential waveforms joined at the various breakpoints in the dynamic routes [12]. Due to complex and diversified dynamic routes with multiple asymptotically stable equilibrium points, 6-lobe CCM is chosen to illustrate the successful switching from lower conductance state (resp., higher resistance state) to higher conductance state (resp., lower resistance state) or vice-versa along with switching failure.

Example 1.

Successful switching from lower conductance state Q₁ to higher conductance state Q₅.

The dynamic route map, in Figure 4a, shows the example of a successful switching of the 6-lobe CCM from low conductance state Q₁ to high conductance state Q₅ when a pulse input with an amplitude V_A= 5.5 V, and width Δw = 7.48 s is applied. According to Sect. II-A, the applied pulse with V_A = 5.5 V is equivalent to translating the red curve f(x, 0) upwards by 5.5 units, as shown by the blue curve f(x, 5.5). The dynamic route starting from low conductance state Q₁ (x = 3) at t = 0^- would jump abruptly from Q₁ on red curve to a point directly above Q₁ on the blue curve (yellow circle) at t = 0⁺ (shown with upward green arrow) as the pulse input increases from 0 V to 5.5 V. Since the blue curve is located above the x-axis (where dx/dt > 0), its motion can only move to the right until time t = Δw. At t = Δw, the square pulse returns to zero and the point x_Δw(t = Δw) = 26.5 (shown with green circle) on the blue curve (f(x, 5.5)) reverts back abruptly to the same point on the red curve (shown with light cyan circle followed by a downward green arrowhead). On red curve (f(x, 0)), state variable x(t) = x_Δw(t) diverges away from unstable equilibrium point Q₄ (x = 25) and must continue to move rightward along the dynamical movement of DRM (i.e., dx/dt > 0) until it converges to the low-resistance memory state Q₅ (x = 35), as indicated with black arrowheads in Figure 4a.

The exponential trajectories of x_n(t) related to the individual piecewise linear segments are shown in Figure 4b. The total time period needed for the x(t) (x(t) is the collective trajectory of all exponential trajectories x_n(t) that originated from each straight-line segments of DRM between Q₁ and Q₅.) trajectory to reach to Q₅ from Q₁ is t_fp = 17.2 s, although the applied pulse is removed at t = Δw = 7.48 s. This phenomenon illustrates the local fading memory attributes of 6-lobe CCM, but reveals the opportunity of utilizing it as a multistate memory device.

Example 2.

Successful switching from higher conductance state Q₅ to lower conductance state Q₁.

To switch from high conductance state Q₅ to low conductance state Q₁ of the 6-lobe CCM, a negative pulse with amplitude V_A = −5.5 V and width Δw_b = 7.684 s is applied. The dynamic route and the state trajectories x(t) of switching kinetics from Q₅ to Q₁ are shown in Figure 4c,d, respectively. Figure 4c shows that the dynamic route starting from Q₅ (x = 35) on red curve jumps abruptly downward by −5.5 units at t = 0⁺, as shown with blue curve f(x, −5.5). The state variable x(t) then moves towards the lower conductance state Q₁ as dx/dt < 0. At t_b = Δw_b, when the negative input is removed, state variable x_Δwb (t_b = Δw_b) = 8.9 on blue curve returns to the exact same position on the red curve and continues to move towards Q₁ (x = 3) as dx/dt < 0. The exponential trajectories of x_n(t) from memory state Q₅ to Q₁ is shown in Figure 4d where the x_n(t) decreases as the time increases and converges to x(t_f1b) = 3 which is regarded as the Q₁ memory state. The 6-lobe CCM exhibits dissimilar switching time in spite of similar pulse amplitude and greater pulse width as the switching time from higher to lower conductance states, t_fpb = 20.701 s, is greater than t_f = 17.2 s. This reveals that the CCM exhibits similar anti-symmetrical switching complication like as other memristive multistate memory devices.

Example 3.

Switching failure from lower conductance state Q₁ to higher conductance state Q₅.

Amplitude V_A and pulse width Δw of an applied input pulse plays a crucial role in the switching kinetics of memory states of the 6-lobe CCM. An inappropriate pulse amplitude or pulse width may result in switching failures which illustrated in Figure 5. An appropriate pulse amplitude V_A = 5.5 V with a pulse width Δw = 7 s is applied to the 6-lobe CCM to switch the memory state from Q₁ to Q₅. Figure 5 shows that the exponential trajectories are converging to memory state Q₃ (x = 15) rather than converging to memory state Q₅ (x = 35). This switching failure happens as the state variable x(t) fails to cover the distance of x(t) > X_Q4 = 25 with a pulse width Δw = 7 s. Before the removal of input, the trajectories of state variable x(t) reaches to a point x_Δw(t = Δw) = 23.812 which lies in the left-hand side of Q₄ (x = 25), as shown in Figure 5a. According to Section 2.1, any point lies in the left-side of Q₄ (x = 25) should follow the dynamic route dx/dt < 0 (as shown with black arrowhead in Figure 2) and converges to equilibrium state Q₃ and in this case, the state variable x(t) follows the same route dx/dt < 0 and converges to Q₃ (x = 15) rather converging to memory state Q₅ (x = 35), as shown in Figure 5b.

To overcome the switching failure problem, this review article includes the universal formulas (For detail derivation and explanation regarding the universal formulas please refer to ref. [12] and its supplementary materials.) that is required to determine the appropriate pulse amplitude V_A and pulse width Δw. To do so, the exponential trajectories of state variable x_n(t) and the time t_fn that required for the trajectorial movement from any initial point x(t_in) to the end of straight-line segment of DRM are computed. The exponential trajectory of state variable x_n(t) of a straight-line segment of the DRM at an equilibrium point Q_n is determined as

$$x_n\left(t\right)=Q_n-mv\left(t\right)\left(1-e^{m\left(t-t_{in}\right)}\right)-\left(Q_n-x(t_{in})\right)e^{m\left(t-t_{in}\right)},$$

(13)

where, n represents the number of equilibrium points and m represents the sign value of the straight-line slope,

$$m=sgn\left(\frac{{\frac{dx}{dt}|}_{start}-{ \frac{dx}{dt}|}_{end}}{x_{start}- x_{end}}\right),$$

(14)

and t_in is the initial time of the straight-line segment; whereas, x(t_in) represents the initial state at t_in. The time (t_fn), that required for the trajectory of x_n(t) to move from any initial point x(t_in) to the end of the straight-line segment of DRM, can be defined as

$$t_{fn}=t_{in}+\underset{\Delta t_{fn}}{\underbrace{\frac{1}{m}ln\left[\left|\frac{Q_n-mv\left(t\right)-x\left(t_{fn}\right)}{Q_n-mv\left(t\right)-x\left(t_{in}\right)}\right|\right]}}.$$

(15)

The complete movement of the exponential trajectories of state variable x_n(t) can be determined by accumulating all the individual exponential trajectories of the straight-line segments of DRM,

$$x\left(t\right)={{\displaystyle \sum }}_{n=1}^p{x}_n\left(t\right) (t_{in}\le t<t_{fn}),$$

(16)

where there trajectories of x_n(t) only valid over t_in ≤ t < t_fn and p represent the total number of PWL segments of the DRM between initial point x(t_in)and final converged equilibrium point Q_n.

The appropriate pulse amplitude V_A is determined as

$$V_A>Q_{\left(n-1\right)}-x\left(t_{0\left(n-1\right)}\right),$$

(17)

where Q_(n-1) and x(t_0(n-1)) represent the immediate before equilibrium point and the initial state of the resultant memory state Q_n.

The pulse width Δw is defined as

$$\Delta w={{\displaystyle \sum }}_{n=0}^q{t}_{fn} \left(x\left(t_{in}\right)\le x\left(t\right)\le x_{\Delta w}\left(t= \Delta w\right)\right)),$$

(18)

where q represents the number of straight-line segments of the DRM over x(t_in) ≤ x(t) ≤ x_Δw (t = Δw) and x_Δw is the user-defined state where the applied input is removed. The value of user-defined x_Δw determines whether the alteration of memory states is going to be successful or not. For example, in spite choosing x_Δw (t = Δw) > X = 25(Q₄) in Figure 4a, any user-define state value x_Δw (t = Δw) ≤ X = 25(Q₄) results in unsuccessful switching between Q₁ and Q₅ and the resultant exponential trajectory converges to Q₃ memory state, as shown in Figure 5.

These formulas (Equations (13)–(18)) are universal as they can be applicable to any piecewise linear dynamic routes for any DC or pulse input and with any number of segments. Moreover, the universal formulas in Equations (17) and (18) compute the minimum pulse amplitude and width, which can be used to solve the anti-symmetrical switching complications, in Example 2. Unlike other memristive multistate memory devices which require empirical approach, the CC memristors are defined by universal analytical formulas to determine the appropriate pulse amplitude and width for successful switching from lower conductance state to higher conductance state or vice-versa.

4. Local Activity and Bifurcation Analysis

Local activity principle predicts the presence of complex phenomena in a nonlinear dynamical system [23]. Particularly it affirms that a nonlinear circuit made of 2-terminal circuit elements, and/or more complicated 2-terminal devices, can exhibit complex bifurcation phenomena, such as oscillation and chaos, if and only if the circuit contains at least one nonlinear locally-active element. The fundamental deep mathematical theorem given in [23] allows testing the locally active phenomenon of a device about some equilibrium points, i.e., DC operating points.

According to the theorem presented in [23], 2-lobe, 4-lobe and 6-lobe CCMs are locally active over the interval −10 V < V < −3.334 V (in Figure 2a), −9 V < V < −3 V (in Figure 2b), and −3 V < V < −1 V (Figure 2c), respectively, as the slope at any point Q over these intervals is negative, i.e., Re [Y(iω)] < 0 at Q and ω = 0 (DC input), which satisfies the locally active criterion of Re [Z(iω)] < 0, or Re [Y(iω)] < 0, for at least one frequency ω [13,14,15,16]. Moreover, all the members of the CCM family exhibit an edge of chaos domains (Edge of Chaos is a relatively small subclass of local activity [16]. For details regarding local activity and edge of chaos please refer to ref. [23]) over the same voltage interval as that of local activities [13,14,15,16].

Nonlinear dynamical systems satisfying the edge of chaos criterion can exhibit bifurcation from a stable equilibrium point regime to a chaotic regime by forced excitation [25]. In a local bifurcation, called the Hopf bifurcation, an equilibrium point of the system’s differential equations loses its stability as a pair of complex conjugate eigenvalues, or equivalently poles of its associated admittance Y(s, V) or impedance Z(s, I), cross the imaginary axis of the complex plane at some critical parameter value μ_c [26]. Hopf bifurcation theorem asserts that under a relatively general situation, a small-amplitude sinusoidal oscillation will emerge for the control parameter μ > μ_c, and whose amplitude A increases proportional to $\sqrt{\mu -{\mu }_c}$, for μ close to μ_c [26,27]. The oscillators made from Chua corsage memristors exhibits Hopf bifurcation as it is endowed with a pair of complex conjugate poles on the imaginary axis (known as Hopf bifurcation points) of the complex plane [13,14,15,16].

The Hopf bifurcation exhibited in the CCM oscillator circuits (The CCM oscillator circuits are designed by connecting the corsage memristors in series with an external inductor and a battery [13,14,15,16].) are classified as supercritical because the typical supercritical amplitude $A_v\left(V\right)=\sqrt{{\overline{x}}^2+{\overline{i}}_L^2}$ at Hopf bifurcation points, shown in Figure 6a,b, is quite similar to the curve computed from the analytical formulas (To avoid the emergence of complex number, the absolute value of (µ − µ_c) is used in the analytical formulas. The critical parameters are μ_c1 = −2.25 V and μ_c2 = −1.75 V for 6-lobe CCM and constants k₁ = 2.65 and k₂ = 8.75 are determined empirically for 6-lobe CCM oscillator circuit [16].) $A_{m1}\left(V\right)=k_1\left[\sqrt{\left|V+{\mu }_{c1}\right|}\right]$ and $A_{m2}\left(V\right)=k_2 \left[\sqrt{\left|V+{\mu }_{c2}\right|}\right]$ with control parameter µ = V and critical parameter μ_c1 and μ_c2 [16]. In this review article, the supercritical Hopf bifurcation theorem is analyzed using 6-lobe CCM oscillator circuit. However, the same bifurcation analogies and amplitude equations hold for 2-lobe and 4-lobe CCM oscillator circuits except for the critical parameter of μ_c1 and μ_c2, and constants k₁ and k₂.

According to the supercritical Hopf bifurcation theorem [26,27], the 6-lobe CCM oscillator circuit must exhibit a small stable near-sinusoidal oscillation, i.e., a limit cycle, over a small range of V beyond the critical parameter value (For better understanding about the choice of critical parameters μ_c1 = −2.25 V and μ_c2 = −1.75 V please refer to Sect. 4.3 and Figure 13 of ref. [16]) μ_c1 = V = −2.25 V. Figure 7a and d show that the transient waveforms converge to 2 asymptotically stable equilibrium points $Q_0^1\left(0.7, -1.127\right)$ for the parameter value V = −2.3 V, (which is near, but to the left of the first Hopf bifurcation point μ_c1 = V = −2.25 V (see inset of Figure 13 in ref. [16])), and $Q_0^2\left(1.3, -2.873\right)$ for V = −1.7 V (which is near, but to the left of the second Hopf bifurcation point μ_c2 = V = −1.75 V), respectively. However, the transient waveforms generated by 6-lobe CCM from two different initial states (x(0) = 0.95, i_L (0) = −2.031) and (x(0) = 0.8, i_L (0) = −1.43) in Figure 7b converge to the yellow stable limit cycle for V = −2.23 V (which is near, but to the right of the first Hopf bifurcation point μ_c1 = V = −2.25 V). Moreover, transient waveforms generated from two different initial states (x(0) = 1.1, i_L (0) = −2.431) and (x(0) = 1.2, i_L (0) = −3.53) for V = −1.77 (which is near, but to the right of the second Hopf bifurcation point μ_c2 = V = −1.75 V (see inset of Figure 13 in ref. [16])) converge to a larger yellow limit cycle shown in Figure 7c. The numerical simulation results shown in Figure 7 affirm that the 6-lobe CCM oscillator circuit exhibits a stable limit cycle when the bifurcation parameter μ = V is chosen between the Hopf bifurcation points at μ_c1 = V = −2.25 V and μ_c1 = V = −1.75 V, as predicted by the supercritical Hopf bifurcation theorem [16]. Similar supercritical Hopf bifurcation analogies also exhibits in 2-lobe and 4-lobe CCM oscillator circuits [13,14,15].

5. Physical Realization of CCM Family

Chua corsage memristors, shown in Figure 8a, can be physically realized in circuit by including the switching kinetics closer to the behavioral attributes of each segment of PWL dynamic route map. A passive nonlinear-resistive two-port and a dynamic first-order one-port are cascaded to design an emulator circuit for CCM memristor [10], as shown in Figure 8b. The passive nonlinear-resistive two-port is composed of parallel connected Graetz bridges [17] with anti-serial diodes and the dynamic first-order one-port is made up of a C-R parallel circuit. Two set of Graetz bridge are used to supply double amount of input current to the dynamic first-order one-port, i.e., C-R parallel circuit, for faster switching of memory states.

The DC V-I curve of active and locally active resistor R₀ in dynamic one-port, in Figure 8b, should exhibit the same number of contiguous breakpoints to that of the DC V-I curves of CCMs. For example, the DC V-I curve of R₀ for 2-lobe CCM emulator must have two breakpoints, whereas, for 4-lobe and 6-lobe emulator the DC V-I curve of R₀ should exhibit four and six contiguous breakpoints, respectively.

To design the nonlinear resistor R₀ for CCM emulators, circuit theoretic analysis is conducted on opamps to obtain the desired DC V-I breakpoints at specific voltages to that of CC memristors. The driving point characteristic of a single positive and negative feedback op-amp circuit provides two breakpoints on its piecewise linear DC V-I curve [28]. Therefore, only a single positive and negative feedback op-amp circuit is sufficient to design an active and locally active R₀ for 2-lobe CCM emulator, as shown in Figure 9a. However, two and three parallel-connected opamp circuits are required to design a four and six breakpoint piecewise linear DC V-I curves for 4-lobe and 6-lobe CCMs, respectively, as shown in Figure 9b,c. The circuit theoretic analysis for designing the CCM emulator circuit is conducted on 6-lobe CC memristor, as it has the highest number of breakpoints on its contiguous six lobes corsage DC V-I curve.

The circuit components and parameters of the parallel-connected opamps, in Figure 9c, are exactly same except the negative feedback resistances (R₆₄₁, R₆₄₂, and R₆₄₃). The effective saturation voltage (βE_sat) of an individual op-amp circuit is determine by the negative feedback resistance which plays a crucial role to achieve the desired V-I breakpoints at specified voltages, such as V= ±3 V, V= ±5 V, and V= ±7 V (The 6-lobe CCM has six breakpoints on its DC V-I curve at V = {±3 V, ±5 V, ±7 V} as shown in Figure 2c). However, the positive feedback path of the op-amp circuits might arise difficulties with the driving-point and transfer function. Such complication can be resolved by replacing the op-amp circuit with three ideal models, such as “– Saturation region”, “Linear region”, and “+ Saturation region”. According to the circuit theoretic approach presented in [12], the three ideal models generate the following combine current (i_n) of an individual opamp circuit for an input voltage v,

$$i_n =\underset{-\mathit{Saturation} \mathit{Region} (v\le -\beta E_{sat})}{\underbrace{\left[\frac{1}{R_{67n}}\right[v(1+\frac{R_{67n}}{R_{67n}})+E_{sat}\left]\right]}}+\underset{\mathit{Linear} \mathit{Region} (-\beta E_{sat}\le v\le \beta E_{sat})}{\underbrace{\left[\frac{1}{R_{67n}}\right[v(1+\frac{R_{67n}}{R_{67n}})-v_{on}\left]\right]}}+\underset{+\mathit{Saturation} \mathit{Region} (v\ge \beta E_{sat})}{\underbrace{\left[\frac{1}{R_{67n}}\right[v(1+\frac{R_{67n}}{R_{67n}})-E_{sat}\left]\right]}}$$

(19)

where n = {1, 2, and 3} denotes the operating opamp circuit. Figure 10a shows the mathematically computed V-i_n plots of the individual currents of opamp circuits. Observe that each V-I curves has two breakpoints at specific voltage at V = ± 2.82 V, V = ± 4.95 V, and V = ± 6.99 V. The value of the breakpoints are a bit dissimilar to that of 6-lobe CCM (V = {±3 V, ±5 V, ±7 V}) as the measured resistive parameters (R₆₃₁ = R₆₃₂ = R₆₃₃ = 0.985K, R₆₆₁ = R₆₆₂ = R₆₆₃ = 100.5K, R₆₇₁ = R₆₇₂ = R₆₇₃ = 1.001K, R₆₄₁ = 3.888K, R₆₄₂ = 1.797K, R₆₄₃ = 0.987K) are used in simulation.

The total current of parallel-connected opamp circuit is equal to the summation of all individual opamp currents, $i ={\displaystyle \sum }_{n=1}^3{i}_n.$ The mathematical simulation of V-I curve and the resistance of active and locally active R₀ (R₀ = V/I) are shown in Figure 10b, whereas, the SPICE simulation and circuit implementation waveforms are shown in Figure 10c, and d, respectively. Observe from circuit implementation waveforms, in Figure 10d, that the locally active R₀ remains almost constant at R₀₁ = 137Ω over an input voltage range −2.16 V < V < 2.16 V, except for a tiny interval at the origin. For ±2.16 V < V < ± 4.05 V, ±4.05 V < V < ±5.74 V, and V > ±5.74 V, R₀ increase from 137 Ω to 204 Ω, 204 Ω to 312 Ω, and 312 Ω to R_max (very large resistance value), respectively. However, the increment rate of R₀ is dissimilar for each voltage range which reveals that the slope is constant in a particular voltage range, but inconstant for different voltage ranges. This suggests that the active and locally active R₀ exhibits four distinct memory states, namely, R₀₁, R₀₂, R₀₃, and R₀₄ as shown in Figure 10b–d.

The numerical values of DC V-I breakpoints and the resistance ranges of nonlinear resistor R₀ (in Figure 10b–d) for mathematical modeling, SPICE simulation, and circuit implementation are unequal. The reason behind such inequality is the non-ideal circuit components of the SPICE module and the non-ideal characteristic of the implemented opamps along with noise induction from DC power supply and oscilloscope probe. Although the breakpoints of DC V-I curves in Figure 2c and Figure 10b–d are quantitatively different, but qualitatively same. This reveals that the DC V-I curve of any real nonlinear resistor can be converted into a memristor by applying the basic method explained in [10,11,12] and [18].

However, unlike a passive nonlinear-resistive two-port emulator circuit, the bi-stability and multi-stability phenomena of Chua Corsage Memristors can be realized by a single device as demonstrated in recent literature [29,30,31]. The NbO₂ Mott memristor [29,30] exhibits an analogous dynamic route to that of 2-lobe CCM which has two stable and one unstable equilibrium points on its dynamic route map (dT/dt vs. T (Figure 1 [29])). The state switching attributes of NbO₂ memristor are identical to 2-lobe CCM and regarded as bi-stable device. The universal formulas of switching kinetics (in Section 3) can be applicable to NbO₂ Mott memristor as the PWL dynamic route, and switching kinetics are explicitly similar to 2-lobe CCM. In addition, HfOx/AlOy-based homeothermic memristor [31] has a similar number of stable equilibrium states (i.e., four temperature-dependent equilibrium states corresponding to its four dynamic conductances (Figure 3 in [31])) to that of 6-lobe CCM. When driven by DC input, the homeothermic memristor exhibits four distinct DC V-I curves corresponding to its four temperature-dependent dynamic conductances (Figure 3e and f in [31]) which is identical to 6-lobe CCM (shown in Figure 2c and Figure 10). In spite of the quantitative dissimilarities, the NbO₂ Mott memristor and homeothermic memristor qualitative exhibit the bi-stability and multi-stability phenomena of CC memristors.

6. Concluding Remarks

This review article presents an in-depth and rigorous analysis of the nonlinear dynamical attributes, switching kinetics, and physical realization of Chua corsage memristors (CCMs). The versatile CCMs exhibit multiple stable equilibria on their complex and diversified, dynamic route map (DRM) and power-off plot (POP). Due to the presence of a higher degree of versatility in DRM, the CC memristors have a variety of dynamic paths in response to different initial conditions which reveals a highly nonlinear DC V-I curves. Unlike most published highly-nonlinear DC V-I curves which have several disconnected branches, the DC V-I curves of CCMs are contiguous. Moreover, the parametric representation and DC V-I curves of CCMs have an explicit analytical equation, which rarely happens.

The multiple stable equilibria on the DRM of CCMs reveal that it can be utilized as binary and multistate memory device whose exponential state trajectories for a particular linear piecewise segment, time period that required for the state trajectorial movement of the particular PWL segment, and the appropriate pulse amplitude and width that required for successful memory state switching can easily be determined from the universal formulas presented in Sect. 3. These universal formulas are applicable to any PWL DRM curves with any number of segments for any DC or pulse input.

Another impressive feature of CCMs is the locally active negative slope region of the DC V-I curves which gives rise to complex phenomenon, such as oscillation, by exploiting the edge of chaos and supercritical Hopf bifurcation theorem.

Last, but not least, the off-the-shelf active and locally active resistor (R₀) in CCM emulators (designed with opamp or parallel-connected opamp circuits) is capable of emulating the attributes of the CCM DC V-I curves and proved that a memristor could be implemented using any real nonlinear resistor. Moreover, NbO₂ Mott memristor and HfO_x/AlO_y-based homeothermic memristor reveals that the bi-stability and multi-stability phenomena of Chua corsage memristors can also be realized with a single physical device.