Spectrum Modeling of Out-of-Band Intermodulation for Dual-Band RF Amplifiers in OFDM Modulation

Abstract

Dual-band RF amplifiers play increasingly important roles in next-generation mobile communication systems including 5G, and the out-of-band intermodulation products are often not negligible since they generate interference to adjacent channels. In this article, following our previous modeling of cross-modulation for amplified dual-band signals, an analytical expression of out-of-band intermodulation for dual-band orthogonal frequency-division multiplexing signals is derived using the third-order intercept points $I{P}_3$. The experimental measurement results validate the proposed analytical expression.

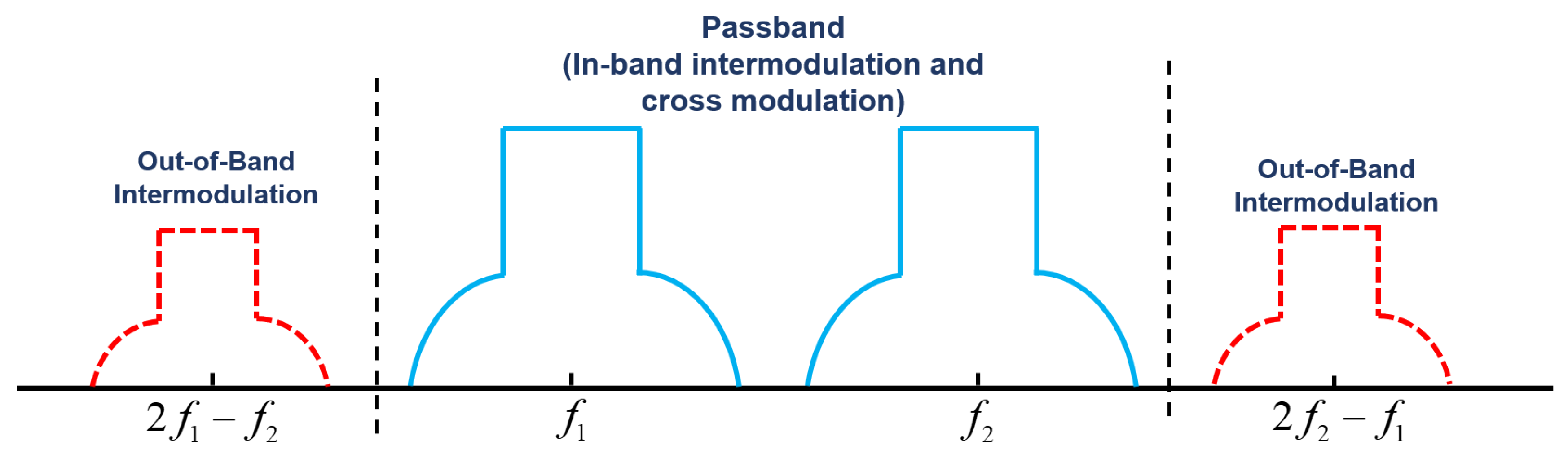
1. Introduction

To address the increasing demands of modern wireless communication terminals that cover different standards, multiband (or multi-standard) RF transmitters and receivers are the key elements for the latest and future wireless transmission systems [1], such as cognitive radios (CRs) [2,3,4,5], 4G LTE-advanced [6,7], and 5G [8,9,10]. In our previous work, the intermodulation (IM) for single-band signals caused by the nonlinearity of RF amplifiers was first studied [11,12]. The in-band intermodulation and cross-modulation (CM) for the amplified dual-band spectrum then was later derived in [13,14].

However, when the spectrum gets more crowed, especially in 5G, more frequency bands are used, which implies the out-of-band intermodulation [13] from the dual-band amplifiers must be considered, because it will cause the interference to other users’ channels, and degrade the modulation quality of the transmitter and the sensitivity of receiver [15]. Figure 1 illustrates the amplified dual-band spectrum including out-of-band intermodulation (red dot lines). The dual-band signals which are divided into the carrier frequencies via $\mathsf{\Delta }f(\mathsf{\Delta }f=|f_2-f_1\left|\right)$ are transmitted simultaneously. For the dual-band amplified signals, the power spectra at the RF amplifier output can be classified into two parts. The first part (blue solid lines) is attributed to linear amplification, IM and CM, which has been derived in [14]. The second part (red dot lines) is referred to as out-of-band IM in Figure 1, located at $\mathsf{\Delta }f$ away from the lower or upper carrier frequencies, which is discussed in this article. Taking 5G NR (new radio) [16] for example, if the amplifier is used to amplify the concurrent signals centered at 1870 MHz (in downlink operating band n3) and 1935 MHz (in downlink operating band n2), the out-of-band intermodulation products will center at 1805 MHz and 2000 MHz, which are located in downlink operating band n3 and band n70 respectively, and will affect the designated downlink transmissions in those two bands. Thus, the interference caused by out-of-band intermodulation will affect the designated downlink transmissions in those two bands. Bandpass filtering or digital predistortion (DPD) techniques are often used to linearize the out-of-band intermodulation such as [17].

In this article, we derived an explicit expression of the spectrum regrowth for the amplified dual-band orthogonal frequency-division multiplexing (OFDM) signals including the out-of-band intermodulation. This result expands the previous spectrum model [14] to a larger range outside the passband. While the dual two-tone test in [13,18,19] could be useful for locating the frequency range of the out-of-band interferences, the proposed out-of-band model of dual-band power spectrum could locate and quantify the out-of-band distortions/interferences.

2. Spectrum Model

2.1. Calculating the Correlation for the Dual-Band OFDM Output Signals

Based on ([14], Equation (3)), the input dual-band OFDM signal can be expressed as:

$$s\left(t\right)={\tilde{s}}_1\left(t\right)cos\left(2\pi f_{c_1}t\right)+{\tilde{s}}_2\left(t\right)cos\left(2\pi f_{c_2}t\right)$$

(1)

where ${\tilde{s}}_1\left(t\right)$ is the OFDM signal in one band centered at frequency $f_{c_1}$ with bandwidth $B_1$, and ${\tilde{s}}_2\left(t\right)$ is the OFDM signal in the other band centered at $f_{c_2}$ with $B_2$. ${\tilde{s}}_1\left(t\right)$ and ${\tilde{s}}_2\left(t\right)$ are the baseband representation, which equal to $|{\tilde{s}}_1\left(t\right)|e^{j{\theta }_1\left(t\right)}$ and $|{\tilde{s}}_2\left(t\right)|e^{j{\theta }_2\left(t\right)}$, respectively. The power spectrum density (PSD) of ${\tilde{s}}_1\left(t\right)$ and ${\tilde{s}}_2\left(t\right)$ can be expressed respectively as follows [14]:

$$P_{{\tilde{s}}_1}\left(f\right)=\left\{\begin{array}{cc}\frac{N_1}{2},& \left|f\right|\le B_1\hfill \\ 0,& \left|f\right|>B_1\hfill \end{array}\right.$$

and

$$P_{{\tilde{s}}_2}\left(f\right)=\left\{\begin{array}{cc}\frac{N_2}{2},& \left|f\right|\le B_2\hfill \\ 0,& \left|f\right|>B_2\hfill \end{array}\right.$$

(2)

where $N_1{B}_1$ and $N_2{B}_2$ are the powers of ${\tilde{s}}_1\left(t\right)$ and ${\tilde{s}}_1\left(t\right)$, respectively.

From [14], we know the third-order term of Taylor series model generally dominates in the nonlinear effect. Using the third-order Taylor series model of RF amplifiers ([14], Equation (6)) and (1), the output amplified dual-band OFDM signals are described as:

$$\begin{array}{ll}y\left(t\right)\hfill & =[a_1{\tilde{s}}_1\left(t\right)+\frac{3}{4}{a}_3{\tilde{s}}_1^3\left(t\right)+\frac{3}{2}{a}_3{\tilde{s}}_1{\tilde{s}}_2^2]cos\left(2\pi f_{c_1}t\right)\hfill \\ & +[a_2{\tilde{s}}_2\left(t\right)+\frac{3}{4}{a}_3{\tilde{s}}_2^3\left(t\right)+\frac{3}{2}{a}_3{\tilde{s}}_2{\tilde{s}}_1^2]cos\left(2\pi f_{c_2}t\right)\hfill \\ & +\frac{3}{4}{a}_3{\tilde{s}}_1^2\left(t\right){\tilde{s}}_2\left(t\right)[cos(4\pi f_{c_1}t+2\pi f_{c_2}t)+cos(4\pi f_{c_1}t-2\pi f_{c_2}t)]\hfill \\ & +\frac{3}{4}{a}_3{\tilde{s}}_2^2\left(t\right){\tilde{s}}_1\left(t\right)[cos(2\pi f_{c_1}t+4\pi f_{c_2}t)+cos(4\pi f_{c_2}t-2\pi f_{c_1}t)]\hfill \\ & +\frac{1}{4}{a}_3{\tilde{s}}_1^{3}cos\left(6\pi f_{c_1}t\right)\hfill \\ & +\frac{1}{4}{a}_3{\tilde{s}}_2^{3}cos\left(6\pi f_{c_2}t\right)\hfill \end{array}$$

(3)

To simplify the expression of (3), six new terms ${\tilde{y}}_1\left(t\right)$, ${\tilde{y}}_2\left(t\right)$, ${\tilde{y}}_3\left(t\right)$, ${\tilde{y}}_4\left(t\right)$, ${\tilde{y}}_5\left(t\right)$, and ${\tilde{y}}_6\left(t\right)$ are defined as:

$${\tilde{y}}_1\left(t\right)=a_1{\tilde{s}}_1\left(t\right)+\frac{3}{4}{a}_3{\tilde{s}}_1^3\left(t\right)+\frac{3}{2}{a}_3{\tilde{s}}_1\left(t\right){\tilde{s}}_2^2\left(t\right)$$

(4)

$${\tilde{y}}_2\left(t\right)=a_1{\tilde{s}}_2\left(t\right)+\frac{3}{4}{a}_3{\tilde{s}}_2^3\left(t\right)+\frac{3}{2}{a}_3{\tilde{s}}_2\left(t\right){\tilde{s}}_1^2\left(t\right)$$

(5)

$${\tilde{y}}_3\left(t\right)=\frac{3}{4}{a}_3{\tilde{s}}_1^2\left(t\right){\tilde{s}}_2\left(t\right)$$

(6)

$${\tilde{y}}_4\left(t\right)=\frac{3}{4}{a}_3{\tilde{s}}_2^2\left(t\right){\tilde{s}}_1\left(t\right)$$

(7)

$${\tilde{y}}_5\left(t\right)=\frac{1}{4}{a}_3{\tilde{s}}_1^3\left(t\right)$$

(8)

$${\tilde{y}}_6\left(t\right)=\frac{1}{4}{a}_3{\tilde{s}}_2^3\left(t\right)$$

(9)

Using (4)–(9), (3) can be rewritten as:

$$\begin{array}{cc}\hfill y\left(t\right)& ={\tilde{y}}_1\left(t\right)cos\left(2\pi f_{c_1}t\right)+{\tilde{y}}_2\left(t\right)cos\left(2\pi f_{c_2}t\right)\hfill \\ \hfill & +{\tilde{y}}_3\left(t\right)cos(4\pi f_{c_1}t+2\pi f_{c_2}t)+{\tilde{y}}_3\left(t\right)cos(4\pi f_{c_1}t-2\pi f_{c_2}t)\hfill \\ \hfill & +{\tilde{y}}_4\left(t\right)cos(2\pi f_{c_1}t+4\pi f_{c_2}t)+{\tilde{y}}_4\left(t\right)cos(4\pi f_{c_2}t-2\pi f_{c_1}t)\hfill \\ \hfill & +{\tilde{y}}_5\left(t\right)cos\left(6\pi f_{c_1}t\right)\hfill \\ \hfill & +{\tilde{y}}_6\left(t\right)cos\left(6\pi f_{c_2}t\right)\hfill \end{array}$$

(10)

When the frequency segmentation between the two carrier-frequency bands $\mathsf{\Delta }f=|f_{c_2}-f_{c_1}|$ is large, the last six terms in (10) centered at $(2f_{c_1}\pm f_{c_2})$, $(2f_{c_2}\pm f_{c_1})$, $3f_{c_1}$ and $3f_{c_2}$, respectively, are considered far away from the spectrum bands of interest. Therefore, after the band-pass filtering, the out-of-band spectral components in (10) are removed [14].

In this article, we now consider the situation that the frequency segmentation $\mathsf{\Delta }f=|f_{c_2}-f_{c_1}|$ is small. Therefore, the two terms in (10) centered at $2f_{c_2}-f_{c_1}$ and $2f_{c_1}-f_{c_2}$ are difficult to be filtered, thus remain in consideration. After the band-pass filtering, the last four terms in (10) centered at $(2f_{c_1}+f_{c_2})$, $(2f_{c_2}+f_{c_1})$, $3f_{c_1}$ and $3f_{c_2}$, respectively, are far away from the passband and are thus removed using band-pass filtering. Therefore, the filtered spectrum (spectrum near passbands) is truncated to:

$$\begin{array}{cc}\hfill y\left(t\right)& ={\tilde{y}}_1\left(t\right)cos\left(2\pi f_{c_1}t\right)+{\tilde{y}}_2\left(t\right)cos\left(2\pi f_{c_2}t\right)\hfill \\ \hfill & +{\tilde{y}}_3\left(t\right)cos(4\pi f_{c_1}t-2\pi f_{c_2}t)+{\tilde{y}}_4\left(t\right)cos(4\pi f_{c_2}t-2\pi f_{c_1}t)\hfill \end{array}$$

(11)

From (11), in order to be comparable with the physical measurement, the power spectrum density (PSD) of $y\left(t\right)$ can be calculated as [14,18]:

$$P_y\left(f\right)=\frac{1}{2}\left\{P_{{\tilde{y}}_1}(f-f_{c_1})+P_{{\tilde{y}}_2}(f-f_{c_2})+P_{{\tilde{y}}_3}[f-(2f_{c_1}-f_{c_2})]+P_{{\tilde{y}}_4}[f-(2f_{c_2}-f_{c_1})]\right\}$$

(12)

Compared to ([14], Equation (19)), the last two terms in are the distortions caused by out-of-band intermodulation. The PSD terms, $P_{{\tilde{y}}_1}\left(f\right)$ and $P_{{\tilde{y}}_2}\left(f\right)$ in (12), contain linear amplification, in-band IM products, and CM products, which all have already been discussed in [14]. The PSD terms, $P_{{\tilde{y}}_3}\left(f\right)$ and $P_{{\tilde{y}}_4}\left(f\right)$ in (12), which represent out-of-band intermodulation can be calculated from the correlation functions $R_{{\tilde{y}}_3}\left(\tau \right)$ of ${\tilde{y}}_3\left(t\right)$ and $R_{{\tilde{y}}_4}\left(\tau \right)$ of ${\tilde{y}}_4\left(t\right)$ using Wiener-Khintchine theorem [17] as:

$$P_{{\tilde{y}}_i}\left(f\right)={\int }_{-\infty }^{\infty }{R}_{{\tilde{y}}_i}\left(\tau \right)e^{-j2\pi f\tau }d\tau (i=1,2,3\mathrm{or}4)$$

(13)

To simplify the calculation, only the derivation of $R_{{\tilde{y}}_3}\left(\tau \right)$ will be explained in detail. $R_{{\tilde{y}}_4}\left(\tau \right)$ can be derived using the similar method. The correlation $R_{{\tilde{y}}_3}\left(\tau \right)$ is defined as:

$$R_{{\tilde{y}}_3}\left(\tau \right)=E\left\{{\tilde{y}}_3\left(t\right){\tilde{y}}_3(t+\tau )\right\}$$

(14)

where $E\{·\}$ is the mathematical expectation of $\{·\}$. By substituting (6) into (14), $R_{{\tilde{y}}_3}\left(\tau \right)$ can be expressed as:

$$\begin{array}{cc}\hfill R_{{\tilde{y}}_3}\left(\tau \right)& =E\left\{{\tilde{y}}_3\left(t\right){\tilde{y}}_3(t+\tau )\right\}\hfill \\ \hfill & =E\left\{\frac{3}{4}{a}_3{\tilde{s}}_1^2\left(3\right){\tilde{s}}_2\left(t\right)\frac{3}{4}{a}_3{\tilde{s}}_1^2(t+\tau ){\tilde{s}}_2(t+\tau )\right\}\hfill \\ \hfill & =\frac{9}{16}{a}_3^{2}E\left\{{\tilde{s}}_1^2\left(t\right){\tilde{s}}_2\left(t\right){\tilde{s}}_1^2(t+\tau ){\tilde{s}}_2(t+\tau )\right\}\hfill \end{array}$$

(15)

Using the formula of Isserlis’ theorem [20], (15) can then be derived as (see Appendix A):

$$R_{{\tilde{y}}_3}\left(\tau \right)=\frac{9}{16}{a}_3^2\left[\frac{N_{2}sin\left(2\pi B_2\tau \right)}{2\pi \tau }{\left(N_1{B}_1\right)}^2+2\frac{N_{2}sin\left(2\pi B_2\tau \right)}{2\pi \tau }{\left[\frac{N_{1}sin\left(2\pi B_1\tau \right)}{2\pi \tau }\right]}^2\right]$$

(16)

$R_{{\tilde{y}}_4}\left(\tau \right)$ can be derived similarly as:

$$\begin{array}{cc}\hfill R_{{\tilde{y}}_4}\left(\tau \right)& =E\left\{{\tilde{y}}_4\left(t\right){\tilde{y}}_4(t+\tau )\right\}\hfill \\ \hfill & =\frac{9}{16}{a}_3^2\left[\frac{N_{1}sin\left(2\pi B_1\tau \right)}{2\pi \tau }{\left(N_2{B}_2\right)}^2+2\frac{N_{1}sin\left(2\pi B_1\tau \right)}{2\pi \tau }{\left[\frac{N_{2}sin\left(2\pi B_2\tau \right)}{2\pi \tau }\right]}^2\right]\hfill \end{array}$$

(17)

2.2. The Power Spectrum Density of Amplified Signals

By using (13) and (16), $P_{{\tilde{y}}_3}\left(f\right)$ can be derived as:

$$\begin{array}{cc}\hfill P_{{\tilde{y}}_3}\left(f\right)& =\mathcal{F}\left\{R_{{\tilde{y}}_3}\left(\tau \right)\right\}\hfill \\ \hfill & =\frac{9}{16}{a}_3^2\mathcal{F}\left\{R_{{\tilde{s}}_2}\left(\tau \right){\left(N_1{B}_1\right)}^2+2R_{{\tilde{s}}_2}\left(\tau \right)R_{{\tilde{s}}_1}^2\left(\tau \right)\right\}\hfill \\ \hfill & =\frac{9}{16}{a}_3^2{\left(N_1{B}_1\right)}^2\mathcal{F}\left\{R_{{\tilde{s}}_2}\left(\tau \right)\right\}+\frac{9}{8}{a}_3^2\mathcal{F}\left\{R_{{\tilde{s}}_2}\left(\tau \right)R_{{\tilde{s}}_1}^2\left(\tau \right)\right\}\hfill \end{array}$$

(18)

where $\mathcal{F}\{·\}$ is defined as the Fourier transform of $\{·\}$. Based on ([14], Equations (4), (25) and (49)), $\mathcal{F}\left\{R_{{\tilde{s}}_2}\left(\tau \right)\right\}$ and $\mathcal{F}\left\{R_{{\tilde{s}}_2}\left(\tau \right)R_{{\tilde{s}}_1}^2\left(\tau \right)\right\}$ can be described respectively as:

$$\mathcal{F}\left\{R_{{\tilde{s}}_2}\left(\tau \right)\right\}=\left\{\begin{array}{cc}\frac{N_2}{2},& \left|f\right|\le B_2\\ 0,& \left|f\right|>B_2\end{array}\right.$$

(19)

and

$$\mathcal{F}\left\{R_{{\tilde{s}}_2}\left(\tau \right)R_{{\tilde{s}}_1}^2\left(\tau \right)\right\}=\left\{\begin{array}{cc}\frac{N_1^2{N}_2}{8}\left(-f^2+4B_1{B}_2-B_2^2\right),\hfill & \left|f\right|\le B_2\hfill \\ \frac{N_1^2{N}_2}{8}\left(4B_1{B}_2-2B_2\left|f\right|\right),\hfill & B_2<\left|f\right|\le 2B_1-B_2\hfill \\ \frac{N_1^2{N}_2}{16}{\left(2B_1+B_2-\left|f\right|\right)}^2,\hfill & 2B_1-B_2<\left|f\right|\le 2B_1+B_2\hfill \\ 0,\hfill & \left|f\right|\ge 2B_1+B_2\hfill \end{array}\right.$$

(20)

By substituting (19) and (20) into (18), $P_{{\tilde{y}}_3}\left(f\right)$ can be derived as:

$$\begin{array}{c}{P}_{{\tilde{y}}_3}\left(f\right)=\hfill \\ \left\{\begin{array}{cc}\begin{array}{c}\frac{1}{B_2}{P}_{o1}^2{P}_{o2}{10}^{\frac{-I{P}_3}{5}}+\frac{1}{2B_1^2{B}_2}\hfill \\ ·P_{o1}^2{P}_{o2}{10}^{\frac{-I{P}_3}{5}}\left(-f^2+4B_1{B}_2-B_2^2\right),\hfill \end{array}\hfill & \left|f\right|\le B_2\hfill \\ \begin{array}{c}\frac{1}{2B_1^2{B}_2}{P}_{o1}^2{P}_{o2}{10}^{\frac{-I{P}_3}{5}}\hfill \\ ·\left(4B_1{B}_2-2B_2\left|f\right|\right),\hfill \end{array}\hfill & B_2<\left|f\right|\le 2B_1-B_2\hfill \\ \begin{array}{c}\frac{1}{4B_1^2{B}_2}{P}_{o1}^2{P}_{o2}{10}^{\frac{-I{P}_3}{5}}\hfill \\ ·{\left(2B_1+B_2-\left|f\right|\right)}^2,\hfill \end{array}\hfill & 2B_1-B_2<\left|f\right|\le 2B_1+B_2\hfill \\ 0,\hfill & \left|f\right|>2B_1+B_2\hfill \end{array}\right.\hfill \end{array}$$

(21)

where $P_{o1}$ is the linear part of the output power for ${\tilde{s}}_1\left(t\right)$ and $P_{o2}$ is the linear part of the output power for ${\tilde{s}}_2\left(t\right)$ [11,12], which are

$$P_{o1}=\frac{a_1^2{N}_1{B}_2}{2}$$

(22)

and

$$P_{o2}=\frac{a_1^2{N}_2{B}_2}{2}$$

(23)

Equation (21) describes the PSD of the first left part of the out-of-band intermodulation. Similarly, the right part of the out-of-band intermodulation $P_{{\tilde{y}}_4}\left(f\right)$ can be calculated as:

$$\begin{array}{c}{P}_{{\tilde{y}}_4}\left(f\right)=\hfill \\ \left\{\begin{array}{cc}\begin{array}{c}\frac{1}{B_1}{P}_{o1}{P}_{o2}^2{10}^{\frac{-I{P}_3}{5}}\hfill \\ +\frac{1}{2B_1^2{B}_2}{P}_{o1}{P}_{o2}^2{10}^{\frac{-I{P}_3}{5}}\left(-f^2+4B_1{B}_2-B_2^2\right),\hfill \end{array}\hfill & \left|f\right|\le 2B_2-B_1\hfill \\ \begin{array}{c}\frac{1}{B_1}{P}_{o1}{P}_{o2}^2{10}^{\frac{-I{P}_3}{5}},\hfill \\ +\frac{1}{4B_1{B}_2^2}{P}_{o1}{P}_{o2}^2{10}^{\frac{-I{P}_3}{5}}·[-f^2+\left(2B_1-4B_2\right)\hfill \\ ·\left|f\right|-B_1^2+4B_2^2+4B_1{B}_2]\hfill \end{array}\hfill & 2B_2-B_1<\left|f\right|\le B_1\hfill \\ \frac{1}{4B_1{B}_2^2}{P}_{o1}{P}_{o2}^2{10}^{\frac{-I{P}_3}{5}}{\left(B_1+2B_2-\left|f\right|\right)}^2,\hfill & B_1<\left|f\right|\le B_1+2B_2\hfill \\ 0,\hfill & \left|f\right|>B_1+2B_2\hfill \end{array}\right.\hfill \end{array}$$

(24)

Based on (12), we now could decompose $P_y\left(f\right)$ into:

$$P_y\left(f\right)=P_{y_{passband}}\left(f\right)+P_{y_{out-of-band}}\left(f\right)$$

(25)

where $P_{y_{passband}}\left(f\right)$ is attributed to linear amplification, in-band IM and CM, while $P_{y_{out-of-band}}\left(f\right)$ is attributed to out-of-band only. $P_{y_{passband}}\left(f\right)$ can be written as ([14], Equation (54)), and the observations related to $P_{y_{passband}}\left(f\right)$ can be found in [14]. So as to obtain $P_{y_{out-of-band}}\left(f\right)$, we need to shift $P_{{\tilde{y}}_3}\left(f\right)$ and $P_{{\tilde{y}}_4}\left(f\right)$ to carrier frequencies $2f_{c_1}-f_{c_2}$ and $2f_{c_2}-f_{c_1}$, respectively. $P_{y_{out-of-band}}\left(f\right)$ then equals to half of the summation of those two shifted spectrum items as

$$\begin{array}{l}{P}_{y_{out-of-band}}\left(f\right)=\frac{1}{2}(P_{{\tilde{y}}_3}(f-(2f_{c_1}-f_{c_2}))+P_{{\tilde{y}}_4}(f-(2f_{c_2}-f_{c_1})))\hfill \\ =\left\{\begin{array}{cc}\begin{array}{c}\frac{1}{2B_2}{P}_{o1}^2{P}_{o2}{10}^{\frac{-I{P}_3}{5}}\hfill \\ +\frac{1}{4B_1^2{B}_2}{P}_{o1}^2{P}_{o2}{10}^{\frac{-I{P}_3}{5}}\hfill \\ ·\left\{-{\left[f-\left(2f_{c_1}-f_{c_2}\right)\right]}^2+4B_1{B}_2-B_2^2\right\},\hfill \end{array}\hfill & \left|f-\left(2f_{c_1}-f_{c_2}\right)\right|\le B_2\hfill \\ \begin{array}{c}\frac{1}{4B_1^2{B}_2}{P}_{o1}^2{P}_{o2}{10}^{\frac{-I{P}_3}{5}}\hfill \\ ·\left[4B_1{B}_2-2B_2\left|f-\left(2f_{c_1}-f_{c_2}\right)\right|\right],\hfill \end{array}\hfill & B_2<\left|f-\left(2f_{c_1}-f_{c_2}\right)\right|\le 2B_1-B_2\hfill \\ \begin{array}{c}\frac{1}{8B_1^2{B}_2}{P}_{o1}^2{P}_{o2}{10}^{\frac{-I{P}_3}{5}}\hfill \\ ·{\left[2B_1+B_2-\left|f-\left(2f_{c_1}-f_{c_2}\right)\right|\right]}^2,\hfill \end{array}\hfill & 2B_1-B_2<\left|f-\left(2f_{c_1}-f_{c_2}\right)\right|\le 2B_1+B_2\hfill \\ \begin{array}{c}\frac{1}{2B_1}{P}_{o1}{P}_{o2}^2{10}^{\frac{-I{P}_3}{5}}\hfill \\ +\frac{1}{4B_1{B}_2^2}{P}_{o1}{P}_{o2}^2{10}^{\frac{-I{P}_3}{5}}\hfill \\ ·\left\{-{\left[f-\left(2f_{c_2}-f_{c_1}\right)\right]}^2-B_1^2+4B_1{B}_2\right\},\hfill \end{array}\hfill & \left|f-\left(2f_{c_2}-f_{c_1}\right)\right|\le 2B_2-B_1\hfill \\ \begin{array}{c}\frac{1}{2B_1}{P}_{o1}{P}_{o2}^2{10}^{\frac{-I{P}_3}{5}}\hfill \\ +\frac{1}{8B_1{B}_2^2}{P}_{o1}{P}_{o2}^2{10}^{\frac{-I{P}_3}{5}}\hfill \\ ·\{-{\left[f-\left(2f_{c_2}-f_{c_1}\right)\right]}^2\hfill \\ +\left(2B_1-4B_2\right)\left|f-\left(2f_{c_2}-f_{c_1}\right)\right|\hfill \\ -B_1^2+4B_2^2+4B_1{B}_2\},\hfill \end{array}\hfill & 2B_2-B_1<\left|f-\left(2f_{c_2}-f_{c_1}\right)\right|\le B_1\hfill \\ \begin{array}{c}\frac{1}{8B_1{B}_2^2}{P}_{o1}{P}_{o2}^2{10}^{\frac{-I{P}_3}{5}}\hfill \\ ·{\left[B_1+2B_2-\left|f-\left(2f_{c_2}-f_{c_1}\right)\right|\right]}^2,\hfill \end{array}\hfill & B_1<\left|f-\left(2f_{c_2}-f_{c_1}\right)\right|\le B_1+2B_2\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(26)

By comparing ([14], Equation (54)) and (26), it can be seen that the in-band spectra will not be interfered by the out-of-band distortions. In Figure 2, A numerical case is shown with $f_{c_1}=864$ MHz, $f_{c_2}$ = 886 MHz, $B_1=B_2=7$ MHz, $I{P}_3=26.1$ dBm, $P_{o1}=-2$ dBm, $P_{o2}=1$ dBm. The blue dash waveform shows $P_y\left(f\right)$ without CM and out-of-band intermodulation, and the red solid waveform shows $P_y\left(f\right)$. The difference between the two lines indicates that the impact of out-of-band intermodulation is clear. Also, from Figure 2, we can see that $P_{y_{out-of-band}}\left(f\right)$ has a clear interference if there are other signals centered around 842 MHz or 908 MHz in those channels.

As a special case, if either ${\tilde{s}}_1\left(t\right)$ or ${\tilde{s}}_2\left(t\right)$ is zero, $P_y\left(f\right)$ will be completely deduced to the single-band signal spectrum as in ([11], Equation (25)). Subsequently, the CM and out-of-band IM due to dual bands in Figure 2 will all disappear. Of course, only one single band in blue will remain.

3. Experimental Setup and Verification

The measurement setup is described in Figure 3, which consists of the Tektronix AWG 70002A arbitrary waveform generator as frequency up-conversion units and DACs, the Tektronix RSA5126B real-time spectrum analyzer for capturing the signal from the output of the RF amplifier for further algorithm verification, the Mini-Circuit LNA ZFL-1000LN+ as the device under test, and a PC running MATLAB to verify the analytical prediction with the experimental measurements.

Based on the standards of LTE operating bands [21], a 7 MHz bandwidth with an 864 MHz center frequency was chosen for the left band, and a 7 MHz bandwidth with an 886 MHz center frequency was chosen for the left band. The number of subcarriers for each band is 470. In Figure 4, it can be clearly observed that the theoretically predicted PSD (the red line) matches the experimental results (the blue line).

Since only third-order nonlinearity is considered in this manuscript, there are some visible misalignments in the shoulder areas between theoretical calculation and experimental measurement shown in Figure 4. These misalignments are generated by high-order nonlinearities and memory effects.

In order to further improve the accuracy of this model, higher order nonlinearities and memory effects will be considered in our future study.

4. Conclusions

In this article, we expanded our dual-band spectrum modeling, from in-band IM and CM previously, to out-of-band intermodulation, which will be used to evaluate the interference to adjacent channels. The dual-band spectrum model could help spectrum planners and regulators to identify where the interferences will be.