An Efficient Resource Allocation for Massive MTC in NOMA-OFDMA Based Cellular Networks

Abstract

To alleviate random access congestion and support massive-connections with less energy consumption for machine-type communications (MTC) in the 5G cellular network, we propose an efficient resource allocation for massive MTC (mMTC) with hybrid non-orthogonal multiple access (NOMA)-orthogonal frequency division multiple access (OFDMA). First, a hybrid multiple access scheme, including the NOMA-based congestion-alleviating access scheme (NCAS) and OFDMA-based congestion-alleviating access scheme (OCAS), is proposed, in which the NOMA based devices coexist with OFDMA based ones. Then, aiming at maximizing the system access capacity, a traffic-aware resource blocks (RBs) allocation is investigated to optimize RBs allocation for preamble transmission and data packets transmission, as well as to optimize the RBs allocation between NCAS and OCAS for the RBs usage efficiency improvement. Next, aiming at the problem of high computational complexity and improving energy efficiency in hybrid NOMA-OFDMA based cellular M2M communications, this paper proposes an improved low complexity power allocation algorithm. The feasibility conditions of power allocation solution under the maximum transmit power constraints and quality of service (QoS) requirements of the devices is investigated. The original non-convex optimization problem is solved under the feasibility conditions by two iterative algorithms. Finally, a device clustering scheme is proposed based on the channel gain difference and feasible condition of power allocation solution, by which NOMA based devices and OFDMA based devices can be determined. Simulation results show that compared with non-orthogonal random access and transmission (NORA-DT), the proposed resource allocation scheme for hybrid NOMA-OFDMA systems can efficiently improve the performance of access capacity and energy efficiency.

1. Introduction

Machine-type communications (MTC), also known as machine-to-machine (M2M) communications, is an emerging technology that boosts the development of the Internet of Things (IoT) by providing ubiquitous connectivity and services [1,2]. Due to the diverse set of MTC applications and services [3,4], the current view on the 5G wireless system categorizes MTC into two: (1) massive MTC (mMTC) supplying a massive number of low-data rate and low-cost devices and (2) ultra-reliable low-latency MTC (uMTC) supporting message transmission with high reliability and low latency [5]. According to Machina Research [6], the number of machine-type communications devices (MTCDs) will reach 27 billion in 2024. Each MTCD performs a random access (RA) procedure for initial uplink access to connect and synchronize with its base station (BS) [7]. However, a large number of MTCDs may be triggered and attempt to access the BS within a relatively short time, which leads to severe RA congestion, high power consumption, unexpected delay, and radio resource wastage [8]. Therefore, alleviating RA congestion and supporting massive-connections have been deemed as the most important for IoT in the 5G network [9].

There have been some solutions addressing the RA congestion problem. Access class barring (ACB) scheme is regarded as an efficient approach to control traffic load [10,11,12,13,14]. The study in [10,11] investigated an analytical model and simulation model to evaluate the performance of the ACB scheme. The authors in [12] proposed a dynamic ACB method to increase the access success probability. In [13], the authors optimized ACB factor and uniform backoff window size to improve the success access. The authors in [14] proposed a learning automata-based ACB scheme to control the massive M2M traffic under the interference of human-to-human (H2H) traffic. Reference [15,16,17,18,19,20,21] tackled the RA congestion problem by efficiently utilizing the radio resources. In [15], the authors proposed a novel pipelined contention resolution scheme based on distributed queuing to improve the utilization of preamble resources. In [16], a collision-aware resource access scheme was proposed to reduce the collisions on the granted physical resource blocks (PRBs). In [17], an enhanced spatial group-based RA scheme was presented to reduce collision probability. The authors in [18] proposed a dynamic preamble grouping strategy based on delay-sensitive characteristics. While in [19], the authors proposed an optimal scheme to dynamically adjust the number of random access channel resources between delay-sensitive devices and delay-tolerant ones. In [20], an adaptive resource allocation scheme was introduced to allocate different amounts of random access resources to M2M applications with distinct delay requirements. Reference [21] considered the resource allocation between physical random access channel (PRACH) and physical uplink shared channel (PUSCH) for orthogonal random access and data transmission to resolve the congestion problem in the RA procedure.

However, in the aforementioned schemes, only one MTCD was allowed to use the scheduled data channel, otherwise, the RA procedure failed. The objective of high spectral efficiency and massive connectivity needs to be further improved [22]. As one of the key technologies for 5G cellular networks, non-orthogonal multiple access (NOMA) with successive interference cancellation (SIC) technique permits multiple users sharing the same radio resources, which could achieve high spectral efficiency and massive connectivity compared with orthogonal multiple access (OMA) [23,24]. There are also some studies on the usage of M2M communications in NOMA systems [25,26,27,28,29,30,31,32,33]. The works in [25,26,27,28] targeted sum rate maximization, and the energy efficiency maximization of NOMA for M2M communications were studied in [29,30,31,32,33]. For a given set of NOMA clusters, standard convex optimization [29], difference of convex programming [30], and Lagrange duality methods [25,31,32,33] were employed, respectively, for power control. User clustering is also a key factor on the performance of uplink NOMA. In [25], the users were grouped into the clusters based on the difference of channel conditions between users. In [26], a novel MTCD pairing scheme was introduced based upon the distance between the BS and the MTCDs. In [27], each strong channel gain device was allocated to the appropriate cluster as a cluster head. In [28], location-based schemes were proposed to place MTCDs in a cluster.

The aforementioned studies mainly focus on the theoretical analysis of the power allocation scheme in the data transmission process, and few studies have considered the realization of NOMA for alleviating the RA congestion problem. Motivated by the idea of NOMA and SIC, the authors in [34] proposed a SIC-based non-orthogonal random access (NORA) scheme to alleviate the access congestion problem, in which multiple users can transmit preamble on the same RBs. Based on [34], the authors in [35] proposed a resource allocation scheme, which can allocate uplink resources between PRACH and PUSCH reasonably for non-orthogonal random access and data transmission (NORA-DT). While the total number of RBs allocated to PRACH and PUSCH was fixed, even the MTCDs may not be able to process over the whole RBs. In [34,35], the BS utilized the difference of time of arrival to identify collided MTCDs with the identical preamble and performed SIC based on the channel conditions obtained through preamble detection. As the number of collided MTCDs at the BS increases, both the preamble collision detection and the user separation complexity increase. In addition, the power control schemes in [34,35] just ensured that collided MTCDs have diverse arrived power, while the limited energy of MTCDs was not considered.

Given an SIC receiver cannot perfectly cancel co-channel interferences, the performance of NOMA will be degraded, and NOMA may not satisfy the quality of service (QoS) of user equipment in some scenarios, while OMA techniques can significantly reduce the inter-user interference. Hence, in a practical scenario, it becomes more beneficial to consider a combination of NOMA and the existing access technology, for example, orthogonal frequency division multiple access (OFDMA), to support a larger number of MTCDs. However, a combination of NOMA and OFDMA for M2M communication over cellular networks faces some challenges. One of these challenges is the management of uplink radio resources. Therefore, we propose a traffic-aware resource allocation scheme for hybrid NOMA-OFDMA based cellular M2M communications. The main contribution of this work are listed below:

• We propose a NOMA-based congestion-alleviating access scheme (NCAS) to improve the access capacity and resource efficiency accompanied with OFDMA-based congestion-alleviating access scheme (OCAS) for the hybrid NOMA-OFDMA based cellular M2M communication systems. The MTCDs in NCAS and OCAS are allowed to send data with optimal power allocation solution right after preamble transmission without explicitly establishing a connection, which could reduce the scheduling signaling overhead and simplify the access process. Different from OCAS, a device called cluster head (CH) transmit preambles in NCAS, so that the number of MTCDs that directly transmit preambles to the BS can be greatly reduced.
• We propose a traffic-aware resource blocks (RBs) allocation scheme consisting of two sub-problems for the hybrid multiple access systems. The first sub-problem is used to optimize RBs allocation between PRACH and PUSCH given the sum of RBs allocated to PRACH and PUSCH for NCAS, while the second one optimizes the RBs allocation between NCAS and OCAS. NOMA based MTCDs and OFDMA based MTCDs, respectively, compete for uplink resources allocated for NCAS and OCAS to transmit preamble and data packets. To alleviate the RA congestion problem, the number of MTCDs that compete for uplink resources allocated for NCAS and OCAS are restricted by the traffic-aware access barring schemes.
• We formulate an energy efficiency maximization problem such that the MTCDs’ power allocation can be optimized under the maximum transmit power constraint and QoS requirement of the MTCD. The feasibility conditions of the power allocation solution are determined as linear constraints of the CH. The original non-convex optimization problem is transformed into the pseudo-concave function of the CH by using the difference of received power. Then the transformed problem is solved under the feasibility conditions by two iterative algorithms. The first algorithm is used to optimize the energy efficiency by using the Dinkelbach method, while the second one optimizes the power allocation solution under the energy efficiency optimized in the first algorithm.
• We design a device clustering scheme to group devices into different clusters. The proposed scheme provides the range of channel gain differences as the condition of grouping, which exploits the channel gain and maximum transmit power constraint of the devices. If the channel gain differences among devices can satisfy the condition of grouping, then these devices are treated as NOMA based MTCDs, which compete for uplink resources allocated for NCAS. Otherwise, these devices are treated as OFDMA based MTCDs, which compete for uplink resources allocated for OCAS.
• We evaluate the energy efficiency and access capacity performance of the resource allocation for the hybrid NOMA-OFDMA based cellular M2M communication systems. Simulation results show that the proposed resource allocation scheme can efficiently improve the system access capacity and energy efficiency compared with NORA-DT.

The rest of this paper is organized as follows. The system model and NOMA based congestion-alleviating access scheme is presented in Section 2. The optimization of the number of RBs for the hybrid NOMA-OFDMA based M2M communication systems is focused in Section 3. The channel model and problem formulation is proposed in Section 4. The power allocation for the hybrid NOMA-OFDMA based M2M communications is solved in Section 5. The MTCD clustering algorithm is presented in Section 6. Numerical results are provided in Section 7, and concluding remarks are given in Section 8.

Notations: Lowercase boldface letters denote vectors. $\left|·\right|$ denotes the absolute value. $O\left(·\right)$ is reserved for complexity estimates. $\mathcal{X}\backslash x$ denotes that component x is not included in the set $\mathcal{X}$, and $\mathcal{X}\left(m\right)$ denotes the m-th element of set $\mathcal{X}$.

2. System Model and NOMA Based Congestion-Alleviating Access Scheme

2.1. System Model

As shown in Figure 1, we consider an uplink of the NOMA-OFDMA scenario with a cellular-enabled M2M network, which contains a BS and U MTCDs. We denote u as index for the u-th MTCD where $u\in \left\{1,2,\cdots ,U\right\}$. In LTE, both the uplink and downlink transmissions are divided into frames of duration of 10 ms, where each frame is composed of 10 sub-frames. Each sub-frame contains two slots, where each slot can contain 6 to 110 RBs [36]. The available radio resources are separately managed for NCAS and OCAS. Assuming the available number of RBs in each RA cycle is q, and $\theta$ is the RBs allocation factor between NCAS and OCAS. Then the number of RBs allocated for NCAS is $q\theta$, and the number of RBs allocated for OCAS is $q\left(1-\theta \right)$. Furthermore, the RBs of NCAS are split into two subsets, i.e., PRACH resource and PUSCH resource. The RBs of OCAS are also split into PRACH resource and PUSCH resource. Denote $n_1$ and $n_2$ as the number of PRACH RBs allocated for NCAS and OCAS, respectively. Then the number of PUSCH RBs allocated for NCAS and OCAS is $q\theta -n_1$ and $q\left(1-\theta \right)-n_2$.

A PRACH consists of six physical RBs in a subframe, which occupies 864 subcarriers [37]. Assuming $\eta$ preamble sequences are mapped to the central 839 subcarriers while the rest 25 subcarriers are reserved for guard band in each RA cycle. Therefore, $\eta n_1/\phantom{\eta n_{1}6}6$ and $\eta n_2/\phantom{\eta n_{2}6}6$ preambles can be constructed for NCAS and OCAS, respectively. $n_1$ and $n_2$ are integer multiples of six. Suppose an MTCD uses one PUSCH for a fixed-size data packet transmission, then the number of available PUSCH for NCAS is $\left(q\theta -n_1\right)/\phantom{\left(q\theta -n_1\right)\delta }\delta$, and the number of available PUSCH for OCAS is $\left(q\left(1-\theta \right)-n_2\right)/\phantom{\left(q\left(1-\theta \right)-n_2\right)\delta }\delta$.

2.2. NOMA Based Congestion-Alleviating Access Scheme

For the hybrid NOMA-OFDMA based cellular M2M communication system, NCAS and OCAS are jointly used to improve the system access capacity. The system access capacity is defined as the expected number of MTCDs that successfully transmit data packets. We adopt the orthogonal random access and data transmission scheme [21] as the OCAS in this paper. In this subsection, we give a detailed description of the NCAS, which consists of NOMA cluster establishment, access barring, preamble transmission, data channel scheduling, power back-off and data packet transmission, SIC and acknowledge (ACK). Before each RA cycle begins, BS broadcasts the configuration of RBs for PRACH (i.e., $n_1$) and the ACB parameters (denoted by $R_1$) via a downlink control channel.

Step 1. NOMA cluster establishment. This step is to discover clustered MTCDs and select a cluster head (CH). The proposed MTCD clustering scheme is investigated in Section 6.

Step 2. Access barring. The CH randomly selects a number out of the uniform distribution between zero and one. Then the CH compares the number with the ACB parameter. If the number is no more than the ACB parameter, the CH participates in random access; otherwise, the CH reattempts after a random back-off.

Step 3. Preamble transmission. The CH randomly selects one preamble from the preambles constructed for NCAS and transmits the preamble on PRACH for random access. After that, the CH broadcasts the list of power back-off index and the identity (ID) of other MTCDs in a NOMA cluster. The index of the transmitted preamble on PRACH is also attached. The MTCD checks if its MTCD ID is included in the list. If included, it goes to step 4 to receive RAR. Otherwise, it reattempts in the next RA cycle.

Step 4. Data channel scheduling. After detecting the preambles transmitted by CHs, the BS sends random access response (RAR) through the downlink channel. A RAR message contains scheduling information that associates a preamble index to the corresponding scheduled data channel. Given all MTCDs in a NOMA cluster know the index of the transmit preamble sequence, they are expected to receive the same RAR.

Step 5. Power back-off and data packet transmission. When the MTCD in a NOMA cluster receives RAR, it checks if the RAR message matches the preamble sequence sent by CH. Upon receiving a matching RAR, the MTCD adjusts the transmit power based on the power back-off index and transmits the data packet on the assigned PUSCH.

Step 6. SIC reception and ACK. The BS performs SIC and decodes the data packets from each PUSCH one by one. Then the BS sends the ACK message and the MTCD’s ID via the control channel. After receiving an ACK message, all the MTCDs in a NOMA cluster report to an upper layer that the data packet is successfully transmitted. If the MTCD cannot receive the RAR message or any ACK message, it is regarded as a failed data transmission.

3. Optimization of the Number of RBs for the Hybrid NOMA-OFDMA Based M2M Communications

In this section, a traffic-aware RBs allocation consisting of two sub-problems for the hybrid multiple access systems is investigated. The first sub-problem is used to optimize RBs allocation between PRACH and PUSCH given the sum of RBs allocated to PRACH and PUSCH for NCAS, while the second one optimizes the RBs allocation between NCAS and OCAS since the MTCDs may not be able to process over the whole available RBs.

3.1. Optimization of the Number of RBs for the PRACH Given the Number of RBs for the NCAS

In this subsection, the closed-form analytic expression for the access capacity in NCAS is derived. Then the optimal number of PRACH RBs allocated for NCAS given $q\theta$ is obtained by maximizing the access capacity function. According to step 3 in NCAS, each CH randomly selects one preamble from $\eta n_1/\phantom{\eta n_{1}6}6$ preambles and transmits it on behalf of the multiplexing MTCDs in a NOMA cluster on PRACH. Let $B_i$ denote the number of CHs selecting preamble i in each cycle. Let $S_i=1$ represent that the BS schedules data channel for detected preamble i. According to the NCAS, if $B_i=1$, $S_i=1$, the cluster selecting preamble i can transmit data packets on the assigned data channel. Therefore, the access capacity obtained by NCAS is given as

$$Acc=M·\left\{Pr\left[S_i=1,B_i=1\right]·\left(\eta n_1/\phantom{\eta n_{oma}6}6\right)\right\}$$

(1)

where M is the number of multiplexing MTCDs in the cluster. $Pr\left[S_i=1,B_i=1\right]·\left(\eta n_1/\phantom{\eta n_{oma}6}6\right)$ is the expected number of the clusters that can transmit data packets on the assigned data channel, where $Pr\left[S_i=1,B_i=1\right]$ is the probability that the BS schedules data channel for the preamble i, where the preamble i is selected by only one CH. $Pr\left[S_i=1,B_i=1\right]$ is given by

$$\begin{array}{cc}\hfill Pr\left[S_i=1,B_i=1\right]& =Pr\left[\left.B_i=1\right|S_i=1\right]·\frac{Pr\left[B_i\ge 1,S_i=1\right]}{Pr\left[\left.B_i\ge 1\right|S_i=1\right]}\hfill \\ \hfill & =Pr\left[\left.B_i=1\right|B_i\ge 1\right]·Pr\left[B_i\ge 1,S_i=1\right]\hfill \\ \hfill & =Pr\left[B_i=1\right]Pr\left[S_i=1\left|B_i\ge 1\right.\right]\hfill \end{array}$$

(2)

Since a preamble receiving the scheduling information of PUSCH must be detected by the BS, $Pr\left[B_i=1\left|S_i=1\right.\right]=Pr\left[B_i=1\left|B_i\ge 1\right.\right]$ and $Pr\left[\left.B_i\ge 1\right|S_i=1\right]=1$ in (2). Assuming the number of NOMA CHs selecting a preamble follows the Poisson distribution with mean $u_1/\phantom{u_1\left(\eta n_1/\phantom{\eta n_{1}6}6\right)}\left(\eta n_1/\phantom{\eta n_{1}6}6\right)$. Therefore, the probability that preamble i is selected by l CHs is [38]

$$Pr\left[B_i=l\right]={\left(\frac{6u_1}{\eta n_1}\right)}^{l}exp\left(-\frac{6u_1}{\eta n_1}\right)\phantom{{\left(\frac{6u_1}{\eta n_1}\right)}^{l}exp\left(-\frac{6u_1}{\eta n_1}\right)l!}/l!$$

(3)

In Equation (2), $Pr\left[S_i=1\left|B_i\ge 1\right.\right]$ is the probability that the BS sends the scheduling information of PUSCH for the detected preamble i, which is given by

$$\begin{array}{cc}\hfill \mathrm{E}\left[V_1^{\mathrm{sched}}\right]& ={\displaystyle \sum _{m=1}^{6n_1}}\mathrm{E}\left[V_1^{\mathrm{sched}}\left|V_1^{\mathrm{detect}}=m\right.\right]Pr\left[V_1^{\mathrm{detect}}=m\right]\hfill \\ \hfill & ={\displaystyle \sum _{m=1}^{6n_1}}{n}_{1}Pr\left[S_i=1\left|B_i\ge 1\right.\right]Pr\left[V_1^{\mathrm{detect}}=m\right]\hfill \\ \hfill & =Pr\left[S_i=1\left|B_i\ge 1\right.\right]\mathrm{E}\left[V_1^{\mathrm{detect}}\right]\hfill \end{array}$$

(4)

where $\mathrm{E}\left[V_1^{\mathrm{sched}}\right]$ is the expected number of detected preambles obtaining the data channel scheduled by BS, and $\mathrm{E}\left[V_1^{\mathrm{detect}}\right]$ is the expected number of preambles that is detected by BS. $\mathrm{E}\left[V_1^{\mathrm{detect}}\right]$ is given by

$$\begin{array}{cc}\hfill \mathrm{E}\left[V_1^{\mathrm{detect}}\right]& =\left(\eta n_1/\phantom{\eta n_{1}6}6\right)·Pr\left[B_i\ge 1\right]\hfill \end{array}$$

(5)

where $Pr\left[B_i\ge 1\right]$ is the preamble detection probability based on the assumption that the BS can detect the preamble i if and only if preamble i is selected by one or more CHs. Therefore, $Pr\left[B_i\ge 1\right]$ is given by

$$Pr\left[B_i\ge 1\right]=1-Pr\left[B_i=0\right]$$

(6)

when the variance of $V^{\mathrm{detect}}$ is relatively small, we can get the following approximation.

$$\mathrm{E}\left[V_1^{\mathrm{sched}}\right]\simeq min\left\{\mathrm{E}\left[V_1^{\mathrm{detect}}\right],\left(q\theta -n_1\right)/\phantom{\left(q\theta -n_1\right)\delta }\delta \right\}$$

(7)

From Equations (3)–(7), $Pr\left[S_i=1\left|B_i\ge 1\right.\right]$ is derived as

$$\begin{array}{cc}\hfill Pr\left[S_i=1\left|B_i\ge 1\right.\right]& =\mathrm{E}\left[V_1^{\mathrm{sched}}\right]\phantom{\mathrm{E}\left[V_1^{\mathrm{sched}}\right]\mathrm{E}\left[V_1^{\mathrm{detect}}\right]}/\mathrm{E}\left[V_1^{\mathrm{detect}}\right]\hfill \\ \hfill & =min\left\{1,\frac{6\left(q\theta -n_1\right)}{\delta \eta n_1\left(1-exp\left(-\frac{6u_1}{\eta n_1}\right)\right)}\right\}\hfill \end{array}$$

(8)

Based on Equations (1)–(3) and (8), we can get the access capacity in NCAS as follows,

$$Acc=min\left\{M{u}_{1}exp\left(-\frac{6u_1}{\eta n_1}\right),\frac{6M{u}_1\left(q\theta -n_1\right)}{\delta \eta n_1\left(exp\left(\frac{6u_1}{\eta n_1}\right)-1\right)}\right\}$$

(9)

Given $q\theta$, the access capacity function can be expressed as

$$\varsigma \left(u_1,n_1,M;q\theta \right)=min\left\{\alpha \left(u_1,n_1,M\right),\beta \left(u_1,n_1,M;q\theta \right)\right\}$$

(10)

where $\alpha \left(u_1,n_1,M\right)=M{u}_{1}exp\left(-\frac{6u_1}{\eta n_1}\right)$, $\beta \left(u_1,n_1,M;q\theta \right)=\frac{6M{u}_1\left(q\theta -n_1\right)}{\delta \eta n_1\left(exp\left(\frac{6u_1}{\eta n_1}\right)-1\right)}$. To maximize the access capacity function in Equation (10), the optimal number of PRACH RBs allocated for NCAS, denoted by $n^{*}\left(u_1;q\theta \right)$, is given by $n^{*}\left(u_1;q\theta \right)=argmax\varsigma \left(u_1,n_1,M;q\theta \right)$.

Proposition 1.

Given $q\theta$, the optimal solution that maximize $\alpha \left(u_1,n_1,M\right)$ exists when $u_1=x_i$, and $n_1=n^{+}\left(x_i;q\theta \right)$, where $x_i=-\eta iln\left(1-\frac{q\theta -6i}{\delta \eta i}\right)$ and $n^{+}\left(x_i;q\theta \right)=6i$. i is an integer, and $i\in \left[⌊q\theta /\phantom{q\theta \left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+1,⌈q\theta /\phantom{q\theta 6}6⌉-1\right]$, where ⌊⌋ denotes the bottom integer function, and ⌈⌉ denotes the ceil integer function.

Proof of Proposition 1. 

$\alpha \left(u_1,n_1,M\right)$ is an increasing function of $n_1$, while $\beta \left(u_1,n_1,M;q\theta \right)$ is a convex function of $n_1$. Therefore, $\alpha \left(u_1,n_1,M\right)$ is a maximum value when $\alpha \left(u_1,n_1,M\right)=\beta \left(u_1,n_1,M;q\theta \right)$, i.e.,

$$M{u}_{1}exp\left(-\frac{6u_1}{\eta n_1}\right)=\frac{6M{u}_1\left(q\theta -n_1\right)}{\delta \eta n_1\left(exp\left(\frac{6u_1}{\eta n_1}\right)-1\right)}$$

(11)

$u_1$ is formulated as

$$u_1=-\frac{\eta n_1}{6}ln\left(1-\frac{6\left(q\theta -n_1\right)}{\delta \eta n_1}\right)$$

(12)

Due to $ln\left(1-\frac{6\left(q\theta -n_1\right)}{\delta \eta n_1}\right)<0$ and $1-\frac{6\left(q\theta -n_1\right)}{\delta \eta n_1}>0$, we have $\frac{6q\theta }{6+\delta \eta }<n_1<q\theta$. Let $n_1=6i$, thus $i\in \left[⌊q\theta /\phantom{q\theta \left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+1,⌈q\theta /\phantom{q\theta 6}6⌉-1\right]$. Substituting $6i$ into Equation (12), we can get $x_i=-\eta iln\left(1-\frac{q\theta -6i}{\delta \eta i}\right)$. Therefore, the optimal solution that maximizes $\alpha \left(u_1,n_1,M\right)$ exists when $u_1=x_i$, and $n_1=6i$. □

Proposition 2.

Given $u_1$ and $q\theta$, the optimal solution that maximizes $\beta \left(u_1,n_1,M;q\theta \right)$ exists when $n_1=n^{-}\left(u_1;q\theta \right)$, where $n^{-}\left(u_1;q\theta \right)=6⌈j⌉$, $j={\left\{\frac{\eta }{u_1}{W}_0\left(-exp\left(-1-\frac{6u_1}{\eta q\theta }\right)\right)+\frac{\eta }{u_1}+\frac{1}{q\theta }\right\}}^{-1}$.

Proof of Proposition 2. 

Assuming $n_1=6j$, then $\beta \left(u_1,j,M;q\theta \right)=\frac{M{u}_1\left(q\theta -6j\right)}{\delta \eta j\left(exp\left(\frac{u_1}{\eta j}\right)-1\right)}$. Define $f\left(x\right)=\frac{M{u}_1\left(q\theta x-6\right)}{\delta \eta \left(exp\left(\frac{u_{1}x}{\eta }\right)-1\right)}$, where $x=1/\phantom{1j}j$. Let $\frac{\partial f\left(x\right)}{\partial x}=0$, we can have

$$exp\left(-\frac{u_{1}x}{\eta }\right)=-\frac{u_{1}x}{\eta }+1+\frac{6u_1}{\eta q\theta }$$

(13)

with the Lambert W function, x can be expressed as

$$x=\frac{\eta }{u_1}{W}_0\left(-exp\left(-1-\frac{6u_1}{\eta q\theta }\right)\right)+\frac{\eta }{u_1}+\frac{6}{q\theta }$$

(14)

In Equation (14), $W_0$ is the principal branch of the Lambert W function. As $x=1/\phantom{1j}j$, we can get

$$j={\left\{\frac{\eta }{u_1}{W}_0\left(-exp\left(-1-\frac{6u_1}{\eta q\theta }\right)\right)+\frac{\eta }{u_1}+\frac{1}{q\theta }\right\}}^{-1}$$

(15)

Then, $n^{-}\left(u_1;q\theta \right)=6⌈j⌉$ since the number of PRACH RBs is integer multiples of six. Therefore, $\beta \left(u_1,n_1,M;q\theta \right)$ is maximum when $n_1=n^{-}\left(u_1;q\theta \right)$. □

From above, it can be known that if $n^{+}\left(x_i;q\theta \right)<n^{-}\left(x_i;q\theta \right)$, the optimal PRACH RBs to maximize the access capacity function is given by $n^{*}\left(x_i;q\theta \right)=n^{-}\left(x_i;q\theta \right)$. If $n^{+}\left(x_i;q\theta \right)\ge n^{-}\left(x_i;q\theta \right)$, the optimal PRACH RBs to maximize the access capacity function is given by $n^{*}\left(x_i;q\theta \right)=n^{+}\left(x_i;q\theta \right)$. However, the computation is intensive since $n^{+}\left(x_i;q\theta \right)$ and $n^{-}\left(x_i;q\theta \right)$ need to be solved many times with the change of $x_i$ and $q\theta$. To relieve the computational burden and to realize the optimal PRACH RBs for different $u_1$, we propose a low-complexity optimal solution for $n^{*}\left(u_1;q\theta \right)$ based on the traffic load ranges derived in Algorithm 1. As shown in Algorithm 1, by determining the range to which $u_1$ belongs, we can directly obtain the optimal solution of the number of PRACH RBs for the NCAS given the value of q and $\theta$. In addition, the number of NOMA CHs that compete for uplink resources is restricted to alleviate the RA congestion problem by the traffic-aware ACB with a computed ACB factor R.

Algorithm 1 RBs Allocation for PRACH for the NCAS
1:	Initialize q, $\theta$, $u_1$, $Count=0$.
2:	for$i=⌊q\theta /\phantom{q\theta \left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+1$ to $⌈q\theta /\phantom{q\theta 6}6⌉-1$ do
3:	Calculating $n^{+}\left(x_i;q\theta \right)$ and $x_i$ based on Proposition 1.
4:	Calculating $n^{-}\left(x_i;q\theta \right)$ based on Proposition 2.
5:	if $n^{+}\left(x_i;q\theta \right)<n^{-}\left(x_i;q\theta \right)$ then
6:	$count=count+1$;
7:	end if
8:	end for
9:	$i_a=⌊q\theta /\phantom{q\theta \left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+count$, $i_b=⌈q\theta /\phantom{q\theta 6}6⌉-1$.
10:	if$u_1\in \left(x_{i+1},x_i\right]$, $\forall i\in \left[i_a,i_b\right)$then
11:	$n^{*}\left(u_1;q\theta \right)=6i$, $R=1$. (See Appendix A.)
12:	end if
13:	if$u_1\in \left(0,x_{i_b}\right]$then
14:	$n^{*}\left(u_1;q\theta \right)=6i_b$, $R=1$.
15:	end if
16:	if$u_1\in \left(x_{i_a},+\infty \right)$then
17:	$n^{*}\left(u_1;q\theta \right)=6i_a$, $R=x_{i_a}/\phantom{x_{i_a}{u}_1}{u}_1$. (See Appendix B.)
18:	end if

3.2. Optimization of the Number of RBs for the Hybrid NOMA-OFDMA Based M2M Communications

In the above subsection, the number of RBs between PRACH and PUSCH is optimized given $u_1$ and $q\theta$. In this subsection, how to optimize the RBs allocation factor $\theta$ is studied. In Figure 2, we present the number of success clusters (i.e., the number of NOMA clusters that successfully transmit data packets) against the number of NOMA CHs when $\theta =0.5$, 0.6, 0.8, 1. For this graph, we set $\eta =24$, $\delta =1$. As can be seen from Figure 2, for different $\theta$, the number of success clusters first increases to its maximum and then achieves a stable level as the number of CHs increases. This is because the ACB scheme is incorporated to control the number of CHs when the number of CHs is higher than the optimal number of participating CHs. Through comparison of the results for different $\theta$, we can find that when the number of CHs is less than 14, the number of success clusters when $\theta =0.5$, 0.6, 0.8, 1 are completely closed. When the number of CHs is less than 18, the number of success clusters when $\theta =0.6,0.8,1$ are completely closed. When the number of CHs is less than 24, the number of success clusters when $\theta =0.8,1$ are completely closed.

From Figure 2, it is known that the NOMA based MTCDs may not be able to process over the whole available RBs in some cases. Therefore, the number of RBs for the NCAS should be adaptively changed for different numbers of CHs to avoid the resource wastage. The BS can utilize the unused RBs for OCAS to improve the resource usage efficiency. The optimal RBs allocation factor between NCAS and OCAS is derived in Algorithm 2. $\theta$ is initialized as $6/\phantom{6q}q$ and increased by $6/\phantom{6q}q$. Based on Algorithm 1, we can get the optimal PRACH RBs for different traffic load range given $\theta$. By Algorithm 2, we can get the optimal RBs allocation factor ${\theta }^{*}$ through comparing the number of success clusters for $\theta$ ($\theta <1$) with that for $\theta =1$. Then we can get the optimal number of RBs allocated for NCAS and OCAS, i.e., $q{\theta }^{*}$ and $q\left(1-{\theta }^{*}\right)$ given q and $u_1$.

According to the NCAS and OCAS, the optimal number of PRACH RBs for NCAS (i.e., $n^{*}\left(u_1;q{\theta }^{*}\right)$) and OCAS (i.e., $n^{*}\left(u_2;q\left(1-{\theta }^{*}\right)\right)$) should be decided before each RA cycle begins, as well as the ACB factor for NCAS (i.e., $R_1$) and OCAS (i.e., $R_2$) given the number of uplink available RBs. For doing this, we consider the following three cases.

Case 1: $u_1\le x_{⌊q/\phantom{q\left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+i_a}$, $u_2\le x_{⌊q\left(1-{\theta }^{*}\right)/\phantom{q\left(1-{\theta }^{*}\right)\left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+i_{a^{\prime }}}$, where $x_{⌊q/\phantom{q\left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+i_a}$ is the optimal number of NOMA clusters allowed to access the network when the whole available RBs are allocated to NCAS, and $x_{⌊q\left(1-{\theta }^{*}\right)/\phantom{q\left(1-{\theta }^{*}\right)\left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+i_{a^{\prime }}}$ is the optimal number of OFDMA based MTCDs allowed to access the network when $q\left(1-{\theta }^{*}\right)$ RBs are allocated to OCAS. $x_{⌊q/\phantom{q\left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+i_a}$ and $x_{⌊q\left(1-{\theta }^{*}\right)/\phantom{q\left(1-{\theta }^{*}\right)\left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+i_{a^{\prime }}}$ can be obtained by Algorithm 1 given $\theta =1$ and $\theta =1-{\theta }^{*}$, respectively.

Both the number of MTCDs that compete for uplink resources allocated for NCAS and OCAS are lower than the optimal number of participating MTCDs. Therefore, the ACB schemes are not activated, i.e., $R_1=1$. $R_2=1$. Let $\theta \leftarrow 1-{\theta }^{*}$, $u_1\leftarrow u_2$. Repeat line 2-18, then we can obtain the optimal number of PRACH RBs $n^{*}\left(u_2;q\left(1-{\theta }^{*}\right)\right)$ for OCAS by Algorithm 1. Then the system access capacity in the hybrid NOMA-OFDMA based cellular M2M communication systems is

$$\begin{array}{c}max\varsigma \left(u_1,n_1,M;q\theta \right)+max\varsigma \left(u_2,n_2;q\left(1-\theta \right)\right)\hfill \\ =M{u}_{1}exp\left(-\frac{6u_1}{\eta n^{*}\left(u_1;q{\theta }^{*}\right)}\right)+u_{2}exp\left(-\frac{6u_2}{\eta n^{*}\left(u_2;q\left(1-{\theta }^{*}\right)\right)}\right)\hfill \end{array}$$

(16)

Case 2: $u_1\le x_{⌊q/\phantom{q\left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+i_a}$, $u_2>x_{⌊q\left(1-{\theta }^{*}\right)/\phantom{q\left(1-{\theta }^{*}\right)\left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+i_{a^{\prime }}}$.

The number of MTCDs that compete for uplink resources allocated for NCAS is lower than the optimal number of participating NOMA clusters. While the number of MTCDs that compete for uplink resources allocated for OCAS is higher than the optimal number of participating MTCDs, and the ACB scheme is used to control the number of MTCDs with the ACB parameter $R_2=\frac{x_{⌊q\left(1-{\theta }^{*}\right)/\phantom{q\left(1-{\theta }^{*}\right)\left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+i_{a^{\prime }}}}{u_2}$. The optimal number of PRACH RBs allocated for OCAS is $6\left(⌊q\left(1-{\theta }^{*}\right)/\phantom{q\left(1-{\theta }^{*}\right)\left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+i_{a^{\prime }}\right)$. Then the system access capacity in the hybrid NOMA-OFDMA based cellular M2M communication systems is

$$\begin{array}{c}max\varsigma \left(u_1,n_1,M;q\theta \right)+max\varsigma \left(u_2,n_2;q\left(1-\theta \right)\right)\hfill \\ =M{u}_{1}exp\left(-\frac{6u_1}{\eta n^{*}\left(u_1;q{\theta }^{*}\right)}\right)+u_2{R}_{2}exp\left(-\frac{u_2{R}_2}{\eta \left(⌊q^{*}/\phantom{q\left(1-{\theta }^{*}\right)\left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+i_{a^{\prime }}\right)}\right)\hfill \end{array}$$

(17)

Case 3: $u_1>x_{⌊q/\phantom{q\left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+i_a}$.

The number of MTCDs that compete for uplink resources allocated for NCAS is higher than the optimal number of participating NOMA clusters, and the ACB scheme should be used to control the number of NOMA clusters with the ACB parameter $R_1=\frac{x_{⌊q/\phantom{q\left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+i_a}}{u_1}$. The optimal number of PRACH RBs allocated for NCAS is $6\left(⌊q/\phantom{q\left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+i_a\right)$. Then the system access capacity in the hybrid NOMA-OFDMA based cellular M2M communication systems is

$$max\varsigma \left(u_1,n_1,M;q\theta \right)=M{u}_1{R}_{1}exp\left(-\frac{u_1{R}_1}{\eta \left(⌊q/\phantom{q\left(6+\delta \eta \right)}\left(6+\delta \eta \right)⌋+i_a\right)}\right)$$

(18)

Algorithm 2 Optimal RBs allocation factor between NCAS and OCAS
1:	Initialize $\theta =6/\phantom{6q}q$, $u_1$. $Indicator=0$.
2:	Calculating $i_a$ by Algorithm 1 when $\theta =1$.
3:	while$s\le ⌈q/\phantom{q6}6⌉$ and $Indicator=0$ do
4:	$\theta =6s/\phantom{6sq}q$. Calculating $i_a$ by Algorithm 1, and let $i_{a^{\prime }}=i_a$.
5:	for $j=i_{a^{\prime }}$ to $⌈q\theta /\phantom{q\theta 6}6⌉-1$ do
6:	$y_{j-i_{a^{\prime }}+1}=-\eta jln\left(1-\frac{q\theta -6j}{\delta \eta j}\right)$.
7:	end for
8:	for $i=i_a$ to $⌈q/\phantom{q6}6⌉-2$ do
9:	if $x_{i-i_a+2}<u_1\le x_{i-i_a+1}$ then
10:	for $j=i_{a^{\prime }}$ to $⌈q\theta /\phantom{q\theta 6}6⌉-2$ do
11:	if $y_{j-i_{a^{\prime }}+2}<u_1\le y_{j-i_{a^{\prime }}+1}$ then
12:	if $\left|u_{1}exp\left(-\frac{u_1}{\eta i}\right)-u_{1}exp\left(-\frac{u_1}{\eta j}\right)\right|<1$ then
13:	${\theta }^{*}=\theta$, $n^{*}\left(u_1;q{\theta }^{*}\right)=6j$, $Indicator=1$.
14:	end if
15:	end if
16:	end for
17:	end if
18:	end for
19:	$x=x+1$.
20:	end while

4. Channel Model and Problem Formulation

According to step 5 in NCAS, upon receiving a matching RAR, the MTCD adjusts the transmit power based on power back-off index and transmits data packet on the assigned PUSCH. In this section, we formulate the energy-efficient power allocation as an optimization problem in the data transmission procedure for the hybrid NOMA-OFDMA based cellular M2M communication systems.

4.1. Channel Model

Let us consider a general M-MTCD uplink NOMA system in which M MTCDs transmit the data packets to the BS over the same PUSCH. Denote $U{E}_{k,m}$ as the m-th MTCD in the k-th cluster, where $m\in \mathcal{M}=\left\{1,2,\cdots ,M\right\}$, and $k\in \mathcal{K}=\left\{1,2,\cdots ,K\right\}$, K is the number of clusters. $h_{k,m}=g_{k,m}{l}_{k,m}$ is the channel coefficient from $U{E}_{k,m}$ to the BS, where $g_{k,m}$ is assumed to have Rayleigh fading channel gain, and $l_{k,m}=\frac{\sqrt{G_l}\lambda }{4\pi d_{k,m}}$ is the path loss function between $U{E}_{k,m}$ and the BS at distance $d_{k,m}$ [39], where $G_l$ is a product of the transmit and receive antenna field radiation patterns in the line-of-sight (LOS) direction, and $\lambda$ is the signal wavelength. Without loss of generality, ${\left|h_{k,1}\right|}^2\ge \cdots \ge {\left|h_{k,m}\right|}^2\ge {\left|h_{k,m+1}\right|}^2\ge \cdots \ge {\left|h_{k,M}\right|}^2$. In uplink NOMA, the MTCD’s signal with the highest channel gain is decoded first at the BS. Thus, the achievable data rate of $U{E}_{k,m}$ depends on the interferences from $U{E}_{k,i}$, $i>m$, whereas the $U{E}_{k,M}$ achieves an intra-cell interference-free data rate. Consequently, the achievable data rate for $U{E}_{k,m}$, $\forall m=1,2,\cdots ,M$, in a M-MTCD uplink NOMA cluster can be expressed as

$$R_{k,m}=B_{sc}\sum _{m=1}^M{log}_2\left(1+\frac{p_{k,m}{\left|h_{k,m}\right|}^2}{{\sum }_{i=m+1}^M{p}_{k,i}{\left|h_{k,i}\right|}^2+{\sigma }^2}\right)$$

(19)

where $B_{sc}$ is the transmission bandwidth of each PUSCH, $p_{k,m}$ is the transmission power of $U{E}_{k,m}$, and ${\sigma }^2=N_0{B}_{sc}$ is the variance of additive white Gaussian noise (AWGN), where $N_0$ is the noise power spectral density. The achievable data rate for OFDMA based MTCDs are also obtained by Equation (19) with $M=1$ according to the OFDMA protocol.

4.2. Problem Formulation

We desire to maximize the energy efficiency (EE) while providing MTCDs’ QoS guarantees by finding the optimal power allocation. EE is defined as the ratio of the achievable sum rate of the MTCDs to the total power consumption. The overall EE of the system can be given by

$$\mathrm{E}\mathrm{E}=\sum _{k\in K}\mathrm{E}{\mathrm{E}}_k$$

(20)

where $\mathrm{E}{\mathrm{E}}_k$ is the EE of the k-th cluster, which is defined as

$$\mathrm{E}{\mathrm{E}}_k=\frac{{\displaystyle \sum _{m\in \mathcal{M}}}{R}_{k,m}}{{\displaystyle \sum _{m\in \mathcal{M}}}{p}_{k,m}}$$

(21)

We derive the optimal power allocation policy that maximizes the EE per cluster and, in turn, maximizes the overall EE. Thereby, the EE maximization problem while satisfying MTCDs’ QoS guarantees for the hybrid NOMA-OFDMA system is formulated as

$$\begin{array}{cc}\hfill & \underset{\mathbf{p}}{max}\frac{{\displaystyle \sum _{m\in \mathcal{M}}}{R}_{k,m}}{{\displaystyle \sum _{m\in \mathcal{M}}}{p}_{k,m}}\hfill \end{array}$$

(22a)

$$\begin{array}{cc}\hfill & \mathrm{s}.\mathrm{t}.p_{k,m}\le p_{k,m}^{max},\forall m\in \mathcal{M}\hfill \end{array}$$

(22b)

$$\begin{array}{cc}\hfill & R_{k,m}\ge \stackrel{\wedge }{R_{k,m}},\forall m\in \mathcal{M}\hfill \end{array}$$

(22c)

where $\mathbf{p}=\left(p_{k,1},p_{k,2},\cdots p_{k,M}\right)$ is the transmit power vector. $p_{k,m}^{max}$ is the maximum transmission power of $U{E}_{k,m}$. $\stackrel{\wedge }{R_{k,m}}$ denotes the minimum data rate requirement of $U{E}_{k,m}$. (22b) and (22c) is the maximum transmit power of MTCD and the MTCDs’ QoS requirements constraint, respectively.

5. Power Allocation for the Hybrid NOMA-OFDMA Based Cellular M2M Communication Systems

5.1. Feasibility Condition

In this subsection, the feasibility conditions of the power allocation solution to satisfy the constraints in Equation (22) is investigated. According to step 6 in NCAS, diverse arrived power is required to separate the multiplexed MTCDs by the BS. Define $\rho$ as the difference of arrived power among multiplex MTCDs at the BS, i.e., the second MTCD’s arrived power is $\rho$ dB lower than that of the first MTCD, and the third MTCD is $\rho$ dB lower than the second MTCD. We define the first MTCD as the CH in a cluster. How to discover clustered MTCDs and select a CH is investigated in Section 6.

Proposition 3.

The uplink transmit power of $U{E}_{k,m}$ can be expressed as

$$p_{k,m}=p_{k,1}\frac{d_{k,m}^2}{d_{k,1}^2}{10}^{\frac{-\left(m-1\right)\rho }{10}}$$

(23)

Proof of Proposition 3. 

The power back-off scheme [40] is introduced. The uplink transmit power of $U{E}_{k,m}$ is expressed by

$$p_{k,m}=min\left\{p_{k,m}^{max},p_{k,u}-\left(m-1\right)\rho +10{log}_{10}\left({\varsigma }_k\right)+wP{L}_{k,m}\right\}$$

(24)

where $p_{k,u}$ represents the target arrived power of the first decoded MTCD of the k-th cluster at BS, ${\varsigma }_k$ denotes the number of allocated RBs for cluster k, while $P{L}_{k,m}$ denotes the downlink pathloss. The factor w denotes to compensate the pathloss difference between downlink and uplink. Since the case that $p_{k,m}$ is the same as $p_{k,m}^{max}$ only occurs in extreme cases, which are not the focus of this paper, the transmit power of $U{E}_{k,m}$ is assumed to be

$$p_{k,m}=p_{k,u}-\left(m-1\right)\rho +10{log}_{10}\left({\varsigma }_k\right)+wP{L}_{k,m}$$

(25)

Based on Equation (25), the difference between $p_{k,m}$ and $p_{k,1}$ can be expressed as

$$p_{k,m}-p_{k,1}=wP{L}_{k,m}-wP{L}_{k,1}-\left(m-1\right)\rho$$

(26)

Given that $x\left[\mathrm{dB}\right]=10{log}_{10}x\left[\mathrm{watt}\right]$, Equation (26) can be expressed in watts by

$$10{log}_{10}\frac{p_{k,m}}{p_{k,1}}=10{log}_{10}\frac{wP{L}_{k,m}}{wP{L}_{k,1}}-\left(m-1\right)\rho$$

(27)

$P{L}_{k,m}$ is modeled by the Free-Space path loss model, and $\frac{P{L}_{k,m}}{P{L}_{k,1}}=\frac{{\left(4\pi d_{k,m}\right)}^2}{G_l{\lambda }^2}\phantom{\frac{{\left(4\pi d_{k,m}\right)}^2}{G_l{\lambda }^2}\frac{{\left(4\pi d_{k,1}\right)}^2}{G_l{\lambda }^2}}/\frac{{\left(4\pi d_{k,1}\right)}^2}{G_l{\lambda }^2}=\frac{d_{k,m}^2}{d_{k,1}^2}$ [36], Equation (27) can be derived as

$$p_{k,m}=p_{k,1}\frac{d_{k,m}^2}{d_{k,1}^2}{10}^{\frac{-\left(m-1\right)\rho }{10}}$$

(28)

 □

Based on Proposition 3 and $p_{k,m}\le p_{k,m}^{max}$, we can get the feasibility condition of power allocation solution of CH as

$$p_{k,1}\le p_{k,m}^{max}\frac{d_{k,1}^2}{d_{k,m}^2}{10}^{\frac{\left(m-1\right)\rho }{10}}$$

(29)

From Equation (29), the maximum power for CH can be expressed as

$${\overline{p}}_{k,1}^{max}=min\left\{p_{k,1}^{max},p_{k,2}^{max}\frac{d_{k,1}^2}{d_{k,2}^2}{10}^{\frac{\rho }{10}},\cdots ,p_{k,M}^{max}\frac{d_{k,1}^2}{d_{k,M}^2}{10}^{\frac{\left(M-1\right)\rho }{10}}\right\}$$

(30)

Therefore, Constraint (22b) can be reformulated as a linear constraint, i.e.,

$$p_{k,1}\le {\overline{p}}_{k,1}^{max}$$

(31)

Substituting Equation (19) into $R_{k,m}\ge \stackrel{\wedge }{R_{k,m}}$, we have

$$p_{k,m}{\left|h_{k,m}\right|}^2-{\phi }_{k,m}{\sum }_{i=m+1}^M{p}_{k,i}{\left|h_{k,i}\right|}^2\ge {\phi }_{k,m}{\sigma }^2$$

(32)

where ${\phi }_{k,m}=2^{\stackrel{\wedge }{R_{k,m}}\phantom{\stackrel{\wedge }{R_{k,m}}{B}_0}/B_{sc}}-1$, $m=1,2,\dots ,M$. Based on Proposition 3 and ${\left|h_{k,m}\right|}^2={\left|g_{k,m}\right|}^2{l}_{k,m}^2$, we can get the other feasibility condition of power allocation solution of CH as

$$\frac{l_{k,1}^2}{{\sigma }^2}{10}^{\frac{-\left(m-1\right)\rho }{10}}{\left|g_{k,m}\right|}^2-\frac{l_{k,1}^2}{{\sigma }^2}{\phi }_{k,m}{\sum }_{i=m+1}^M{10}^{\frac{-\left(i-1\right)\rho }{10}}{\left|g_{k,i}\right|}^2\ge \frac{{\phi }_{k,m}}{p_{k,1}}$$

(33)

Let $a_{k,m}=\frac{l_{k,1}^2}{{\sigma }^2}{\sum }_{i=m}^M{10}^{\frac{-\left(i-1\right)\rho }{10}}{\left|g_{k,i}\right|}^2$, $b_{k,m}=\frac{l_{k,1}^2}{{\sigma }^2}{\sum }_{i=m+1}^M{10}^{\frac{-\left(i-1\right)\rho }{10}}{\left|g_{k,i}\right|}^2$, then Equation (33) is reformulated as

$$p_{k,1}\ge \frac{{\phi }_{k,m}}{a_{k,m}-\left({\phi }_{k,m}+1\right)b_{k,m}}$$

(34)

From Equation (34), we can get the minimum power required to satisfy the minimum rate requirement for CH as

$$p_{k,1}^{min}=max\left\{\frac{{\phi }_{k,1}}{a_{k,1}-\left({\phi }_{k,1}+1\right)b_{k,1}},\frac{{\phi }_{k,2}}{a_{k,2}-\left({\phi }_{k,2}+1\right)b_{k,2}},\cdots ,\frac{{\phi }_{k,M}}{a_{k,M}-\left({\phi }_{k,M}+1\right)b_{k,M}}\right\}$$

(35)

Therefore, Constraint (22c) can be reformulated as a linear constraint, i.e.,

$$p_{k,1}\ge p_{k,1}^{min}$$

(36)

Once the above feasibility condition of the CH’s power allocation solution are satisfied, Equation (22) is feasible.

5.2. Power Allocation for EE Maximization

Based on Proposition 3 and ${\left|h_{k,m}\right|}^2={\left|g_{k,m}\right|}^2{l}_{k,m}^2$, $\frac{{\displaystyle \sum _{m\in \mathcal{M}}}{R}_{k,m}}{{\displaystyle \sum _{m\in \mathcal{M}}}{p}_{k,m}}$ is derived as

$$\begin{array}{cc}\hfill \frac{{\displaystyle \sum _{m\in \mathcal{M}}}{R}_{k,m}}{{\displaystyle \sum _{m\in \mathcal{M}}}{p}_{k,m}}& ={\frac{B_{sc}{\displaystyle \sum _{m=1}^M}{log}_2\left(1+\frac{p_{k,1}{l}_{k,1}^2{10}^{\frac{-\left(m-1\right)\rho }{10}}{\left|g_{k,m}\right|}^2}{p_{k,1}{l}_{k,1}^2{\sum }_{i=m+1}^M{10}^{\frac{-\left(i-1\right)\rho }{10}}{\left|g_{k,i}\right|}^2+{\sigma }^2}\right)}{p_{k,1}{l}_{k,1}^2{\displaystyle \sum _{m=1}^M}\frac{1}{l_{k,m}^2}{10}^{\frac{-\left(m-1\right)\rho }{10}}}}_{}\hfill \\ \hfill & =\frac{B_{sc}{\displaystyle \sum _{m=1}^M}{log}_2\left(\frac{p_{k,1}{l}_{k,1}^2\phantom{p_{k,1}{l}_{k,1}^2{\sigma }^2}/{\sigma }^2{\sum }_{i=m}^M{10}^{\frac{-\left(i-1\right)\rho }{10}}{\left|g_{k,i}\right|}^2+1}{p_{k,1}{l}_{k,1}^2\phantom{p_{k,1}{l}_{k,1}^2{\sigma }^2}/{\sigma }^2{\sum }_{i=m+1}^M{10}^{\frac{-\left(i-1\right)\rho }{10}}{\left|g_{k,i}\right|}^2+1}\right)}{p_{k,1}{l}_{k,1}^2{\displaystyle \sum _{m=1}^M}\frac{1}{l_{k,m}^2}{10}^{\frac{-\left(m-1\right)\rho }{10}}}\hfill \\ \hfill & =\frac{B_{sc}{\displaystyle \sum _{m=1}^M}{log}_2\left(1+a_{k,m}{p}_{k,1}\right)-B_{sc}{\displaystyle \sum _{m=1}^M}{log}_2\left(1+b_{k,m}{p}_{k,1}\right)}{c{p}_{k,1}}\hfill \end{array}$$

(37)

where $c=l_{k,1}^2{\displaystyle \sum _{m=1}^M}\frac{1}{l_{k,m}^2}{10}^{\frac{-\left(m-1\right){\rho }_k}{10}}$. Note that $b_{k,1}=a_{k,2}$, $b_{k,2}=a_{k,3}$, ⋯, $b_{k,M_{k-1}}=a_{k,M}$, $b_{k,M}=0$. Then Equation (37) can be rewritten as

$$\frac{{\displaystyle \sum _{m\in \mathcal{M}}}{R}_{k,m}}{{\displaystyle \sum _{m\in \mathcal{M}}}{p}_{k,m}}=\frac{B_{sc}{log}_2\left(1+a_{k,1}{p}_{k,1}\right)}{c{p}_{k,1}}$$

(38)

Accordingly, Problem (22) can be rewritten as

$$\begin{array}{cc}\hfill & \underset{p_{k,1}}{max}\frac{B_{sc}{log}_2\left(1+a_{k,1}{p}_{k,1}\right)}{c{p}_{k,1}}\hfill \end{array}$$

(39a)

$$\begin{array}{cc}\hfill & \mathrm{s}.\mathrm{t}.p_{k,1}\le {\overline{p}}_{k,1}^{max},m\in \mathcal{M}\hfill \end{array}$$

(39b)

$$\begin{array}{cc}\hfill & p_{k,1}\ge p_{k,m}^{min},m\in \mathcal{M}\hfill \end{array}$$

(39c)

In Equation (22), the power allocation solution for $\mathbf{p}=\left(p_{k,1},p_{k,2},\cdots p_{k,M}\right)$ has been transformed to the power allocation solution for $p_{k,1}$ in Equation (39). As a strictly pseudo-concave function, the objective function Equation (39a) can be optimally solved by applying Dinkelbach’s algorithm [41]. The Dinkelbach method is summarized in Algorithm 3. During each iteration, the proposed algorithm needs to solve the following problem, i.e., line 3:

$$\begin{array}{cc}\hfill & \underset{p_{k,1}}{max}\left\{\frac{B_{sc}{log}_2\left(1+a_{k,1}{p}_{k,1}\right)}{c}-\gamma p_{k,1}\right\}\hfill \end{array}$$

(40a)

$$\begin{array}{cc}\hfill & \mathrm{s}.\mathrm{t}.39\left(b\right),39\left(c\right)\hfill \end{array}$$

(40b)

Algorithm 3 The Dinkelbach’s algorithm
1:	Initialize $\gamma =0$, error tolerance $\epsilon \ll 1$.
2:	repeat
3:	Solve the equivalent problem (40) for a given $\gamma$ to obtain the solution $p_{k,1}^{*}$; s.t. (39b), (39c).
4:	$F=B_{sc}{log}_2\left(1+a_{k,1}{p}_{k,1}^{*}\right)-\gamma c{p}_{k,1}^{*}$.
5:	$\gamma =\frac{B_{sc}{log}_2\left(1+a_{k,1}{p}_{k,1}^{*}\right)}{c{p}_{k,1}^{*}}$.
6:	until$\left|F\right|\le \epsilon$

In Algorithm 3, $\gamma$ and $p_{k,1}^{*}$ denote the EE and optimal power solution of (40), respectively. The problem of Equation (40) can be solved by the interior-point method. However, the computation is intensive since Equation (40) needs to be solved many times. To relieve the computational burden, we propose a low-complexity optimal solution for Equation (40). Denote $F=B_{sc}{log}_2\left(1+a_{k,1}{p}_{k,1}\right)-\gamma c{p}_{k,1}$. For $U{E}_{k,1}$, we have $\frac{\partial F}{\partial p_{k,1}}=\frac{B_{sc}{a}_{k,1}}{ln2\left(1+a_{k,1}{p}_{k,1}\right)}-\gamma c$. Setting $\frac{\partial F}{\partial p_{k,1}}=0$, we can get

$$p_{k,1}^0=\frac{B_{sc}}{ln2\gamma c}-\frac{1}{a_{k,1}}$$

(41)

We can get the optimal power allocation for NOMA CH by comparing $p_{k,1}^0$ with its maximum power constraint and minimum power constraint. The optimal power allocation for NOMA CH is specified as

$$p_{k,1}^{*}=\left\{\begin{array}{cc}{p}_{k,1}^{min},& \mathrm{if}{p}_{k,1}^0<p_{k,1}^{min},\\ p_{k,1}^{max},& \mathrm{if}{p}_{k,1}^0>p_{k,1}^{max},\\ p_{k,1}^0,& \mathrm{otherwise}.\end{array}\right.$$

(42)

The specific algorithm is present in Algorithm 4. The minimum required power is first allocated to $U{E}_{k,1}$. Then the power for $U{E}_{k,1}$ is updated using Equation (42) until convergence. Based on Proposition 3, the optimal solution for the m-th MTCD in the k-th cluster is easily obtained by

$$p_{k,m}^{*}=p_{k,1}^{*}\frac{d_{k,m}^2}{d_{k,1}^2}{10}^{\frac{-\left(m-1\right)\rho }{10}}$$

(43)

Algorithm 4 The algorithm for solving problem (39a).
1:	Initialize $p_{k,1}=p_{k,1}^{min}$.
2:	while 1 do
3:	$p_{k,1}^{old}=p_{k,1}$.
4:	$p_{k,1}^0=\frac{B_{sc}}{ln2\gamma c}-\frac{1}{a_{k,1}}$.
5:	if $p_{k,1}^0<p_{k,1}^{min}$ then
6:	$p_{k,1}=p_{k,1}^{min}$.
7:	else if $p_{k,1}^0>p_{k,1}^{max}$ then
8:	$p_{k,1}=p_{k,1}^{max}$.
9:	else
10:	$p_{k,1}=p_{k,1}^0$.
11:	end if
12:	if $\left|p_{k,1}^{old}-p_{k,1}\right|<{10}^{-9}$ then
13:	$\mathbf{break}$;
14:	end if
15:	end while

The optimal solution for OFDMA based MTCDs are also obtained by running the proposed Algorithm 3 with the achievable data rate expressions adjusted.

5.3. Computational Complexity Analysis

In the above subsection, the proposed power allocation algorithm for EE maximization includes Algorithms 3 and 4. According to [41], the convergence of Algorithms 3 is guaranteed. We use $I_4$ to denote the number of iterations for Algorithm 3. Since the EE increases or remains unchanged after each update, and the EE has an upper bound due to the transmit power constraint of each MTCD. Therefore, the convergence of Algorithm 4 is guaranteed. Denote the number of iterations for Algorithm 4 to convergence as $I_5$. Then, the computational complexity of the power allocation algorithm is $O\left(I_4{I}_5\right)$.

6. NOMA Clustering Strategy

In Section 5, we derive the optimal power allocation policy that maximizes the EE per NOMA cluster for a given set of NOMA clusters. In this section, how to group MTCDs into multiple clusters is studied. Since $\rho$ is the difference of target arrived power at the BS among multiplex MTCDs, therefore, to separate $U{E}_{k,m}$ and $U{E}_{k,m+1}$, the difference between received power of $U{E}_{k,m}$ and $U{E}_{k,m+1}$ should not be less than $\rho$ dB, i.e.,

$$p_{k,m}{\left|h_{k,m}\right|}^2-p_{k,m+1}{\left|h_{k,m+1}\right|}^2\ge {10}^{\frac{\rho }{10}}$$

(44)

In Equation (44), the unit of $p_{k,m}$ is watts. Based on Proposition 3 and ${\left|h_{k,m}\right|}^2={\left|g_{k,m}\right|}^2{l}_{k,m}^2$, we can get the clustering condition as

$$\frac{{10}^{\frac{m\rho }{10}}}{l_{k,1}^2\left({\left|g_{k,m}\right|}^2-{\left|g_{k,m+1}\right|}^2{10}^{\frac{-\rho }{10}}\right)}\le p_{{}_{k,1}}^{}\le {\overline{p}}_{k,1}^{max}$$

(45)

From Equation (45), it is evident that, if the difference between Rayleigh fading coefficients of $U{E}_{k,m}$ and $U{E}_{k,m+1}$ satisfies the clustering condition, then $U{E}_{k,m}$ and $U{E}_{k,m+1}$ can be grouped into the same cluster. The MTCD clustering strategy is present in Algorithm 5. $S_{Uncluster}$ is initialized to record the MTCDs who have not been clustered, and the unclustered MTCDs are sorted in the descending order of the Rayleigh fading coefficient. Define $\mathcal{G}$, $\mathcal{L}$, and $\mathcal{P}$ as the set of above unclustered MTCDs’ Rayleigh fading coefficient, large scale fading coefficient, and the maximum allowed transmission power, respectively. Define ${\mathsf{\Lambda }}_k^{\left(i\right)}$ as the Rayleigh fading coefficient of the i-th MTCD in the k-th cluster. The clustering process is as follows: The MTCD with the largest Rayleigh fading coefficient in $S_{Uncluster}$ is selected as the NOMA CH for the k-th cluster, i.e., ${\mathsf{\Lambda }}_k^{\left(1\right)}=\mathcal{G}\left(s\right)$, where $s=1$. If there exists MTCDs in which the Rayleigh fading coefficient satisfies the condition of Equation (45), i.e., line 6 and 18, then these MTCDs can be grouped to the same cluster and removed from $S_{Uncluster}$; otherwise, these MTCDs are removed from $S_{Uncluster}$ and identified as OFDMA based MTCDs.

Algorithm 5 MTCD Clustering Algorithm
1:	Initialize $S_{Uncluster}$, $\mathcal{G}$, $\mathcal{L}$, $\mathcal{R}$ and $\mathcal{P}$. $k=0$.
2:	while$\left\{S_{Uncluster}\ne \varnothing \right\}$do
3:	$k=k+1$. $i=1$, $s=1$. ${\mathsf{\Lambda }}_k^{\left(i\right)}=\mathcal{G}\left(s\right)$. ${\mathrm{Z}}_k^{\left(i\right)}=\mathcal{P}\left(s\right)$.
4:	if $i<M-1$ then
5:	for $j=s+1$ to $\left|S_{Uncluster}\right|$ do
6:	if $\frac{{10}^{\frac{i\rho }{10}}}{{\Gamma }_k^{\left(1\right)}\left({\mathsf{\Lambda }}_k^{\left(i\right)}-\mathcal{G}\left(j\right){10}^{\frac{-\rho }{10}}\right)}\le min\left\{{\mathrm{Z}}_k^{\left(1\right)}\right\}$ then
7:	Add MTCD j to the k-th cluster, and remove MTCD j from $S_{Uncluster}$.
8:	${\mathsf{\Lambda }}_k^{\left(i+1\right)}=\mathcal{G}\left(j\right)$. $i=i+1$.
9:	${\mathrm{Z}}_k^{\left(1\right)}=\left\{{\mathrm{Z}}_k^{\left(1\right)},\mathcal{P}\left(j\right)\frac{\mathcal{L}\left(j\right)}{{\Gamma }_k^{\left(1\right)}}{10}^{\frac{-\left(i-1\right)\rho }{10}}\right\}$.
10:	$\mathbf{break}$;
11:	else
12:	Remove MTCD j from $S_{Uncluster}$.
13:	end if
14:	end for
15:	end if
16:	if $i=M-1$ then
17:	for $j=s+1$ to $\left|S_{Uncluster}\right|$ do
18:	if$\frac{{10}^{\frac{i\rho }{10}}}{{\Gamma }_k^{\left(1\right)}\left({\mathsf{\Lambda }}_k^{\left(i\right)}-\mathcal{G}\left(j\right){10}^{\frac{-\rho }{10}}\right)}\le min\left\{{\mathrm{Z}}_k^{\left(1\right)}\right\}$ and $\frac{{10}^{\frac{\left(i+1\right)\rho }{10}}}{{\Gamma }_k^{\left(1\right)}G\left(j\right)}\le min\left\{{\mathrm{Z}}_k^{\left(1\right)},\mathcal{P}\left(j\right)\frac{\mathcal{L}\left(j\right)}{{\Gamma }_k^{\left(1\right)}}{10}^{\frac{-i\rho }{10}}\right\}$ then
19:	Add MTCD j to the k-th cluster, and remove MTCD j from $S_{Uncluster}$.
20:	${\mathsf{\Lambda }}_k^{\left(i+1\right)}=\mathcal{G}\left(j\right)$.
21:	$\mathbf{break}$;
22:	else
23:	Remove MTCD j from $S_{Uncluster}$.
24:	end if
25:	end for
26:	end if
27:	end while

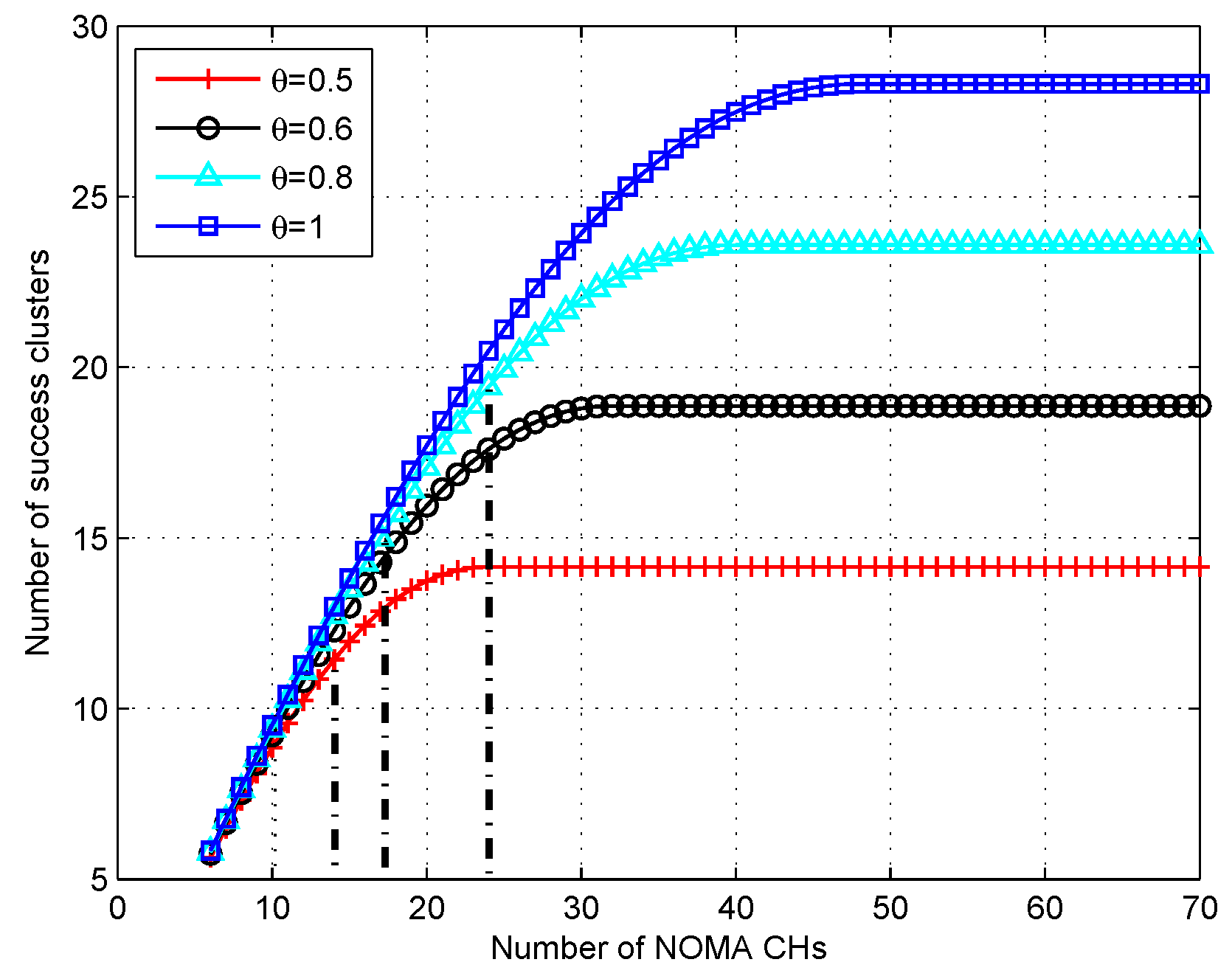
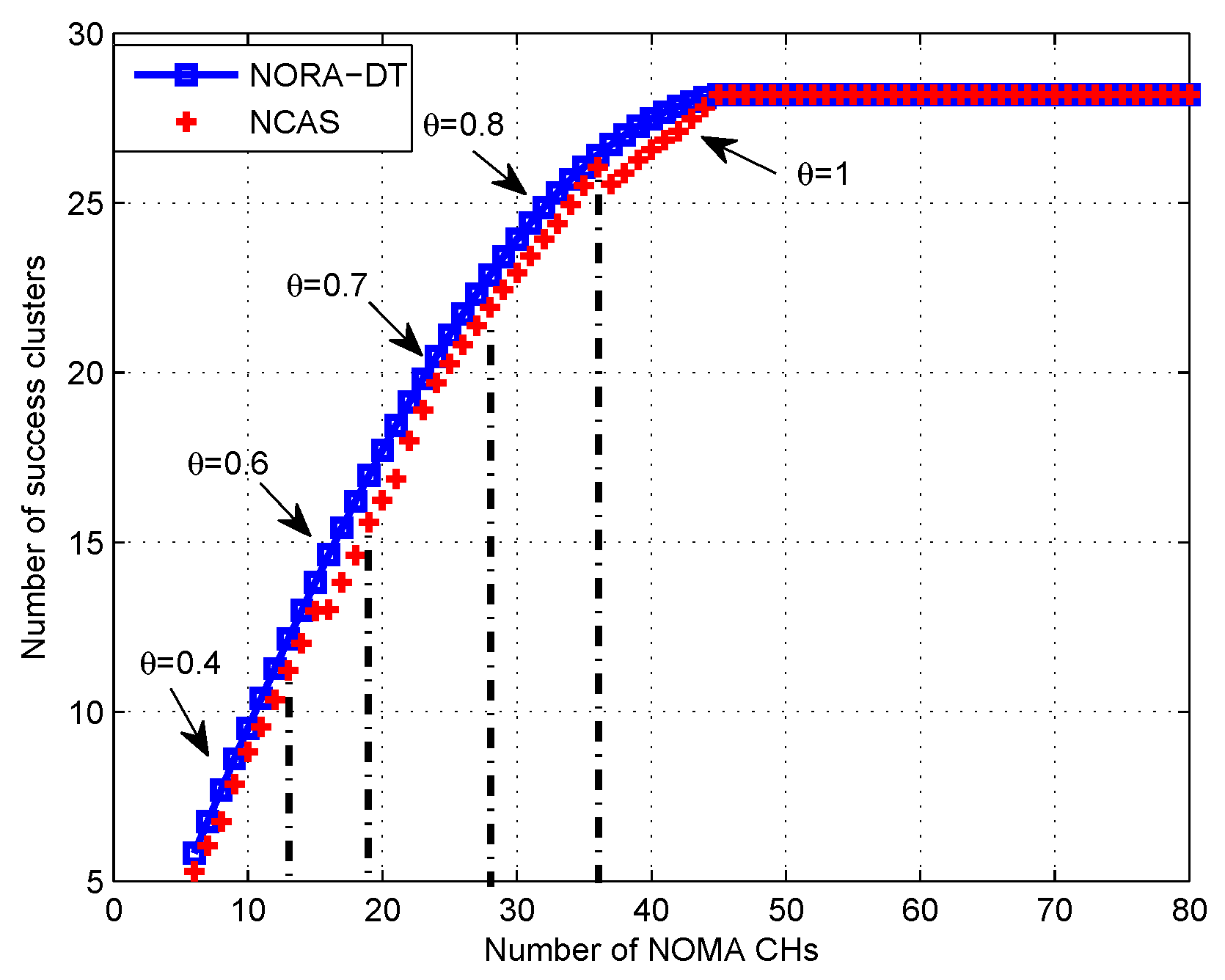
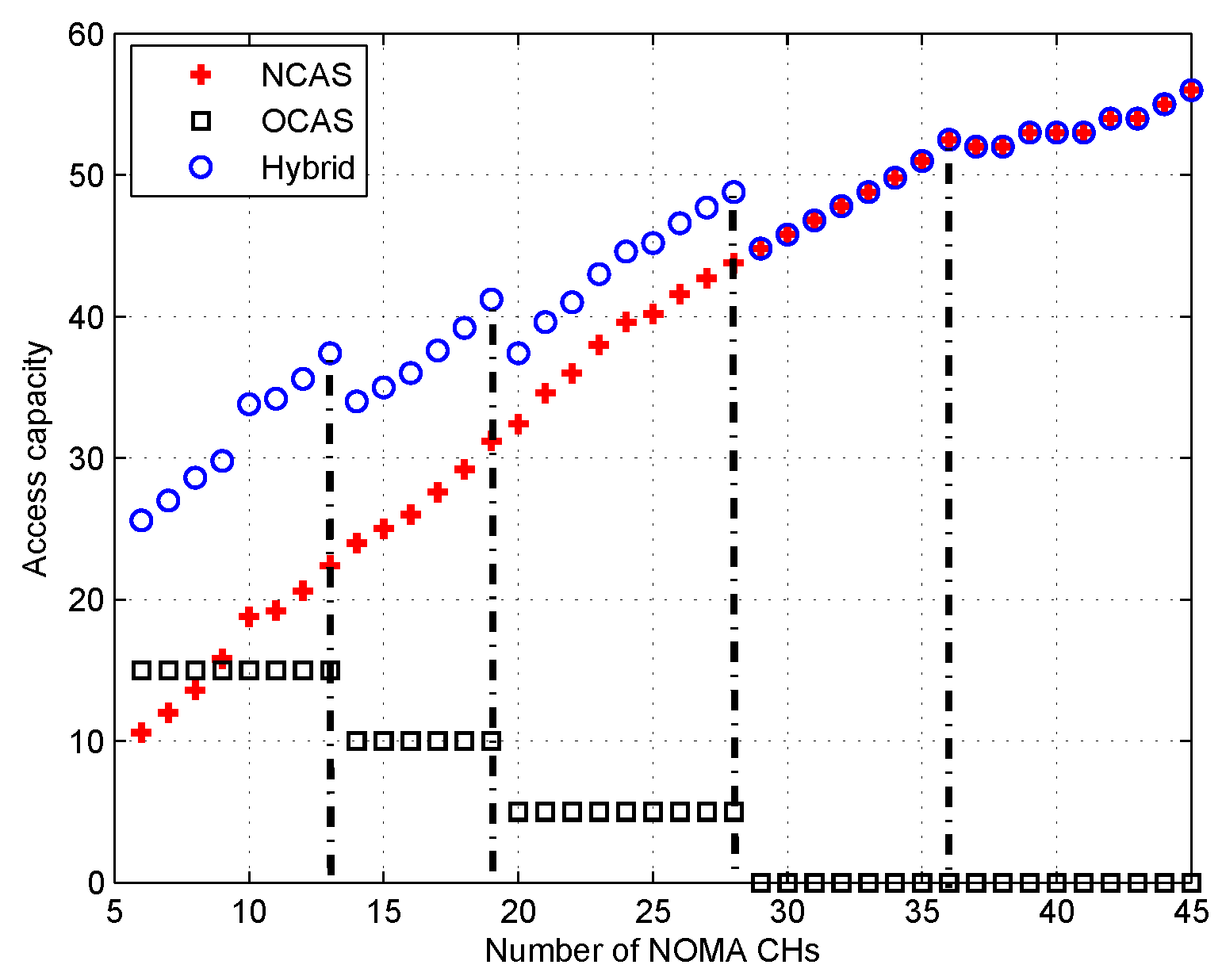
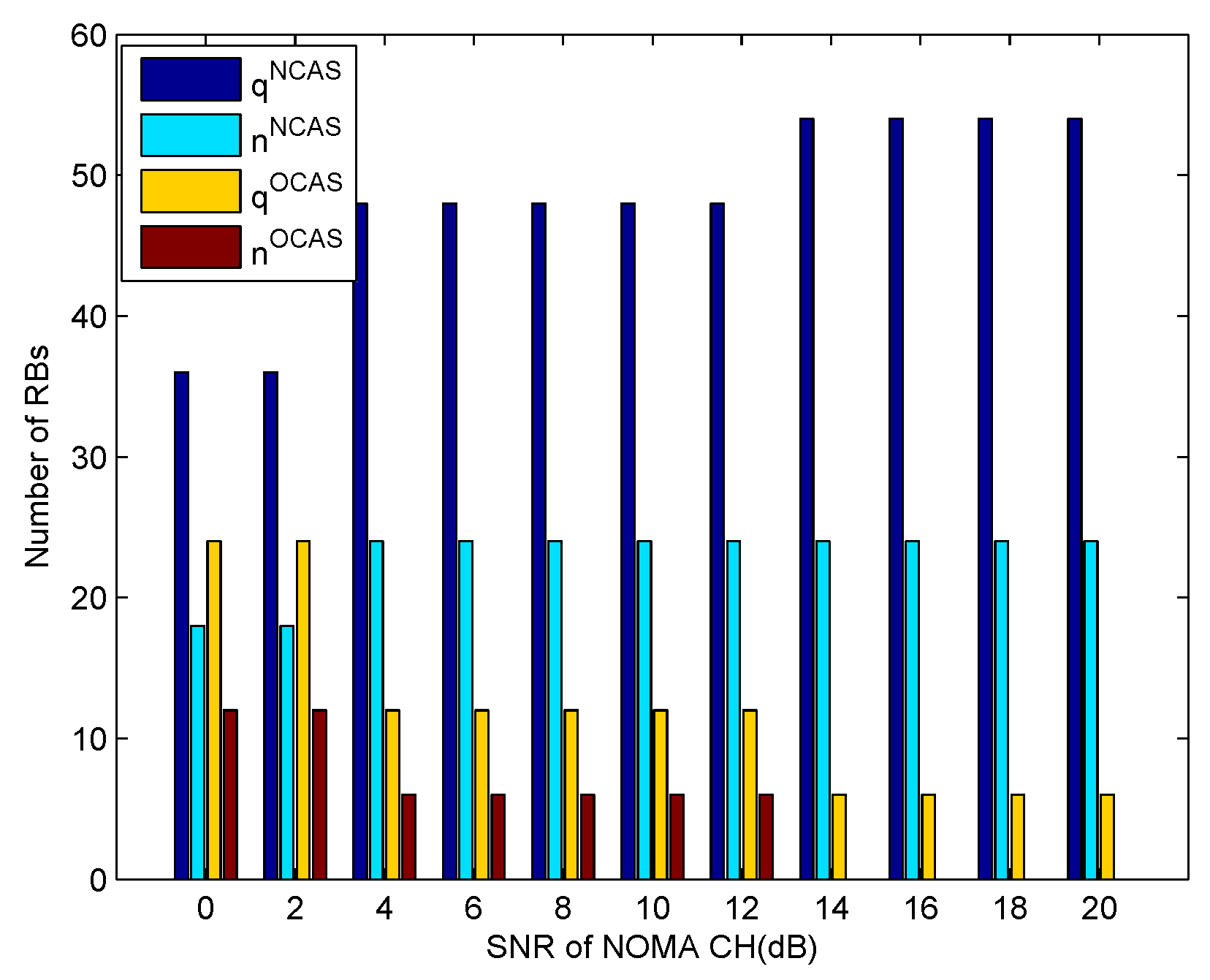
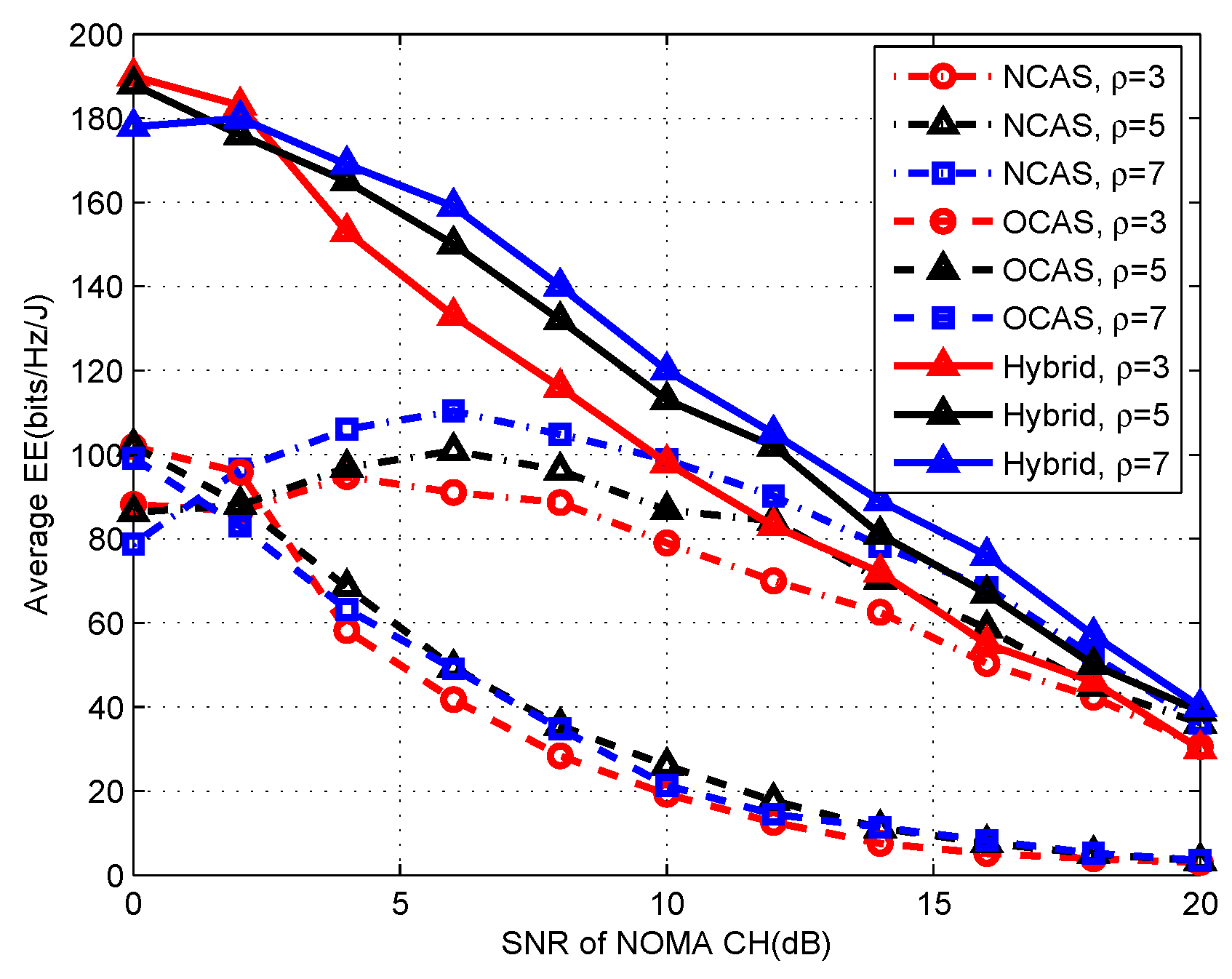
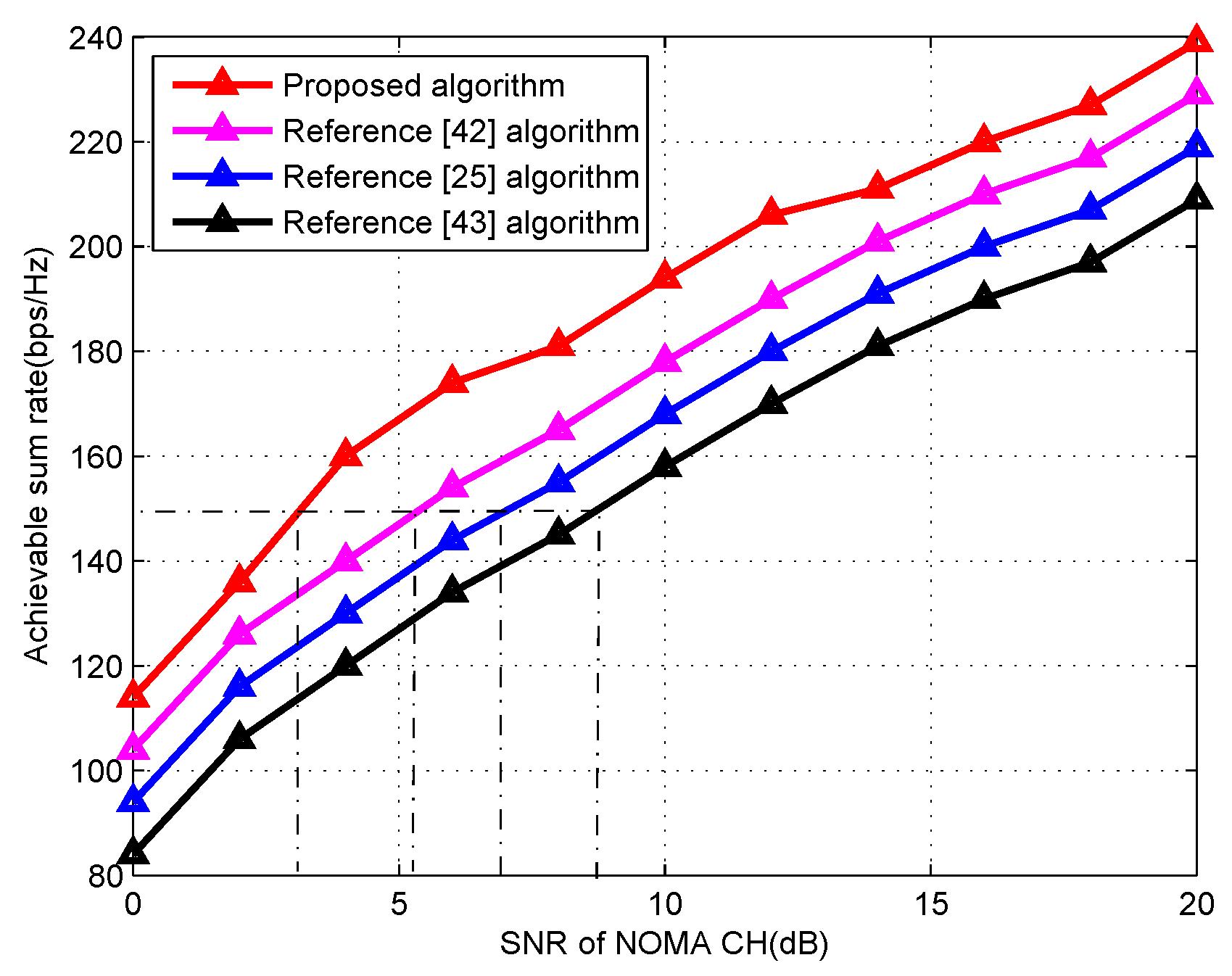
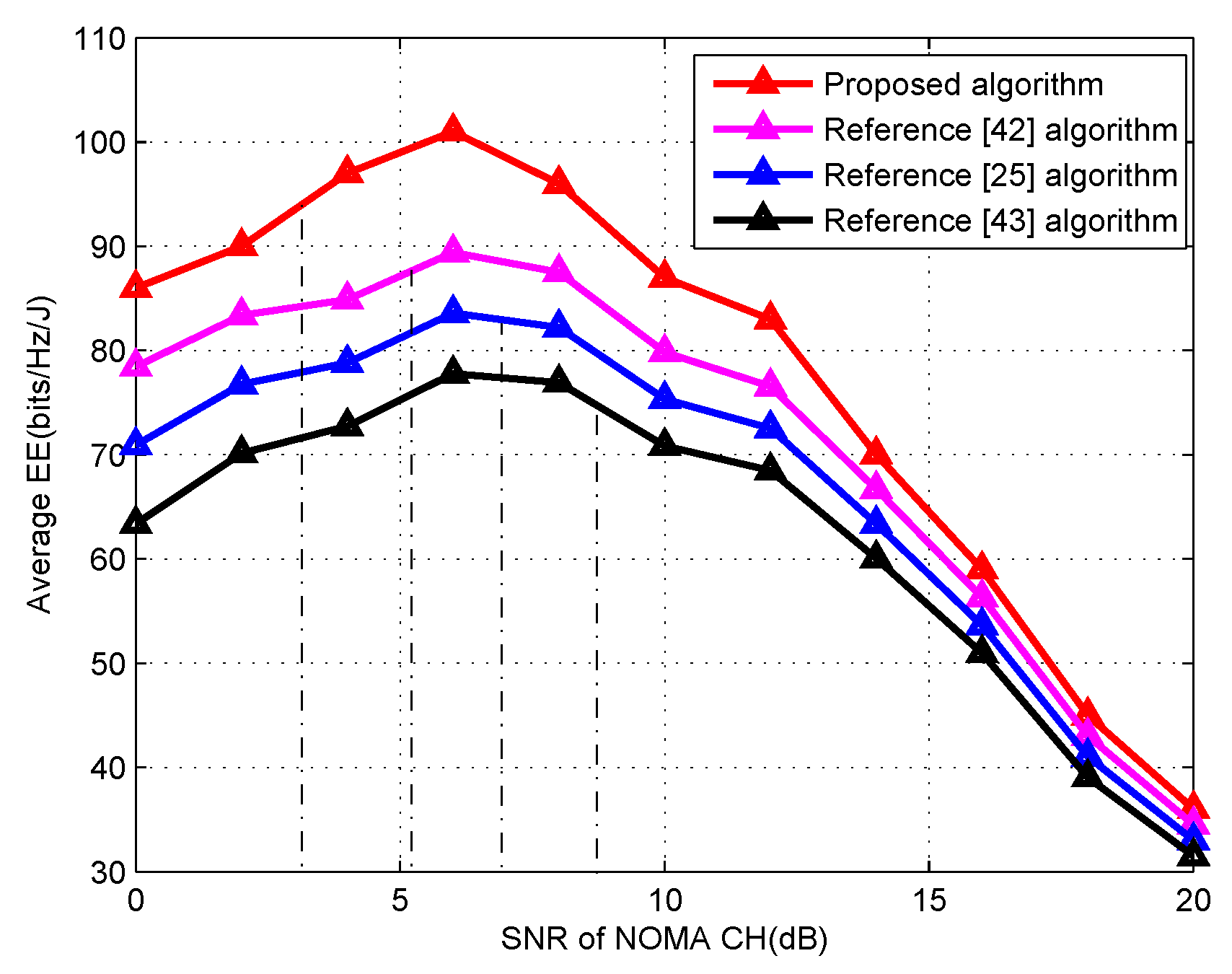
7. Performance Evaluation

In this section, we present the energy efficiency and access capacity performance of the resource allocation for the hybrid NOMA-OFDMA based cellular M2M communication systems. The average EE is quantitatively measured by the bits of information reliably transferred to a receiver per unit consumed energy per unit bandwidth at the transmitter. For simulation, the radius of BS is 1 km. $G_l=1$, and $\lambda =v/\phantom{v{f}_c}{f}_c$, where v is the speed of light and $f_c=2\mathrm{GHz}$. The values of the main simulation parameters are summarized in

Table 1. Simulation Parameters.

Parameters	Value
System bandwidth	20 MHz
Bandwidth of a RB	180 KHz
Number of available RBs, q	60
Number of preambles mapped to one PRACH, $\eta$	24
Number of RBs constituting one PUSCH, $\delta$	1
Maximum transmission power	$15\sim 35$ dBm
Minimum data rate	$1\sim 4$ bps
Number of multiplexing MTCD	2
Variance of additive noise	0 dB

.

Figure 3 presents the comparison between $q^{NCAS}$ and $n^{NCAS}$ for a different number of NOMA clusters. $q^{NCAS}$ is the sum of RBs allocated to PRACH and PUSCH for NCAS, and $n^{NCAS}$ is the number of RBs allocated to PRACH for NCAS. As Figure 3 shows, $q^{NCAS}$ is 24, 36, 42, 48, 54, 60 and $n^{NCAS}$ is 12, 18, 24, 24, 24, 24 when the number of NOMA CHs belongs to $\left(6,13\right]$, $\left(13,19\right]$, $\left(19,20\right]$, $\left(20,28\right]$, $\left(28,36\right]$, $\left(36,45\right]$, respectively. The reason is as follows:

(1) Given $\theta =1$, we can get the traffic load ranges $\left(6,12\right]$, $\left(12,19\right]$, $\left(19,26\right]$, $\left(26,35\right]$, $\left(35,45\right]$ by Algorithm 1. The optimal number of RBs allocated to PRACH is 48, 42, 36, 30, 24 corresponding to different traffic load range.

(2) Given $\theta =0.9$, we can get the traffic load ranges $\left(6,12\right]$, $\left(12,19\right]$, $\left(19,27\right]$, $\left(27,36\right]$ by Algorithm 1. The optimal number of RBs allocated to PRACH is 42, 36, 30, 24 corresponding to different traffic load range.

(3) Given $\theta =0.8$, we can get the traffic load ranges $\left(6,13\right]$, $\left(13,20\right]$, $\left(20,28\right]$, $\left(28,39\right]$ by Algorithm 1. The optimal number of RBs allocated to PRACH is 36, 30, 24, 18 corresponding to different traffic load range.

By analogy, we can also get the traffic load intervals and corresponding number of RBs allocated to PRACH when $\theta$ is 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1. By Algorithm 2, we can get the optimal RBs allocation factor ${\theta }^{*}$ through comparing the performance of access capacity for different $\theta$. Then the optimal number of RBs allocated for NCAS can be obtained by $q^{NCAS}=q{\theta }^{*}$, and the optimal number of RBs allocated to PRACH can be obtained by $n^{NCAS}=n^{*}\left(u_1;q{\theta }^{*}\right)$ for different number $u_1$ of NOMA clusters.

Figure 4 shows the comparison of the number of success clusters among NORA-DT and NCAS for different values of NOMA clusters. In NORA-DT, the total number of RBs allocated to PRACH and PUSCH was fixed even though the MTCDs may not be able to process over the whole RBs. While in the hybrid NOMA-OFDMA systems, the total number of RBs allocated for NCAS can dynamically change according to the number of NOMA clusters. By Algorithm 2, we can get the optimal number of RBs allocated for NCAS (i.e., $q{\theta }^{*}$). As Figure 4 shows, the optimal ${\theta }^{*}$ is 0.4, 0.6, 0.7, 0.8, 0.9, 1 when the number of NOMA clusters belongs to $\left(6,13\right]$, $\left(13,19\right]$, $\left(19,20\right]$, $\left(20,28\right]$, $\left(28,36\right]$, $\left(36,45\right]$, respectively. It means that 40%, 60%, 70%, 80%, 90%, 100% of uplink available RBs are allocated to NCAS for different values of NOMA clusters. We can observe that the number of success clusters in NCAS is similar to that for NORA-DT, which proves the feasibility of Algorithm 2.

Figure 5 shows the comparison of the access capacity among the hybrid NOMA-OFDMA, NCAS, and OCAS for different number of NOMA CHs. With the increase of the number of NOMA CHs, the access capacity in NCAS drastically increases. From Figure 3, we can know $q^{NCAS}$ is 24, 36, 42, 48, 54, 60 when the number of NOMA CHs belongs to $\left(6,13\right]$, $\left(13,19\right]$, $\left(19,20\right]$, $\left(20,28\right]$, $\left(28,36\right]$, $\left(36,45\right]$, respectively. Since the NOMA based MTCDs are not able to process over the whole available RBs. Therefore, the remaining RBs can be provided for OFDMA based MTCDs. We can get the number of RBs allocated for OCAS, denoted by $q^{OCAS}$, is 36, 24, 18, 12, 6, 0 as the number of NOMA CHs belongs to $\left(6,13\right]$, $\left(13,19\right]$, $\left(19,20\right]$, $\left(20,28\right]$, $\left(28,36\right]$, $\left(36,45\right]$, respectively. The maximum number of OFDMA based MTCDs allowed to access the network and the optimal number of PRACH RBs given $q^{OCAS}$ are also obtained by running the proposed Algorithm 1. Then we can get the maximum access capacity supported in OCAS. As shown in Figure 5, the access capacity in OCAS is non-increasing since the number of RBs allocated for OCAS is reduced for a different range of the number of NOMA CHs. Furthermore, it can be seen that the access capacity in hybrid NOMA-OFDMA is improved compared with that in NCAS until the number of NOMA CHs exceeds 28.

Figure 6 shows the comparison of the access capacity among the hybrid NOMA-OFDMA, NCAS, and OCAS for a different number of OFDMA based MTCDs. With the increase of the number of OFDMA based MTCDs, the access capacity in OCAS drastically increases. $q^{OCAS}$ is 24, 36, 42, 48, 54, 60 when the number of OFDMA based MTCDs belongs to $\left(6,13\right]$, $\left(13,19\right]$, $\left(19,20\right]$, $\left(20,28\right]$, $\left(28,36\right]$, $\left(36,45\right]$, respectively. Since the OFDMA based MTCDs are not able to process over the whole available RBs, the remaining RBs can be provided for NOMA based MTCDs. The number of RBs allocated for NCAS is 36, 24, 18, 12, 6, 0 as the number of OFDMA based MTCDs belongs to $\left(6,13\right]$, $\left(13,19\right]$, $\left(19,20\right]$, $\left(20,28\right]$, $\left(28,36\right]$, $\left(36,45\right]$, respectively. The optimal number of NOMA CHs and the optimal number of PRACH RBs given $q^{NCAS}$ are obtained by running the proposed Algorithm 1. As shown in Figure 5, the access capacity in NCAS is non-increasing. Furthermore, we can observe that the access capacity in hybrid NOMA-OFDMA in Figure 6 is less than that in Figure 5. Therefore, in the proposed RBs allocation scheme, sufficient resources allocated for NCAS is ensured compared to OCAS since NOMA can support more MTCDs than OCAS.

Figure 7 shows the comparison of the access capacity among the hybrid NOMA-OFDMA, NCAS, and OCAS, $\rho =3$, 5, and 7 dB. The number U of uniformly distributed MTCDs is 60. With the increase of the SNR of CH, the access capacity of NCAS first increases then achieves a stable level, while the access capacity of OCAS drops greatly. It means that NCAS can effectively improve the access capacity by supporting more and more NOMA clusters, which contributes the most compared with OCAS. The performance of the hybrid NOMA-OFDMA is obviously better than the performance of NCAS with a lower SNR. We can observe that the performance gaps between the hybrid NOMA-OFDMA and NCAS are lower when the SNR of CH is increasing. The performance gap between the hybrid NOMA-OFDMA and NCAS stands at about 40.7% when the SNR of CH is 0 dB and dramatically deteriorates to 6.9% when the SNR of CH is 8 dB. When the SNR of NOMA CH exceeds 12 dB, the performance of the hybrid NOMA-OFDMA and NCAS are completely closed. That is, the access capacity is mainly contributed by NCAS. As the SNR of CH increases, by decreasing $\rho$, the access capacity of NCAS increases, while the access capacity of OCAS decreases. Furthermore, the access capacity of the hybrid NOMA-OFDMA can reach at least 50 for different values of SNR of CH, accounting for 84% of all MTCDs.

Figure 8 shows the comparison among $q^{NCAS}$, $n^{NCAS}$, $q^{OCAS}$, and $n^{OCAS}$ for different values of the SNR of NOMA CH, $\rho =5$ dB, $U=60$. $n^{OCAS}$ is the number of RBs allocated to PRACH for OCAS. We can observe that with the increase of the SNR of NOMA CH, $q^{NCAS}$ and $n^{NCAS}$ gradually increase, while $q^{OCAS}$ and $n^{OCAS}$ gradually drop. This is because as the SNR of NOMA CH increases, the number of MTCDs that compete for uplink resources allocated for OCAS drops greatly, while the number of MTCDs that compete for uplink resources allocated for NCAS increases. Therefore, the more the resources allocated to NCAS, the less the resources are available for OCAS. In addition, $n^{OCAS}=0$ as the SNR of NOMA CH exceeds 12 dB, and $q^{OCAS}$ is relatively small. This is because the number of MTCDs that compete for uplink resources allocated for OCAS is relatively small as the SNR of NOMA CH exceeds 12 dB.

Figure 9 shows the comparison of average EE among the hybrid NOMA-OFDMA, NCAS, and OCAS for different values of the SNR of CH, $\rho =3$, 5, and 7 dB, $U=60$. As seen in the figure, as the SNR of NOMA CH increases, the performance of average EE in OCAS decreases, and the average EE of NCAS first increases to its maximum and then decreases. However, OCAS plays a key role compared with NCAS when the SNR of NOMA CH is small. While with the increase of the SNR of NOMA CH, NCAS plays a key role, and we also observe that when the SNR of NOMA CH is small, by increasing $\rho$, the performance of the average EE decreases. When the value of the SNR of NOMA CH becomes larger, by increasing $\rho$, the performance of average EE increases. The reason is that for uplink, the power allocation strategy needs to ensure the difference of received power at BS among multiplex MTCDs. As the difference (i.e., $\rho$) increases, the accuracy of SIC in decoding multiple MTCDs increases.

Figure 10 compares the achievable sum-rate of the proposed algorithm and the sub-optimal user clustering algorithm [25], the greedy algorithm (GA) based user grouping [42], random user grouping algorithm [43]. As can be seen from Figure 10, with the increase of the SNR of NOMA CH, the performance of the achievable sum-rate increases for all algorithms. In addition, we can notice that the performance of the proposed algorithm outperforms that of the reference [25,42,43] with different SNR of NOMA CH. Although the principle of reference [25,42,43] algorithms is to keep the difference of channel conditions between users in the group, the reference [25,42,43] algorithms cannot promise enough channel difference, which degrades the SIC decoding performance and the achievable sum-rate performance. While in the proposed algorithm, the range of channel gain differences is provided as the condition of grouping, which exploits the channel gain and maximum transmit power constraint of the devices. If the channel gain differences among devices can satisfy the condition of grouping, then these devices can be divided into the same cluster. In addition, when the achievable sum-rate of the proposed algorithm is the same as reference [25,42,43] algorithms (taking 150 as a target achievable sum-rate), the SNR of NOMA CH of the proposed algorithm is smaller than that of the reference [25,42,43] algorithms. Based on Proposition 3, the SNR of NOMA CH is derived as $CH\_SNR=10{log}_{10}\frac{{\left|g_{k,1}\right|}^2}{{\sum }_{i=2}^M{10}^{\frac{-\left(i-1\right)\rho }{10}}{\left|g_{k,i}\right|}^2+{\sigma }^2\phantom{{\sigma }^2\left(p_{k,1}{l}_{k,1}^2\right)}/\left(p_{k,1}{l}_{k,1}^2\right)}$ dB. As $p_{k,1}$ decreases, the SNR of NOMA CH decreases. Therefore, the proposed algorithm can realize the same achievable sum-rate of the reference [25,42,43] algorithms at a smaller transmission power.

Figure 11 shows the comparison of average EE of the proposed algorithm and the sub-optimal user clustering algorithm [25], the GA based user grouping [42], random user grouping algorithm [43]. As can be seen from Figure 11, the performance of the proposed algorithm is improved comparing with the performance of reference [25,42,43] algorithms. Both the proposed method and reference [25,42,43] algorithms have the maximum energy efficiency with a lower SNR of NOMA CH, and the energy efficiency decrease at a higher SNR of NOMA CH. The reason for the decrease of average EE is that with the increase of the SNR of NOMA CH, user grouping and power allocation strategy are more difficult to meet the minimum data rate requirements and the maximum transmission power of all multiplexing user. From Figure 10, we can get the SNR of NOMA CH of the proposed algorithm and reference [25,42,43] algorithms when the target achievable sum-rate is 150. Then from Figure 11, the average EE of the proposed algorithm and reference [25,42,43] algorithms can be obtained under the target achievable sum-rate. It can be seen that the performance of the proposed algorithm is obviously better than the performance of reference [25,42,43] algorithms.

8. Conclusions

In this paper, we have studied the issue of resource allocation for hybrid NOMA-OFDMA based cellular M2M communication systems with the goal of maximizing system access capacity and energy efficiency. NCAS and OCAS were investigated for NOMA based RA and OFDMA based RA, respectively. A traffic-aware RBs allocation scheme consisting of two sub-problems was proposed for the hybrid multiple access systems. The first sub-problem was used to optimize RBs allocation between PRACH and PUSCH given the sum of RBs allocated to PRACH and PUSCH for NCAS, while the second one optimized the RBs allocation between NCAS and OCAS. The energy efficiency maximization problem in the hybrid NOMA-OFDMA systems was formulated. Under the maximum transmit power constraints and QoS requirements of the devices, the feasibility conditions of a power allocation solution was derived. The original non-convex optimization problem was transformed into the pseudo-concave optimization problem based on the power back-off scheme, and was solved under the feasibility conditions by two iterative algorithms. Based on the channel gain difference and the feasibility conditions of power allocation solution, a device clustering scheme was proposed to decide the devices selecting NCAS or OCAS. By simulation, we showed that the proposed traffic-aware resource allocation scheme for hybrid NOMA-OFDMA based cellular M2M communication systems significantly improves the system access capacity, as well as the energy efficiency.