1. Introduction
With the development of wireless communication system, the next industrial revolution is on the way. The fifth generation (5G) communication technology brings the industrial Internet of things (IIoT) into the era of Industry 4.0 [
1]. Head mounted displays, handheld terminals, collaborative robots, and automated guided vehicles (AGV) are widely deployed in industrial factory to achieve more intelligent information interaction. Due to the exponential growth of mobile data traffic, the problem of spectrum scarcity is getting worse. To meet the requirements of IIoT, unlicensed 60 GHz spectrum has aroused extensive attention due to the continuously available spectrum resources [
2]. However, the signal transmission in this band suffers from high propagation loss [
3]. Therefore, large-scale antenna should be used to improve the diversity gains at the transceiver [
4].
To further extend the coverage range, beamforming techniques are also adopted to provide directional gain. Typically, the hybrid beamforming architecture is used to realize massive multiple-input multiple-output (MIMO) due to the high cost of RF chains and power consumption in traditional full-digital beamforming [
5]. Considering the difficulty to acquire perfect channel state information (CSI), the analog beamformer usually performs beam alignment through a specific pre-defined codebooks. Although the codebook-based beam alignment techniques are more convenient to be adopted on the inexpensive RF phase shifters, the latency and signaling overhead will be increased during beam management [
6,
7].
Compared with the static scenario, beam misalignment probability increases greatly in a dynamic IIoT environment. The communication links are prone to interruption due to the rapid changes of mobile user’s location. To update and reconstruct the communication beam, some beam tracking methods have been proposed in the literature. The three-stage search method in [
8] narrows the beam range step by step to reduce the time complexity. However, when the size of antenna arrays increases, the time complexity of this method is still very high. Two pre-established codebook fingerprints are constructed in [
9] to obtain the optimal beam pairs at the current location. Although the proposed method provides high performance with larger antenna arrays, the database construction is time consuming. Since communication is mainly through LOS component in dynamic scenario, its beam direction can be tracked based on the user’s location and velocity. Prior works developed in [
10,
11,
12,
13,
14] attempt to obtain location of the user to track the beam. The angle of arrival (AOA) and angle of departure (AOD) can determine the channel, which can then be used to construct the optimal beamforming precoding vector directly [
11]. To achieve accurate location information, an uplink time-difference-of-arrival (TDOA) measurement is considered in [
12] at multiple Remote Radio Heads (RRHs). In addition, to track and predict the position more precisely, the Extend Kalman Filter (EKF) is adopted. Device Positioning is another way to get a user’s location, which can be achieved by global navigation satellite-based systems (GNSS), radar, cameras, and laser scanners (lidar) [
13,
14].
With the use of larger antenna array and narrower beams at unlicensed 60 GHz spectrum, a higher latency and signaling overhead of the beam tracking will be caused by the increasing of the number of beams. To deal with this problem, in addition to reducing the complexity of the beam tracking algorithm, a suitable beam switching time should also be found to minimize the signaling overhead. To the best of our knowledge, there are few studies aiming to investigate the update frequency of beam alignment during terminal motion. It is naturally to leverage channel coherence time for beam alignment. However, the channel coherence time is only a few milliseconds or less at the 60 GHz mmWave bands. As a result, it is impossible to align beams by the channel coherence time in terms of the frame structure in the 5G protocol. To determine a suitable beam switching time, we derive the beam coherent time. Moreover, we propose a trajectory prediction and channel monitoring aided fast beam tracking (TCFBT) scheme to further reduce the latency and overhead for beam alignment. In other words, we first derive a beam coherent time to reduce the frequency of beam alignment. Then, a Gaussian process-based sector prediction algorithm is presented to narrow the scope of beam searching. Finally, the optimal beam pairs are selected by the joint directional Listen before talk (LBT) and beam training algorithm proposed in the following.
In conclusion, the main contributions of this paper can be summarized as follows:
We derive the beam coherent time based on DFT codebook to indicate the terminals switching their beams. Moreover, we quantify the beam pointing error and the beam coherence time and discover that the beam coherence time is much longer than the mmWave channel coherence time. Consequently, the beam coherence time is more suitable for beam tracking with mobile terminal.
We propose a two-stage heuristic TCFBT scheme to ensure the fairness and availability of the beams for 5G mobile terminal in unlicensed 60 GHz. In other words, a Gaussian process-based sector predict algorithm is adopted to determine the corresponding sectors at the transceivers in the first stage. Then, a joint directional LBT and beam training algorithm is proposed in the second stage to obtain the optimal beam pair links in the current moment. The proposed scheme reduces the searching range of the beam set by trajectory prediction and channel monitoring. Therefore, the latency and overhead are further reduced to a large degree.
The symbolic notation we use in this paper is shown in
Table 1.
The rest of this paper is organized as follows. In
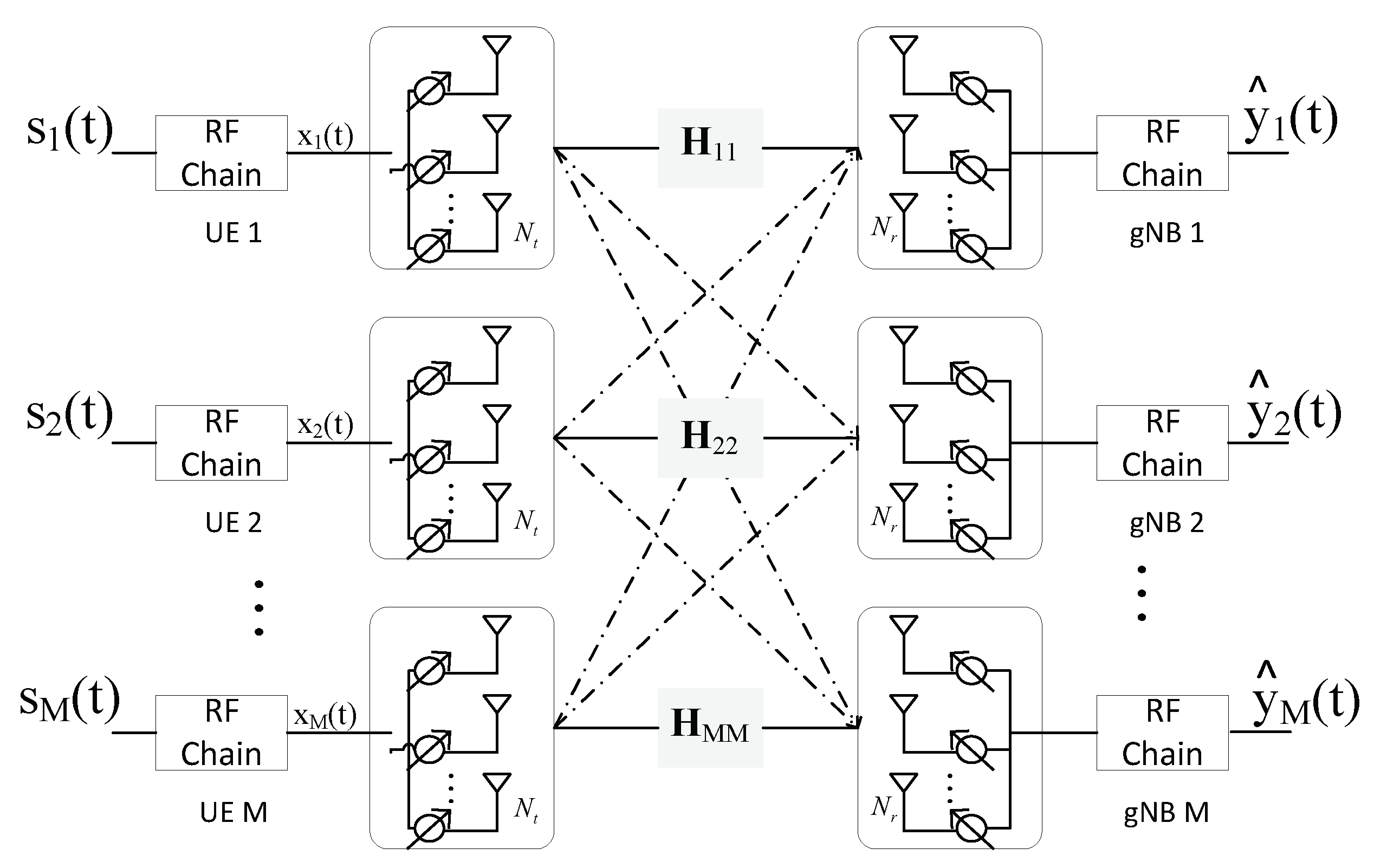
Section 2, the considered system model is described, including the multi-user single links in mobility scenario, receive signal structures with analog beamforming and channel model. To reduce the frequency of beam searching, the beam coherent time is derived in
Section 3. In
Section 4, we present the TCFBT scheme, including a Gaussian process-based prediction algorithm and the joint directional LBT and beam training algorithm. After that, the performance of our algorithm is evaluated by the system-level simulations in
Section 5, while the conclusions are drawn in
Section 6.
3. Beam Coherent Time
In the process of terminal movement, it is much more frequent to switch beam according to channel coherent time. To determine a more reasonable beam switching time, we first quantify the beam pointing error and the beam coherence time for the LOS cases in this section. Then, two types of function are proposed to fit the probability density function (PDF) of antenna pattern. It should be noticed that the analysis is based on a single link, while the derived beam coherent time is also applicable to multiple links since the time is only related to the user’s speed, time, and beam direction (or the beam width).
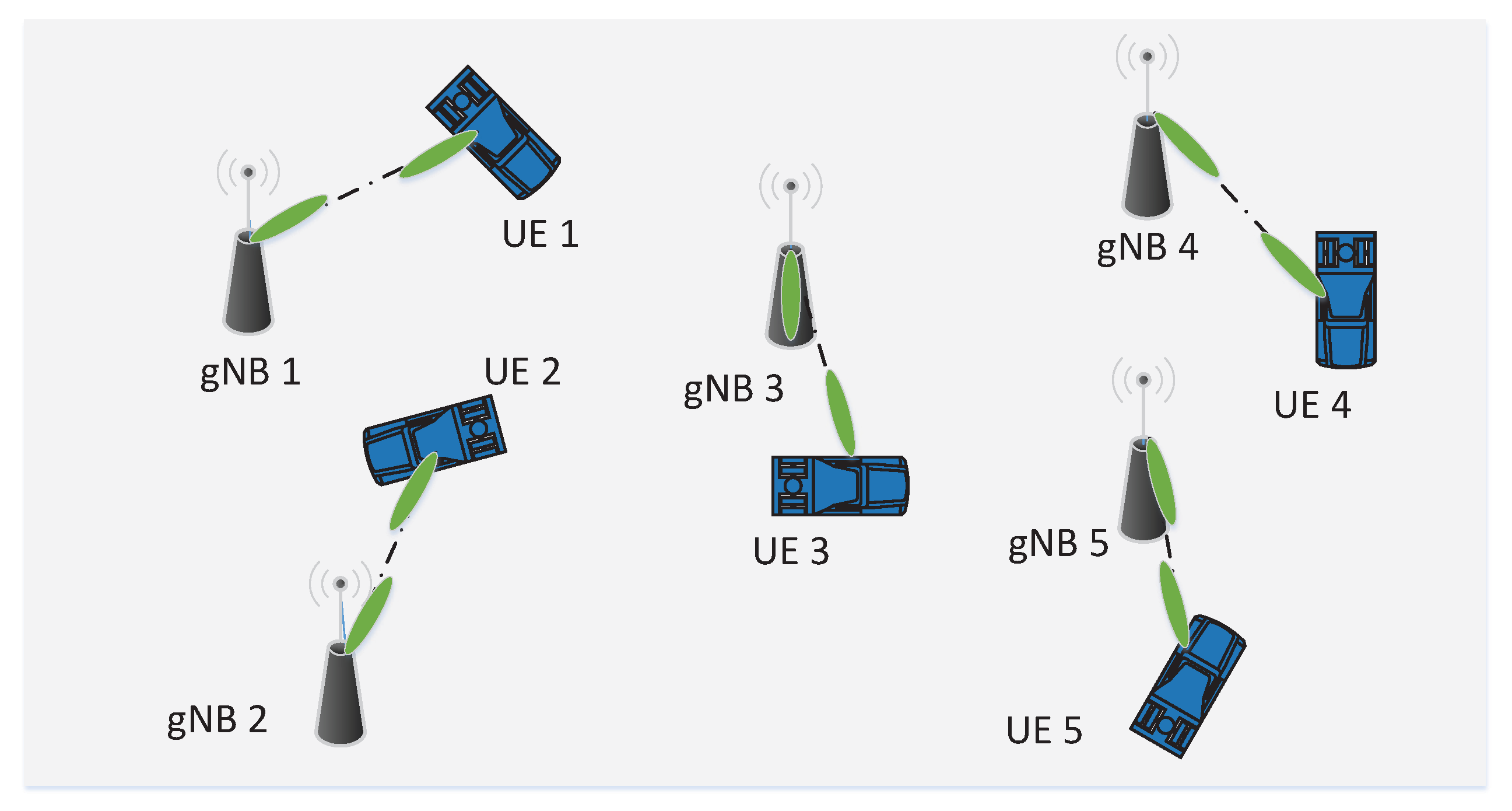
The model we use to evaluate the beam misalignment is the two-dimensional motion model shown in
Figure 3. Let the UE point at gNB have beam direction
at time
t and move with a constant speed
v along the straight line to reach point B at time
. Take the UE side as an example; the beam pointing error is defined as
over a short period of time
. As a result, the distance from A to B can be denoted as
. Assuming the distance from the gNB to the UE is
S at time
t, we quantify the relationship between the user’s speed, time and beam direction according to the law of sines for triangle, i.e.,
When the angle
is small,
, the beam pointing error is derived as
To evaluate the relationship between beam pointing error and receive power, we introduce the concept of beam coherence time. It is defined as the average time that the beam can stay aligned [
16]. In other words, when the received power
P at time
drops to a certain degree compared with the power at time
t due to channel variation, it is considered that the beam misalignment occurs at this time. In this case,
is defined as the beam coherence time, i.e.,
where
is the threshold representing the decline degree of the received power. Because the power is proportional to the beam pattern
G, Equation (
9) can be written as
at beam switching moment. Moreover, we adopt a specific DFT codebook [
17] as a predefined codebook to generate the communication beam pattern. The codebook can be generated by
where
and
represent the antenna element index and the beam pattern index, respectively.
Since the received power
P can be expressed as the gain of antenna beam pattern approximately, the study in [
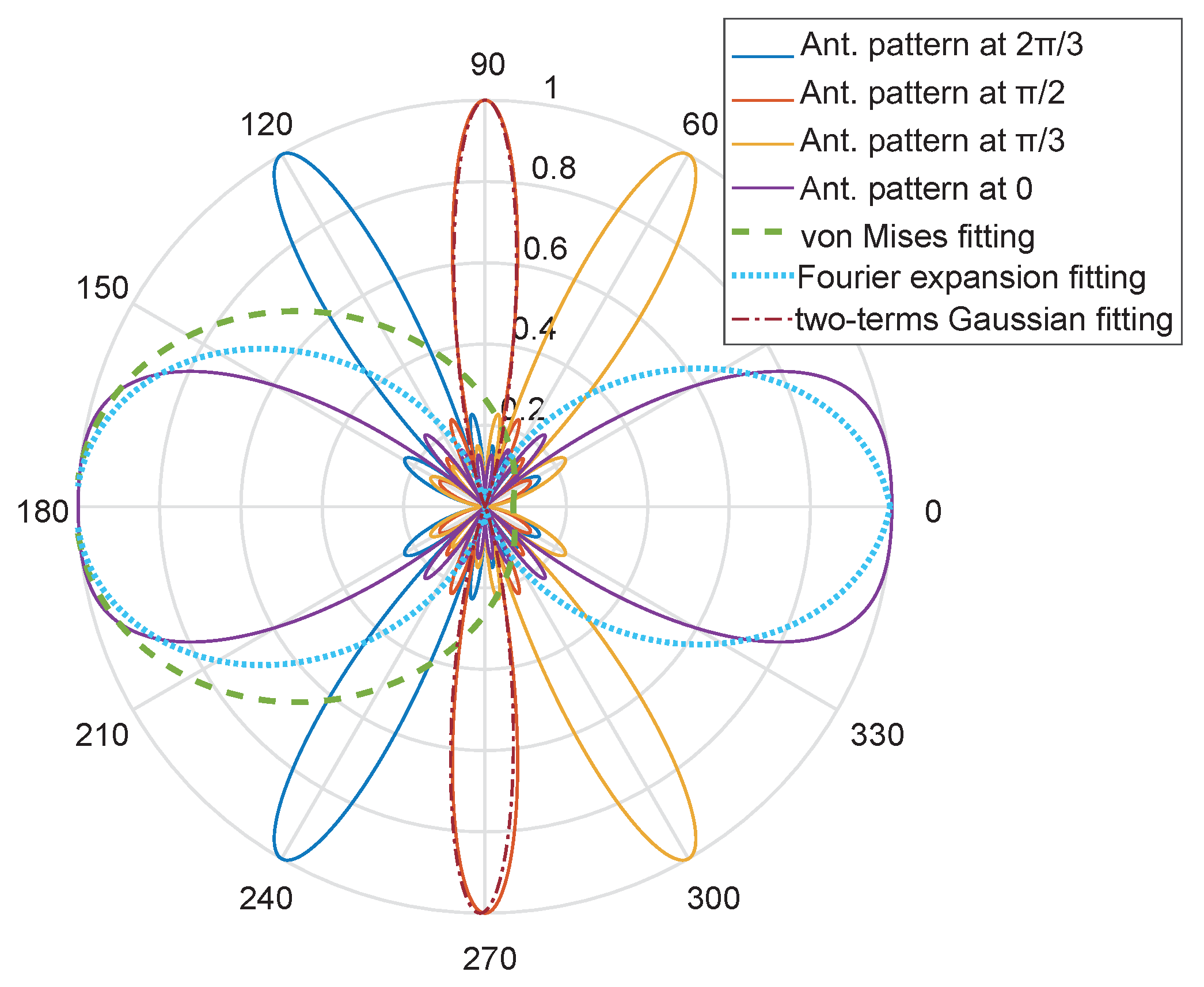
16] adopts von Mises distribution to fit the probability density function (PDF) of antenna beam pattern. However, von Mises cannot fit the antenna beam pattern exactly. As a result, we select Fourier expansion of triangular (FET) and two-term Gaussian function (TGF) to fit the PDF of DFT beam pattern more accurately. The fitting functions are shown as
where
are regression coefficients under the confidence probability of
which can be calculated by least square estimator. As shown in
Figure 4, the root mean square error (RMSE) in FET fitting is
for the first column vector with the largest beamwidth in DFT codebook. The fitting precision becomes better as the number of Fourier expansion terms increases. For the other column vector in DFT codebook, the RMSE in TGF fitting is
. Both are much smaller than the von Mises distribution (RMSE with
for the first column vector) proposed in [
16]. It should be noticed that the FET fitting is appropriate for the case where the beamwidth is greater than or equal to
, and TGF fitting is suitable for the beams with beamwidth less than
. Taking FET fitting as an example, the beam coherence time is
and the derivative process can be seen in
Appendix A.
Therefore, the beam coherent time is then defined as the corresponding beam switching time. Instead of switching beams in each shorter channel coherent time, the UE only need to switch their beams at the beginning of each beam coherent time, which can reduce the latency and overhead to a large extent.
4. Trajectory Prediction and Channel Monitoring Aided Fast Beam Tracking Scheme
As discussed above, we derive an appropriate beam coherent time to decrease the frequency of beam alignment. In this section, we propose a two-stage heuristic TCFBT scheme to reduce the latency
in the problem in Equation (
6) and signaling overhead in the process of beam training. A sector prediction algorithm based on Gaussian process classifier is adopted in the first stage to acquire the beam subset, which reduces the space of beam training and is more suitable for beam tracking in mobile scenario. Then, we leverage directional LBT in the second stage to further decrease the range of beam training. To be more specific, we divide the 360-degree spatial region of the transceiver into a limited set of sectors, and the sector prediction algorithm is used to predict the sector indices of the transceivers. After that, the joint directional LBT and beam training algorithm (JDLBT) is used in the selected sector to obtain the optimal beam pair. Finally, we analyze the complexity of the proposed two-stage scheme.
4.1. Gaussian Process-Based Sector Prediction Algorithm
In the light of the study in [
18], a Gaussian process is a collection of random variables, any finite number of which have a joint Gaussian distribution. Therefore, we adopt the GP-based machine learning algorithm to build a prediction model for coordinate prediction. The aim of the GP-based algorithm is to find the input-output mappings of the position coordinates from the observation data. After that, we use the geometric model described in
Section 4.1.1 and
Section 4.1.2 to establish the relationship between position coordinates and sectors.
Considering a standard GP regression model,
where
x is the one-dimension coordinate value of each mobile user in the xy-plane and
z is the output predicted coordinate value on the same direction.
is the regression function with the mean function of
and covariance function
.
n is the Gaussian noise that follows i.i.d
.
Define a training set
with length L,
, where
is a matrix of input coordinate value and
is a matrix of output predicted coordinate value, respectively. For each
, it represents the historical observations during each beam coherent time
and can be denoted as
.
is defined as the predicted coordinate value during the same beam coherent time
. It should be noticed that
can be represented by either x-coordinate value or y-coordinate value of the mobile user in the xy-plane here. Assuming that the input of test dataset is
and the output is
, the distribution with the zero mean function can be written as
where
represents the covariance function. As a result, the prediction distribution can be denoted as
The predicted coordinate value can be obtained by the mean function in Equation (
15), which means the predicted coordinates can be achieved by using expression
. Then, the following two steps can be processed to predict the corresponding sector.
As shown in
Figure 3, we assume that the coordinate of UE is
, and the coordinate of gNB is
. The initial pointing direction
at UE side is denoted as
. As a result, we derive
. Assume that the transceivers pre-divide the beam radiation space into eight sectors. Take the transmitter as an example, the relationship between coordinate and the antenna sector can be obtained by using the following steps.
4.1.1. Step 1
First, the transmitter should determine the range of the AOD. When , it indicates . If , , it represents , and, if , , . When , it means .
4.1.2. Step 2
Then, the transmitter will calculate the AOD by . After that, the transmitter will search the range of sector sets to determine the sector index based on the corresponding .
After sector prediction, each 5G mobile user i and the corresponding gNB i can select their optimal beam pairs from the beamforming codebooks in the predicted transceiver sectors, and this subset is denoted as and , respectively.
4.2. Joint Directional LBT and Beam Training Algorithm
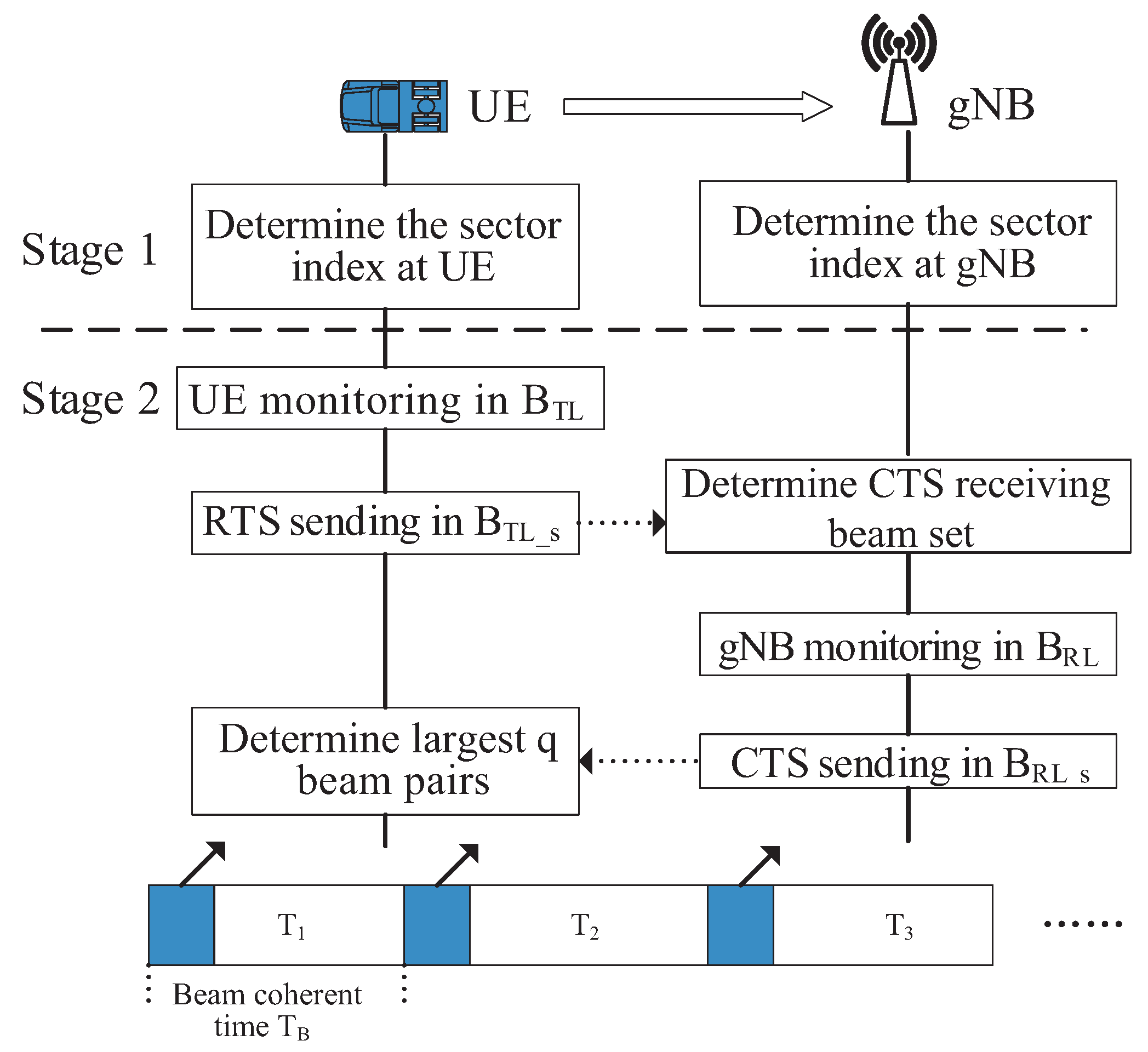
Although the size of beam training set decreases, we can also use directional LBT to further narrow the scope of beam training. Therefore, we design a JDLBT algorithm to obtain the optimal beam pairs. Specifically, the transceivers execute directional LBT on the beam training subset , which are selected by the first stage, and ensure that the interference is under the CCA threshold . With the help of request to send reference signal (RTS) and clear to send reference signal (CTS), the optimal communication beam pairs are then determined during beam training process. It should be noticed that the latency of JDLBT will be much less than the duration of each beam coherent time.
We divide the JDLBT into four stages: UE monitoring, RTS sending, gNB monitoring, and CTS sending. Based on channel reciprocity theory between uplink and downlink, the details are describe as follows.
4.2.1. UE Monitoring
The UE sweeps the beam set … which belongs to the selected sector according to the angle correlation and detects the channel energy on each beam direction. If the co-channel interference is lower than the CCA threshold , the transmitter will choose these beams as a subset of to send RTS in the next stage. The subset is denoted as .
4.2.2. RTS Sending
The UE sends RTS on each beam direction in . At the same time, the gNB carries out a sector beam sweeping during each beam transmission cycle. Based on sounding reference signal (SRS), the gNB sorts the reference signal receiving power (RSRP) of the receiving beams in descending order after times of beam sweeping. Then, the the largest p beam indices in RSRP are sent to UE and adopted as the CTS receiving beam set at UE.
4.2.3. gNB Monitoring
In a similar way, the gNB scans its monitoring beam set … in the corresponding receiving beam sector. Then, the gNB performs CCA detection on those beam direction to pick out a subset of , which is used for CTS sending in the next stage, denoted as .
4.2.4. CTS Sending
At the end of the procedure, the gNB sends CTS by sweeping each beams in to occupy the channels. Meanwhile, the UE sweeps the largest p beams in RSRP which are selected by RTS sending stage in each beam transmission cycle. According to the RSRP, the transceiver determine the largest q beam pairs as the communication beam set. Further, the optimal beam pairs are chosen as the current communication beams. Finally, the UE will report the beam index to gNB.
It should be noticed that the exposed node problem and hidden node problem can be solved with the help of RTS/CTS in JDLBT [
19]. The JDLBT enables exposed node to establish a communication link with limited interference, and prevents hidden node form the link by stop sending CTS on beams with strong interference. In conclusion, the JDLBT avoids duplicating beam sweeping in the process of directional LBT and succeeding beam training, and reduces the latency and signaling overhead significantly. The range of beam set is further reduced with the help of the directional LBT.
The procedure of the TCFBT scheme is summarized in
Figure 5.
4.3. Complexity Analysis
We analyze the complexity of TCFBT scheme in each beam coherent time in this subsection. Taking IEEE 802.15.3c three-stage search algorithm as the baseline [
8], which is much less complex than ergodic searching, the complexity of the independent beam searching is
, and it needs extra
beam pair links in the RTS/CTS sending process. Moreover, it requires
times channel monitoring at UE side and
times channel monitoring in gNB before beam training. Therefore, the total complexity is less than or equal to
, which is relatively high for beam tracking with mobile users.
When channel monitoring combines with beam tracking, the complexity become much lower than the independent scheme. Thanks to the sector prediction algorithm, the beam training set is narrowed to
at the UE and
at the gNB. In the process of RTS sending, the beam pair links are
times, while the complexity is
at CTS sending. As a result, the complexity of the proposed TCFBT scheme is
. As shown in
Table 2, we assume there are eight sectors at the gNB and the size of alternative beam set p is equal to 3. The beam pair links are largely reduced by using TCFBT scheme.