1. Introduction
Traditional authentication procedures and protocols were constructed upon the state-of-the-art cryptographic algorithms that fundamentally operate over the use of secret keys stored in non-volatile memory. Such memory-based cryptographic methods are subjected to invasive and side-channel attacks [
1,
2,
3], increasing the cost of maintaining secure transactions and processes. In addition, the intensive processing nature of such classical cryptographic algorithms makes them unsuitable for the IoT environment. Therefore, Physical Unclonable Functions (PUFs) have emerged as a lightweight memoryless solution to provide security requirements for limited-resource Internet of Things (IoT) devices. PUF utilizes physical variations in integrated circuits to output unique responses that are unreproducible even by manufacturers. Even if the exact design is implemented and the same challenge set is used, the responses generated in one circuit should be uniquely distinguished from another one, making them appropriate for providing security requirements at a low cost, due to the elimination of non-volatile memory.
The notion of PUFs was first proposed in [
4,
5] which later led to the introduction of delay-based Arbiter PUF (APUF) by [
6]. Among all proposed designs of delay-based arbiter PUF, XOR PUF designs have been thought to be one of the most resistant designs against possible attacks due to the use of XOR operation. However, XOR PUFs have been reported to be mathematically cloneable by machine learning-based methods and suffer from a low unpredictability rate [
7,
8,
9,
10]. Recently, Double Arbiter PUFs (DAPUFs) have been proposed by [
11] as an enhancement against machine learning attacks. Authors in [
11] argue that both 3-1 DAPUF and 4-1 DAPUF are secure against modeling attacks. Although authors in [
12] could successfully break the security of 3-1 DAPUF using a very large set of CRPs, 17 million CRPs, they failed to make a breakthrough 4-1 DAPUF using the same set of CRPs.
In this paper, we examine the robustness and unpredictability of DAPUF using silicon data to evaluate the reliability of DAPUF designs in reproducing the exact key given the same set of input challenges, to what extent challenge sets of a given design is biased, and the uniqueness of a key produced from one circuit to another when the same design and challenge set is used. Since the introduction of DAPUF designs, to the best of our knowledge, the proposed DAPUF designs have not been thoroughly investigated since its introduction, and the performance evaluations were carried out using a very limited number of CRPs. This has motivated us to perform a detailed analysis of DAPUF that contributes to the literature in the following:
Perform comprehensive performance evaluations on all proposed designs of DAPUF and their counterparts from XOR PUF using different sets of CRPs generated from FPGA chips.
Examine the security of each proposed design using FPGAs data drawn from the implemented DAPUF designs on FPGA boards. Thus:
- -
By reconstructing the 3-1 DAPUF design in our FPGA boards, we were able to break the security of 3-1 DAPUF design and substantially lower the number of CRPs required from 17 million CRPs, as reported by [
12], to 500 k only with a higher accuracy rate.
- -
We were able to successfully model 4-1 DAPUF that has never been cloned at the time of writing this paper.
The rest of the paper is organized as follows:
Section 1.1 gives an overview of delay-based arbiter PUF.
Section 1.2 discusses related work on DAPUF, and
Section 1.3 points out areas that need to be revisited and our contributions on DAPUF.
Section 2 describes performance evaluations developed in [
13,
14] that we rely on to perform our analysis on DAPUF designs. In
Section 3, we explain our experimental setup which includes FPGA implementation, CRP generation, and our machine learning attack model.
Section 4 presents our results for performance evaluations, modeling attacks, and detailed discussion on what is the preferred design. Finally, concluding remarks are provided in
Section 5.
1.1. Background on Delay Based Arbiter PUFs
Since the design of both XOR PUF and DAPUF consist of multiple arbiter PUFs, it is essential to understand the structure of an arbiter PUF design. The initial design of arbiter PUFs that was introduced in [
15,
16] is illustrated in
Figure 1. It consists of two parallel paths on which electric signals (input challenge) race against each other simultaneously through n-stages to reach the Arbiter. Each stage contains a pair of multiplexers and the challenge bit decides which path will be taken by the signal. The final stage is connected with an arbiter using two latches from top and bottom paths. The signal that reaches the arbiter input bit first will take the value of 1, otherwise 0. The response in n-stage arbiter PUF could take
different paths. However, it turns out that the output of arbiter PUF could be predicted using machine learning attack depending on a model of additive delay model [
6] that could be represented as a linear specification problem, which makes it vulnerable against machine learning attacks.
XOR PUF, illustrated in
Figure 2, was proposed in [
17] to enhance the resilience of arbiter PUF. XOR PUF is composed of N number of arbiter PUFs and the response from each arbiter is XORed to generate the output response of XOR PUF. While XOR PUF has evidently added more complexity by introducing nonlinearity to the design [
8], the response of XOR PUF can be predicted using machine learning techniques [
7,
8,
9].
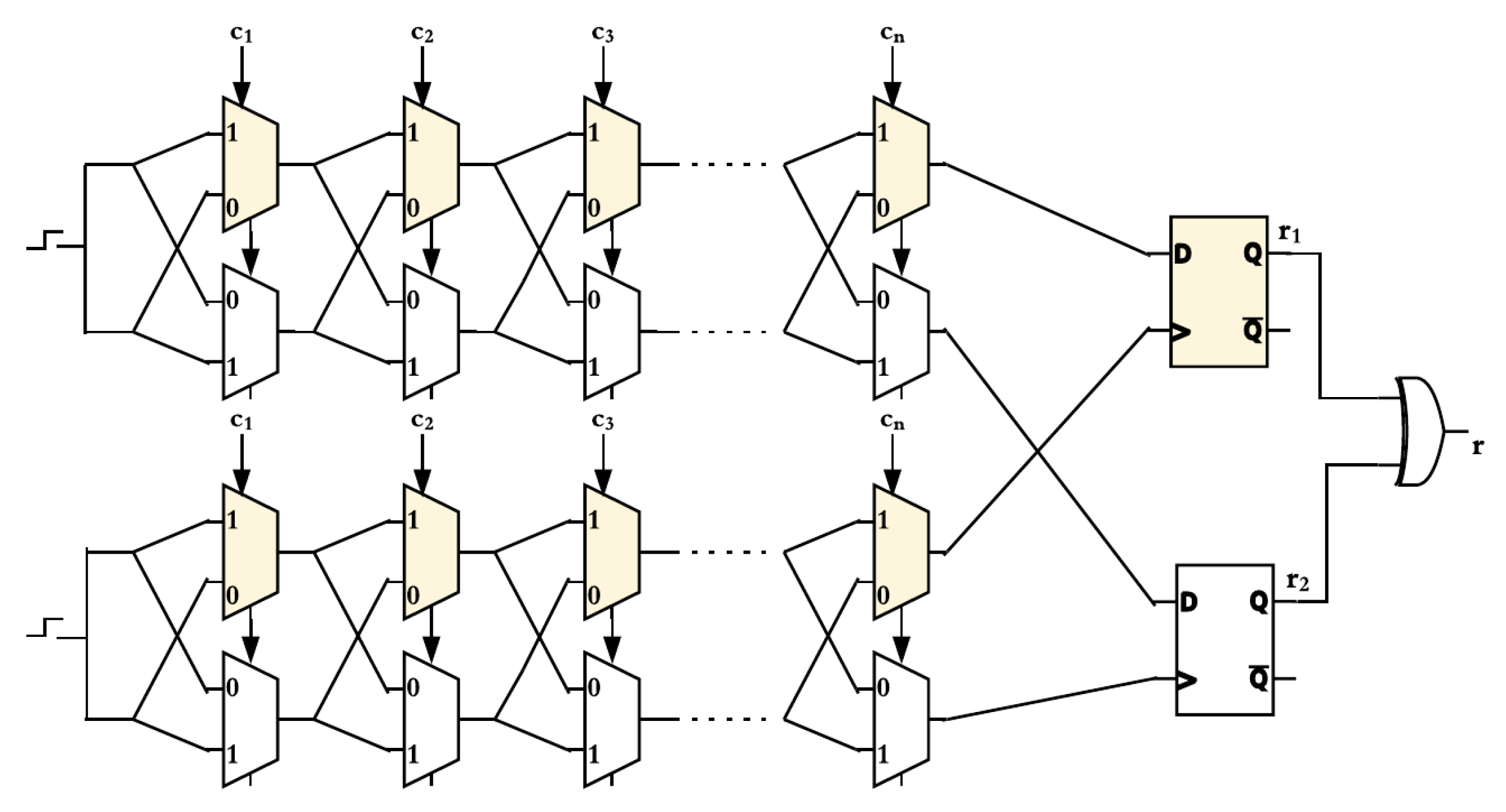
DAPUF has recently been proposed in [
18] to add further complexity to the modeled design of Arbiter PUF as illustrated in
Figure 3. Three DAPUF designs have been introduced in [
11,
18] which are (2-1, 3-1, and 4-1 DAPUF) shown in
Figure 4,
Figure 5 and
Figure 6, respectively. In DAPUF, it requires N(N-1) internal bit XORing, one from each arbiter, to get the response of N-1 DAPUF.
DAPUF is similar to XOR PUF in that N ≥ 2 arbiters are required for any of their designs. However, unlike XOR PUF where each arbiter receives the top and bottom delay signals from the same APUF, each arbiter in DAPUF will take either the top delay lines or the bottom delay lines in similar proportions. DAPUF requires N(N-1) XORing to get the one bit-response of N-1 DAPUF, while it takes N-XORed responses to generate the one-bit output response of N-XOR PUF.
1.2. Related Work
Previous work on XOR PUF and DAPUF can be split into performance evaluation and security analysis. Performance evaluation, on one hand, is based on evaluation metrics introduced in [
13,
14] that allow us to examine and compare the suitability of each proposed design of delay-based arbiter PUF. Performance analysis is based on hardware primitives in which each proposed design is implemented using FPGA boards. Each implemented design on FPGA utilizes the inherited variation in the ICs to generate the challenge–response pairs.
Performance evaluation on XOR PUF is well reported in the literature [
10,
19,
20,
21,
22,
23] using different components (also known as streams) and number of stages. However, there is very limited number of research conducted on the implementation and experimentation of DAPUFs. Authors of [
24] have examined and compared three different designs which are XOR PUF, PAPUF, and DAPUF. However, their implemented design of DAPUF, shown in
Figure 3, is not similar to those implemented in [
11,
18]. In particular, the response from each arbiter has to be XORed to generate the one-bit response of any DAPUF design, a part that has prevented them from conducting their analysis on different DAPUF designs. The only paper that reported performance analysis on all DAPUF designs is from the same authors that proposed the design of DAPUF [
11], in which they analyzed the performance of DAPUF and compare it with that of XOR PUF using three evaluation metrics.
Security analysis, on the other hand, is pivotal to the applicability of any PUF design. In fact, XOR PUF and DAPUF, with multiple components and different number stages, were primarily introduced to enhance the resilience of arbiter PUF design against machine learning attacks. The tolerance of XOR PUFs against machine learning attack have been extensively studied in [
7,
9,
10,
22] and they were able to impersonate them using different machine learning techniques. DAPUF designs have shown more resilience against machine learning attacks compared to XOR PUF. Authors of [
11] reported that 3-1 DAPUF and 4-1 DAPUF are secure against machine learning attacks, but their findings were based on small sets of CRPs. Other work on DAPUF utilized 17 million real CRPs to successfully attack 3-1 DAPUF, while they report that 4-1 DAPUF remains secure even when deep learning techniques are used and 17 million real CRPs are employed [
12]. Authors of [
25] have simulated 2-1, 3-1, and 4-1 DAPUF designs and were able to virtually counterfeit all designs using different sets of CRPs.
1.3. Motivation and Contribution
Previous work on DAPUF lack in two essential aspects. First, more comprehensive performance evaluations are required to examine each of the implemented design. Studies on XOR PUF include correctness and diffuseness; these performance metrics are not reported in DAPUF work. Performance analysis on DAPUF conducted in [
11] uses a very limited number of CRPs.
Our goal is to evaluate the performance of each proposed design of DAPUF using five evaluation metrics, and the reported results of each evaluated design are based on 60,000 CRPs with 32 iterations and each experiment is repeated 32 times. Our experiments include comparisons between DAPUF designs and their counterparts from XOR PUF using similar experimental setups.
The second area that needs to be revisited is the security analysis on DAPUF. Authors of [
11] examined the resilience of DAPUF using small sets of CRPs with 1000 training samples and 10,000 test samples, and they concluded that 3-1 DAPUF and 4-1 DAPUF are secure against machine learning attacks. However, it is important to examine the tolerance of DAPUF when a sufficient amount of CRPs can be acquired. The security of DAPUF designs have also been studied in [
12] using deep learning. However, employing deep learning techniques may raise the issue of overfitting on the trained model, and the model will perform worse on the data outside the trained model [
26]. Their approach to solving this problem was to dropout layers at the end of the network and increase the set of CRPs to 17 million. While this has helped them to model 3-1 DAPUF with an 86% accuracy rate, their approach had no efficiency gain and failed to model 4-1 DAPUF. Our approach is to use a rather simpler model by employing a neural network-based attack model that enables us to successfully model all the proposed design of DAPUF, namely 2-1, 3-1, and 4-1 DAPUF and their counterparts 2, 3, and 4 XOR PUF. Our modeled attack reduced the number of CRPs required to successfully attack any DAPUF design with a higher accuracy rate compared to the literature.
2. Performance Evaluation of PUF
Several types of PUF designs have been proposed since the initiation of PUFs including delay-based Arbiter PUFs, Ring Oscillator PUFs [
17], Lightweight Secure PUFs [
27], etc. These designs can be complicated by increasing the number of stages and/or by increasing the number of components embedded in the design. While sophisticating the design can surely enhance the resilience of a PUF instance against attacks, it raises the question of what are the trade-offs brought by these complications. For this reason, a number of evaluation metrics have been proposed to evaluate the performance of PUF designs. These metrics can be classified into intra-chip and inter-chip evaluation metrics. The former is related to examinations of a PUF design performance within a device which are randomness, correctness, steadiness, and diffuseness, while the latter examines how unique the output of a PUF design is when the same challenge is given to different devices, called a uniqueness test. These performance metrics are explained in detail next, and all notations used in these metrics are shown in
Table 1.
2.1. Performance Metrics
2.1.1. Randomness
Randomness measures how balanced the output of a PUF in producing numbers of 0’s and numbers of 1’s. The proper output of a PUF should be uniformly distributed between 0’s and 1’s. Randomness, defined in [
13], is calculated using the hamming weight from running multiple tests using different sets of CRPs:
where
is the output frequency of 1’s generated from device
k, and
is the
i-bit response of a challenge set
s when examined at test
t on device
k. The randomness of a device is calculated as follows:
The ideal value is equal to 1 when ( i.e., when the data are balanced). The higher the deviation to either or , the more unbalanced the data are.
2.1.2. Steadiness
Evaluation of a PUF design should consider factors that may influence the ability to reproduce the exact key under different work environments. One factor is related to power voltage that could impact signal variations within the device. Noise due to environmental variability such as temperature in the working area may also affect the delay in ICs. To measure the influence of these variables, multiple tests have to be made using the same devices and keeping the number of CRPs fixed. Hori et al. [
13] introduced one way to measure steadiness of a response bit as follows:
where
takes the value of one when the output has repeatedly produced the exact key (i.e., when
or
). The value of
is zero if
when it fails to emulate similar responses for the same challenge sets.
2.1.3. Correctness
The reliability of a PUF is also exposed to internal factors that could impact the accuracy of the responses from a given challenge set. One source of incorrect responses is due to damage that does not destroy the IC entirely, but rather influence the permanent variations in the device. Aging of the examined device could potentially affect identification degradation after lengthy use [
16]. The correctness of the device is measured using the fractional Hamming distance as follows [
13]:
where
is the correct
i-bit response that is determined by the majority voting from the set of all challenges, while
is the response to the same bit challenge through
T tests. Thus, correctness is calculated as the sum of the normalized Hamming distance between the “correct” bit and the response of that specific challenge when generated multiple times.
2.1.4. Diffuseness
Each challenge set in a PUF is expected to output unique responses that could be utilized as a secret key. One approach to examining the validity of this key is to evaluate how it is different from any other key produced by the same device. Diffuseness, introduced in [
13], is calculated using the fractional Hamming distance of all possible keys generated by the device as follows:
where
and
are the bit response of challenge set
s and
m, respectively. Since it is inevitable for any PUF design to share common bit-responses in such multi-bit settings, Hori et al. [
13] prove that the upper bound of the sum of Hamming distance for all possible key is
The highest value is 1 when reaches the upper bound, while it takes the value of 0 if all of the generated keys from different challenge sets are identical.
2.1.5. Uniqueness
All of the above metrics are concerned about the nature of challenge–response pairs within the same device. The metric that measures to what extent CRP sets’ behavior vary among different devices is called Uniqueness. It evaluates how different the response of one PUF device from the response generated from another device when the same design implemented and the same set of challenges is given to both devices. Since the response on any PUF design relies on the inherited delay variation, it is crucial to examine if responses from a specific challenge set can be replicated using a different device. Maiti et al. [
14] show one way to measure uniqueness using the hamming distance between responses generated from different devices from a given challenge as follows:
where
n and
m are two different PUF devices, and
and
are the
i-bit responses generated from a given challenge. The uniqueness of all challenges is averaged out to obtain the uniqueness of the response uniqueness of all experimented tests set. Hori et al. [
13] proposed a similar approach, but they differ in the normalization value where the ideal value is one instead of one half as follows:
and the upper bound is similar to the one shown in randomness.
3. Experimental Setup
3.1. FPGA Hardware and Utilized Software in the Experiments
Our hardware implementation procedures follow [
10] to build in XOR PUF and DAPUF instances. Three Artix-7 FPGA devices have been used to implement both designs which we shall refer to A, B, and C. We used VHDL on Xilinx Vivado, edition 15.4 HL, that is capable of describing signal variations in ICs and synthesize HDL designs. Xilinx SDK is utilized to capture the input/output functioning using C language.
Core voltage in Artix-7 is set to 1V with 30 mv tolerance and the junction temperature is between 0–85 °C. The reported ambient temperature is around 26 °C during all performed experiments. When generating the CRPs, fluctuation in power voltage and variations in the temperature are reflected in the stability metric [
14]. In our experiments, correctness and steadiness metrics evaluate how consistent the responses generated from any design are under these conditions. In case of placing 2-1 DAPUFs on the circuit, the first stream gates’ placement starts from X1Y100 to X32Y100 and X1Y101 to X32Y101 and connected to an arbiter D-FF, and the second stream starts from X1Y102 to X32Y102 and X1Y103 to X32Y103 connected to arbiter D-FF. The top and bottom MUXes of each stage are placed on the same slice. The same procedure is followed to place all designs. The number of gates allocated in each implemented designs on FPGA is calculated as follows:
The number of components and arbiters differ in each of the implemented designs, while the number of XOR gate is equal to 1 in all designs. This shows that the cost of implementing DAPUFs is higher than their counterparts from XOR PUFs.
3.2. CRP Generation
We implement all proposed designs of DAPUF (2-1, 3-1, and 4-1 DAPUF) and their counterparts from XOR PUF (2, 3, and 4 XOR PUF). Each design is implemented on three FPGA boards which results in a total of 18 implementations, and the challenge length is 64-bit in all tested designs. Each extracted CRP could take one path ranging from 0– where n is the number of challenge bits in the implementation.
Several papers have evaluated the performance of PUF designs using sets of CRPs ranging from 128 as in [
13,
14,
18,
19] to 32,768 CRPs in [
21]. Although increasing the number of accumulated CRPs does not imply a better approximation to the true distribution, Ref. [
23] shows that the model accuracy increases when more CRPs are used. Considering the trade-offs between enhancing model accuracy and the cost brought by increasing the number of CRPs, we limited the number of CRPs generated in our performance evaluations to 60,000 CRPs with 32 iterations.
Each of the challenge sets is utilized to examine randomness and diffuseness of each design. To evaluate the steadiness of each design, each challenge set is repeated instantly 32 times. The correctness of all designs is evaluated when the whole experiment on each device and for each design is iterated 32 times. We evaluate uniqueness by examining how different the responses of 60,000 CRPs from each design are when generated on each device. This procedure will capture factors that may have some impacts on the reported results such as heat on the device or the frequency of power voltage. The reported results for each performance evaluation metric of each design is the average from all of the three FPGA boards.
Generating the required CRPs for performance experiments in all XOR PUFs and DAPUF designs took an approximately similar time. Each design on each device takes around 128 min, and the total time to generate all required CRPs is 38.4 h. These CRPs are used to evaluate the performance of each design on different devices using five performance metrics, and evaluation of each design takes approximately 9 h, which brings the total time required to examine all devices to 54 h.
3.3. Machine Learning Attacks
Our work also covers the security of all DAPUF instances and relevant XOR PUF designs. To compare our security analysis with the literature, the challenge length is set to 64-bits in all designs. We use neural networks that utilize Scikit-learn [
28] in our modeling attack with Multi-Layer Perceptron (MLP) that is capable of handling nonlinearity in both designs. Our machine learning attack model employs Rectified Linear Unit (ReLU) to learn the parameters of each PUF design. The Adaptive Moment Estimation (ADAM) optimizer [
29] enabled us to achieve high accuracies and successfully model all examined designs.
It is preferable to find a globally optimal solution using the smallest number of parameters, and that model with higher degree of freedoms is expected to perform worse than smaller networks that are trained to zero error [
30]. XOR PUFs and DAPUF designs could be modeled using NN based attack without the need to employ more sophisticated deep learning techniques. In our modeling attack, we found that three hidden layers derive the best accuracy for all implemented designs. The number of neurons employed varies based on the complexity of the examined design, the number of components implemented, and the number of CRPs used. In implementations with large CRPs, the number of neurons in each layer is
for XOR PUF designs [
7] and
for DAPUF designs where
n is the number of streams in each design. When small sets of CRPs are used, the number of neurons should be decreased to model DAPUF designs with higher accuracy rates. A summary of MLP parameters is listed in
Table 2.
We generated a variety of CRPs sets to examine the security of DAPUFs and XOR PUFs. Our approach is to examine the resilience of each evaluated design when different sets of CRPs are attainable. In all experiments, each CRPs set is split into 85% training set and 15% test set. The breakability of each design is tested using 100 k, 500 k, and one million generated CRPs which allow us to demonstrate the resilience of each examined design. While we are able to make a breakthrough in most of the proposed designs by utilizing only 100 k, the number of CRPs required increases with the number of components embedded in the design.
Since the security of the implemented designs is influenced by the inherited properties of each FPGA board, our experiments use CRPs generated from three FPGA boards. The reported results of all implemented designs are based on the average of 10 trials using more than 28 million CRPs.
5. Conclusions
This paper evaluates the performance and the security of all proposed designs of DAPUF, namely 2-1, 3-1, 4-1 DAPUF, and their counterparts from XOR PUF which are 2, 3, 4 XOR PUF. We generated different sets of real CRP to analyze the performance of each design using five evaluation metrics proposed in [
13,
14]. Our experiments show that DAPUF designs have better uniqueness, but this came at the cost in the stability of the responses generated from given challenge sets. XOR PUFs are more stable but suffer from low uniqueness since over 90% of responses generated in one device could be replicated on another device. Overall, increasing the number of components in any design has a positive impact on both diffusion and uniqueness, while it has an adverse effect on both steadiness and correctness of the responses generated from DAPUF designs.
Our analysis also covers the security of both DAPUF designs and their counterparts from XOR PUFs. Results of the machine learning attack shows that all XOR PUF designs and 2-1 DAPUF and 3-1 DAPUF designs can be impersonated when only 100k CRPs are attainable. Ref. [
12] 4-1 DAPUF is a sophisticated design that has not been impersonated at the time of writing this paper even when 17 million CRPs are used. We are able to successfully predict the response of 4-1 DAPUF design with 81% accuracy rate using 1 million CRPs.
Our results contradict with [
11] that 3-1 DAPUF is the preferred design and we show that there are no strict preferences toward any DAPUF over other designs. Experimental results in [
11] show that the 3-1 DAPUF design has a better randomness and steadiness than 4-1 DAPUF while uniqueness is almost ideal in both designs, in which they conclude that 3-1 DAPUF is the preferred design. However, our experiments show that that 4-1 DAPUF is more secure and has better uniqueness than 3-1 DAPUF, while the responses of 3-1 DAPUF are more stable. Finally, stability of the responses is essential to the applicability of a PUF, and responses from XOR PUFs have been shown to be more stable than DAPUF designs.