Reliable Surrogate Modeling of Antenna Input Characteristics by Means of Domain Confinement and Principal Components
Abstract
:1. Introduction
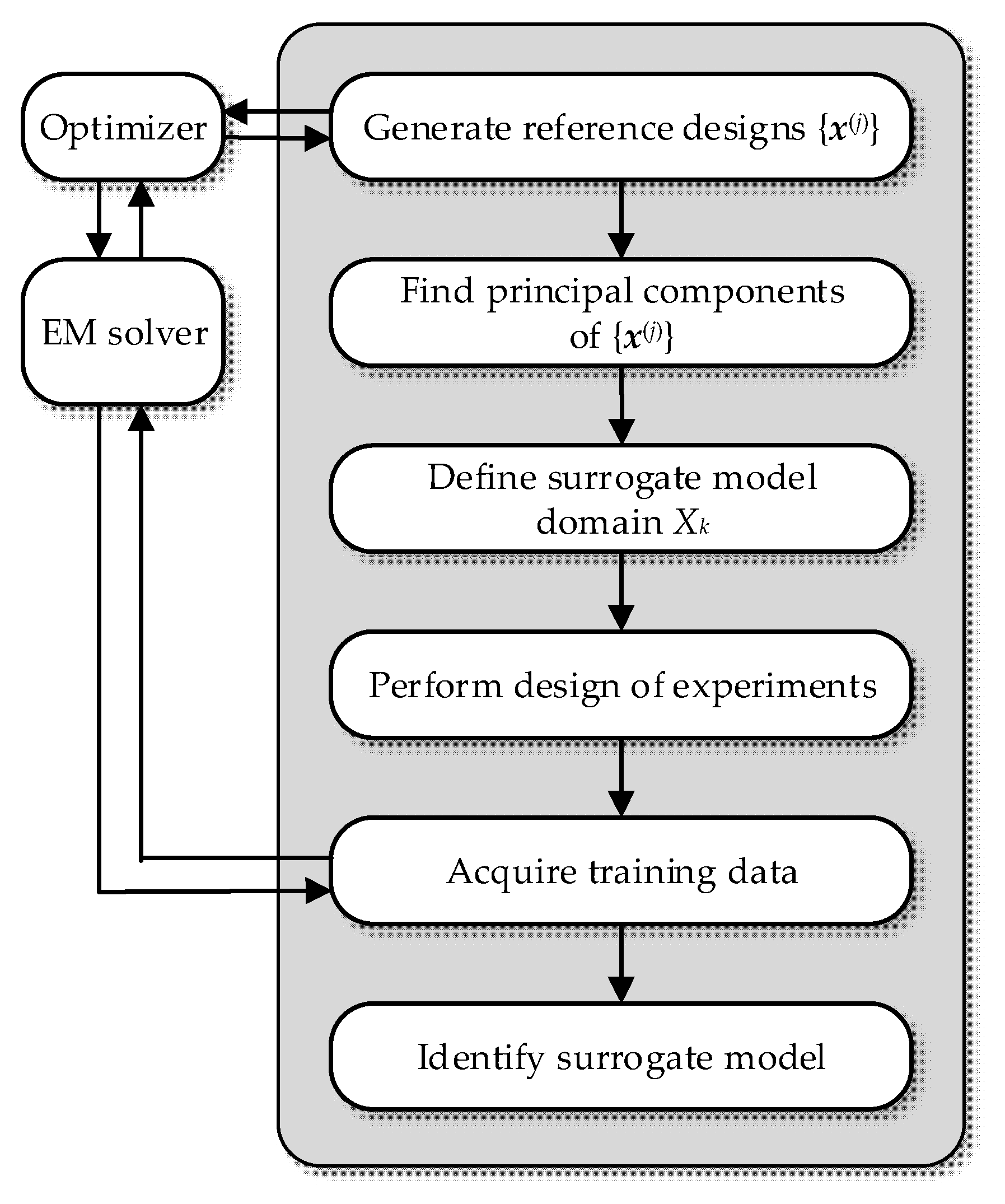
2. Surrogate Modeling in Constrained Domains Using Principal Component Analysis
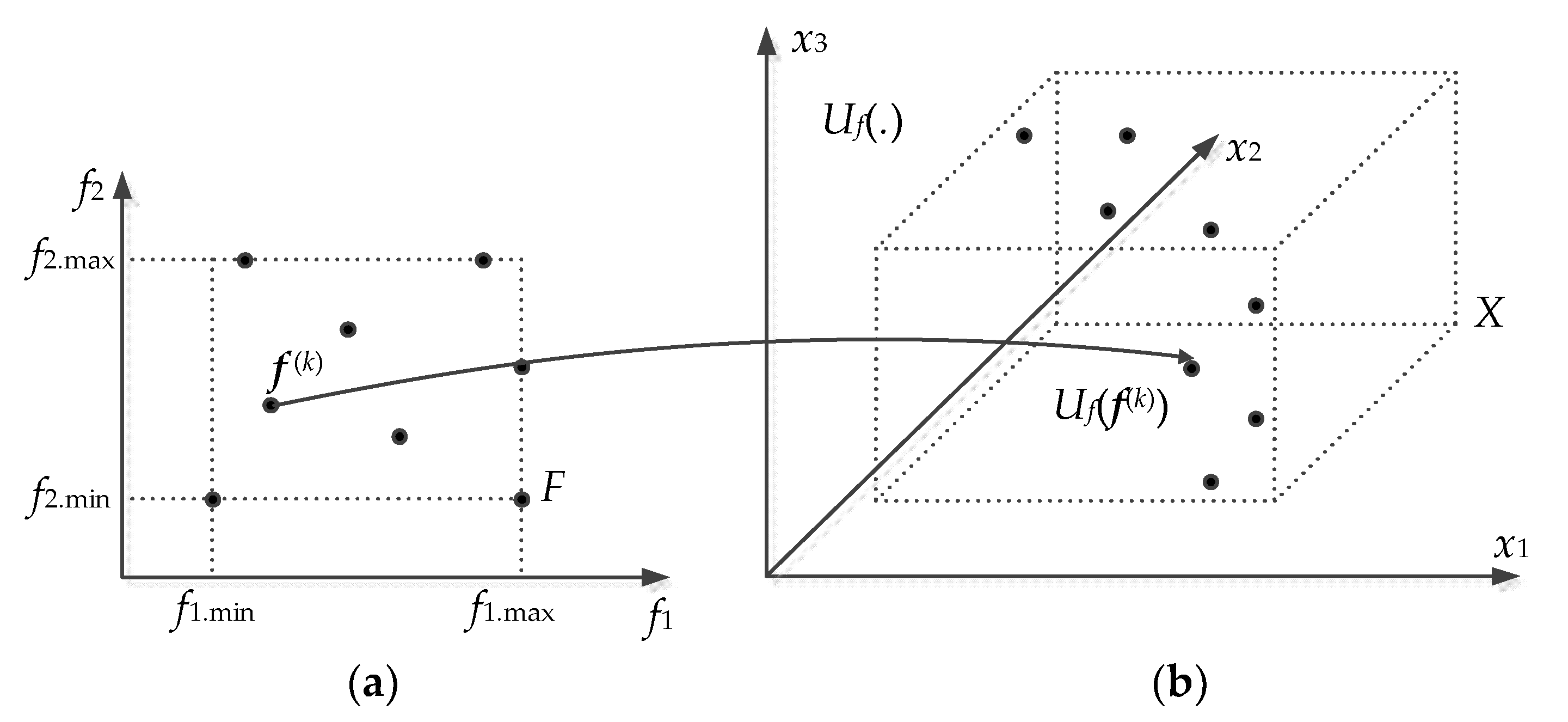
2.1. Fundamental Components of the Modeling Process: Parameter and Objective Spaces
2.2. Pre-Optimized Data and Principal Component Analysis
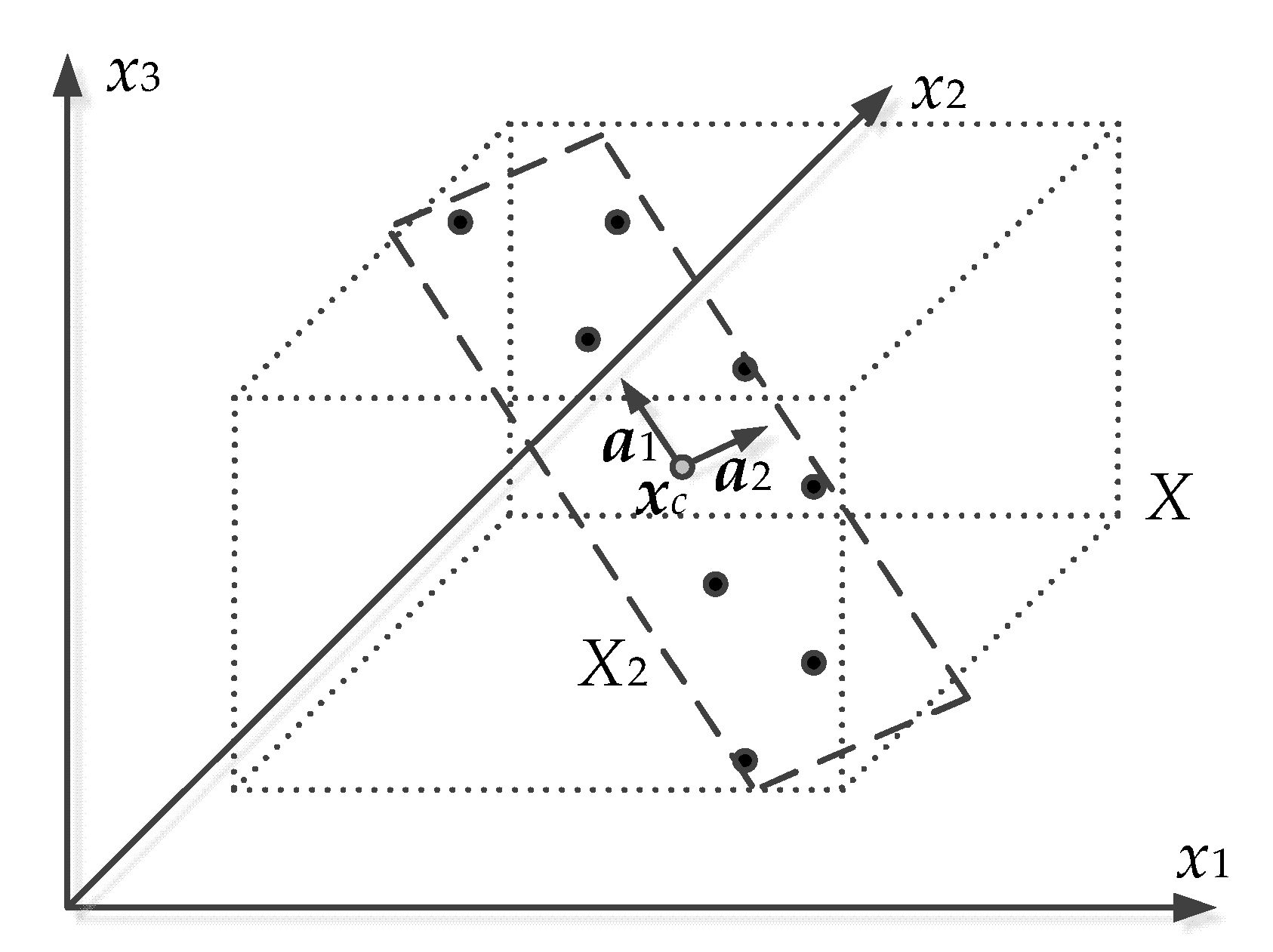
2.3. Defining the Surrogate Model Domain
2.4. Sampling Procedure and Model Identification
2.5. Design Applications: Optimizing the Surrogate
3. Validation and Benchmarking
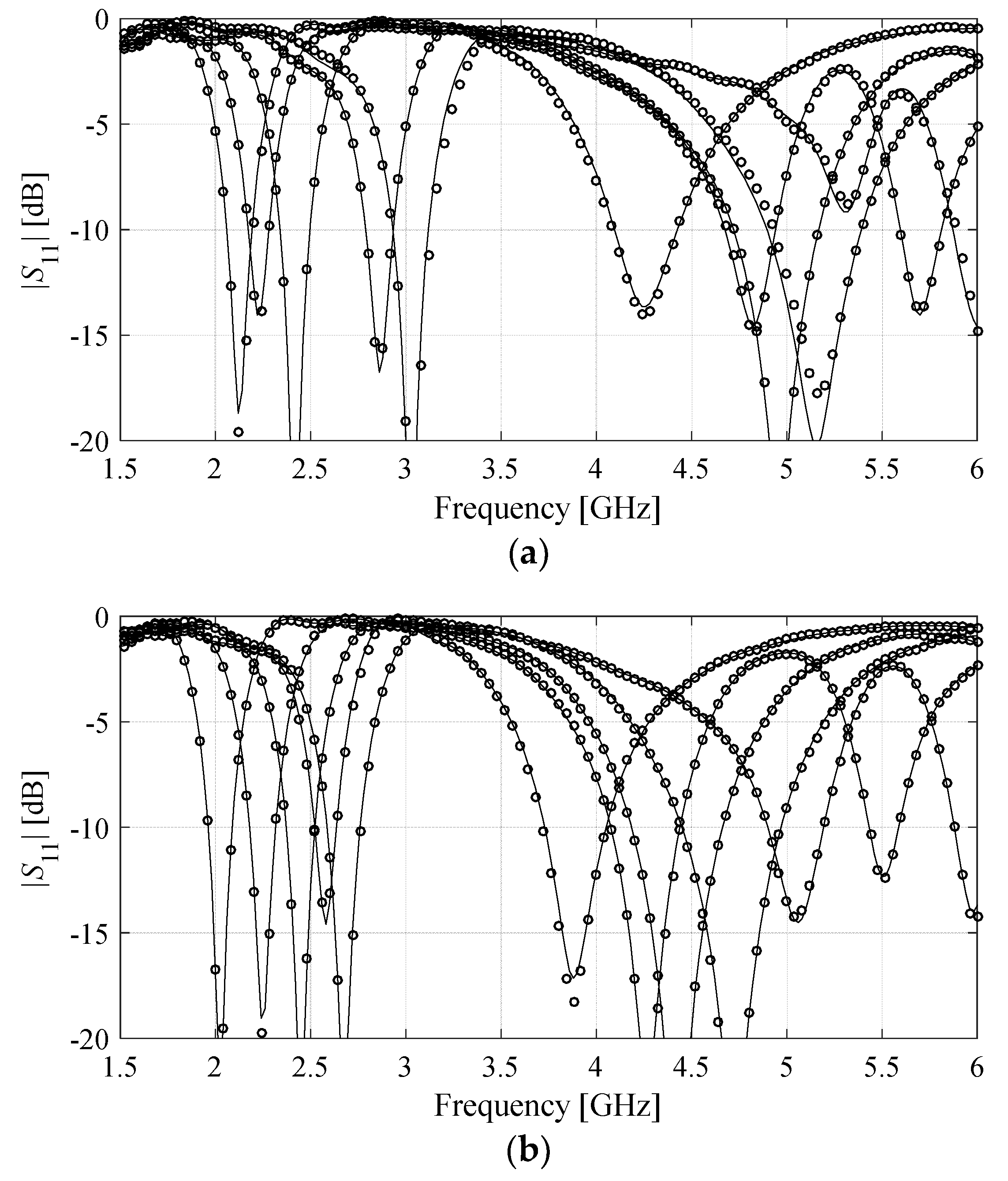
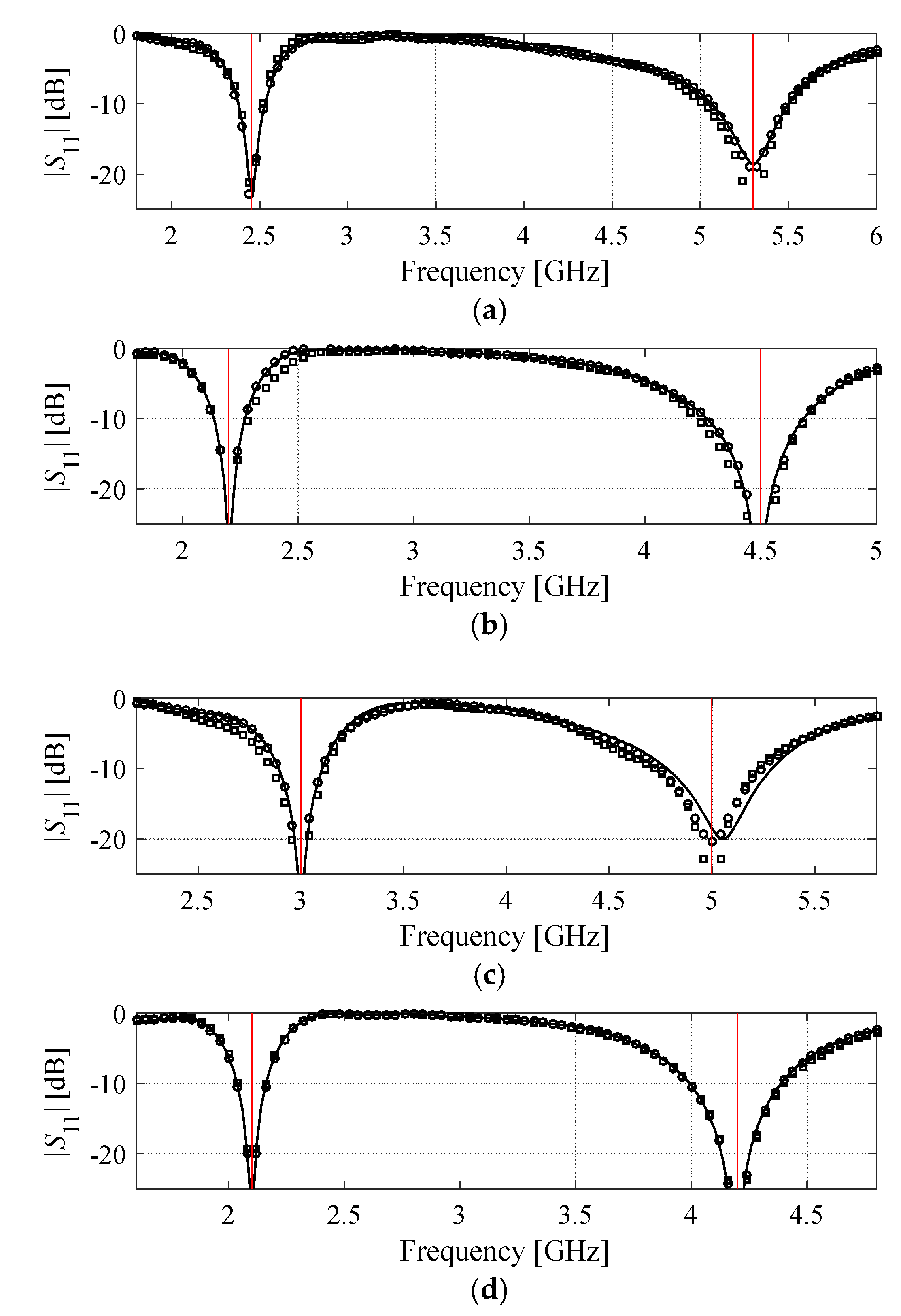
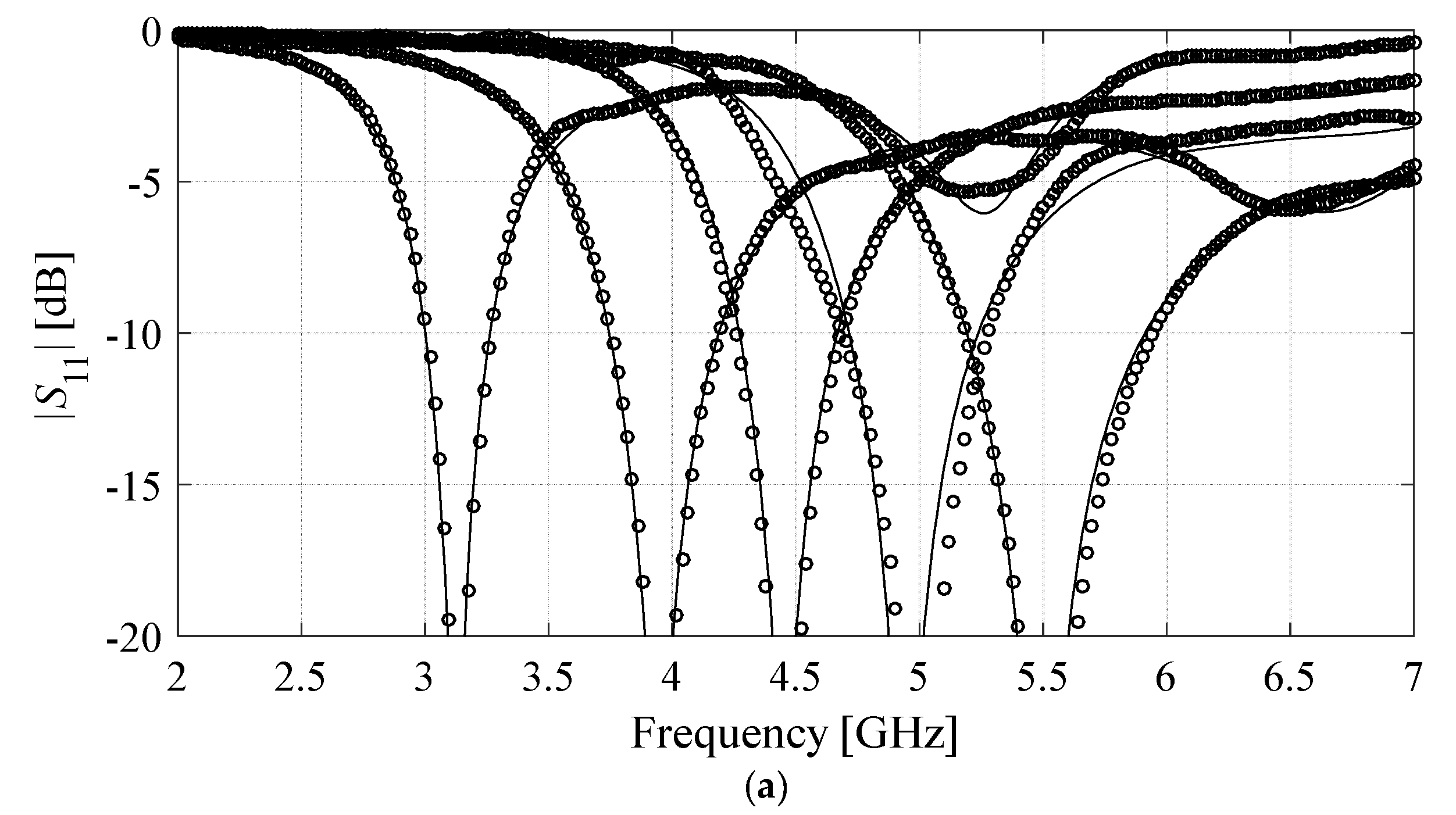
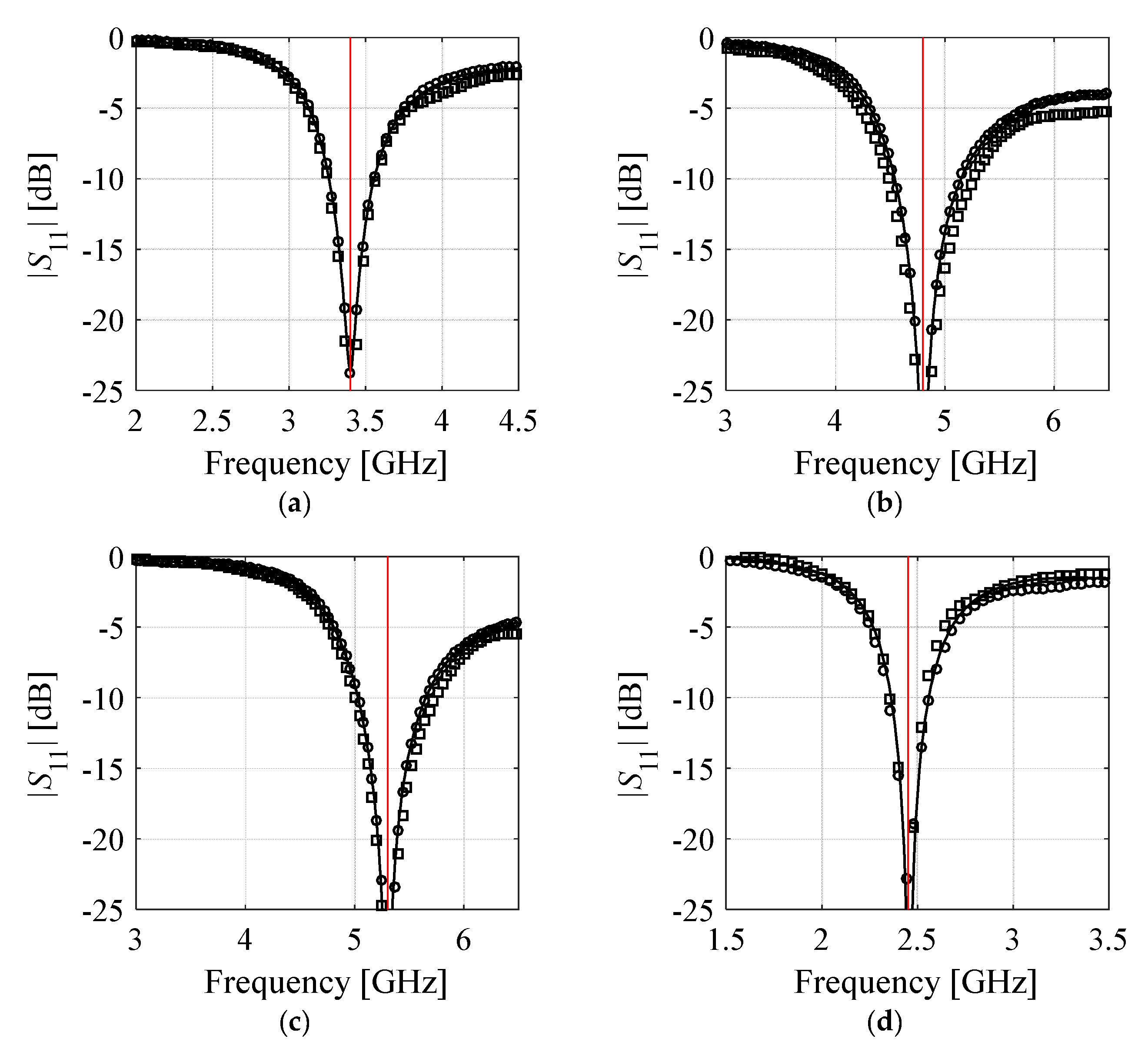
3.1. Example 1: Dual-Band Dipole Antenna
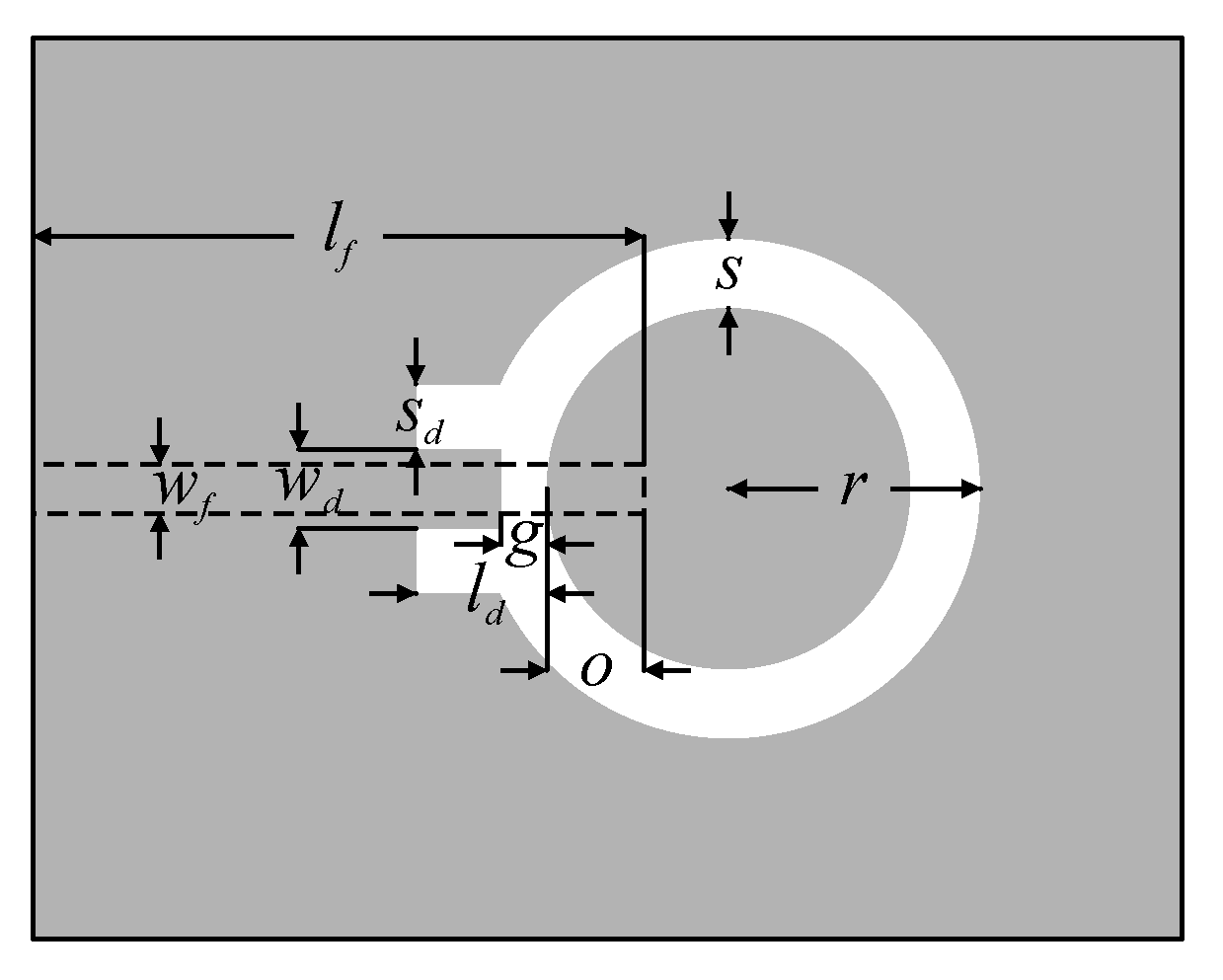
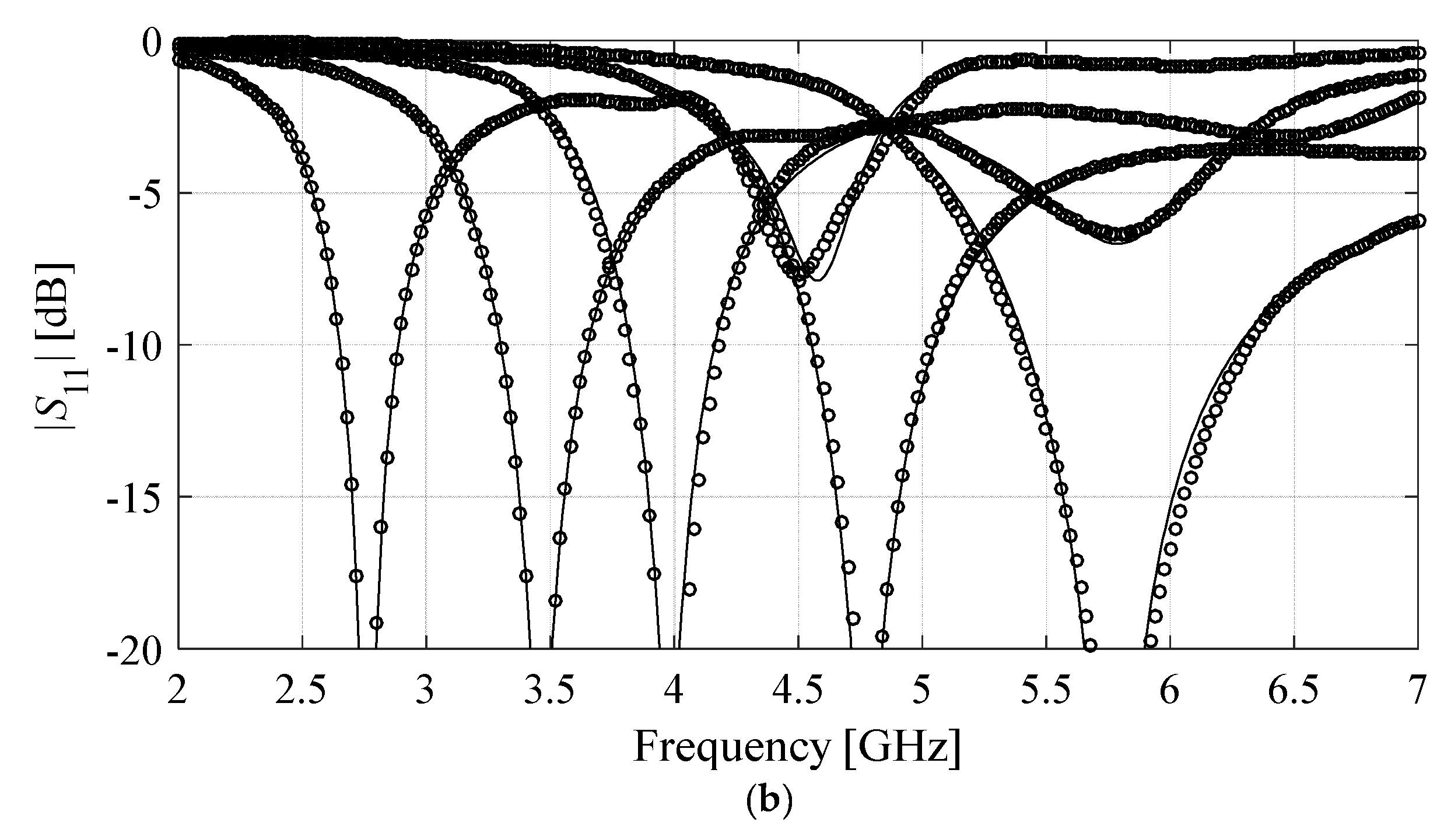
3.2. Example 2: Ring Slot Antenna
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guo, J.; Cui, L.; Li, C.; Sun, B. Side-edge frame printed eight-port dual-band antenna array for 5G smartphone applications. IEEE Trans. Ant. Prop. 2018, 66, 7412–7417. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Ren, A.; Wang, H.; Sim, C.Y.D. TCM-based hepta-band antenna with small clearance for metal-rimmed phone applications. IEEE Trans. Ant. Wirel. Prop. Lett. 2018, 18, 717–721. [Google Scholar] [CrossRef]
- Liao, W.J.; Hsieh, C.Y.; Dai, B.Y.; Hsiao, B.R. Inverted-F/slot integrated dual-band four-antenna system for WLAN access point. IEEE Ant. Wirel. Prop. Lett. 2015, 14, 847–850. [Google Scholar] [CrossRef]
- Kumar, A.; Ansari, A.Q.; Kanaujia, B.; Kishor, J.; Kumar, S. An ultra-compact two-port UWB-MIMO antenna with dual band-notched characteristics. AEU Int. J. Electr. Comm. 2019, 114, 152997. [Google Scholar] [CrossRef]
- Majidzadeh, M. Linear and circular polarization radiation through a modified 270° square ring-fed 2×2 array antenna. AEU Int. J. Electr. Comm. 2019, 98, 164–173. [Google Scholar] [CrossRef]
- Wu, J.; Sarabandi, K. Compact omnidirectional circularly polarized antenna. IEEE Trans. Ant. Prop. 2017, 65, 1550–1557. [Google Scholar] [CrossRef]
- Kurgan, P.; Koziel, S. Selection of circuit geometry for miniaturized microwave components based on concurrent optimization of performance and layout area. AEU Int. J. Electr. Comm. 2019, 108, 287–294. [Google Scholar] [CrossRef]
- Lakbakhsh, A.; Afzal, M.U.; Esselle, K.P. Multiobjective particle swarm optimization to design a time-delay equalizer metasurface for an electromagnetic band-gap resonator antenna. IEEE Ant. Wirel. Prop. Lett. 2017, 16, 915. [Google Scholar]
- Zhang, J.; Zhang, C.; Feng, F.; Zhang, W.; Ma, J.; Zhang, Q.J. Polynomial chaos-based approach to yield-driven EM optimization. IEEE Trans. Microw. Theory Tech. 2018, 66, 3186–3199. [Google Scholar] [CrossRef]
- Hassan, A.S.O.; Abdel-Malek, H.L.; Mohamed, A.S.A.; Abuelfadl, T.M.; Elqenawy, A.E. Statistical design centering of RF cavity linear accelerator via non-derivative trust region optimization. In Proceedings of the 2015 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO), Ottawa, ON, Canada, 11–14 August 2015; pp. 1–3. [Google Scholar]
- Kouassi, A.; Nguyen-Trong, N.; Kaufmann, T.; Lallechere, S.; Bonnet, P.; Fumeaux, C. Reliability-aware optimization of a wideband antenna. IEEE Trans. Ant. Prop. 2016, 64, 450–460. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Darvish, A.; Ebrahimzadeh, A. Improved fruit-fly optimization algorithm and its applications in antenna array synthesis. IEEE Trans. Ant. Prop. 2018, 66, 1756–1766. [Google Scholar] [CrossRef]
- Dong, J.; Li, Q.; Deng, L. Fast multi-objective optimization of multi-parameter antenna structures based on improved MOEA/D with surrogate-assisted model. AEU Int. J. Electr. Comm. 2017, 72, 192–199. [Google Scholar] [CrossRef] [Green Version]
- Koziel, S.; Mosler, F.; Reitzinger, S.; Thoma, P. Robust microwave design optimization using adjoint sensitivity and trust regions. Int. J. RF Microw. CAE 2012, 22, 10–19. [Google Scholar] [CrossRef]
- Wang, J.; Yang, X.S.; Wang, B.Z. Efficient gradient-based optimization of pixel antenna with large-scale connections. IET Microw. Ant. Prop. 2018, 12, 385–389. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Expedited optimization of antenna input characteristics with adaptive Broyden updates. Eng. Comp. 2020, 37, 851–862. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Variable-fidelity simulation models and sparse gradient updates for cost-efficient optimization of compact antenna input characteristics. Sensors 2019, 19, 1806. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhao, Z.; Wang, J.; Dan, G. Antenna array beam pattern synthesis based on trust region method. In Proceedings of the 2014 IEEE 17th International Conference on Computational Science and Engineering, Chengdu, China, 19–21 December 2014; pp. 859–862. [Google Scholar]
- Bandler, J.W.; Mohamed, A.S.; Bakr, M.H. TLM-based modeling and design exploiting space mapping. IEEE Trans. Microw. Theory Techn. 2005, 53, 2801–2811. [Google Scholar] [CrossRef] [Green Version]
- Tu, S.; Cheng, Q.S.; Zhang, Y.; Bandler, J.W.; Nikolova, N.K. Space mapping optimization of handset antennas exploiting thin-wire models. IEEE Trans. Ant. Propag. 2013, 61, 3797–3807. [Google Scholar] [CrossRef]
- Koziel, S.; Leifsson, L. Simulation-Driven Design by Knowledge-Based Response Correction Techniques; Springer: New York, NY, USA, 2016. [Google Scholar]
- Koziel, S.; Unnsteinsson, S.D. Expedited design closure of antennas by means of trust-region-based adaptive response scaling. IEEE Ant. Wirel. Prop. Lett. 2018, 17, 1099–1103. [Google Scholar] [CrossRef]
- Su, Y.; Lin, J.; Fan, Z.; Chen, R. Shaping optimization of double reflector antenna based on manifold mapping. In Proceedings of the 2017 International Applied Computational Electromagnetics Society Symposium (ACES), Firenze, Italy, 1–4 August 2017. [Google Scholar]
- Easum, J.A.; Nagar, J.; Werner, D.H. Multi-objective surrogate-assisted optimization applied to patch antenna design. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; pp. 339–340. [Google Scholar]
- Hassan, A.K.; Etman, A.S.; Soliman, E.A. Optimization of a novel nano antenna with two radiation modes using kriging surrogate models. IEEE Photonics J. 2018, 10, 4800807. [Google Scholar] [CrossRef]
- de Villiers, D.I.L.; Couckuyt, I.; Dhaene, T. Multi-objective optimization of reflector antennas using kriging and probability of improvement. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; pp. 985–986. [Google Scholar]
- Chen, Y.; Tian, Y.B.; Qiang, Z.; Xu, L. Optimisation of reflection coefficient of microstrip antennas based on KBNN exploiting GPR model. IET Microw. Ant. Prop. 2018, 12, 602–606. [Google Scholar] [CrossRef]
- Koziel, S. Fast simulation-driven antenna design using response-feature surrogates. Int. J. RF Microw. CAE 2015, 25, 394–402. [Google Scholar] [CrossRef]
- Simpson, T.W.; Pelplinski, J.D.; Koch, P.N.; Allen, J.K. Metamodels for computer-based engineering design: Survey and recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef] [Green Version]
- Chávez-Hurtado, J.L.; Rayas-Sánchez, J.E. Polynomial-based surrogate modeling of RF and microwave circuits in frequency domain exploiting the multinomial theorem. IEEE Trans. Microw. Theory Tech. 2016, 64, 4371–4381. [Google Scholar] [CrossRef] [Green Version]
- Jacobs, J.P. Characterization by Gaussian processes of finite substrate size effects on gain patterns of microstrip antennas. IET Microw. Ant. Prop. 2016, 10, 1189–1195. [Google Scholar] [CrossRef] [Green Version]
- Kabir, H.; Wang, Y.; Yu, M.; Zhang, Q.J. Neural network inverse modeling and applications to microwave filter design. IEEE Trans. Microw. Theory Tech. 2008, 56, 867–879. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Leary, S.; Bhaskar, A.; Keane, A. Optimal orthogonal-array-based latin hypercubes. J. Appl. Stat. 2003, 30, 585–598. [Google Scholar] [CrossRef] [Green Version]
- Santner, T.J.; Williams, B.J.; Notz, W.I. Space-filling designs for computer experiments. In The Design and Analysis of Computer Experiments; Springer Series in Statistics; Springer: New York, NY, USA, 2003; pp. 121–161. [Google Scholar]
- Crombecq, K.; Laermans, E.; Dhaene, T. Efficient space-filling and non-collapsing sequential design strategies for simulation-based modeling. Eur. J. Oper. Res. 2011, 214, 683–696. [Google Scholar] [CrossRef] [Green Version]
- Koziel, S. Low-cost data-driven surrogate modeling of antenna structures by constrained sampling. IEEE Ant. Wirel. Propag. Lett. 2017, 16, 461–464. [Google Scholar] [CrossRef]
- Koziel, S.; Sigurdsson, A.T. Triangulation-based constrained surrogate modeling of antennas. IEEE Trans. Ant. Prop. 2017, 66, 4170–4179. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Performance-based nested surrogate modeling of antenna input characteristics. IEEE Trans. Ant. Prop. 2019, 67, 2904–2912. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Beachkofski, B.; Grandhi, R. Improved Distributed Hypercube Sampling; Paper AIAA 2002–1274; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2002. [Google Scholar]
- Chen, Y.-C.; Chen, S.-Y.; Hsu, P. Dual-band slot dipole antenna fed by a coplanar waveguide. In Proceedings of the 2006 IEEE Antennas and Propagation Society International Symposium, Albuquerque, NM, USA, 9–14 July 2006; pp. 3589–3592. [Google Scholar]
- Queipo, N.V.; Haftka, R.T.; Shyy, W.; Goel, T.; Vaidynathan, R.; Tucker, P.K. Surrogate based analysis and optimization. Prog. Aerosp. Sci. 2005, 41, 1–28. [Google Scholar] [CrossRef] [Green Version]


| Number of Training Samples | Relative RMS Error | ||||||
|---|---|---|---|---|---|---|---|
| Conventional Models | Nested Kriging Model [37] | Proposed Model (Domain Confinement with PCA) | |||||
| Kriging | RBF | k = 2 | k = 3 | k = 4 | k = 6 | ||
| 50 | 21.7% | 24.9% | 9.9% | 2.9% | 8.6% | 11.7% | 15.9% |
| 100 | 17.3% | 19.8% | 6.4% | 1.5% | 5.2% | 8.6% | 11.0% |
| 200 | 12.6% | 14.3% | 4.4% | 1.4% | 2.9% | 5.8% | 8.1% |
| 400 | 9.3% | 10.5% | 3.8% | 1.2% | 1.9% | 4.3% | 5.8% |
| 800 | 7.2% | 8.7% | 3.4% | 1.1% | 1.5% | 3.0% | 4.6% |
| Target Operating Conditions | Geometry Parameter Values [mm] | ||||||
|---|---|---|---|---|---|---|---|
| f1 [GHz] | f2 [GHz] | l1 | l2 | l3 | w1 | w2 | w3 |
| 2.45 | 5.30 | 33.1 | 8.76 | 17.9 | 0.31 | 2.70 | 1.98 |
| 2.20 | 4.50 | 34.2 | 5.76 | 18.3 | 0.47 | 4.21 | 1.75 |
| 3.00 | 5.00 | 29.7 | 11.10 | 20.3 | 0.33 | 2.47 | 1.16 |
| 2.10 | 4.20 | 35.4 | 5.30 | 19.0 | 0.54 | 4.83 | 1.68 |
| Number of Training Samples | Relative RMS Error | ||||||
|---|---|---|---|---|---|---|---|
| Conventional Models | Nested Kriging Model [37] | Proposed Model (Domain Confinement with PCA) | |||||
| Kriging | RBF | k = 2 | k = 3 | k = 4 | k = 6 | ||
| 50 | 56.9% | 61.0% | 19.4% | 5.7% | 18.0% | 26.9% | 29.6% |
| 100 | 50.8% | 53.2% | 12.9% | 2.2% | 9.4% | 15.9% | 23.4% |
| 200 | 35.8% | 37.9% | 7.7% | 1.9% | 5.5% | 9.8% | 14.3% |
| 400 | 31.5% | 34.1% | 5.1% | 1.3% | 2.7% | 5.4% | 9.6% |
| 800 | 25.6% | 27.2% | 3.7% | 0.8% | 2.1% | 3.9% | 7.3% |
| Target Operating Conditions | Geometry Parameter Values [mm] | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| f0 [GHz] | ε | lf | ld | wd | r | s | sd | o | g |
| 3.4 | 3.5 | 25.2 | 5.82 | 1.25 | 11.6 | 4.81 | 3.04 | 4.74 | 1.08 |
| 4.8 | 2.2 | 22.6 | 5.12 | 0.58 | 9.66 | 4.01 | 4.08 | 5.17 | 1.46 |
| 5.3 | 3.5 | 22.9 | 4.59 | 0.45 | 8.48 | 3.57 | 4.61 | 5.14 | 1.76 |
| 2.45 | 4.3 | 27.9 | 6.82 | 2.02 | 14.23 | 5.87 | 1.67 | 4.29 | 0.53 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pietrenko-Dabrowska, A.; Koziel, S. Reliable Surrogate Modeling of Antenna Input Characteristics by Means of Domain Confinement and Principal Components. Electronics 2020, 9, 877. https://doi.org/10.3390/electronics9050877
Pietrenko-Dabrowska A, Koziel S. Reliable Surrogate Modeling of Antenna Input Characteristics by Means of Domain Confinement and Principal Components. Electronics. 2020; 9(5):877. https://doi.org/10.3390/electronics9050877
Chicago/Turabian StylePietrenko-Dabrowska, Anna, and Slawomir Koziel. 2020. "Reliable Surrogate Modeling of Antenna Input Characteristics by Means of Domain Confinement and Principal Components" Electronics 9, no. 5: 877. https://doi.org/10.3390/electronics9050877
APA StylePietrenko-Dabrowska, A., & Koziel, S. (2020). Reliable Surrogate Modeling of Antenna Input Characteristics by Means of Domain Confinement and Principal Components. Electronics, 9(5), 877. https://doi.org/10.3390/electronics9050877






