A Non-WSSUS Channel Simulator for V2X Communication Systems
Abstract
:1. Introduction
2. Motivation and Related Work
3. Multicarrier Data Frames of the DSRC and LTE-V2X Standards
3.1. General Overview of IEEE 802.11p and LTE-V2X Specifications
3.2. Mathematical Model of the Received Signal in Multicarrier Systems
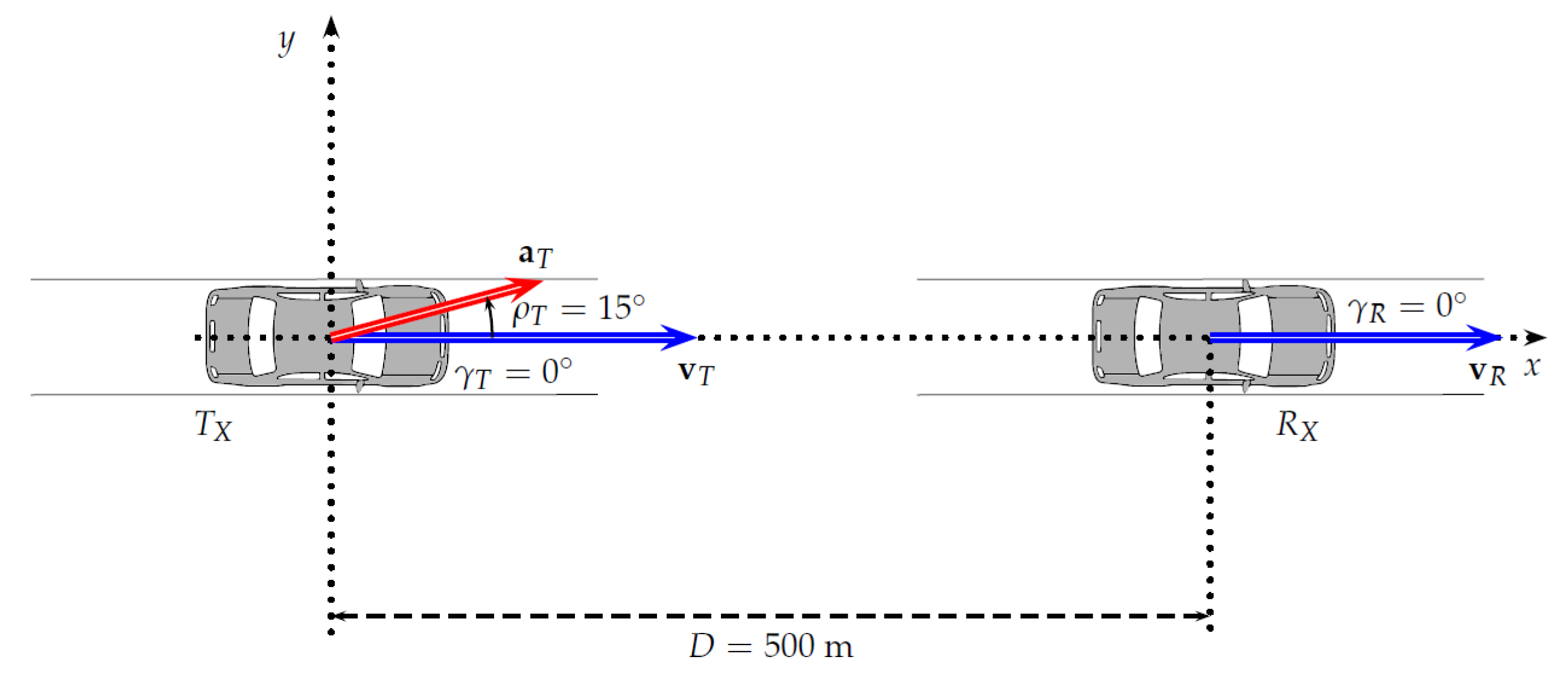
4. Reference Channel Model
4.1. Description of the Reference Propagation Environment
4.2. Mathematical Model of the Channel Transfer Function
5. The Proposed Vehicular Channel Simulator
6. Simulation Examples
6.1. Channel Estimation Techniques for the IEEE 802.11p Standard
6.1.1. Least Squares Estimator
6.1.2. Spectral Temporal Averaging Technique
6.2. Simulation Setup
- Scenario I: Intersection. The MSs move in such a way that they approach each other with angles and , and both and acceleration components point in the same direction of their corresponding initial speeds (i.e., and ). The motion of the MSs resembles a safety scenario where vehicles circulate on two streets that intersect at one point. This scenario is depicted in Figure 5.
- Scenario II: Overtaking maneuver. A vehicle accelerates and changes its direction of motion aiming to overtake the one in front of it. For this scenario, we assume that both vehicles start moving in the same direction , but the transmitting station has an acceleration component with angle , which modifies its trajectory over time. In the case of the receiving vehicle, this one has no acceleration component, i.e., . Figure 6 illustrates this scenario where the two vehicles start on the same lane.
- Scenario III: Opposite lanes. Two vehicles are approaching each other on opposite parallel lanes of a highway environment. This scenario is shown in Figure 7, where we consider the angles and to describe the motion of the vehicles in opposite directions over parallel lanes.
6.3. Results of Changes of the Initial Speed
6.4. Results of Changes of the Frame Length
6.5. Results over Non-Isotropic Scattering
6.6. Results of the STA Modification Proposal
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| 3GPP | Third-Generation Partnership Project |
| 5G | fifth-generation |
| AOA | angle of arrival |
| AOD | angle of departure |
| AWGN | additive white Gaussian noise |
| BER | bit error rate |
| CIR | channel impulse response |
| C-V2X | cellular-based V2X |
| DMRS | demodulation reference signal |
| DSRC | dedicated short-range communications |
| D2D | device-to-device |
| F2M | fixed-to-mobile |
| GI | guard interval |
| IEEE | Institute of Electrical and Electronics Engineers |
| i.i.d. | independent and identically distributed |
| IO | interfering object |
| ITS | intelligent transportation systems |
| LS | least squares |
| LTE | Long-Term Evolution |
| LTE-V2X | LTE-based V2X |
| LTS | long training symbols |
| MSs | mobile stations |
| OFDM | orthogonal frequency division multiplexing |
| RB | resource blocks |
| SC-FDMA | single carrier frequency division multiple access |
| SOC | sum-of-cisoids |
| STA | spectral temporal averaging |
| STS | short training symbols |
| TF | time and frequency |
| V2X | vehicle-to-everything |
| V2I | vehicle-to-infrastructure |
| V2N | vehicle-to-network |
| V2P | vehicle-to-pedestrian |
| V2V | vehicle-to-vehicle |
| WLAN | wireless local area network |
| WSS | wide sense stationary |
| WSSUS | wide sense stationary uncorrelated scattering |
References
- Dimitrakopoulos, G.; Demestichas, P. Intelligent Transportation Systems: Systems Based on Cognitive Networking Principles and Management Functionality. IEEE Veh. Technol. Mag. 2010, 5, 77–84. [Google Scholar] [CrossRef]
- Aoyagi, S.; Le, Y.; Shimizu, T.; Takahashi, K. Mobile Application to Provide Traffic Congestion Estimates and Tourism Spots to Promote Additional Stopovers. Future Internet 2020, 12, 83. [Google Scholar] [CrossRef]
- Papadimitratos, P.; Fortelle, A.L.; Evenssen, K.; Brignolo, R.; Cosenza, S. Vehicular Communication Systems: Enabling Technologies, Applications, and Future Outlook on Intelligent Transportation. IEEE Commun. Mag. 2009, 47, 84–95. [Google Scholar] [CrossRef] [Green Version]
- Kenney, J.B. Dedicated Short-Range Communications (DSRC) Standards in the United States. Proc. IEEE 2011, 99, 1162–1182. [Google Scholar] [CrossRef]
- Karagiannis, G.; Altintas, O.; Ekici, E.; Heijenk, G.; Jarupan, B.; Lin, K.; Weil, T. Vehicular Networking: A Survey and Tutorial on Requirements, Architectures, Challenges, Standards and Solutions. IEEE Commun. Surv. Tutor. 2011, 13, 584–616. [Google Scholar] [CrossRef]
- Uzcátegui, R.A.; Acosta-Marum, G. WAVE: A Tutorial. IEEE Commun. Mag. 2009, 47, 126–133. [Google Scholar] [CrossRef]
- Seo, H.; Lee, K.; Yasukawa, S.; Peng, Y.; Sartori, P. LTE Evolution for Vehicle-to-Everything Services. IEEE Commun. Mag. 2016, 54, 22–28. [Google Scholar] [CrossRef]
- Chen, S.; Hu, J.; Shi, Y.; Peng, Y.; Fang, J.; Zhao, R.; Zhao, L. Vehicle-to-Everything (V2X) Services Supported by LTE-Based Systems and 5G. IEEE Commun. Stand. Mag. 2017, 1, 70–76. [Google Scholar] [CrossRef]
- Bazzi, A.; Cecchini, G.; Menarini, M.; Masini, B.; Zanella, A. Survey and Perspectives of Vehicular Wi-Fi versus Sidelink Cellular-V2X in the 5G Era. Future Internet 2019, 11, 122. [Google Scholar] [CrossRef] [Green Version]
- Soto, I.; Jimenez, F.; Calderon, M.; Naranjo, J.E.; Anaya, J.J. Reducing Unnecessary Alerts in Pedestrian Protection Systems Based on P2V Communications. Electronics 2019, 8, 1–26. [Google Scholar]
- IEEE. IEEE Std. 802.11-2010 (Revision of IEEE Std 802.11-1999), Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications. Amendment 6: Wireless Access in Vehicular Environments, Part 11th ed.; IEEE: New York, NY, USA, 2010; pp. 1–2793. [Google Scholar]
- Wang, X.; Mao, S.; Gong, M. An Overview of 3GPP Cellular Vehicle-to-Everything Standards. Get Mob. Mob. Comput. Commun. 2017, 21, 19–25. [Google Scholar] [CrossRef]
- Khan, U.A.; Lee, S. Three-Dimensional Resource Allocation in D2D-Based V2V Communication. Electronics 2019, 8, 1–15. [Google Scholar]
- 3rd Generation Partnership Project. 3GPP TR 21.914 V14.0.0 (2018-05) 3rd Generation Partnership Project; Technical Specification Group Services and System Aspects; Release 14 Description; Summary of Rel-14 Work Items (Release 14); 3GPP: Valbonne, France, 2018. [Google Scholar]
- 3rd Generation Partnership Project. 3GPP TR 21.916 V0.4.0 (2020-03) 3rd Generation Partnership Project; Technical Specification Group Services and System Aspects; Release 16 Description; Summary of Rel-16 Work Items (Release 16); 3GPP: Valbonne, France, 2019. [Google Scholar]
- Viriyasitavat, W.; Boban, M.; Tsai, H.; Vasilakos, A. Vehicular Communications: Survey and Challenges of Channel and Propagation Models. IEEE Veh. Technol. Mag. 2015, 10, 55–66. [Google Scholar] [CrossRef] [Green Version]
- Atallah, R.F.; Khabbaz, M.J.; Assi, C.M. Vehicular Networking: A Survey on Spectrum Access Technologies and Persisting Challenges. Elsevier Veh. Commun. 2015, 2, 125–149. [Google Scholar] [CrossRef]
- Khan, U.A.; Lee, S. Multi-Layer Problems and Solutions in VANETs: A Review. Electronics 2019, 8, 1–19. [Google Scholar]
- Bakhshi, G.; Saadat, R.; Shahtalebi, K. Modeling and Simulation of MIMO Mobile-to-Mobile Wireless Fading Channels. Int. J. Antennas Propag. 2012, 2012, 1–13. [Google Scholar] [CrossRef]
- Qiuming, Z.; Xinglin, L.; Ning, L.; Xiaomin, C. An Improved Sum-of-Sinusoids Channel Simulator Based on Brownian Motion. In Proceedings of the 2014 International Symposium on Antennas and Propagation Conference, Kaohsiung, Taiwan, 2–5 December 2014; pp. 407–408. [Google Scholar]
- Ma, Y.; Pätzold, M. A Wideband One-Ring MIMO Channel Model Under Non-Isotropic Scattering Conditions. In Proceedings of the VTC Spring 2008-IEEE Vehicular Technology Conference, Marina Bay, Singapore, 11–14 May 2008; pp. 424–429. [Google Scholar]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables and Stochastic Processes, 4th ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Bernadó, L.; Zemen, T.; Tufvesson, F.; Molisch, A.F.; Mecklenbrauker, C.F. The (In-)validity of the WSSUS Assumption in Vehicular Radio Channels. In Proceedings of the 2012 IEEE 23rd International Symposium on Personal, Indoor and Mobile Radio Communications-(PIMRC), Sydney, Australia, 9–12 September 2012; pp. 1757–1762. [Google Scholar]
- Bernadó, L.; Zemen, T.; Tufvesson, F.; Molisch, A.F.; Mecklenbrauker, C.F. Delay and Doppler Spreads of Nonstationary Vehicular Channels for Safety-Relevant Scenarios. IEEE Trans. Veh. Technol. 2014, 63, 82–93. [Google Scholar] [CrossRef] [Green Version]
- Mecklenbrauker, C.; Molisch, A.; Karedal, J.; Tufvesson, F.; Paier, A.; Bernardo, L.; Zemen, T.; Klemp, O.; Czink, N. Vehicular Channel Characterization and its Implications for Wireless System Design and performance. Proc. IEEE 2011, 99, 1189–1212. [Google Scholar] [CrossRef]
- Narrainen, J.; Besnier, P.; Gatsinzi Ibambe, M. A Geometry-Based Stochastic Approach to Emulate V2V Communications’ Main Propagation Channel Metrics. Int. J. Microw. Wirel. Technol. 2016, 8, 455–461. [Google Scholar] [CrossRef]
- Ivan, I.; Besnier, P.; Bunion, X.; Danvic, L.L.; Drissi, M. On the Simulation of Weibull Fading for V2X Communications. In Proceedings of the 2011 11th International Conference on ITS Telecommunications, St. Petersburg, Russia, 23–25 August 2011; pp. 86–91. [Google Scholar]
- Li, Y.; Ai, B.; Cheng, X.; Lin, S.; Zhong, Z. A TDL Based Non-WSSUS Vehicle-to-Vehicle Channel Model. Int. J. Antennas Propag. 2013, 2013, 1–8. [Google Scholar] [CrossRef]
- Li, Y.; Ai, B.; Michelson, D.G.; Lin, S.; Wang, Q.; Zhong, Z. A Method for Generating Correlated Taps in Stochastic Vehicle-to-Vehicle Channel Models. In Proceedings of the 2015 IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, Scotland, 1–14 May 2015; pp. 1–5. [Google Scholar]
- Jeruchim, M.C.; Balaban, P.; Shanmugan, K.S. Simulation of Communication Systems, 2nd ed.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Gutierrez, C.A.; Patzold, M.; Dahech, W.; Youssef, N. A Non-WSSUS Mobile-to-Mobile Channel Model Assuming Velocity Variations of the Mobile Stations. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference(WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Fernandez, J.A.; Borries, K.; Cheng, L.; Kumar, B.V.K.V.; Stancil, D.D.; Bai, F. Performance of the 802.11p Physical Layer in Vehicle-to-Vehicle Environments. IEEE Trans. Veh. Technol. 2012, 61, 3–14. [Google Scholar] [CrossRef]
- Vatalaro, F.; Forcella, A. Doppler spectrum in mobile-to-mobile communications in the presence of three-dimensional multipath scattering. IEEE Trans. Veh. Technol. 1997, 46, 213–219. [Google Scholar] [CrossRef]
- Patel, C.; Stuber, G.; Pratt, T. Simulation of Rayleigh-faded mobile-to-mobile communication channels. IEEE Trans. Commun. 2005, 53, 1876–1884. [Google Scholar] [CrossRef]
- Pätzold, M.; Hogstad, B.O.; Youssef, N. Modeling, analysis, and simulation of MIMO mobile-to-mobile fading channels. IEEE Trans. Wirel. Commun. 2008, 7, 510–520. [Google Scholar] [CrossRef]
- Zajić, A.G.; Stüber, G.L. Space-Time Correlated Mobile-to-Mobile Channels: Modelling and Simulation. IEEE Trans. Veh. Technol. 2008, 57, 715–726. [Google Scholar] [CrossRef]
- Zajić, A.G.; Stüber, G.L.; Pratt, T.G.; Nguyen, T. Wideband MIMO Mobile-to-Mobile Channels: Geometry-Based Statistical Modeling With Experimental Verification. IEEE Trans. Veh. Technol. 2009, 58, 517–534. [Google Scholar] [CrossRef]
- Zajić, A.G.; Stüber, G.L. Three-Dimensional Modeling and Simulation of Wideband MIMO Mobile-to-Mobile Channels. IEEE Trans. Wirel. Commun. 2009, 8, 1260–1275. [Google Scholar] [CrossRef]
- Cheng, X.; Yao, Q.; Wen, M.; Wang, C.X.; Song, L.Y.; Jiao, B.L. Wideband Channel Modeling and Intercarrier Interference Cancellation for Vehicle-to-Vehicle Communication Systems. IEEE J. Sel. Areas Commun. 2013, 31, 434–448. [Google Scholar] [CrossRef]
- Walter, M.; Shutin, D.; Fiebig, U.C. Delay-Dependent Doppler Probability Density Functions for Vehicle-to-Vehicle Scatter Channels. IEEE Trans. Antennas Propag. 2014, 62, 2238–2249. [Google Scholar] [CrossRef]
- Karedal, J.; Tufvesson, F.; Czink, N.; Paier, A.; Dumard, C.; Zemen, T.; Mecklenbräuker, C.; Molisch, A.F. A Geometry-Based Stochastic MIMO Model for Vehicle-to-Vehicle Communications. IEEE Trans. Wirel. Commun. 2009, 8, 3646–3657. [Google Scholar] [CrossRef] [Green Version]
- Gutiérrez, C.A.; Gutiérrez-Mena, J.T.; Luna-Rivera, J.M.; Campos-Delgado, D.U.; Velázquez, R.; Pätzold, M. Geometry-Based Statistical Modeling of Non-WSSUS Mobile-to-Mobile Rayleigh Fading Channels. IEEE Trans. Veh. Technol. 2017, 67, 362–377. [Google Scholar] [CrossRef] [Green Version]
- Gutiérrez, C.A.; Jaime-Rodríguez, J.J.; Luna-Rivera, J.M.; Campos-Delgado, D.U.; Vázquez-Castillo, J. Modeling of non-WSSUS Double-Rayleigh Fading Channels for Vehicular Communications. Wirel. Commun. Mob. Comput. 2017, 2017, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Wang, C.X.; He, Y.; Alwakeel, M.M.; Aggoune, E.H.M. 3D wideband non-stationary geometry-based stochastic models for non-isotropic MIMO vehicle-to-vehicle channels. IEEE Trans. Wirel. Commun. 2015, 14, 6883–6895. [Google Scholar] [CrossRef]
- Iqbal, R.; Abhayapala, T.D. Impact of mobile acceleration on the statistics of Rayleigh fading channel. In Proceedings of the Australian Communication Theory Workshop (AusCTW), Adelaide, Australia, 5–7 February 2007; pp. 122–128. [Google Scholar]
- Pätzold, M.; Borhani, A. A non-stationary multipath fading channel model incorporating the effect of velocity variations of the mobile station. In Proceedings of the WCNC: Wireless Communications and Networking Conference, Honolulu, HI, USA, 3–6 February 2014; pp. 194–199. [Google Scholar]
- Dahech, W.; Pätzold, M.; Gutiérrez, C.A.; Youssef, N. A Non-Stationary Mobile-to-Mobile Channel Model Allowing for Velocity and Trajectory Variations of the Mobile Stations. IEEE Trans. Wirel. Commun. 2017, 16, 1987–2000. [Google Scholar] [CrossRef]
- Jiang, K.; Chen, X.; Zhu, Q.; Chen, L.; Xu, D.; Chen, B. A Novel Simulation Model for Nonstationary Rice Fading Channels. Wirel. Commun. Mob. Comput. 2018, 2018, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Imbert, S.; Leturc, X.; LeMartret, C.J. On the simulation of correlated mobile-to-mobile fading channels for time-varying velocities. In Proceedings of the 2018 International Conference on Military Communications and Information Systems (ICMCIS 2018), Mazowieckie, Poland, 22–23 May 2018; pp. 1–8. [Google Scholar]
- Gutiérrez, C.A.; Pätzold, M.; Ortega-Silva, N.; Azurdia-Meza, C.A.; Maciel-Barbosa, F.M. Doppler Shift Characterization of Wideband Mobile Radio Channels. IEEE Trans. Veh. Technol. 2019, 68, 12375–12380. [Google Scholar] [CrossRef]
- von Mises, R. Über die ‘Ganzzahligkeit’ der Atomgewichte und verwandte Fragen. Phys. Z. 1918, 19, 490–500. [Google Scholar]
- Pätzold, M. Mobile Radio Channels, 2nd ed.; John Wiley and Sons: Chichester, UK, 2011. [Google Scholar]
- Gutiérrez, C.A.; Pätzold, M. The Generalized Method of Equal Areas for the Design of Sum-of-Cisoids Simulators for Mobile Rayleigh Fading Channels with Arbitrary Doppler Spectra. Wirel. Commun. Mob. Comput. 2011, 13, 951–966. [Google Scholar] [CrossRef]
- Gutiérrez, C.A.; Pätzold, M. The Design of Sum-of-Cisoids Rayleigh Fading Channel Simulators Assuming non-Isotropic Scattering Conditions. IEEE Trans. Wirel. Commun. 2010, 9, 1308–1314. [Google Scholar] [CrossRef] [Green Version]
- Hogstad, B.O.; Gutiérrez, C.A.; Pätzold, M.; Crespo, P.M. Classes of Sum-of-Cisoids Processes and Their Statistics for the Modeling and Simulation of Mobile Fading Channels. EURASIP J. Wirel. Commun. Netw. 2013, 2013, 125. [Google Scholar] [CrossRef] [Green Version]
- Jaime-Rodríguez, J.; Gutiérrez, C.A.; Luna-Rivera, M.; Campos-Delgado, D.U.; Velazquez, R. Comparative Performance Analysis of Two Channel Estimation Techniques for DSRC Systems Based on the IEEE 802.11p Standard. In Proceedings of the 34th IEEE Convention of Central America and Panama (CONCAPAN XXXIV), Panama City, Panama, 12–14 November 2014; pp. 1–6. (In Spanish). [Google Scholar]
- Jaime-Rodríguez, J.J.; Gómez-Vega, C.A.; Gutiérrez, C.A.; Luna-Rivera, J.M.; Campos-Delgado, D.U.; Velázquez, R. A Monte Carlo Simulator of non-WSSUS Rayleigh Fading Channels for Vehicular Communications. In Proceedings of the 2018 IEEE 38th Central America and Panama Convention (CONCAPAN XXXVIII), San Salvador, El Salvador, 7–9 November 2018; pp. 1–6. [Google Scholar]
- Ortega, N.M.; Azurdia-Meza, C.A.; Gutierrez, C.A.; Gómez-Vega, C.A. Second Order Statistics and BER Performance Analysis of a non-WSSUS V2X Channel Model that Considers Velocity Variations. In Proceedings of the 2019 IEEE Latin-American Conference on Communications (LATINCOM), Salvador, Brazil, 11–13 November 2019; pp. 1–6. [Google Scholar]
- Gómez-Vega, C.A.; Jaime-Rodríguez, J.J.; Gutiérrez, C.A.; Velázquez, R. Bit error rate performance analysis of vehicular communication systems considering velocity variations of the mobile stations. In Proceedings of the 2017 IEEE 37th Central America and Panama Convention (CONCAPAN XXXVII), Managua, Nicaragua, 15–17 November 2017; pp. 1–6. [Google Scholar]










| Parameter | IEEE 802.11p | LTE-V2X |
|---|---|---|
| Data subcarriers () | 48 | 600 |
| Pilot () | 4 subcarriers | 4 symbols |
| Frequency spacing between subcarriers () | 156.25 kHz | 15 kHz |
| Guard interval | 1.6 s | 4.69 s |
| Symbol duration without Guard interval | 6.4 s | 66.31 s |
| Total symbol duration () | 8 s | 71 s |
| Description | Parameter |
|---|---|
| Velocity vector of | |
| Velocity vector of | |
| Acceleration vector of | |
| Acceleration vector of | |
| Position of the ℓ-th IO with respect to the reference point | |
| position seen from the ℓ-th IO | |
| Initial distance between and | D |
| Radius of the ring of IOs around | d |
| Mean of the AOA distribution | |
| Concentration parameter of the AOA distribution |
| GenerateChannel(, , , , , , , , ) |
|---|
| Set system parameters according to the standard: |
| Bandwidth B |
| Carrier Frequency |
| Total number of subcarriers |
| Symbol duration |
| Subcarriers spacing |
| Compute gains for the IOs |
| Generate random variables for the IOs: |
| Phase shift |
| AOAs with von Mises distribution |
| AODs following (8) |
| Compute maximum Doppler frequencies due to initial speed and |
| Compute Doppler frequency shift due to initial speed |
| Compute time-varying maximum Doppler frequencies due to acceleration |
| and for |
| for ℓ=0 to |
| Compute time-varying Doppler frequency shift |
| due to acceleration for |
| Compute time-varying propagation delays for |
| end for |
| Compute channel transfer function matrix with elements |
| for and |
| function generateSystem |
|---|
| Set simulation and system parameters: |
| Number of data symbols F |
| Total number of transmitted symbols K |
| Total number of subcarriers |
| Number of pilots and data subcarriers , |
| Number of iterations n |
| Vector for the Eb/No values P |
| Set parameters for the propagation scenario: |
| Number of IOs |
| MSs initial speeds, acceleration components, and direction parameters |
| , , , , , , , and |
| Scattering parameters |
| Initial distance D (between and ) |
| Ring radius d (between and the ℓ-th IO) |
| Generate training and data symbols randomly |
| Modulate training and data symbols |
| Organize training and data symbols in matrix |
| Initialize accumulated number of errors |
| for i=0 to |
| Call GenerateChannel(, , , , , , , , ) |
| to compute channel transfer function matrix |
| Simulate data transmission over |
| Add AWGN |
| Perform transmission scheme to be evaluated |
| Conduct channel equalization |
| Demodulate data |
| Compute and accumulate number of errors on B |
| end for |
| Average B over n iterations to obtain the BER |
| Scenario I | Scenario II | Scenario III | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial MS speed | 20 | 40 | 80 | 100 | 20 | 40 | 80 | 100 | 20 | 40 | 80 | 100 | |
| (km/h) | |||||||||||||
| Estimator | BER | Required Eb/No (dB) | |||||||||||
| LS | 4.73 | 5.12 | 8.69 | 16.51 | 4.67 | 5.37 | 13.54 | NA | 4.81 | 5.29 | 12.88 | NA | |
| STA () | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| STA () | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| LS | 16.99 | NA | NA | NA | 16.94 | NA | NA | NA | 16.91 | NA | NA | NA | |
| STA () | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| STA () | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| Scenario I | Scenario II | Scenario III | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frame length | 16 | 32 | 64 | 128 | 16 | 32 | 64 | 128 | 16 | 32 | 64 | 128 | |
| F | |||||||||||||
| Estimator | BER | Required Eb/No (dB) | |||||||||||
| LS | 4.00 | 4.61 | 5.08 | 7.92 | 3.98 | 4.52 | 5.37 | 10.70 | 3.87 | 4.55 | 5.41 | 10.31 | |
| STA () | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| STA () | 4.48 | 7.05 | NA | NA | 4.50 | 7.15 | NA | NA | 4.43 | 6.98 | NA | NA | |
| LS | 15.37 | 17.06 | NA | NA | 15.34 | 16.63 | NA | NA | 15.18 | 16.79 | NA | NA | |
| STA () | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| STA () | 16.10 | 34.38 | NA | NA | 15.66 | 39.99 | NA | NA | 15.79 | 32.36 | NA | NA | |
| Scenario I | Scenario II | Scenario III | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean AOA | 0 () | 0 | 0 () | 0 | 0 () | 0 | |||||||
| Estimator | BER | Required Eb/No (dB) | |||||||||||
| LS | 5.67 | 4.32 | 5.87 | 5.88 | 6.11 | 8.14 | 5.12 | 4.43 | 6.06 | 4.27 | 5.44 | 7.16 | |
| STA () | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| STA () | 9.18 | 6.98 | 11.86 | 12.02 | 10.78 | NA | 9.00 | 6.94 | 10.85 | 7.03 | 9.67 | 19.03 | |
| LS | NA | 16.03 | 17.53 | 17.33 | NA | 20.14 | 17.35 | 15.88 | NA | 15.11 | 17.76 | 19.89 | |
| STA () | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| STA () | NA | 22.09 | NA | NA | NA | NA | NA | 21.18 | NA | 18.98 | NA | NA | |
| LS | NA | NA | 38.90 | 29.67 | NA | 31.93 | NA | 39.75 | NA | 24.94 | NA | NA | |
| STA () | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | |
| STA () | NA | NA | NA | NA | NA | NA | NA | NA | NA | 32.82 | NA | NA | |
| Scenario I | Scenario II | Scenario III | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frame length | 16 | 32 | 64 | 128 | 16 | 32 | 64 | 128 | 16 | 32 | 64 | 128 | |
| F | |||||||||||||
| Estimator | BER | Required Eb/No (dB) | |||||||||||
| Mod. STA () | 4.85 | 6.01 | 7.18 | 8.75 | 4.85 | 6.05 | 7.29 | 8.68 | 4.81 | 6.11 | 7.35 | 8.7 | |
| Mod. STA () | 15.88 | 17.21 | 18.67 | 22.46 | 15.93 | 17.15 | 19.05 | 21.83 | 15.76 | 17.36 | 18.97 | 21.99 | |
| Mod. STA () | 29.96 | 31.04 | 38.9 | NA | 27.06 | 30.68 | 38.66 | NA | 27.1 | 30.96 | 39.2 | NA | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaime-Rodríguez, J.J.; Gómez-Vega, C.A.; Gutiérrez, C.A.; Luna-Rivera, J.M.; Campos-Delgado, D.U.; Velázquez, R. A Non-WSSUS Channel Simulator for V2X Communication Systems. Electronics 2020, 9, 1190. https://doi.org/10.3390/electronics9081190
Jaime-Rodríguez JJ, Gómez-Vega CA, Gutiérrez CA, Luna-Rivera JM, Campos-Delgado DU, Velázquez R. A Non-WSSUS Channel Simulator for V2X Communication Systems. Electronics. 2020; 9(8):1190. https://doi.org/10.3390/electronics9081190
Chicago/Turabian StyleJaime-Rodríguez, José Jimmy, Carlos Antonio Gómez-Vega, Carlos A. Gutiérrez, José Martín Luna-Rivera, Daniel Ulises Campos-Delgado, and Ramiro Velázquez. 2020. "A Non-WSSUS Channel Simulator for V2X Communication Systems" Electronics 9, no. 8: 1190. https://doi.org/10.3390/electronics9081190
APA StyleJaime-Rodríguez, J. J., Gómez-Vega, C. A., Gutiérrez, C. A., Luna-Rivera, J. M., Campos-Delgado, D. U., & Velázquez, R. (2020). A Non-WSSUS Channel Simulator for V2X Communication Systems. Electronics, 9(8), 1190. https://doi.org/10.3390/electronics9081190







