High Precision Sparse Reconstruction Scheme for Multiple Radar Mainlobe Jammings
Abstract
:1. Introduction
2. Problem Statement
3. Methodology
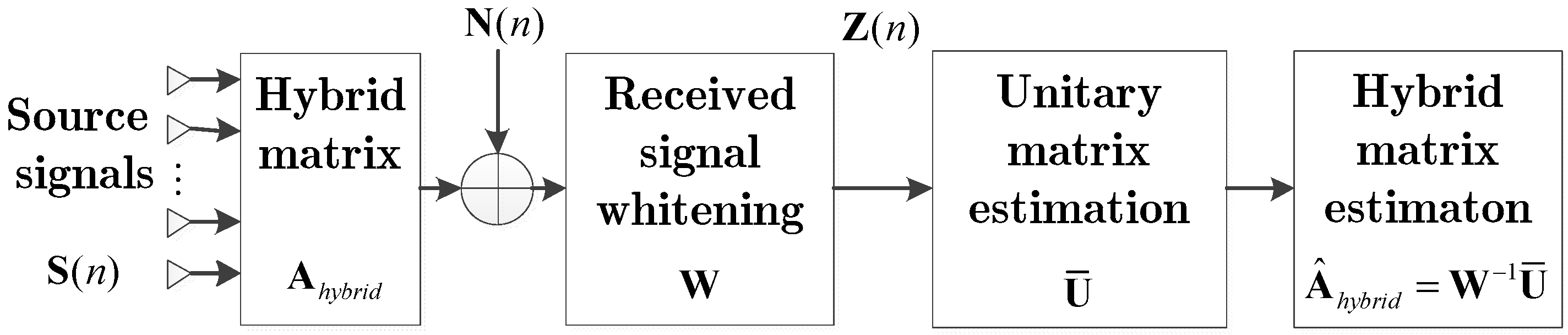
3.1. Steering Vector Estimation Based on Fourth-Order Cumulant Matrix
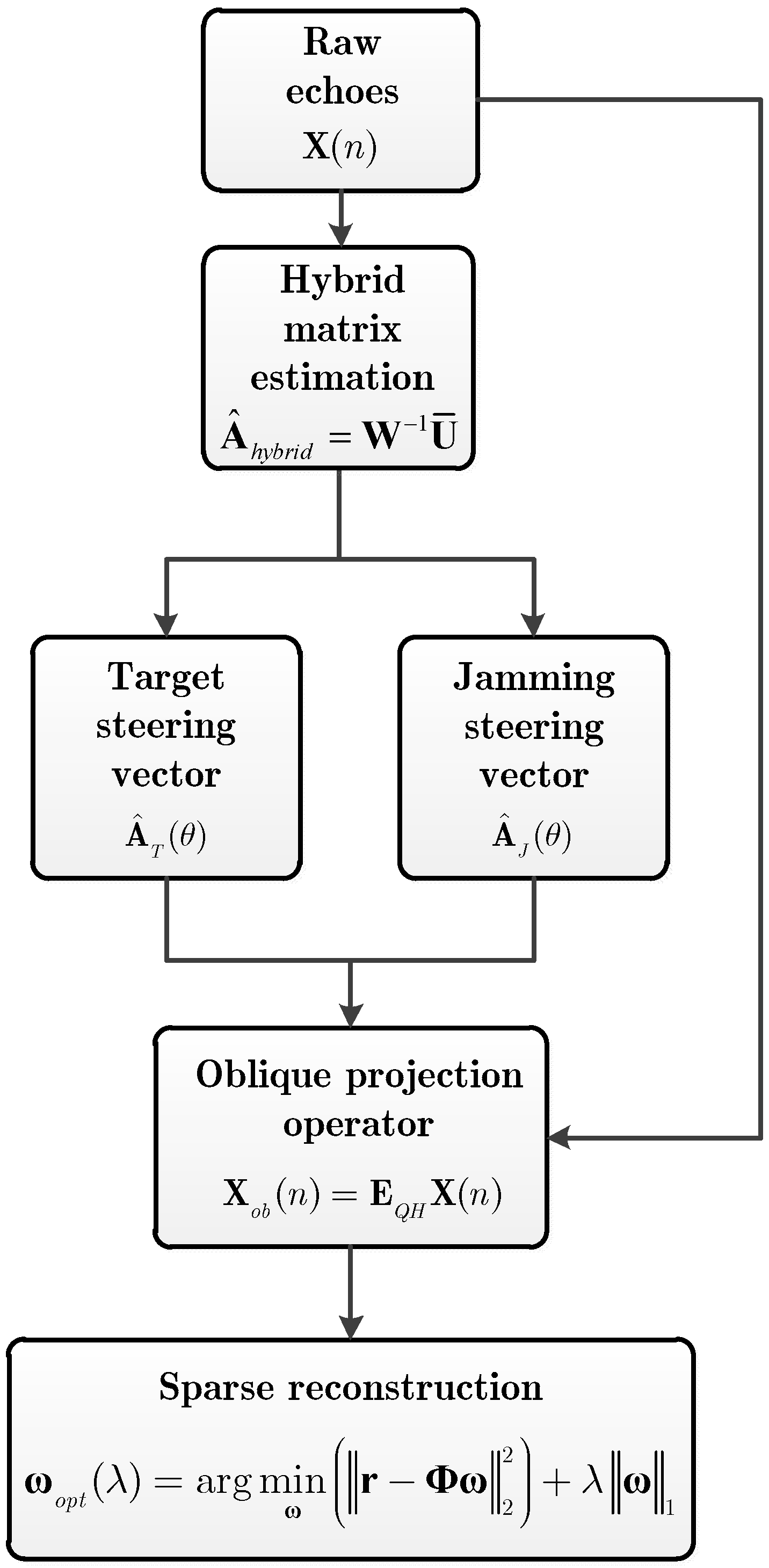
3.2. Sparse Reconstruction with Jamming Suppression Based on OP-SBL Algorithm
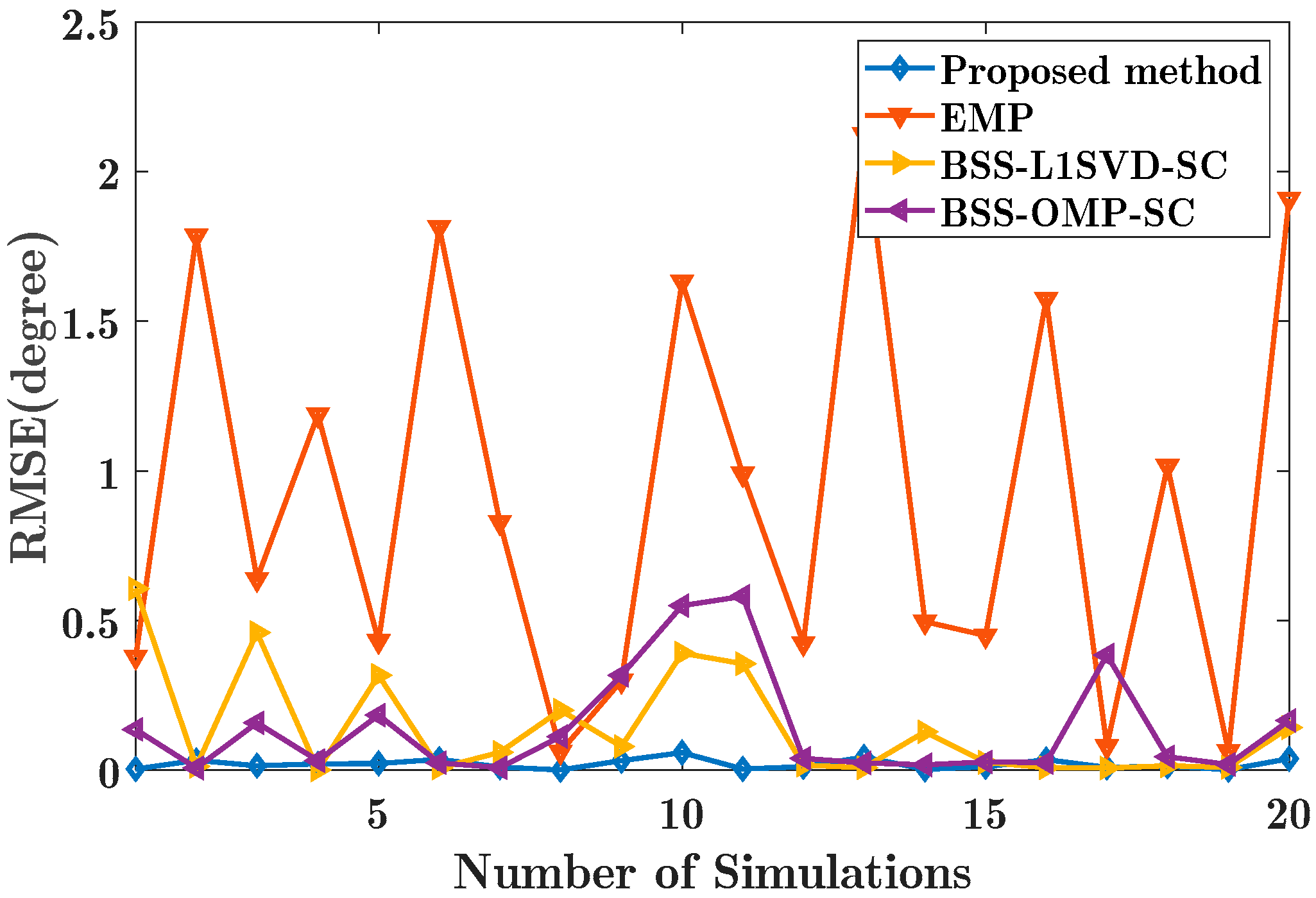
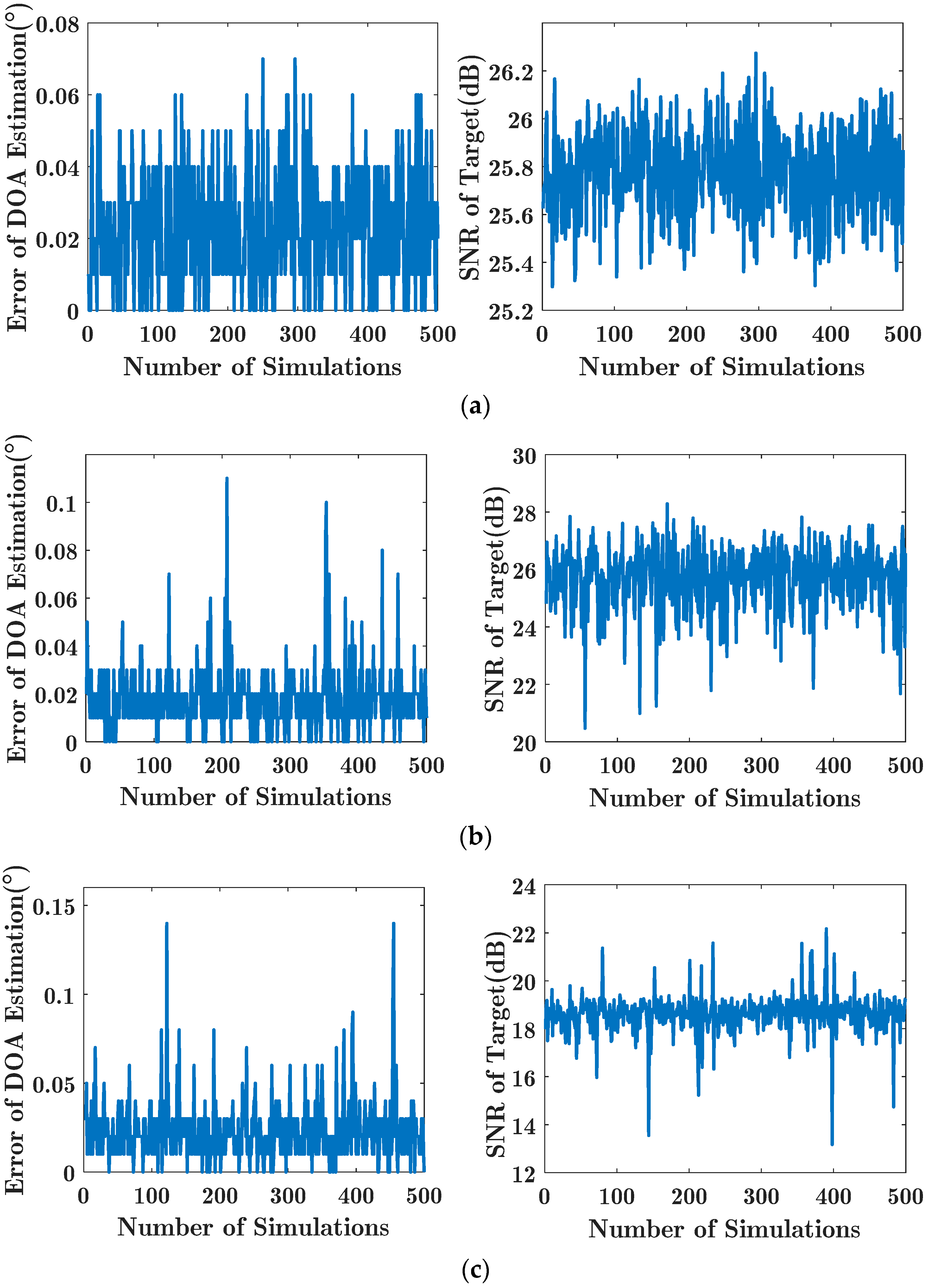
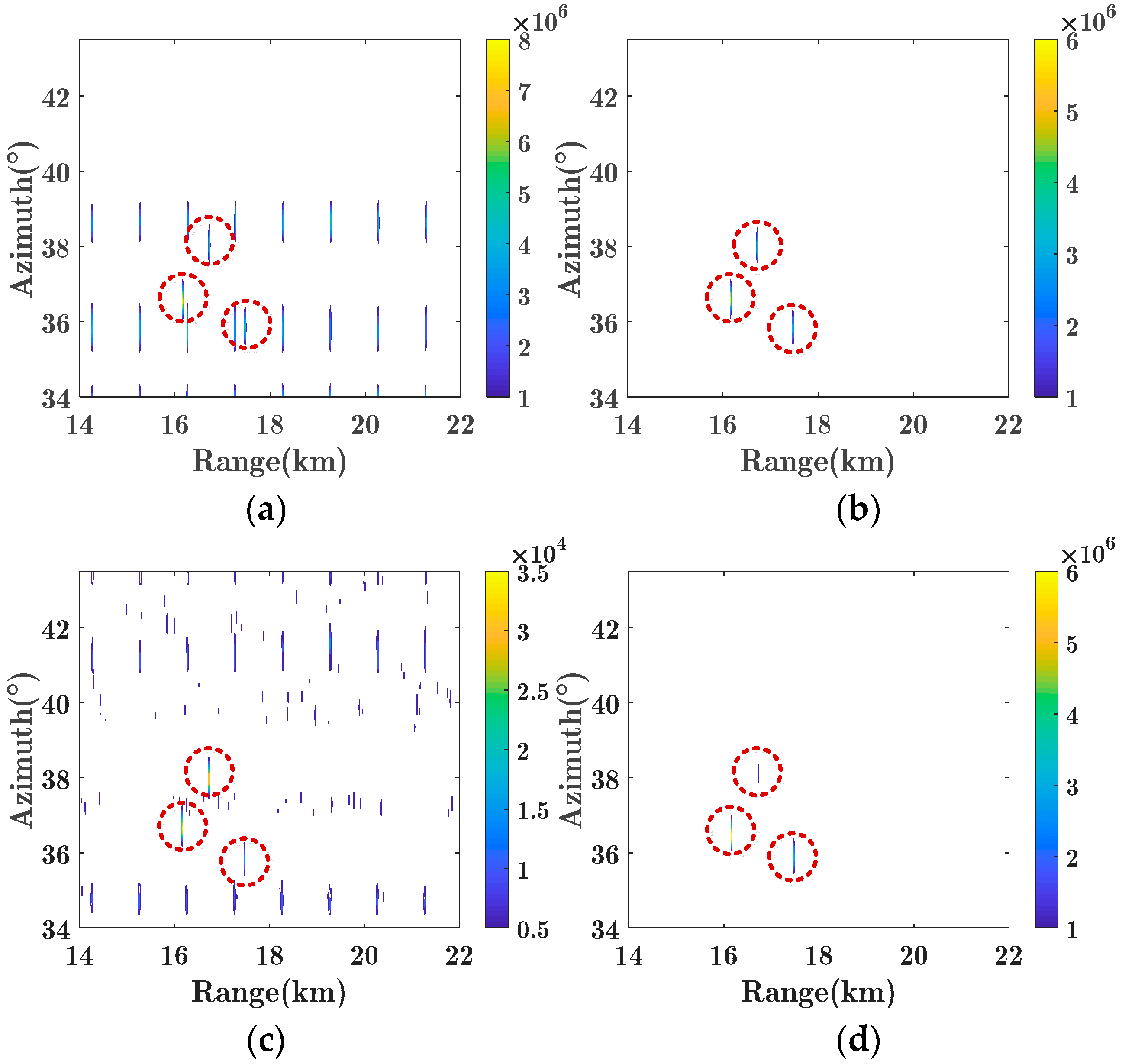
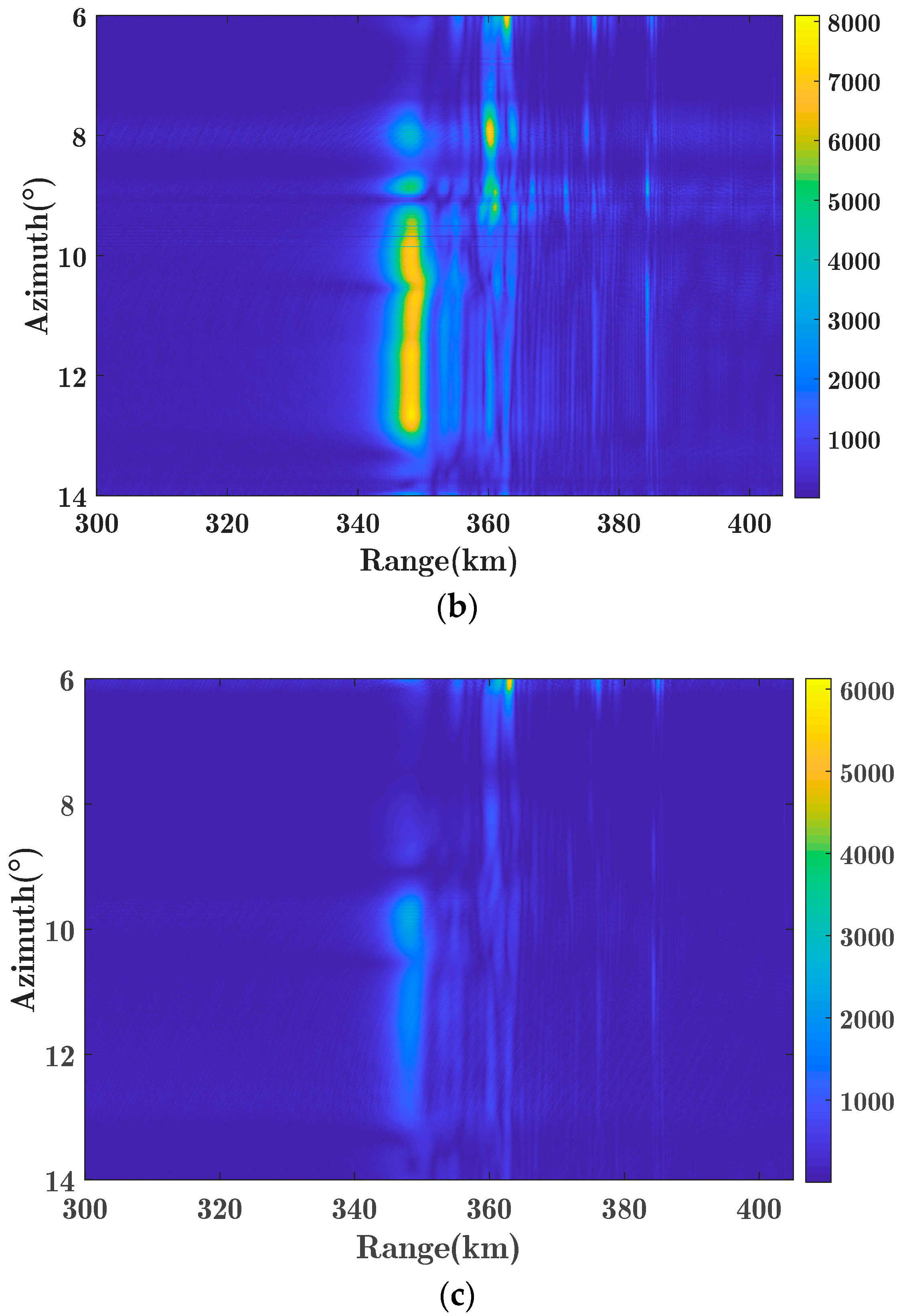
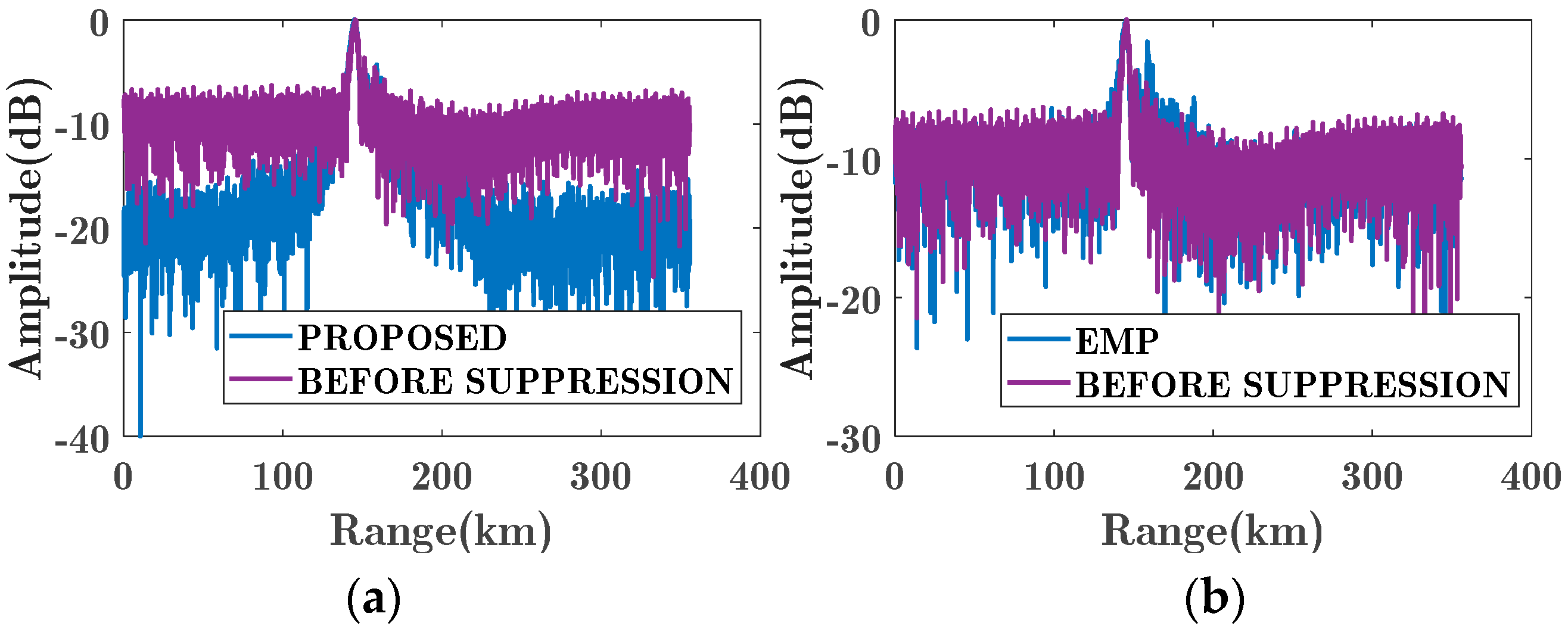
4. Experimental Results
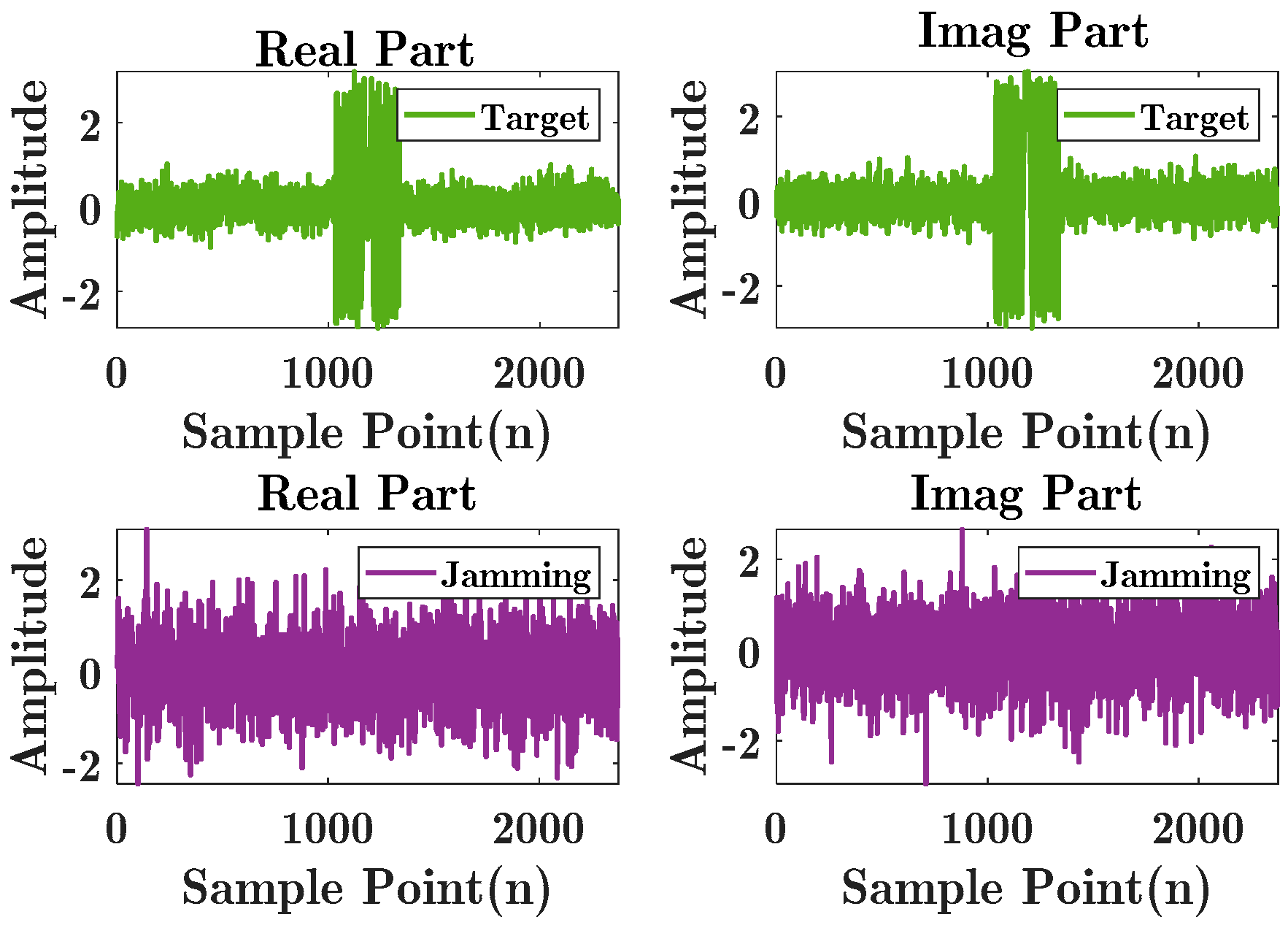
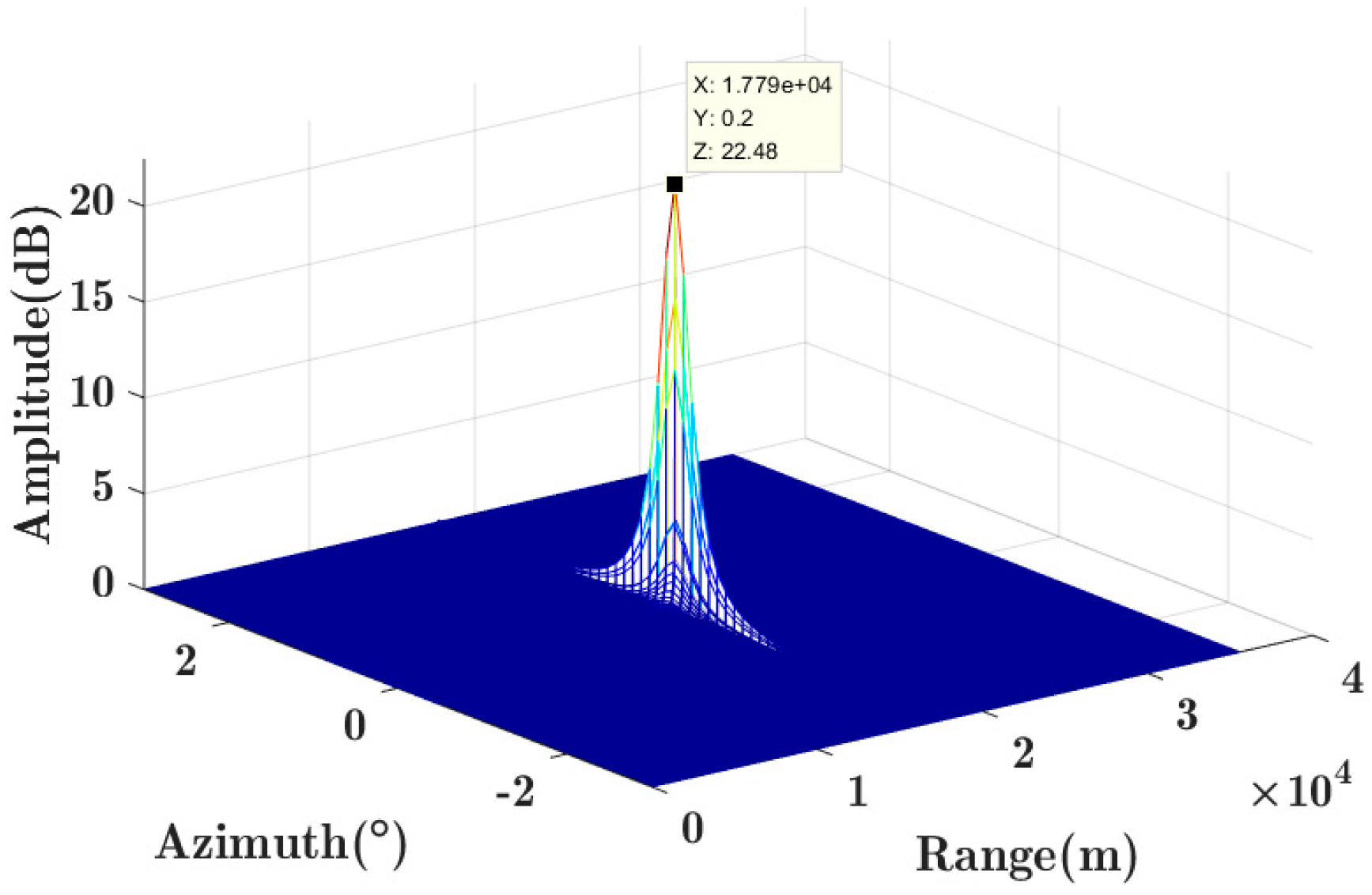
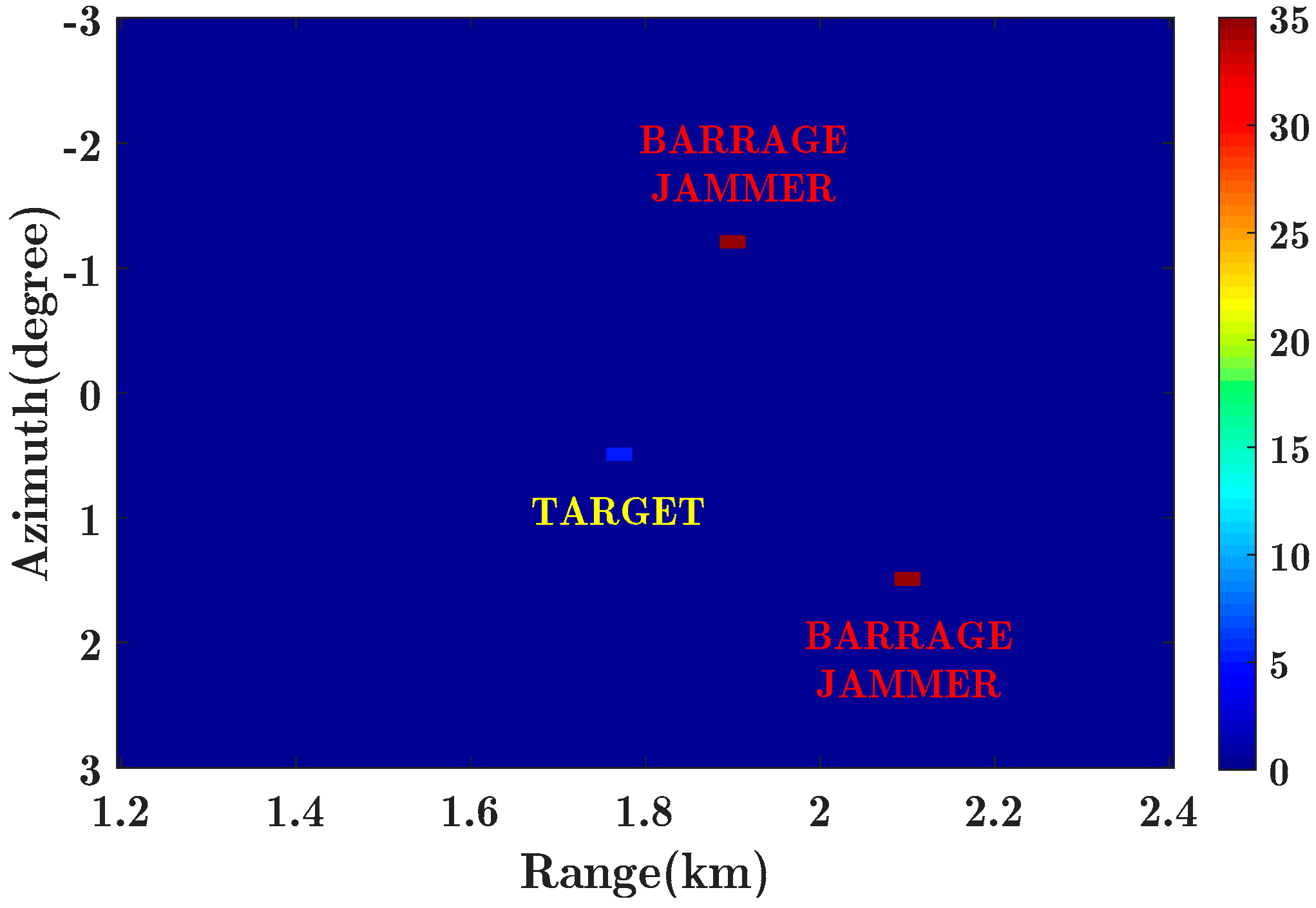
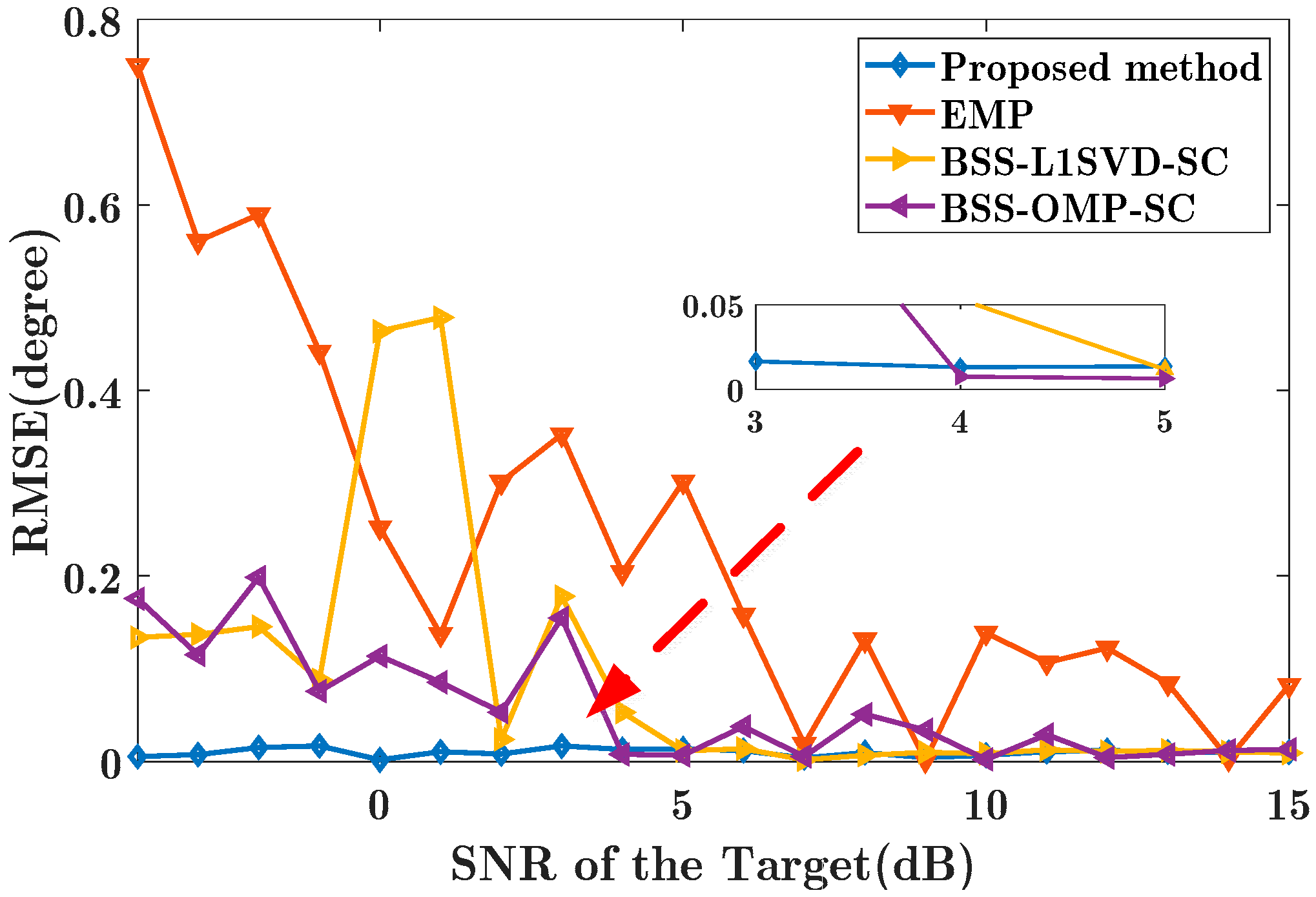
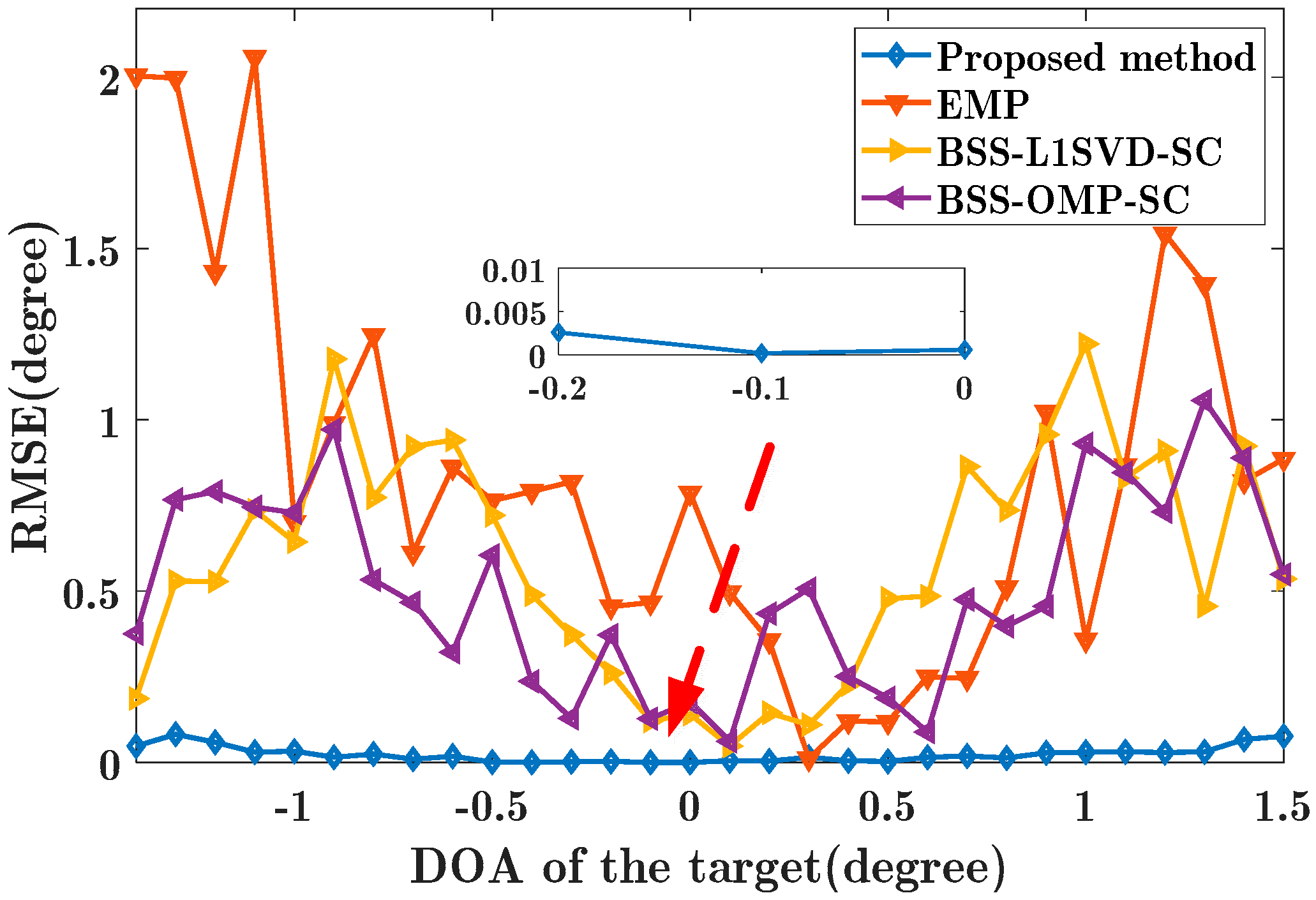
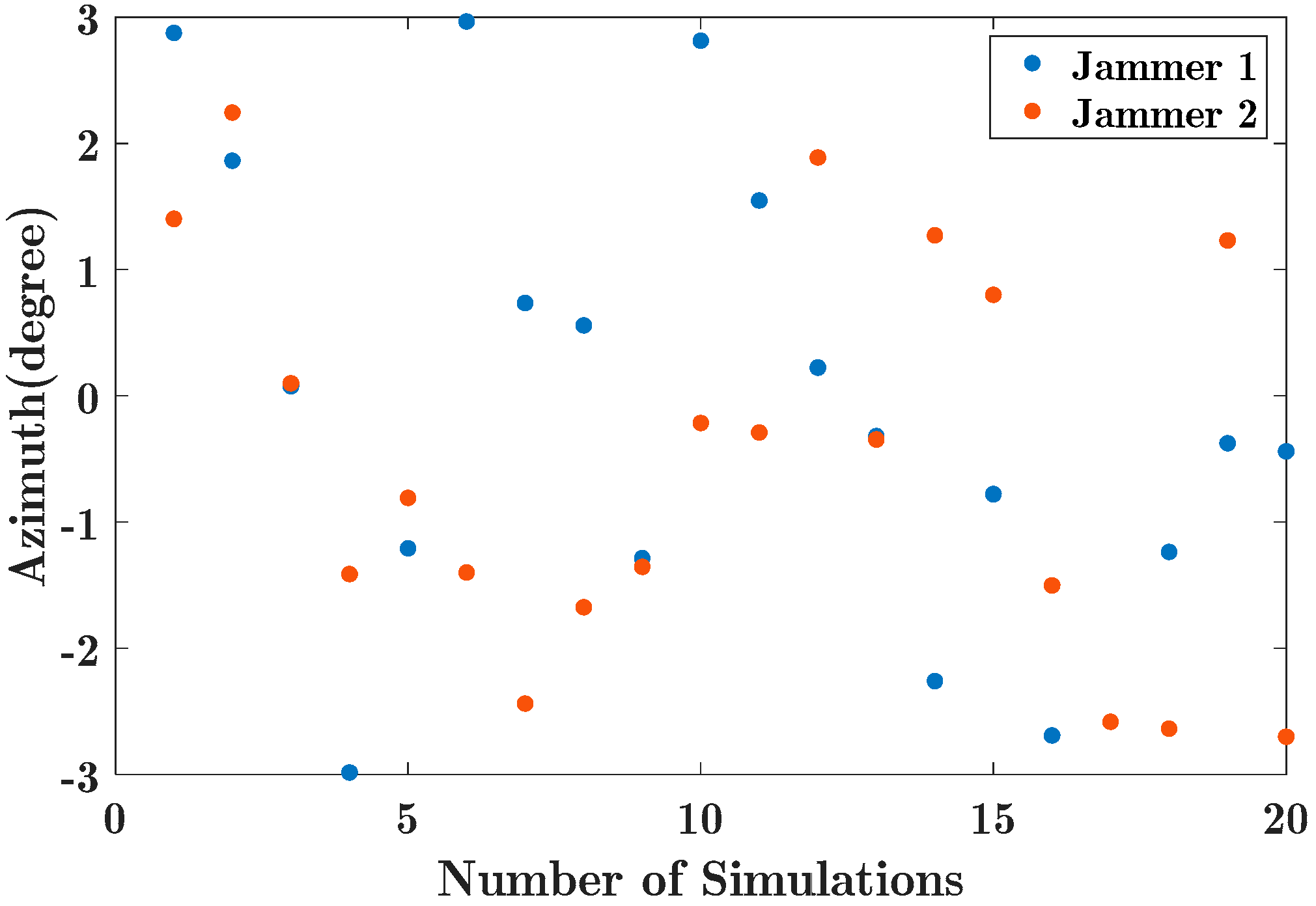
4.1. Simulation Study
4.2. Experimental Data Verification Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Garmatyuk, D.; Narayanan, R. ECCM capabilities of an ultrawideband bandlimited random noise imaging radar. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 1243–1255. [Google Scholar] [CrossRef]
- Yu, K.-B.; Murrow, D. Adaptive digital beamforming for angle estimation in jamming. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 508–523. [Google Scholar] [CrossRef]
- Mears, M.J. Cooperative electronic attack using unmanned air vehicles. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 3339–3347. [Google Scholar]
- Hoshuyama, O.; Sugiyama, A.; Hirano, A. A robust adaptive beamformer for microphone arrays with a blocking matrix using constrained adaptive filters. IEEE Trans. Signal Process. 1999, 47, 2677–2684. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Z.; Zeng, T.; Long, T.; Sarkar, T.K. Mainlobe Interference Suppression Based on Eigen-Projection Processing and Covariance Matrix Reconstruction. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1369–1372. [Google Scholar] [CrossRef]
- Shen, M.; Wu, D.; Zhu, D. An ultra-low sidelobe ADBF algorithm for digital array. J. Electromagn. Waves Appl. 2012, 26, 1611–1618. [Google Scholar] [CrossRef]
- Dai, H.; Wang, X.; Li, Y.; Liu, Y.; Xiao, S. Main-Lobe Jamming Suppression Method of using Spatial Polarization Characteristics of Antennas. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2167–2179. [Google Scholar] [CrossRef]
- Li, S.; Zhang, L.; Liu, N.; Zhang, J.; Zhao, S. Adaptive detection with conic rejection to suppress deceptive jamming for frequency diverse MIMO radar. Digit. Signal Process. 2017, 69, 32–40. [Google Scholar] [CrossRef]
- Lan, L.; Liao, G.; Xu, J.; Zhang, Y.; Fioranelli, F. Suppression Approach to Main-Beam Deceptive Jamming in FDA-MIMO Radar Using Nonhomogeneous Sample Detection. IEEE Access 2018, 6, 34582–34597. [Google Scholar] [CrossRef]
- Cui, G.; Ji, H.; Carotenuto, V.; Iommelli, S.; Yu, X. An adaptive sequential estimation algorithm for velocity jamming suppression. Signal Process. 2017, 134, 70–75. [Google Scholar] [CrossRef]
- Cui, G.; Yu, X.; Yuan, Y.; Kong, L. Range jamming suppression with a coupled sequential estimation algorithm. IET Radar Sonar Navig. 2018, 12, 341–347. [Google Scholar] [CrossRef]
- Bofill, P.; Zibulevsky, M. Underdetermined blind source separation using sparse representations. Signal Process. 2001, 81, 2353–2362. [Google Scholar] [CrossRef] [Green Version]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef] [Green Version]
- Falco, N.; Benediktsson, J.A.; Bruzzone, L. Spectral and Spatial Classification of Hyperspectral Images Based on ICA and Reduced Morphological Attribute Profiles. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6223–6240. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.I.; Jung, K.; Kim, H.J. Face recognition using kernel principal component analysis. IEEE Signal Process. Lett. 2002, 9, 40–42. [Google Scholar] [CrossRef] [Green Version]
- Yin, S.; Zhao, X.; Wang, W.; Gong, M. Efficient multilevel image segmentation through fuzzy entropy maximization and graph cut optimization. Pattern Recognit. 2014, 47, 2894–2907. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, Y.; Zhang, X. A blind source separation-based anti-jamming method by space pre-whitening. In Proceedings of the 2016 7th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 26–28 August 2016; pp. 454–457. [Google Scholar]
- Ge, M.; Cui, G.; Yu, X.; Huang, D.; Kong, L. Mainlobe jamming suppression via blind source separation. In Proceedings of the 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018; pp. 0914–0918. [Google Scholar]
- Zhou, B.; Li, R.; Liu, W.; Wang, Y.; Dai, L.; Shao, Y. A BSS-based space–time multi-channel algorithm for complex-jamming suppression. Digit. Signal Process. 2019, 87, 86–103. [Google Scholar] [CrossRef]
- Guo, S.; Wang, J.; Chen, G.; Wang, J.; Jun, W. Mainlobe interference suppression based on independent component analysis in passive bistatic radar. IET Signal Process. 2018, 12, 1193–1201. [Google Scholar] [CrossRef]
- Ge, M.; Cui, G.; Kong, L. Mainlobe jamming suppression for distributed radar via joint blind source separation. IET Radar Sonar Navig. 2019, 13, 1189–1199. [Google Scholar] [CrossRef]
- Ge, M.; Cui, G.; Yu, X.; Kong, L. Main lobe jamming suppression via blind source separation sparse signal recovery with subarray configuration. IET Radar Sonar Navig. 2020, 14, 431–438. [Google Scholar] [CrossRef]
- Wipf, D.; Rao, B. Sparse Bayesian Learning for Basis Selection. IEEE Trans. Signal Process. 2004, 52, 2153–2164. [Google Scholar] [CrossRef]
- Pedzisz, M.; Mansour, A. Automatic modulation recognition of MPSK signals using constellation rotation and its 4th order cumulant. Digit. Signal Process. 2005, 15, 295–304. [Google Scholar] [CrossRef]






| Parameter Name | Value |
|---|---|
| Radar center frequency | 10 GHz |
| Signal bandwidth | 2.5 GHz |
| Pulse duration | 150 µs |
| Sampling frequency | 3 MHz |
| Modulation form | LFM |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Zhu, D.; Zhang, J. High Precision Sparse Reconstruction Scheme for Multiple Radar Mainlobe Jammings. Electronics 2020, 9, 1224. https://doi.org/10.3390/electronics9081224
Cheng Y, Zhu D, Zhang J. High Precision Sparse Reconstruction Scheme for Multiple Radar Mainlobe Jammings. Electronics. 2020; 9(8):1224. https://doi.org/10.3390/electronics9081224
Chicago/Turabian StyleCheng, Yuan, Daiyin Zhu, and Jindong Zhang. 2020. "High Precision Sparse Reconstruction Scheme for Multiple Radar Mainlobe Jammings" Electronics 9, no. 8: 1224. https://doi.org/10.3390/electronics9081224
APA StyleCheng, Y., Zhu, D., & Zhang, J. (2020). High Precision Sparse Reconstruction Scheme for Multiple Radar Mainlobe Jammings. Electronics, 9(8), 1224. https://doi.org/10.3390/electronics9081224




