Full Range Capacitor Voltage Balance PWM Strategy for Diode-Clamped Multilevel Inverter
Abstract
:1. Introduction
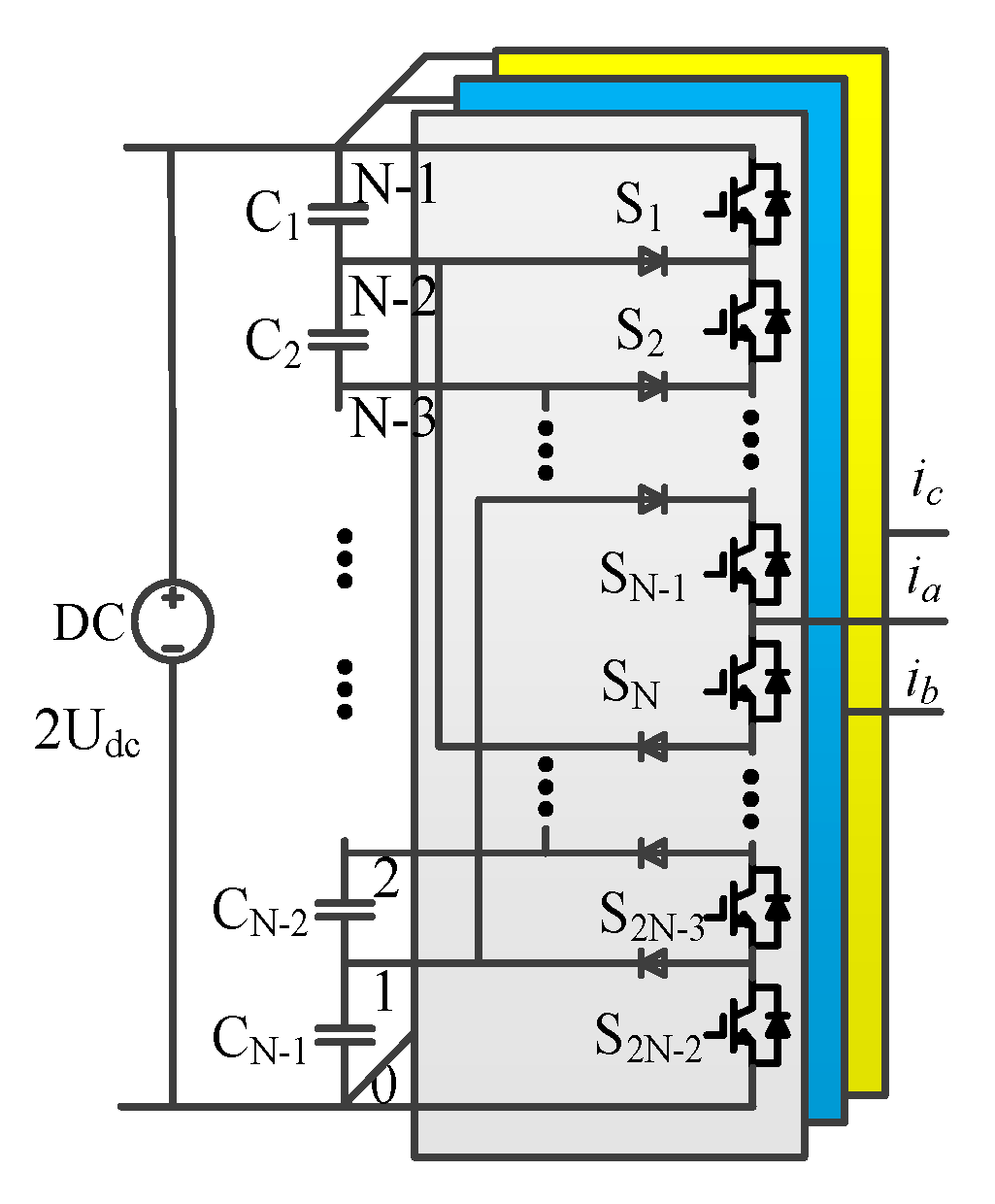
2. DCMLI and its Modulation Model
2.1. DCMLI
2.2. The PWM Model for DCMLI
2.3. Review of VSVPWM for DCMLI
3. The Proposed FRCVBPWM for DCMLI
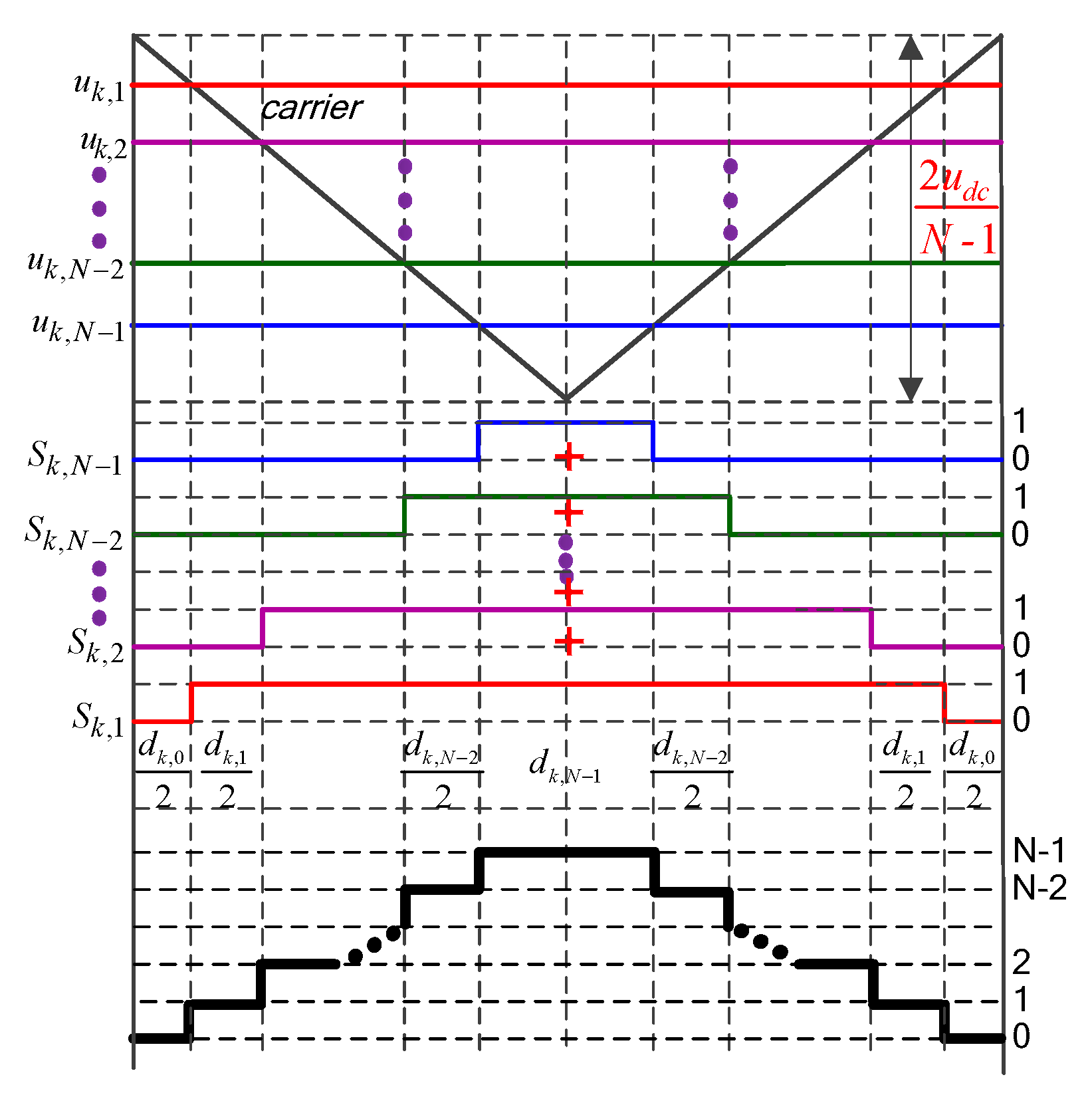
3.1. The Proposed FRCVBPWM
3.2. The Duty Ratio Calculation under Different Modes in One Switching Cycle
4. Selecting the Mode Based on the Switching Loss
5. The Implementation of FRCVBPWM
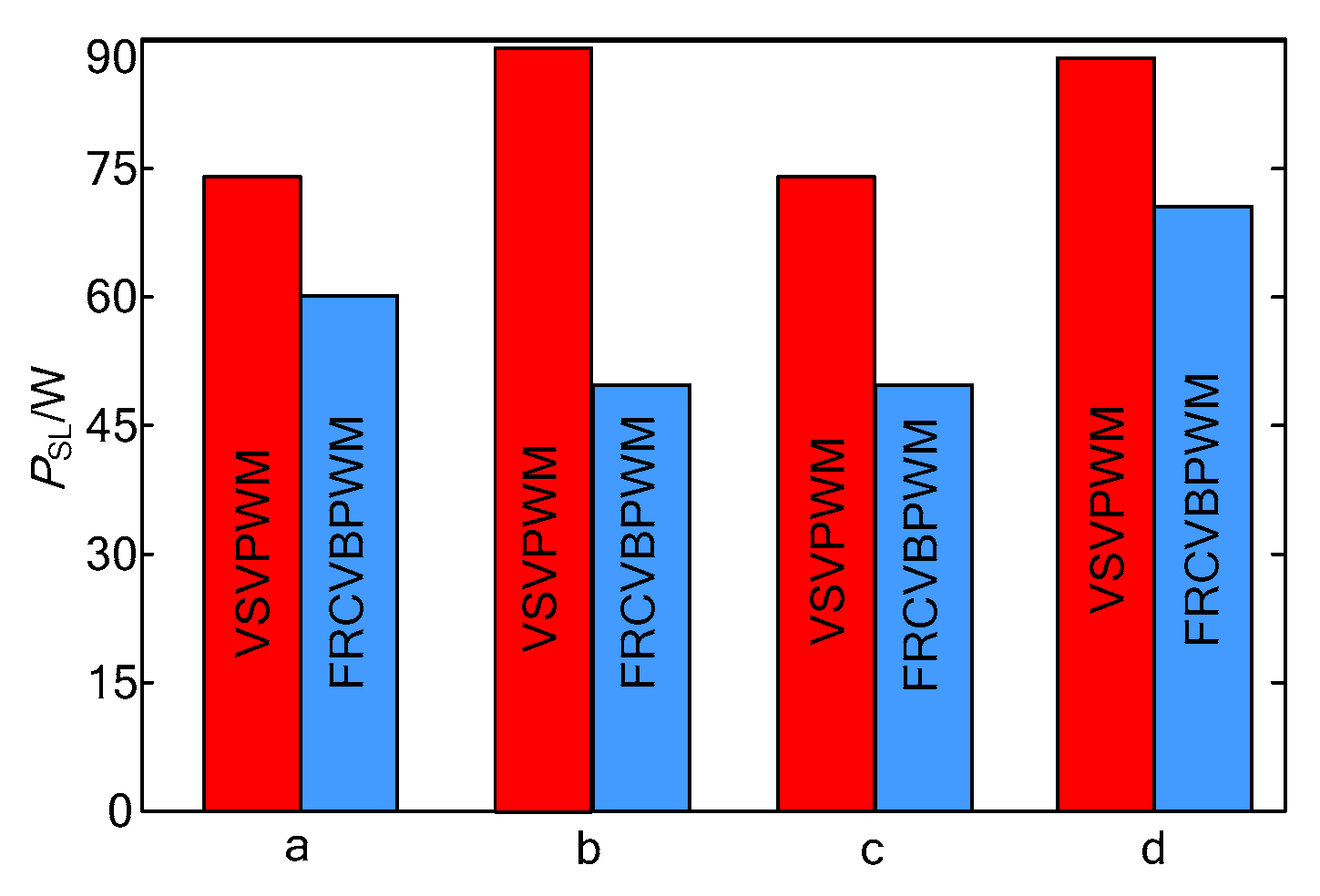
6. Switching Loss Analysis
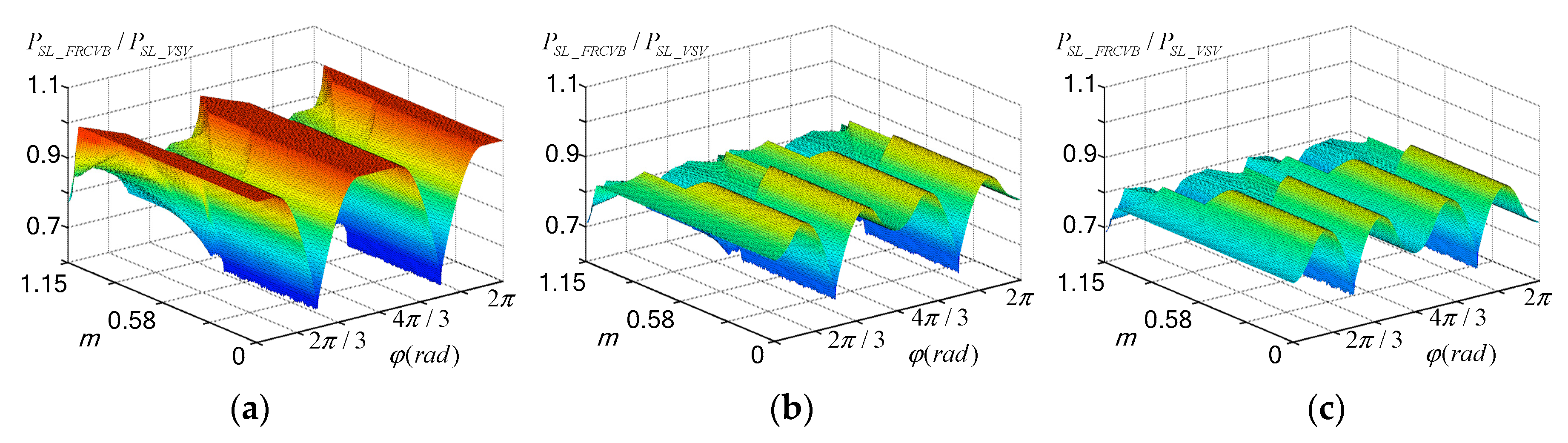
7. Experimental Verification
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rodríguez, J.; Lai, J.; Peng, F. Multilevel inverters: A survey of topologies, controls and applications. IEEE Trans. Ind. Electron. 2002, 49, 724–738. [Google Scholar] [CrossRef] [Green Version]
- Delmas, L.; Meynard, T.A.; Foch, H.; Gateau, G. Comparative study of multilevel topologies: NPC, multicell inverter and SMC with IGBT. In Proceedings of the IEEE 2002 28th Annual Conference of the Industrial Electronics Society, Sevilla, Spain, 5–8 November 2002; pp. 828–833. [Google Scholar]
- Renge, M.M.; Suryawanshi, H.M. Five-level diode clamped inverter to eliminate common mode voltage and reduce dv/dt in medium voltage rating induction motor drives. IEEE Trans. Power Electron. 2008, 23, 1598–1607. [Google Scholar] [CrossRef]
- Franquelo, L.G.; Rodriguez, J.; Leon, J.I.; Kouro, S.; Portillo, R.; Prats, M.A.M. The age of multilevel converters arrives. IEEE Trans. Ind. Electron. 2008, 2, 28–39. [Google Scholar] [CrossRef] [Green Version]
- Norambuena, M.; Kouro, S.; Dieckerhoff, S.; Rodriguez, J. Reduced multilevel converter: A novel multilevel converter with reduced active switches. IEEE Trans. Ind. Electron. Early Access 2018, 65, 3636–3645. [Google Scholar] [CrossRef]
- Lee, J.S.; Lee, K.B. A carrier-based PWM method for neutral-point ripple reduction of a 3-level inverter. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 2095–2100. [Google Scholar]
- Shen, J.; Schroder, S.; Duro, B.; Roesner, R. A neutral-point balancing controller for a three-level inverter with full power-factor range and low distortion. IEEE Trans. Ind. Electron. 2013, 49, 138–148. [Google Scholar] [CrossRef]
- Gupta, K.; Khambadkone, A.M. A simple space vector PWM scheme to operate a three-level NPC inverter at high modulation index including over modulation region, with neutral point balancing. IEEE Trans. Ind. Electron. 2007, 43, 751–760. [Google Scholar]
- Dordevic, O.; Jones, M.; Levi, E. A comparison of carrier-based and space vector PWM techniques for three-level five-phase voltage source inverters. IEEE Trans. Ind. Inform. 2013, 9, 609–619. [Google Scholar] [CrossRef]
- McGrath, B.P.; Holmes, D.G.; Meynard, T. Reduced PWM harmonic distortion for multilevel inverters operating over a wide modulation range. IEEE Trans. Power Electron. 2006, 21, 941–949. [Google Scholar] [CrossRef]
- Chen, J.; He, Y.; Hasan, S.U.; Liu, J. A comprehensive study on equivalent modulation waveforms of the SVM sequence for three-level inverters. IEEE Trans. Power Electron. 2015, 30, 7149–7158. [Google Scholar] [CrossRef]
- Qin, J.; Saeedifard, M. Capacitor voltage balancing of a five-level diode-clamped converter based on a predictive current control strategy. In Proceedings of the 2011 Twenty-Sixth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 6–11 March 2011; pp. 1656–1660. [Google Scholar]
- Rodriguez, J.; Pontt, J.; Silva, C.A.; Correa, P.; Lezana, P.; Cortes, P.; Ammann, U. Predictive current control of a voltage source inverter. IEEE Trans. Ind. Electron. 2007, 54, 495–503. [Google Scholar] [CrossRef]
- Busquets-Monge, S.; Alepuz, S.; Bordonau, J.; Peracaula, J. Voltage balancing control of diode-clamped multilevel converters with passive front-ends. IEEE Trans. Power Electron. 2008, 23, 1751–1758. [Google Scholar] [CrossRef]
- Saeedifard, M.; Iravani, R.; Pou, J. Analysis and control of DC capacitor voltage drift phenomenon of a passive front-end five level converter. IEEE Trans. Ind. Electron. 2007, 54, 3255–3266. [Google Scholar] [CrossRef]
- Lewicki, A.; Krzeminskiv, Z.; Abu-Rub, H. Space-Vector Pulsewidth modulation for three-level NPC converter with the neutral point voltage control. IEEE Trans. Ind. Electron. 2011, 58, 5076–5086. [Google Scholar] [CrossRef]
- Saeedifard, B.M.; Iravani, R.; Pou, J. Control and DC-capacitor voltage balancing of a space vector-modulated five-level STATCOM. IEEE Trans. Power Electron. 2009, 2, 203–215. [Google Scholar] [CrossRef]
- Hasegawa, K.; Akagi, H. A new DC-voltage-balancing circuit including a single coupled inductor for a five-level diode clamped PWM inverter. IEEE Trans. Ind. Electron. 2011, 47, 841–852. [Google Scholar] [CrossRef]
- Shu, Z.; He, X.; Wang, Z.; Qiu, D.; Jing, Y. Voltage balancing approaches for diode-clamped multilevel converters using auxiliary capacitor-based circuits. IEEE Trans. Power Electron. 2013, 28, 2111–2124. [Google Scholar] [CrossRef]
- Busquets-Monge, S.; Bordonau, J.; Boroyevich, D.; Somavilla, S. The nearest three virtual space vector PWM—A modulation for the comprehensive neutral-point balancing in the three-level NPC inverter. IEEE Power Electron. Lett. 2004, 2, 11–15. [Google Scholar] [CrossRef]
- Hu, C.; Yu, X.; Holmes, D.G.; Shen, W.; Wang, Q.; Luo, F.; Liu, N. An improved virtual space vector modulation scheme for three-level active neutral-point-clamped inverter. IEEE Trans. Power Electron. 2017, 32, 7419–7434. [Google Scholar] [CrossRef]
- Liu, P.; Duan, S.; Yao, C.; Chen, C. A double modulation wave CBPWM strategy providing neutral-point voltage oscillation elimination and CMV reduction for three-level NPC inverters. IEEE Trans. Ind. Electron. 2018, 65, 16–26. [Google Scholar] [CrossRef]
- Monge, S.B.; Alepuz, S.; Rocabert, J.; Bordonau, J. Pulse width modulations for the comprehensive capacitor voltage balance of n-Level three-leg diode-clamped converters. IEEE Trans. Power Electron. 2009, 24, 1364–1375. [Google Scholar] [CrossRef] [Green Version]
- Charumit, C.; Kinnares, V. Discontinuous SVPWM techniques of three-leg VSI-fed balanced two-phase loads for reduced switching losses and current ripple. IEEE Trans. Power Electron. 2015, 30, 2191–2204. [Google Scholar] [CrossRef]





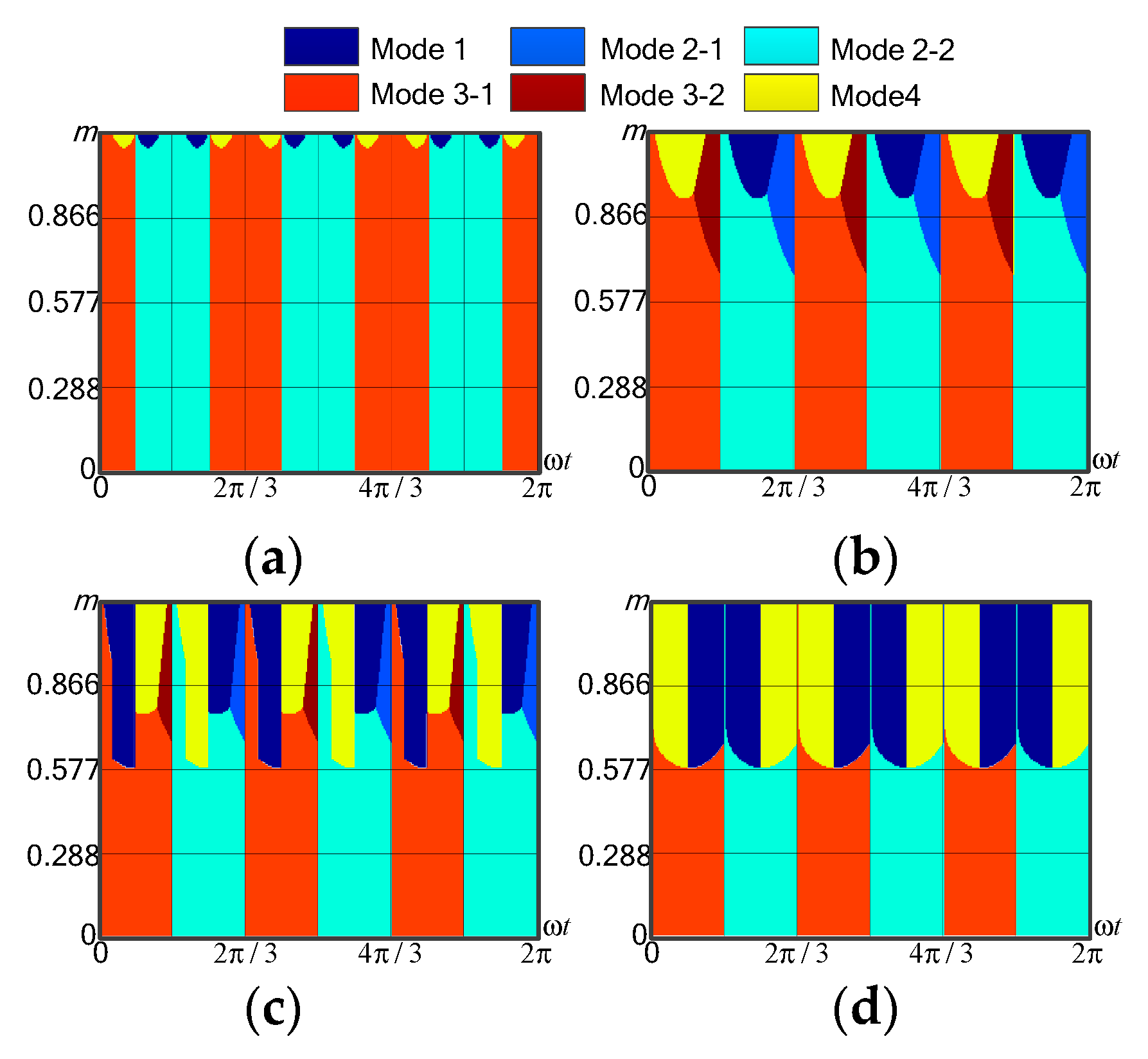




| MAX_PB/MID_N − 1/MIN_N − 2 | MAX_PB/MIN_N − 1/MID_N − 2 | MIN_NB/MAX_N − 1/MID_N − 2 | MIN_NB/MID_N − 1/MAX_N − 2 | |
|---|---|---|---|---|
| umax | 0 | 0 | N − 1 | N − 2 |
| umid | N − 1 | N − 2 | N − 2 | N − 1 |
| umin | N − 2 | N − 1 | 0 | 0 |
| Mode | Duty Ratio | Mode | Duty Ratio |
|---|---|---|---|
| Mode 1: MAX_PB/MID_N − 1/MIN_N − 2 | Mode 2-1: MAX_PB/MIN_N − 1/MID_N − 2 (The output sequence of the phase corresponding to umid is composed of levels 1... , N − 1) | ||
| Mode 2-2: MAX_PB/MIN_N − 1/MID_N − 2 (The output sequence of the phase corresponding to umid is composed of levels 0..., N − 2) | Mode 3-1: MIN_NB/MAX_N − 1/MID_N − 2 (The output sequence of the phase corresponding to umid is composed of levels 1..., N − 1) | ||
| Mode 3-2: MIN_NB/MAX_N − 1/MID_N − 2 (The output sequence of the phase corresponding to umid is composed of levels 0..., N − 2) | Mode 4: MIN_NB/MID_N − 1/MAX_N − 2 |
| Three-Level | Five-Level | ...-Level | N-Level | |
|---|---|---|---|---|
| FRCVBPWM | 3 | 7 | ... | 2N − 3 |
| VSVPWM | 4 | 10 | ... | 3N − 5 |
| Parameter | Value |
|---|---|
| DC side voltage | 200 V |
| Upper and lower capacitance values | 1000 μF |
| Load factor with high PF 1 (ZH1) | 2ejπ/12 Ω |
| Load factor with high PF 2 (ZH2) | 6ejπ/12 Ω |
| Load factor with low PF 1 (ZL1) | 2ej5π/12 Ω |
| Load factor with low PF 2 (ZL2) | 6ej5π/12 Ω |
| Fundamental frequency | 50 Hz |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, J.; Xiao, B.; Gui, Z.; Jiang, W. Full Range Capacitor Voltage Balance PWM Strategy for Diode-Clamped Multilevel Inverter. Electronics 2020, 9, 1263. https://doi.org/10.3390/electronics9081263
Wang J, Wang J, Xiao B, Gui Z, Jiang W. Full Range Capacitor Voltage Balance PWM Strategy for Diode-Clamped Multilevel Inverter. Electronics. 2020; 9(8):1263. https://doi.org/10.3390/electronics9081263
Chicago/Turabian StyleWang, Jinping, Juncan Wang, Benxian Xiao, Zaiyi Gui, and Weidong Jiang. 2020. "Full Range Capacitor Voltage Balance PWM Strategy for Diode-Clamped Multilevel Inverter" Electronics 9, no. 8: 1263. https://doi.org/10.3390/electronics9081263
APA StyleWang, J., Wang, J., Xiao, B., Gui, Z., & Jiang, W. (2020). Full Range Capacitor Voltage Balance PWM Strategy for Diode-Clamped Multilevel Inverter. Electronics, 9(8), 1263. https://doi.org/10.3390/electronics9081263