As URT systems, particularly in large cities, are a combination of complex interrelations, the proposed methodology aims at better capturing the most relevant efficiency and sustainability indicators to optimize transport infrastructures, from planning to real-time operation. Furthermore, as an additional outcome of this methodology, open-data repositories could be enriched with new data sources such as occupancy rates, queueing times, URT network elements capacities (e.g., stations) as well as CO2 footprints.
3.2. Efficiency and Sustainability Key Performance Indicators (KPIs) for URT
The output of EDA is the estimation of state-of-the-art Key Performance Indicators (KPIs), as well as defining new ones based on large-scale data. For instance, new KPIs that can be defined are the number of trains per line that could be estimated based on the travel time and the rail frequencies. Moreover, another KPI, the number of passengers per line, can be estimated from the number of trains and the entry/exit numbers at the stations of a line. Finally, URT CO2 footprint can be estimated from the annual supply (in GWh) and the breakdown by source of the consumed electricity and their CO2 respective footprints.
Additional candidate KPIs that can be modeled after big-data sources are:
Occupancy ratio: considering 100% occupancy ratio equals to all seated places plus 4 standing people per m2.
Trains Per Hour (TPH): the number of trains that enter and leave a given station per hour, monitoring real-time traffic conditions.
Travel time: from origin to destination, involving an URT journey.
Excess Journey Time: is the additional time on top of scheduled time.
The definition, measurement, and analysis of the evolution of KPIs is key to improve the efficiency, security, convenience, and sustainability of existing URT. In fact, the public availability of these KPIs might support that personalized preferences for route selection can be expanded to, for instance, the occupancy rate, for ensuring the availability of seating space, CO2 footprint, or risk of an excess journey time higher than 10 min. Currently the preferences for route selection are quite rigid, the faster route, or manifest preference for a transport mode, although eventually passengers are considering additional factors, as seen when analyzing, anonymously, their routes using Wi-Fi data.
3.3. Data Envelopment Analysis (DEA) for Assessing Efficiency and Sustainability of Public Transport
DEA is a non-parametric method to measure the performance of entities, called Decision-Making Units (DMUs). A DMU can be a factory, a bank branch, a hospital and, as in our paper, a transport mode, an URT line, or an URT station. The initial DEA models consider Constant Return to Scale (CRS or CCR for Charnes, Cooper, and Rodhes), which ignores the fact that different DMUs could be operating at different scales. In our scenario, it would not make any distinction between two URT lines, one with 6 stations and another with 60 stations. To overcome the drawback the Variable Returns to Scale (VRS or BCC for Banker, Charnes, and Cooper) mode [
44] was introduced, ensuring that DMUs are only benchmarked against DMUs of similar size.
Figure 3 presents an example of four DMUs and both CRS and VRS efficiency frontiers. DMU 1 is the only one in CRS efficiency frontier (the only efficient in CRS), maximizing the output/input ratio, whereas DMUs 1, 2 and 3 are in VRS efficiency frontier (the three are efficient in VRS, DMU 2 in low input values and DMU 3 in high input values). Further to VRS, a wide range of DEA models have been designed for measuring efficiency and capacity specializing the original models into different types of problems.
DEA models can be classified in either input-oriented or output-oriented models.
Figure 4 shows an inefficient DMU (DMU 4 or C) to exemplify both approaches. Input-oriented efficiency is BA/CA. Output-oriented efficiency is CD/ED. With input-oriented DEA, a DMU computes the potential savings of inputs in case of operating efficiently (in
Figure 4 reducing the inputs from C to B while providing the same output). In contrast, with output-oriented DEA, a DMU measures its potential output increase given its inputs do not vary (in
Figure 4 increasing the outputs from C to E while using the same amount of input, D. If C were in the frontier, so C = B = E, the efficiency would be 1.
The bad/undesirable outputs, in our case CO
2 emissions, have been treated as inputs reversing traditional DEA models [
45,
46]. This technique is based on the fact that undesirable outputs can be treated as inputs when there is a combination of undesirable and desirable outputs. The objective is to minimize the undesirable output, so considering it as input the function looks for its minimization.
A DEA model is a particular selection of inputs and outputs to analyze the efficiency of DMUs. In previous DEA assessments of transit lines, labor, capital, and energy have been used as inputs and vehicle-kms and passenger-kms have been used as outputs. In the absence of actual costs of labor, fuel/energy, and other operational expenses for individual transport lines, it is reasonable to assume that the cost of operating a line is related to its travel time, round-trip distance, and the number of stations/bus stops [
35]. Additional, when alternative transport options are being considered, the cost is usually the single input whereas travel time savings, patronage (people for each transport mode), and car trips removed are outputs, as shown in [
38], a study that implemented a constant returns of scale–output-oriented (CRS–O) model.
Figure 5 presents our candidate DEA models for: (a) assessing different transport modes from the traveler’s viewpoint (for route planning), and (b) analyzing URT lines from the operator/local authority perspective. The analyzed DMUs are the available transport modes (e.g., URT, bus, car, taxi, walking, and cycling) for the first model, and the available URT lines, usually in the range of 1 to 24 lines (e.g., New York has the highest number of metro lines, 24, followed by Beijing 23, Seoul 23, Shanghai 17, Paris 16, Moscow 14, and Tokyo 13). CRSs are considered for both models, in the transport modes model because route planning is generally used for one traveler (or a small group) and DMUs operate in the same scale, whereas URT lines, for a given URT network, are usually directly comparable.
The selection of inputs and outputs is especially relevant in this scenario due to the large number of available variables and the modest sample size. Following the cardinality constraints introduced in [
39], the recommended number of variables for these two CRS models is 3 (in case of considering VRS it would be 2). The selected variables depend eventually on EDA on the available data; however, a tentative output is the number of passengers, and the models can be considered input-oriented, designed for minimizing inputs when moving a given number of people.
In the first model CO
2 emissions, an undesirable output, have been treated as input, as already mentioned, while considering the overall cost the only true input [
38]. Here, as the model is from the passenger viewpoint, the overall cost is the transport fare (or the direct costs incurred) plus the monetary value of the passenger time. As most of the mobility is associated with commuting to work, the passenger time value can be estimated at the cost of unskilled working time, although this can be configured on a per-passenger basis for personalized route planning. The selection of these two inputs, which combined with the output reaches the recommended number of variables (3), is original, selected after using EDA on the available data, which contrasts with state-of-the-art indicators for route planning such as travel time and fare cost.
With regards to the URT lines model, two tentative inputs, subject to change due to EDA conclusions on the available data for a given URT network, are considered: (1) the number of stations per line as estimate of the capital costs (CAPEX); and (2) weekly frequencies as operating costs (OPEX).
The related literature in public transport generally uses the actual investment as CAPEX; however, when considering URT lines it is neither directly disaggregated per lines, nor comparable across the time (e.g., 20th century vs. 21st century URT lines). The number of stations per line has been selected as input due to the wide availability of this KPI, although generally indirectly, derived from the longest URT route obtained from online route planning/maps services and applications. The line length, although it is a more popular metric and it is also widely available, has not been selected after EDA on the available data (data sourced from [
47]) as long lines usually have generally lower investment due to a higher ratio of above-ground to underground construction, especially in suburban areas where distance between stations tend to be higher. In fact, in [
47], a reference paper in CAPEX in Urban Rail only considers costs per kilometer, a state-of-the-art KPI, which shows a higher variability than the cost per station (e.g., in 16 European URT projects, after discarding 3 outliers, the cost per kilometer ranges from 26.7 to 88.3 M USD
$, whereas the cost per station ranges, for the same projects, from 39.4 M to 83.1 USD
$), with lower standard deviation. Additionally, stations have a share of 25–30% of the infrastructure costs, which favors the selection of the number of stations versus line length as CAPEX.
Regarding OPEX inputs, the related literature in public transport generally uses the price of labor and the price of fuel. However, they are not particularly useful for comparing different lines within the same URT system, as they are set at the operator level. Labor and energy consumption can vary per line, although this level of detailed data is generally not available. Nevertheless, a variable directly related to OPEX that is generally available per line is the number of weekly frequencies. EDA on route planning data shows different patterns for weekdays and for weekends, so the week is the selected period. This input, in combination with the number of stations (the other input), are the selected variables for this DEA model after EDA on publicly available data from URT systems.
The shortlisted inputs (e.g., number of stations and weekly frequencies) have a relevant positive correlation with most of the state-of-the-art inputs, such as the line length, labor force, and number of URT cars, as shown from EDA on [
47] and validated in
Section 4 (e.g., using LU lines key parameters), thus making it a highly representative selection, with higher discriminatory power and simplicity thanks to minimizing redundancy. Furthermore, the shortlisted inputs are directly obtained from route planning services and applications (e.g., Apple Maps, Bing Maps, Google Maps, and services such as Rome2rio.com that, as of today, includes worldwide 176,885 rail lines from 4151 operators), significantly easier than collecting data from other sources, some of them not available publicly. Finally, in case of availability of data, our candidate inputs for a more representative model would be car capacities, consider line branches, and breakdown passengers into time bands (a.m./p.m. peak versus off-peak). The selection of these additional candidate inputs, which add relevant information about URT efficiency, is one of the outcomes of the previous step, defining new indicators from EDA.
These DEA models have been computed using the solver software that comes with the reference DEA book by Cooper [
6]. To illustrate DEA concepts this subsection concludes with an example of DEA analysis, computing the efficiency of London Underground (LU) lines, the use case to validate the proposed models, using for clarity purposes a simplified URT lines DEA model, with a single input, the number of stations, and a single output, the number of passengers.
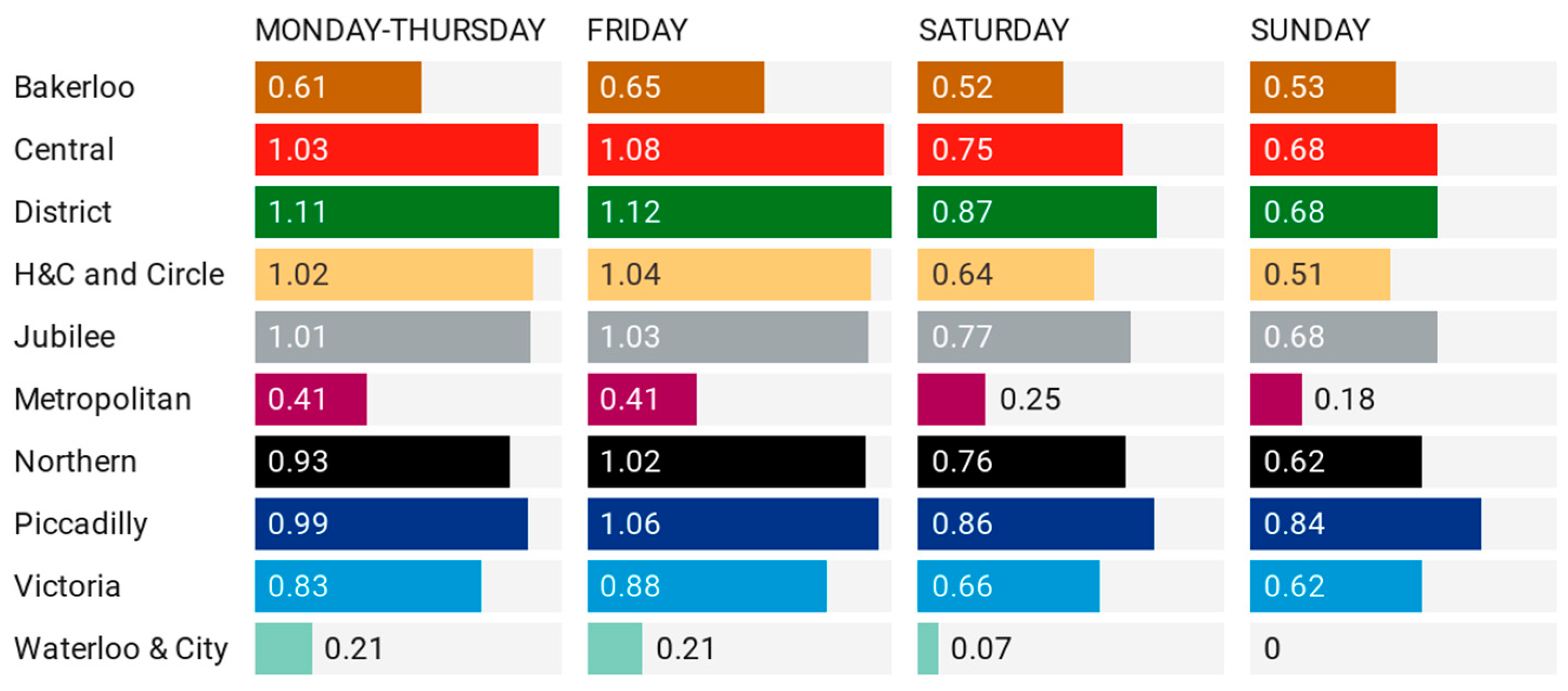
Table 1 summarizes the input and output data, as well as the results provided by the solver. As there is a single input/output the resolution is direct.
The DMU Victoria maximizes the production function (weekly passengers per station), 363,000, so it scores 1. Compared to the first DMU of the list, Bakerloo, with 98,000 passengers per station, 26.9% of 363,000, thus scoring 0.269. This is a CRS model, similar to the two proposed models, so the production function is the same for all DMUs, not varying at scale (as for VRS). Since there is a fixed number of stations, the key parameter is the number of passengers that maximizes the efficiency for each line, so the model has been computed as output-oriented. In fact, the highest ratio, 363,000 passengers per station, has been used to compute the projection of passengers, presented in
Table 1, as well as the difference between the projection and the actual line passengers. Thus, for Bakerloo, ranking 6th in Efficiency, the projection is 9.08 million passengers, +272% over the actual number of passengers, 2.44 million passengers. Alternatively, models can be computed following an input-oriented approach, thus minimizing the required number of stations to achieve the maximum ratio. Thus, for Bakerloo line, it would need to carry 2.44 million passengers with 6.7 stations (2.44/0.353), which is 73.1% less stations (1 minus its efficiency score, 0.269).
Figure 6 represents graphically the 10 DMUs (URT LU lines) using their coordinates (number of passengers as y axis and number of stations as x axis). The production function, CRS, achieves its maximum value for Victoria, thus scoring 1 in efficiency. Please note that the CRS function starts at the origin (0,0). The remaining DMUs score below 1, depending on its ratio passengers/station compared to the optimal. The least efficient is Metropolitan, graphically it can be seen that it has the minimum slope to the origin. The figure also helps to understand how to measure inefficiency. Using Bakerloo as a sample, on the one hand, for input-oriented, the CRS optimal function requires 73,1% less stations (6.7 stations) for moving 2.44 million passengers. On the other hand, for output-oriented, CRS optimal function can move 9.08 million passengers, +272%, with 25 stations.