Battery Energy Management of Autonomous Electric Vehicles Using Computationally Inexpensive Model Predictive Control

Abstract

With the emergence of vehicle-communication technologies, many researchers have strongly focused their interest in vehicle energy-efficiency control using this connectivity. For instance, the exploitation of preview traffic enables the vehicle to plan its speed and position trajectories given a prediction horizon so that energy consumption is minimized. To handle the strong uncertainties in the traffic model in the future, a constrained controller is generally employed in the existing researches. However, its expensive computational feature largely prevents its commercialization. This paper addresses computational burden of the constrained controller by proposing a computationally tractable model prediction control (MPC) for real-time implementation in autonomous electric vehicles. We present several remedies to achieve a computationally manageable constrained control, and analyze its real-time computation feasibility and effectiveness in various driving conditions. In particular, both warmstarting and move-blocking methods could relax the computations significantly. Through the validations, we confirm the effectiveness of the proposed approach while maintaining good performance compared to other alternative schemes.

1. Introduction

For the last few years, many experts in the field of automotive research have claimed that self-driving cars will become commonplace in the near future. Although there are still technical difficulties for commercializing self-driving cars, at least a certain degree of automation in the vehicles is expected to be available soon [1,2].

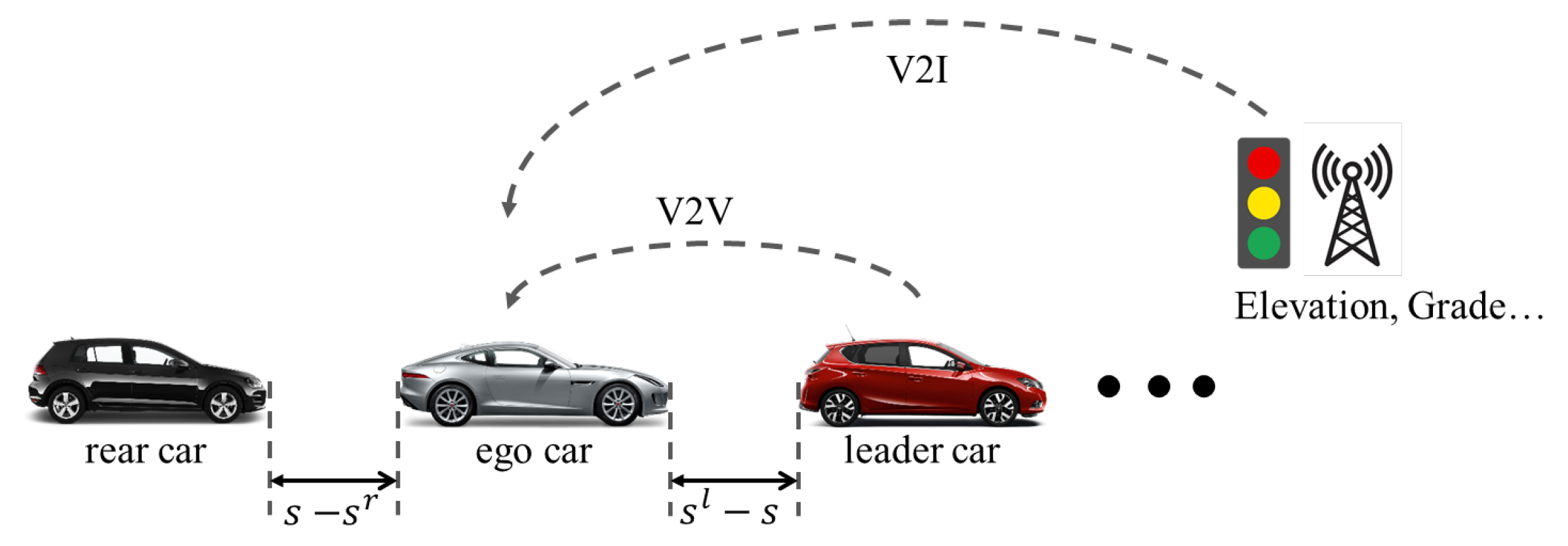
With the advent of new features in self-driving cars, novel approaches to optimize the energy efficiency of vehicles have become available. In general, human-driver behaviors are based on their own driving habits on the roads, which are not consistent with the traffic flow [3]. Self-driving cars, in contrast, can plan optimally their trajectories by exploiting real-time traffic information [4,5,6]. For example, many short and long-range traffic information using vehicle-to-vehicle (V2V), vehicle-to-infrastructure (V2I), and, more generally, vehicle-to-everything (V2X) communication (see Figure 1) provide useful traffic information, which the self-driving cars can effectively use in real time. For example, the geometry information of the route is available through the pre-loaded maps and the future traffic density is also available through the V2X technologies. Therefore, unlike human drivers, self-driving cars can make suitable decisions based on real-time traffic flow so as to optimize their energy efficiency.

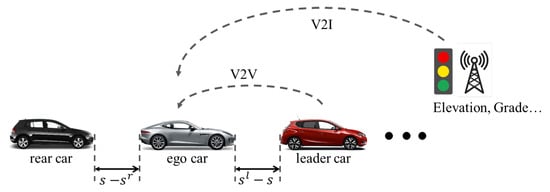
Figure 1. Increased levels of automation and connectivity through vehicle-to-everything (V2X) communication.

However, since the traffic dynamics are complex and nonlinear, there is a non-negligible computational burden associated with long-term real-time traffic prediction. Moreover, since the traffic predicted by the self-driving car in the long run become uncertain (e.g., traffic disturbances, unexpected changes in human-driver behavior), it is required to choose an appropriate length of the prediction horizon to effectively exploit the current traffic information.

Although there have been numerous researches that show the benefits of vehicle speed- and position-trajectory planning in terms of energy efficiency, to the best of our knowledge, practical aspects, such as the length of the prediction horizon and its relative computational burden, have not been discussed in the existing literature on self-driving cars. In order to achieve high performance while ensuring computational feasibility, this paper deals with the above-mentioned practical concerns for real production vehicles.

Also, in this paper, the battery-electric vehicle (BEV) is assumed to be ego vehicle that needs to be controlled, so, using connectivity technologies (i.e., V2X), the optimal battery energy management is our ultimate goal.

1.1. Literature Review

So far, there have been many research interests in the optimization of energy efficiency using constrained control theories. In general, both vehicle- and powertrain-level optimizations are used to achieve specific control objectives while ensuring constraint satisfaction. For example, the vehicle speed and position are planned in a way that minimizes the energy consumption, while at the same time the operating points in the powertrain such as engine, motor, and transmission are moved to the optimum area.

In particular, the BEV that is entirely powered by the electric motors is promising platform for the autonomous vehicles due to its environmental benefits and low operating cost. In [7], as compared to the internal-combustion engine vehicle, the benefit of BEV in terms of energy requirement per unit distance has been confirmed when both powertrain types were utilized as the fully autonomous vehicles. In addition, the synergies between shared autonomous vehicle fleets and electric vehicle has also been proposed in [8]. For this reason, this paper also employs the BEV as our vehicle platform and the minimization of battery energy consumption of BEV has been pursued.

To achieve this goal, one representative method is to adopt dynamic programming (DP), which ensures global optimality by exploring all possible combinations of the trajectories. DP requires, however, the entire traffic prediction before the trip. In [9], global optimum speed trajectory of the vehicle could be obtained using DP, but future traffic environments even including pre-known of the leading vehicle’s speed profiles are assumed to be given initially. That is, DP is mainly suitable for offline computation and is thus not implementable in real time due to the heavy computational burden. However, the control performance using DP is meaningful as a benchmark to investigate the maximum achievable control performance.

To manage the computational complexity of DP, another well-known trajectory optimization approach is Pontryagin Minimum Principle (PMP), which has been utilized in [10], for example. Note that only the necessary condition for optimality is guaranteed, and the method still requires a long-term prediction. Moreover, two-point boundary value problem associated with PMP conditions cannot be easily solved numerically. Unfortunately, most literature that employ the PMP [10,11] do not handle the tractability of their optimal controller rigorously.

Although these two approaches, i.e., DP and PMP, have shown the effectiveness when planning the optimal trajectory, these methods are usually effective for the deterministic system. However, the interactions between the road participants in the traffic cannot be modelled in deterministic way. To handle the such uncertainties in the traffic prediction, stochastic DP [12], Q-learning-based PMP [13], and reinforcement learning [14,15] have been considered, but the analysis on the practical aspects like computational tractability is omitted. Additionally, since these methods are based on Markov decision process, where the relationship between the control action and probability are pre-determined, these methods cannot ensure robustness when the vehicle is in an unexpected situation [16].

The above-mentioned two approaches, that is, DP and PMP, are the most popular methods and provide an optimal-state-trajectory framework. However, as discussed, the heavy computational burden prevents the introduction of such techniques in production vehicles. Also, the requirement of long-term preview information in DP and PMP is not usually available in the real-world traffic since the traffic is significantly influenced by the unexpected uncertainties. To address this, the method that re-calculate the optimal trajectory once the new traffic information become available can be considered. More appropriately, the popular receding-horizon control, model predictive control (MPC) [17,18], can be used to update a short-term traffic prediction at each time instant, which effectively approximates the long-term traffic prediction of DP and PMP by means of real-time trajectory corrections using the current state estimate.

Unlike the internal-combustion engine vehicle where the pulse-and-glide driving strategy is assumed to the optimal way to increase the fuel economy, it is well-known that speed smoothing of the BEV can optimize the energy efficiency of the electric motor [19]. Therefore, the speed trajectory of the BEV should be flatten as much as possible for the prediction horizon to prevent battery spikes, while satisfying the safety constraints. Also, the battery temperature that significantly influences the battery efficiency should be maintained in the appropriate ranges. Taking these all into consideration, we can conclude that the MPC that can handle the state and control constraints is appropriate method for the battery energy management of the autonomous BEV.

In [20,21,22,23], MPC is designed using short-term prediction and it has been confirmed that, to a certain degree, this method is effective to improve energy efficiency. However, the computational burdens depending on the several important factors in MPC such as sampling-time and length of the prediction time were not analyzed thoroughly. To the best of our knowledge, computational load reduction in MPC for real-time computational feasibility has not been discussed in the literature of self-driving cars, and this paper will reveal the critical factors determining the computational burden in MPC. Finally, several remedies to increase the feasibility of the MPC will be suggested.

1.2. Research Contribution

The primary contributions of this paper can be summarized as follows.

First, to overcome the technical shortcomings of a nominal MPC, several methods that enable the real-time implementation of the optimizer are proposed, and its effectiveness is verified through various case studies. Depending on the driving conditions, the computational-time constraint violation rate is reduced around 35% compared to the one of a nominal MPC, but the control performance is similar to each other, which is our central argument.

Secondly, an appropriate prediction-horizon selection for MPC for BEVs control is studied by comparing the performances with the one of DP. In most works employing MPC for trajectory optimization and control, the procedure determining the horizon length is omitted, but our approach starts with this important aspect considering the implementation in real hardware. As compared to the control results of nominal MPC and DP, the proposed method can reduce the computational burden significantly while minimizing the performance degradation in terms of the battery state-of-charge (SOC) reduction.

1.3. Paper Organization

This paper is organized as follows. Section 2 introduces the vehicle- and battery-dynamics models, and the optimization control problem is formulated in Section 3. Next, the central part of this paper is described in Section 4, which proposes a method to reduce the computational complexity of MPC. Section 6 demonstrates the effectiveness of our approach through simulations, and Section 7 concludes the paper.

2. Vehicle and Battery Dynamics

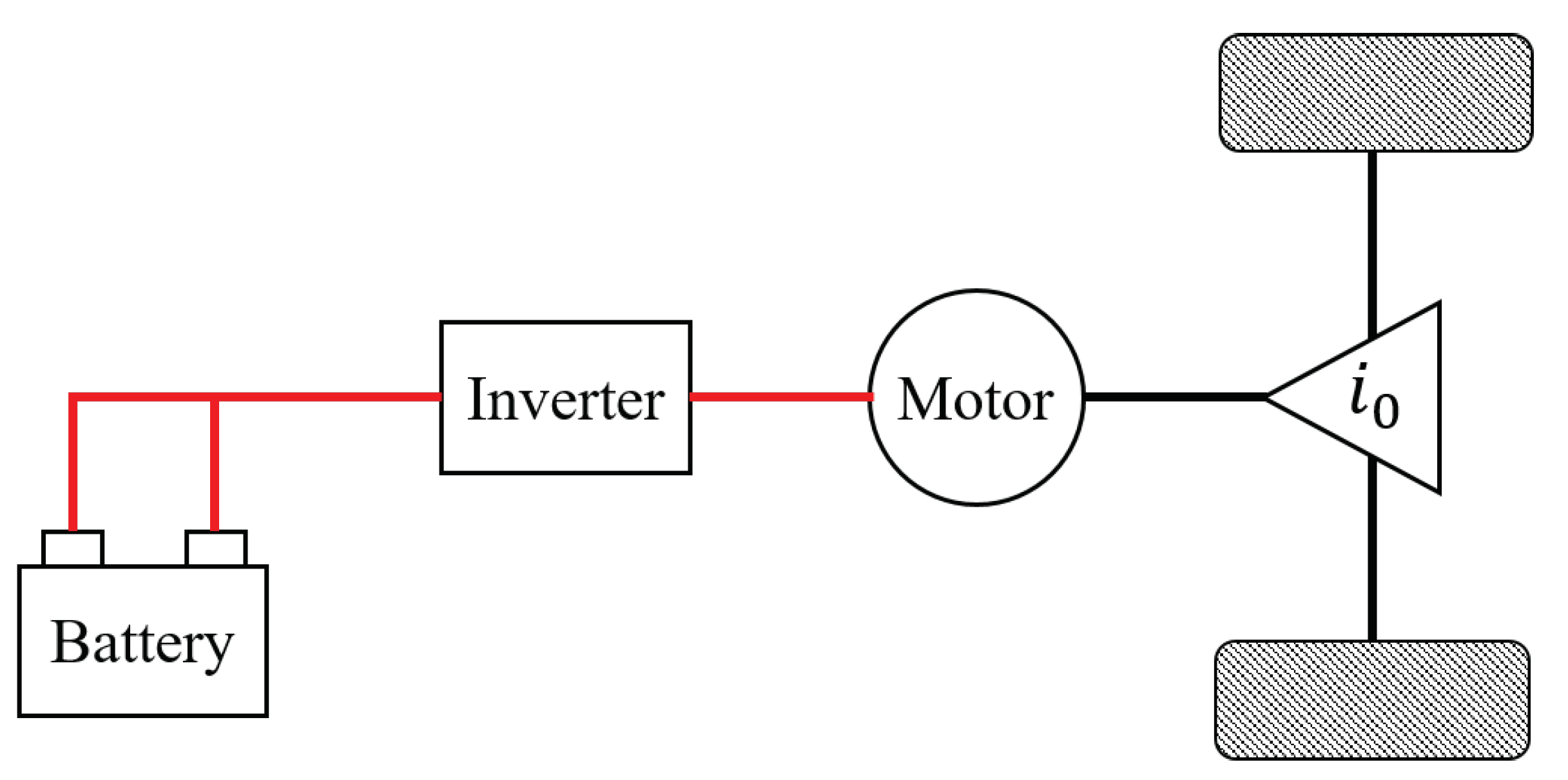
Since the interest of this study is to optimize the energy efficiency of the BEVs, relevant vehicle and powertrain dynamics are modeled first. Note that, compared to other types of vehicles, BEVs have a simple structure, as shown in Figure 2. Since the power is transmitted through a single path, the energy loss is only determined by the efficiency of each actuator depending on the operating points. Before designing the controller, the central parts of BEVs are simplified and modeled in this section.

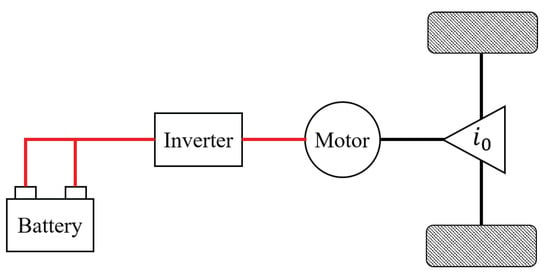
Figure 2. Schematic of a battery-electric vehicle.

2.1. Vehicle Longitudinal Dynamics

Consider the point-mass longitudinal dynamics of the vehicle. We assume that the effective mass of the vehicle, which normally accounts for the vehicle static and rotational effect together, is approximately equivalent to the vehicle mass [24]. Accordingly, the continuous-time longitudinal dynamics are given by

$$\begin{array}{cc}\dot{s}=v,\hfill & \hfill \end{array}$$

(1)

$$\begin{array}{c}\dot{v}=\left(\frac{T_{\mathrm{m}}+T_{\mathrm{b}}}{mr}\right)i_0-\frac{\rho A_{\mathrm{f}}{C}_{\mathrm{d}}{v}^2}{2m}-gsin\theta -\gamma gcos\theta ,\hfill \end{array}$$

(2)

where $s\in \mathbb{R}$ is the vehicle position, $v\in \mathbb{R}$ is the vehicle speed, $m>0$ is the vehicle mass, $T_{\mathrm{m}}\in \mathbb{R}$ and $T_{\mathrm{b}}\in \mathbb{R}$ are the motor and friction brake torques, respectively, $r>0$ is the wheel radius, $i_0>0$ is the final gear ratio, $\rho >0$ is the air density, $A_{\mathrm{f}}>0$ is the frontal area of the vehicle, $C_{\mathrm{d}}\ge 0$ is the aerodynamic drag coefficient, $\theta \in (-\pi /2,\pi /2)$ is the road inclination that influences the energy consumption significantly but assumed to be zero in this paper, $g>0$ is the gravitational constant, and $\gamma \ge 0$ is the coefficient of rolling resistance. Note that $\theta$ is a function of the position, that is, $\theta \left(s\right),$ and that the rolling friction is kinetic, that is, $\gamma =0$ for $v=0.$ In the remainder of this paper, we consider $T_{\mathrm{b}}=0$ without a significant loss of generality.

In actual fact, several parameters that are assumed to be constant such as m and $\theta$ influence the vehicle’s energy efficiency significantly. Also, the other constant parameters vary depending on driving conditions, so the parameter estimations are needed for the accurate energy-efficiency calculation. However, for simplicity, this paper does not consider the varying-parameters, but it should be treated in the future.

To apply digital control methods, the continuous-time mode (Equations (1) and (2)) is discretized using the Euler-forward method

$$x_{k+1}^{\mathrm{v}}=x_k^{\mathrm{v}}+g^{\mathrm{v}}(x_k^{\mathrm{v}},u_k^{\mathrm{v}})T_{\mathrm{s}},$$

(3)

where $x_k^{\mathrm{v}}\triangleq {\left[s_k{v}_k\right]}^{\mathrm{T}}$, $u_k^{\mathrm{v}}\triangleq T_{m,k}$, $g^{\mathrm{v}}:{\mathbb{R}}^2\times \mathbb{R}\to {\mathbb{R}}^2$ is the vehicle dynamics function vector that aggregates in a column the right-hand side of Equations (1) and (2), and $T_{\mathrm{s}}>0$ is the sampling time.

2.2. Battery Dynamics

2.2.1. Continuous-Time SOC Dynamics

The continuous-time battery SOC dynamics is given by

$$\dot{\mathrm{SOC}}=-\frac{I_{\mathrm{b}}}{C_{\mathrm{b}}},$$

(4)

where $\mathrm{SOC}\in [0,1]$ is the state of charge of the battery, $I_{\mathrm{b}}\in \mathbb{R}$ is the battery current, and $C_{\mathrm{b}}>0$ is the battery capacity and is assumed to be constant.

The battery current $I_{\mathrm{b}}$ is a function of the open-circuit voltage $V_{\mathrm{oc}}\in \mathbb{R}$, the battery resistance $R_{\mathrm{b}}>0$, and the battery-power consumption $P_{\mathrm{b}}\in \mathbb{R}$ as,

$$I_{\mathrm{b}}=\frac{V_{\mathrm{oc}}-\sqrt{V_{\mathrm{oc}}^2-4R_{\mathrm{b}}{P}_{\mathrm{b}}}}{2R_{\mathrm{b}}},$$

(5)

where

$$P_{\mathrm{b}}=\left\{\begin{array}{cc}\frac{P_{\mathrm{m}}}{{\eta }_{\mathrm{b}}^{+}}\hfill & \mathrm{for}{P}_{\mathrm{m}}\ge 0,\hfill \\ \frac{P_{\mathrm{m}}}{{\eta }_{\mathrm{b}}^{-}}\hfill & \mathrm{for}{P}_{\mathrm{m}}<0,\hfill \end{array}\right.$$

(6)

${\eta }_{\mathrm{b}}^{+}\in (0,1)$ is the battery-depletion efficiency, ${\eta }_{\mathrm{b}}^{-}>1$ is the battery-recharge efficiency, and $P_{\mathrm{m}}$ is the motor-output power.

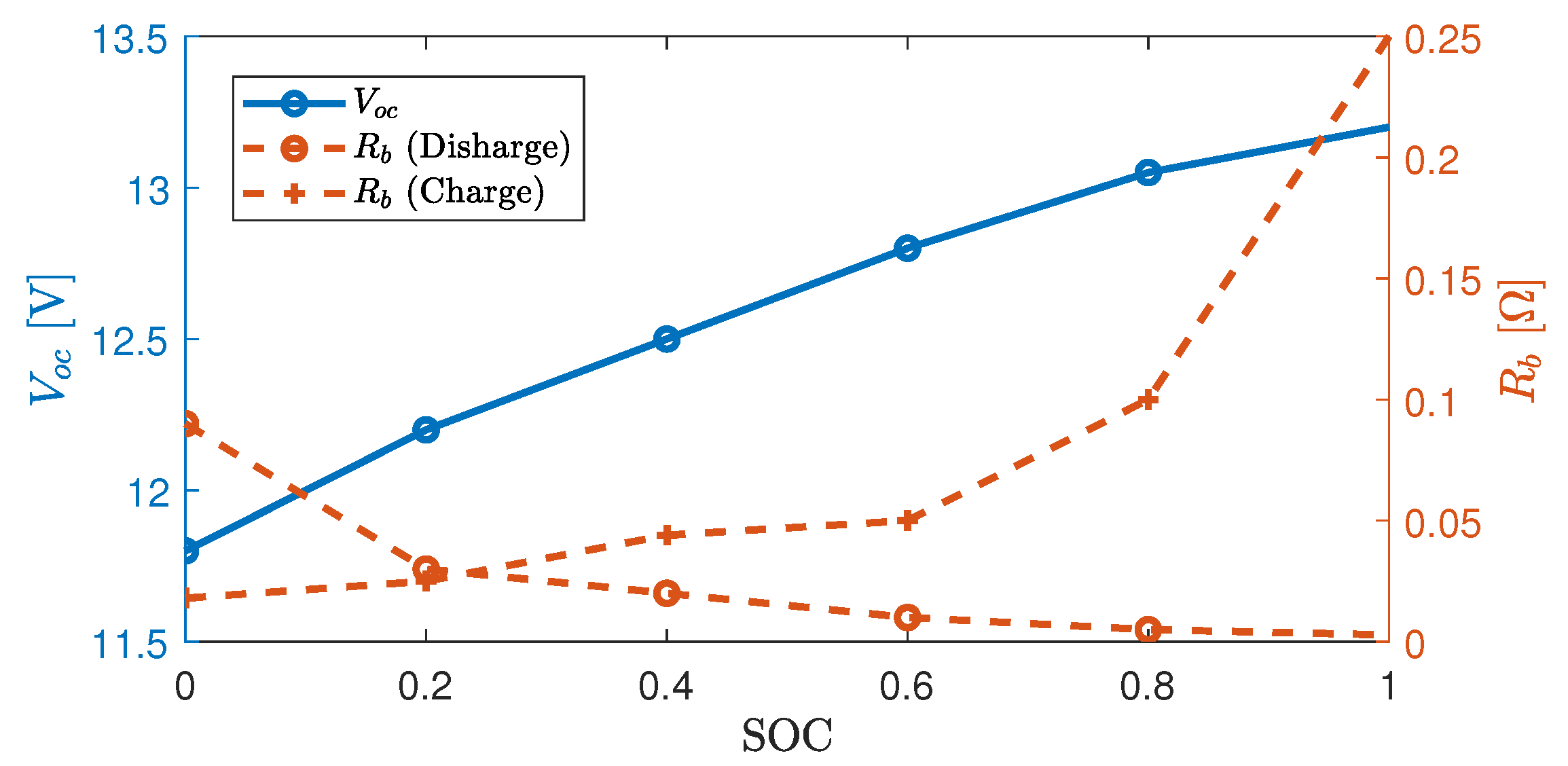
The SOC dynamics is captured more accurately by accounting for the variations of $V_{\mathrm{oc}}$ and $R_{\mathrm{b}}$, which are functions of SOC, as illustrated in Figure 3.

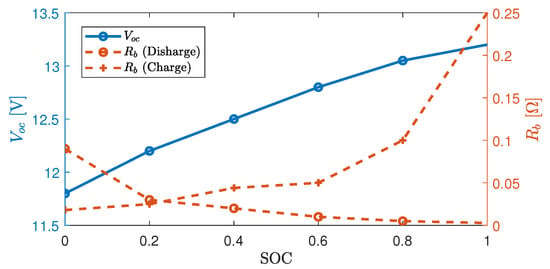
Figure 3. Variation of the open-circuit voltage $V_{\mathrm{oc}}$ and internal resistance $R_{\mathrm{b}}$ as functions of state-of-charge (SOC).

Note that, in practice, the variations of $V_{\mathrm{oc}}$ and $R_{\mathrm{b}}$ are relatively small compared to $P_{\mathrm{b}}$ during driving time. Therefore, the battery-output power $P_{\mathrm{b}}$ mainly contributes to the battery SOC changes in Equation (4). In general, $P_{\mathrm{b}}$ is used as a control input in the battery dynamics. Note that $P_{\mathrm{b}}$ depends also on the motor-output power $P_{\mathrm{m}},$ whose dynamics are described hereafter.

2.2.2. Motor Dynamics

The motor-output power is determined by the motor torque $T_{\mathrm{m}}$, motor speed ${\omega }_{\mathrm{m}}\triangleq \frac{v}{r}{i}_0,$ and motor efficiency ${\eta }_{\mathrm{m}}$ as

$$P_{\mathrm{m}}=\frac{T_{\mathrm{m}}{\omega }_{\mathrm{m}}}{{\eta }_{\mathrm{m}}(T_{\mathrm{m}},{\omega }_{\mathrm{m}})}.$$

(7)

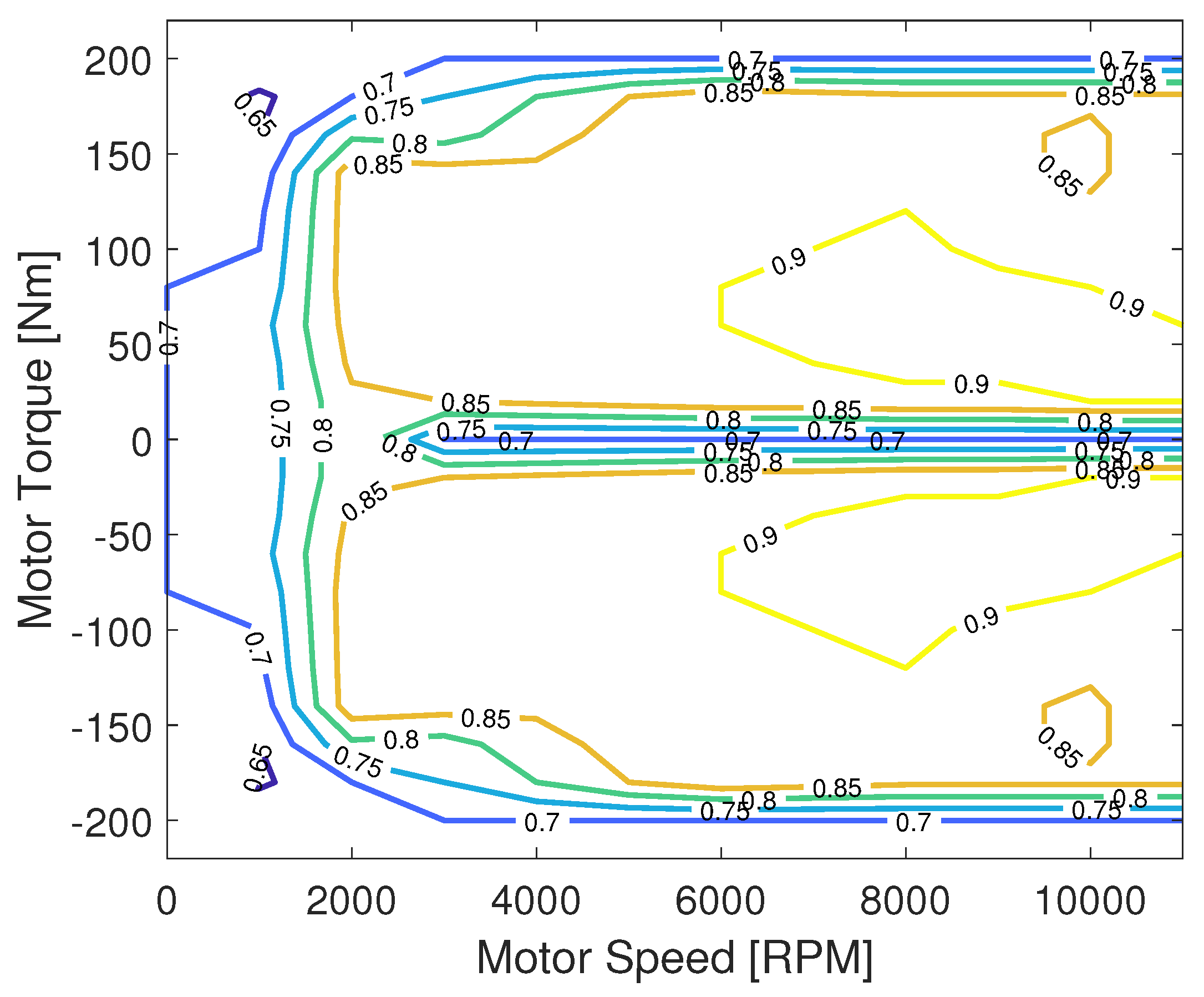
Note that the motor efficiency ${\eta }_{\mathrm{m}}$ is a function of the motor operating points, which depend on $T_{\mathrm{m}}$ and $w_{\mathrm{m}}$ (see Figure 4). Furthermore, we assume that the motor efficiency is mirrored in terms of propulsion and regenerative braking, that is, ${\eta }_{\mathrm{m}}(T_{\mathrm{m}},{\omega }_{\mathrm{m}})={\eta }_{\mathrm{m}}(-T_{\mathrm{m}},{\omega }_{\mathrm{m}})$.

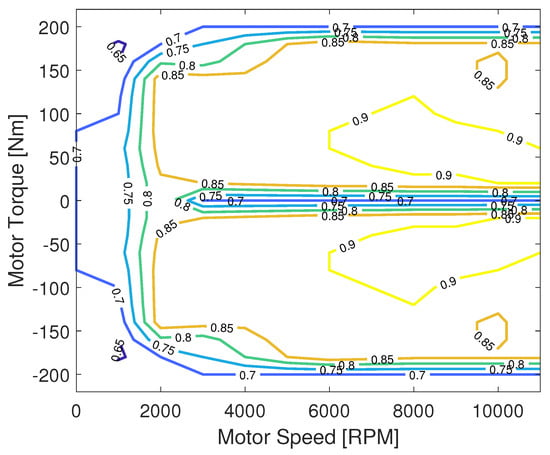
Figure 4. Motor efficiency map.

2.2.3. Discrete-Time Battery Dynamics

By combining Equations (4)–(7) and using the Euler-forward method, the continuous-time SOC dynamics Equation (4) can be discretized as

$${\mathrm{SOC}}_{k+1}={\mathrm{SOC}}_k+g^{\mathrm{s}}({\mathrm{SOC}}_k,T_{\mathrm{m},k})T_{\mathrm{s}},$$

(8)

where $g^{\mathrm{s}}:[0,1]\times \mathbb{R}\to [0,1]$ is the SOC dynamics function vector, which aggregates as a column the right-hand side of Equations (4) and (5).

2.3. Discrete-Time Model for Implementation

The discrete-time model of the vehicle and battery dynamics for digital implementation are given by

$$\begin{array}{cc}\hfill x_{k+1}& =x_k+f(x_k,u_k)T_{\mathrm{s}},\hfill \end{array}$$

(9)

where $x_k\triangleq {\left[s_k{v}_k{\mathrm{SOC}}_k\right]}^{\mathrm{T}},$ $u_k\triangleq T_{\mathrm{m}},$ and $f\triangleq {[{\left(g^{\mathrm{v}}\right)}^{\mathrm{T}}{\left(g^{\mathrm{s}}\right)}^{\mathrm{T}}]}^{\mathrm{T}}.$ In this paper, we assume that, for all $k\ge 0,$ the state $x_k$ is available, and thus, an observer needs not to be built. Based on Equation (9), the optimization control problem and several optimization methods will be described in Section 3.

3. Optimal Control Problem Formulation

In this paper, we assume that the controlled car (ego car) is driving between a leader and rear car. Additionally, the ego car is able to send and receive information through V2X communication (see Figure 1). In this case scenario, the ego car can plan its future trip by predicting the traffic dynamics while ensuring safety constraints between the leader and rear cars. Assuming that the rear car behaves rationally, it is possible to ignore its behavior in the optimization formulation [25]. In addition, this paper assumes only a single lane, which means that no lane changing is considered. However, in reality, such interactions between the ego vehicle and adjacent vehicles might occur frequently and influence on the ego vehicle’s trajectory planning. In this paper, however, we exclude the above-mentioned situations, which are left to our future work.

The objective of the optimization formulation is to minimize the battery-output power over a given route by optimizing the speed profile.

Let $N>0$ be the discrete-time prediction horizon, define ${\widehat{x}}_{i|k}\triangleq {[{\widehat{s}}_{i|k}{\widehat{v}}_{i|k}{\widehat{\mathrm{SOC}}}_{i|k}]}^{\mathrm{T}}$ as the i-step-ahead state predicted at step k, let ${\widehat{\omega }}_{\mathrm{m},i|k}$ be the i-step-ahead motor speed predicted at step $k,$ and define ${\widehat{U}}_k\triangleq {[{\widehat{u}}_{0|k}\cdots {\widehat{u}}_{N-1|k}]}^{\mathrm{T}}\in {\mathbb{R}}^N$ as the sequence of control inputs computed at step $k.$ Using Equation (9), the optimization problem at step k is given by

$$\begin{array}{cc}\underset{{\widehat{U}}_k}{min}{J}_k({\widehat{U}}_k)=\sum _{i=0}^{N-1}{P}_{b,i}({\widehat{u}}_{i|k},{\widehat{x}}_{i|k}),\hfill & \hfill \\ \mathrm{s}.\mathrm{t}.\hfill & \hfill \end{array}$$

(10a)

$$\begin{array}{cc}{\widehat{x}}_{i+1|k}={\widehat{x}}_{i|k}+f({\widehat{x}}_{i|k},{\widehat{u}}_{i|k})T_{\mathrm{s}},\hfill & \hfill \end{array}$$

(10b)

$$\begin{array}{cc}{\widehat{x}}_{0|k}={\left[s_k{v}_k{\mathrm{SOC}}_k\right]}^{\mathrm{T}},\hfill & \hfill \end{array}$$

(10c)

$$\begin{array}{cc}{v}_{\min }\le {\widehat{v}}_{i+1|k}\le v_{\max },\hfill & \hfill \end{array}$$

(10d)

$$\begin{array}{c}{\tau }_{\min }({\widehat{v}}_{i+1|k}+\delta )\le s_{i+1}^l-{\widehat{s}}_{i+1|k}\le {\tau }_{\max }({\widehat{v}}_{i+1|k}+\delta )\hfill \end{array}$$

(10e)

$$\begin{array}{cc}{\mathrm{SOC}}_{\min }\le {\widehat{\mathrm{SOC}}}_{i+1|k}\le {\mathrm{SOC}}_{\max }\hfill & \hfill \end{array}$$

(10f)

$$\begin{array}{ccc}\hfill & T_{\mathrm{m},i}^{\min }\left({\widehat{\omega }}_{\mathrm{m},i|k}\right)\le {\widehat{u}}_{i|k}\le T_{\mathrm{m},i}^{\max }\left({\widehat{\omega }}_{\mathrm{m},i|k}\right)\hfill & \hfill \end{array}$$

(10g)

$$\begin{array}{cc}i=0,\cdots ,N-1,\hfill & \hfill \end{array}$$

(10h)

where $s^l$ is the deterministic position of leader car provided by driving cycle, $0\le v_{\min }<v_{\max },$ $0<{\tau }_{\min }<{\tau }_{\max }$ are the minimum/maximum time headways, $\delta >0$ is the velocity bound, ${\mathrm{SOC}}_{\min }<{\mathrm{SOC}}_{\max }\in [0,1],$ and $T_{\mathrm{m},i}^{\min }:\mathbb{R}\to \mathbb{R}$ and $T_{\mathrm{m},i}^{\max }:\mathbb{R}\to \mathbb{R}$ are given constraint functions at step j that depend on ${\widehat{\omega }}_{\mathrm{m},i|k}.$

Note that the problem formulation (10a)–(10h) is a receding-horizon problem formulation if the problem must be solved for all $k\ge 0.$ The terms (10d)–(10f) are the state constraints, and (10g) is the control constraint. The constraint bounds are reasonable values according to the driving conditions on US roads [26]. In particular, depending on the ego car’s speed, (10e) indicates the reasonable varying position constraint between the ego car and leader car.

4. Practical Considerations for Real-Time Implementation of MPC

The receding-horizon control problem (10a)–(10h) can be solved using standard nonlinear solvers. We expect superior control performance in MPC for long prediction horizons in the case where the model matches the plant and the solver gives the global optimal solution at each step. However, for implementation reasons, an appropriate prediction-horizon length should be chosen.

In this section, we first give the performance benchmark of DP when the prediction horizon is the entire trip of the ego car. Next, for real-time implementation in MPC, we propose a simplification of the cost function in order to reduce computational complexity. A numerical analysis is carried out to highlight the impact of an increase in N on performance and computational feasibility of MPC.

All simulations presented in this paper are carried out using MATLAB R2020a, Windows 10, Intel Core i7-9700 CPU @ 3.00 Ghz, and 16 GB RAM. Furthermore, the continuous-time dynamics are integrated by ode45 and the control is constant between samples.

4.1. Dynamic Programming

In this subsection, the deterministic DP algorithm is employed to solve (10a)–(10h) for the entire trip. In general, DP is not applicable in practice because DP requires all future reference inputs and disturbances in advance, indicating that DP is a noncausal controller [27,28]. For example, the entire speed trajectory of the leader car should be provided, which is not reasonable in reality. However, in many applications, the control performance using DP is usually assumed to be the best solution that guarantees global optimality. Therefore, employing DP is meaningful as a benchmark, with which the control performance of other causal controllers can be compared. In this paper, we will compare MPC with DP benchmark performance.

DP solves the optimization problem (10a)–(10h) by setting $k=0$ and $N=N_{\mathrm{dp}},$ where $N_{\mathrm{dp}}>0$ is the discrete-time prediction horizon of the entire trip. Note that, as DP is used once and thus does not depend on the actual time step $k,$ we omit the index k in (10a)–(10h) in this subsection.

For all $j\ge 0,$ let ${\mathcal{X}}_j$ be the feasible state-constraint set (10d)–(10f) at predicted step j, let ${\mathcal{X}}_N$ be the terminal state-constraint set, and let ${\mathcal{U}}_j$ be the feasible control-constraint set (10g) at predicted step j. Next, define the discretized-state set $\tilde{X}\triangleq \{{\tilde{x}}_1,\dots ,{\tilde{x}}_i,\dots ,{\tilde{x}}_{\ell }\}\subset {\mathcal{X}}_j,$ for all $0\le j\le N,$ where ${\tilde{x}}_i$ is the i-th node of $\tilde{X},$$i\in \{1,\dots ,\ell \},$ and $\ell >0$ is the total number of discretized states in $\tilde{X}$.

Using the principle of optimality [29], the optimal control policy for the node ${\tilde{x}}_i$ is obtained by backward induction, where ${\widehat{x}}_0={\tilde{x}}_i$ in (10c). In particular, starting from the optimal final stage cost

$$\begin{array}{c}\hfill {\mathcal{J}}_N\left({\tilde{x}}_i\right)=\underset{{\widehat{u}}_N\in {\mathcal{U}}_N}{min}{P}_{\mathrm{b},N}({\widehat{u}}_N,{\tilde{x}}_i),\end{array}$$

(11)

where $N=N_{\mathrm{dp}},$ the DP backward recursion is given by

$$\begin{array}{c}\hfill {\mathcal{J}}_j\left({\tilde{x}}_i\right)=\underset{{\widehat{u}}_j\in {\mathcal{U}}_j}{min}[P_{b,j}({\widehat{u}}_j,{\tilde{x}}_i)\\ \hfill +{\mathcal{J}}_{j+1}({\tilde{x}}_i+f({\tilde{x}}_i,{\widehat{u}}_j)T_{\mathrm{s}})],\end{array}$$

(12)

where $j\in \{N-1,\dots ,0\}.$ Accordingly, the optimal control policy $\pi$ for each node ${\tilde{x}}_i$ is mapped by

$$\pi =\{{\mu }_0\left(x\right),{\mu }_1\left(x\right),\cdots ,{\mu }_{N_{\mathrm{dp}}-1}\left(x\right)\},$$

(13)

where ${\mu }_i:{\mathbb{R}}^3\to \mathbb{R}$ is the mapping function and $i=0,\dots ,N_{\mathrm{dp}}-1.$ Accordingly, Equation (13) can be used to find the optimal control input in a forward simulation.

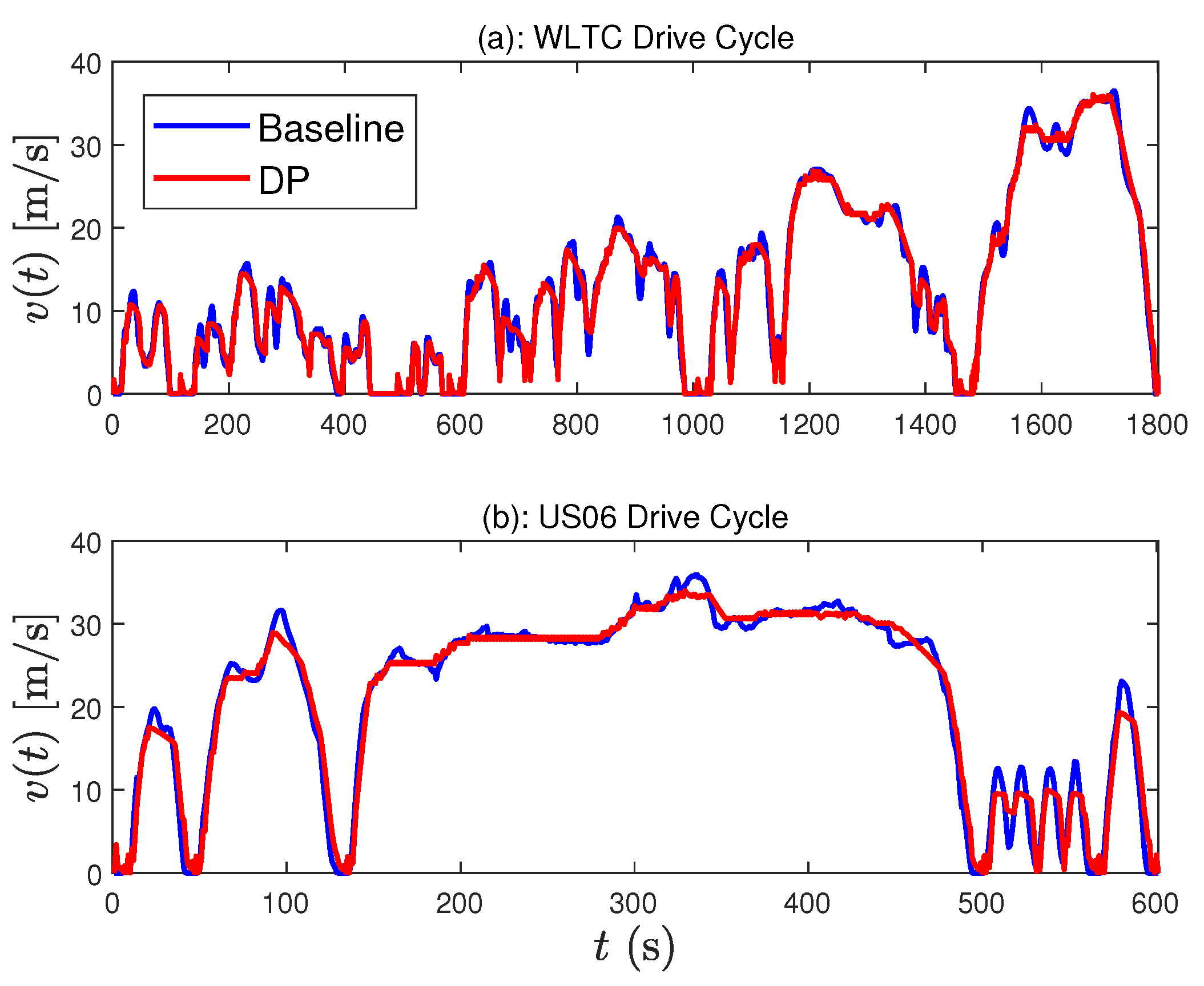
In this paper, we use the generic DP function in Matlab, that is, dpm [30]. An appropriate grid number for the state and control variables must be specified to avoid the curse of dimensionality. Doing so, the computation is completed approximately in five minutes while satisfying all constraints, as illustrated in Figure 5. The entire vehicle speed trajectories for two drive cycles, i.e., WLTC, US06, are optimized so as to minimize the cost and enforce the constraints. One distinguished feature is that the speed profile when applying DP is flattened as much as possible to prevent spikes in the battery current.

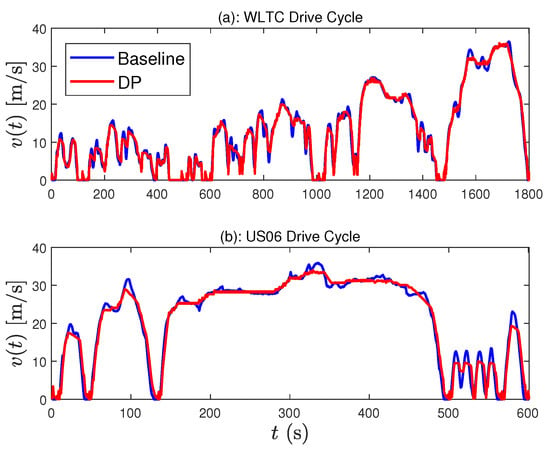
Figure 5. Comparison of the speed trajectories obtained by dynamic programming (DP) and human-driver maneuvers with (a) WLTC and (b) US06.

The battery SOC consumption for each drive cycle is compared in Table 1, which shows that DP can significantly improve the energy efficiency of BEV around 14 to 20%. These control performances are considered ideal, so we will use these as our benchmark. However, as mentioned, DP is not implementable in real time due to the computational complexity and strong assumptions on command and disturbance preview.

Table 1. Comparison of the battery state-of-charge (SOC) consumption (%) with the speed profiles obtained by dynamic programming (DP) and nominal speed.

Drive Cycle	Baseline	DP	Improvement (%)
WLTC	17.55	14.96	14.76
US06	13.41	10.74	19.90

Since the cost function is nonconvex and the dynamics are nonlinear, several local minima may be presented. However, as DP computes all costs for every node by backward induction, it can be said that the obtained performance ensures global optimality.

4.2. Model Predictive Control

4.2.1. Quadratic Cost Simplification

In the previous section, the nonlinear function $P_{\mathrm{b}}$ is used as a cost when applying DP, which gives a globally optimal result by backward induction. However, for real-time computation, a computationally tractable method is required. In particular, we show in this section that the nonlinear cost $P_{\mathrm{b}}$ can be approximated by a quadratic cost.

In [19], by assuming constant actuator efficiencies, the motor power $P_{\mathrm{b}}$ can be simplified as

$$P_{\mathrm{b}}\approx P_{\mathrm{m}}\approx \frac{T_{\mathrm{m}}v}{r}{i}_0+\alpha T_{\mathrm{m}}^2$$

(14)

where $\alpha >0$ is a tunable motor parameter. Note that, even though the cost is greatly simplified compared to the original $P_{\mathrm{b}}$, Equation (14) is still nonlinear and depends on the value of $\alpha$, which modifies the overall control performance significantly.

In this paper, the cost function is further simplified as follows. Since the objective of this study is to minimize the battery SOC reduction, the fluctuation of $I_{\mathrm{b}}$ should be minimized according to Equation (4). It also can be interpreted that the sudden changes in the control input u, which cause $I_{\mathrm{b}}$ fluctuations, should be avoided as much as possible. Therefore, for all $k\ge 0,$ another minimization of a quadratic cost in place of Equation (10a) is used by eliminating the first term in Equation (14), that is,

$$\begin{array}{cc}\hfill \underset{{\widehat{u}}_{i|k}\in {\mathcal{U}}_{i|k}}{min}\sum _{i=0}^{N-1}{P}_{\mathrm{b},i}({\widehat{x}}_{i|k},{\widehat{u}}_{i|k})& \approx \underset{{\widehat{u}}_{i|k}\in {\mathcal{U}}_{i|k}}{min}\sum _{i=0}^{N-1}{\widehat{u}}_{i|k}^2,\hfill \end{array}$$

(15)

where ${\mathcal{U}}_{i|k}$ is the i-step-ahead constraint Equation (10g) at step $k.$

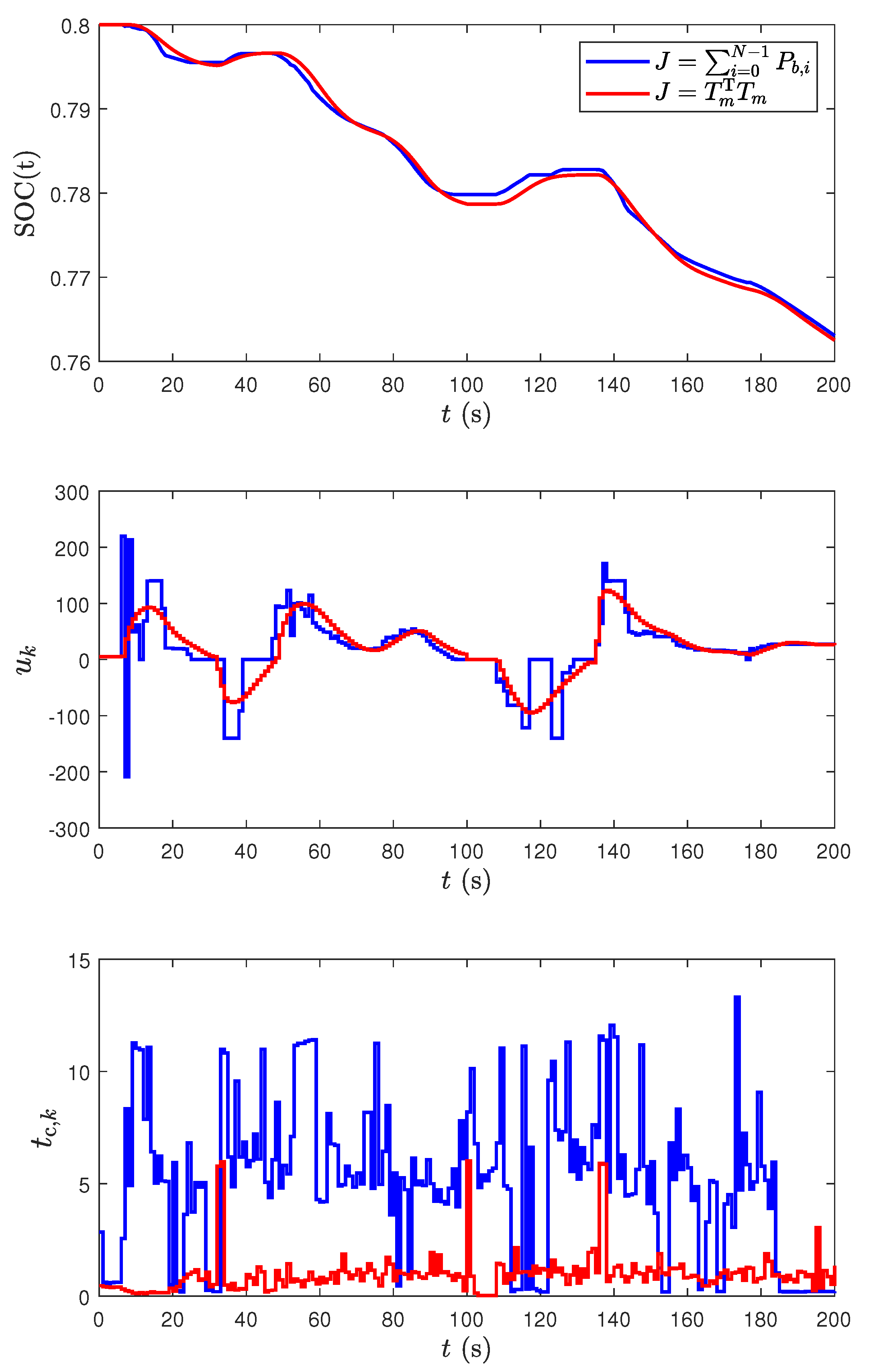
To verify the above assumption, the simulation results using the cost functions (10a) and (15) are compared in Figure 6. It is important to note that the SOC reductions for both cases are almost the same. Due to the nonconvexity in $P_{\mathrm{b}}$, the control fluctuates a lot to search the optimum point at every step, and is sometimes stuck at the local minimum points, as shown in the middle plot of Figure 6.

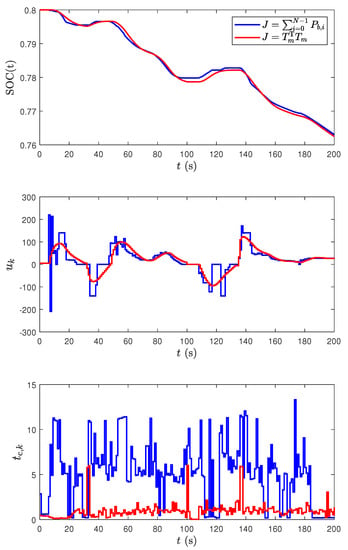
Figure 6. Comparison of the simulation results using the different cost functions with $N=10$ and $T_{\mathrm{s}}=1$ s. The top plot shows the battery SOC trajectories, the middle plot shows the control input evolutions, and the bottom plot shows the computation times $t_{\mathrm{c},k}$ at each step $k.$

In contrast, by exploiting the quadratic form (15), the computation time at each step is significantly reduced compared to the original form, as shown in the bottom plot of Figure 6.

Therefore, it can be concluded that the nonlinear cost (10a) can be replaced with the quadratic cost (15) without sacrificing too much performance in terms of the battery SOC reduction.

4.2.2. Real-Time Computational Feasibility

One of the major issues in MPC is the computational burden when we handle large or fast dynamics-related systems. Moreover, a long prediction horizon increases the computational complexity significantly, even though a longer horizon provides better performance in the ideal case.

In this subsection, an appropriate prediction horizon for our problem that takes into account the relationship between performance and real-time implementation feasibility is analyzed. The nonlinear solver fmincon in MATLAB is used to solve the optimization control problem (10a)–(10h), where the sampling time is specified as $T_{\mathrm{s}}=1$ s in all cases. That is, the computation should be completed in 1 s at each step.

By solving the optimization problem, we obtain the optimal sequence ${\widehat{U}}_k^{*}$ at each step k and only the first element ${\widehat{u}}_{0|k}^{*}$ is applied, which is the principle of receding horizon control. To see the relationship between the control performance and the prediction horizon, we gradually increase the prediction horizon while observing the required computations for each horizon. Note that it is possible to achieve superior performance with faster computation by using other advanced solvers, e.g., tailored NLP solvers using inexact and real-time iteration solution strategies [31]. However, for the purpose of comparison, we utilize the same solver for all simulations.

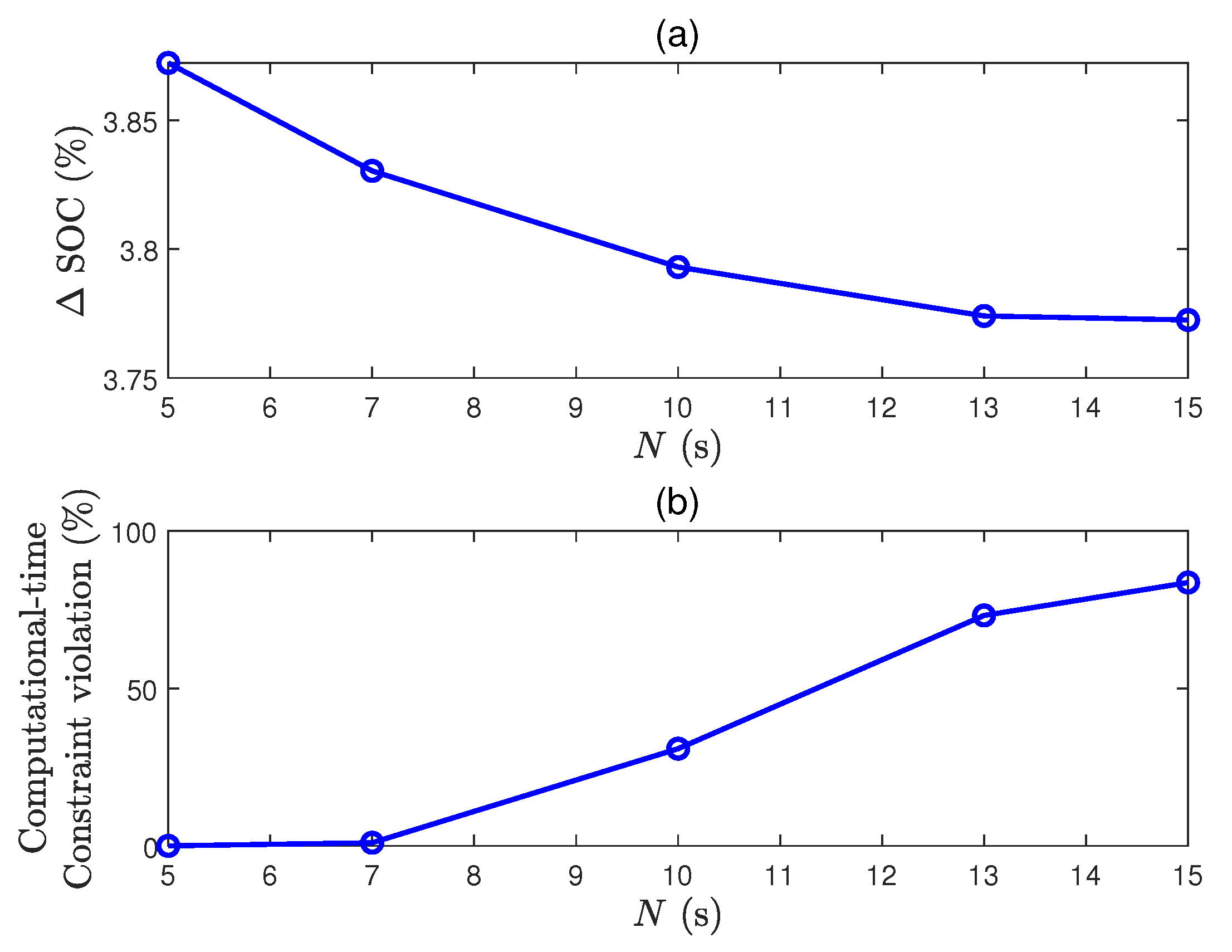
As shown in Figure 7, better control performance in terms of the battery SOC reduction can be achieved by increasing N. However, the required average computation time for each step exceeds the sample time $T_{\mathrm{s}}$, meaning that fmincon is not implementable in real time.

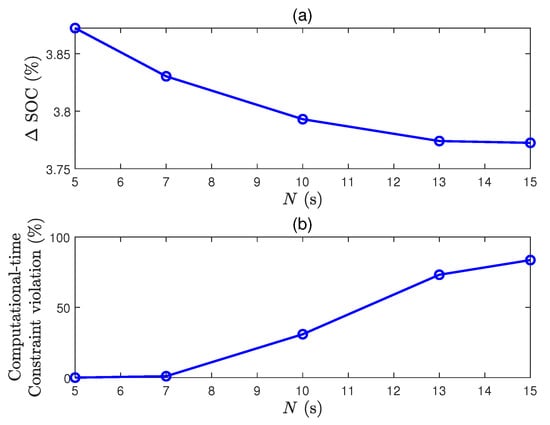
Figure 7. (a) Battery SOC reductions with respect to N, and (b) computational burdens with respect to N. The computational-time constraint violation represents the ratio between the number of occurrences where $t_{\mathrm{c}}>T_{\mathrm{s}}$ and the number of samples of the entire experiment.

It can be concluded that $N=10$ is sufficient to optimize the energy efficiency of our BEV, but the computational burden should be reduced for implementation. A collection of methods to deal with the computational complexity of MPC is proposed in the next section.

5. Strategies for Computational Load Reduction in MPC

In the previous section, an appropriate prediction horizon for MPC is determined heuristically. The computational load is, however, unmanageable with the specified horizon. In this section, we suggest a collection of strategies, which potentially reduce the computational load of MPC. In particular, we describe sampling-time adjustment, warmstarting, and move-blocking strategies, and explain their possible impact upon performance.

5.1. Sampling-Time Adjustment

A sampling-time increase is expected to reduce the computational load of MPC as, for a similar preview of the trajectories, the prediction horizon N decreases. However, note that, as $T_{\mathrm{s}}$ increases, crucial intersampled information might be ignored during prediction causing potential performance degradation of MPC, especially regarding constraint satisfaction. In the following, we numerically investigate the impact of larger sampling times in MPC.

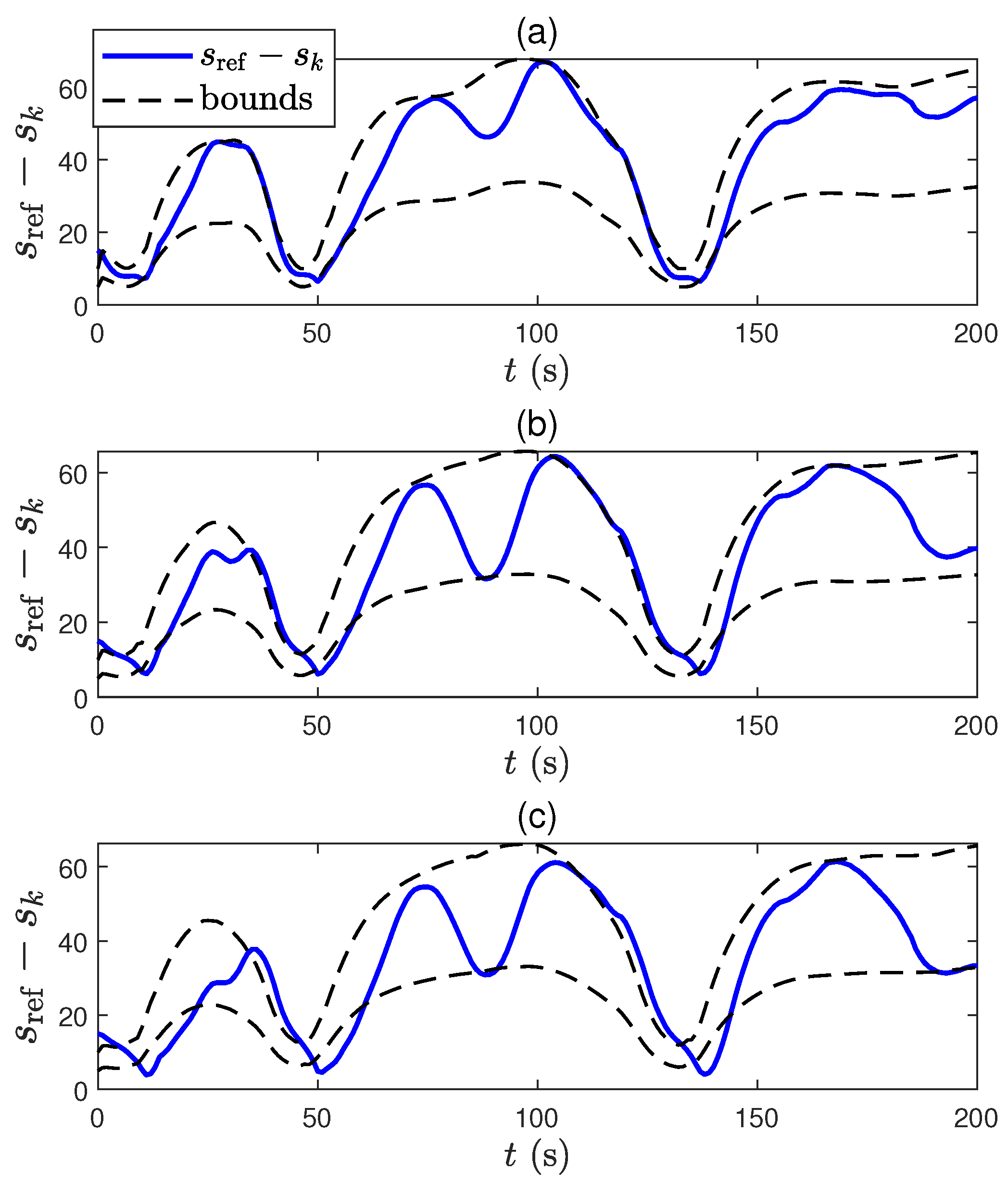
As shown in Figure 8, the position constraints between the ego car and leader car, which are hard constraints, are sometimes violated as $T_{\mathrm{s}}$ increases. As expected, we observe that the average computation time proportionally decreases as $T_{\mathrm{s}}$ increases, and the result is omitted since it is obvious. In fact, due to the inaccuracy of intersampling model information, MPC cannot handle the constraints when the vehicle is close to the bounds (see e.g., at 40 s in Figure 8b,c).

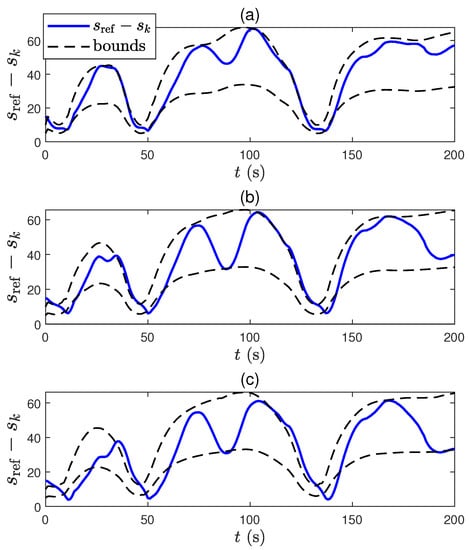
Figure 8. Distance difference between ego car and leader car with (a) $T_{\mathrm{s}}=1$ s, (b) $T_{\mathrm{s}}=2$ s, and (c) $T_{\mathrm{s}}=3$ s.

5.2. Warmstarting

Another remedy for computational burden reduction is warmstarting [32]. Warmstarting is a method that supplies an initial guess of the sequence of controls to the solver rather than using a constant initial control sequence, typically, a vector of zeros. In general, supplying an initial guess is useful when dealing with nonconvex problems and nonlinear solvers because the solvers can easily get stuck to a local minimum point. In addition, this scheme also prevents cases with singularities by avoiding regions close to the initial condition.

Specifically, instead of starting the optimizer with the initial control sequence ${\widehat{U}}_{k,0}={[0\cdots 0]}^{\mathrm{T}}$, we use the previous optimal solution, which is computed at $k-1,$ at the current step k as

$$\begin{array}{c}\hfill {\widehat{U}}_{k,0}=\left\{\begin{array}{cc}{[0\cdots 0]}^{\mathrm{T}},\hfill & k=0,\hfill \\ {\widehat{U}}_{k-1}^{*}(2:\mathrm{end}){\widehat{U}}_{k-1}^{*}{\left(\mathrm{end}\right)]}^{\mathrm{T}},\hfill & k>0,\hfill \end{array}\right.\end{array}$$

(16)

where ${\widehat{U}}_{k-1}^{*}(2:\mathrm{end})\triangleq {[u_{1|k-1}^{*}\cdots u_{N-1|k-1}^{*}]}^{\mathrm{T}}\in {\mathbb{R}}^{N-1}$ is the optimal control sequence computed at step $k-1,$ which is truncated from the second component to the N-th component. Note that the last element ${\widehat{U}}_{k-1}^{*}\left(\mathrm{end}\right)$ is copied twice in ${\widehat{U}}_{k,0}$ so as to match the number of components in the array to N components.

The effectiveness of adopting warmstarting strategy is summarized in Table 2. Although the improvement is not very significant, it can be said that adopting warmstarting is usually helpful.

Table 2. Comparison of the average computation time with and without warmstarting.

	Without Warmstarting	With Warmstarting
$N=15$	2.5336 s	2.5210 s
$N=20$	2.5646 s	2.5512 s

5.3. Move Blocking

To reduce the computational load of MPC, a move-blocking strategy is considered [33]. Move-blocking strategy is similar to control-horizon strategy, where the control is free to move for the first initial prediction steps and then blocked. The difference is that, after the free initial moves of the control, move-blocking strategy blocks the control for several consecutive intervals, whereas control-horizon strategy blocks the last control for the remainder of the prediction horizon.

Control-horizon strategy is described as follows. At step $k,$ instead of solving the optimization problem with the optimal control sequence ${\widehat{U}}_k\in {\mathbb{R}}^N$, we use the alternative sequence ${\widehat{U}}_k^{\prime }\in {\mathbb{R}}^{N_{\mathrm{c}}+1},$ where $N_{\mathrm{c}}$ is the control horizon and $0<N_{\mathrm{c}}<N.$ The relationship between ${\widehat{U}}_k$ and ${\widehat{U}}_k^{\prime }$ is given by

$${\widehat{U}}_k=T_{\mathrm{c}}{\widehat{U}}_k^{\prime },$$

(17)

where $T_{\mathrm{c}}\in R^{N\times (N_{\mathrm{c}}+1)}$ is the control-horizon matrix and is defined by

$$T_{\mathrm{c}}\triangleq \mathrm{blkdiag}(I_{N_{\mathrm{c}}},1_{(N-N_{\mathrm{c}})\times 1})\in {\mathbb{R}}^{N\times (N_{\mathrm{c}}+1)},$$

(18)

where $I_n$ is the n-by-n identity matrix, and $1_{m\times n}$ is the m-by-n matrix of ones.

A variation of the control-horizon strategy is adopted in this paper, which is the move-blocking strategy. The motivation of this variation is that, since the reference position of the leader car can vary significantly in the future, blocking the control over a large interval yields constraint violation and, in some cases, suboptimality or infeasibility. Therefore, we divide the prediction horizon into several blocking intervals. Accordingly, the control-horizon matrix is modified to the move-blocking matrix

$$\begin{array}{c}\hfill T_{\mathrm{b}}=\mathrm{blkdiag}(I_{k_{\mathrm{b}}},1_{k_{\mathrm{b}}\times 1},\dots ,1_{k_{\mathrm{b}}\times 1},1_{k_{\mathrm{r}}\times 1})\in {\mathbb{R}}^{N\times N_{\mathrm{b}}},\end{array}$$

(19)

where $0<k_{\mathrm{b}}<N$ is the number of control moves blocked at each interval (except the first interval), $k_{\mathrm{r}}$ is the remainder of the division $N/k_{\mathrm{b}}$ (if zero, then this term disappears), and $N_{\mathrm{b}}\triangleq \mathrm{ceil}(N/k_{\mathrm{b}})-1+k_{\mathrm{b}}$ is the length of ${\widehat{U}}_k^{\prime }$ using move-blocking strategy. With this move-blocking matrix, the control is free to move for the first $k_{\mathrm{b}}$ steps, and, afterwards, blocked for $k_{\mathrm{b}}$ steps consecutively within $N_{\mathrm{b}}-k_{\mathrm{b}}$ intervals. An example of move-blocking sequence using the proposed method is shown in Figure 9 with $k_{\mathrm{b}}=3$ and $N=10.$

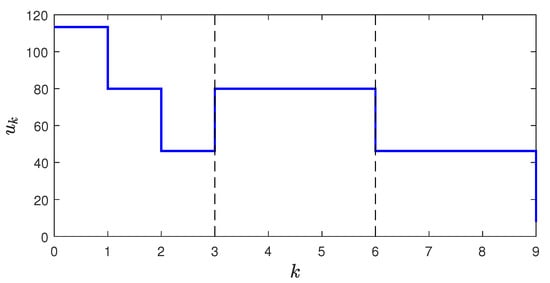
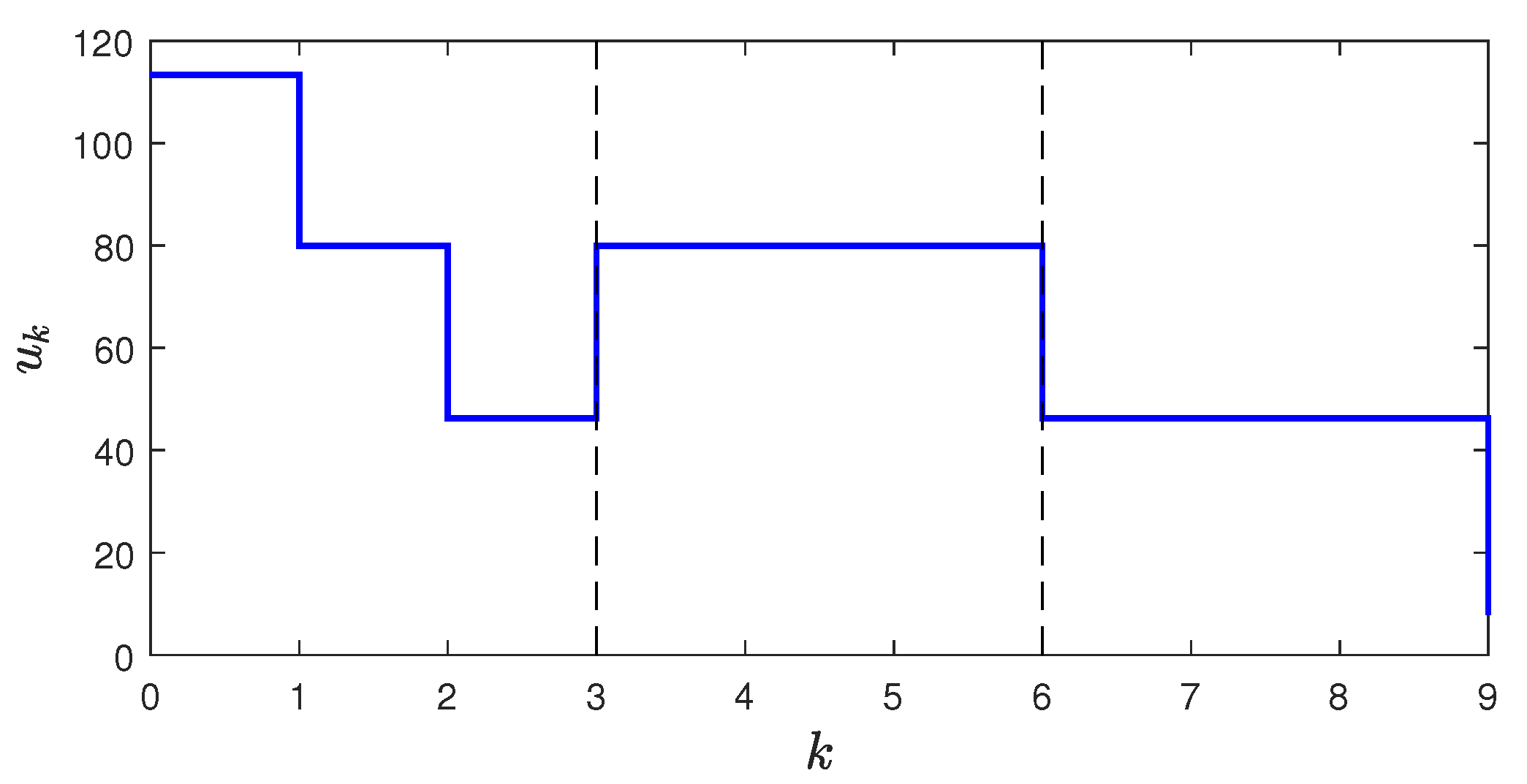
Figure 9. Control sequence using move-blocking strategy, where $k_{\mathrm{b}}=3$ and $N=10.$ The first three moves are free, then blocked in consecutive blocks of three controls. Note that $N_{\mathrm{b}}=6,$ $k_{\mathrm{r}}=1,$ and the last control is within a separate block from $k=9$ to $k=10.$

6. Simulation Results

So far, several methods to reduce the computational burden of MPC have been discussed. In this section, the effectiveness of the proposed strategies is verified for two driving cycles, namely, WLTC and US06. The parameters of the simulations are listed in Table 3. The model parameters are extracted from the Ford Focus BEV model in ADVISOR [34], which is a high-fidelity simulator with the aim of analyzing the vehicle-energy efficiency.

Table 3. Simulation Parameters.

Symbol	Description	Value (Unit)
m	Vehicle total mass	1445 (kg)
r	Wheel radius	0.3166 (m)
$A_{\mathrm{f}}$	Vehicle frontal area	2.06 (m${}^2$)
$C_{\mathrm{d}}$	Aerodynamic drag coefficient	0.312
$\rho$	Air density	1.2 (kg/${\mathrm{m}}^3$)
$\theta$	road inclination	0 (${}^{\circ }$)
$\gamma$	Rolling resistance coefficient	0.0086
$i_0$	Final drive ratio	4.2
$v^{\min },v^{\max }$	Acceptable range of speed	(0, 150} (km/h)
$C_{\mathrm{b}}$	Battery capacity	55 (Ah)
${\eta }_{\mathrm{b}}^{+}$	Battery-depletion efficiency	0.9
${\eta }_{\mathrm{b}}^{-}$	Battery-recharge efficiency	1.11
${\tau }_{\min },{\tau }_{\max }$	max/min time headway	$\{1,2\}$ (s)
N	Prediction horizon	10
$T_{\mathrm{s}}$	Sampling time	1 (s)
$k_{\mathrm{b}}$	Control moves blocked	3

The following simulations compare control performance between the proposed method and other strategies, i.e., nominal MPC and DP. As mentioned earlier, the performance using DP can be considered as ideal. Therefore, if the performance using our approach closely matches the one of DP with a computationally manageable complexity, it can be said that the main objective of this study is achieved. Also, compared to the nominal MPC, the computational complexity should be reduced with the almost same control performance.

Simulation 1: WLTC driving cycle. The results in urban-driving scenario obtained from the proposed method and DP are compared in Figure 10. Since the state and control trajectories using the nominal MPC are very similar to those of our approach, we omit the plots with the nominal MPC.

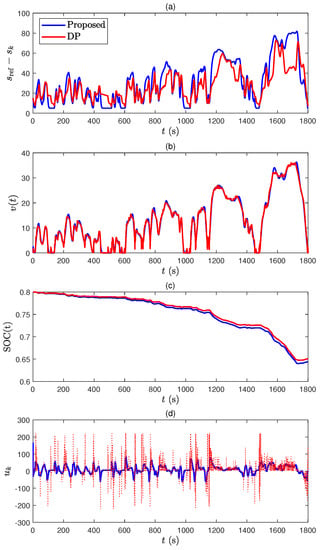
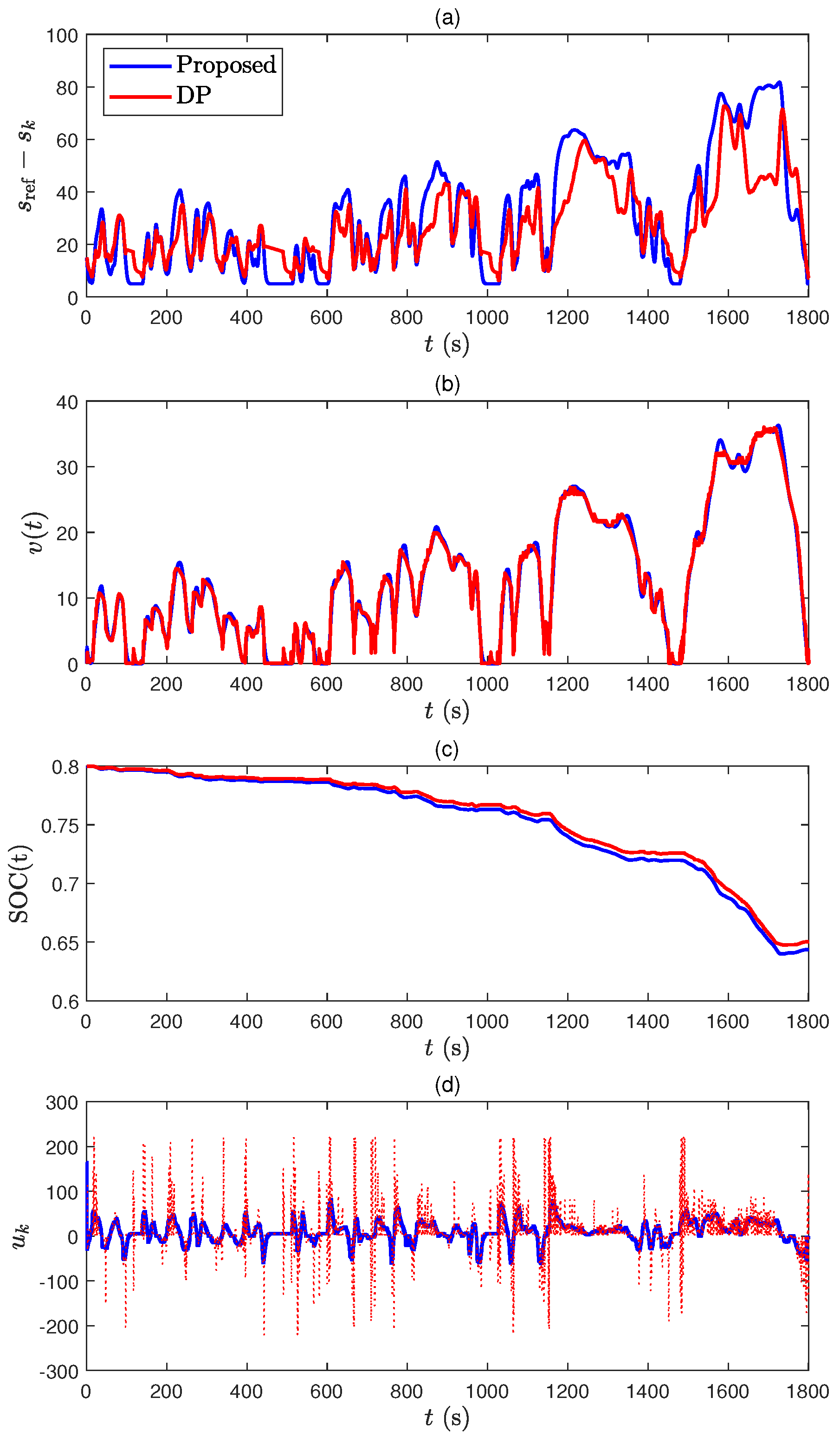
Figure 10. Comparison between model prediction control (MPC) and DP for the WLTC driving cycle, (a) distance difference between ego car and leader car, (b) speed profiles, (c) battery SOC trajectories, and (d) control trajectories.

Note that the appropriate distances between the self-driving car and leader car are maintained for both methods, as shown in Figure 10a. Depending on the self-driving car speed, the time-varying upper- and lower- bounds (10e) are specified in the predictions. No constraint violation occurs for MPC and DP. The entire speed trajectories are very similar to each other, but slightly different in Figure 10b. The battery SOC trajectories are depicted in Figure 10c and the SOC consumption using the proposed method is very similar to that of DP, which verifies the effectiveness of our approach. Since DP explores all possible combinations of control and state pairs, the control input in Figure 10d sometimes changes rapidly because DP is just designed to minimize the cost function without considering the physical relationship between the actuator and vehicle. Therefore, the control performance using DP is exaggerated to some extent, but it can serve as a benchmark that only considers the minimization of the cost.

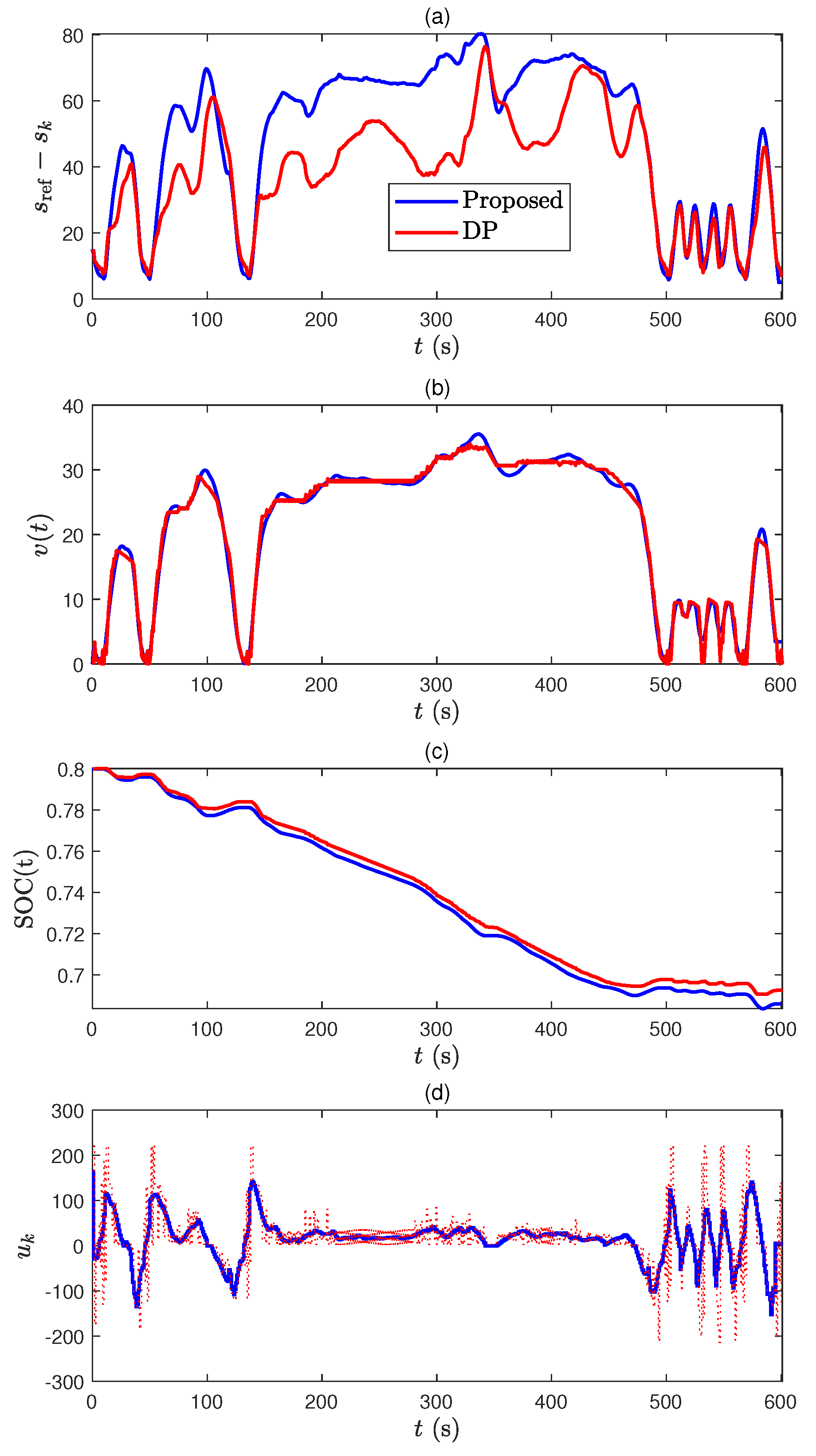
The trajectories of $s,$ $v,$ and $\mathrm{SOC}$ are shown in Figure 11a–c. From the battery SOC trajectory in Figure 11c, the proposed MPC, which is computationally tractable, can give a solution that is very close to the globally optimum solution obtained by DP. Moreover, the trajectories obtained by DP sometimes physically do not make sense and should be corrected for hardware implementation. Since the nonlinear model used in this paper only captures the primary dynamics of the vehicle and powertrain, the control input using DP in Figure 11d cannot ensure a globally optimum solution in real production vehicle. Therefore, in reality, we expect that the performance gap between DP and our approach is much closer to each other, but the computational burden is significantly reduced with our approach, which is the central argument of this paper.

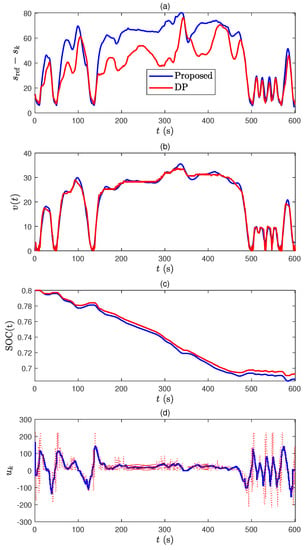
Figure 11. Comparison between MPC and DP in US06 driving cycle, (a) distance difference between ego-car and leader-car, (b) speed profiles, (c) battery SOC trajectories, and (d) control trajectories.

Simulation 2: US06 drive cycle. The US06 drive cycle represents the case of a highway-driving scenario. The results are shown in Figure 11.

Discussion.Table 4 and Figure 12 support the above claims. As expected, the speed modification that minimizes $T_{\mathrm{m}}^2$ is effective in terms of battery SOC reduction. As expected, the proposed MPC with move-blocking method does not outperform the nominal MPC but is very close to that of nominal MPC in terms of battery SOC reduction performance (see Table 4). Unfortunately, the control performances of our approach and nominal MPC shows the significant difference by comparing with DP result, but DP is not implementable in the real-time and trajectories from the DP do not consider the physical limitation of the actuator.

Table 4. $\Delta \mathrm{SOC}$ obtained by different optimized speed trajectories (the values in parentheses describe the improvements compared to the baseline).

	WLTC	US06
Baseline	17.55	13.41
Proposed	15.64 (10.88%)	11.42 (14.83%)
Nominal MPC	15.42 (12.14%)	11.30 (15.73%)
DP	14.96 (14.76%)	10.74 (19.90%)

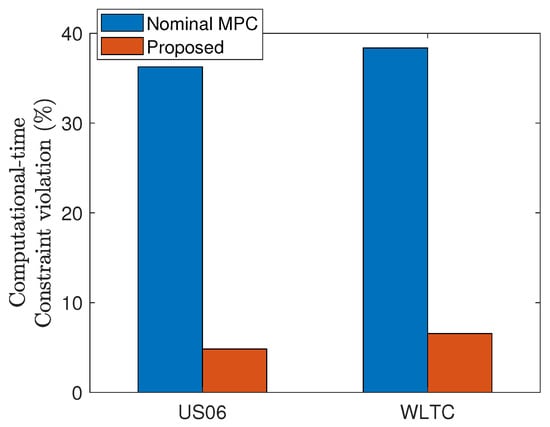
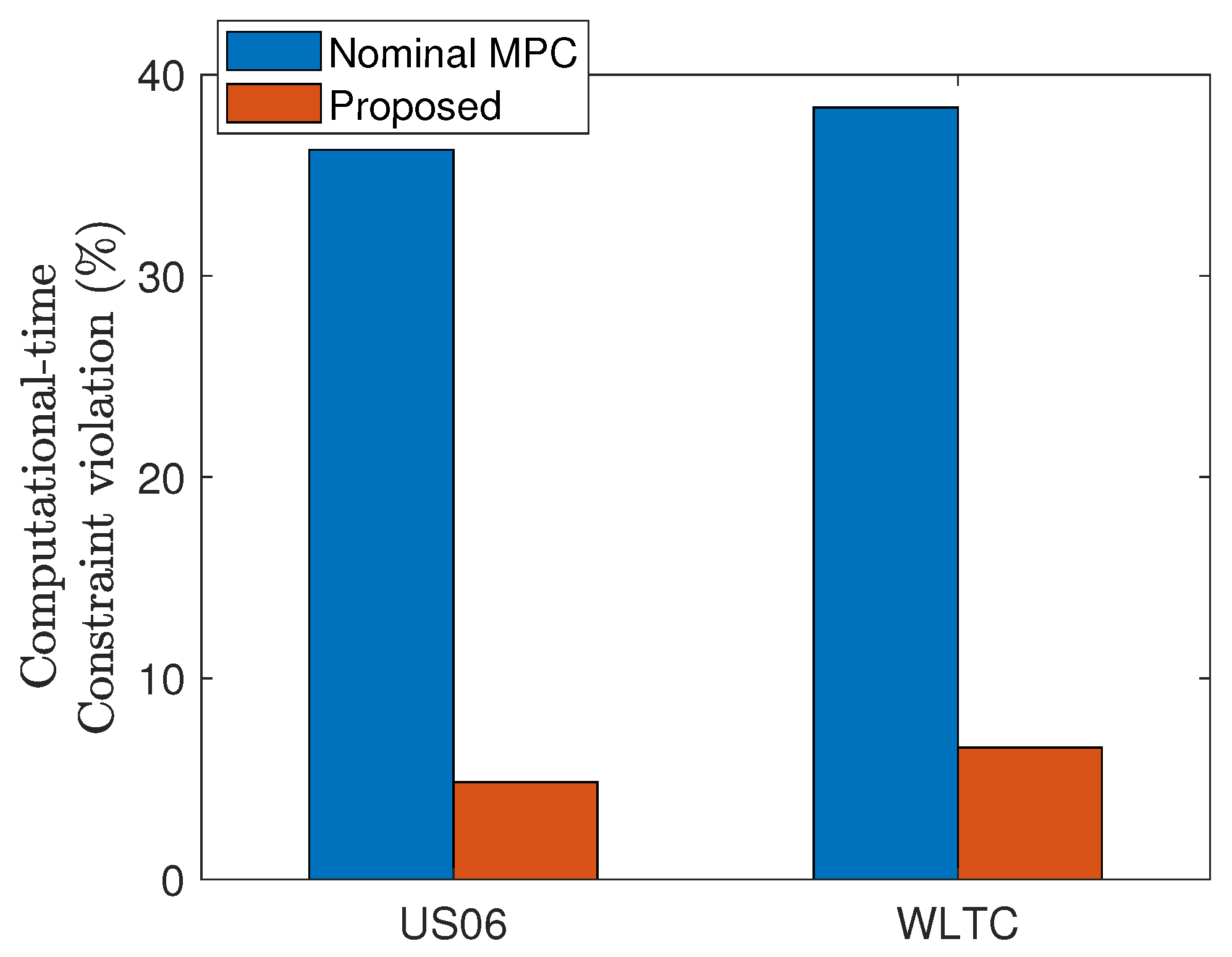
Figure 12. Comparison of the computational-time constraint violation rates obtained by nominal MPC and proposed method.

Note that the computational-time constraint violation rate is significantly reduced with the proposed method (see Figure 12). Even though our approach sometimes exceeds the sampling period $T_{\mathrm{s}}$, some remedies to handle this issue are possible. For example, we can further reduce the computation time by replacing the language from MATLAB to C, which is essentially needed for hardware implementation. Also, constraint relaxation and the introduction of faster solvers instead of fmincon can be alternative solutions, which are left to our future works.

7. Conclusions

There have been extensive approaches in the literature to apply MPC in automotive control applications, but its computational feasibility was not clearly reviewed. This paper investigated several methods to reduce the computational complexity of a nominal MPC implemented in a battery-electric vehicle (BEV). First, an appropriate prediction horizon for our optimization control problem was determined with a nominal MPC, and we concluded that the control performance of nominal MPC closely matches the one of DP, which is assumed to be globally optimal. Next, to ensure real-time feasibility, adopting move-blocking strategy, with warmstarting and large sampling times, significantly reduces the computational burden compared to a nominal MPC without sacrificing too much of the control performance in terms of battery state-of-charge (SOC) reduction. Methods that provide further reduction of the computation load for real-time implementation of MPC in hardware will be our future work. In addition, a lot of constraint violations are expected to occur with the proposed approach when the reference value varies significantly. To overcome such a shortcoming, the relaxation of the constraints with the proposed approach is also left to our future work.