Short-Transient Discrete Time-Variant Filter Dedicated for Correction of the Dynamic Response of Force/Torque Sensors
Abstract
:1. Introduction
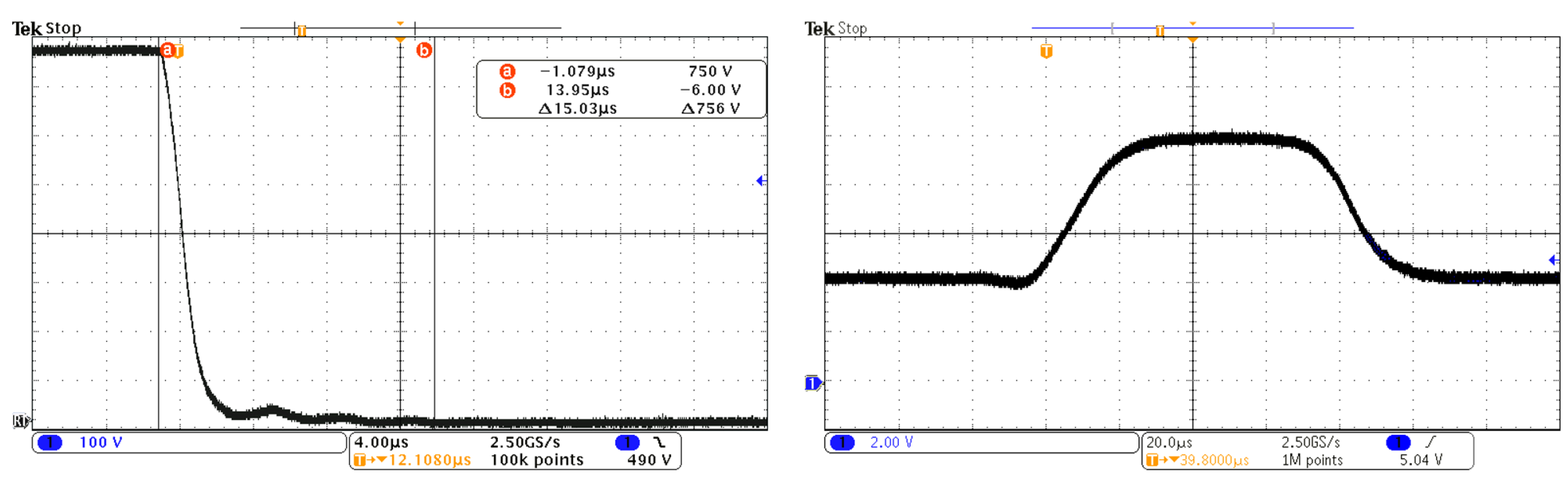
2. Properties of Commercial Filters Implemented in JR3 Force/Torque Sensors
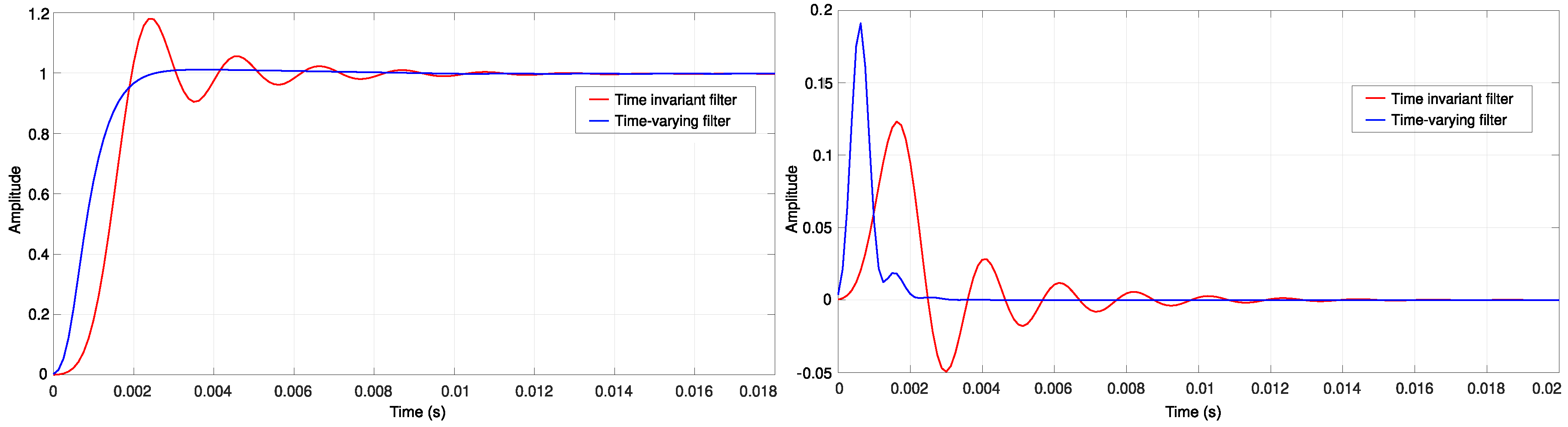
3. Discrete Time-Varying Filter With Reduced Transient Response
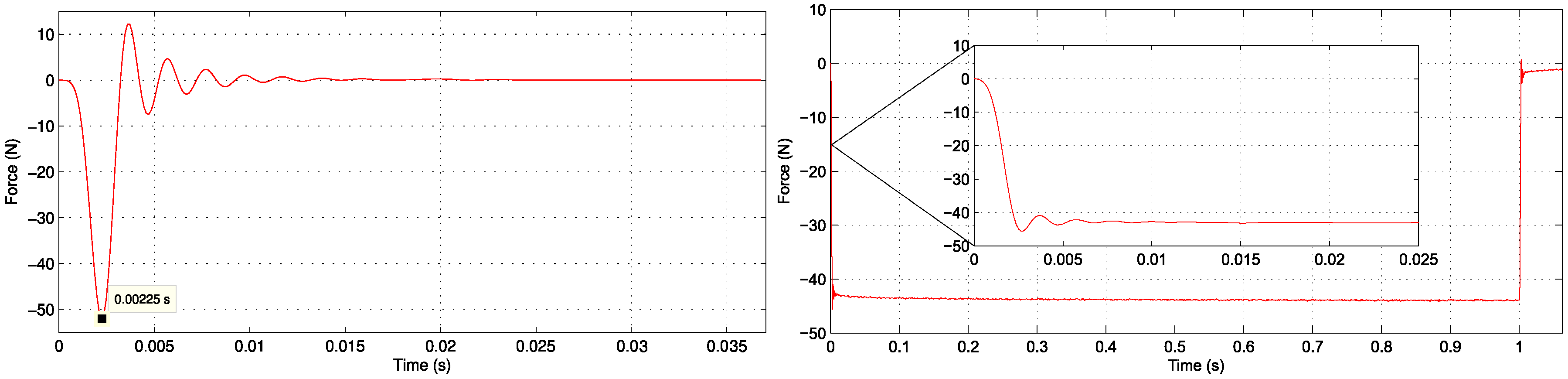
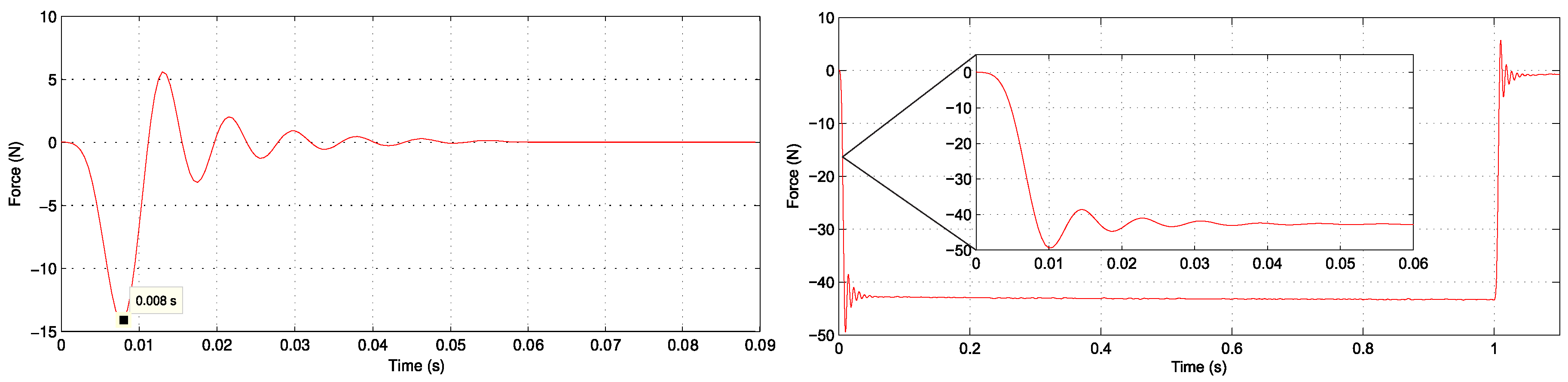
4. Experimental Setup
5. Experimental Results
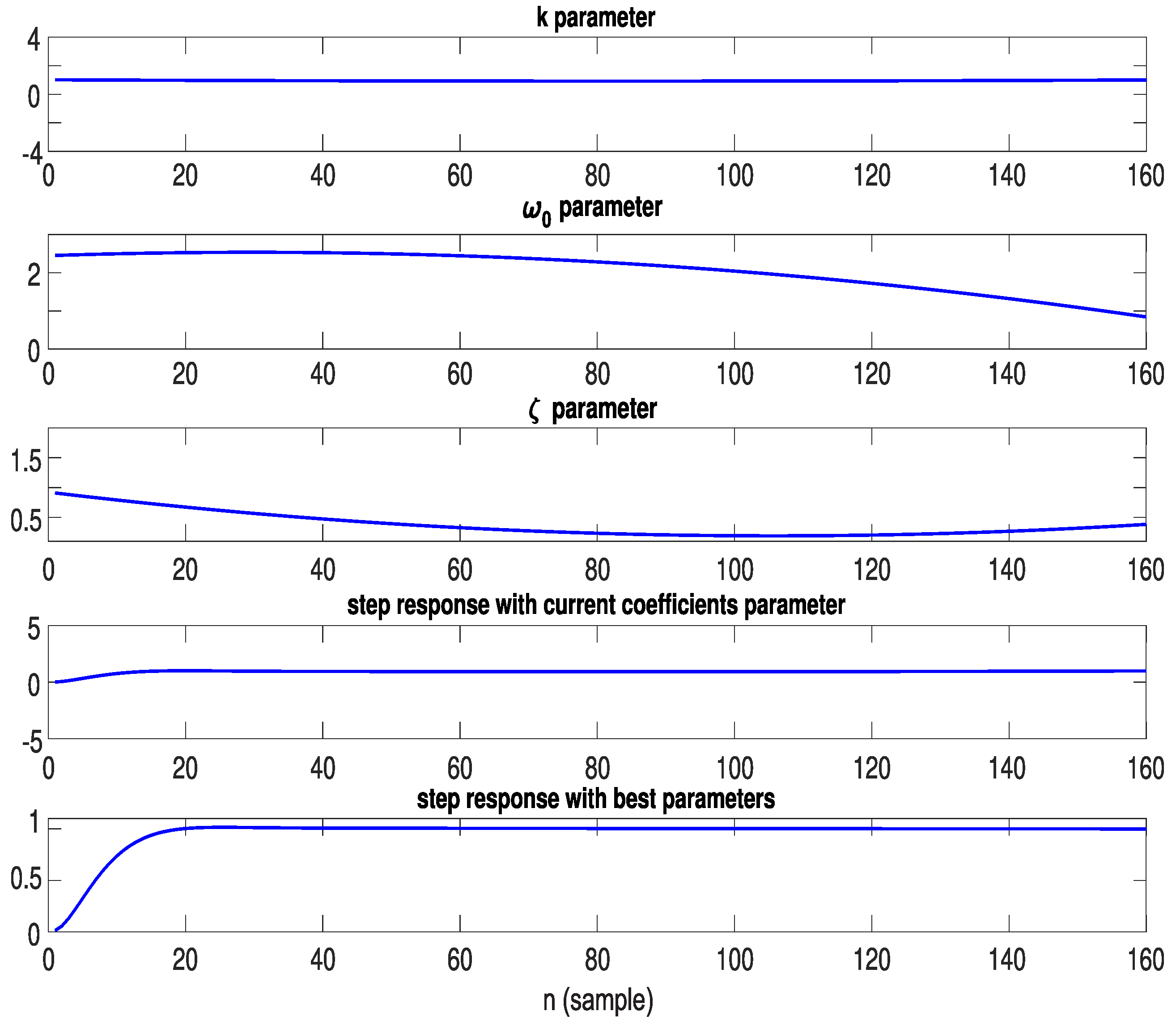
6. Optimization Routine
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Zhu, Z.; Hu, H. Robot Learning from Demonstration in Robotic Assembly: A Survey. Robotics 2018, 7, 17. [Google Scholar]
- Chen, G.; Li, Z.; Shi, S.; Wang, Y. Force Detection and Control of Redundant Manipulator for Unknown Environment. In Proceedings of the 14th IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 19–21 June 2019. [Google Scholar]
- Kondratenko, Y.P.; Duro, R.J. Advances in Intelligent Robotics and Collaborative Automation; River Publishers: Gistrup, Denmark, 2015. [Google Scholar]
- Liu, L.; Xi, N.; Li, W.-J.; Zhao, X.; Shen, Y. (Eds.) Special Issue “Sensors for Robots”. In Sensors; MDPI: Basel, Switzerland, 2016. [Google Scholar]
- Jeong, S.; Takahashi, T. Impact Force Reduction of Manipulators Using a Dynamic Acceleration Polytope and Flexible Collision Detection Sensor. Adv. Robot. 2012, 367–383. [Google Scholar] [CrossRef]
- Malm, T.; Salmi, T.; Marstio, I.; Montonen, J. Dynamic safety system for collaboration of operators and industrial robots. Open Eng. 2019, 9, 61–71. [Google Scholar] [CrossRef]
- Wahrburg, A.; Boes, J.; Listmann, K.D.; Dai, F.; Matthias, B.; Ding, H. Motor-Current-Based Estimation of Cartesian Contact Forces and Torques for Robotic Manipulators and Its Application to Force Control. Trans. Autom. Sci. Eng. 2018, 15, 879–886. [Google Scholar] [CrossRef]
- Yen, S.H.; Tang, P.C.; Lin, Y.C.; Lin, C.Y. Development of a Virtual Force Sensor for a Low-Cost Collaborative Robot and Applications to Safety Control. Sensors 2019, 19, 2603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kucuk, S. Serial and Parallel Robot Manipulators. In BoD – Books on Demand; IntechOpen: London, UK, 2012. [Google Scholar]
- Marvel, J. Sensors for safe, collaborative robots in smart manufacturing. In Proceedings of the IEEE Sensors, Glasgow, UK, 29 Ocober–1 November 2017. [Google Scholar]
- Li, C.; Gu, X.; Xiao, X.; Lim, C.M.; Ren, H. Flexible Robot With Variable Stiffness in Transoral Surgery. Trans. Mechatron. 2020, 25, 1–10. [Google Scholar] [CrossRef]
- DIppolito, P.; Alonge, F.; Cucco, E. Contact Estimation in Robot Interaction. Int. J. Adv. Robot. Syst. 2014, 11, 96. [Google Scholar] [CrossRef] [Green Version]
- JR3. Available online: https://www.jr3.com/resources/product-manuals?download=36:5907e-legacy-pci-receiver-manual (accessed on 1 May 2020).
- Osypiuk, R.; Kroeger, T. A three-loop model-following control structure: Theory and implementation. Int. J. Control 2010, 83, 97–104. [Google Scholar] [CrossRef]
- Osypiuk, R.; Piskorowski, J.; Kubus, D. A method of improving the dynamic response of 3D force/torque sensors. Mech. Syst. Signal Process. 2016, 68, 366–377. [Google Scholar] [CrossRef]
- Orchard, H.J.; Willson, A.N. Elliptic functions for filter design. IEEE Trans. Circ. Syst. 1997, 44, 273–287. [Google Scholar] [CrossRef]
- Vlcek, M.; Unbehauen, R. Degree, ripple, and transition width of elliptic filters. IEEE Trans. Circ. Syst. 1989, 36, 469–472. [Google Scholar] [CrossRef]
- Piskorowski, J.; Barcinski, T. Dynamic compensation of load cell response: A time-varying approach. Mech. Syst. Signal Process. 2008, 22, 1694–1704. [Google Scholar] [CrossRef]
- Piskorowski, J.; Gutierrez de Anda, M.A. A new class of continuous-time delay-compensated parameter-varying lowpass elliptic filters with improved dynamic behavior. IEEE Trans. Circ. Syst. I Reg. Pap. 2009, 56, 179–189. [Google Scholar] [CrossRef]
- Gutierrez de Anda, M.A.; Sarmiento Reyes, L.A.; Martinez, L.H.; Piskorowski, J.; Kaszynski, R. The reduction of the duration of the transient response in a class of continuous-time LTV filters. IEEE Trans. Circ. Syst. II Exp. Briefs 2009, 56, 102–106. [Google Scholar] [CrossRef]
- Piskorowski, J. Digital Q-varying notch IIR filter with transient suppression. IEEE Trans. Instrum. Meas. 2010, 59, 866–872. [Google Scholar] [CrossRef]
- Okoniewski, P.; Piskorowski, J. Stability analysis of linear time-varying IIR filter with equalized group delay characteristic. In Proceedings of the 18th International Conference on Methods and Models in Automation and Robotics, Miedzyzdroje, Poland, 26–29 August 2013. [Google Scholar]
- Johnson, C.D.; Zhu, J. New results for linear, time-varying, discretetime systems. In Proceedings of the Twenty-Third Southeastern Symposium on System Theory, Columbia, SC, USA, 10–12 March 1991. [Google Scholar]
- FANUC. Available online: https://pdf.directindustry.com/pdf/fanuc-europe-corporation/force-sensor/32007-834751.html (accessed on 1 May 2020).
- Zhang, H.-X.; Ryoo, Y.-J.; Byun, K.-S. Development of Torque Sensor with High Sensitivity for Joint of Robot Manipulator Using 4-Bar Linkage Shape. Sensors 2016, 16, 991. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kubus, D.; Kröger, T.; Wahl, F.M. On-line rigid object recognition and pose estimation based on inertial parameters. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1402–1408. [Google Scholar]
- Janschek, K. Mechatronic Systems Design: Methods, Models, Concepts; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]






| [rad/s] | [rad/s] | [rad/s] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Hz | 457.0789 | 0.8775 | 12.9716 | 653.0697 | 0.4257 | 12.2994 | 775.1774 | 0.1200 | 65.5222 | |
| Hz | 1895.78 | 0.8777 | 12.9716 | 2606.34 | 0.4257 | 12.2994 | 3093.70 | 0.1200 | 62.522 |
| Time Invariant Filter 500 Hz | Time-Varying Filter 500 Hz | Time Invariant Filter 125 Hz | Time-Varying Filter 125 Hz | |
|---|---|---|---|---|
| RiseTime [s] | 0.001 | 0.0013 | 0.0041 | 0.0031 |
| SettlingTime [s] | 0.007 | 0.0023 | 0.0270 | 0.0105 |
| SettlingMin | 0.9046 | 0.9058 | 0.9056 | 0.9028 |
| SettlingMax | 1.1797 | 1.0112 | 1.1572 | 1.0754 |
| Overshoot [%] | 18.2402 | 1.3528 | 15.8869 | 7.7583 |
| PeakTime [s] | 0.0025 | 0.0039 | 0.0100 | 0.0076 |
| Time Invariant Filter 500 Hz | Time-Varying Filter 500 Hz | Time Invariant Filter 125 Hz | Time-Varying Filter 125 Hz | |
|---|---|---|---|---|
| SettlingTime [s] | 0.0105 | 0.0021 | 0.0412 | 0.0208 |
| Min | −0.0496 | −0.0003 | −0.0112 | −0.0069 |
| Max | 0.1232 | 0.1911 | 0.0304 | 0.0444 |
| MinTime [s] | 0.0031 | 0.0047 | 0.0120 | 0.0092 |
| MaxTime [s] | 0.0018 | 0.0007 | 0.0067 | 0.0035 |
| Time Invariant Filter 500 Hz | Time-Varying Filter 500 Hz | Time Invariant Filter 125 Hz | Time-Varying Filter 125 Hz | |
|---|---|---|---|---|
| SettlingTime [s] | 0.0105 | 0.0019 | 0.0412 | 0.0206 |
| Min | −0.0496 | −0.0004 | −0.0112 | −0.0071 |
| Max | 0.1232 | 0.1912 | 0.0304 | 0.0443 |
| MinTime [s] | 0.0031 | 0.0045 | 0.0120 | 0.0089 |
| MaxTime [s] | 0.0018 | 0.0005 | 0.0067 | 0.0031 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okoniewski, P.; Osypiuk, R.; Piskorowski, J. Short-Transient Discrete Time-Variant Filter Dedicated for Correction of the Dynamic Response of Force/Torque Sensors. Electronics 2020, 9, 1291. https://doi.org/10.3390/electronics9081291
Okoniewski P, Osypiuk R, Piskorowski J. Short-Transient Discrete Time-Variant Filter Dedicated for Correction of the Dynamic Response of Force/Torque Sensors. Electronics. 2020; 9(8):1291. https://doi.org/10.3390/electronics9081291
Chicago/Turabian StyleOkoniewski, Piotr, Rafał Osypiuk, and Jacek Piskorowski. 2020. "Short-Transient Discrete Time-Variant Filter Dedicated for Correction of the Dynamic Response of Force/Torque Sensors" Electronics 9, no. 8: 1291. https://doi.org/10.3390/electronics9081291
APA StyleOkoniewski, P., Osypiuk, R., & Piskorowski, J. (2020). Short-Transient Discrete Time-Variant Filter Dedicated for Correction of the Dynamic Response of Force/Torque Sensors. Electronics, 9(8), 1291. https://doi.org/10.3390/electronics9081291






