Reduced-Reflection Multilayer PCB Microstrip with Discontinuity Characterization

Abstract

In the era of technology and communication, printed circuit boards (PCBs) can be found in a myriad of devices—from ordinary household items, to state of the art custom metrology equipment. Different types of component for wireless communications are available and come in various packages, supplied by multiple manufacturers. The signal landpads for some high-frequency connectors and components, encapsulated in larger packages, are usually wider than the controlled impedance trace, thereby introducing unwanted impedance mismatch and resulting in signal reflections. The component land pad and microstrip width a discrepancy issue can be found in both complex high-density industrial devices and system-level academic research papers. This paper addresses the topic of compensating discontinuities, introduced by signal pads, which are wider than the target impedance microstrip, characterizes the difference between the compensated and uncompensated microstrip with discontinuity, and proposes a generalized guideline on compensating for the introduced impedance change in multilayer PCBs. The compensation method is based upon carefully designing the stackup of the PCB allowing for a reference plane cutout under the discontinuity to even out the impedance mismatch. A 6-layer PCB with IT180A dielectric material containing three structures has been manufactured and characterized using an Agilent E8363B vector network analyzer (VNA). A 4–12 dB improvement in S₁₁ response in the whole frequency range up to 10 GHz, compared to that when no compensation has been applied, was observed.

1. Introduction

In today’s modern world, printed circuit boards (PCBs) can be found in a myriad of devices—from ordinary household items, to state of the art custom metrology equipment. With the upcoming leap from 4G to 5G telecommunications and 4th industrial revolution [1], wireless technology becomes a mandatory part of every electronics device. Different types of component for wireless communications, which come in various packages supplied by multiple manufacturers, are at the disposal of a modern electronics design engineer and architect. These include high-frequency amplifiers, filters, baluns, mixers, isolators, connectors and many more [2,3,4]. The physical size of the latter components is usually related to certain specifications, including power handling, bandwidth or operating frequency. 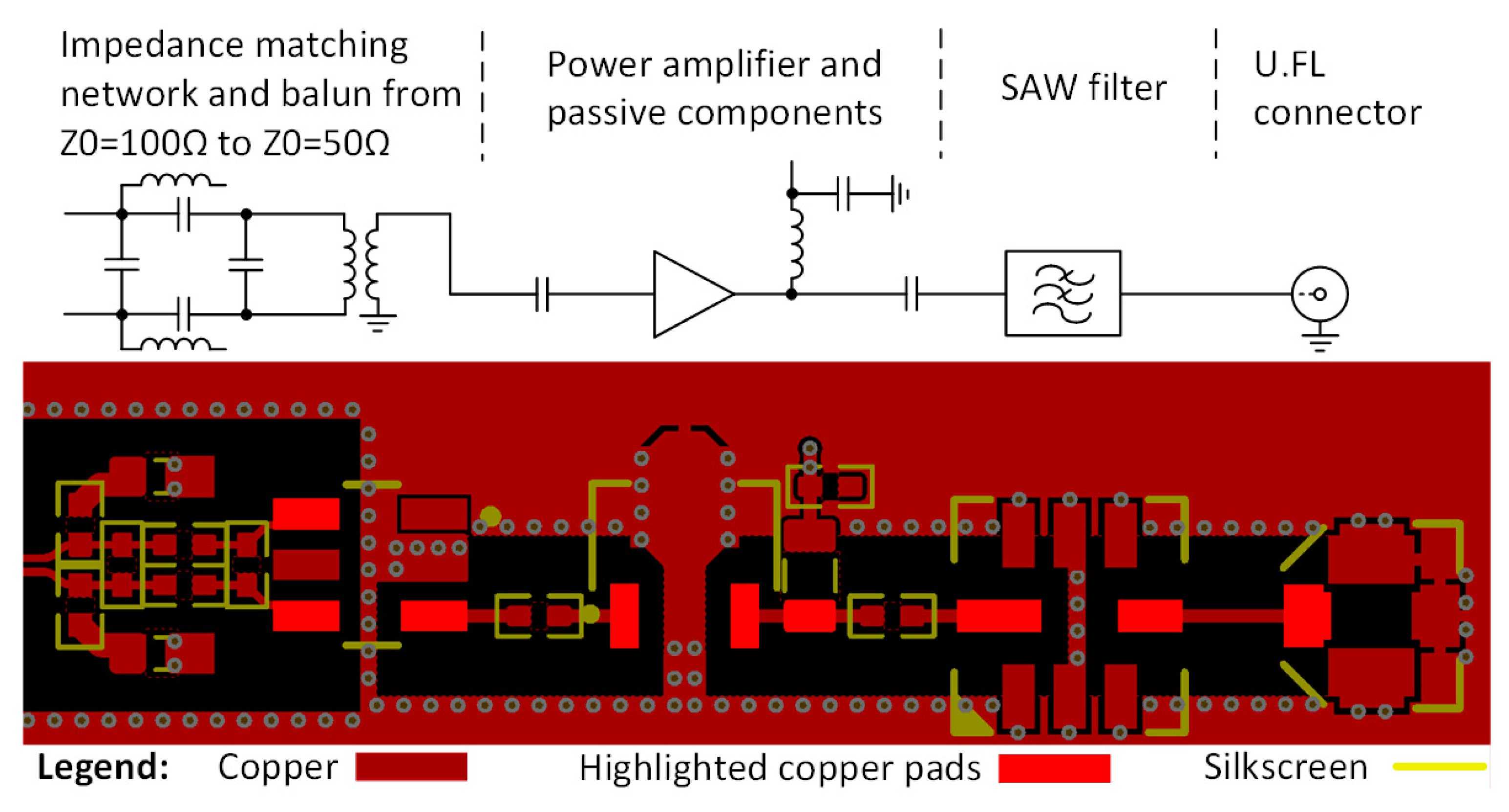An example of a common circuit in a modern radio frequency (RF) device is shown in Figure 1. The latter figure depicts a conversion from differential to single-ended microstrip using a balun, which is then fed into a wideband amplifier. The output of the amplifier is connected to a filter and then fed into a ultra-small surface-mount coaxial connector (U.FL) connector. The signal path contains parts aimed at altering the passing signal differently, whether it’s amplification, filtering, phase shifting, etc.

Despite the differences in manufacturers, packages and the parts’ purpose, the characteristic impedance (Z0) in RF chains is usually defined and constant. In this case, the impedance for single-ended tracks should be 50 Ω, and for differential 100 Ω. The signal landpads for some high-frequency connectors and components, encapsulated in larger packages, are wider than the controlled impedance trace, therefore introducing unwanted impedance mismatch in the chain and resulting in signal reflections. These pads are highlighted in the example chain in Figure 1. Modern wireless standards aim at reducing power consumption and increasing the data throughput [5,6], but the reflections, which occur due to larger signal landpads, reduce the overall power efficiency and increase noise levels, thus decreasing reliability. The component land pad and microstrip width discrepancy issue can mainly be found in complex high-density industrial devices due to the vast variety of components used, although in some cases, it can be also met analyzing PCBs discussed in system-level academic research papers [7,8]. The designer cannot simply reduce the component landpad size, which is provided by the manufacturer in technical notes and datasheets, in order to meet the width of the microstrip, as the PCB assembly process will be corrupted. Modern high-density industrial device PCBs are multilayer, thus the discussed topic is relevant for both modern and future designs.

Modern PCB manufacturing processes provide capabilities of fabricating boards with 30 conductor layers and more [9,10], including structures like blind and buried vias, back-drilling through-hole vias, and a myriad of dielectric materials (from typical FR4-based to high-speed low-loss Rogers Corp. materials [11]). One of the largest problems in fabricating a multilayer PCB is layer alignment, but nowadays manufacturers align 0.1 mm diameter microvias with 0.1 mm copper annular ring around them [9,10].

This paper addresses the topic of compensating discontinuities, introduced by signal pads, which are wider than the target impedance microstrip, which characterizes the difference between the compensated and uncompensated microstrip with discontinuity and proposes a generalized guideline on compensating for the introduced impedance change in multilayer PCBs. The paper is organized as follows: existing methods and techniques of compensating discontinuities are discussed in the second section, the third section describes the research setup. The latter section is followed by discussing the simulation and measurement results as well as providing a guideline for how to compensate for discontinuities in multilayer PCBs. Conclusions and references are provided at the end of the paper.

2. Existing Discontinuity Compensation Techniques

Microstrip discontinuities have been a topic of research for many years, exploring different junctions, bends, steps etc. [12]. The latter topic is even more relevant in today’s high-speed device era with research and recommendations found in industrial application notes, research papers, and similar topics revealed in patents. Paper [13] proposes a step in width discontinuity compensation method, which is based on obtaining the optimal chamfer angle θ and demonstrates a 60° taper to be the best solution for frequencies up to 10 GHz. Paper [14] presents a Klopfenstein (Dolph–Chebyshev) taper in order to compensate for the increased width and demonstrates s very good measurement response of S₁₁ ≤ −20 dB up to 3 GHz. The drawback of the latter taper is its length of L = 72.6 mm. Paper [15] authors conducted research around the microstrip step change in width and step change in substrate thickness at the same physical location canceling the effect of each other. Their approach was to characterize a wider microstrip, which narrowed down to an inductive discontinuity with and without tapering in the frequency range from 1 GHz to 6 GHz. The main target application is to reduce reflections from PCB microstrips which are connected to bare silicon directly. Application note [16] presents impedance measurements of capacitive and inductive discontinuities in an impedance-controlled microstrip and stripline transmission in the time domain region. This also points out the importance of modern metrology systems to be capable of determining them accurately. Application note [17] recommends cutouts under the surface mount direct current (DC) block capacitor land pads in a 25 Gbps system. Application note [18] recommends smooth transitions as the best solution if the microstrip width varies, with multi-step or single-step transitions held as those exerting poor performance. Patent [19] reveals a multilayer PCB via with the reference layer copper clearance on all layers around the via in order to maintain a constant characteristic impedance. The patent also shows the reference layer under the microstrip which connects to the latter via following the trace as close as possible in order to maintain the characteristic impedance of the microstrip and avoid introducing an inherent discontinuity. Patent [20] reveals an impedance discontinuity compensator for electronic package bondwire inductance in the form of a microstrip capacitive step.

Although applying tapers is the only way to reduce the effect of impedance mismatch in a two-layer PCB, it usually requires a large area which is rarely available in densely packed layouts. Moreover, there is a handful of papers covering the topic of discontinuity compensation in multilayer PCBs and the aforementioned research papers and application notes do not analyze the differences in multilayer PCB stackups and the possibilities of applying microstrip discontinuity compensation techniques, as well as not quantitatively characterizing the differences. Thus, the main objective of this research is to propose a technique of reducing microstrip discontinuities, introduced by component land pads, in multilayer PCBs and quantitatively characterize the difference between a microstrip discontinuity with and without compensation.

3. Research Setup Description

The devices under test (DUTs) are three separate structures, all of which have been designed on the 1st (top, L1) copper layer in a 6-layer PCB with impedance control ensured by the manufacturer. The dielectric material used is IT180A and is characterized up to 10 GHz. The nominal 50 Ω microstrip width is w₁ = 0.325 mm, when the reference layer (L2) is spaced h₁₂ = 0.173 mm from the microstrip and the average dielectric constant ε_r = 4.2 and has been calculated using electromagnetic field (EM) solvers Saturn PCB Toolkit and Agilent ADS. The DUTs are shown in Figure 2 with all design parameters listed and described in

Table 1. Detailed device under test (DUT) structure description.

Parameter	Value	Comment
Z0	50 Ω	Target microstrip impedance
-	18 μm (0.5 oz)	Final external layer copper foil thickness
-	36 μm (1 oz)	Final internal layer copper foil thickness
-	IT180A	Dielectric material. Rated up to 10 GHz
εr/Dk	4.2	Average dielectric constant value for prepreg and core layers
tan δ	0.015	Dielectric material loss tangent
h12	0.173 mm	Dielectric height between top copper layer and reference copper layer on L2
h23	0.5 mm	Dielectric height between L2 copper layer and L3 copper layer
w1	0.325 mm	50 Ω microstrip width
w2	0.55 mm	RF connector signal pin land pad width
w3	0.9 mm	Discontinuity width
d1	1.4 mm	Distance to side reference plane
d2	1 mm
d3	1.15 mm
l1	13 mm	Total microstrip length
l2	0.9 mm	RF connector signal pin land pad length
l3	3.825 mm	Discontinuity length
l4	4.16 mm	Distance from SubMiniature version A (SMA) connector pad to discontinuity
RL	51 Ω	1% tolerance, 0402 package, same manufacturing batch

.

The base structure, presented in Figure 2a, is a 50 Ω microstrip with no discontinuity and loaded with a R_L = 51 Ω resistor encapsulated in a 0402 surface mount package. This structure serves as a reference to which all other measurements are compared.

Figure 2b presents a loaded 50 Ω microstrip with a discontinuity in the middle. Although the signal pads of components might not be as long as the discontinuity in this structure, the length l₃ = 3.825 mm has been selected to vividly depict the impact of discontinuity compensation.

The width of the discontinuity is set to be around 3 times larger than the width of the microstrip w₃ ≈ 3∙w₁ and is a value which is close to industrial designs similar to that, shown example Figure 1. According to the microstrip parameters in Table 1, the impedance of the discontinuity without compensation is calculated to be Z_{disc.,w/o comp} = 26 Ω. Lastly, Figure 2c presents a cutout in the reference plane on layer L2 under the microstrip, when the compensation is applied.

The discontinuity compensation technique is based on trying to maintain the characteristic impedance Z0 by manipulating the capacitance or inductance of the discontinuity according to:

$$Z0=\sqrt{L/C}$$

(1)

where L is the inductance of the microstrip segment unit length and C is its capacitance per length [21]. A narrower than the nominal microstrip width w₁ discontinuity presents a series distributed inductor, the value of which depends on the width and distance to the reference plane and is found according to:

$$L=\mu d/w$$

(2)

where μ is the magnetic permeability, d is the distance to reference plane and w is the width of the microstrip segment [21]. The width w₃ of the discontinuity in Table 1 is larger, compared to the nominal microstrip width w₁, therefore presenting a lower inductance and larger capacitance values for the latter segment. A distributed capacitance per unit length value is calculated according to

$$C={\epsilon }^{\prime }w/d$$

(3)

where ε^′ is the real part of the relative complex permittivity and is related to the stored energy within the dielectric, w is the width of the microstrip segment, and d is its distance to the reference plane [21].

According to Equation (3), the only way of reducing the capacitance C without introducing dielectric material changes (keeping a constant ε), which would make the manufacturing process either impossible or very costly, is to increase the distance between the plates d.

Thus, the reference plane for the microstrip discontinuity segment is “moved” to the next copper layer, making the distance between the discontinuity and the reference plane on L3 larger and equal to h₁₂ + h₂₃ = 0.673 mm. This makes the calculated impedance of the compensated discontinuity Z_{disc.,w comp} = 62 Ω instead of Z_{disc.,w/o comp} = 26 Ω, when the reference plane was L2. It should also be noted that, because the reference layer for each of the microstrip segment changes from L2 to L3 and then back to L2, vias connecting the reference planes should be as close as possible to the structure in order for the return currents to flow following the path of least impedance. The detailed stackup of the 6-layer PCB discussed in this paper is presented in Figure 3a, while the generalized microstrip discontinuity compensation technique in multilayer PCBs is shown in Figure 3b.

The compensation would be even more precise (Z_{disc.,w comp} = 53 Ω) under the same conditions, if the total dielectric thickness between copper layers L1 and L3 was h₁₂ + h₂₃ = 0.5 mm, but the DUT structures were designed on a standard 1.6 mm (±10%) thickness PCB, which served as a part of a complex transceiver project. This leads to a point that if the designer has more degrees of freedom in layer count (see Figure 3c), or can reduce the thickness of a 4-layer or 6-layer PCB from standard 1.6 mm to 1.2 mm and below, then the compensation can level out the impedance mismatch.

In an 8-layer board, shown in Figure 3c, the core layer thickness is naturally smaller, compared to that of a 6-layer board, when the overall thickness of the PCB is the same. This leads to a possibility of adding cutouts in several reference planes (Figure 3c) under the discontinuity to compensate for the mismatch, ensuring a proper electrical connection between the reference planes with nearby vias.

4. Measurement Results and Discussion

The fabricated DUT structures are presented in Figure 4a. The first structure, named “RF test 1”, corresponds to the loaded 50 Ω microstrip shown in Figure 2a with a solid reference layer on L2. The structure named “RF test 2” represents the microstrip with discontinuity and without compensation, and corresponds to Figure 2b with a solid reference layer on L2. Finally, “RF test 3” is the microstrip with discontinuity and with compensation, and corresponds to Figure 2b with a reference layer L2 cutout shown in Figure 2c. All DUTs have been loaded using a 0402 package 51 Ω 1% tolerance resistor form the same batch. The scattering parameter (S-parameter) measurements have been done using Agilent E8363B vector network analyzer (VNA) calibrated in the range from 20 MHz to 10 GHz accounting for the length of the cable, which connects the DUT to the VNA. The structures presented in Figure 4 have also been simulated using EM simulator Agilent ADS, replicating the precise stackup.

The S-parameter simulation (dashed) and measurement (solid) results are presented in Figure 4b. The loaded microstrip with no discontinuity “RF test 1” simulation and measurement results in green reveal the matched characteristic impedance threshold when loading the microstrip line with a surface mount resistor. The matching quality is perfect (S₁₁ < −25 dB) up to around 2 GHz. The worst performance is seen in the frequency range between 8–9 GHz, where the S₁₁ curve reaches slightly above −10 dB.

“RF test 2” in orange corresponds to the microstrip line containing a discontinuity, which is not compensated using reference layer cutouts. Both simulation and measurement results match ideally with a slight resonance at around 3 GHz. Comparing the threshold “RF test 1” and “RF test 2” curves, an expectedly large (from 2.5 dB to 34 dB) difference in S₁₁ response over the whole frequency range can be observed.

Finally, the curves in blue represent “RF test 3”, and correspond to the microstrip line containing a discontinuity, which is compensated using a reference layer cutout on L2. The measurement and simulation results resemble each other with the measurement S₁₁ curve shifted by around 1 GHz to the lower side and containing slight resonances around 2.8 GHz and 3.8 GHz. Comparing “RF test 2” with no compensation to “RF test 3” with the introduced cutout, an improvement of 4–12 dB can be observed in the whole frequency range, with “RF test 3” curve shape resembling the threshold “RF test 1” curve. As a result, the reference layer cutout under the discontinuity provides a sufficient improvement in matching the discontinuity to the characteristic impedance of the signal path.

The observed resonances are a result of the 0402 surface mount load resistor package parasitics (mainly package lead inductance), as well as the introduced discontinuities in the SubMiniature version A (SMA) connector to microstrip transition and solder joints.

Based on the simulation and measurement results for a single discontinuity pad (Figure 4b), the principle is extrapolated to a part of the common RF chain (Figure 1). The simulated radio-frequency chain consists of a power amplifier (named PA) PGA-102+ [2] encapsulated in a SOT89 package connected to a 0805 size surface mount inductor and a RF3336C [22] surface acoustic wave (SAW) filter which is fed into a U.FL connector. The simulated amplifier chain and the corresponding schematic are presented in Figure 5a. In order to omit the characteristics of the selected parts and evaluate only the impact of the package footprint, the landpads are bypassed (shorted) by means of a transmission line as shown in Figure 5b.

The latter figure is similar to a distributed band-pass filter, therefore the S-parameter response is expected to be characteristic of the mentioned filter type. Figure 5c presents a reference plane with cutouts on L2 when the discontinuity compensation technique is applied. Landpad sizes and PCB stackup information, used in the simulation, are presented in

Table 2. Simulated amplifier chain landpad sizes.

Parameter	Value	Comment
w1	0.325 mm	50 Ω microstrip width
A1	0.6 mm × 0.5 mm	0402 package surface mount capacitor pad area
A2	0.7 mm × 1.6 mm	PGA-102+ amplifier in SOT89 package landpad area
A3	1.3 mm × 0.8 mm	0805 package surface mount choke inductor pad area
A4	2.1 mm × 0.8 mm	SF2237C saw filter package input landpad area
A5	1.6 mm × 0.8 mm	SF2237C saw filter package output landpad area
A6	1.2 mm × 1.6 mm	U.FL connector RF pin landpad area
-	>2∙w1	Distance to side reference plane
lchain	20 mm	Total microstrip length
-	IT180A	Dielectric material. Rated up to 10 GHz
h12	0.173 mm	Dielectric height between top copper layer and reference copper layer on L2. IT180A 1086 × 1 + 2113 × 1 prepreg material.
h23	0.355 mm	Dielectric height between L2 copper layer and L3 copper layer. IT180A 7628 × 2 core material.
tan δ	0.015	Dielectric material loss tangent
-	18 μm (0.5 oz)	Final external layer copper foil thickness
-	36 μm (1 oz)	Final internal layer copper foil thickness
εr/Dk	4.2	Average dielectric constant value for prepreg and core layers

. It can also be noticed, that the 0402 size surface mount DC block capacitor landpads with an area A₁ are not included in the compensation, as the width is only 0.175 mm larger than the 50 Ω microstrip width w₁. If this pad width deviation from w₁ was to be compensated, the distance to the reference plane (thickness of the dielectric) should have been much smaller than h₁₂.

The amplifier chain with bypassed components (Figure 5b) S-parameter simulation results are presented in Figure 6. The latter figure contains three solid S₁₁ and dashed S₂₁ simulation result curves. Results in green describe a l_chain = 20 mm long transmission line simulation with no components, which serves as a reference for return loss S₁₁ and insertion loss S₂₁ values. Results in orange correspond to the amplifier chain simulation with bypassed components (Figure 5b) and a solid reference plane on layer L2. Results in blue describe the amplifier chain simulation with bypassed components (Figure 5b) and a reference plane with cutouts, when the compensation technique is applied (Figure 5c). The introduced compensation technique for multiple pads in the amplifier chain provides an overall improvement of more than 5 dB in return loss S₁₁ results according to Figure 6.

According to the reflection coefficient formula [21]:

$$S_{11}=V_1^{-}/V_1^{+}$$

(4)

where V₁⁺ and V₁⁻ are the forward and reflected powers accordingly, the improvement in reflection loss S₁₁ could be a result of the reflected wave being attenuated because of the increased losses S₂₁ (thus reducing the reflected power V₁⁻) in the simulated amplifier chain.

In order to exclude the latter, return loss simulation is presented in Figure 6. The losses in the l_chain = 20 mm long transmission line (green dashed curve) serve as a reference to which the results are compared. When no compensation is applied (orange dashed curve), the reflected signal distorts the forward signal, and thus the insertion loss S₂₁ is increased up to 0.4 dB in the range of 1–2 GHz and more in the higher frequency range. When the compensation technique is applied (blue dashed curve), the insertion loss S₂₁ is improved and the curve resembles the losses of a transmission line without any discontinuity (green dashed curve).

Thus, when dealing with transmission lines which connect multiple components, such as amplifiers, filters, connectors and etc., the introduced pad discontinuity compensation can reduce losses in the chain by more than 0.5 dB, depending on the number of pads.

The latter research is a case study in multilayer PCBs, as there are various dielectric materials with different properties which make up differing thickness PCBs with multiple copper layer count variations. Although the presented technique is successfully applied to a 6-layer stackup, the overall design approach is universal and could be applied to other PCBs with differing layer counts and materials. Based on the presented simulation and measurement results, a generalized guideline for compensating microstrip discontinuities in a multilayer PCB is proposed:

(1)

Define the PCB layer count, dielectric material, its thickness between the copper layer, containing microstrips, and the reference plane and thickness of the copper layers.

(2)

Calculate the width of the target characteristic impedance Z0 trace and lay out the design.

(3)

Compensate for capacitive or inductive discontinuities introduced by wider or narrower than the Z0 microstrip signal pads if the stackup makes it feasible. In order for the compensation to be successful, the core and prepreg layer thicknesses should be as even as possible. A 4-layer board design is the hardest to successfully implement the compensation. If the 4-layer PCB is standard 1.6 mm thickness, then the core and prepreg layer thicknesses vary around 6 times, and the added reference layer cutout as a measure of compensation will not provide the desired result, thus leaving only the option of adding tapers. If there is a way to reduce the overall thickness of the PCB (for example, to a manufacturable 0.8 mm) and select prepreg to a core layer thickness ratio of around ½ or less, reference plane cutout compensation becomes possible. The 6-layer PCB stackups, as demonstrated in this paper, are easier to handle, but still require careful core and prepreg layer thickness selection. Standard thickness boards with 8 layers and more are the most suited for the compensation to be implemented successfully, due to the core and prepreg layer thicknesses being almost identical.

(4)

Vias in close proximity to the reference plane change under the discontinuity are mandatory for the reverse currents to flow following the path of least impedance.

(5)

The reference plane under the microstrip and the cutouts under discontinuities must not contain any other crossing planes (for example, power) or traces in order not to distort the path of return currents.

Comparing the proposed compensation technique for multilayer PCBs to the currently available microstrip discontinuity techniques, it can be noted that the closest approaches to the proposed one are found in [15,17]. The major difference is that the latter papers either address PCB to bare silicon transitions or very high-speed (25 Gbps and higher) digital communication scenarios. Other mentioned papers and technical datasheets suggest using different size tapers, which greatly increase the area and are not quite suitable for dense designs. This paper emphasizes the possibilities and advantages of compensating for microstrip discontinuities in a frequency range, which covers the operation of most of the modern electronics devices and quantitatively characterizes the improvements in S₁₁ and S₂₁ parameters. The proposed design approach is universal and is not dependent on the multilayer PCB layer count (which in this paper is suggested to be more than 4 for standard thickness PCBs), dielectric materials used or other fabrication requirements and provides significant improvements in return and transmission losses. Moreover, the proposed design approach only requires cutouts under larger component pads and affects neither the area of the layout nor the overall cost of the PCB, as no specific fabrication requirements are requested, thus is well within the capabilities of most modern PCB fabrication facilities.

Thus, an S₁₁ response improvement of 4–12 dB can be observed in the whole frequency range up to 10 GHz, when the microstrip discontinuity is compensated for using a carefully designed stackup, as shown in a 6-layer PCB presented in this paper, and following the listed design guidelines. The advantage of applying the proposed discontinuity compensation technique in multilayer PCBs compared to other proposed techniques (for example, different variations of tapers, etc.) is reduced losses without increasing the area of the microstrip structure with the expense of introducing cutouts in the reference plane below. The extrapolated simulation shows, that when compensating multiple pads in a transmission line with components, the overall S₁₁ improves by more than 6 dB and the S₂₁ is reduced to almost the value of losses in a transmission line of the same length.

5. Conclusions

This paper addresses the topic of compensating discontinuities, introduced by signal pads, which are wider than the target impedance microstrip. A 6-layer PCB with IT180A dielectric material containing three structures has been manufactured and characterized using Agilent E8363B VNA. The first structure had no discontinuity, the second had an uncompensated capacitive discontinuity and the third had the same capacitive discontinuity but with compensation. The compensation method is based upon carefully designing the stackup of the PCB allowing for a reference plane cutout under the discontinuity to even out the impedance mismatch. This led to a measured S₁₁ response improvement of 4–12 dB in the whole frequency range up to 10 GHz, compared to that when no compensation was applied. Simulation of an amplifier chain with multiple pads, which make up discontinuities, revealed a return loss S₁₁ improvement of more than 5 dB and an insertion loss S₂₁, which resembles that of a transmission line. Based on the presented gathered results, a generalized guideline for compensating microstrip discontinuities in multilayer PCBs is proposed. The more copper layers a PCB contains, the closer the thicknesses of core and prepreg are to each other, allowing for a more precise discontinuity impedance matching to the characteristic impedance of the microstrip.