A Novel SRAM PUF Stability Improvement Method Using Ionization Irradiation
Abstract
:1. Backgrounds
2. Introduction
- Modifying Cell Structure
- Aging Injection
- Masking and Preselection
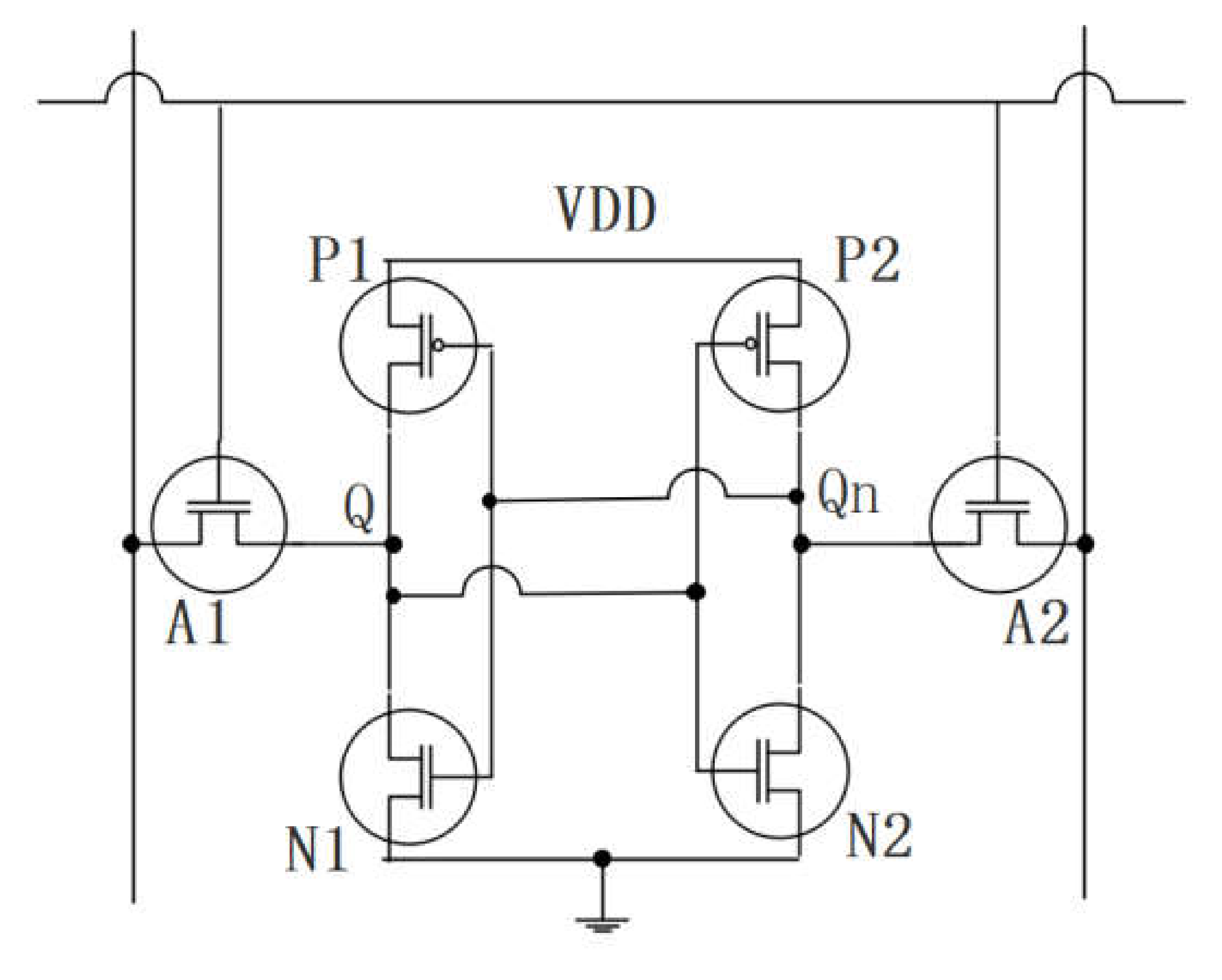
3. Principles of Proposed Methodology
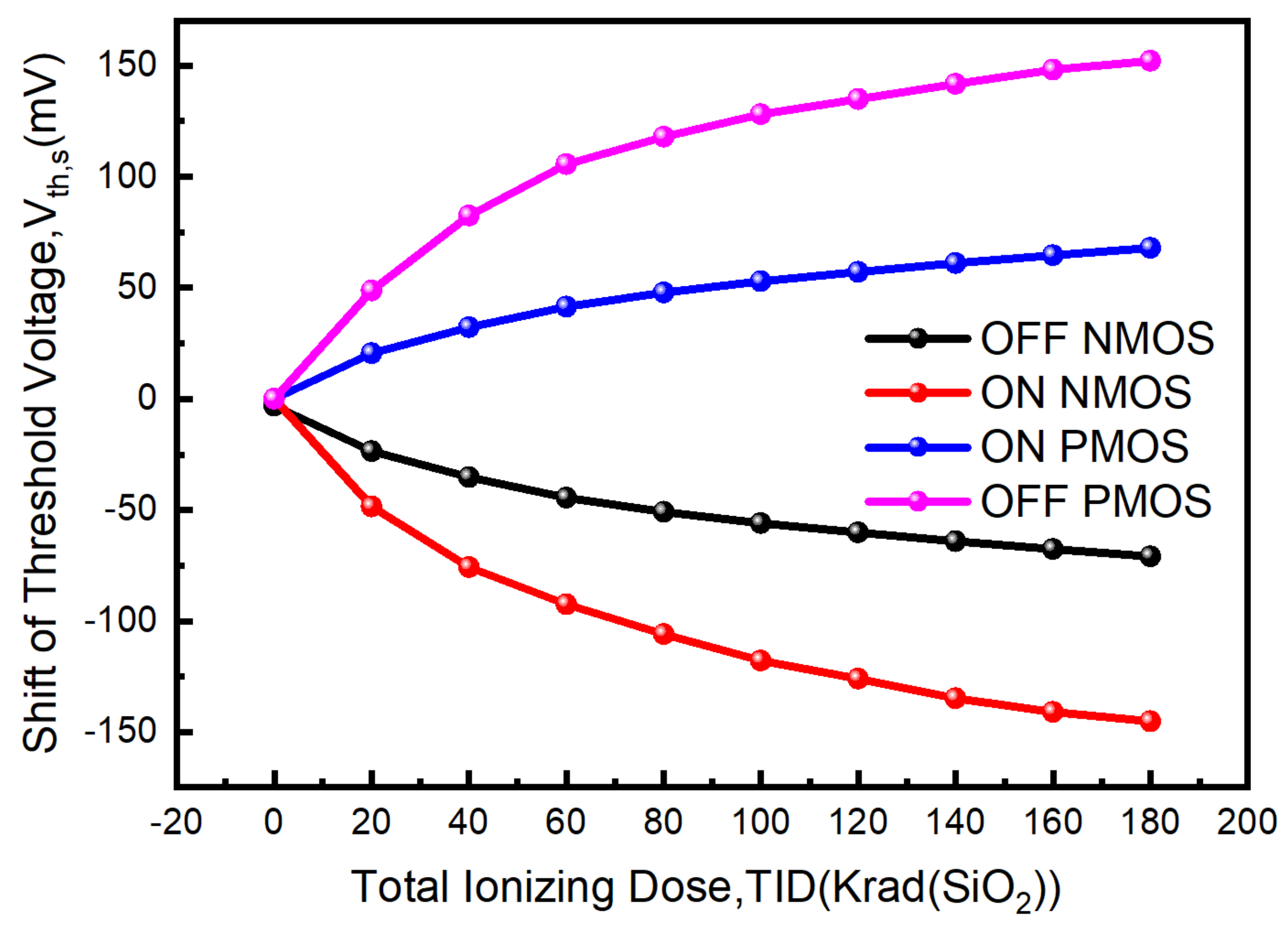
3.1. TID Effect on Transistors’ Threshold Voltages
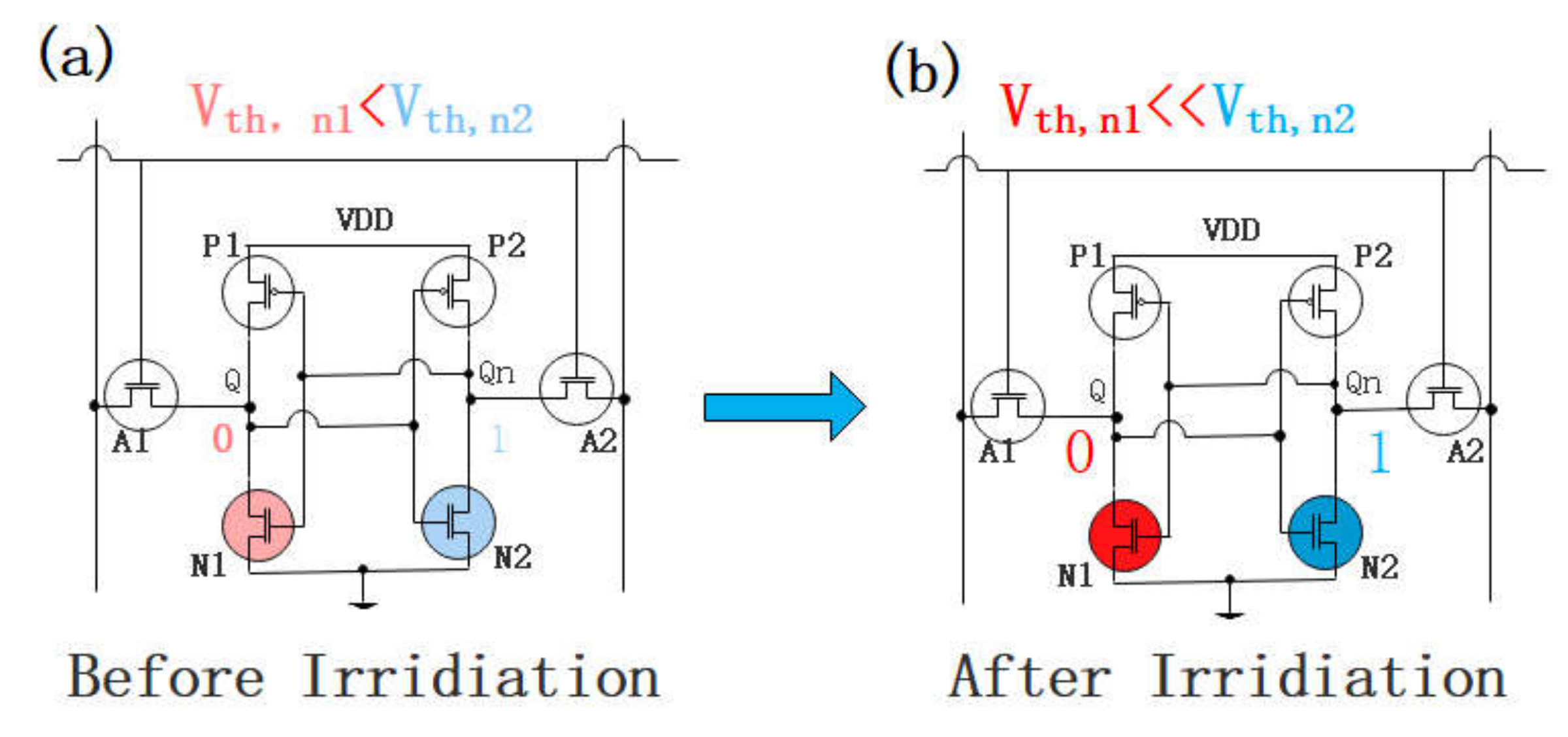
3.2. Physical Mechanisms of Stability Improvement Benefiting from TID Effect
4. Simulations
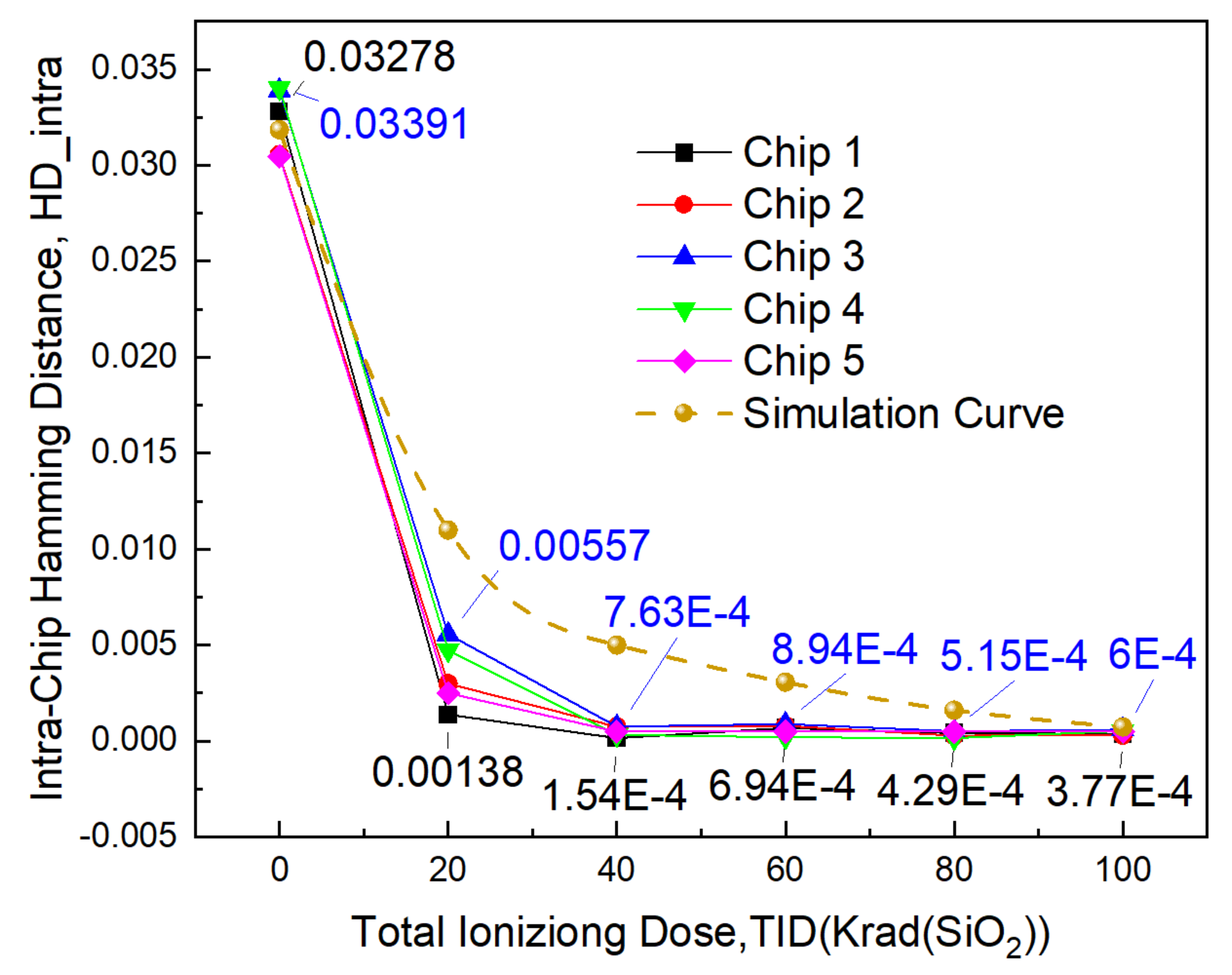
5. Experimental Verification
5.1. Devices and Experiment Sets
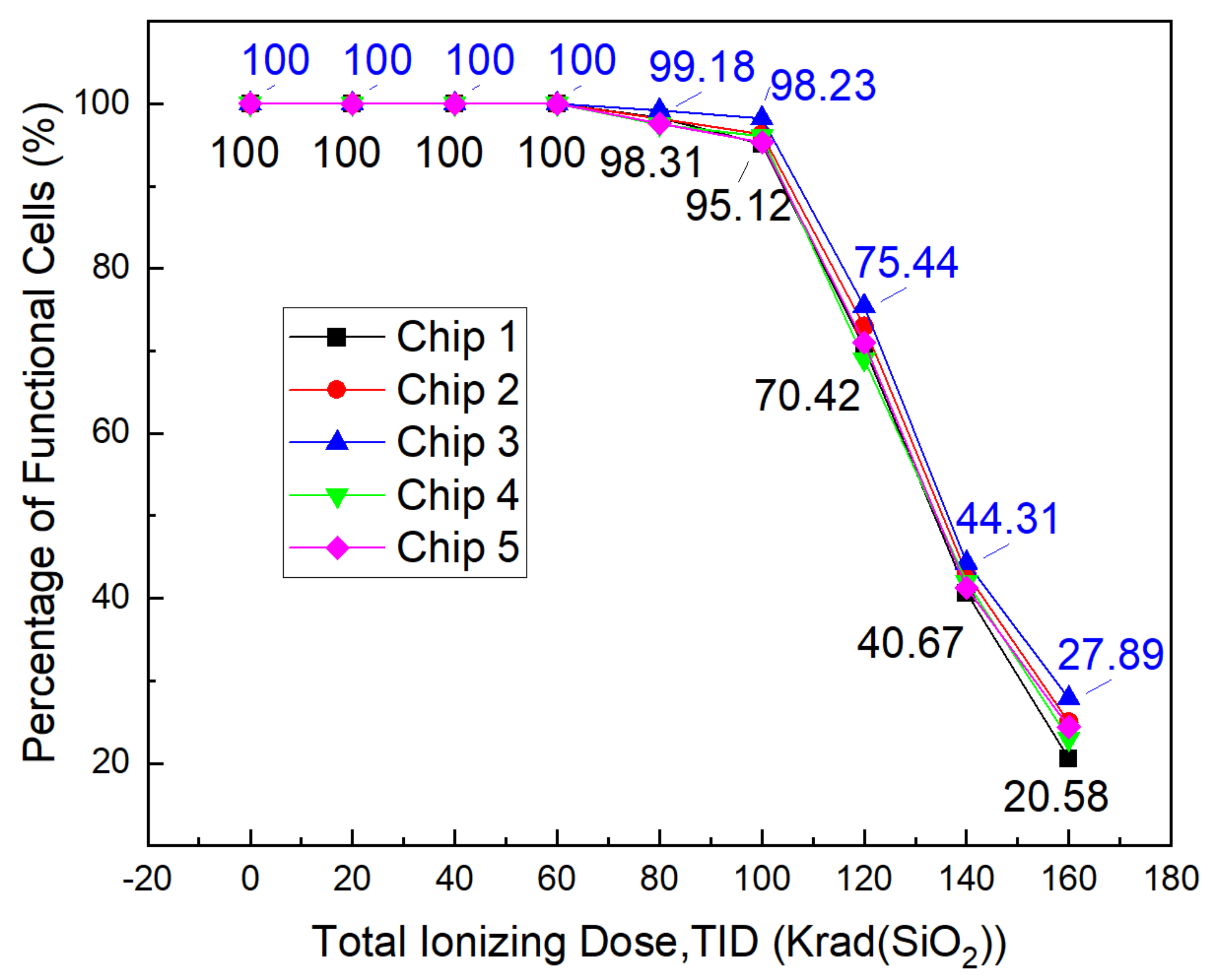
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- McGrath, T.; Bagci, I.E.; Wang, Z.M.; Roedig, U.; Young, R.J. A PUF taxonomy. Appl. Phys. Rev. 2019, 6, 011303. [Google Scholar] [CrossRef] [Green Version]
- Van Der Leest, V.; Van Der Sluis, E.; Schrijen, G.-J.; Tuyls, P.; Handschuh, H. Efficient Implementation of True Random Number Generator Based on SRAM PUFs. In Computer Vision; Springer Science and Business Media LLC: Berlin, Germany, 2012; Volume 6805, pp. 300–318. [Google Scholar]
- Bohm, C.; Hofer, M. Physical Unclonable Functions in Theory and Practice. In Physical Unclonable Functions in Theory and Practice; Springer Science and Business Media LLC: Berlin, Germany, 2013; pp. 16–19. [Google Scholar]
- AlAmro, M.; Mursi, K.T.; Zhuang, Y.; Aseeri, A.; Alkatheiri, M.S. Robustness and Unpredictability for Double Arbiter PUFs on Silicon Data: Performance Evaluation and Modeling Accuracy. Electronics 2020, 9, 870. [Google Scholar] [CrossRef]
- Cao, Y.; Robson, A.J.; Alharbi, A.; Roberts, J.; Woodhead, C.; Noori, Y.J.; Bernardo-Gavito, R.; Shahrjerdi, D.; Roedig, U.; Fal’Ko, V.I.; et al. Optical identification using imperfections in 2D materials. 2D Materials 2017, 4, 045021. [Google Scholar] [CrossRef]
- Liu, W.; Yu, Y.; Wang, C.; Cui, Y.; O’Neill, M.; Weiqiang, L. RO PUF design in FPGAs with new comparison strategies. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015. [Google Scholar]
- Lim, D.; Lee, J.; Gassend, B.; Suh, G.; Van Dijk, M.; Devadas, S. Extracting secret keys from integrated circuits. IEEE Trans. Very Large Scale Integr. Syst. 2005, 13, 1200–1205. [Google Scholar] [CrossRef]
- Guajardo, J.; Kumar, S.S.; Schrijen, G.-J.; Tuyls, P. FPGA Intrinsic PUFs and Their Use for IP Protection. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, Vienna, Austria, 10–13 September 2007. [Google Scholar]
- Maes, R.; Rozic, V.; Verbauwhede, I.; Koeberl, P.; Van Der Sluis, E.; Van Der Leest, V. Experimental evaluation of Physically Unclonable Functions in 65 nm CMOS. In Proceedings of the European Solid State Device Research Conference (SSCIRC), Bordeauz, France, 17 September 2012. [Google Scholar]
- Fruhashi, K.; Shiozaki, M.; Fukushima, A.; Murayama, T.; Fujino, T. The arbiter-PUF with high uniqueness utilizing novel arbiter circuit with Delay-Time Measurement. In Proceedings of the IEEE International Symposium of Circuits and Systems (ISCAS), Seoul, South Korea, 20–23 May 2012. [Google Scholar]
- Intrinsic ID. Intrinsic ID SRAM PUF Technology. Available online: https://www.intrinsic-id.com/sram-puf/ (accessed on 26 April 2020).
- Mispan, M.S.; Duan, S.; Halak, B.; Zwolinski, M. A reliable PUF in a dual function SRAM. Integration 2019, 68, 12–21. [Google Scholar] [CrossRef]
- Liu, M.; Zhou, C.; Tang, Q.; Parhi, K.K.; Kim, C.H. A data remanence based approach to generate 100% stable keys from an SRAM physical unclonable function. In Proceedings of the IEEE/ACM International Symposium on Low Power Electronics and Design (ISLPED), Portland, OR, USA, 27–29 August 2007. [Google Scholar]
- NXP. NXP Secures the Edge with Two Industry-First Multi-Core Arm Cortex-M33 Solutions. Available online: https://www.nxp.com/search?keyword=AN12292&start=0 (accessed on 3 August 2020).
- Intrinsic ID. QuiddiKey®. Available online: https://www.intrinsic-id.com/products/quiddikey/ (accessed on 3 June 2020).
- Microsemi. Libero SoC v11.6 Resources Archive. Available online: https://www.microsemi.com/product-directory/design-resources-archive/5086-libero-soc-v11-6-resources-archive (accessed on 10 October 2019).
- Schrijen, G.-J.; Van Der Leest, V. Comparative analysis of SRAM memories used as PUF primitives. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 12–16 March 2012. [Google Scholar]
- Kiamehr, S.; Golanbari, M.S.; Tahoori, M.B. Leveraging aging effect to improve SRAM-based true random number generators. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Lausanne, Switzerland, 27–31 March 2017. [Google Scholar]
- Bhargava, M.; Mai, K. A High Reliability PUF Using Hot Carrier Injection Based Response Reinforcement. In Proceedings of the of International Conference on Cryptographic Hardware and Embedded Systems, Santa Barbara, CA, USA, 19–22 August 2013. [Google Scholar]
- Jang, J.-W.; Ghosh, S. Design and analysis of novel SRAM PUFs with embedded latch for robustness. In Proceedings of the Sixteenth International Symposium on Quality Electronic Design, Santa Clara, CA, USA, 2–4 March 2015. [Google Scholar]
- Okumura, S.; Yoshimoto, S.; Kawaguchi, H.; Yoshimoto, M. A 128-bit Chip Identification Generating Scheme Exploiting Load Transistors’ Variation in SRAM Bitcells. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2012, 95, 2226–2233. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Wang, P.; Zhang, Y. Highly stable data SRAM-PUF in 65nm CMOS process. In Proceedings of the IEEE 10th International Conference on ASIC.; Institute of Electrical and Electronics Engineers (IEEE), Shenzen, China, 28–31 October 2013. [Google Scholar]
- Garg, A.; Kim, T.T.; Garg, A. Design of SRAM PUF with improved uniformity and reliability utilizing device aging effect. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Melbourne, Australia, 1–5 June 2014. [Google Scholar]
- Garg, A.; Lee, Z.C.; Lu, L.; Kim, T.T.-H. Improving uniformity and reliability of SRAM PUFs utilizing device aging phenomenon for unique identifier generation. Microelectron. J. 2019, 90, 29–38. [Google Scholar] [CrossRef]
- Xiao, K.; Rahman, M.; Forte, D.; Huang, Y.; Su, M.; Tehranipoor, M. Bit selection algorithm suitable for high-volume production of SRAM-PUF. In Proceedings of the IEEE International Symposium on Hardware-Oriented Security and Trust (HOST), Arlington, VA, USA, 6–7 May 2014. [Google Scholar]
- Mathew, S. A 0.19 pJ/b PVT-variation-tolerant hybrid physically unclonable function circuit for 100in 22nm CMOS. In Proceedings of the IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 9–13 February 2014. [Google Scholar]
- Shifman, Y.; Miller, A.; Keren, O.; Weizmann, Y.; Shor, J. A Method to Improve Reliability in a 65-nm SRAM PUF Array. IEEE Solid-state Circuits Lett. 2018, 1, 138–141. [Google Scholar] [CrossRef]
- Lee, M.; Cho, S.; Lee, N.; Kim, J. New Radiation-Hardened Design of a CMOS Instrumentation Amplifier and its Tolerant Characteristic Analysis. Electronics 2020, 9, 388. [Google Scholar] [CrossRef] [Green Version]
- Esqueda, I.S. Modeling of Total Ionizing Dose Effects in Advanced Complementary Metal-oxide-Semiconductor Technologies. Ph.D Thesis, Arizona State University, Tempe, AZ, USA, 2011. [Google Scholar]
- Ma, T.-P.; Dressendorfer, P.V. Phenomenological description of ionizing radiation effects. In Ionizing Radiation Effects in MOS Devices and Circuits; John Wiley & Sons: New York, NY, USA, 1989; pp. 35–43. [Google Scholar]
- Setyawan Sajim, A. Open-Source Software-Based SRAM-PUF for Secure Data and Key Storage Using Off-The-Shelf SRAM. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2018. [Google Scholar]
- Wu, P.-C.; Yeh, C.-Y.; Tsai, H.-H.; Juang, Y.-Z. Low-frequency noise reduction technique for accelerometer readout circuit. In Proceedings of the IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Jeju, South Korea, 25–28 October 2016. [Google Scholar]








| Solution | Original 𝐻𝐷_𝑖𝑛𝑡𝑟𝑎 | Improved 𝐻𝐷_𝑖𝑛𝑡𝑟𝑎 | Operation | Tape Out | Time-Cost | Memory Use Ratio | |
|---|---|---|---|---|---|---|---|
| This work | Ionization irradiation | 0.033 | 10−4 | simple | no | 13 min | above 99% |
| [21] | Modifying cell structure | 0.037 | 0.0138 | complex | yes | - | - |
| [24] | Aging injection | ~0.014 | ~0.003 | simple | no | at least 6 h | above 99% |
| [13] | Preselection | - | close to 0 | simple | no | - | 1‰ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Jiang, C.; Gu, K.; Zhong, L.; Fang, W.; Dai, G. A Novel SRAM PUF Stability Improvement Method Using Ionization Irradiation. Electronics 2020, 9, 1498. https://doi.org/10.3390/electronics9091498
Zhang X, Jiang C, Gu K, Zhong L, Fang W, Dai G. A Novel SRAM PUF Stability Improvement Method Using Ionization Irradiation. Electronics. 2020; 9(9):1498. https://doi.org/10.3390/electronics9091498
Chicago/Turabian StyleZhang, Xu, Chunsheng Jiang, Ke Gu, Le Zhong, Wen Fang, and Gang Dai. 2020. "A Novel SRAM PUF Stability Improvement Method Using Ionization Irradiation" Electronics 9, no. 9: 1498. https://doi.org/10.3390/electronics9091498
APA StyleZhang, X., Jiang, C., Gu, K., Zhong, L., Fang, W., & Dai, G. (2020). A Novel SRAM PUF Stability Improvement Method Using Ionization Irradiation. Electronics, 9(9), 1498. https://doi.org/10.3390/electronics9091498





