Modeling and Analysis of the Fractional-Order Flyback Converter in Continuous Conduction Mode by Caputo Fractional Calculus
Abstract
:1. Introduction
2. Fundamentals
2.1. Fractional Calculus
2.2. The Basic Model of the Fractional-Order Inductor and Capacitor
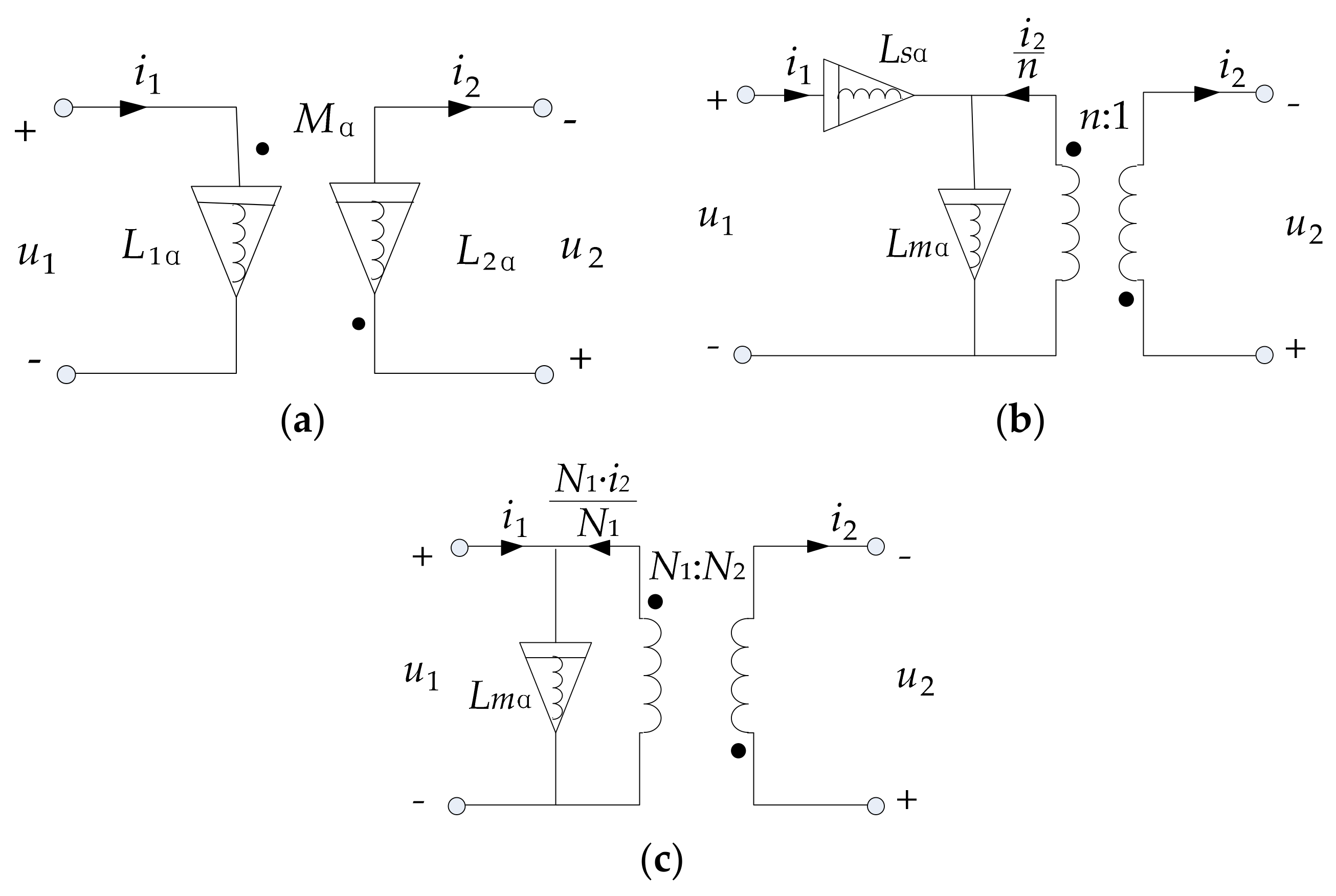
2.3. The Equivalent Circuit of the Fractional-Order Mutual Inductance
3. Mathematical Model of the Fractional-Order Flyback Converter
4. State-Space Average Modeling and Analysis of the Fractional-Order Flyback Converter
4.1. State-Space Average Modeling and Analysis of the Fractional-Order Flyback Converter
4.2. DC Analysis
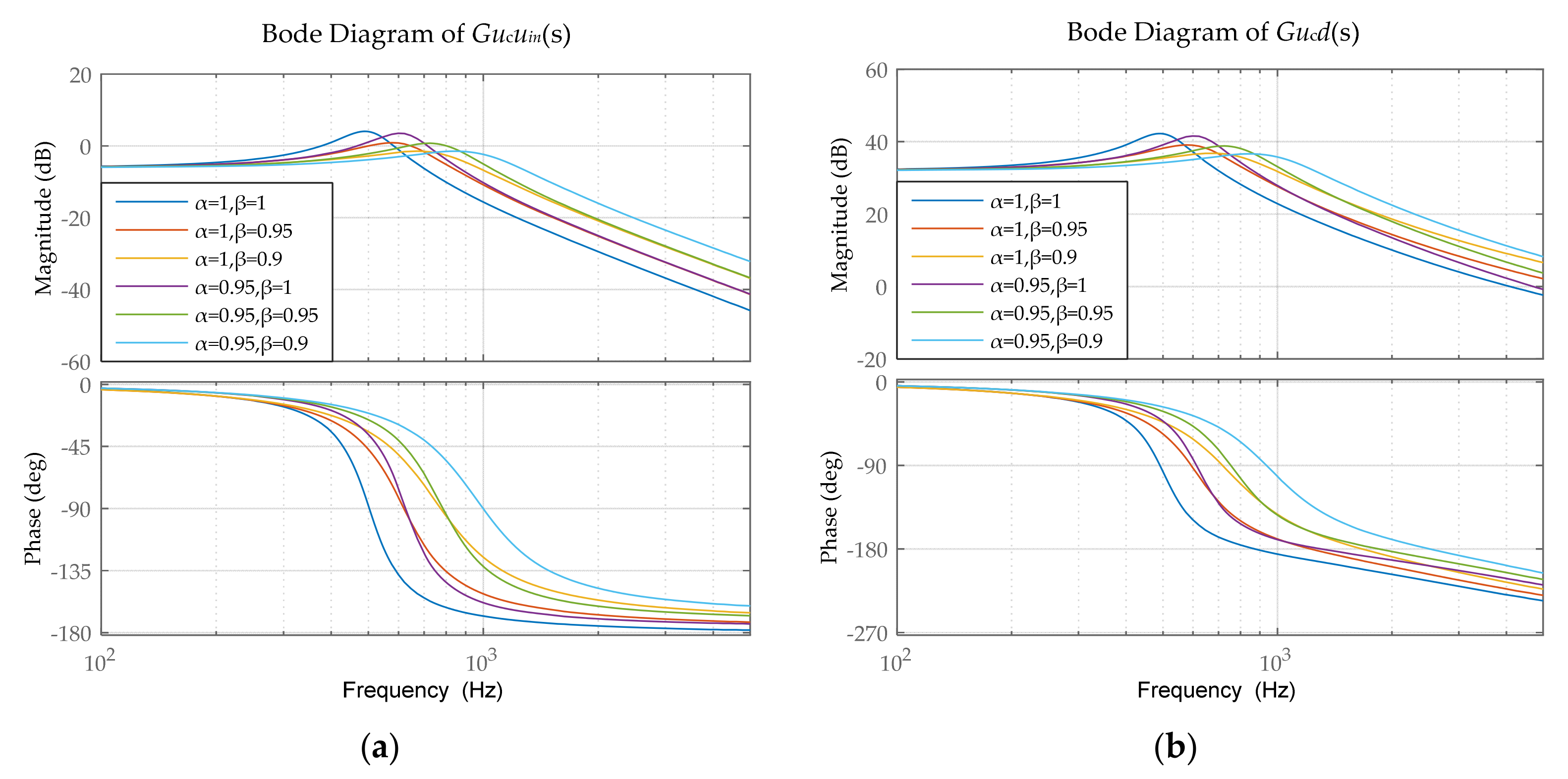
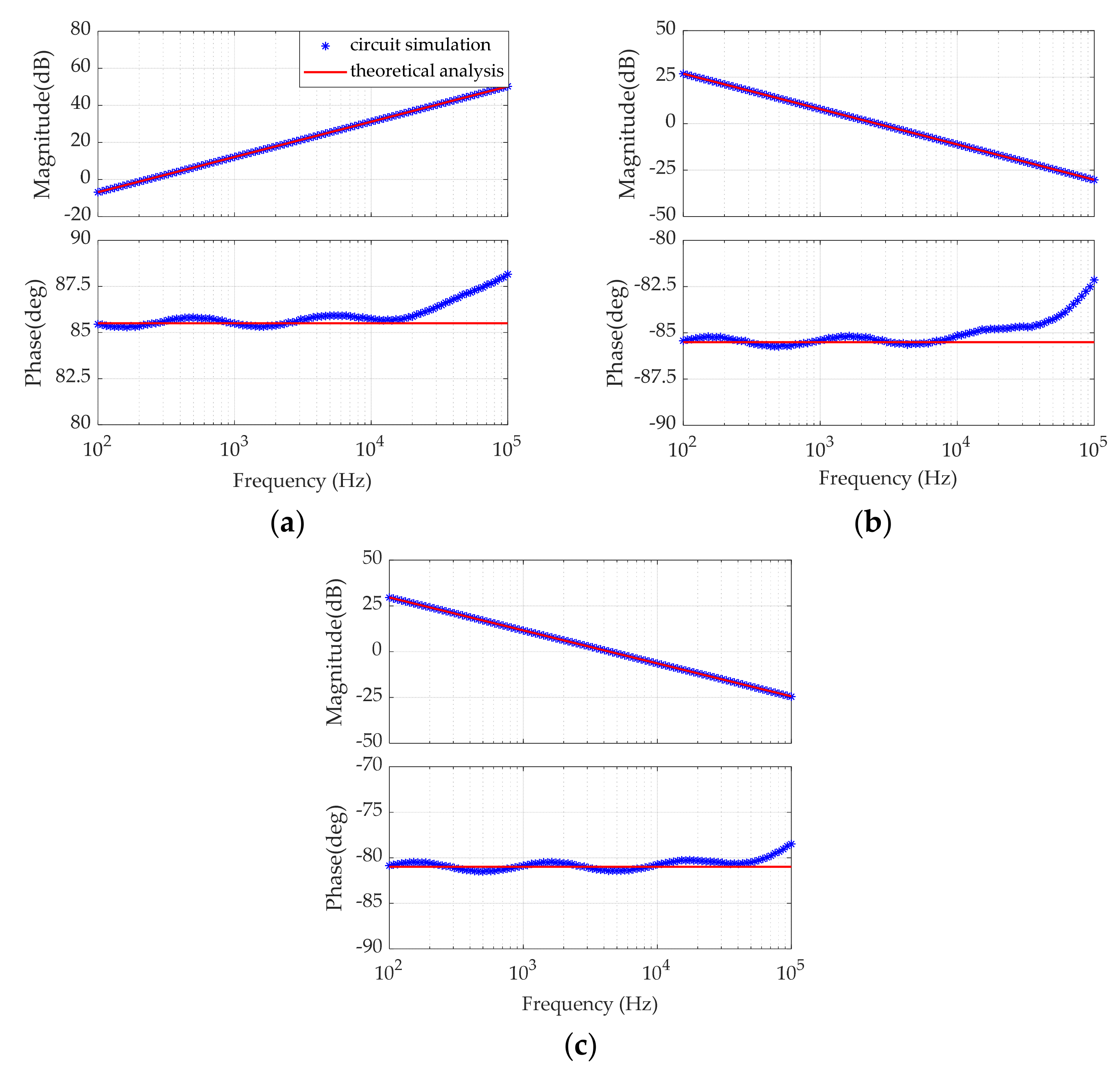
4.3. AC Analysis
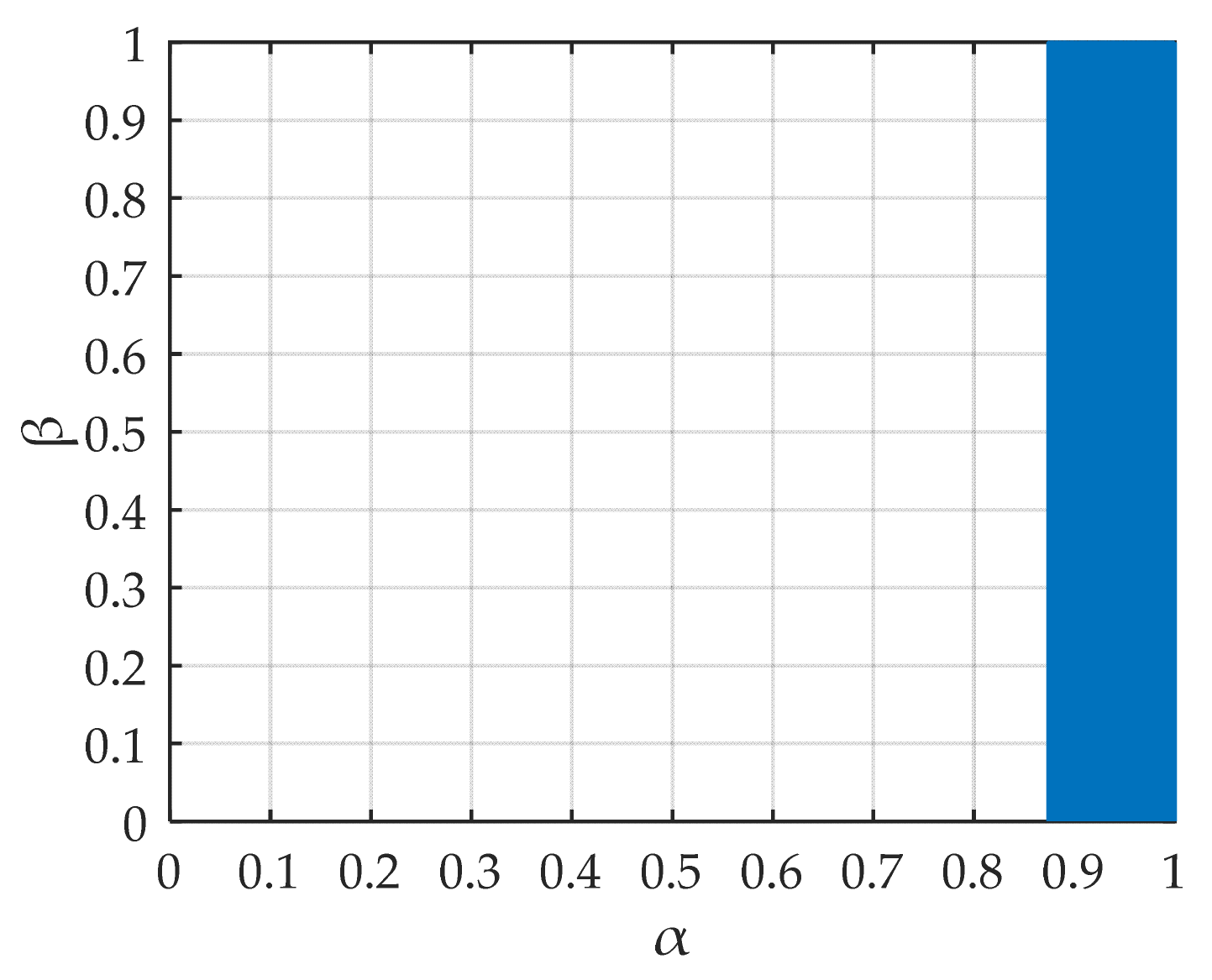
5. Simulation
5.1. The Rational Approximation Method for the Fractional-Order Inductor and Capacitor
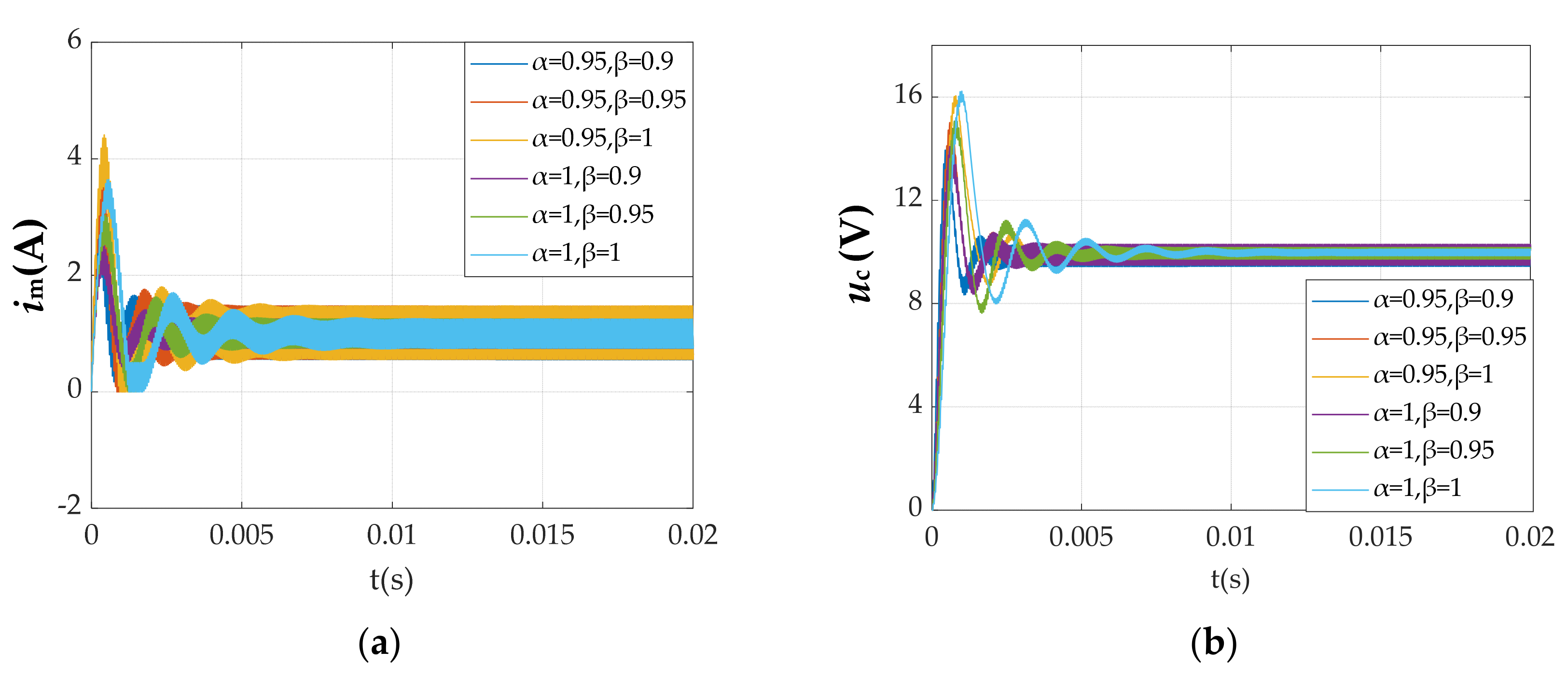
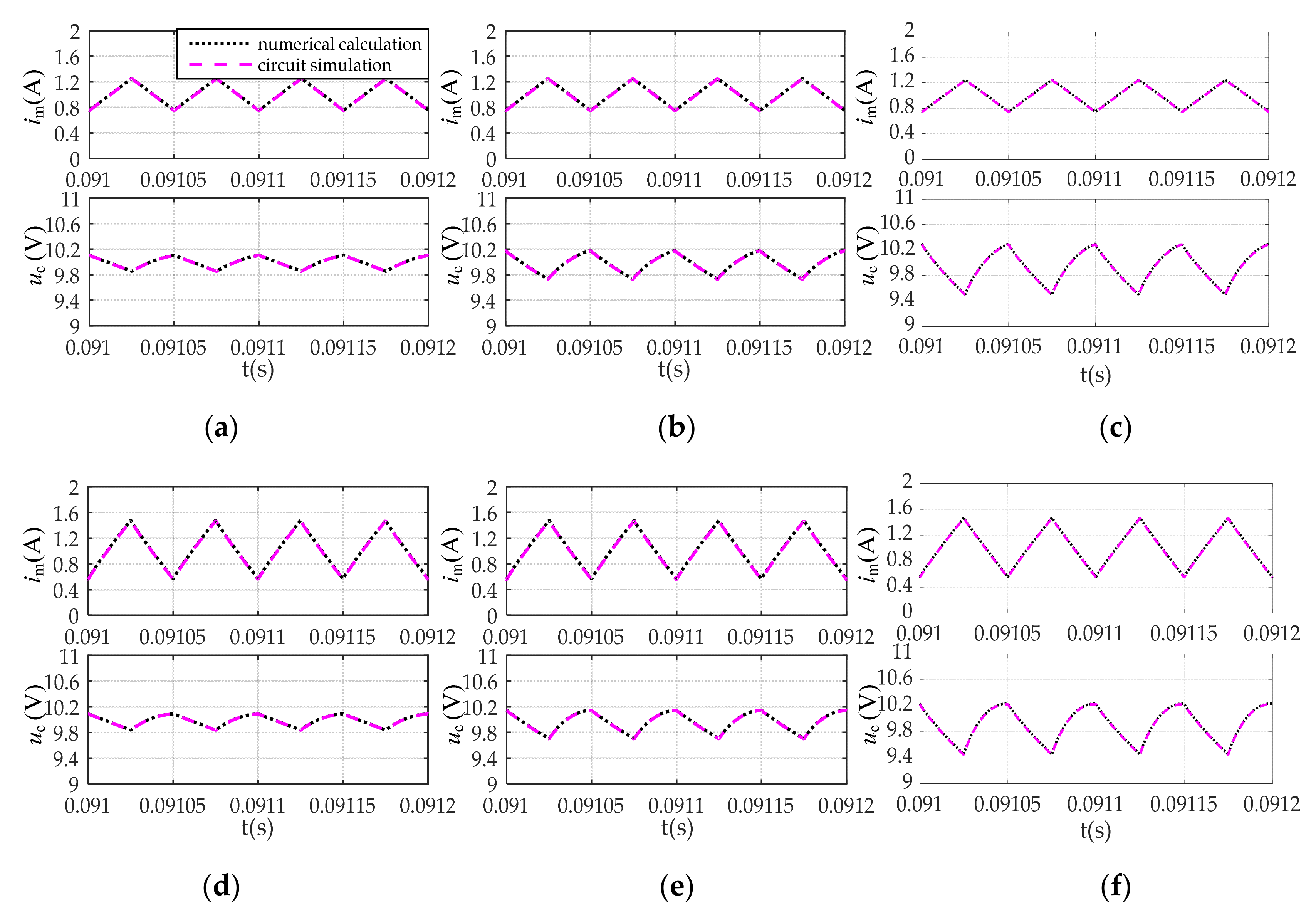
5.2. Simulations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, Q.; Chen, D.; Zhao, T.B.; Chen, Y.Q. Fractional calculus in image processing: A review. Fract. Calc. Appl. Anal. 2016, 19, 1222–1249. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.W.; Zhang, B.; Shu, X.J.; Wei, Z.H. Fractional-order autonomous circuits with order larger than one. J. Adv. Res. 2020, 25, 217–225. [Google Scholar] [CrossRef] [PubMed]
- Zou, C.F.; Zang, L.; Hu, X.S. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef] [Green Version]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.A.T.; Bates, J.H.T. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Liu, H.; Pan, Y.; Li, S.; Chen, Y. Adaptive fuzzy backstepping control of fractional-order nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2209–2217. [Google Scholar] [CrossRef]
- Radwan, A.G. Resonance and quality factor of the RLβCα fractional circuit. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 377–385. [Google Scholar] [CrossRef]
- Jiang, Y.W.; Zhang, B.; Zhou, J. A Fractional-order resonant wireless power transfer system with inherently constant current output. IEEE Access 2020, 8, 23317–23323. [Google Scholar] [CrossRef]
- Jonscher, A.K. Dielectric Relaxation in Solids; Chelsea Dielectric Press: London, UK, 1983. [Google Scholar]
- Westerlund, S.; Ekstam, L. Capacitor theory. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 826–839. [Google Scholar] [CrossRef]
- Jesus, I.S.; Machado, J.A.T. Development of fractional order capacitors based on electrolyte processes. Nonlinear Dyn. 2009, 56, 45–55. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.W.; Zhang, B. High-power fractional-order capacitor with 1<α<2 based on power converter. IEEE Trans. Ind. Electron. 2018, 65, 3157–3164. [Google Scholar] [CrossRef]
- Westerlund, S. Dead Matter has Memory! Phys. Scr. 1991, 43, 174–179. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Galhano, A.M.S.F. Fractional order inductive phenomena based on the skin effect. Nonlinear Dyn. 2012, 68, 107–115. [Google Scholar] [CrossRef]
- Soltan, A.; Radwan, A.G.; Soliman, A.M. Fractional-order mutual inductance: Analysis and design. Int. J. Circuit Theory Appl. 2016, 44, 85–97. [Google Scholar] [CrossRef]
- Ahmad, W. Power factor correction using fractional capacitors. In Proceedings of the 2003 International Symposium on Circuits and Systems, Thailand, Bangkok, 25–28 May 2003. [Google Scholar]
- Martínez, R.; Bolea, Y.; Grau, A.; Martínez, H. Fractional DC/DC converter in solar-powered electrical generation systems. In Proceedings of the IEEE Conference on Emerging Technologies & Factory Automation, Mallorca, Spain, 22–25 September 2009. [Google Scholar]
- Kianpoor, N.; Yousefi, M.; Bayati, N.; Hajizadeh, A.; Soltani, M. Fractional order modelling of DC-DC boost converters. In Proceedings of the IEEE 28th International Symposium on Industrial Electronics (SIE), Vancouver, BC, Canada, 12–14 June 2019. [Google Scholar]
- Wang, F.Q.; Ma, X.K. Fractional order modeling and simulation analysis of Boost converter in continuous conduction mode operation. Acta Phys. Sin. 2011, 60, 070506. [Google Scholar]
- Tan, C.; Liang, Z.S. Modeling and simulation analysis of fractional-order Boost converter in pseudo-continuous conduction mode. Acta Phys. Sin. 2014, 63, 070502. [Google Scholar]
- Chen, X.; Chen, Y.F.; Zhang, B.; Qiu, D.Y. A modeling and analysis method for fractional-order DC–DC converters. IEEE Trans. Power Electron. 2017, 32, 7034–7044. [Google Scholar] [CrossRef]
- Wang, F.Q.; Ma, X.K. Modeling and analysis of the fractional order Buck converter in DCM operation by using fractional calculus and the circuit-averaging technique. J. Power Electron. 2013, 13, 1008–1015. [Google Scholar] [CrossRef] [Green Version]
- Wei, Z.H.; Zhang, B.; Jiang, Y.W. Analysis and modeling of fractional-order Buck converter based on Riemann-Liouville Derivative. IEEE Access 2019, 7, 162768–162777. [Google Scholar] [CrossRef]
- Wu, C.G.; Si, G.Q.; Zhang, Y.B.; Yang, N.N. The fractional-order state-space averaging modeling of the Buck–Boost DC/DC converter in discontinuous conduction mode and the performance analysis. Nonlinear Dyn. 2015, 79, 689–703. [Google Scholar] [CrossRef]
- Yang, N.N.; Liu, C.X.; Wu, C.J. Modeling and dynamics analysis of the fractional-order Buck-Boost converter in continuous conduction mode. Chin. Phys. B 2012, 21, 080503. [Google Scholar] [CrossRef] [Green Version]
- Fang, S.C.; Wang, X.G. Modeling and analysis method of fractional-order buck–boost converter. Int. J. Circuit Theory Appl. 2020. [Google Scholar] [CrossRef]
- Xie, L.L.; Liu, Z.P.; Zhang, B. A Modeling and Analysis Method for CCM Fractional Order Buck—Boost Converter by Using R–L Fractional Definition. J. Electr. Eng. Technol. 2020, 15, 1651–1661. [Google Scholar] [CrossRef]
- Radwan, A.G.; Emira, A.A.; AbdelAty, A.M.; Azar, A.T. Modeling and analysis of fractional order DC-DC converter. ISA Trans. 2018, 82, 184–199. [Google Scholar] [CrossRef] [PubMed]
- Zhu, P.F.; Wei, Y.F.; Zheng, Z.; Wang, X.W.; Ma, F.J. Fractional modelling and simulation for single-phase PWM rectifier. J. Eng. 2019, 16, 1675–1678. [Google Scholar] [CrossRef]
- Sharma, M.; Rajpurohit, B.S.; Agnihotri, S.; Rathore, A.K. Development of Fractional Order Modeling of Voltage Source Converters. IEEE Access 2020, 8, 131750–131759. [Google Scholar] [CrossRef]
- Xu, J.H.; Li, X.C.; Liu, H.; Meng, X.R. Fractional-Order Modeling and Analysis of a Three-Phase Voltage Source PWM Rectifier. IEEE Access 2020, 8, 13507–13515. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999; pp. 78–81. [Google Scholar]
- Sarafraz, M.S.; Tavazoei, M.S. Passive realization of fractional-order impedances by a fractional element and RLC components: Conditions and procedure. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 585–595. [Google Scholar] [CrossRef]
- Duan, J.S.; An, J.Y.; Xu, M.Y. Solution of system of fractional differential equations by Adomian decomposition method. Appl. Math. 2007, 22, 7–12. [Google Scholar] [CrossRef]
- Xue, D.Y. Fractional Calculus and Fractional-Order Control; Science Press: Beijing, China, 2018; pp. 115–123. [Google Scholar]





| i | α = 0.95 | β = 0.95 | β = 0.9 | |||
|---|---|---|---|---|---|---|
| Ri (Ω) | Li (mH) | Ri (Ω) | Ci (mF) | Ri (Ω) | Ci (mF) | |
| 1 | 5.123 k | 4.8 | 1.952 m | 0.484 | 7.337 m | 0.121 |
| 2 | 523.188 | 4.9 | 19.113 m | 0.494 | 63.945 m | 0.139 |
| 3 | 58.181 | 5.5 | 0.712 | 0.549 | 0.512 | 0.174 |
| 4 | 6.522 | 6.2 | 1.533 | 0.616 | 4.074 | 0.219 |
| 5 | 0.732 | 6.9 | 13.667 | 0.691 | 32.365 | 0.275 |
| 6 | 0.082 | 7.7 | 121.907 | 0.774 | 257.266 | 0.346 |
| 7 | 0.0091 | 8.6 | 1.095 k | 0.862 | 2.058 k | 0.433 |
| 8 | 0.943 m | 8.9 | 10.609 k | 0.890 | 17.579 k | 0.507 |
| 9 | 12.78 u | 1.2 | 0.782 M | 0.121 | 0.611 M | 0.146 |
| (α,β) | (1,1) | (1,0.95) | (1,0.9) | (0.95,1) | (0.95,0.95) | (0.95,0.9) |
| overshoot(V) | 16.220 | 15.151 | 14.180 | 16.044 | 15.001 | 14.090 |
| setting time(s) | 0.01023 | 0.00641 | 0.00419 | 0.00743 | 0.00476 | 0.00329 |
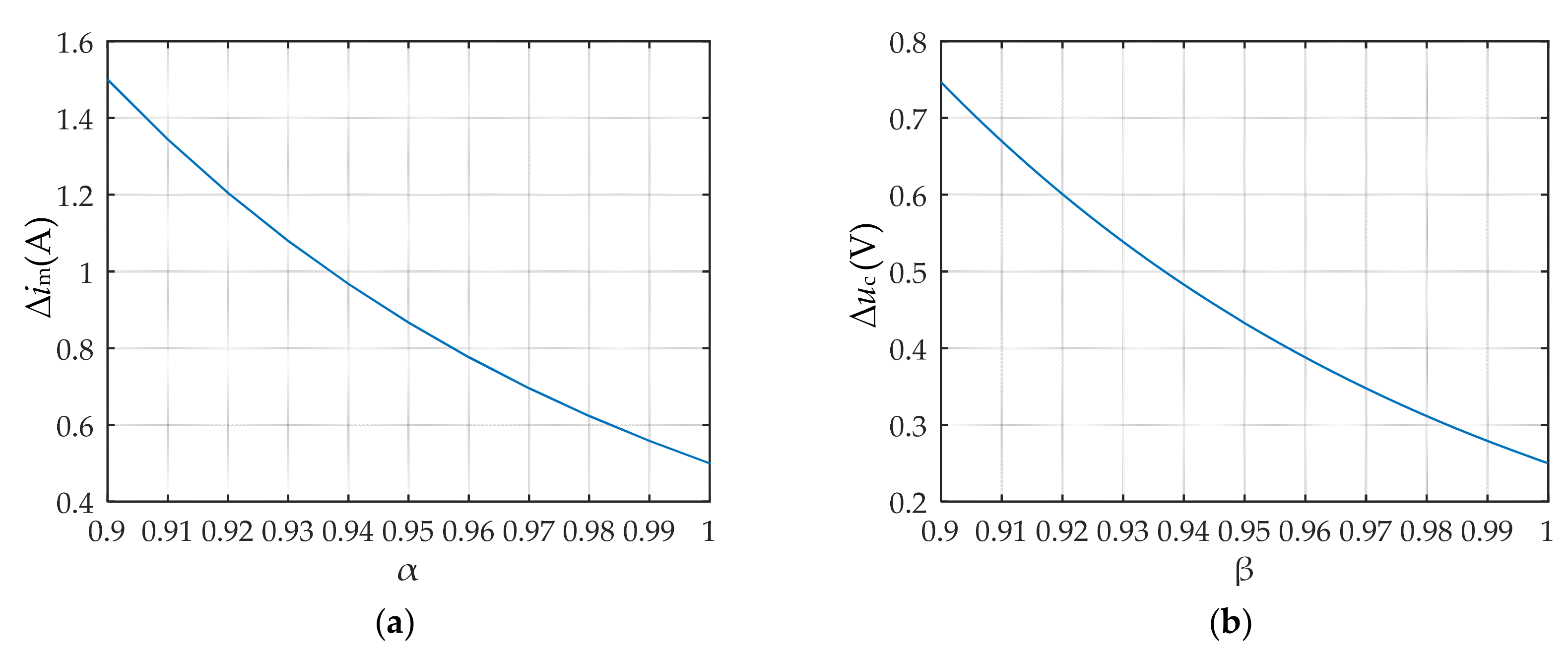
| (α,β) | Uc (V) | Im (A) | ∆im (A) | ∆uc (V) |
|---|---|---|---|---|
| (1,1) | 9.989/10 | 0.998/1 | 0.500/0.5 | 0.249/0.25 |
| (1,0.95) | 9.970/10 | 0.996/1 | 0.500/0.5 | 0.447/0.433 |
| (1,0.9) | 9.928/10 | 0.992/1 | 0.500/0.5 | 0.796/0.747 |
| (0.95,1) | 9.980/10 | 1.015/1 | 0.911/0.867 | 0.249/0.25 |
| (0.95,0.95) | 9.955/10 | 1.013/1 | 0.914/0.867 | 0.442/0.433 |
| (0.95,0.9) | 9.901/10 | 1.006/1 | 0.914/0.867 | 0.776/0.747 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Xie, F.; Chen, Y.; Xiao, W.; Zhang, B. Modeling and Analysis of the Fractional-Order Flyback Converter in Continuous Conduction Mode by Caputo Fractional Calculus. Electronics 2020, 9, 1544. https://doi.org/10.3390/electronics9091544
Yang C, Xie F, Chen Y, Xiao W, Zhang B. Modeling and Analysis of the Fractional-Order Flyback Converter in Continuous Conduction Mode by Caputo Fractional Calculus. Electronics. 2020; 9(9):1544. https://doi.org/10.3390/electronics9091544
Chicago/Turabian StyleYang, Chen, Fan Xie, Yanfeng Chen, Wenxun Xiao, and Bo Zhang. 2020. "Modeling and Analysis of the Fractional-Order Flyback Converter in Continuous Conduction Mode by Caputo Fractional Calculus" Electronics 9, no. 9: 1544. https://doi.org/10.3390/electronics9091544
APA StyleYang, C., Xie, F., Chen, Y., Xiao, W., & Zhang, B. (2020). Modeling and Analysis of the Fractional-Order Flyback Converter in Continuous Conduction Mode by Caputo Fractional Calculus. Electronics, 9(9), 1544. https://doi.org/10.3390/electronics9091544






