Modified Analytical Technique for Multi-Objective Optimal Placement of High-Level Renewable Energy Penetration Connected to Egyptian Power System
Abstract
:1. Introduction
1.1. Motivation
1.2. Related Work
1.3. Contributions
- Develop a modified analytical technique based on energy calculation to select the optimal location of high-level penetration RES in the IEEE 33-bus and 69-bus distribution systems and the realistic 25-bus 500 kV EPS, taking into account maximum load capacity. The GA method based on power calculation has been developed to select the optimal location of high-level penetration RES in the realistic 25-bus 500 kV EPS.
- Development of a multi-objective energy-based algorithm to select the optimal location of PV systems, as well as wind farms, to reduce annual total energy losses and improve the voltage profile.
- A fair comparison of the proposed algorithm based on power and energy calculations with previous works, which used the PSO and GA algorithms, was performed to demonstrate the efficiency and feasibility of the proposed algorithm for the IEEE 33-bus and IEEE 69-bus distribution systems. For the realistic 25-bus 500 kV EPS, the optimal locations of RES obtained by the proposed algorithm based on power and energy calculations are compared with those obtained by the GA algorithm.
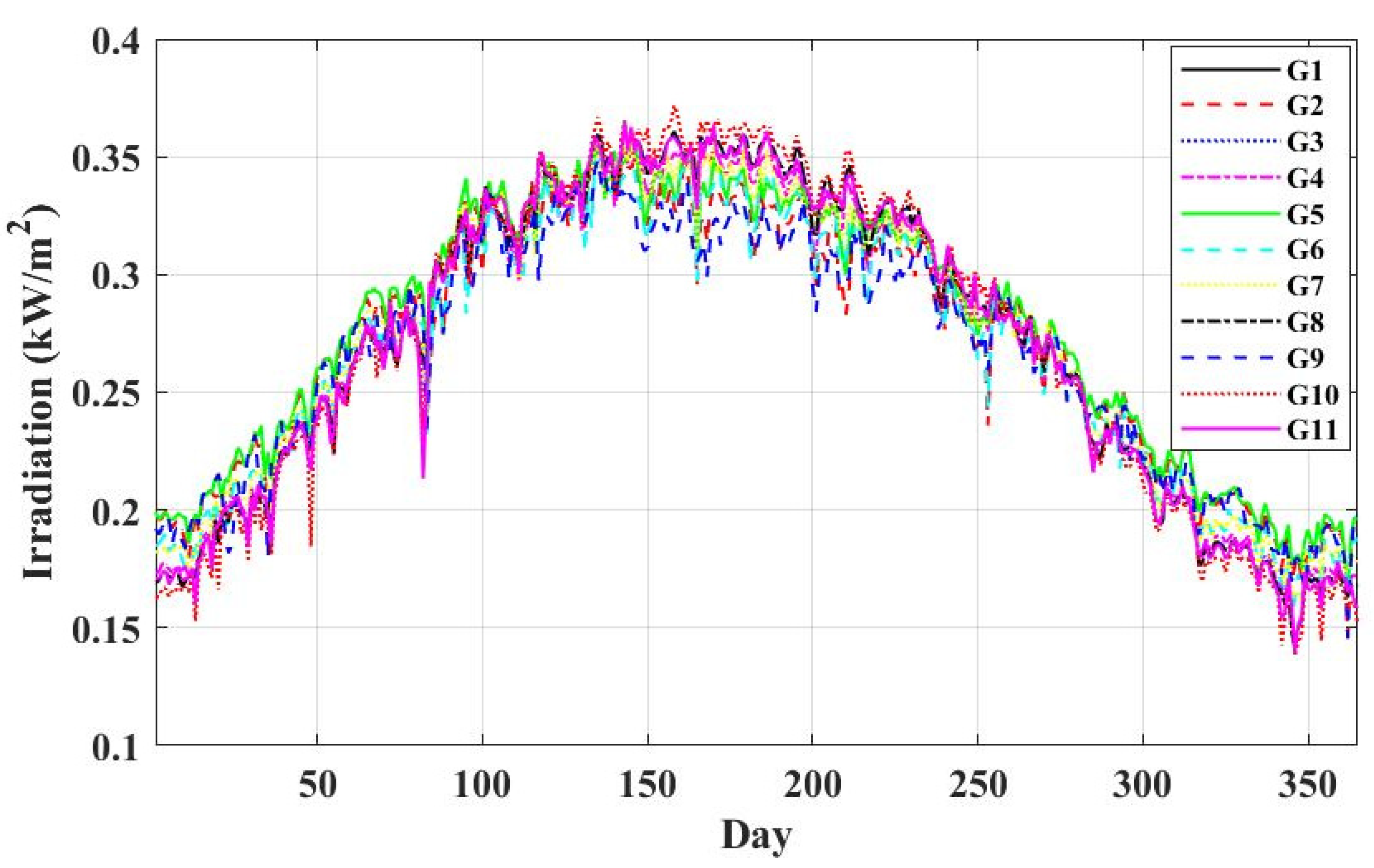
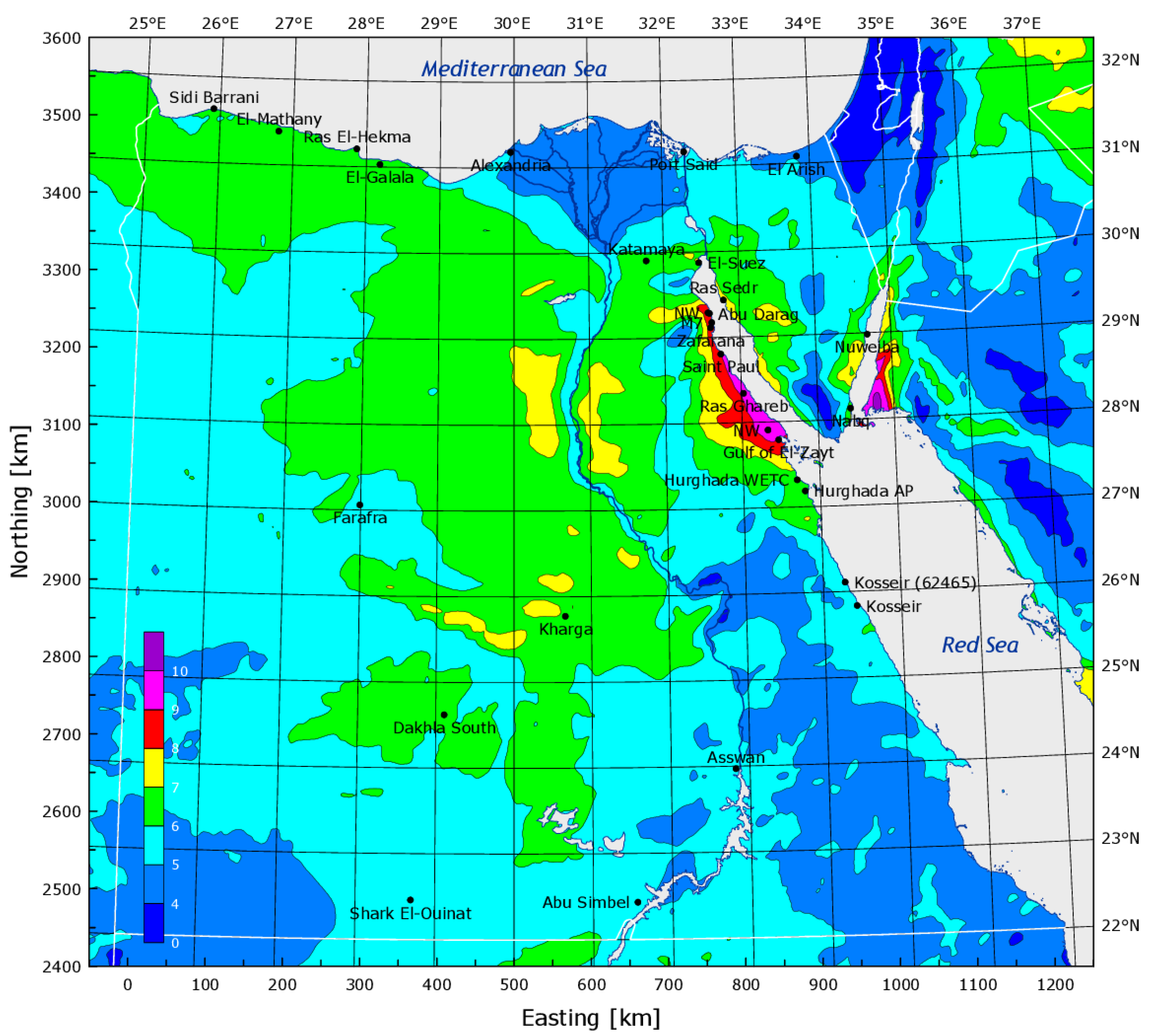
- Examine the effect of the RES connection on the performance of the 500 kV Egyptian Power system, taking into account weather data for solar radiation and wind speed. This data was obtained from the NASA website for the period 1 January 2021 to 31 December 2021.
- This paper has been organized as follows: Section 2 describes the proposed method and the research method for calculating the optimal location of RES based on the power flow of the power system consisting of the PV system or the wind system; Section 3 contains the description of the test systems and the PV and wind projects in Egypt, the results of optimization applied to the tested power systems, and the discussion of the results; while Section 4 concludes the highlights of this research.
2. Research Method
2.1. Power Flow of Grid-Connected RES
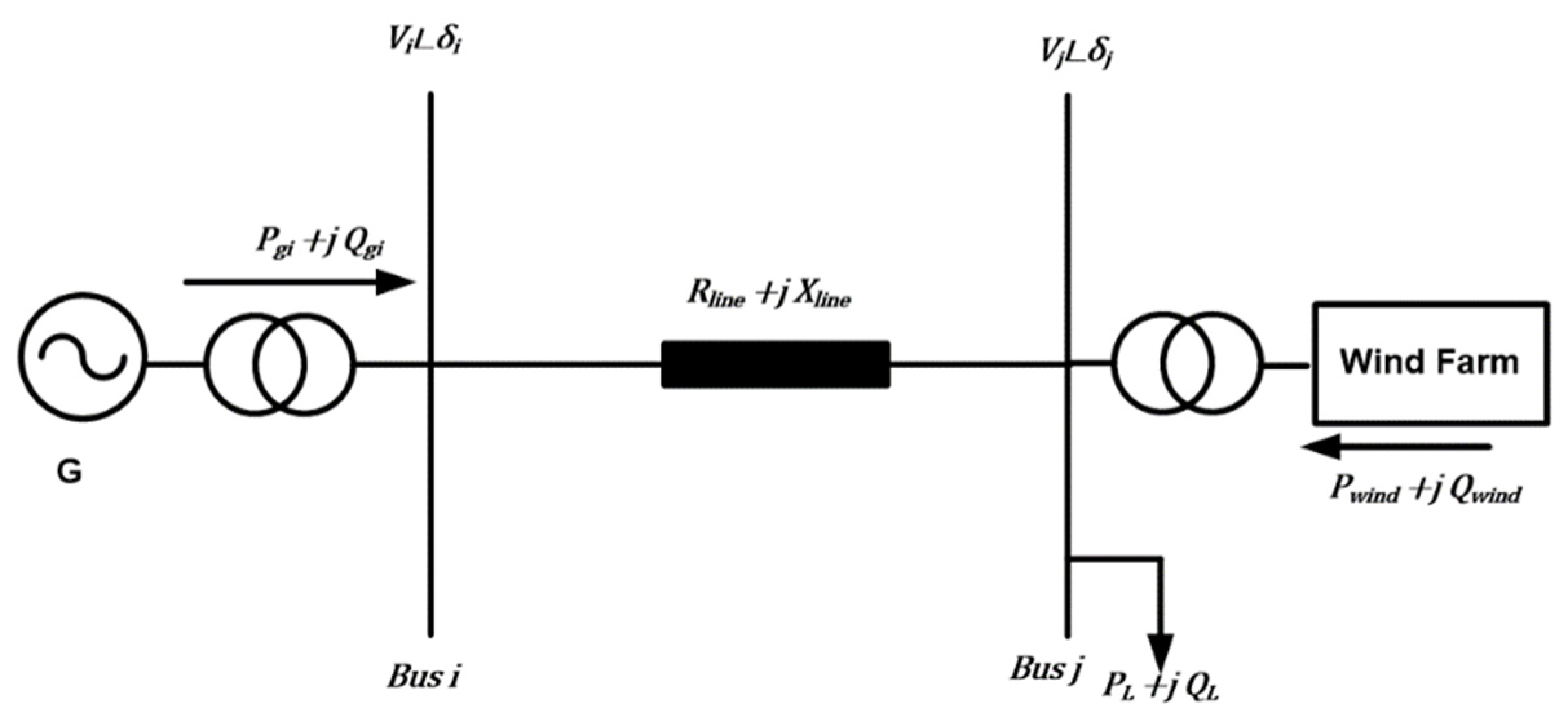
2.1.1. PV System Model in Power Flow
2.1.2. Wind Farm Model in Power Flow
2.2. Objective Function
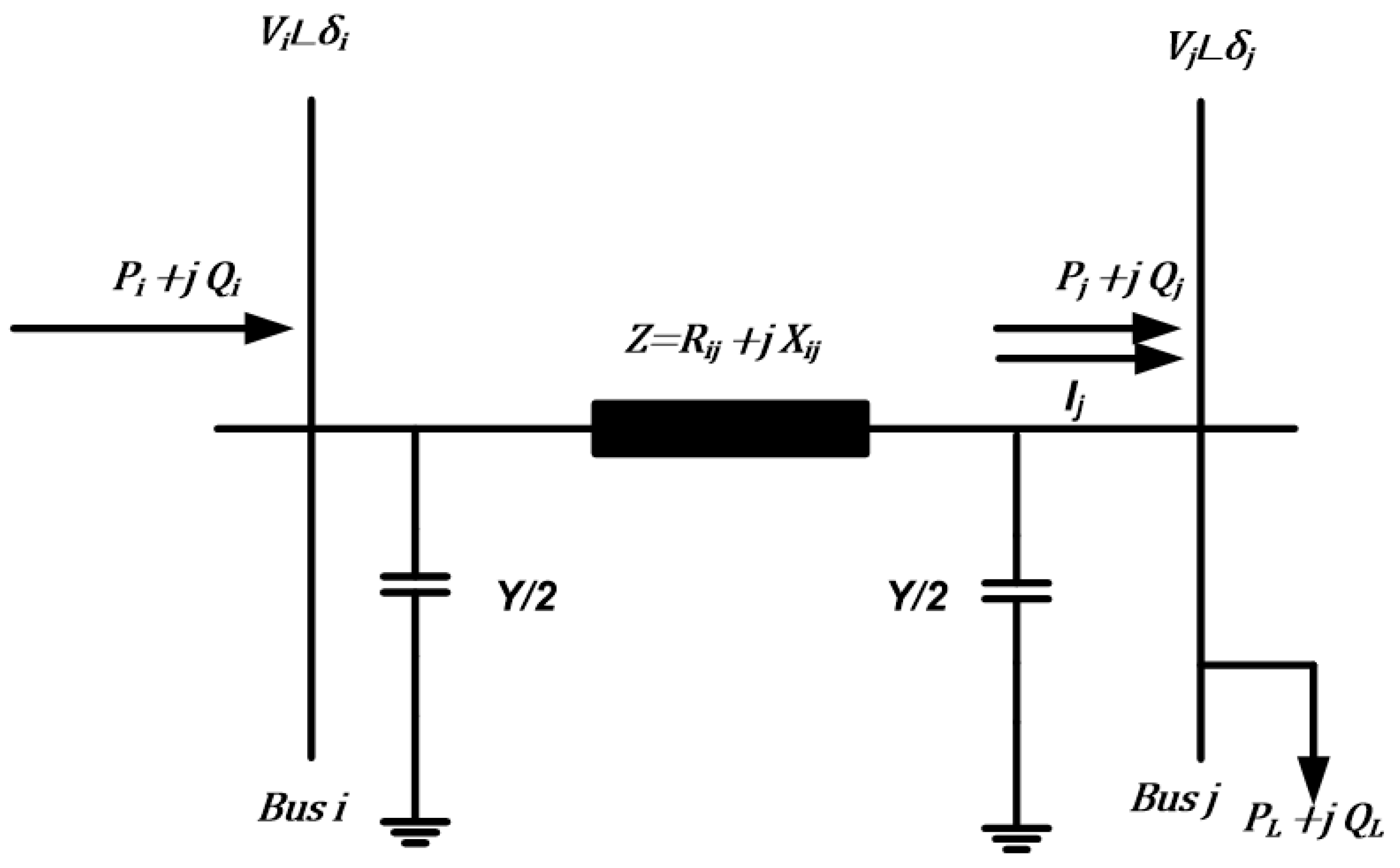
2.2.1. Active Energy Loss
2.2.2. Voltage Deviation
2.2.3. The Maximum Load Ability of the System
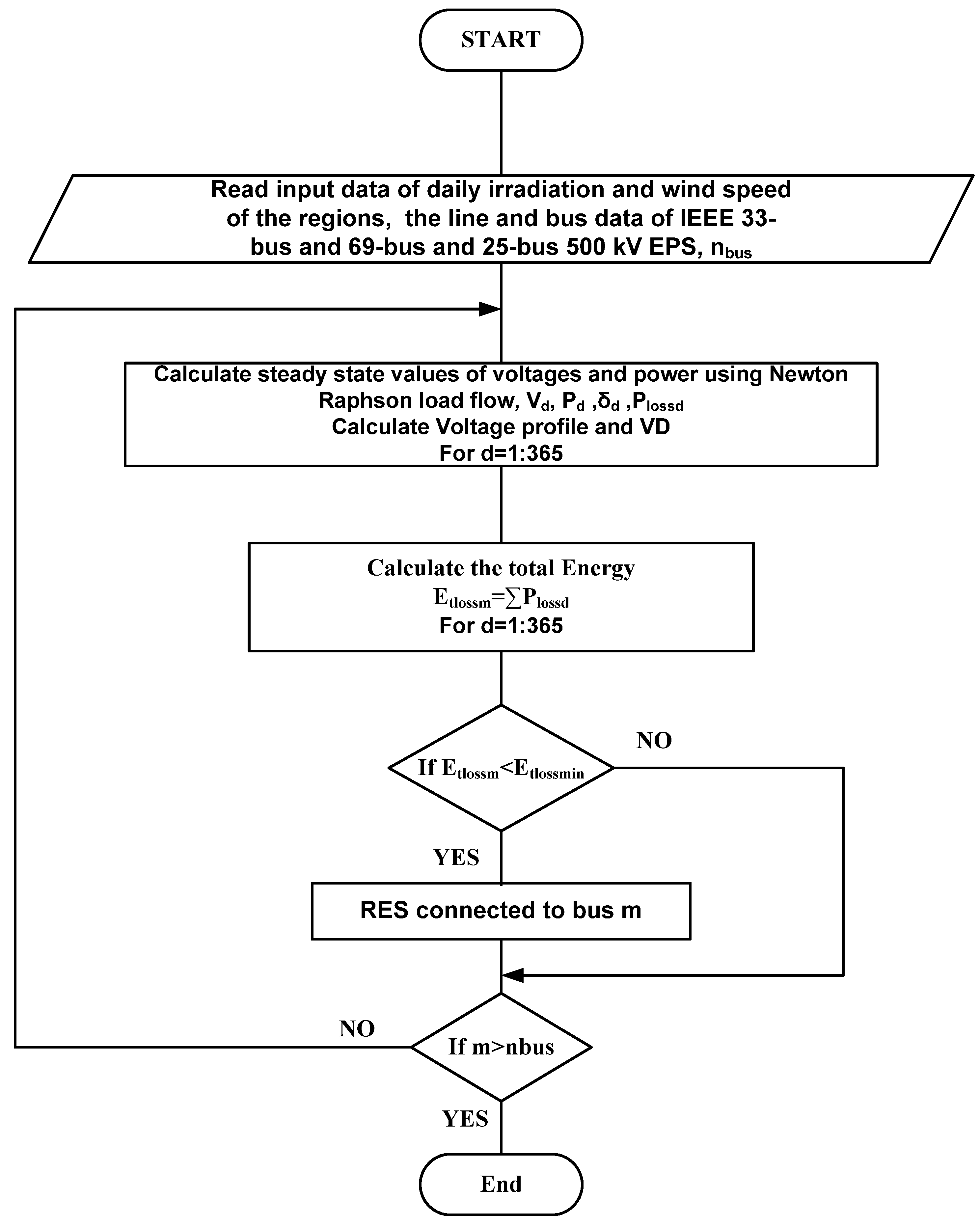
2.3. The Proposed Algorithm
2.3.1. Selection of the Best Locations of Full Captured Power RESs
- Select the number of RES: one (PV system or wind farm).
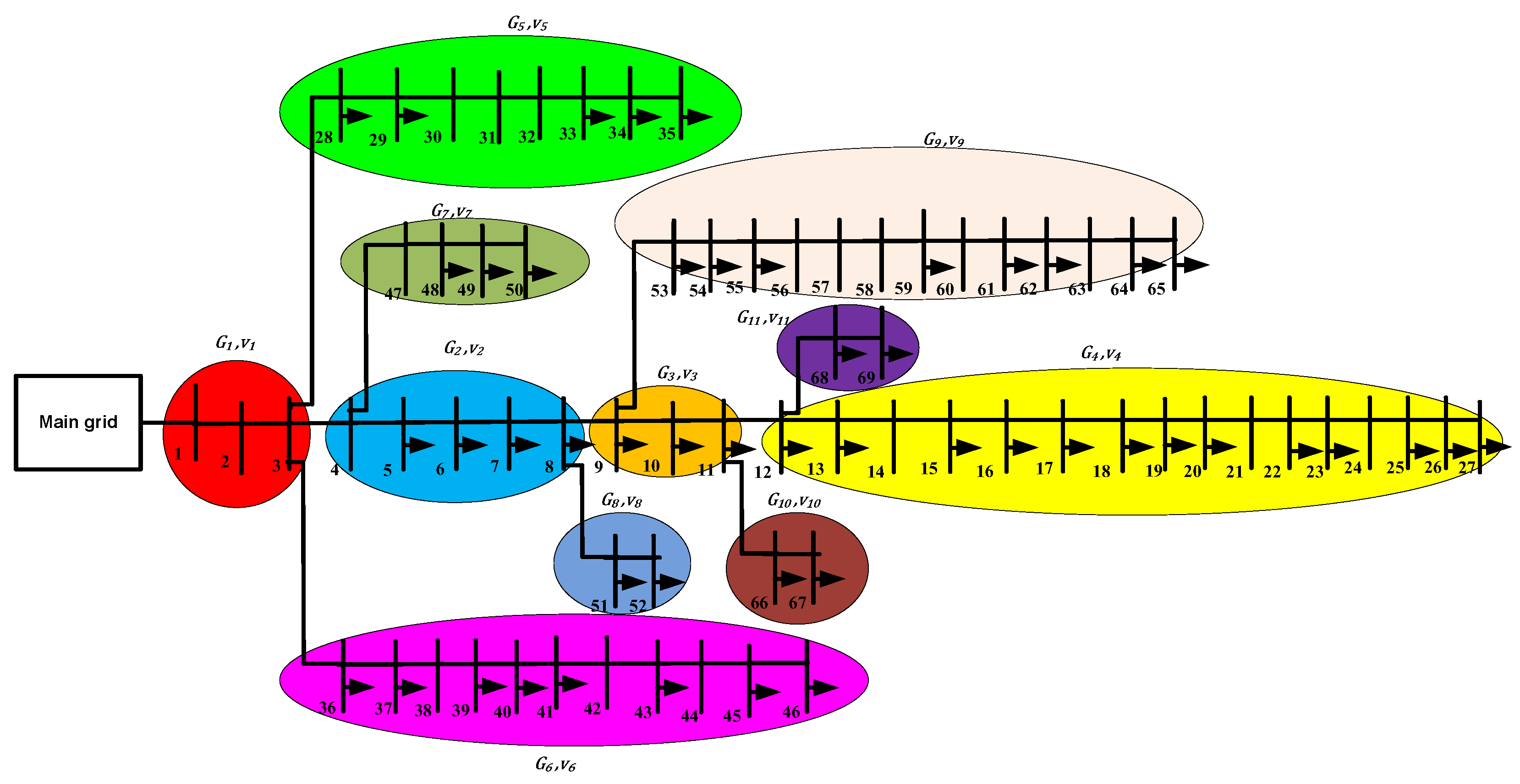
- Choose RES connected to bus No. 1 of IEEE 33-bus and 69-bus distribution systems, and realistic 25-bus 500 kV EPS.
- Start calculating the active and reactive power of RES depending on the weather condition, solar irradiation for the PV system, and wind speed for the wind farm.where and are irradiation intensity and wind speed at bus 1. Their values were obtained from the NASA website for the period 1 January 2021 to 31 December 2021.
- Calculate the power flow of the 25-bus 500 kV EPS with RES
- Calculate , voltage profile.
- Repeat steps 4 and 5 for in a year
- Calculate and minimum voltage deviation.
- Repeat steps 3–7 with the RES bus connected to bus No. 2 to nbus.
- Choose a bus with which RES can be connected, achieving the minimum annual total energy and voltage deviation. Figure 4 shows the flowchart for selecting the bus of RES.
- When selecting the bus of one RES, it can be used for the number of RESs: two, three, or four. The steps from 2 to 8 are repeated to select the second bus for the second RES, increasing the number of buses in the IEEE 33-bus and 69-bus distribution systems and the realistic 25-bus 500 kV EPS by one (nbus + 1).
- When selecting the bus for the second RES, it can be used for three or four RES. Steps 2 through 8 are repeated to select the third bus for the third RES, increasing the number of buses in the IEEE 33-bus and 69-bus distribution systems and the realistic 25-bus 500 kV EPS by two (nbus + 2).
- When selecting the bus of the third RES, it can also be used for the bus of the fourth RES. Steps 2 through 8 are repeated to select the fourth bus for the fourth RES, increasing the number of buses in the IEEE 33-bus and 69-bus distribution systems and the realistic 25-bus 500 kV EPS by three (nbus + 3).
2.3.2. The Maximum Load Capacity of 500 kV EPS with RESs
- Increase the load by 1% as Equation (27)
- Calculate the power flow of EPS with RESs
- Calculate , and voltage profile.
- Repeat steps 4 and 5 for in a year
- Detect the convergence of the power flow of the system
2.3.3. Performance of 500 kV EPS without and with RES Projects
- Run power flow for 500 kV EPS without RESs, 500 kV EPS with RESs (in operation), and 500 kV EPS with RESs (in operation and under construction).
- Calculate RES power per day using the weather data (obtained from the NASA website).
- Calculate the power flow of EPS with RES
- Calculate , voltage profile, and voltage deviation
- Repeat steps 4 and 5 for in a year
2.4. Particle Swarm Optimization [44]
2.5. Genetic Algorithm [45]
3. Results and Analysis
3.1. Systems under Study
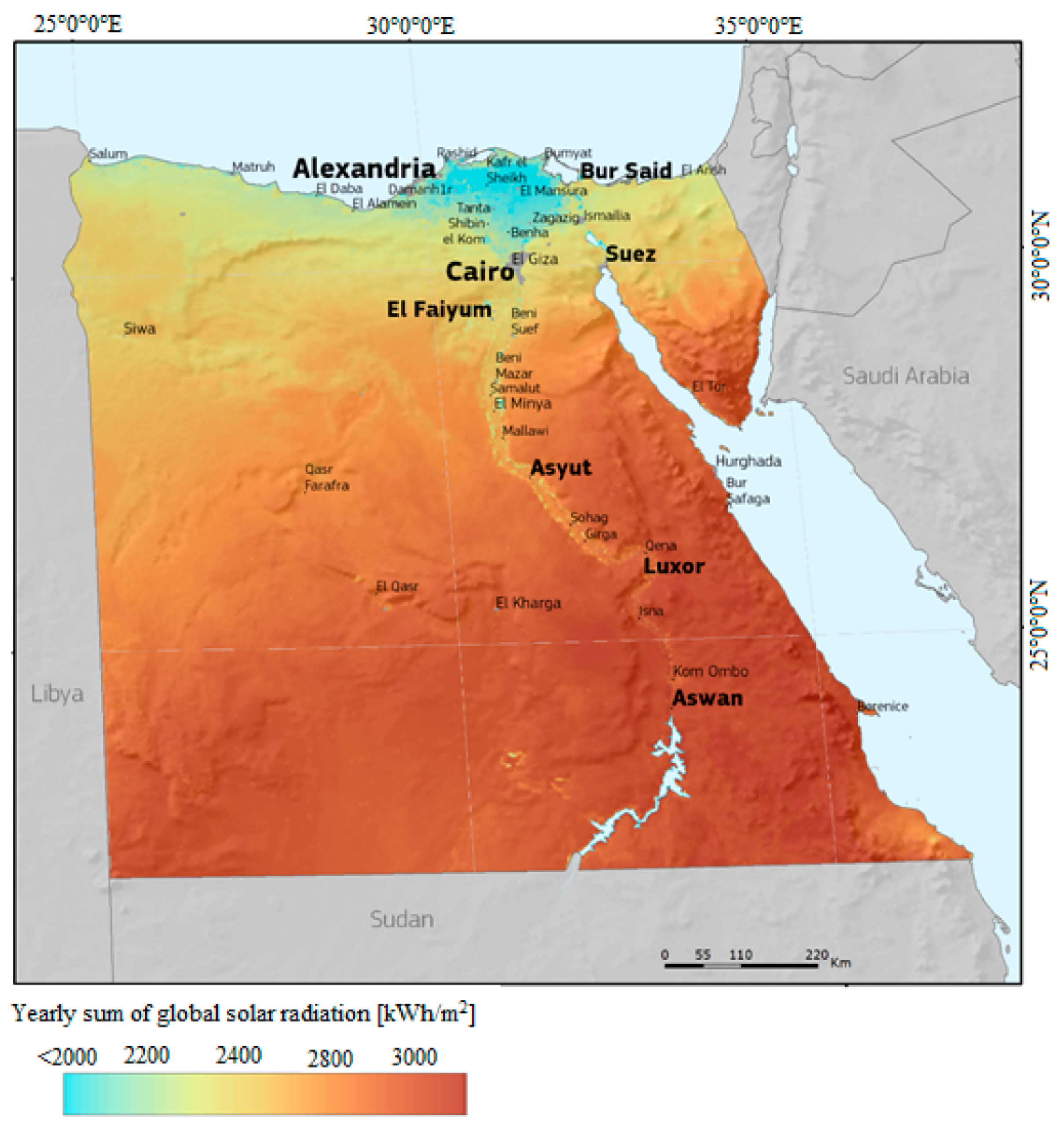
3.1.1. New Renewable Energy Projects in Egypt
3.1.2. PV Projects
3.1.3. Wind Energy Projects
- A wind power plant project with a capacity of 250 MW in the private sector (Lakela Company) is under construction, and many BOO (“Build, own, and operate”) projects have a capacity of 750 MW.
- Ras Ghareb Wind Farm (262 MW); A wind project is being developed near the Gulf of Suez, approximately 30 km northwest of Ras Ghareb, Egypt.
- A wind power plant in West Nile (200 MW).
3.2. Results and Discussion
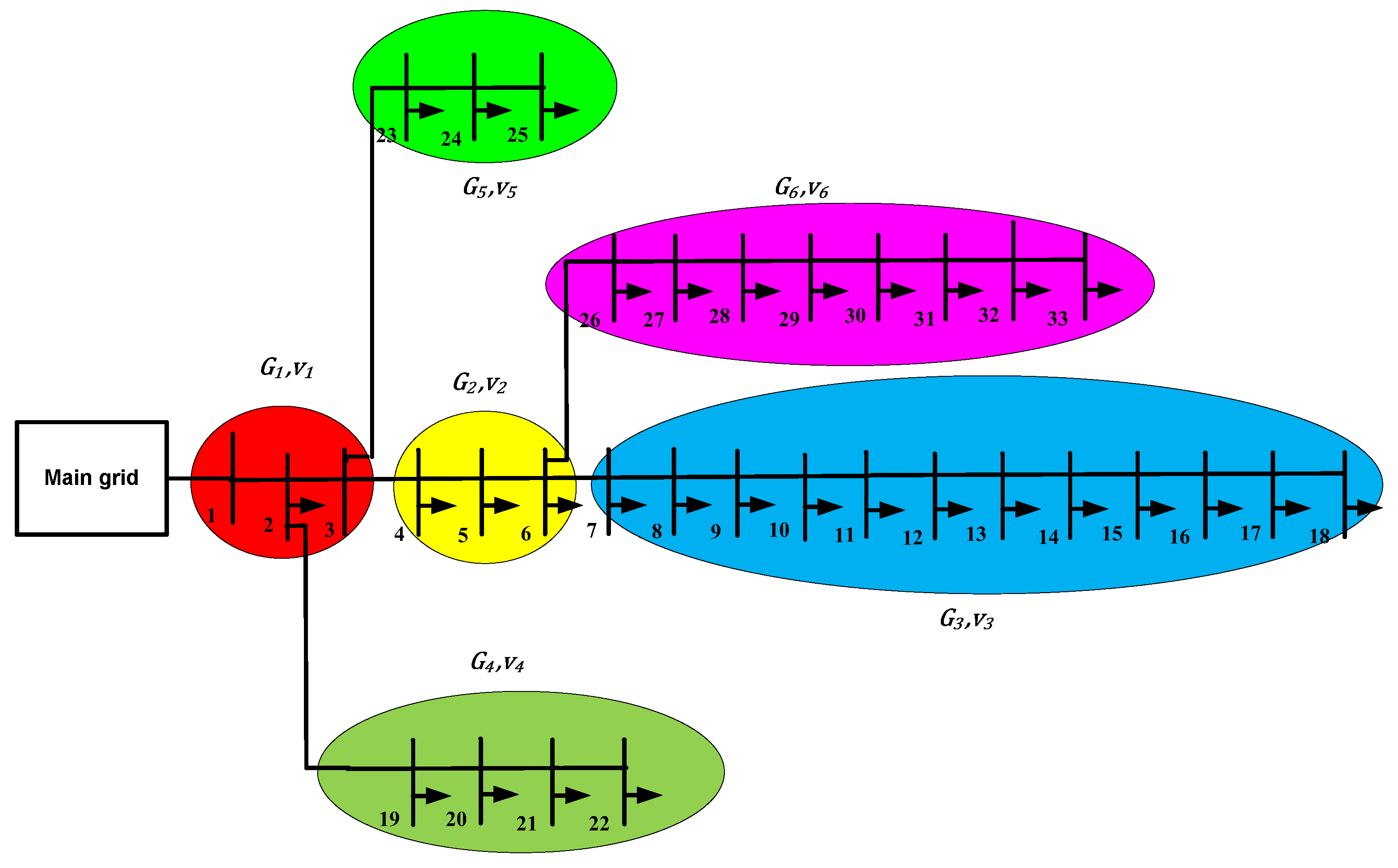
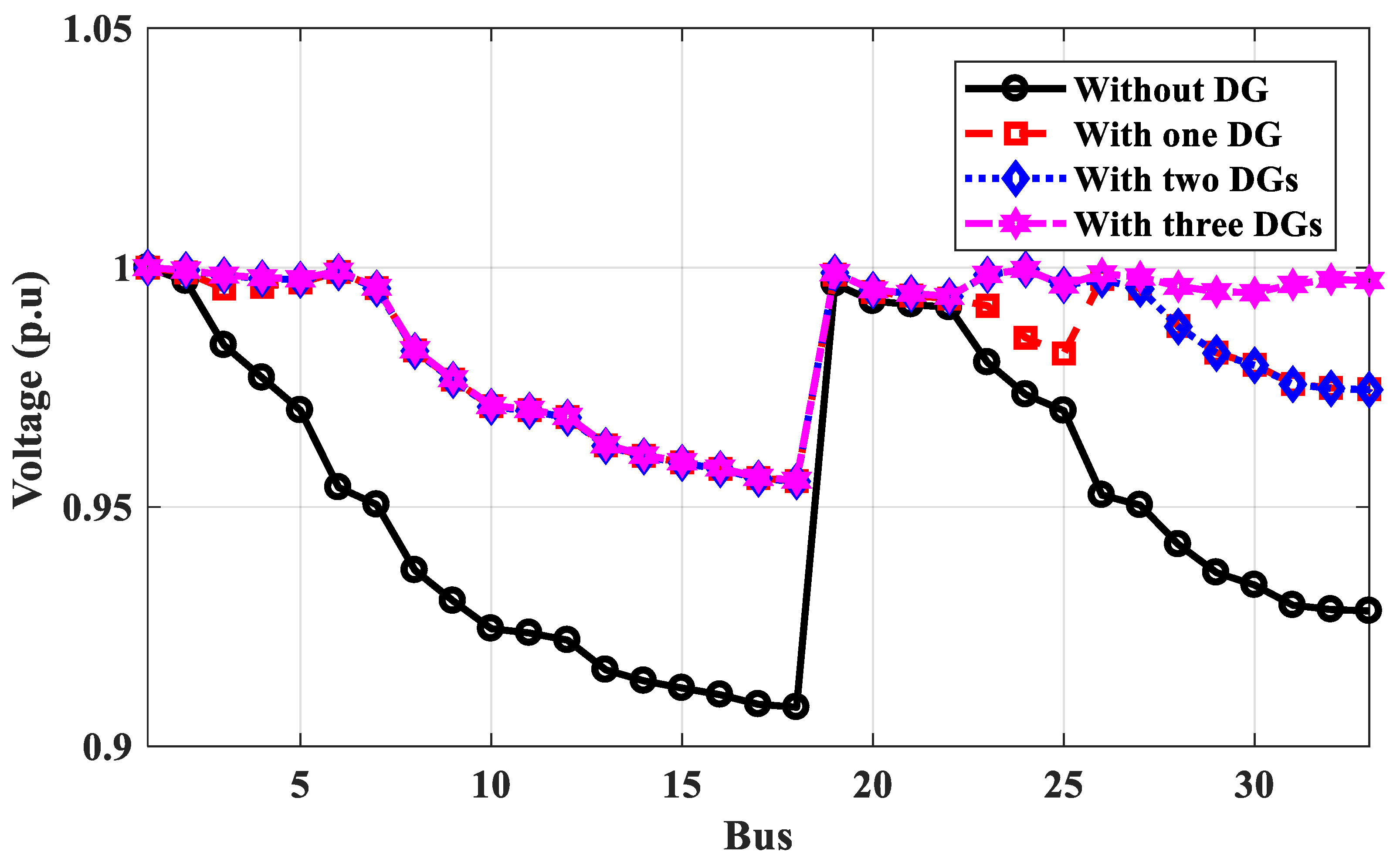
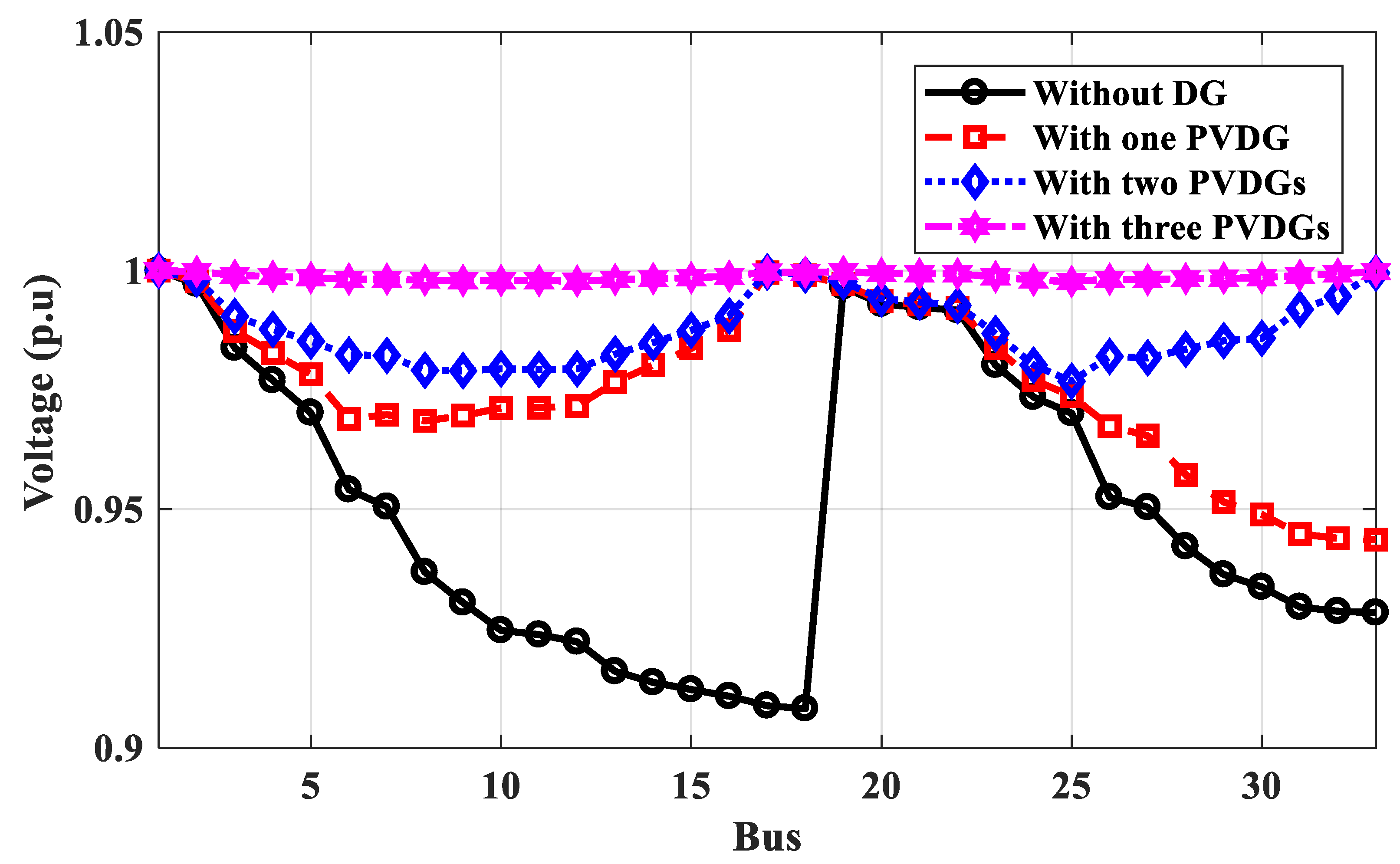
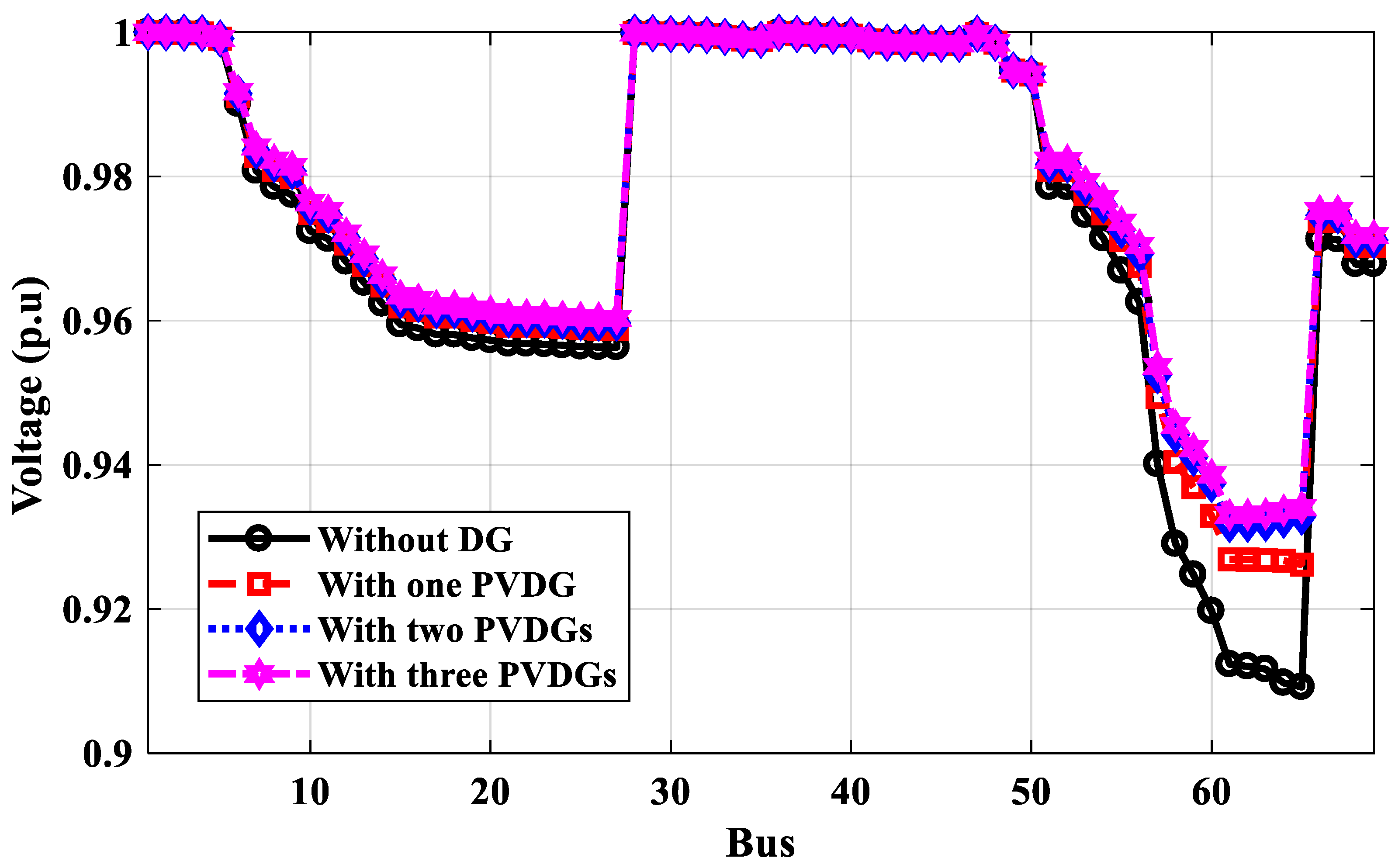
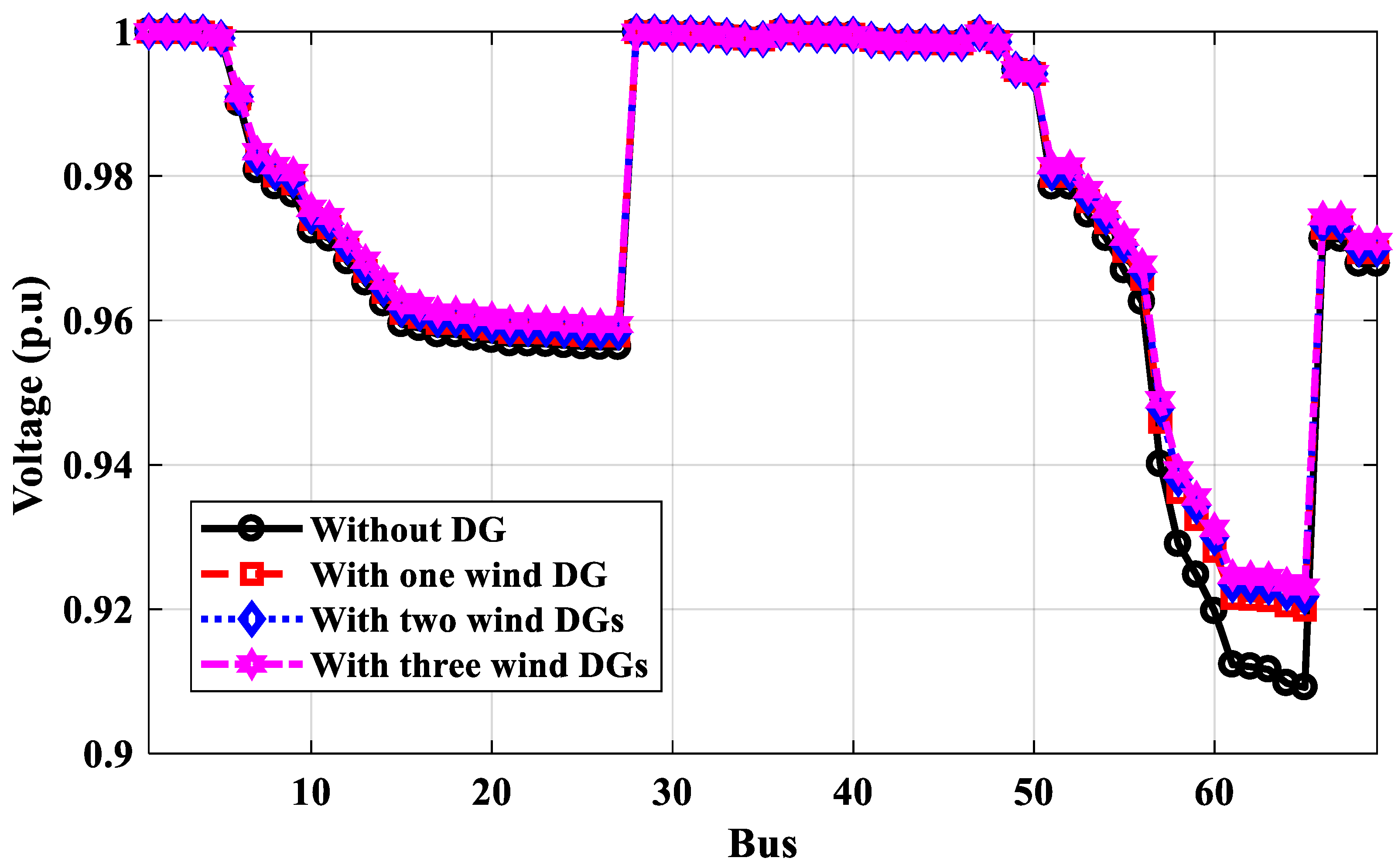
3.2.1. Case 1: IEEE 33-Bus Performance
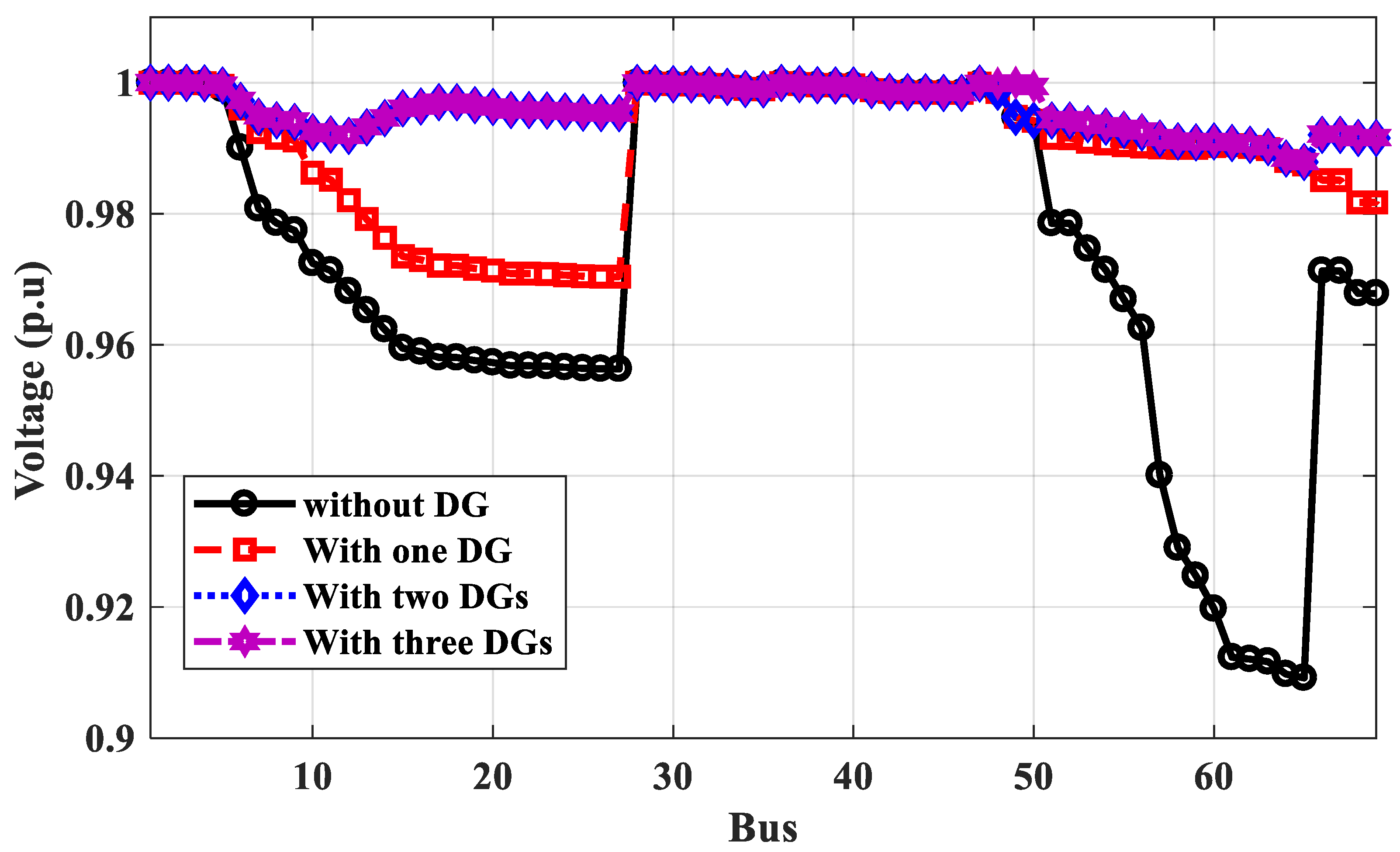
3.2.2. Case 2: IEEE 69-Bus Performance
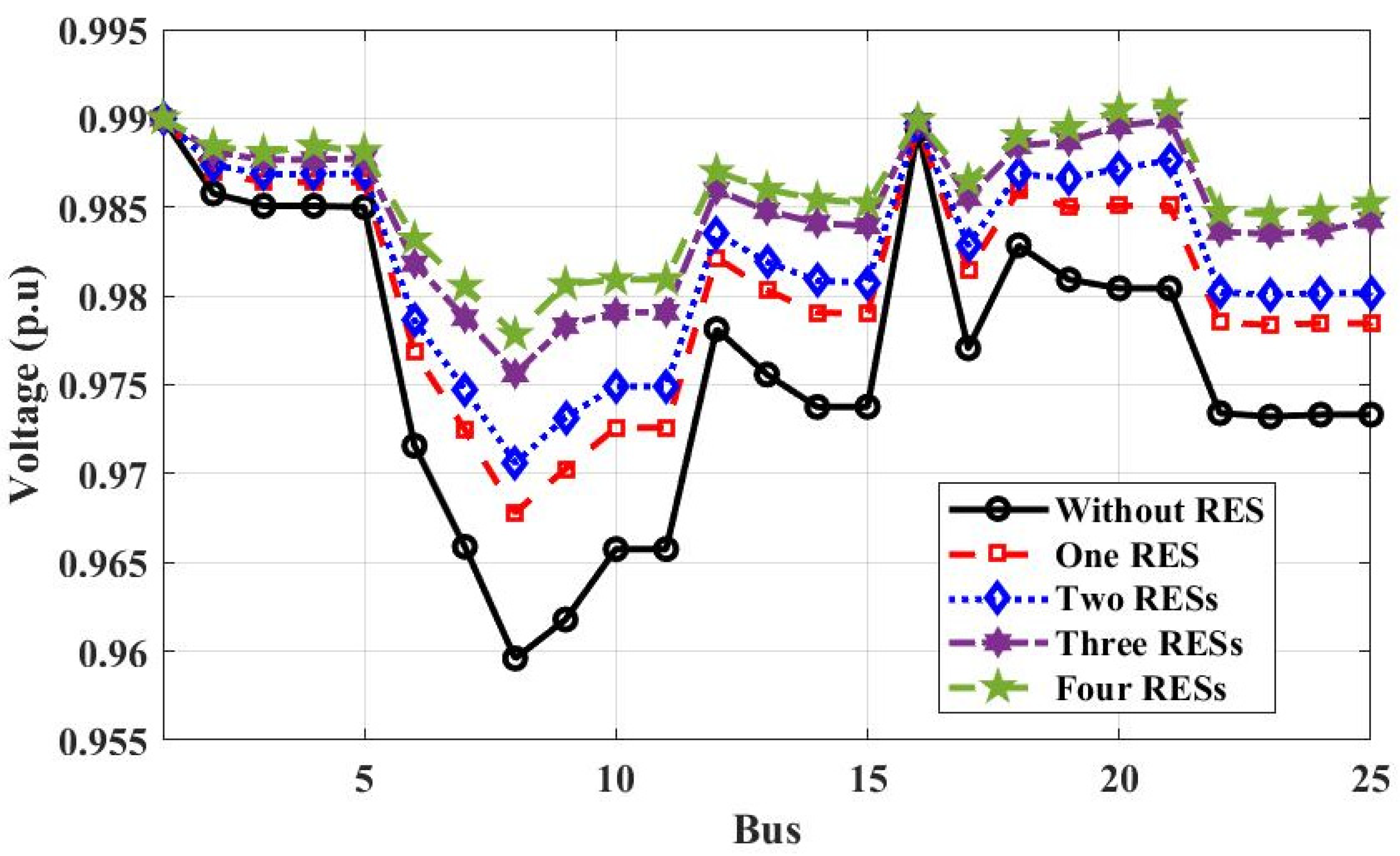
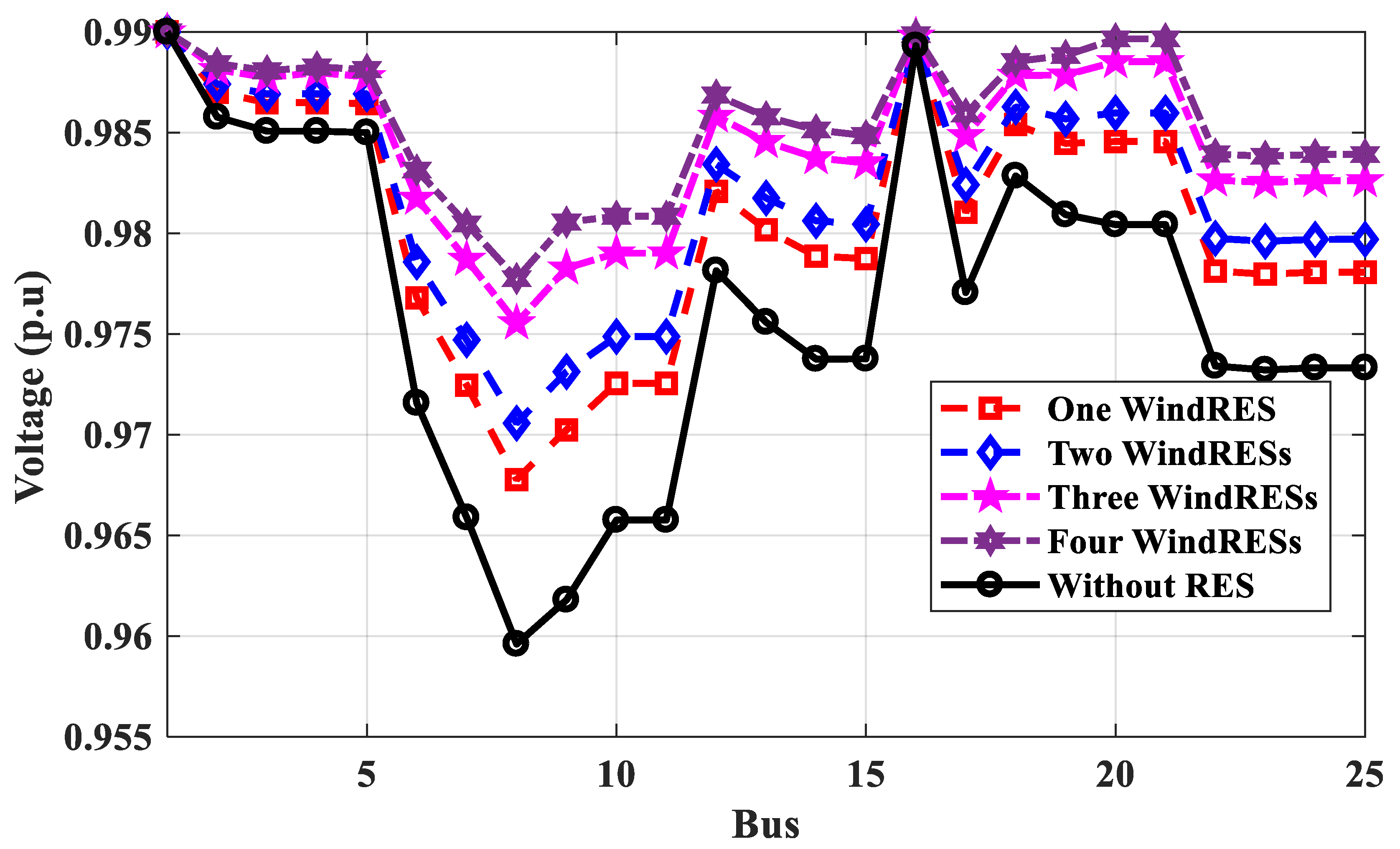
3.2.3. Case 3: The Performance of the Egyptian Power System with Maximum Penetration RES
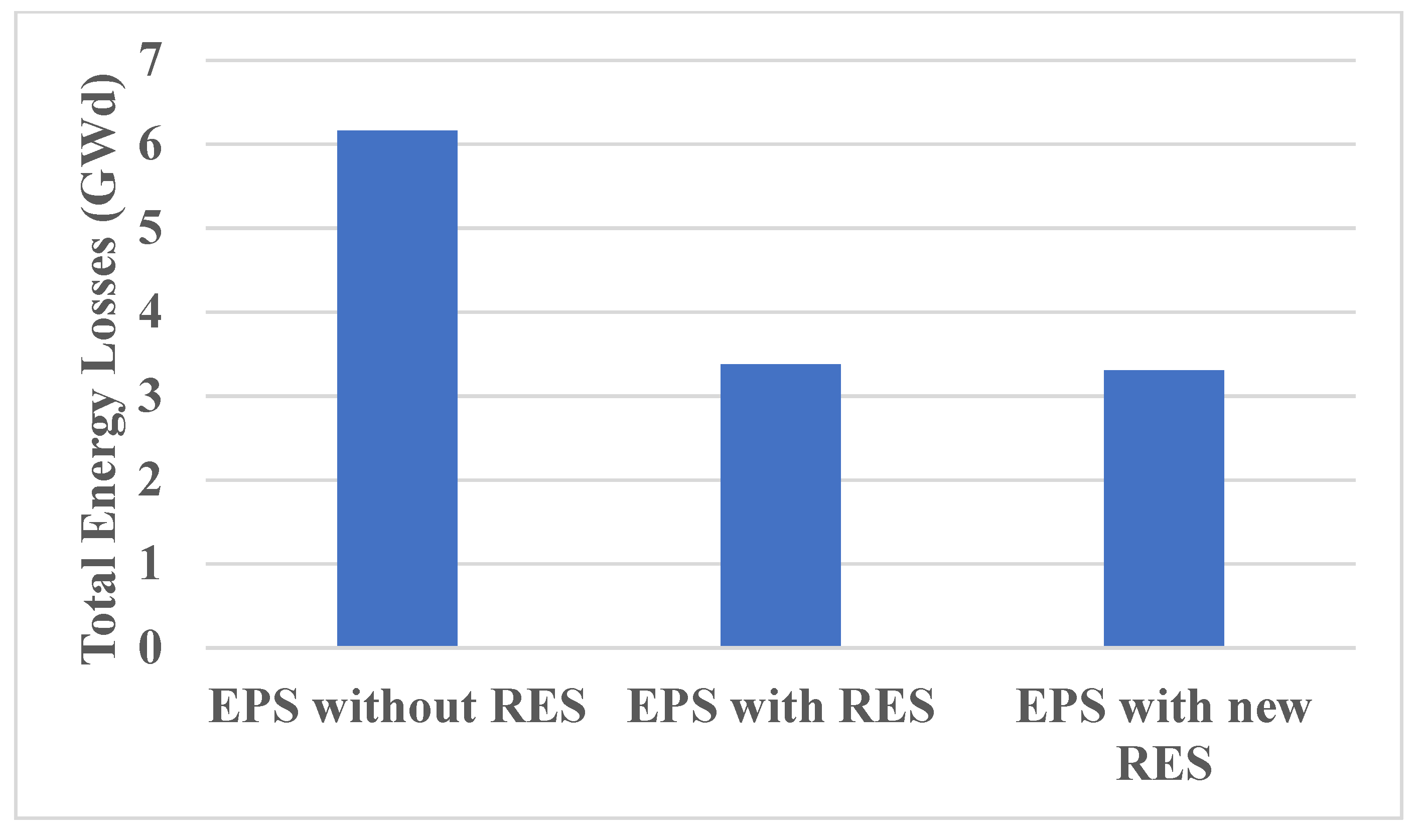
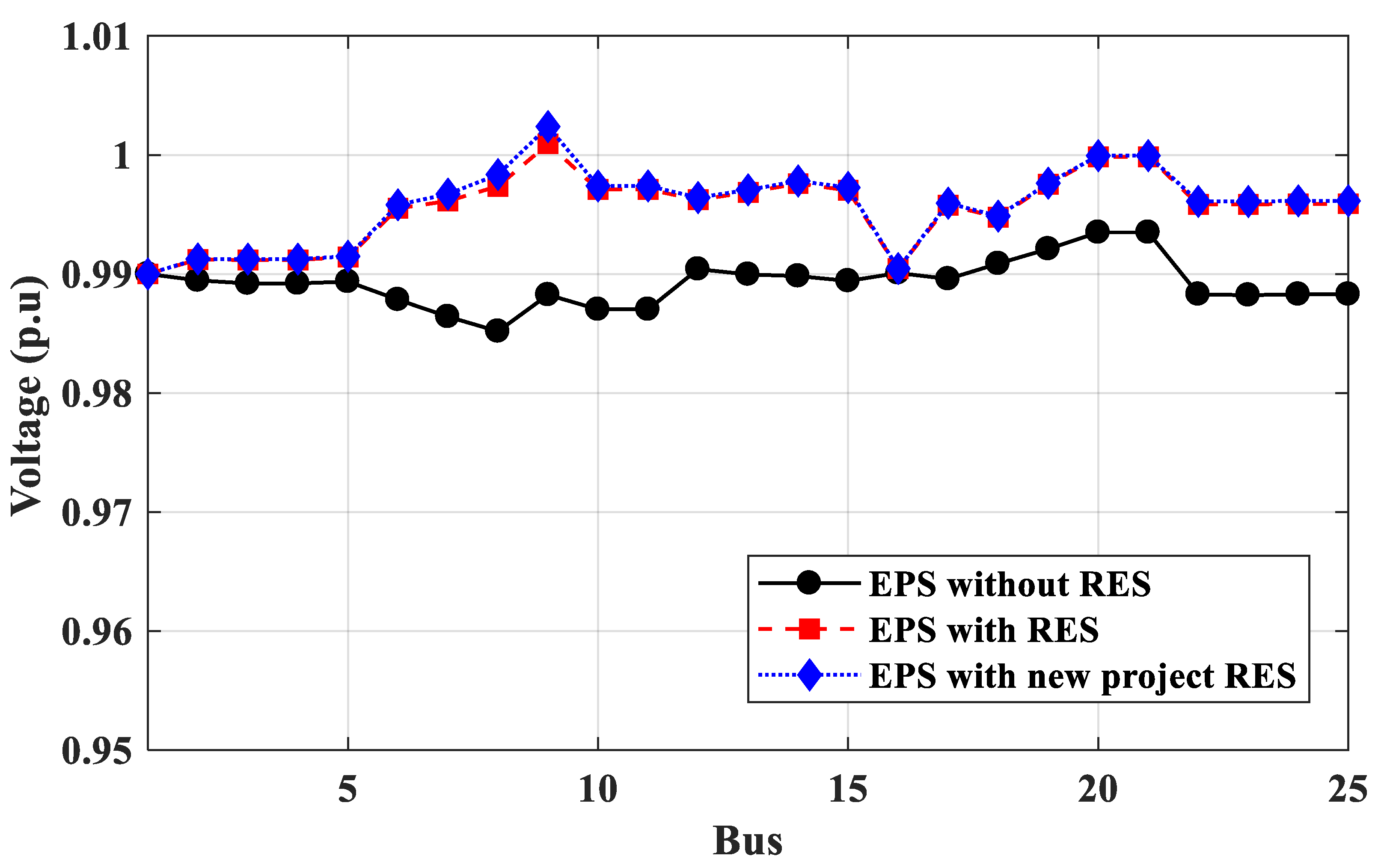
3.2.4. Case 4: Performance of Egyptian Power System with and without RES Projects
4. Conclusions
- The modified multi-objective function was developed for determining the optimal locations of RES buses in IEEE 33-bus and 69-bus distribution systems, as well as the realistic 25-bus 500 kV EPS based on minimum power losses or annual energy losses and the operation stability of the system depending on weather conditions. The proposed technique obtained the optimal locations of the weather-adjusted RES, such as PV systems or wind systems, based on energy calculations, which improved the voltage profile better than those locations based on power calculations, where the effective values of output power have been used to obtain optimal weather-adjusted locations.
- The proposed technique obtained the optimal locations of the weather-adjusted RES, such as PV systems or wind systems, based on energy calculations, which improved the voltage profile better than those locations based on power calculations by about 2%. Additionally, the annual energy losses decrease by about 7% for one RES to 4% for four RESs, where the effective values of output power have been used to obtain optimal weather-adjusted locations.
- The optimal locations of DGs selected by the proposed technique are better than those selected by PSO and GA, and the power loss of the system calculated by the proposed method is better than its values using PSO and GA for tested IEEE 33-bus and 69-bus systems. The voltage profile has been improved by about 2% for each bus, and the power losses have decreased from 174 to 45.4 kW for the IEEE 33-bus system and from 225 to 57 kW for the IEEE 69-bus system.
- The optimal locations of DGs based on energy calculations differ from those based on power calculations and depend on the type of DG (the PV system or the wind system). The effective value of the output power of DG, depending on the weather conditions, differs from its nominal value. The proposed technique used these effective values to obtain the optimal weather-adjusted locations.
- The performance of 25-bus 500 kV EPS was improved by adding RES; the total energy loss per year has been reduced by about 47%, and the voltage buses of 25-bus 500 kV EPS have been improved by 0.1 p.u.
- With an increase in the number of PV system projects, the overall energy loss will be decreased by increasing the voltage profile and operation stability of 25-bus 500 kV EPS. However, increasing the number of wind farm projects does not always give good system stability because some regions are characterized by low wind speeds throughout the year.
- The maximum load capacity obtained using the load ability algorithm can be fed from the 25-bus 500 kV EPS with 9 GW of RESs depending on weather conditions and available areas for the construction of new PV systems and wind farm projects in Egypt. The hydrogen production and industrial loads, as well as the increasing load demand every year due to the development in different regions of Egypt, can be fed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| GA | PSO |
|---|---|
| population = 10 and number of iterations = 100 | population = 50, ω = 1, c1 = 2, c2 = 2 and number of iterations = 100 |
References
- Abdel-Gawad, N.M.; Hamza, A.S.H.; Hassanin, H.M.; Mahmoud, S.A.; El-Debeiky, S. Improving Voltage Profile in the Egyptian National Power System (Enps) Using Simultaneously Three Specific Remedial Actions for Reactive Power Com-pensation. Online J. Power Energy Eng. 2017, 2, 177–187. [Google Scholar]
- Kotb, K.M.; Elkadeem, M.R.; Khalil, A.; Imam, S.M.; Hamada, M.A.; Sharshir, S.W.; Dan, A. A fuzzy decision-making model for optimal design of solar, wind, diesel-based RO desalination integrating flow-battery and pumped-hydro storage: Case study in Baltim, Egypt. Energy Convers. Manag. 2021, 235, 113962. [Google Scholar] [CrossRef]
- Hemeida, M.G.; Ibrahim, A.A.; Mohamed, A.-A.A.; Alkhalaf, S.; El-Dine, A.M.B. Optimal allocation of distributed generators DG based Manta Ray Foraging Optimization algorithm (MRFO). Ain Shams Eng. J. 2021, 12, 609–619. [Google Scholar] [CrossRef]
- Ali, Z.M.; Diaaeldin, I.M.; El-Rafei, A.; Hasanien, H.M.; Aleem, S.H.A.; Abdelaziz, A.Y. A novel distributed generation planning algorithm via graphically-based network reconfiguration and soft open points placement using Archimedes optimization algorithm. Ain Shams Eng. J. 2021, 12, 1923–1941. [Google Scholar] [CrossRef]
- Karunarathne, E.; Pasupuleti, J.; Ekanayake, J.; Almeida, D. The Optimal Placement and Sizing of Distributed Generation in an Active Distribution Network with Several Soft Open Points. Energies 2021, 14, 1084. [Google Scholar] [CrossRef]
- Alham, M.; Gad, M.F.; Ibrahim, D.K. Potential of wind energy and economic assessment in Egypt considering optimal hub height by equilibrium optimizer. Ain Shams Eng. J. 2023, 14, 101816. [Google Scholar] [CrossRef]
- Omara, M.A.; Nassar, I.A. Voltage quality in delta Egypt network and its impact in oil industry. Energy Rep. 2019, 5, 29–36. [Google Scholar] [CrossRef]
- Hassan, A.S.; Othman, E.A.; Bendary, F.M.; Ebrahim, M.A. Distribution systems techno-economic performance optimization through renewable energy resources integration. Array 2021, 9, 100050. [Google Scholar] [CrossRef]
- Abdalla, O.H.; Abdel Ghany, A.M.; Fayek, H.H. Development of a Digital Model of the Egyptian Power Grid for Steady-State and Transient Studies. In Proceedings of the 11th International Conference on Electrical Engineering ICEENG 2018, Cairo, Egypt, 3–5 April 2018; pp. 1–15. [Google Scholar]
- Hassan, A.S.; Younes, A.H.H.; El Saad, M.M.A.; Bendary, F.M. Technical and Economic As-sessment of Integrating DG Resources into a Realistic Egyptian Distribution Network. In Proceedings of the 23rd International Conference on Electricity Distribution Lyon, Lyon, France, 15–18 June 2015; pp. 1–5. [Google Scholar]
- El-Ela, A.A.A.; Allam, S.M.; Shehata, N.K. Optimal Allocation of a Hybrid Wind Energy-Fuel Cell System Using Different Optimization Techniques in the Egyptian Distribution Network. Energy Power Eng. 2021, 13, 17–40. [Google Scholar] [CrossRef]
- Elsayed, A.M.; Mishref, M.M.; Farrag, S.M. Distribution system performance enhancement (Egyptian distribution system real case study). Int. Trans. Electr. Energy Syst. 2018, 28, e2545. [Google Scholar] [CrossRef]
- Molzahn, D.K.; Hiskens, I.A.; Lesieutre, B.C. Calculation of Voltage Stability Margins and Certification of Power Flow Insolvability Using Second-Order Cone Programming. In Proceedings of the 2016 49th Hawaii International Conference on System Sciences (HICSS), Koloa, HI, USA, 5–8 January 2016; pp. 1–10. [Google Scholar] [CrossRef]
- Ali, Z.M.; Diaaeldin, I.M.; Aleem, S.H.E.A.; El-Rafei, A.; Abdelaziz, A.Y.; Jurado, F. Scenario-Based Network Reconfiguration and Renewable Energy Resources Integration in Large-Scale Distribution Systems Considering Parameters Uncertainty. Mathematics 2021, 9, 26. [Google Scholar] [CrossRef]
- Salem, A.A.; Eldesouky, A.A.; Farahat, A.A.; Abdelsalam, A.A. New Analysis Framework of Lyapunov-Based Stability for Hybrid Wind Farm Equipped With FRT: A Case Study of Egyptian Grid Code. IEEE Access 2021, 9, 80320–80339. [Google Scholar] [CrossRef]
- Diaaeldin, I.M.; Aleem, S.H.E.A.; El-Rafei, A.; Abdelaziz, A.Y.; Ćalasan, M. Op-timal Soft Open Points Operation and Distributed Generations Penetration in a Reconfigured Egyptian Distribution Network. In Proceedings of the 25th International Conference on Information Technology (IT), Montenegro, Zabljak, 16–20 February 2021; pp. 1–6. [Google Scholar]
- Mobarak, Y.A. Voltage Collapse Prediction for Egyptian Interconnected Electrical Grid EIEG. Int. J. Electr. Eng. Inform. 2015, 7, 79–88. [Google Scholar] [CrossRef]
- El Hamed, A.M.A.; Ebeed, M.; Refai, A.; El Sattar, M.A.; Elbaset, A.A.; Ahmed, T.A. Application Of Slime Mould Algorithm For Optimal Allocation Of Datacom And Pv System In Real Egyptian Radial Network. Sohag Eng. J. 2021, 1, 16–24. [Google Scholar] [CrossRef]
- Parihar, S.S.; Malik, N. Analysing the impact of optimally allocated solar PV-based DG in harmonics polluted distribution network. Sustain. Energy Technol. Assess. 2022, 49, 101784. [Google Scholar] [CrossRef]
- Fayek, H.H.; Abdalla, O.H. Operation of the Egyptian Power Grid with Maximum Penetration Level of Renewable Energies Using Corona Virus Optimization Algorithm. Smart Cities 2022, 5, 34–53. [Google Scholar] [CrossRef]
- Sultan, H.M.; Kuznetsov, O.N.; Diab, A.A.Z. Modelling and Performance Evaluation of the Egyptian National Utility Grid Based on Real Data. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Moscow and St. Petersburg, Russia, 29 January–1 February 2018; pp. 1–6. [Google Scholar]
- Remha, S.; Chettih, S.; Arif, S. Optimal DG location and sizing for minimum active power loss in radial distribution system using firefly algorithm. Int. J. Energetica 2017, 2, 6–10. [Google Scholar] [CrossRef]
- M’hamdi, B.; Teguar, M.; Tahar, B. Optimal DG Unit Placement and Sizing in Radial Distribution Network for Power Loss Minimization and Voltage Stability Enhancement. Period. Polytech. Electr. Eng. Comput. Sci. 2020, 64, 157–169. [Google Scholar] [CrossRef]
- Abd, M.K.; Cheng, S.J.; Sun, H.S. Optimal DG Placement and Sizing for Power Loss Reduction in a Radial Distribution System using MPGSA and Sensitivity Index Method. In Proceedings of the 2016 IEEE 11th Conference on Industrial Electronics and Applications (ICIEA), Hefei, China, 5–7 June 2016; pp. 1579–1585. [Google Scholar]
- Al Abri, R.S.; El-Saadany, E.F.; Atwa, Y.M. Optimal Placement and Sizing Method to Improve the Voltage Stability Margin in a Distribution System Using Distributed Generation. IEEE Trans. Power Syst. 2013, 28, 326–334. [Google Scholar] [CrossRef]
- Natarajan, M.; Balamurugan, R.; Lakshminarasimman, L. Optimal Placement and Sizing of DGs in the Distribution System for Loss Minimization and Voltage Stability Improvement using CABC. Int. J. Electr. Eng. Inform. 2015, 7, 679–690. [Google Scholar] [CrossRef]
- Kazmi, S.A.A.; Shin, D.R. DG Placement in Loop Distribution Network with New Voltage Stability Index and Loss Minimization Condition Based Planning Approach under Load Growth. Energies 2017, 10, 1203. [Google Scholar] [CrossRef]
- Memarzadeh, G.; Keynia, F. A newindex-basedmethod for optimalDGplacement in distribution networks. Eng. Rep. 2020, 2, e12243. [Google Scholar] [CrossRef]
- Murty, V.; Kumar, A. Optimal placement of DG in radial distribution systems based on new voltage stability index under load growth. Int. J. Electr. Power Energy Syst. 2015, 69, 246–256. [Google Scholar] [CrossRef]
- Haider, W.; Hassan, S.; Mehdi, A.; Hussain, A.; Adjayeng, G.; Kim, C.-H. Voltage Profile Enhancement and Loss Minimization Using Optimal Placement and Sizing of Distributed Generation in Reconfigured Network. Machines 2021, 9, 20. [Google Scholar] [CrossRef]
- Aryanfar, M. Optimal Dispatchable DG Location and Sizing with an Analytical Method, based on a New Voltage Stability Index. Int. J. Res. Technol. Electr. Ind. 2022, 1, 95–104. [Google Scholar] [CrossRef]
- Azad, S.; Amiri, M.M.; Heris, M.N.; Mosallanejad, A.; Ameli, M.T. A Novel Analytical Approach for Optimal Placement and Sizing of Distributed Generations in Radial Electrical Energy Distribution Systems. Sustainability 2021, 13, 10224. [Google Scholar] [CrossRef]
- Prakash, P.; Meena, D.C.; Malik, H.; Alotaibi, M.A.; Khan, I.A. A Novel Analytical Approach for Optimal Integration of Renewable Energy Sources in Distribution Systems. Energies 2022, 15, 1341. [Google Scholar] [CrossRef]
- Aman, M.; Jasmon, G.; Mokhlis, H.; Bakar, A. Optimal placement and sizing of a DG based on a new power stability index and line losses. Int. J. Electr. Power Energy Syst. 2012, 43, 1296–1304. [Google Scholar] [CrossRef]
- Seet, C.C.; Pasupuleti, J.; Khan, M.R.B. Optimal Placement and Sizing of Distributed Generation in Distribution System using Analytical Method. Int. J. Recent Technol. Eng. 2019, 8, 6357–6363. [Google Scholar] [CrossRef]
- Shaik, M.A.; Mareddy, P.L.; Visali, N. Enhancement of Voltage Profile in the Distribution system by Reconfiguring with DG placement using Equilibrium Optimizer. Alex. Eng. J. 2022, 61, 4081–4093. [Google Scholar] [CrossRef]
- Hassan, A.S.; Sun, Y.; Wang, Z. Multi-objective for optimal placement and sizing DG units in reducing loss of power and enhancing voltage profile using BPSO-SLFA. Energy Rep. 2020, 6, 1581–1589. [Google Scholar] [CrossRef]
- Adewuyi, O.B.; Adeagbo, A.P.; Adebayo, I.G.; Howlader, H.O.R.; Sun, Y. Modified Analytical Approach for PV-DGs Integration into a Radial Distribution Network Considering Loss Sensitivity and Voltage Stability. Energies 2021, 14, 7775. [Google Scholar] [CrossRef]
- Mohamed, A.E.; Salah, K.; Hussein, A.; Ehab, E.E. A Novel Approach Based on Honey Badger Algorithm for Optimal Allocation of Multiple DG and Capacitor in Radial Distribution Networks Considering Power Loss Sensitivity. Mathematics 2022, 10, 2081. [Google Scholar] [CrossRef]
- Lakshmi, G.V.N.; Laxmi, A.J.; Veeramsetty, V.; Salkuti, S.R. Optimal Placement of Distributed Generation Based on Power Quality Improvement Using Self-Adaptive Lévy Flight Jaya Algorithm. Clean Technol. 2022, 4, 1242–1254. [Google Scholar] [CrossRef]
- Ntombela, M.; Musasa, K.; Leoaneka, M.C. Power Loss Minimization and Voltage Profile Improvement by System Reconfiguration, DG Sizing, and Placement. Computation 2022, 10, 180. [Google Scholar] [CrossRef]
- Lekhuleni, T.; Twala, B. Distributed Optimal Placement Generators in a Medium Voltage Redial Feeder. Symmetry 2022, 14, 1729. [Google Scholar] [CrossRef]
- Kumar, P.; Swarnkar, N.K.; Ali, A.; Mahela, O.P.; Khan, B.; Anand, D.; Ballester, J.B. Transmission Network Loss Reduction and Voltage Profile Improvement Using Network Restructuring and Optimal DG Placement. Sustainability 2023, 15, 976. [Google Scholar] [CrossRef]
- Bhumkittipich, K.; Phuangpornpitak, W. Optimal Placement and Sizing of Distributed Generation for Power Loss Reduction Using Particle Swarm Optimization. Energy Procedia 2013, 34, 307–317. [Google Scholar] [CrossRef]
- Chandel, A.; Chauhan, D.; Singh, D. Enriched Technique for DG Placement and Sizing by GA Optimization. Am. Eurasian J. Sci. Res. 2017, 12, 260–270. [Google Scholar] [CrossRef]
- Sellami, R.; Sher, F.; Neji, R. An improved MOPSO algorithm for optimal sizing & placement of distributed generation: A case study of the Tunisian offshore distribution network (ASHTART). Energy Rep. 2022, 8, 6960–6975. [Google Scholar] [CrossRef]
- Duong, M.Q.; Pham, T.D.; Nguyen, T.T.; Doan, A.T.; Van Tran, H. Determination of Optimal Location and Sizing of Solar Photovoltaic Distribution Generation Units in Radial Distribution Systems. Energies 2019, 12, 174. [Google Scholar] [CrossRef]

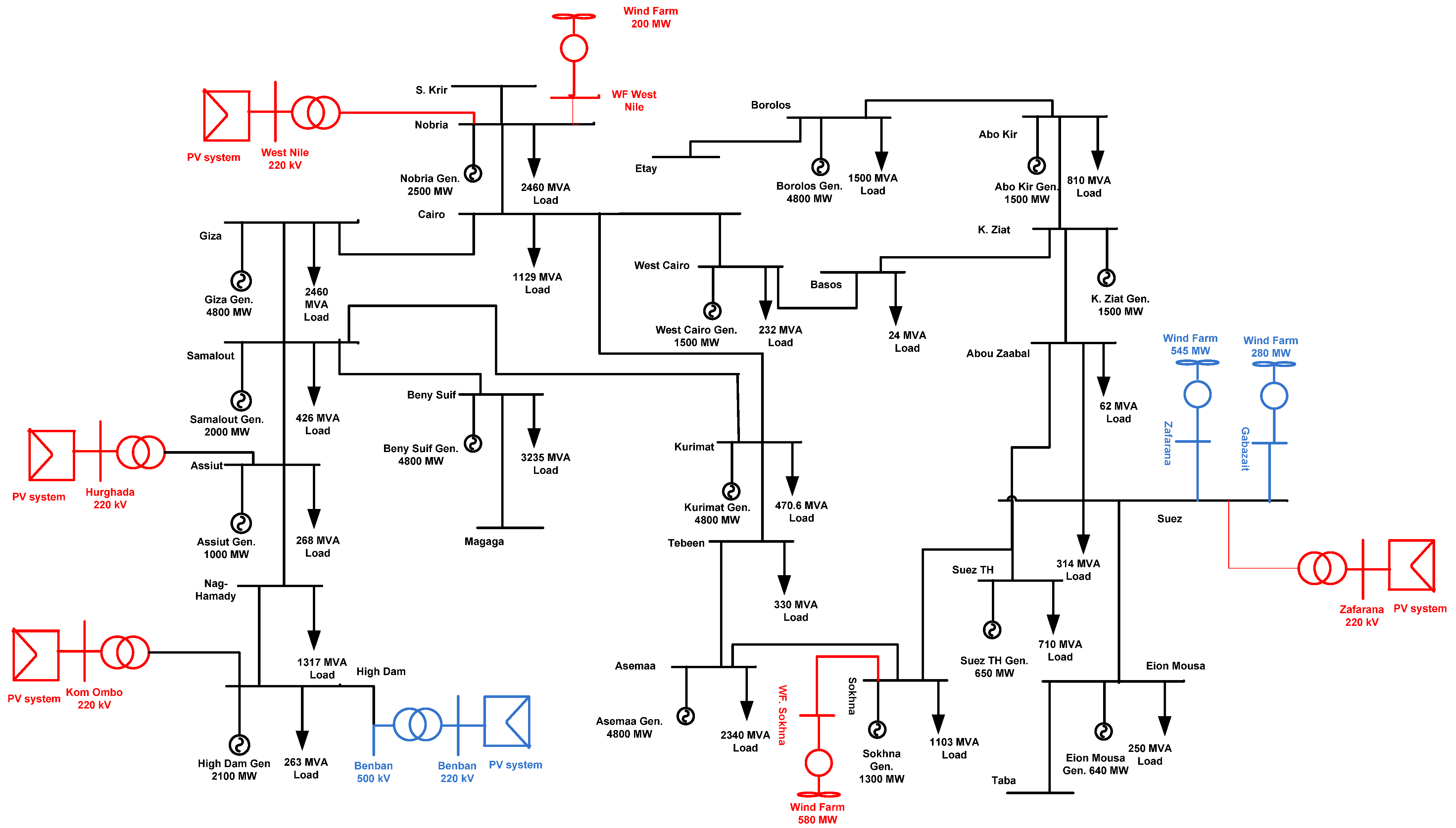




| No. | Name | Pg | Qg | PL | QL |
|---|---|---|---|---|---|
| 1 | West Cairo | 5616 | 2718 | 380.8 | 184.4 |
| 2 | Cairo | 1720 | 832 | 1853.3 | 897.4 |
| 3 | Nobaria | 2048 | 991 | 4038.3 | 1955.3 |
| 4 | S krir | 0 | 0 | 0 | 0 |
| 5 | Giza | 3931 | 1903 | 4038.3 | 1955.3 |
| 6 | Samalout | 0 | 0 | 699.4 | 338.6 |
| 7 | Assiut | 314 | 138 | 440 | 213 |
| 8 | Nag-hammady | 0 | 0 | 2162 | 1046.8 |
| 9 | High damn | 1720 | 832 | 431.8 | 209.1 |
| 10 | Beniswif | 3931 | 1903 | 5310.6 | 2571.4 |
| 11 | Magaga | 0 | 0 | 0 | 0 |
| 12 | Kurimat | 3931 | 1903 | 772.5 | 374 |
| 13 | Tebeen | 0 | 0 | 541.7 | 262.3 |
| 14 | Assemaa | 3931 | 1903 | 3841.3 | 1860 |
| 15 | Sokhna | 1065 | 515 | 1810.7 | 876.7 |
| 16 | Bassos | 0 | 0 | 39.4 | 19.1 |
| 17 | Abo zabaal | 0 | 0 | 101.8 | 49.3 |
| 18 | K zaiat | 1229 | 595 | 0 | 0 |
| 19 | Abo kir | 1229 | 595 | 1329.7 | 643.8 |
| 20 | Borolos | 3931 | 1903 | 2462.4 | 1192.3 |
| 21 | ETAY | 0 | 0 | 0 | 0 |
| 22 | Suez | 0 | 0 | 515.4 | 249.6 |
| 23 | Suez th | 532 | 257 | 1165.5 | 564.3 |
| 24 | Ein Mousa | 524 | 254 | 410.4 | 198.7 |
| 25 | Taba | 0 | 0 | 0 | 0 |
| Total | 35,652 | 17,242 | 32,345.3 | 15,661.6 | |
| Project | Size | Contract |
|---|---|---|
| Kom Ombo | 200 MW | BOO SCHEME |
| West Nile | 600 MW | Sky power and EETC BOO |
| West Nile | 200 MW | EETC BOO |
| West Nile | 600 MW | BOO scheme |
| FIT | 50 MW | EETC PPA |
| FIT | 1415 MW | EETC PPA |
| Hurghada | 20 MW | NREA-JICA EPC scheme |
| Zaafarana | 50 MW | NREA-AFD EPC scheme |
| Kom ombo | 26 MW | NREA-AFD EPC scheme |
| Kom ombo | 50 MW | NREA-AFD EPC scheme |
| Case | Proposed Method | Previous Work | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Based on Power | Based on Energy | Based on Power | ||||||||
| Buses No. | DG Size (MW) | Losses (kW) | Min Voltage | Buses No. | DG Size | Losses | Min Voltage | Ref. [46] | Ref. [47] | |
| Without DG | - | - | 174 | 0.9082@18 | - | - | - | - | PSO | GA |
| One PVDG | 6 | 2.5 | 58.2 | 0.9555@18 | 17 | Prate = 2.5 Pavg = 0.6765 | E = 49,275 (kWd) Pavg = 135 kW/d | 0.9436@33 | 6 | 6 |
| Two PVDGs | 6, 24 | 1.8, 0.9 | 50 | 0.9553@18 | 17, 33 | Prate: 1.8, 0.9 Pav: 0.6224, 0.4010 | E = 47,815 P = 131 | 0.9768@25 | 12, 30 | 6, 15 |
| Three PVDGs | 6, 24, 19 | 1.15, 0.9, 0.5 | 45.4 | 0.9556@18 | 17, 33, 22 | Prate: 1.1, 1.09, 0.5 Pav: 0.2977, 0.2914, 0.0802 | E = 20,075 P = 55 | 0.9977@25 | 9, 24, 30 | 14, 24, 28 |
| One wind DG | 14 | Prate = 2.5 Pav = 1.2936 | E = 46,720 Pav = 128 kW/d | 0.9462@33 | ||||||
| Two wind DGs | 14, 7 | Prate: 1.8, 0.9 Pav: 1.3634, 0.6817 | E = 38,325 Pav = 105 | 0.9654@33 | ||||||
| Three wind DGs | 14, 7, 33 | Prate:1.1, 1.05, 0.5 Pav: 0.8332, 0.8256, 0.3488 | E = 34,675 Pav = 95 | 0.9798@25 | ||||||
| Case | Proposed Method | Previous Work | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Based on Power | Based on Energy | Ref. [46] | Ref. [47] | |||||||
| Buses No. | DG Size (MW) | Losses (kW) | Min Voltage | Buses No. | DG Size | Losses | Min Voltage | |||
| Without DG | - | - | 225 | 0.9092@65 | - | - | - | - | PSO | GA |
| One PVDG | 61 | 1.86 | 100 | 0.9704@27 | 64 | Prate: 1.86 Pav: 0.4957 | E = 65,700 Pav = 180 | 0.9262@65 | 62 | 61 |
| Two PVDGs | 61, 17 | 1.8, 0.7 | 68 | 0.9879@65 | 64, 65 | Prate: 1.8, 0.7 Pav: 0.4797, 0.1866 | E = 57,670 Pav = 158 | 0.9318@61 | 62, 17 | 61, 17 |
| Three PVDGs | 61, 17, 49 | 1.8, 0.7, 0.5 | 57 | 0.9879@65 | 64, 65, 56 | Prate: 1.8, 0.7, 0.5 Pav: 0.4797, 0.1866, 0.1333 | E = 55,845 Pav = 153 | 0.9330@61 | 61, 17, 9 | 61, 18, 49 |
| One wind DG | 64 | Prate: 1.86 Pav: 0.6142 | E = 69,350 Pav = 190 | 0.9200@65 | ||||||
| Two wind DGs | 64, 57 | Prate: 1.8, 0.7 Pav: 0.6142, 0.2311 | E = 66,795 Pav = 183 | 0.9218@65 | ||||||
| Three wind DGs | 64, 57, 9 | Prate: 1.8, 0.7, 0.5 Pav: 0.6142, 0.2311, 0.3787 | E = 64,605 Pav = 177 | 0.9231@65 | ||||||
| Case | Proposed Method | GA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Based on Power | Based on Energy | ||||||||||
| Buses No. | RES Size (MW) | Losses (MW) | Min Voltage | Buses No. | RES Size | Losses | Min Voltage | Buses No. | Losses (MW) | Min Voltage | |
| Without RES | - | - | 195.51 | 0.9596@8 | - | - | - | - | - | 195.51 | 0.9596@8 |
| One PVRES | 2 | 9000 | 127.5 | 0.9678@8 | 16 | Pr: 9000 Pav: 2435.5 | E = 42,969 Pav = 118 | 0.9677@8 | 18 | 123.8 | 0.9678@8 |
| Two PVRESs | 2, 16 | 4500, 4500 | 99.1 | 0.9706@8 | 16, 3 | Pr: 4500, 4500 Pav: 1218, 1248 | E = 34,022 Pav = 93 | 0.9705@8 | 18 21 | 95.1 | 0.9706@8 |
| Three PVRESs | 2, 16, 5 | 3000, 3000, 3000 | 61.5 | 0.9756@8 | 16, 3, 2 | Pr: 3000, 3000, 3000 Pav: 812, 832, 832 | E = 21,530 Pav = 59 | 0.9755@8 | 18 21 25 | 58 | 0.9756@8 |
| Four PVRESs | 2, 16, 5, 3 | 2250, 2250, 2250, 2250 | 47 | 0.9778@8 | 16, 3, 2, 5 | Pr: 2250, 2250, 2250, 2250 Pav: 609, 624, 624, 624 | E = 16,874 Pav = 46 | 0.9777@8 | 4 25 18 21 | 45 | 0.9778@8 |
| one wind RES | 3 | Pr: 9000 Pav: 3501 | E = 42,410 Pav = 116 | 0.9678@8 | |||||||
| Two wind RESs | 3, 2 | Pr: 4500, 4500 Pav: 1751, 1751 | E = 33,706 Pav = 92 | 0.9706@8 | |||||||
| Three wind RESs | 3, 2, 4 | Pr: 3000, 3000, 3000 Pav:1167, 1167, 1167 | E = 21,414 Pav = 59 | 0.9755@8 | |||||||
| Four wind RESs | 3, 2, 4, 16 | Pr: 2250, 2250, 2250, 2250 Pav: 875, 875, 875, 1704 | E = 17,171 Pav = 47 | 0.9777@8 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aref, M.; Oboskalov, V.; El-Shahat, A.; Abdelaziz, A.Y. Modified Analytical Technique for Multi-Objective Optimal Placement of High-Level Renewable Energy Penetration Connected to Egyptian Power System. Mathematics 2023, 11, 958. https://doi.org/10.3390/math11040958
Aref M, Oboskalov V, El-Shahat A, Abdelaziz AY. Modified Analytical Technique for Multi-Objective Optimal Placement of High-Level Renewable Energy Penetration Connected to Egyptian Power System. Mathematics. 2023; 11(4):958. https://doi.org/10.3390/math11040958
Chicago/Turabian StyleAref, Mahmoud, Vladislav Oboskalov, Adel El-Shahat, and Almoataz Y. Abdelaziz. 2023. "Modified Analytical Technique for Multi-Objective Optimal Placement of High-Level Renewable Energy Penetration Connected to Egyptian Power System" Mathematics 11, no. 4: 958. https://doi.org/10.3390/math11040958








