Experimental Study on the Dynamic Characteristics of Gas-Centered Swirl Coaxial Injector under Varying Ambient Pressure
Abstract
:1. Introduction
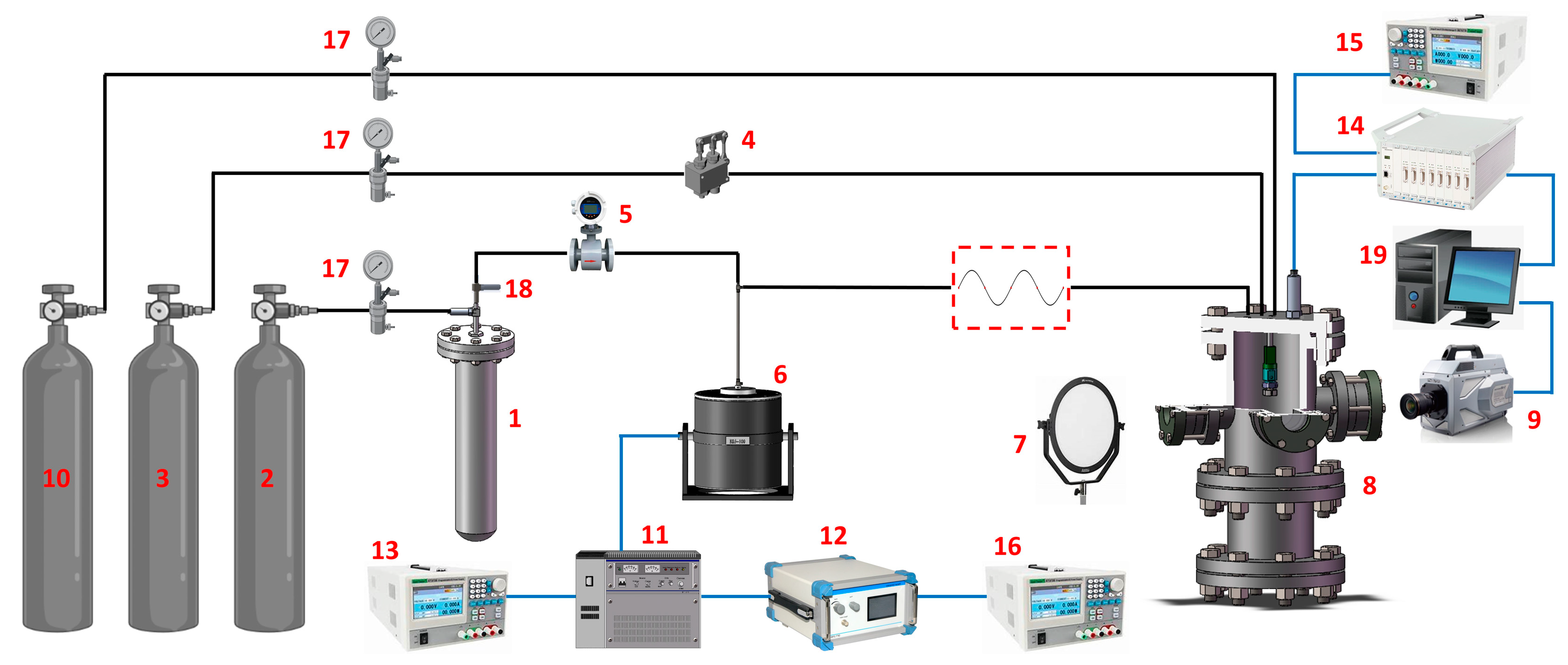
2. Experimental Methods
2.1. Experimental Facilities
2.2. Experimental Conditions
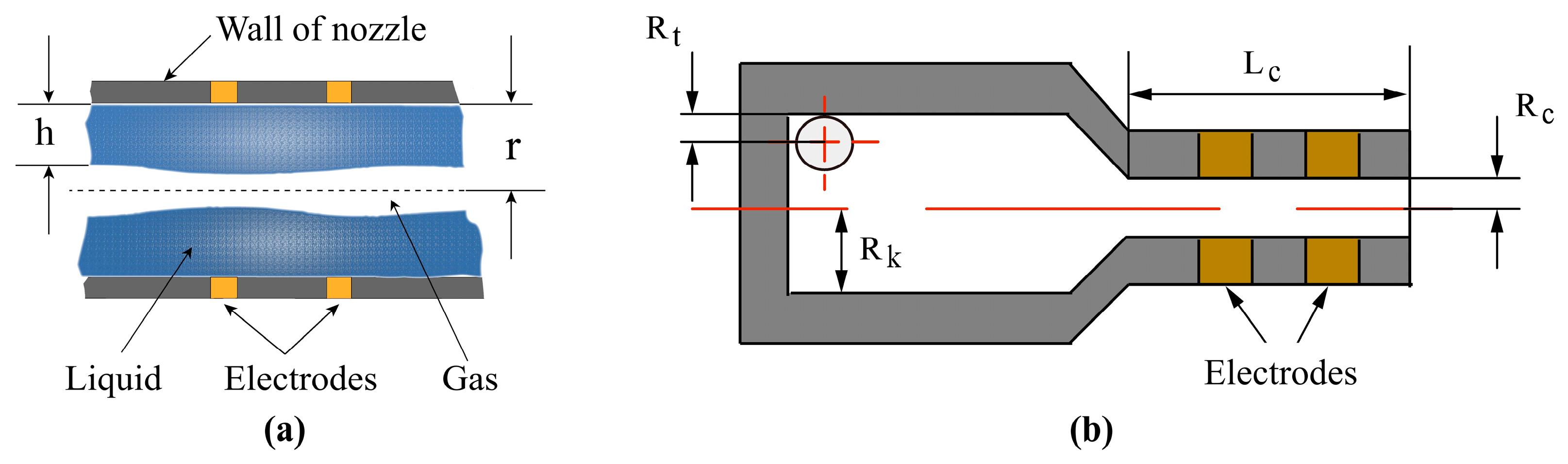
2.3. Experimental Techniques
2.3.1. Inertial Flow Pulsator
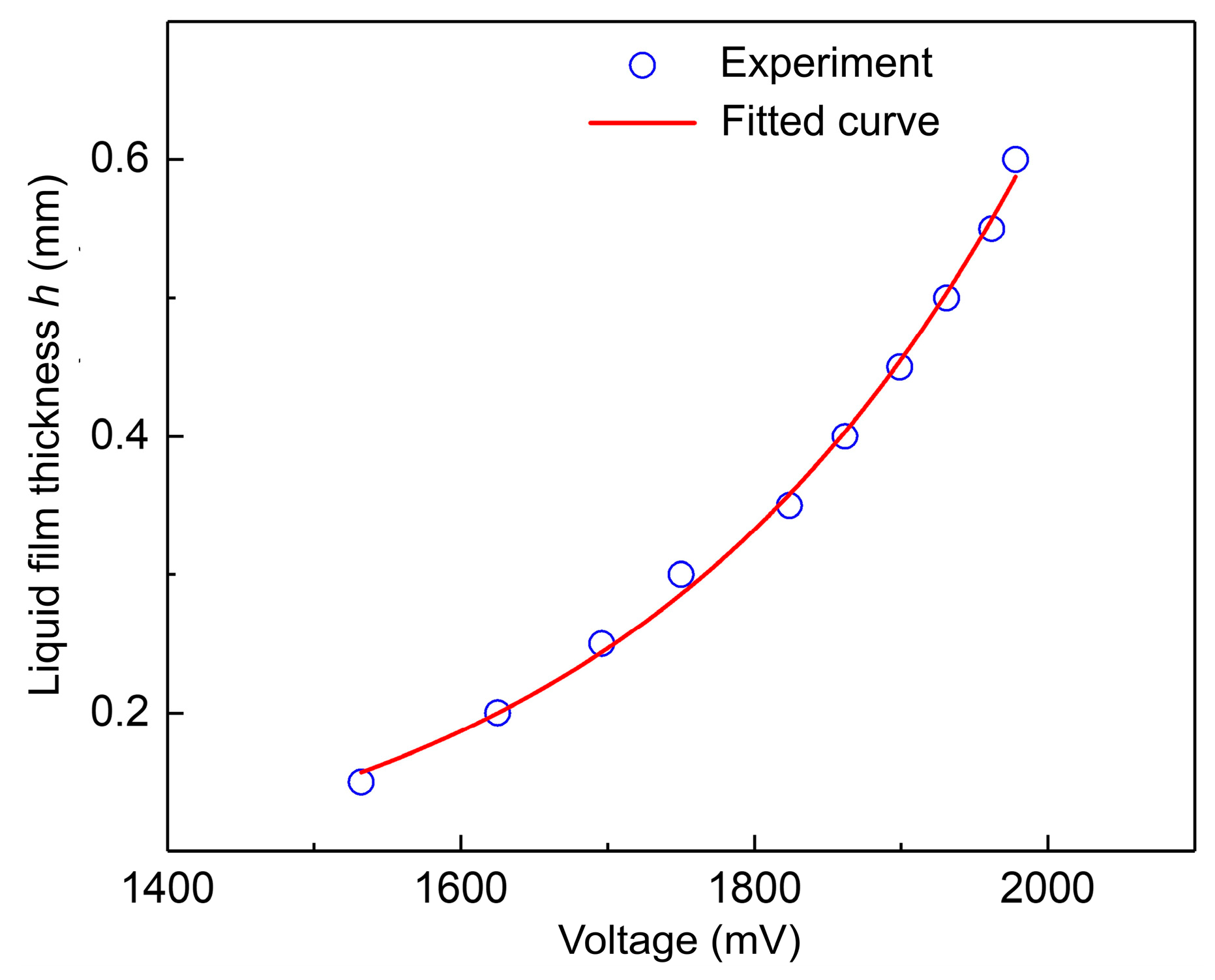
2.3.2. Electric Conductance Method
3. Results and Discussion
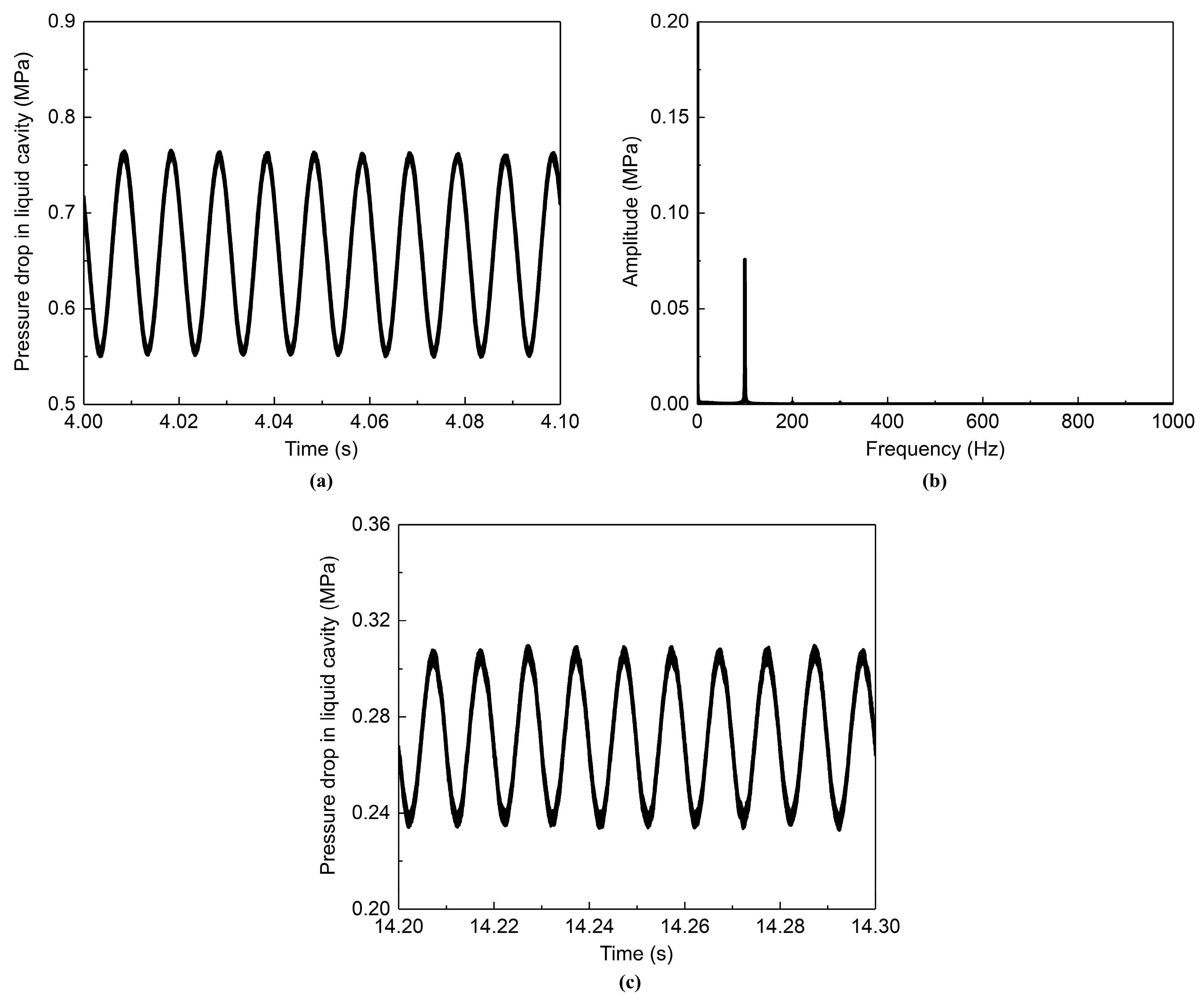
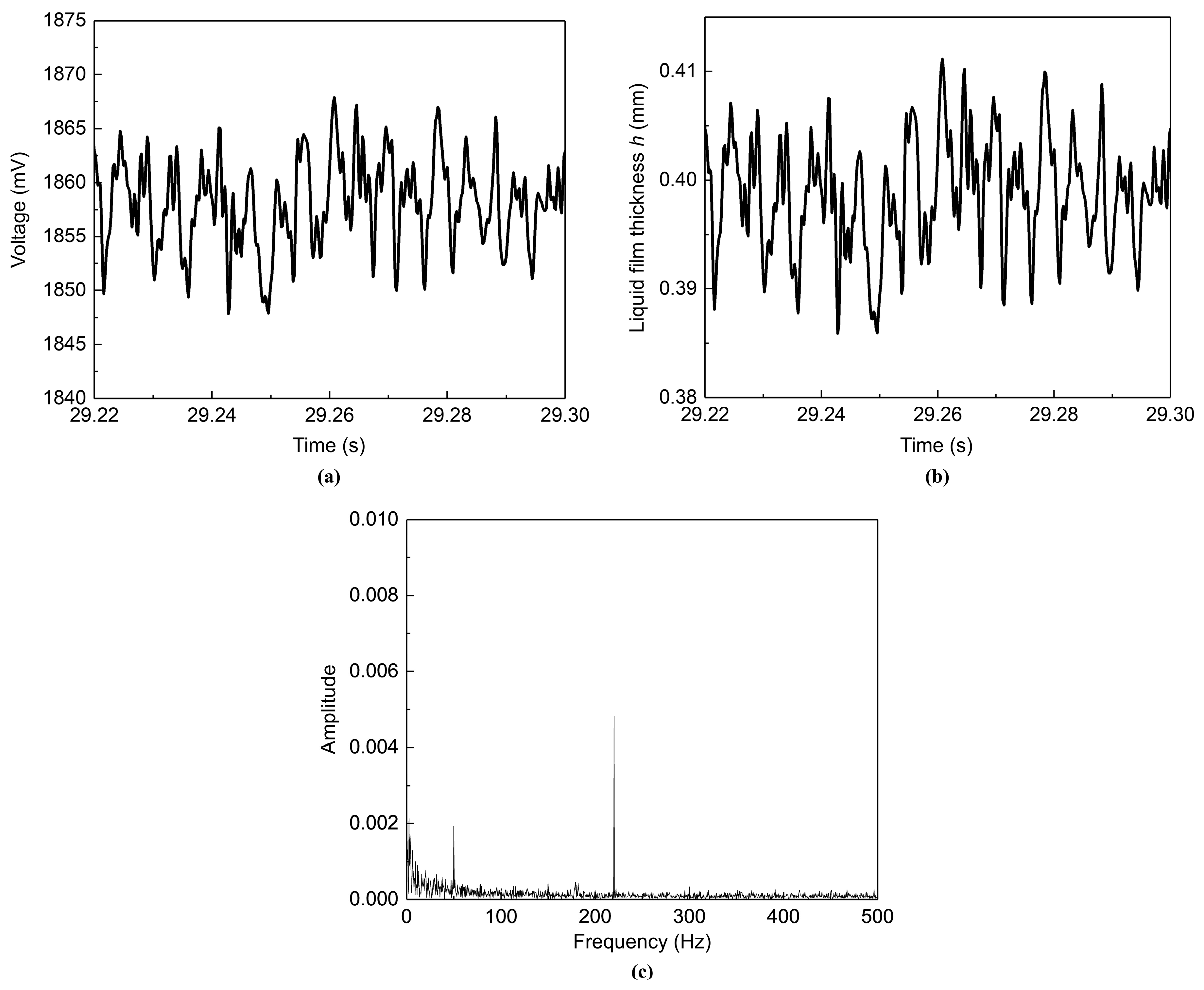
3.1. The Pulsation Test of Inertial Flow Pulsator and the Validation of Operating Conditions
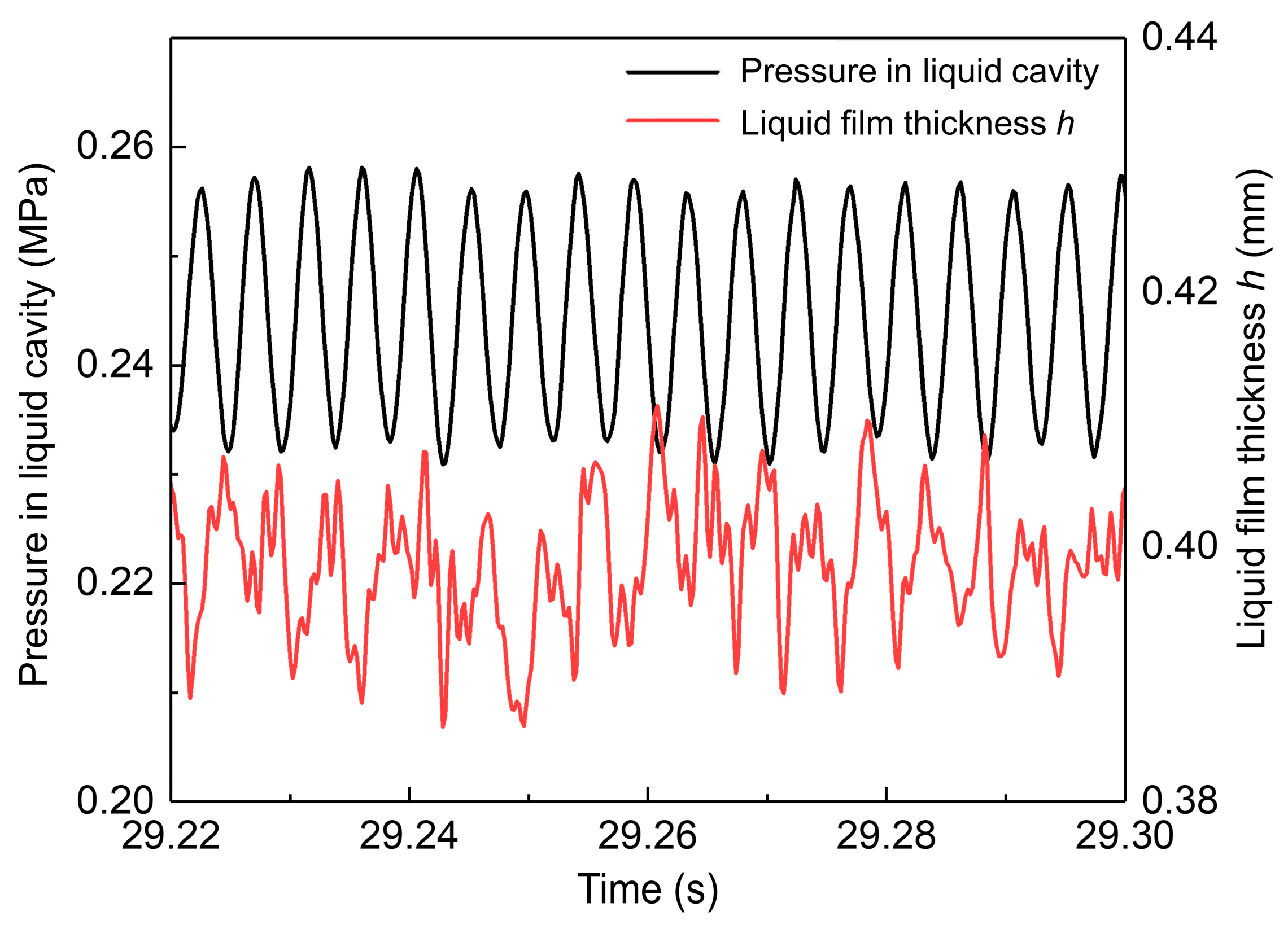
3.2. Steady State
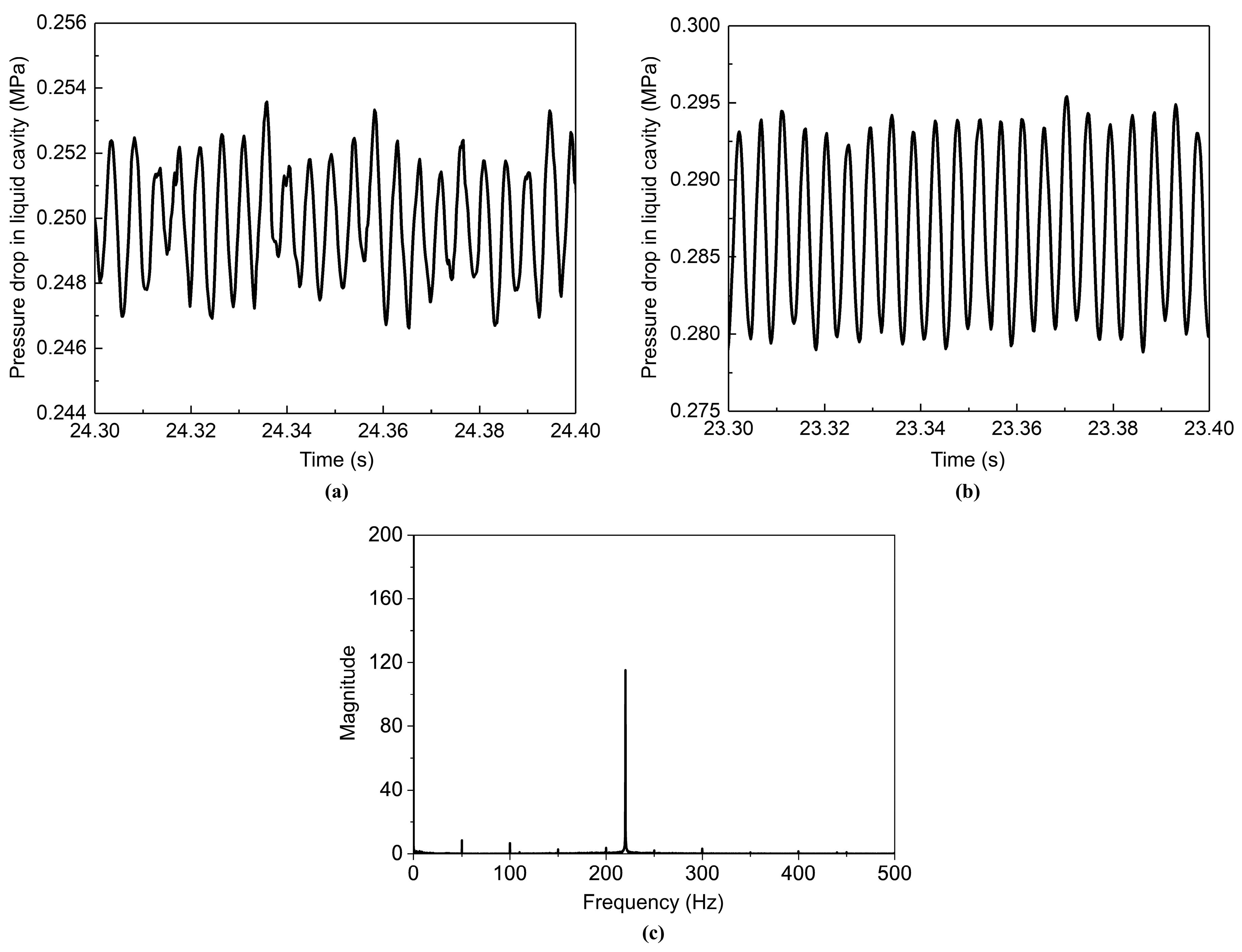
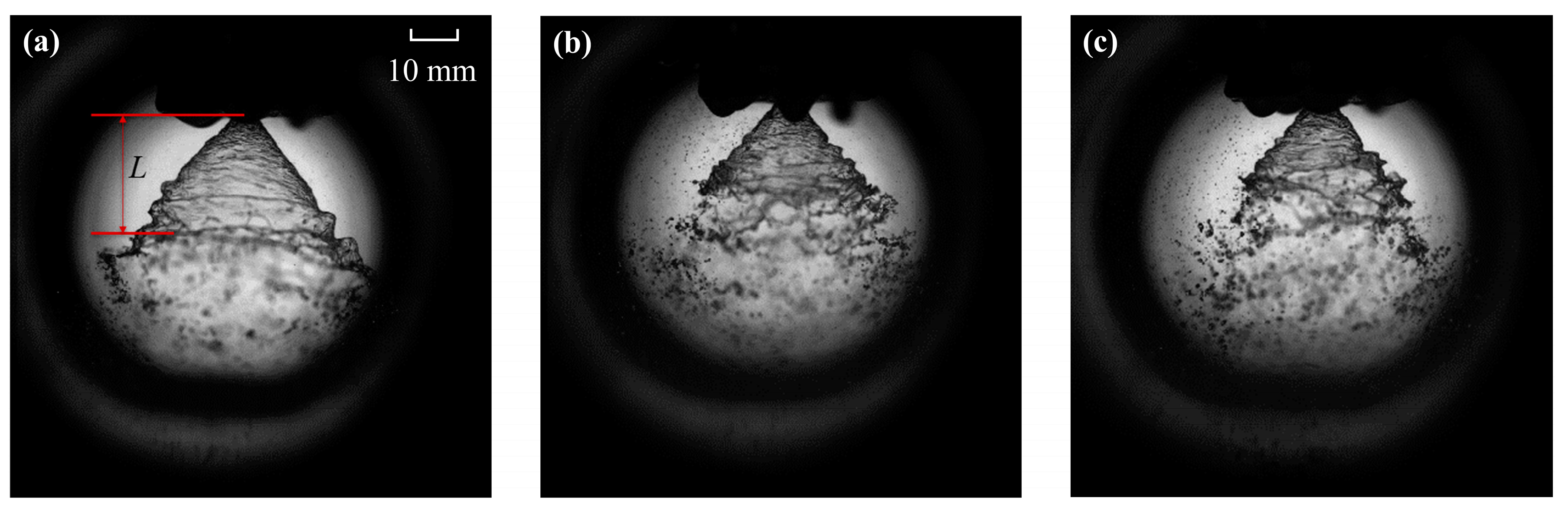
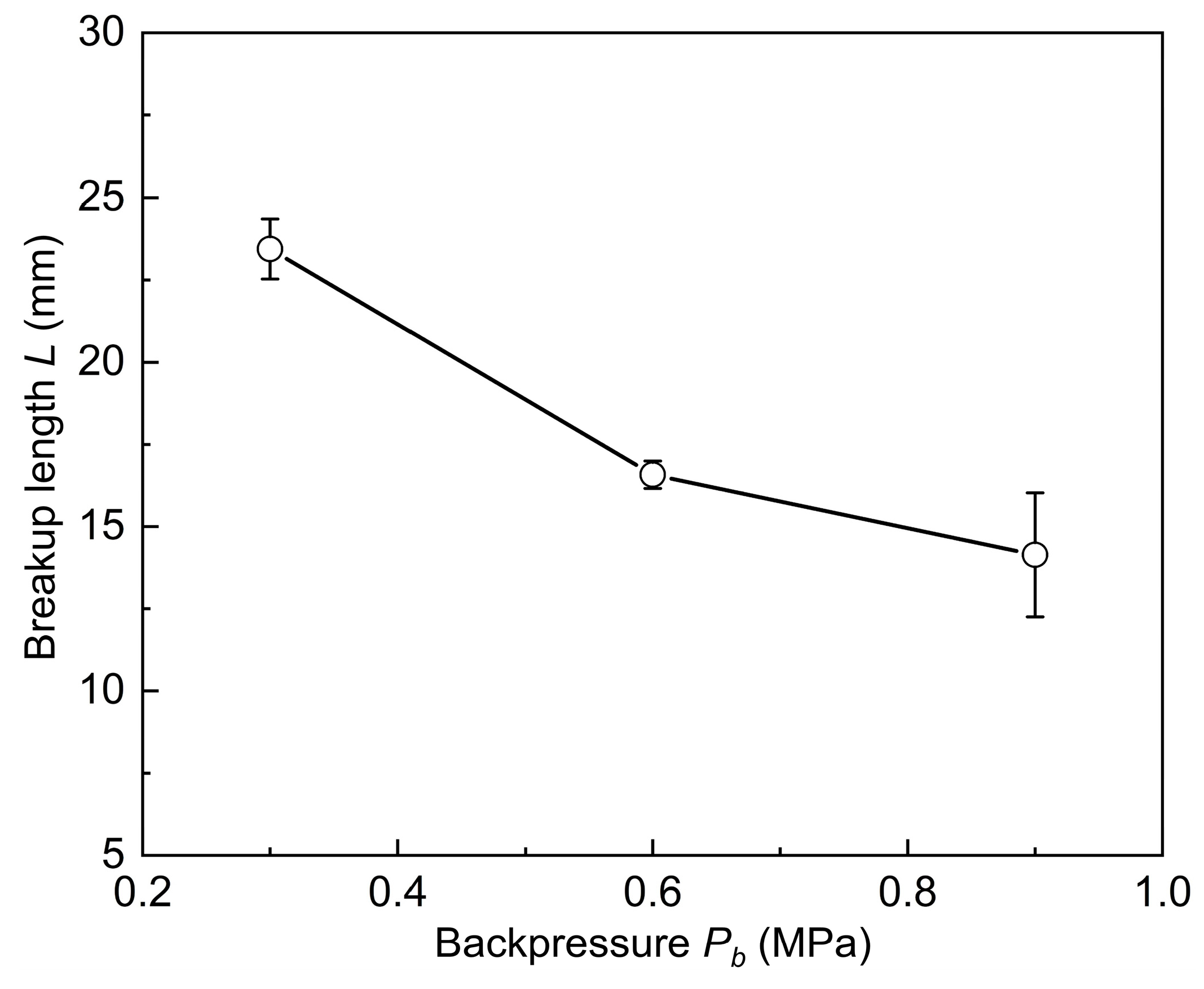
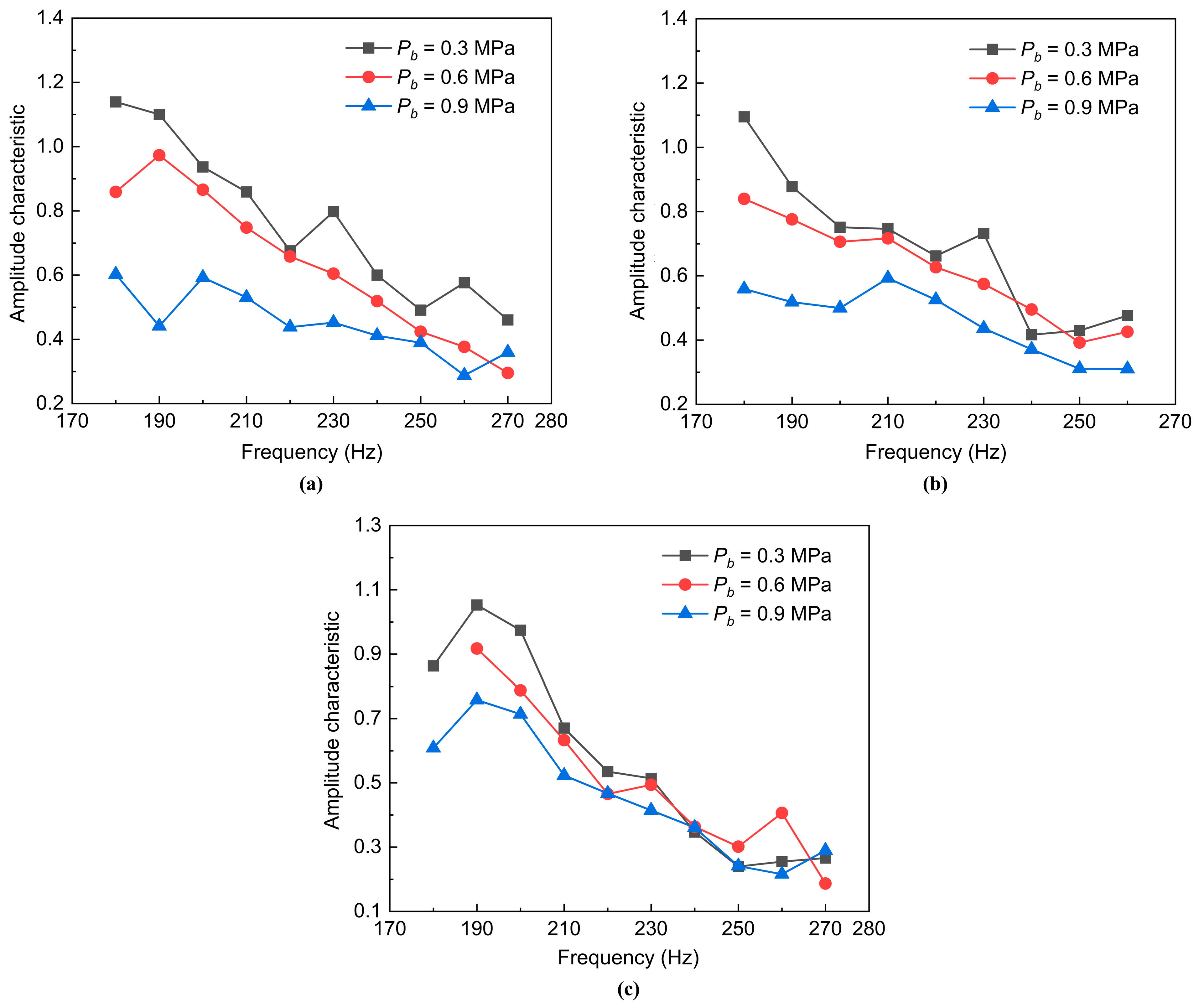
3.3. The Effect of the Chamber Backpressure
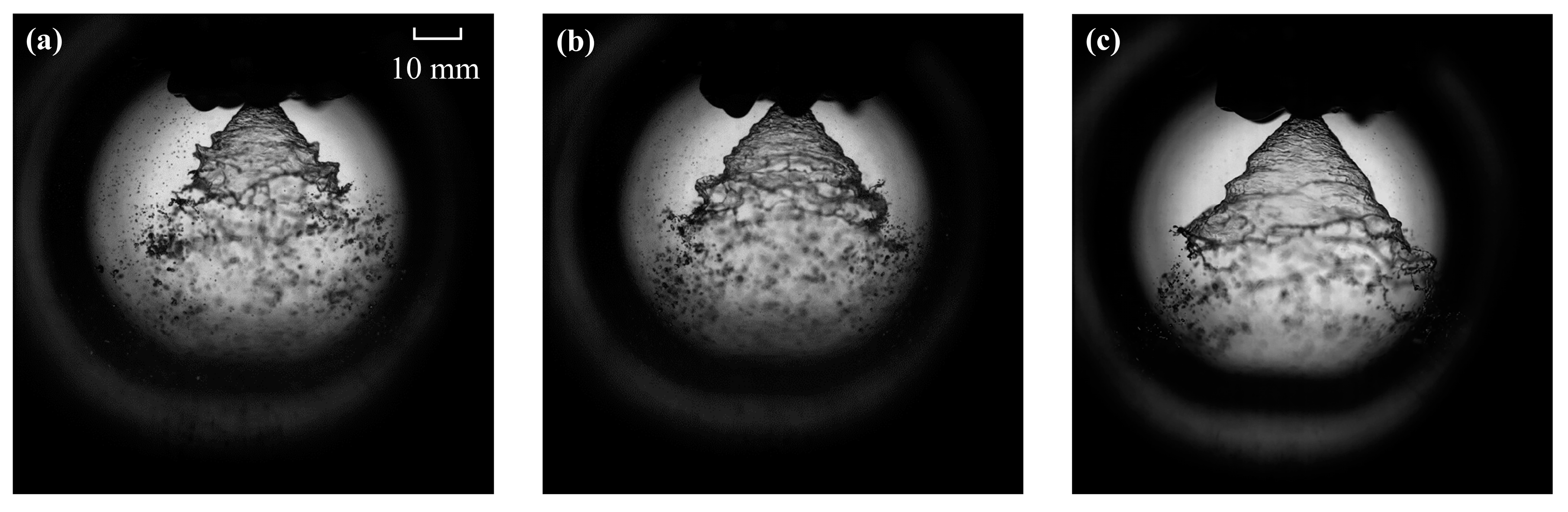
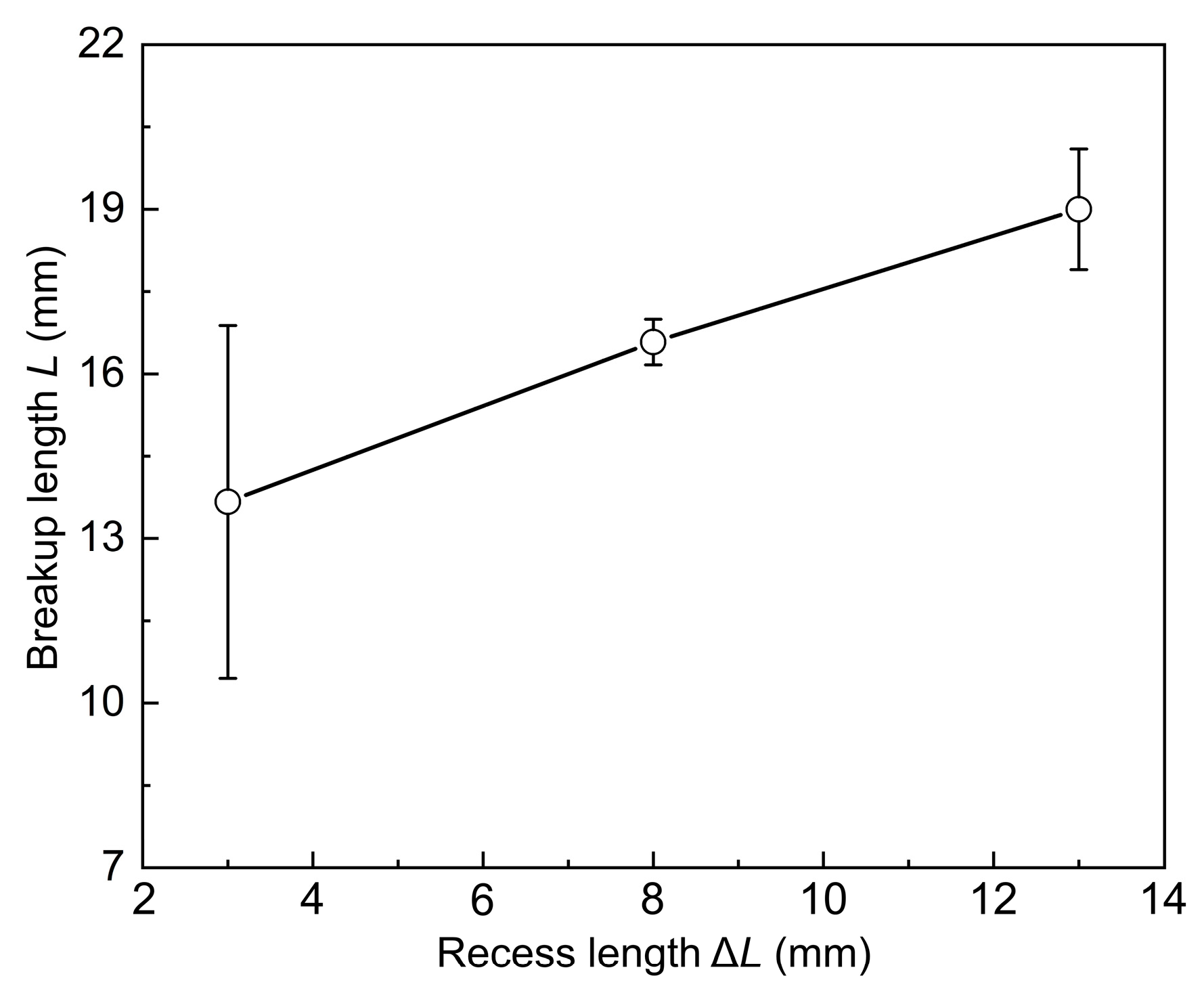
3.4. The Effect of the Recess Length
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kang, Z.; Wang, Z.; Li, Q.; Cheng, P. Review on pressure swirl injector in liquid rocket engine. Acta Astronaut. 2018, 145, 174–198. [Google Scholar]
- Im, J.H.; Cho, S.; Yoon, Y.; Moon, I. Comparative study of spray characteristics of gas-centered and liquid-centered swirl coaxial injectors. J. Propul. Power 2010, 26, 1196–1204. [Google Scholar] [CrossRef]
- Inoue, C.; Watanabe, T.; Himeno, T.; Uzawa, S. Liquid Jet Dynamics and Primary Breakup Characteristics at Near-Field of Coaxial Type Injector. In Proceedings of the 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Nashville, TN, USA, 25–28 July 2010. [Google Scholar]
- Cohn, R.; Strakey, P.; Bates, R.; Talley, D.; Muss, J.; Johnson, C. Swirl Coaxial Injector Development. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003. [Google Scholar]
- Bazarov, V. Influence of Propellant Injector Stationary and Dynamic Parameters on High Frequency Combustion Stability. In Proceedings of the 32nd Joint Propulsion Conference and Exhibit, Lake Buena Vista, FL, USA, 1–3 July 1996. [Google Scholar]
- Harrje, D.T.; Reardon, F.H. Liquid Propellant Rocket Combustion Instability; Scientific and Technical Information Office, National Aeronautics and Space Administration, U.S. Government Printing Office: Washington, DC, USA, 1972; Volume 1. [Google Scholar]
- Ismailov, M.; Heister, S.D. Dynamic response of rocket swirl injectors, part II: Nonlinear dynamic response. J. Propul. Power 2011, 27, 412–421. [Google Scholar] [CrossRef]
- Li, P.; Yang, L.; Fu, Q.; Fang, Z. Spray characteristics of the nanoparticle-containing gel propellants by using an improved single-phase nozzle. Fuel 2022, 315, 122968. [Google Scholar] [CrossRef]
- Ismailov, M.M. Modeling of Classical Swirl Injector Dynamics. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2010. [Google Scholar]
- Liu, L.; Zhang, S.; Fu, Q. Spray characteristics of gel fuel in a gas-centered coaxial swirl injector with variable recess ratios. Fuel 2022, 319, 123766. [Google Scholar] [CrossRef]
- Bazarov, V.G.; Yang, V. Liquid-propellant rocket engine injector dynamics. J. Propul. Power 1998, 14, 797–806. [Google Scholar] [CrossRef]
- Fu, Q.F.; Yang, L.J.; Wang, X.D. Theoretical and experimental study of the dynamics of a liquid swirl injector. J. Propul. Power 2010, 26, 94–101. [Google Scholar] [CrossRef]
- Fu, Q.F.; Yang, L.; Qu, Y.Y.; Gu, B. Geometrical effects on the fluid dynamics of an open-end swirl injector. J. Propul. Power 2011, 275, 929–936. [Google Scholar] [CrossRef]
- Bazarov, V. Non-Linear Interactions in Liquid-Propellant Rocket Engine Injectors. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cleveland, OH, USA, 13–15 July 1998. [Google Scholar]
- Bazarov, V. Self-Pulsations in Coaxial Injectors with Central Swirl Liquid Stage. In Proceedings of the 31st Joint Propulsion Conference and Exhibit, San Diego, CA, USA, 10–12 July 1995. [Google Scholar]
- Yang, V.; Puri, P. Design and Dynamics of Jet and Swirl Injectors. In Liquid Rocket Thrust Chambers; Astronautics and Aeronautics Inc.: Reston, VA, USA, 2004; pp. 19–103. [Google Scholar]
- Park, G.; Oh, S.; Yoon, Y.; Choi, J.Y. Characteristics of gas-centered swirl-coaxial Injector with liquid flow excitation. J. Propul. Power 2019, 35, 624–631. [Google Scholar] [CrossRef]
- Park, G.; Lee, J.; Oh, S.; Yoon, Y.; Sohn, C.H. Characteristics of gas-centered swirl coaxial injector with acoustic excitation of gas flow. AIAA J. 2017, 55, 894–901. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Gadgil, H. Dynamics of self-pulsation in gas-centered swirl coaxial injector: An experimental study. J. Propul. Power 2021, 373, 450–462. [Google Scholar]
- Oh, S.; Park, G.; Kim, S.; Lee, H.; Yoon, Y.; Choi, J.Y. A Study on dynamic characteristics of gas centered swirl coaxial injector varying tangential inlet diameter with liquid pulsation. J. ILASS-Korea 2017, 22, 62–68. [Google Scholar]
- Bai, X.; Cheng, P.; Sheng, L.; Li, Q.; Zhang, X.; Kang, Z. Effects of backpressure on self-pulsation characteristics of liquid-centered swirl coaxial injectors. Int. J. Multiphas. Flow 2019, 116, 239–249. [Google Scholar]
- He, X.; Chen, C.; Yang, Y.; Yan, Z. Experimental study on the flow field distribution characteristics of an open-end swirl injector under ambient pressure. Aerosp. Sci. Technol. 2020, 98, 105691. [Google Scholar]
- Kim, D.; Jeong, W.; Im, J.; Yoon, Y. The Characteristics of Swirl Coaxial Injector under Varying Geometric and Environmental Conditions. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, FL, USA, 11–14 July 2004. [Google Scholar]
- Zhang, Z.; Liu, Y.; Hu, H. Effects of chamber pressure on the kinematic characteristics of spray flows exhausted from an airblast atomizer. Exp. Therm. Fluid Sci. 2022, 130, 110514. [Google Scholar]
- Zhang, L.; Wang, X.; Li, Y.; Yeh, S.T.; Yang, V. Supercritical fluid flow dynamics and mixing in gas-centered liquid-swirl coaxial injectors. Phys. Fluids 2018, 30, 075106. [Google Scholar] [CrossRef]
- Mayer, W.; Tamura, H. Propellant injection in a liquid oxygen/gaseous hydrogen rocket engine. J. Propul. Power 1996, 12, 1137–1147. [Google Scholar] [CrossRef]
- Kenny, R.J.; Hulka, J.R.; Moser, M.D.; Rhys, N.O. Effect of chamber backpressure on swirl injector fluid mechanics. J. Propul. Power 2009, 25, 902–913. [Google Scholar]
- Cho, S.; Park, G.; Chung, Y.; Yoon, Y.; Bazarov, V.G. Surface instability on cryogenic swirl flow at sub-to supercritical conditions. J. Propul. Power 2014, 30, 1038–1046. [Google Scholar] [CrossRef]
- Chen, C.; He, X.; Liu, C.; Yang, Y.; Tang, Z. Experimental study on the flow field distribution characteristics of a gas–liquid swirl coaxial injector under ambient pressure. Aerosp. Sci. Technol. 2021, 114, 106757. [Google Scholar]
- Fu, Q.F.; Yang, L.J.; Qu, Y.Y. Measurement of annular liquid film thickness in an open-end swirl injector. Aerosp. Sci. Technol. 2011, 15, 117–124. [Google Scholar] [CrossRef]
- Bazarov, V.; Lee, E.; Lineberry, D.; Swanner, B.; Frederick, R. Pulsator Designs for Liquid Rocket Injector Research. In Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, OH, USA, 8–11 July 2007. [Google Scholar]
- Chung, Y.; Kim, H.; Jeong, S.; Yoon, Y. Dynamic characteristics of open-type swirl injector with varying geometry. J. Propul. Power 2016, 32, 583–591. [Google Scholar] [CrossRef]
- Kim, D.; Im, J.H.; Koh, H.; Yoon, Y. Effect of ambient gas density on spray characteristics of swirling liquid sheets. J. Propul. Power 2007, 23, 603–611. [Google Scholar] [CrossRef]
- Dombrowski, N.; Hooper, P.C. The effect of ambient density on drop formation in sprays. Chem. Eng. Sci. 1962, 17, 291–305. [Google Scholar] [CrossRef]
- Hagerty, W.W.; Shea, J.F. A study of the stability of plane fluid sheets. J. Appl. Fluid Mech. 1955, 22, 509–514. [Google Scholar] [CrossRef]
- Bazarov, V. Dynamics of Liquid Injectors; Mashinostroenie: Moscow, Russia, 1979; p. 35. [Google Scholar]
- Clark, C.J.; Dombrowski, N. Aerodynamic instability and disintegration of inviscid liquid sheets. Proc. R. Soc. Lond. A. Math. Phys. Sci. 1972, 329, 467–478. [Google Scholar]







| No. | Dt (mm) | Dk (mm) | Dc (mm) | Dg (mm) | Rs (mm) | Lg (mm) | n | A | (mm) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.8 | 4 | 3 | 2 | 0.5 | 10 | 2 | 20 | 13 |
| 2 | 0.8 | 4 | 3 | 2 | 0.5 | 15 | 2 | 20 | 8 |
| 3 | 0.8 | 4 | 3 | 2 | 0.5 | 20 | 2 | 20 | 3 |
| Type | Injector | (MPa) | Qg (L/min) | Pb (MPa) | f (Hz) |
|---|---|---|---|---|---|
| Test 1 | LS | 0.45 | – | 0.5 | 500 |
| Test 2 | LS | 0.65 | – | 1 | 100 |
| Test 3 | LS | 0.3 | – | 1 | 100 |
| Test 4 | LS | 0.45 | – | 1.5 | 500 |
| Test 5 | GCSC 2 | 0.25 | 15 | 0.1 | 200 |
| Exp 1 | GCSC 1 | 0.25 | 15 | 0.3, 0.6, 0.9 | 180–270 |
| Exp 2 | GCSC 2 | 0.25 | 15 | ||
| Exp 3 | GCSC 3 | 0.25 | 15 |
| Rt (mm) | Rk (mm) | Rc (mm) | Lc (mm) | ns | As |
|---|---|---|---|---|---|
| 1 | 3.2 | 1 | 10 | 2 | 2.2 |
| Source of Uncertainty | Component of Standard Uncertainty | |||
|---|---|---|---|---|
| Semibreadth of the Range () | ) | ) | ) | |
| Calibration rod | 0.001 mm | – | 0.0006 mm | |
| Environmental effect | – | – | – | 0 |
| Measurement repeatability | – | – | 0.017 mm | – |
| Combined uncertainty () | 0.017 mm | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Qiao, W.; Gao, Q.; Zhang, D.; Yang, L.; Fu, Q. Experimental Study on the Dynamic Characteristics of Gas-Centered Swirl Coaxial Injector under Varying Ambient Pressure. Aerospace 2023, 10, 257. https://doi.org/10.3390/aerospace10030257
Zhang X, Qiao W, Gao Q, Zhang D, Yang L, Fu Q. Experimental Study on the Dynamic Characteristics of Gas-Centered Swirl Coaxial Injector under Varying Ambient Pressure. Aerospace. 2023; 10(3):257. https://doi.org/10.3390/aerospace10030257
Chicago/Turabian StyleZhang, Xiaoguang, Wentong Qiao, Qixiang Gao, Dingwei Zhang, Lijun Yang, and Qingfei Fu. 2023. "Experimental Study on the Dynamic Characteristics of Gas-Centered Swirl Coaxial Injector under Varying Ambient Pressure" Aerospace 10, no. 3: 257. https://doi.org/10.3390/aerospace10030257
APA StyleZhang, X., Qiao, W., Gao, Q., Zhang, D., Yang, L., & Fu, Q. (2023). Experimental Study on the Dynamic Characteristics of Gas-Centered Swirl Coaxial Injector under Varying Ambient Pressure. Aerospace, 10(3), 257. https://doi.org/10.3390/aerospace10030257







