Human Body Shapes Anomaly Detection and Classification Using Persistent Homology
Abstract
:1. Introduction
- Extract information from human bodies with interpretation in terms of human anatomy;
- Detect scans anomalies;
- Identify and separate human point clouds by gender;
- Classify male and female morphotypes.
2. Methodology
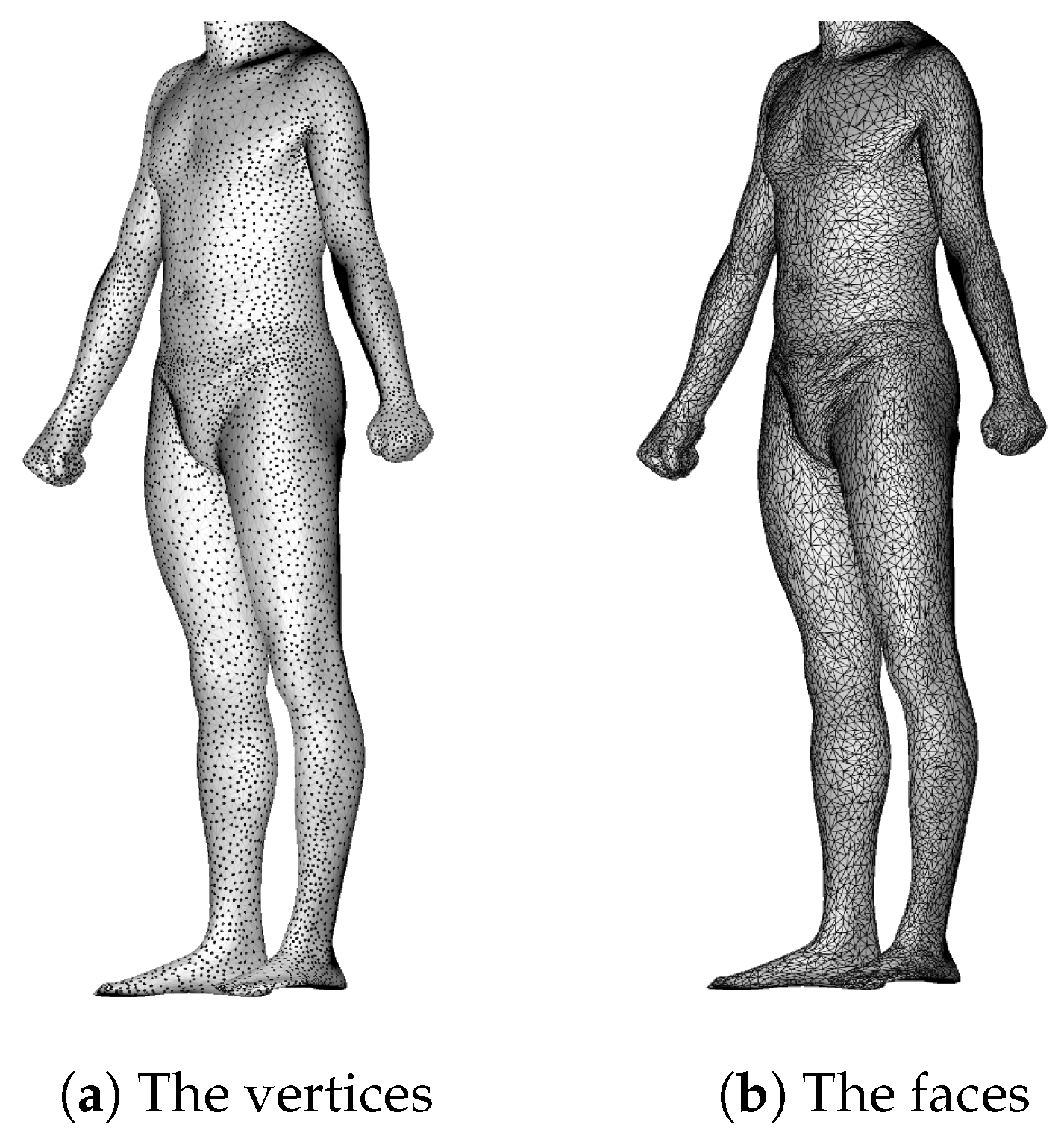
2.1. Dataset
2.2. Persistence Diagrams, Landscapes, Silhouettes and Distances
- : The connected components;
- : The non-homotopic loops;
- : The two-dimensional voids.
2.3. Interpretation of Persistent Homology
- Dimension 0: All homologies are born when the radius of the balls is zero. For each homology , we choose to display the second point of the pair covered at the birth of the homology as its representative.
- Dimension 1: First, we make an undirected graph containing all the points of a set, where each time a pair of points is covered, as the radius of the balls increases, we connect these points by an edge with a weight equal to the radius of the balls. At the birth of a homology , before adding the edge to our graph, we compute the shortest path connecting these two points, which we display by closing it with the segment connecting these points. The lace displayed is a likely representative of this homology. At the death of this homology, we recover the information of the triangle covered by the balls, and we add it to the display to give a general idea of the evolution of our homology.
- Dimension 2: For each homology , we simply display the triangle covered at its birth and the tetrahedron covered at its death.
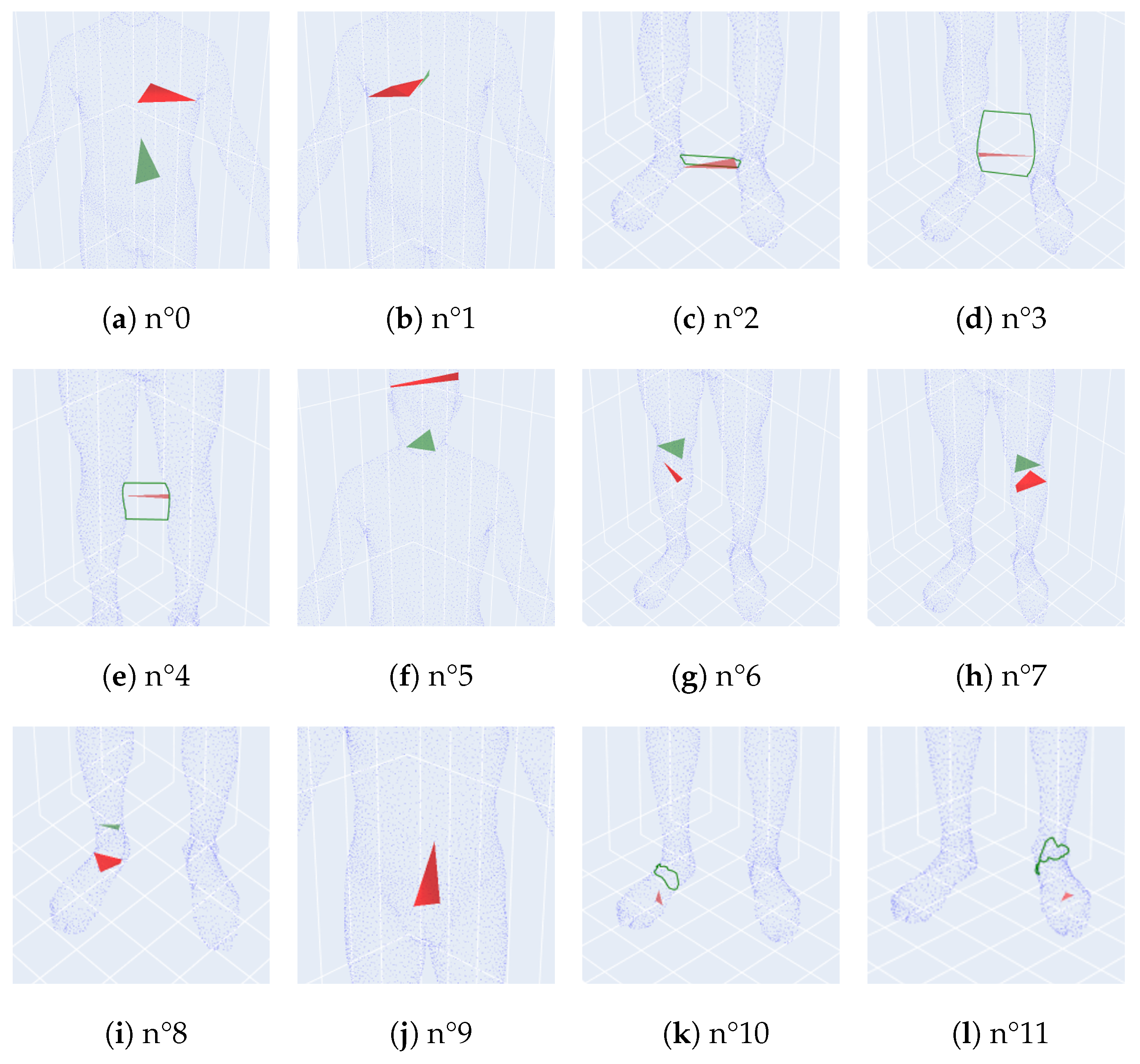
- n°0: corresponding to the left part of the torso,
- n°1: corresponding to the right part of the torso,
- n°2: corresponding to a loop between legs at foot level,
- n°3: corresponding to a loop between legs from ankles to calves,
- n°4: corresponding to a loop between legs from knees to calves,
- n°5: corresponding to the head,
- n°6: corresponding to the right calf,
- n°7: corresponding to the left calf,
- n°8: corresponding to the right foot,
- n°9: corresponding to the whole body,
- n°10: corresponding to a loop around the right foot,
- n°11: corresponding to a loop around the left foot,
- n°12: of all the connected balls.
2.4. Normalization of Point Clouds by Homothety
3. Anomaly Detection
4. Gender Discrimination Index
4.1. Evolution of the GDI Score as a Function of the Number of Clusters
4.2. Restriction to Trunks
5. Human Body Shapes Classification
5.1. Male Morphotypes
5.2. Female Morphotypes
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Simmons, K.; Istook, C.; Devarajan, P. Female Figure Identification Technique (FFIT) for apparel part I: Describing female shapes. J. Text. Appar. Technol. Manag. 2004, 4, 1–16. [Google Scholar]
- Song, H.K.; Ashdown, S. Categorization of lower body shapes for adult females based on multiple view analysis. Text. Res. J. 2011, 81, 914–931. [Google Scholar] [CrossRef]
- Nakamura, K.; Kurokawa, T. Analysis and classification of three-dimensional trunk shape of women by using the human body shape model. Int. J. Comput. Appl. Technol. 2009, 34, 278–284. [Google Scholar] [CrossRef] [Green Version]
- Cottle, F.S. Statistical Human Body Form Classification: Methodology Development and Application; Auburn University: Auburn, AL, USA, 2012. [Google Scholar]
- Hamad, M.; Thomassey, S.; Bruniaux, P. A new sizing system based on 3D morphology clustering. Comput. Ind. Eng. 2017, 113, 683–692. [Google Scholar] [CrossRef]
- Naveed, T.; Zhong, Y.; Hussain, A.; Babar, A.A.; Naeem, A.; Iqbal, A.; Saleemi, S. Female Body Shape Classifications and Their Significant Impact on Fabric Utilization. Fibers Polym. 2018, 19, 2642–2656. [Google Scholar] [CrossRef]
- Pei, J.; Park, H.; Ashdown, S.P. Female breast shape categorization based on analysis of CAESAR 3D body scan data. Text. Res. J. 2019, 89, 590–611. [Google Scholar] [CrossRef]
- Chazal, F.; Michel, B. An Introduction to Topological Data Analysis: Fundamental and Practical Aspects for Data Scientists. Front. Artif. Intell. 2021, 4, 667963. [Google Scholar] [CrossRef] [PubMed]
- Munch, E. A User’s Guide to Topological Data Analysis. J. Learn. Anal. 2017, 4, 47–61. [Google Scholar] [CrossRef] [Green Version]
- Edelsbrunner, H.; Letscher, D.; Zomorodian, A. Topological Persistence and Simplification. Discret. Comput. Geom. 2002, 28, 511–533. [Google Scholar] [CrossRef] [Green Version]
- Zomorodian, A.; Carlsson, G. Computing Persistent Homology. Discret. Comput. Geom. 2005, 33, 249–274. [Google Scholar] [CrossRef] [Green Version]
- Cohen-Steiner, D.; Edelsbrunner, H.; Harer, J. Stability of Persistence Diagrams. In Proceedings of the SCG ’05: Twenty-First Annual Symposium on Computational Geometry, Pisa, Italy, 6–8 June 2005; Association for Computing Machinery: New York, NY, USA, 2005; pp. 263–271. [Google Scholar] [CrossRef]
- Chazal, F.; Cohen-Steiner, D.; Glisse, M.; Guibas, L.J.; Oudot, S.Y. Proximity of Persistence Modules and Their Diagrams. In Proceedings of the SCG ’09: Twenty-Fifth Annual Symposium on Computational Geometry, Aarhus, Denmark, 8–10 June 2009; Association for Computing Machinery: New York, NY, USA, 2009; pp. 237–246. [Google Scholar] [CrossRef] [Green Version]
- Umeda, Y.; Kaneko, J.; Kikuchi, H. Topological data analysis and its application to time-series data analysis. Fujitsu Sci. Tech. J. 2019, 55, 65–71. [Google Scholar]
- Li, C.; Ovsjanikov, M.; Chazal, F. Persistence-Based Structural Recognition. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2003–2010. [Google Scholar] [CrossRef] [Green Version]
- Horak, D.; Maletić, S.; Rajković, M. Persistent homology of complex networks. J. Stat. Mech. Theory Exp. 2009, 2009, P03034. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Sun, J.; Huang, X.; Bowman, G.R.; Singh, G.; Lesnick, M.; Guibas, L.J.; Pande, V.S.; Carlsson, G. Topological methods for exploring low-density states in biomolecular folding pathways. J. Chem. Phys. 2009, 130, 144115. [Google Scholar] [CrossRef] [Green Version]
- Skaf, Y.; Laubenbacher, R. Topological data analysis in biomedicine: A review. J. Biomed. Inform. 2022, 130, 104082. [Google Scholar] [CrossRef]
- Corcoran, P.; Jones, C.B. Topological data analysis for geographical information science using persistent homology. Int. J. Geogr. Inf. Sci. 2023, 37, 712–745. [Google Scholar] [CrossRef]
- Ver Hoef, L.; Adams, H.; King, E.J.; Ebert-Uphoff, I. A Primer on Topological Data Analysis to Support Image Analysis Tasks in Environmental Science. Artif. Intell. Earth Syst. 2023, 2, e220039. [Google Scholar] [CrossRef]
- Mahmmod, B.M.; Abdulhussain, S.H.; Suk, T.; Hussain, A. Fast computation of Hahn polynomials for high order moments. IEEE Access 2022, 10, 48719–48732. [Google Scholar] [CrossRef]
- Jassim, W.A.; Raveendran, P.; Mukundan, R. New orthogonal polynomials for speech signal and image processing. IET Signal Process. 2012, 6, 713–723. [Google Scholar] [CrossRef]
- Abdulhussain, S.H.; Mahmmod, B.M.; Baker, T.; Al-Jumeily, D. Fast and accurate computation of high-order Tchebichef polynomials. Concurr. Comput. Pract. Exp. 2022, 34, e7311. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, Y.; Zhou, Y.; Du, S.; Davis, J.; Yang, R. Semantic Parametric Reshaping of Human Body Models. In Proceedings of the 2014 2nd International Conference on 3D Vision, Tokyo, Japan, 8–11 December 2014; Volume 2, pp. 41–48. [Google Scholar] [CrossRef]
- Chazal, F.; Fasy, B.T.; Lecci, F.; Rinaldo, A.; Wasserman, L. Stochastic Convergence of Persistence Landscapes and Silhouettes. In Proceedings of the SOCG’14: Thirtieth Annual Symposium on Computational Geometry, Kyoto, Japan, 8–11 June 2014; Association for Computing Machinery: New York, NY, USA, 2014; pp. 474–483. [Google Scholar] [CrossRef] [Green Version]
- Bubenik, P. Statistical Topological Data Analysis Using Persistence Landscapes. J. Mach. Learn. Res. 2015, 16, 77–102. [Google Scholar]
- Ward, J.H.W., Jr. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Partitioning around Medoids (Program PAM). In Finding Groups in Data; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1990. [Google Scholar] [CrossRef]
- Mileyko, Y.; Mukherjee, S.; Harer, J. Probability measures on the space of persistence diagrams. Inverse Probl. 2011, 27, 124007. [Google Scholar] [CrossRef] [Green Version]
- Turner, K.; Mileyko, Y.; Mukherjee, S.; Harer, J. Frechet Means for Distributions of Persistence Diagrams. Discret. Comput. Geom. 2014, 52, 44–70. [Google Scholar] [CrossRef] [Green Version]
- Lance, G.N.; Williams, W.T. A general theory of classificatory sorting strategies: II. Clustering systems. Comput. J. 1967, 10, 271–277. [Google Scholar] [CrossRef] [Green Version]
- Davies, D.L.; Bouldin, D.W. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Dunn, J.C. A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]




















| Complete | Ward | K-Medoids | |
|---|---|---|---|
| Body | 0.2 | 0.54 | 0.526 |
| Trunk | 0.21 | 0.553 | 0.582 |
| Ward | K-Means | K-Medoids | |
|---|---|---|---|
| Body | 0.738 | 0.73 | 0.737 |
| Trunk | 0.765 | 0.767 | 0.827 |
| Cluster | ||||||||
|---|---|---|---|---|---|---|---|---|
| Size | 2 | 4 | 50 | 311 | 125 | 273 | 415 | 332 |
| Proportion (in percent) | 0.1 | 0.3 | 3 | 21 | 8 | 18 | 27 | 22 |
| Mean distance | 79.6 | 39.4 | 28.6 | 17.4 | 20.3 | 16.3 | 18.9 | 19.4 |
| Diameter | 79.6 | 53.9 | 62 | 49.6 | 59.2 | 54.6 | 67.1 | 69.4 |
| Distance to the mean | 39.8 | 24.4 | 19.6 | 12.1 | 14.2 | 11.5 | 13.1 | 13.6 |
| Distance mean–medoid | 39.8 | 20.1 | 9 | 3.4 | 5.9 | 6.9 | 5.1 | 6.1 |
| Clusters | |||||||
|---|---|---|---|---|---|---|---|
| Size | 306 | 263 | 403 | 107 | 122 | 112 | 214 |
| Proportion (in percent) | 20 | 17 | 27 | 7 | 8 | 7 | 14 |
| Mean distance | 14.2 | 12.7 | 14.1 | 14.3 | 14 | 19 | 21.3 |
| Diameter | 36.6 | 32 | 32.1 | 31.9 | 38.2 | 59.3 | 62.4 |
| Distance to the mean | 10.1 | 9 | 10.1 | 10.1 | 9.9 | 13.3 | 14.8 |
| Distance mean–medoid | 3.4 | 3.4 | 4.5 | 3.3 | 3.6 | 5.9 | 5.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Rose, S.; Meyer, P.; Bertrand, F. Human Body Shapes Anomaly Detection and Classification Using Persistent Homology. Algorithms 2023, 16, 161. https://doi.org/10.3390/a16030161
de Rose S, Meyer P, Bertrand F. Human Body Shapes Anomaly Detection and Classification Using Persistent Homology. Algorithms. 2023; 16(3):161. https://doi.org/10.3390/a16030161
Chicago/Turabian Stylede Rose, Steve, Philippe Meyer, and Frédéric Bertrand. 2023. "Human Body Shapes Anomaly Detection and Classification Using Persistent Homology" Algorithms 16, no. 3: 161. https://doi.org/10.3390/a16030161
APA Stylede Rose, S., Meyer, P., & Bertrand, F. (2023). Human Body Shapes Anomaly Detection and Classification Using Persistent Homology. Algorithms, 16(3), 161. https://doi.org/10.3390/a16030161









