The Markets of Green Cars of Three Countries: Analysis Using Lotka–Volterra and Bertalanffy–Pütter Models
Abstract
1. Introduction
1.1. Background
1.2. The Diesel Scandal and the Problem of the Paper
2. Methods
2.1. Outline of the Approach
2.2. Data
2.3. BP Model
2.4. Other Growth Models
2.5. Sales and Market Shares
2.6. LV Model
2.7. Calibration
2.8. Data Fitting
2.9. Model Uncertainty
2.10. Simulation
3. Results
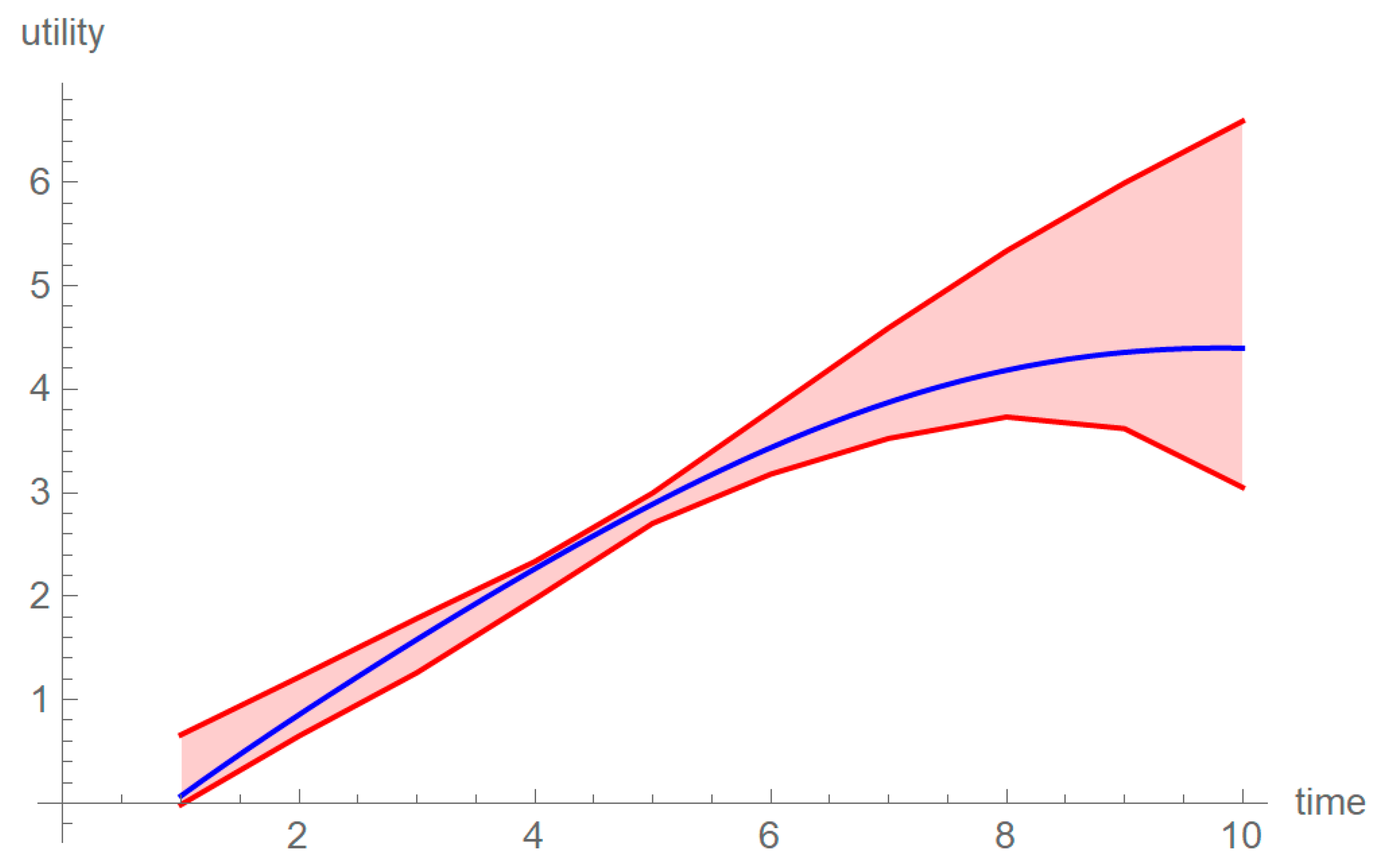
3.1. Graphical Review of Methodology
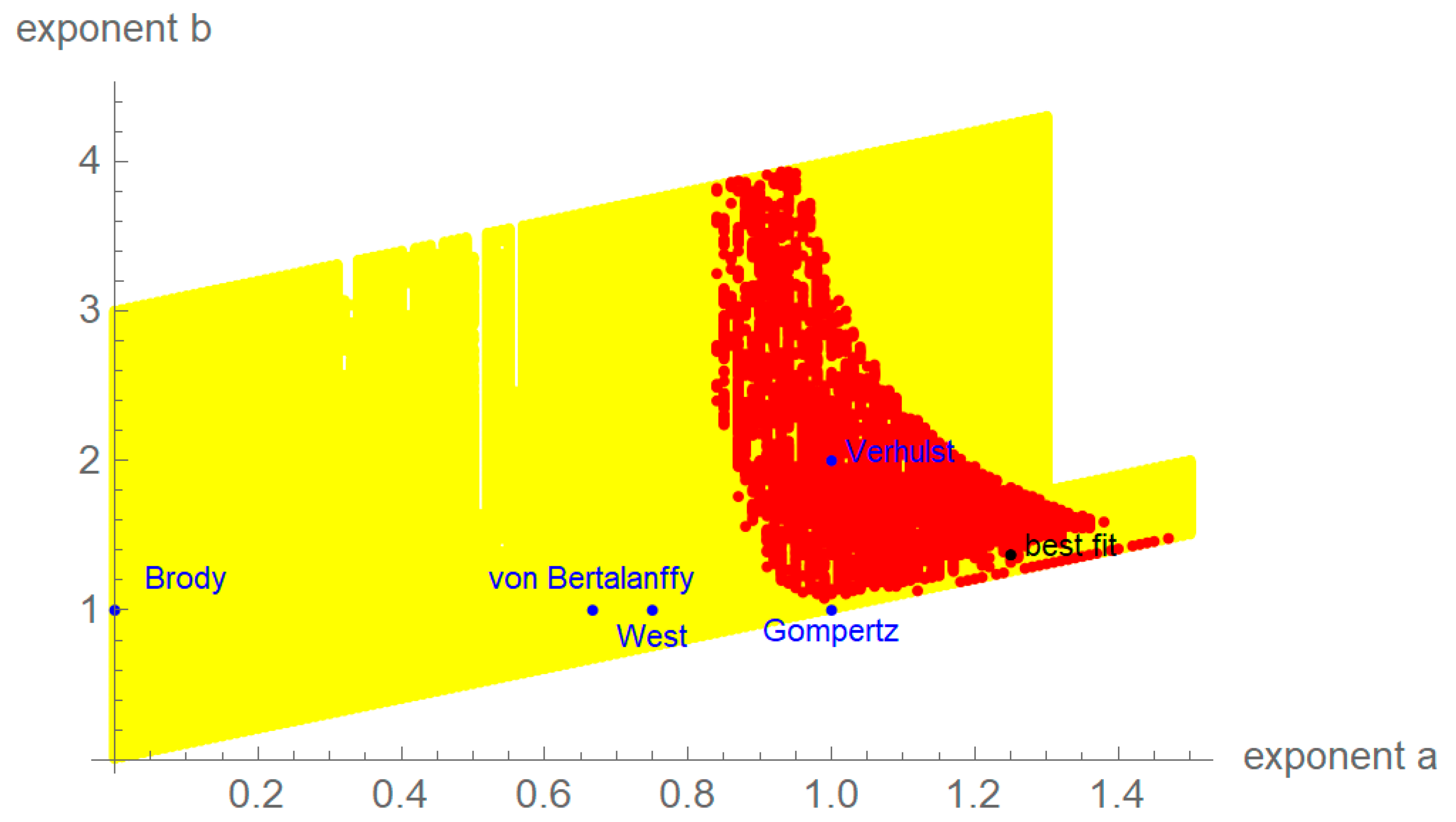
3.2. Best-Fit Exponent Pairs
3.3. Exponent Pairs Leading to Reasonable Fits
3.4. Market Dynamics
3.5. Did the Diesel Scandal Change the Market Dynamics?
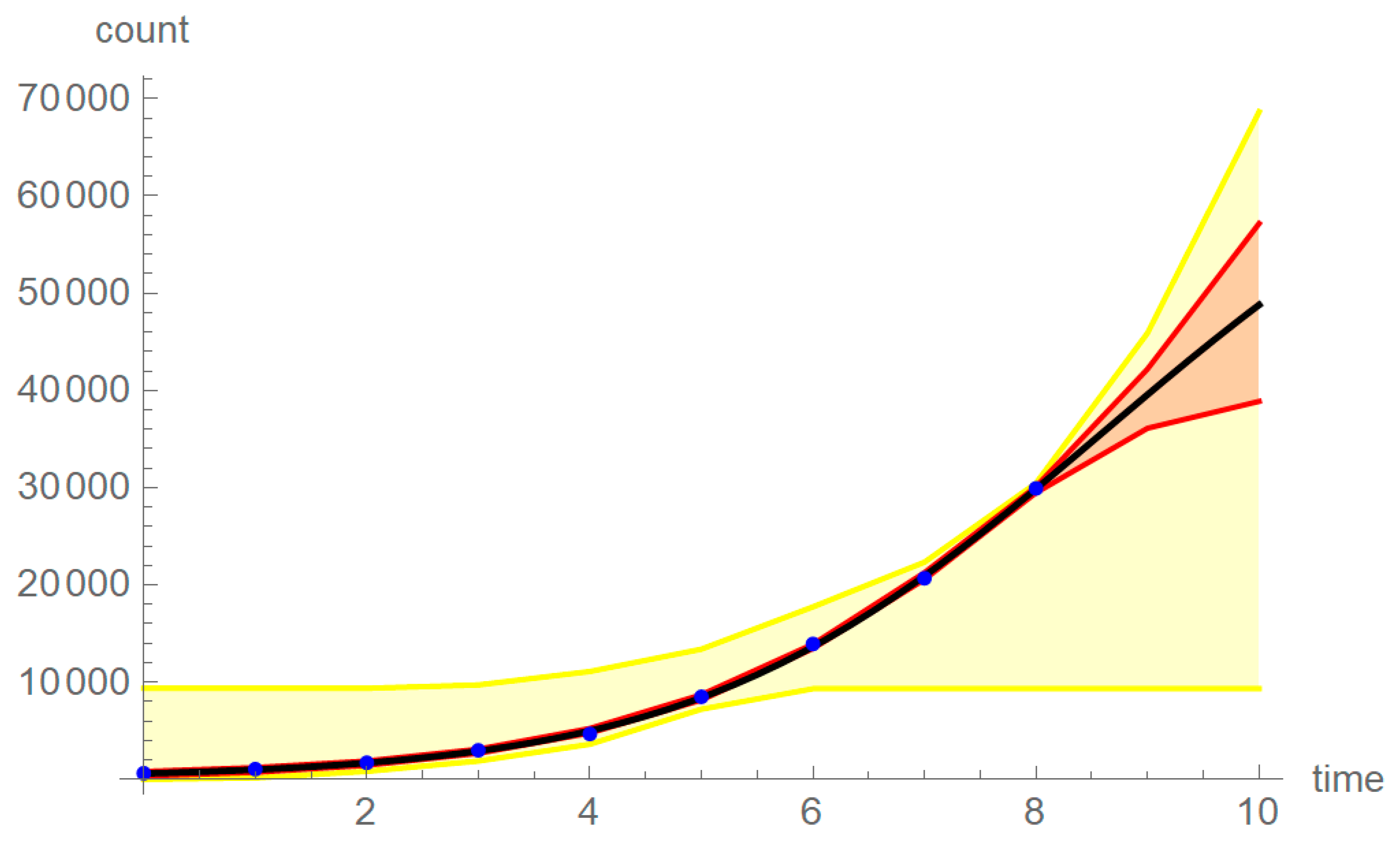
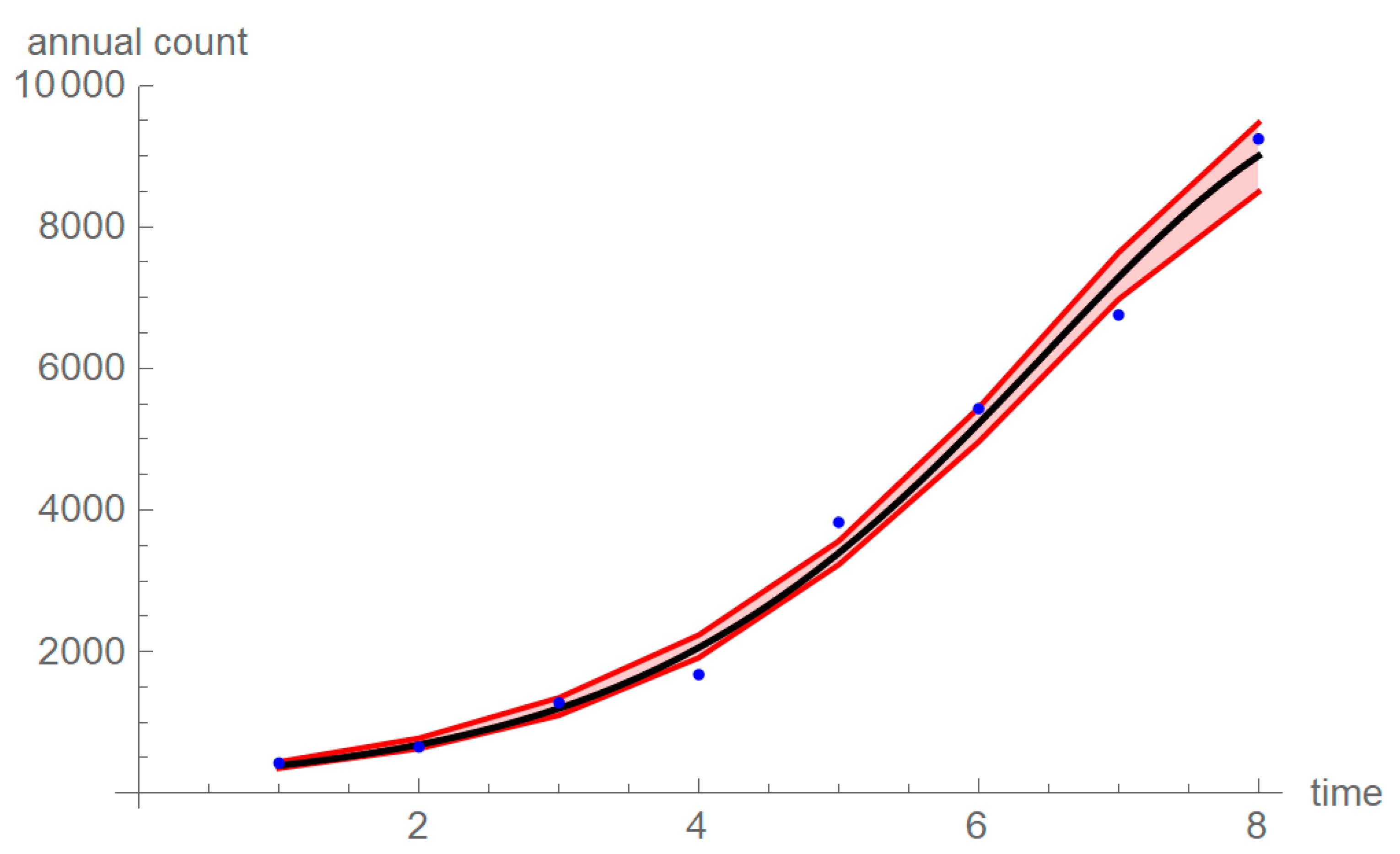
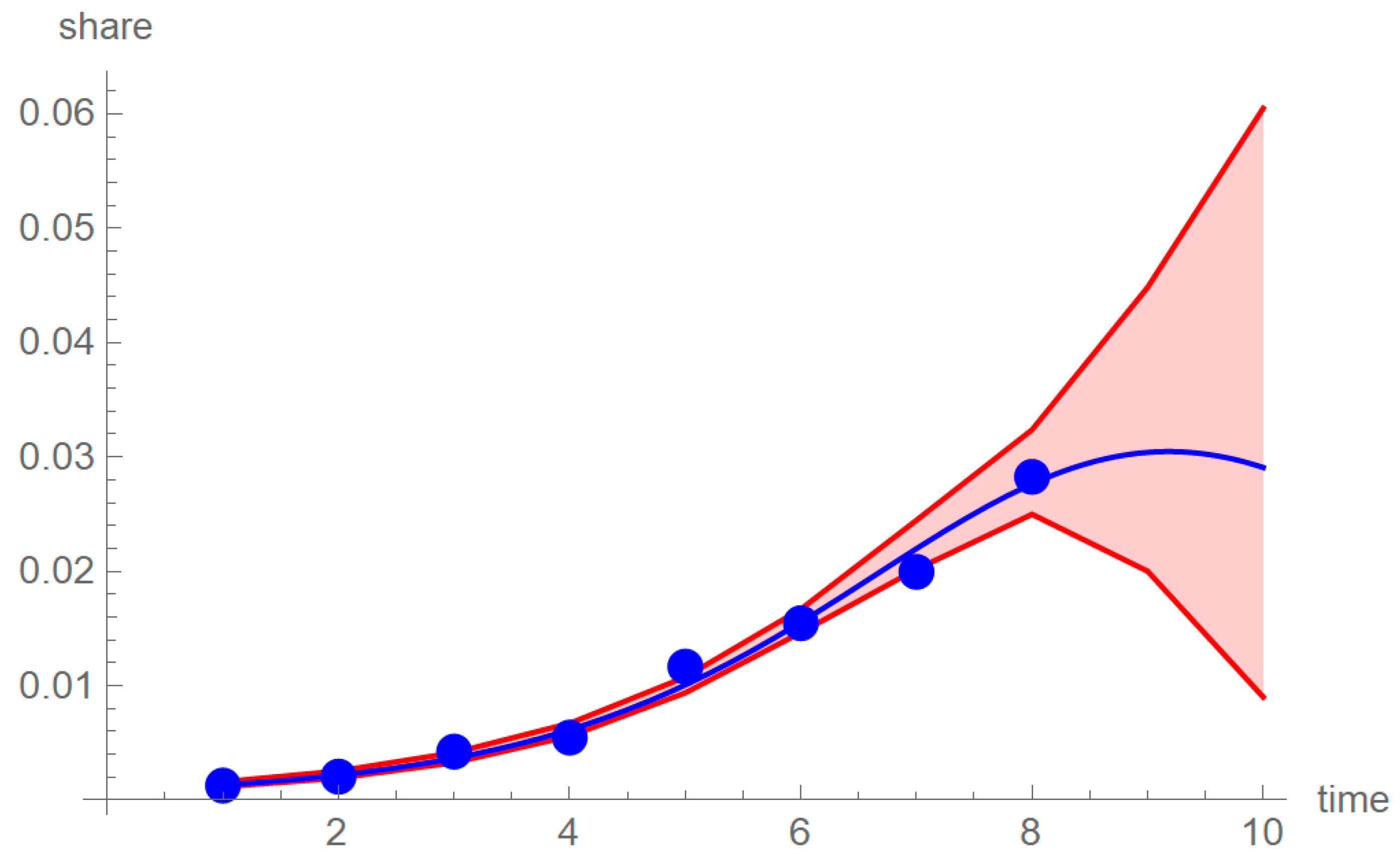
3.6. Forecasts
3.7. Alternative Methodological Approaches
4. Discussion: Outlook on the Open Innovation in the Automotive Industry
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pathak, K.S.; Sood, V.; Singh, Y.; Channiwala, S.A. Real world vehicle emissions: Their correlation with driving parameters. Transp. Res. Part D 2016, 44, 157–176. [Google Scholar] [CrossRef]
- Jonson, J.E.; Borken-Kleefeld, J.; Simpson, D.; Nyiri, A.; Posch, M.; Heyes, C. Impact of excess NOx emissions from diesel cars on air quality, public health and eutrophication in Europe. Environ. Res. Lett. 2017, 12. [Google Scholar] [CrossRef]
- Moshammer, H.; Poteser, M.; Kundi, M.; Lemmerer, K.; Weitensfelder, L.; Wallner, P.; Hutter, H.-P. Nitrogen-dioxide remains a valid air quality indicator. Int. J. Environ. Res. Public Health 2020, 17, 3733. [Google Scholar] [CrossRef] [PubMed]
- Jansson, J.; Pettersson, T.; Mannberg, A.; Brännlund, R.; Lindgren, U. Adoption of alternative fuel vehicles: Influence from neighbors, family, and coworkers. Transp. Res. Part D 2017, 54, 61–73. [Google Scholar] [CrossRef]
- Sun, S.; Wang, W. Analysis on the market evolution of new energy vehicle based on population competition model. Transp. Res. Part D 2018, 65, 36–50. [Google Scholar] [CrossRef]
- Meyer, G.; Müller, B.; Briec, E.; Mazal, C. European Roadmap Electrification of Road Transport. 2012. Available online: https://www.researchgate.net/publication/322625576 (accessed on 10 June 2020).
- Meyer, G.; Bucknall, R.; Breuil, D. Electrification of the Transport System; European Commission: Brussels, Belgium, 2017. [Google Scholar]
- Johnson, K.G.E.; Mollenhauer, K.; Tschöke, H. Handbook of Diesel Engines; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Davenport, C.; Hakim, D. U.S. Sues Volkswagen for Cheating on Emissions Tests. 2016. Available online: https://www.nytimes.com/2016/01/05/business/vw-sued-justice-department-emissions-scandal.html (accessed on 10 June 2020).
- Mansouri, N. A case study of volkswagen unethical practice in diesel emission test. Int. J. Sci. Eng. Appl. 2016, 5, 211–216. [Google Scholar] [CrossRef]
- Hayes, R.E.; Mukadi, L.S.; Votsmeier, M.; Gieshoff, J. Three-way catalytic converter modelling with detailed kinetics and washcoat diffusion. Top. Catal. 2004, 30, 411–415. [Google Scholar] [CrossRef]
- Strittmatter, A.; Lechner, M. Sorting on the used-car market after the Volkswagen emission scandal. J. Environ. Econ. Manag. 2020, 101, 1–41. [Google Scholar] [CrossRef]
- An, Q.; Christensen, M.G.; Ramachandran, A.; Mukkamala, R.R.; Vatrapu, R. Volkswagen’s diesel emission scandal: Analysis of Facebook engagement and financial outcomes. In Proceedings of the Big Data, 7th International Congress, Held as Part of the Services Conference Federation, Seattle, WA, USA, 25–30 June 2018; pp. 260–276. [Google Scholar] [CrossRef]
- Jung, J.C.; Sharon, E. The Volkswagen emissions scandal and its aftermath. Glob. Bus. Organ. Excell. 2019, 38, 6–15. [Google Scholar] [CrossRef]
- Santana, J.C.C.; Miranda, A.C.; Yamamura, C.L.K.; Silva Filho, S.C.; Tambourgi, E.B.; Lee Ho, L.; Berssaneti, F.T. Effects of air pollution on human health and costs: Current situation in São Paulo, Brazil. Sustainability 2020, 12, 4875. [Google Scholar] [CrossRef]
- Johnson, E. Cars and ground-level ozone: How do fuels compare? Eur. Transp. Res. Rev. 2017, 9, 47. [Google Scholar] [CrossRef]
- Brondz, I. To be or not to be …? Part III: Diesel versus electrically powered cars. Voice Publ. 2018, 4, 33–50. [Google Scholar] [CrossRef][Green Version]
- Sullivan, J.L.; Baker, R.E.; Boyer, B.A.; Hammerle, R.H.; Kenney, T.E.; Muniz, L.; Wallington, T.J. CO2 emission benefit of diesel (Versus Gasoline) powered vehicles. Environ. Sci. Technol. 2004, 38, 3217–3223. [Google Scholar] [CrossRef] [PubMed]
- Andersen, O.; Upham, P.; Aall, C. Technological response options after the VW diesel scandal: Implications for engine CO2 emissions. Sustainability 2018, 10, 2313. [Google Scholar] [CrossRef]
- ACEA. The Automobile Industry Pocket Guide, Brussels. 2016. Available online: www.acea.be/uploads/press_releases_files/POCKET_GUIDE_2015-2016.pdf (accessed on 12 June 2020).
- Stanwick, P.; Stanwick, S. Volkswagen emissions scandal: The perils of installing illegal software. Int. Rev. Manag. Bus. Res. 2017, 6, 18–24. [Google Scholar]
- Fu, X.; Zhang, P.; Zhang, J. Forecasting and analyzing internet users of China with Lotka-Volterra model. Asia-Pac. J. Oper. Res. 2017, 34. [Google Scholar] [CrossRef]
- Nguimkeu, P. A simple selection test between the gompertz and logistic growth models. Technol. Forecast. Soc. Chang. 2014, 88, 98–105. [Google Scholar] [CrossRef]
- Pütter, A. Studien über physiologische ähnlichkeit. VI. Wachstumsähnlichkeiten. Pflügers Arch. Für Die Gesamte Physiol. Des Menschen Und Der Tiere 1920, 180, 298–340. [Google Scholar] [CrossRef]
- Statistik Austria. Statistiken: Kraftfahrzeuge Neuzulassungen. 2020. Available online: www.statistik.at (accessed on 4 June 2020).
- Bundesamt, K. Statistik: Neuzulassungsbarometer. 2020. Available online: www.kba.de (accessed on 4 June 2020).
- STAT-TAB. Neue Inverkehrsetzungen von Strassenfahrzeugen nach Fahrzeuggruppe, Fahrzeugart. 2020. Available online: www.pxweb.bfs.admin.ch (accessed on 4 June 2020).
- Sheperd, S.P. A review of system dynamics models applied in transportation. Transp. B 2014, 2, 83–105. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. Ieee Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Ohnishi, S.; Yamakawa, T.; Akamine, T. On the analytical solution for the pütter-bertalanffy growth equation. J. Theor. Biol. 2014, 343, 174–177. [Google Scholar] [CrossRef] [PubMed]
- Bass, F.M. A new product growth model for consumer durables. Manag. Sci. 1969, 15, 215–227. [Google Scholar] [CrossRef]
- Decock, K.; Debackere, K.; van Looy, B. Bass re-visited: Quantifying multi-finality. Preprint 2020. [Google Scholar] [CrossRef]
- Brunner, N.; Kühleitner, M.; Nowak, W.G.; Renner-Martin, K.; Scheicher, K. Comparing growth patterns of three species: Similarities and differences. PLoS ONE 2019, 14, e0224168. [Google Scholar] [CrossRef]
- Adamuthe, A.C.; Thampi, G.K. Technology forecasting: A case study of computational technologies. Technol. Forecast. Soc. Chang. 2019, 143, 181–189. [Google Scholar] [CrossRef]
- Dhakal, T. An analytical model on business diffusion. J. Ind. Eng. Manag. Sci. 2018, 2018, 119–128. [Google Scholar] [CrossRef][Green Version]
- Ma, L.; Wu, M.; Tian, X.; Zheng, G.; Du, Q.; Wu, T. China’s provincial vehicle ownership forecast and analysis of the causes influencing the trend. Sustainability 2019, 11, 3928. [Google Scholar] [CrossRef]
- Nagula, M. Forecasting of fuel cell technology in hybrid and electric vehicles using Gompertz growth curve. J. Stat. Manag. Syst. 2016, 19, 73–88. [Google Scholar] [CrossRef]
- Chatzikomis, C.I.; Spentzas, K.N.; Mamalis, A.G. Environmental and economic effects of widespread introduction of electric vehicles in Greece. Eur. Transp. Res. Rev. 2014, 6, 365–376. [Google Scholar] [CrossRef]
- Verhulst, P.F. Notice sur la loi que la population suit dans son accroissement. Curr. Math. Phys. 1838, 10, 113–121. [Google Scholar]
- Brody, S. Bioenergetics and Growth; Hafner Publishing Company: New York, NY, USA, 1945. [Google Scholar]
- Bertalanffy, L.V. Untersuchungen über die Gesetzlichkeit des Wachstums. I. Allgemeine grundlagen der theorie; mathematische und physiologische gesetzlichkeiten des wachstums bei wassertieren. Arch. Für Entwickl. 1934, 131, 613–652. [Google Scholar] [CrossRef]
- Bertalanffy, L.V. Quantitative laws in metabolism and growth. Q. Rev. Biol. 1957, 32, 217–231. [Google Scholar] [CrossRef] [PubMed]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for ontogenetic growth. Nature 2001, 413, 628–631. [Google Scholar] [CrossRef] [PubMed]
- Richards, F.J. A flexible growth function for empirical use. J. Exp. Bot. 1959, 10, 290–300. [Google Scholar] [CrossRef]
- Gompertz, B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos. Trans. R. Soc. Lond. 1832, 123, 513–585. [Google Scholar]
- Marusic, M.; Bajzer, Z. Generalized two-parameter equations of growth. J. Math. Anal. Appl. 1993, 179, 446–462. [Google Scholar] [CrossRef]
- Lotka, A.J. Analytical Theory of Biological Populations; Translation of 1934 and 1939 Publications; Plenum Press: New York, NY, USA, 1988. [Google Scholar]
- Volterra, V. Variazioni e fluttuazioni del numerod’ individui in specie animali conviventi. Mem. Della R. Accad. Dei Lincei 1926, 6, 31–113. [Google Scholar]
- Smale, S. On the differential equations of species in competition. J. Math. Biol. 1976, 3, 5–7. [Google Scholar] [CrossRef]
- Modis, T. Genetic re-engineering of corporations. Technol. Forecast. Soc. Chang. 1997, 56, 107–118. [Google Scholar] [CrossRef]
- Modis, T. Technological forecasting at the stock market. Technol. Forecast. Soc. Chang. 1999, 62, 173–202. [Google Scholar] [CrossRef]
- Marasco, A.; Picucci, A.; Romano, A. Market share dynamics using Lotka-Volterra models. Technol. Forecast. Soc. Chang. 2016, 105, 49–62. [Google Scholar] [CrossRef]
- Romano, A. Turning the coin: A competition model to evaluate mergers. J. Res. Ind. Organ. 2013, 443935. [Google Scholar] [CrossRef]
- Nevo, A.; Rossi, F. An approach for extending dynamic models to settings with multi-product firms. Econ. Lett. 2008, 100, 49–52. [Google Scholar] [CrossRef]
- Romano, A. A study of tourism dynamics in three italian regions using a nonautonomous integrable lotka–volterra model. PLoS ONE 2016, 11. [Google Scholar] [CrossRef]
- Marasco, A.; Romano, A. Inter-port interactions in the le Havre-Hamburg range: A scenario analysis using a nonautonomous Lotka Volterra model. J. Transp. Geogr. 2018, 69, 207–220. [Google Scholar] [CrossRef]
- Lorenčič, V.; Twrdy, E.; Batista, M. Development of competitive-cooperative relationships among mediterranean cruise ports since 2000. J. Mar. Sci. Eng. 2020, 8, 374. [Google Scholar] [CrossRef]
- Zhang, G.; McAdams, D.A.; Shankar, V.; Darani, M. M Modeling the evolution of system technology performance when component and system technology performances interact: Commensalism and amensalism. Technol. Forecast. Soc. Chang. 2017, 125, 116–124. [Google Scholar] [CrossRef]
- Loibel, S.; Andrade, M.G.; do Val, J.B.R.; de Freitas, A.R. Richards growth model and viability indicators for populations subject to interventions. An. Acad. Bras. Ciências 2010, 82. [Google Scholar] [CrossRef]
- Vidal, R.V.V. Applied simulated annealing. In Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Renner-Martin, K.; Brunner, N.; Kühleitner, M.; Nowak, W.G.; Scheicher, K. Best-fitting growth curves of the von bertalanffy-pütter type. Poult. Sci. 2019, 98, 3587–3592. [Google Scholar]
- Burnham, K.P.; Anderson, D.R. Multi-model inference. Understanding AIC and BIC in model selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Berg, H.A.V.D. Inceptions of biomathematics from Lotka to Thom. Sci. Prog. 2017, 100, 45–62. [Google Scholar] [CrossRef]
- Bühne, J.; Gruschwitz, D.; Hölscher, J.; Klötzke, M.; Kugler, U.; Schimecek, C. How to promote electromobility for European car drivers? Obstacles to overcome for a broad market penetration. Eur. Transp. Res. Rev. 2015, 7. [Google Scholar] [CrossRef]
- Langbroek, J.H.M.; Franklin, J.P.; Susilo, Y.O. The effect of policy incentives on electric vehicle adoption. Energy Policy 2016, 94, 94–103. [Google Scholar] [CrossRef]
- Letmathe, P.; Suares, M. Understanding the impact that potential driving bans on conventional vehicles and the total cost of ownership have on electric vehicle choice in Germany. Sustain. Futures 2020, 2, 100018. [Google Scholar] [CrossRef]
- Brand, C. Beyond ‘dieselgate’: Implications of unaccounted and future air pollutant emissions and energy use for cars in the United Kingdom. Energy Policy 2016, 97, 1–12. [Google Scholar] [CrossRef]
- Horgan, D.C. Modelling market share in the UK grocery retail sector using the nonautonomous lotka-volterra equations. Preprint 2020. [Google Scholar] [CrossRef]
- Pham, V.V.; Cao, D.T. A brief review of technology solutions on fuel injection system of Diesel engine to increase the power and reduce environmental pollution. J. Mech. Eng. Res. Dev. 2019, 42, 1–9. [Google Scholar]
- Hirota, K.; Kashima, S. How are automobile fuel quality standards guaranteed? Evidence from indonesia, malaysia and vietnam. Transp. Res. Interdiscip. Perspect. 2020, 4. [Google Scholar] [CrossRef]
- Yun, J.J.; Jeon, J.; Park, K.; Zhao, X. Benefits and costs of closed innovation strategy: Analysis of Samsung’s galaxy note 7 explosion and withdrawal scandal. J. Open Innov Technol. Mark. Complex. 2018, 4, 20. [Google Scholar] [CrossRef]
- Chiaroni, D.; Chiesa, V.; Frattini, F. Unravelling the process from closed to open innovation: Evidence from mature, asset-intensive industries. RD Manag. 2010, 40, 222–245. [Google Scholar] [CrossRef]
- Yun, J.J.; Jeong, E.; Zhao, X.; Hahm, S.D.; Kim, K. Collective intelligence: An emerging world in open innovation. Sustainability 2019, 11, 4495. [Google Scholar] [CrossRef]
- Yun, J.J.; Zhao, X.; Jung, K.; Yigitcanlar, T. The culture for open innovation dynamics. Sustainability 2020, 12, 76. [Google Scholar] [CrossRef]
- Yun, J.J.; Lee, M.; Park, K.; Zhao, X. Open innovation and serial entrepreneurs. Sustainability 2019, 11, 55. [Google Scholar] [CrossRef]
- Kim, J.; Chun, M.S.; Nhung, D.T.H.; Lee, J. The transition of samsung electronics through its M&A with harman international. J. Open Innov. Technol. Mark. Complex. 2019, 5, 51. [Google Scholar] [CrossRef]
- Kodama, F. Incessant conceptual/industrial transformation of automobiles. J. Open Innov. Technol. Mark. Complex. 2019, 5, 50. [Google Scholar] [CrossRef]
- Hysa, E.; Kruja, A.; Rehman, N.U.; Laurenti, R. Circular economy innovation and environmental sustainability impact on economic growth: An integrated model for sustainable development. Sustainability 2020, 12, 4831. [Google Scholar] [CrossRef]
- Misran, M.F.R.; Roslin, E.N.; Mohd Nur, N. AHP-consensus judgement on transitional decision-making: With a discussion on the relation towards open innovation. J. Open Innov. Technol. Mark. Complex. 2020, 6, 63. [Google Scholar] [CrossRef]
| Year | Hybrid | Electric | Liquid Gas | Natural Gas | Petrol | Diesel | |
|---|---|---|---|---|---|---|---|
| Austria | 2011 | 1310 | 631 | - | 262 | 159,027 | 194,721 |
| 2012 | 2171 | 427 | - | 274 | 143,325 | 189,622 | |
| 2013 | 2573 | 654 | - | 455 | 134,276 | 180,901 | |
| 2014 | 1823 | 1281 | - | 279 | 126,503 | 172,381 | |
| 2015 | 2241 | 1677 | - | 167 | 122,832 | 179,822 | |
| 2016 | 3324 | 3826 | - | 119 | 131,756 | 188,820 | |
| 2017 | 6483 | 5433 | - | 114 | 163,701 | 175,458 | |
| 2018 | 7473 | 6757 | - | 110 | 184,150 | 140,111 | |
| 2019 | 14,304 | 9242 | - | 421 | 176,706 | 126,311 | |
| Germany | 2012 | 21,438 | 2956 | 11,465 | 5215 | 1,555,241 | 1,486,119 |
| 2013 | 24,963 | 6051 | 6255 | 7835 | 1,502,784 | 1,403,113 | |
| 2014 | 22,908 | 8522 | 6234 | 8194 | 1,533,726 | 1,452,565 | |
| 2015 | 22,529 | 12,363 | 4716 | 5285 | 1,611,389 | 1,538,451 | |
| 2016 | 47,996 | 11,410 | 2990 | 3240 | 1,746,308 | 1,539,596 | |
| 2017 | 55,239 | 25,056 | 4400 | 3723 | 1,986,488 | 1,336,776 | |
| 2018 | 98,816 | 36,062 | 4663 | 10,804 | 2,142,700 | 1,111,130 | |
| 2019 | 175,969 | 63,281 | 7256 | 7623 | 2,136,891 | 1,152,733 | |
| Switzerland | 2005 | - | 13 | - | 442 | 185,120 | 74,114 |
| 2006 | 1272 | 9 | - | 1064 | 185,807 | 80,857 | |
| 2007 | 3220 | 19 | - | 1653 | 185,055 | 92,333 | |
| 2008 | 3092 | 24 | - | 1136 | 189,151 | 93,366 | |
| 2009 | 3900 | 57 | - | 1063 | 182,174 | 78,755 | |
| 2010 | 4250 | 201 | - | 721 | 200,576 | 90,547 | |
| 2011 | 5462 | 452 | - | 651 | 211,540 | 109,324 | |
| 2012 | 6708 | 924 | - | 519 | 200,576 | 124,911 | |
| 2013 | 7158 | 1392 | - | 791 | 185,070 | 115,656 | |
| 2014 | 6893 | 1948 | - | 1041 | 180,875 | 113,304 | |
| 2015 | 8785 | 3882 | - | 1080 | 185,469 | 127,899 | |
| 2016 | 10,587 | 3525 | - | 944 | 178,666 | 125,595 | |
| 2017 | 11,846 | 4929 | - | 769 | 183,637 | 113,848 | |
| 2018 | 15,432 | 5411 | - | 805 | 188,847 | 90,360 | |
| 2019 | 26,376 | 13,197 | - | 1252 | 192,430 | 79,618 |
| Country | Typeof Car | Best-Fit Parameter of the BP Model | Goodness of Fit | Data Characteristics | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | p | q | SSE | R2 (%) | NRMSE (%) | Count n | Grid Size | Mean | |||
| Austria | AT | Petrol | 0.27 | 0.60 | 1.83 × 105 | 3.90 × 103 | 3.21 × 10−1 | 2.22 × 109 | 99.82 | 2.19 | 9 | 3.94 × 104 | 7.17 × 105 |
| Diesel | 0.11 | 3.02 | 2.01 × 105 | 4.41 × 104 | 1.79 × 10−14 | 4.62 × 108 | 99.97 | 0.79 | 9 | 3.94 × 104 | 9.06 × 105 | ||
| Electric | 1.25 | 1.37 | 6.04 × 102 | 2.27 × 10−1 | 5.89 × 10−2 | 2.60 × 105 | 99.97 | 1.82 | 9 | 3.99 × 104 | 9.34 × 103 | ||
| Nat. Gas | 0.00 | 0.23 | 2.50 × 102 | 9.73 × 102 | 1.45 × 102 | 7.15 × 104 | 97.63 | 6.85 | 9 | 3.94 × 104 | 1.30 × 103 | ||
| Hybrid | 1.12 | 1.13 | 2.85 × 103 | 1.70 × 10−1 | 5.47 × 10−2 | 5.01 × 106 | 99.63 | 5.11 | 9 | 3.96 × 104 | 1.46 × 104 | ||
| Switzerland | CH | Petrol | 0.19 | 0.76 | 1.87 × 105 | 1.86 × 104 | 1.70 × 100 | 1.09 × 109 | 99.99 | 0.56 | 15 | 3.94 × 104 | 1.51 × 106 |
| Diesel | 0.35 | 3.30 | 9.15 × 104 | 1.09 × 103 | 2.78 × 10−16 | 1.63 × 109 | 99.95 | 1.35 | 15 | 4.46 × 104 | 7.70 × 105 | ||
| Electric | 0.88 | 0.89 | 2.23 × 101 | 2.10 × 100 | 8.11 × 10−1 | 7.04 × 106 | 99.56 | 9.45 | 15 | 3.92 × 104 | 7.25 × 103 | ||
| Nat. Gas | 0.00 | 0.17 | 6.63 × 102 | 1.84 × 103 | 2.08 × 102 | 1.36 × 106 | 99.41 | 4.05 | 15 | 3.94 × 104 | 7.45 × 103 | ||
| Hybrid | 0.80 | 0.81 | 4.47 × 103 | 3.12 × 100 | 1.14 × 100 | 6.94 × 107 | 99.55 | 5.61 | 14 | 3.94 × 104 | 3.97 × 104 | ||
| Germany | GE | Petrol | 0.24 | 0.27 | 1.58 × 106 | 4.15 × 104 | 1.50 × 10−1 | 3.91 × 1010 | 99.97 | 0.94 | 8 | 3.86 × 104 | 7.45 × 106 |
| Diesel | 0.64 | 0.95 | 1.51 × 106 | 2.57 × 102 | 1.48 × 100 | 1.10 × 1010 | 99.99 | 0.57 | 8 | 3.94 × 104 | 6.46 × 106 | ||
| Electric | 1.00 | 1.01 | 6.56 × 103 | 7.08 × 10−1 | 2.23 × 10−1 | 3.36 × 107 | 99.84 | 3.77 | 8 | 3.94 × 104 | 5.44 × 104 | ||
| Nat. Gas | 0.10 | 0.36 | 6.78 × 103 | 2.64 × 103 | 2.75 × 101 | 3.24 × 107 | 98.05 | 7.14 | 8 | 3.94 × 104 | 2.82 × 104 | ||
| Liq. Gas | 0.00 | 0.60 | 1.23 × 104 | 5.97 × 103 | 2.28 × 100 | 9.27 × 106 | 99.08 | 3.61 | 8 | 3.96 × 104 | 2.98 × 104 | ||
| Hybrid | 1.14 | 1.15 | 3.29 × 104 | 7.44 × 10−2 | 4.57 × 10−4 | 2.56 × 108 | 99.84 | 3.41 | 8 | 3.94 × 104 | 1.66 × 105 | ||
| Scenario | 2013 | 2014 | 2015 | 2017 | 2019 | 2021 | |
|---|---|---|---|---|---|---|---|
| Pairwise competition | AT | t = 2:1 70% (88%) | t = 3.5: 100% (100%) | t = 4.5: 99% (100%) | t = 6.5: 98% (97%) | t = 8: 97% (92%) | t = 10: 45% (45%) |
| CH | t = 8: 98% (99%) | t = 9.5: 76% (78%) | t = 10.5: 12% (7%) | t = 12.5: − | t = 14: − | t = 16: − | |
| DE | t = 1: 75% (86%) | t = 1.5: 58% (74%) | t = 2.5: 30% (41%) | t = 4.5: 4% (2%) | t = 7: 35% (18%) | t = 9: 18% (15%) | |
| Diesel as the sole prey | AT | t = 2: 6% (2%) | t = 3.5: − | t = 4.5: 1% (0%) | t = 6.5: 2% (3%) | t = 8: 3% (8%) | t = 10: 2% (4%) |
| CH | t = 8: − | t = 9.5: 21% (20%) | t = 10.5: 84% (90%) | t = 12.5: 93% (91%) | t = 14: 88% (84%) | t = 16: 46% (50%) | |
| DE | t = 1: 12% (4%) | t = 1.5: 24% (12%) | t = 2.5: 54% (49%) | t = 4.5: 94% (97%) | t = 7: 62% (80%) | t = 9: 14% (31%) | |
| Diesel and petrol as the sole prey | AT | t = 2: 24% (10%) | t = 3.5: − | t = 4.5: − | t = 6.5: − | t = 8: − | t = 10: − |
| CH | t = 8: − | t = 9.5: 3% (2%) | t = 10.5: 4% (3%) | t = 12.5: 7% (9%) | t = 14: 12% (16%) | t = 16: 10% (18%) | |
| DE | t = 1: 8% (5%) | t = 1.5: 17% (12%) | t = 2.5: 16% (10%) | t = 4.5: 2% (1%) | t = 7: 3% (2%) | t = 9: 1% (0%) |
| Ctry. | ts0 | ts1 | ts2 | ts3 | ts4 |
|---|---|---|---|---|---|
| Gas | Hybrid | Electric | Petrol | Diesel | |
| AT | 0.39 | 0.42 | 0.50 | 0 | 0.33 |
| CH | 1 | 0.09 | 0.34 | 1 | 0.22 |
| DE | 0 | 0.44 | 0.45 | 0.40 | 0.50 |
| Technology | Good-Fit Model | Comparison of R2 (%) | Alternative | ||||
|---|---|---|---|---|---|---|---|
| a | b | Good Fit | Best Fit | Logistic | Alternative | Model | |
| Diesel | 0.43 | 2.07 | 99.93 | 99.94 | 99.58 | 99.91 | West |
| Petrol | 0.36 | 0.72 | 99.81 | 99.82 | 99.35 | 99.70 | |
| Electric | 0.88 | 0.89 | 99.56 | 99.56 | 99.44 | 99.53 | Gompertz |
| Hybrid | 0.99 | 1.03 | 99.50 | 99.54 | 99.25 | 99.47 | |
| Gas | 0.00 | 0.58 | 97.57 | 97.63 | 95.12 | 97.45 | Brody |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziegler, A.M.; Brunner, N.; Kühleitner, M. The Markets of Green Cars of Three Countries: Analysis Using Lotka–Volterra and Bertalanffy–Pütter Models. J. Open Innov. Technol. Mark. Complex. 2020, 6, 67. https://doi.org/10.3390/joitmc6030067
Ziegler AM, Brunner N, Kühleitner M. The Markets of Green Cars of Three Countries: Analysis Using Lotka–Volterra and Bertalanffy–Pütter Models. Journal of Open Innovation: Technology, Market, and Complexity. 2020; 6(3):67. https://doi.org/10.3390/joitmc6030067
Chicago/Turabian StyleZiegler, Annika Maria, Norbert Brunner, and Manfred Kühleitner. 2020. "The Markets of Green Cars of Three Countries: Analysis Using Lotka–Volterra and Bertalanffy–Pütter Models" Journal of Open Innovation: Technology, Market, and Complexity 6, no. 3: 67. https://doi.org/10.3390/joitmc6030067
APA StyleZiegler, A. M., Brunner, N., & Kühleitner, M. (2020). The Markets of Green Cars of Three Countries: Analysis Using Lotka–Volterra and Bertalanffy–Pütter Models. Journal of Open Innovation: Technology, Market, and Complexity, 6(3), 67. https://doi.org/10.3390/joitmc6030067





