Static Impurities in a Weakly Interacting Bose Gas
Abstract
:1. Introduction
2. Formulation
2.1. Model
2.2. Effective Field Theory Approach
2.3. Limit of Dilute Bose Gas
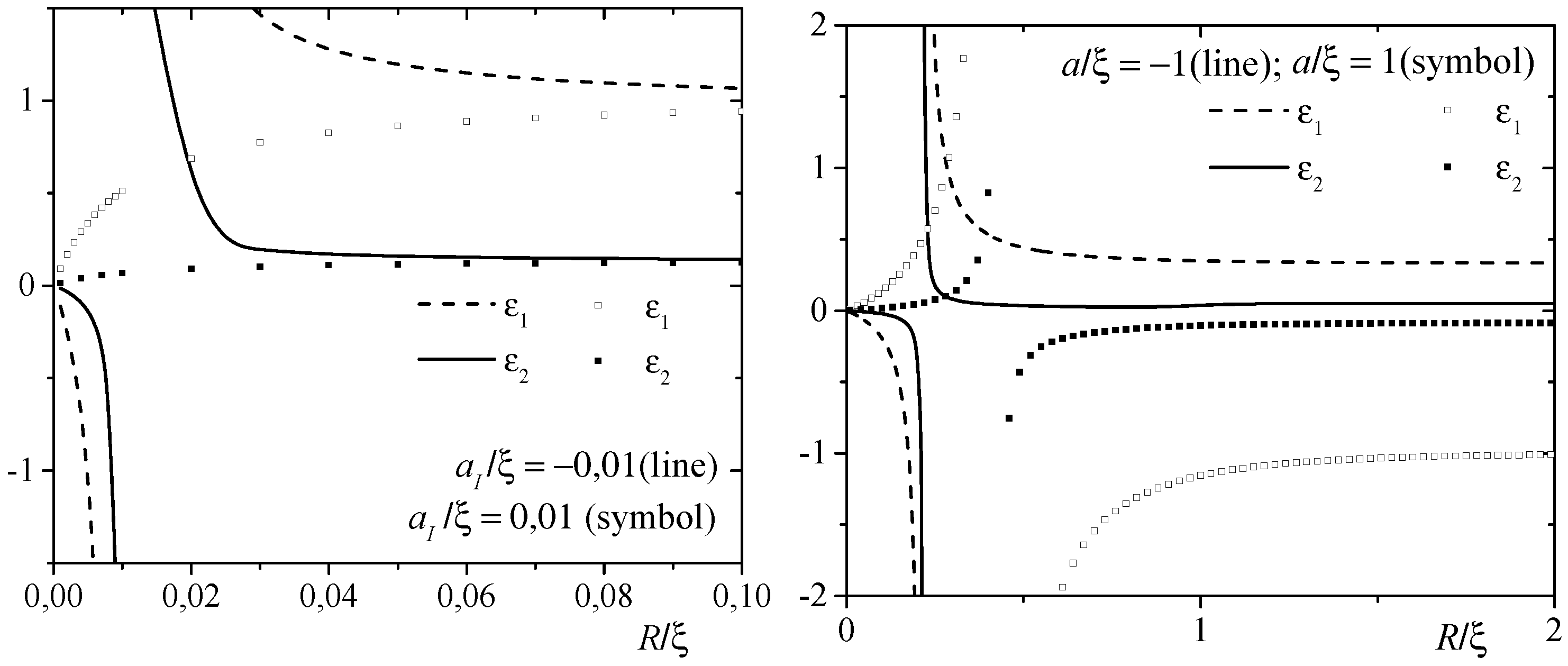
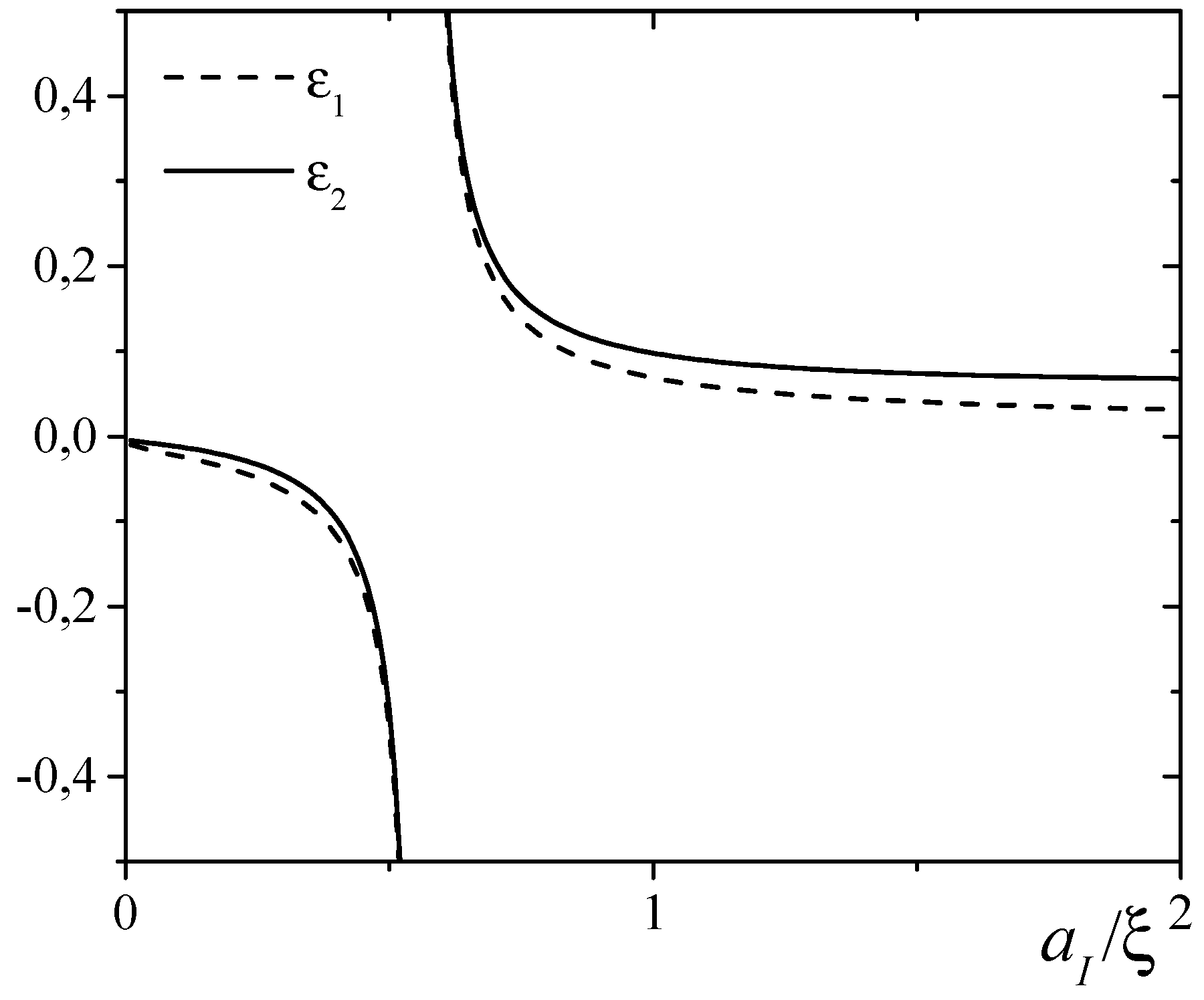
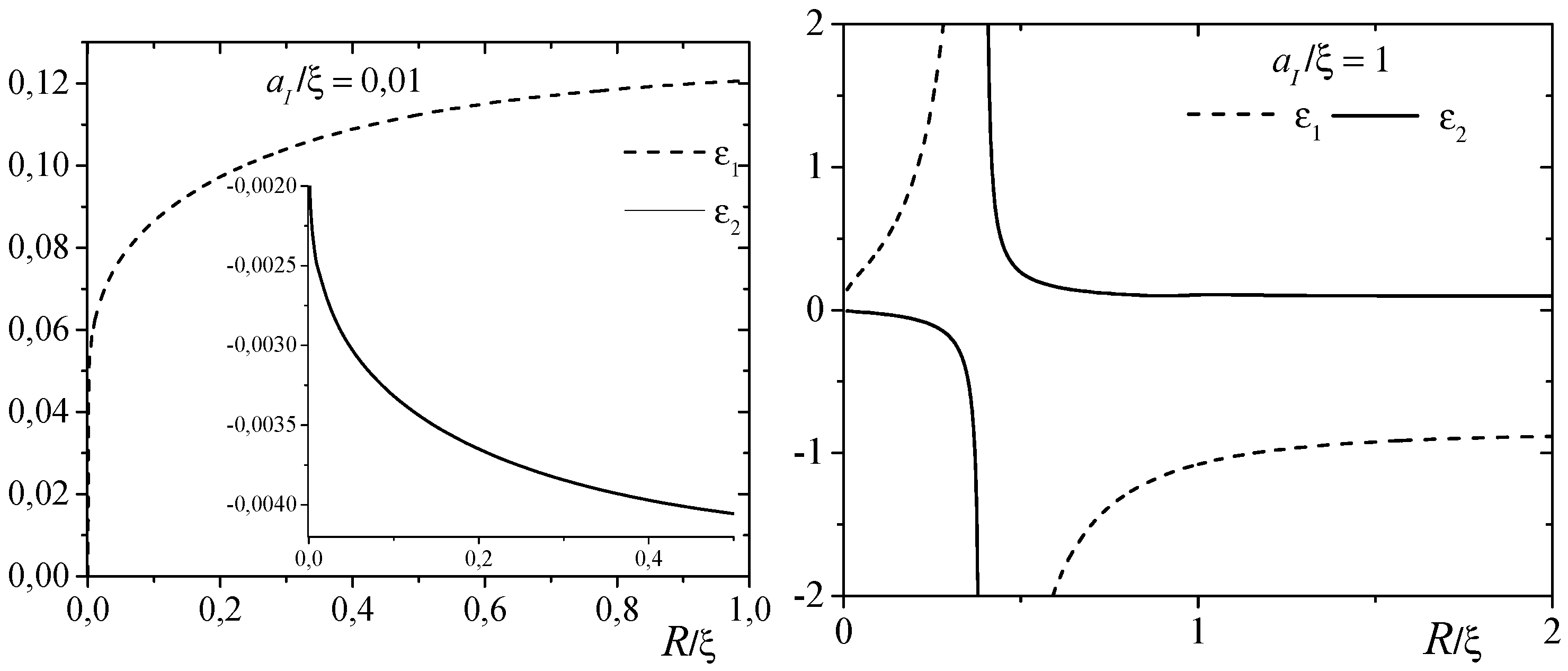
3. Results
3.1. 3D Case
3.2. 2D Case
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Tempere, J.; Casteels, W.; Oberthaler, M.K.; Knoop, S.; Timmermans, E.; Devreese, J.T. Feynman path-integral treatment of the BEC-impurity polaron. Phys. Rev. B 2009, 80, 184504. [Google Scholar] [CrossRef] [Green Version]
- Vlietinck, J.; Casteels, W.; Houcke, K.V.; Tempere, J.; Ryckebusch, J.; Devreese, J.T. Diagrammatic Monte Carlo study of the acoustic and the Bose–Einstein condensate polaron. New J. Phys. 2015, 17, 033023. [Google Scholar] [CrossRef] [Green Version]
- Ardila, L.A.P.; Giorgini, S. Impurity in a Bose-Einstein condensate: Study of the attractive and repulsive branch using quantum Monte Carlo methods. Phys. Rev. A 2015, 92, 033612. [Google Scholar] [CrossRef] [Green Version]
- Grusdt, F.; Shchadilova, Y.E.; Rubtsov, A.N.; Demler, E. Renormalization group approach to the Frohlich polaron model: Application to impurity-BEC problem. Sci. Rep. 2015, 5, 12124. [Google Scholar] [CrossRef] [PubMed]
- Panochko, G.; Pastukhov, V.; Vakarchuk, I. Behavior of the impurity atom in a weakly-interacting Bose gas. Cond. Matt. Phys. 2017, 20, 13604. [Google Scholar] [CrossRef]
- Astrakharchik, G.E.; Pitaevskii, L.P. Motion of a heavy impurity through a Bose-Einstein condensate. Phys. Rev. A 2004, 70, 013608. [Google Scholar] [CrossRef] [Green Version]
- Novikov, A.; Ovchinnikov, M. A diagrammatic calculation of the energy spectrum of quantum impurity in degenerate Bose–Einstein condensate. J. Phys. A Math. Theor. 2009, 42, 135301. [Google Scholar] [CrossRef]
- Christensen, R.S.; Levinsen, J.; Bruun, G.M. Quasiparticle Properties of a Mobile Impurity in a Bose-Einstein Condensate. Phys. Rev. Lett. 2015, 115, 160401. [Google Scholar] [CrossRef] [Green Version]
- Panochko, G.; Pastukhov, V.; Vakarchuk, I. Impurity self-energy in the strongly-correlated Bose systems. Int. J. Mod. Phys. B 2018, 32, 1850053. [Google Scholar] [CrossRef]
- Rath, S.P.; Schmidt, R. Field-theoretical study of the Bose polaron. Phys. Rev. A 2013, 88, 053632. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Sarma, S.D. Variational study of polarons in Bose-Einstein condensate. Phys. Rev. A 2014, 90, 013618. [Google Scholar] [CrossRef] [Green Version]
- Levinsen, J.; Massignan, P.; Parish, M.M. Efimov Trimers under Strong Confinement. Phys. Rev. X 2014, 4, 031020. [Google Scholar] [CrossRef] [Green Version]
- Naidon, P.; Endo, S. Efimov physics: A review. Rep. Prog. Phys. 2017, 80, 056001. [Google Scholar] [CrossRef] [Green Version]
- Levinsen, J.; Parish, M.M.; Bruun, G.M. Impurity in a Bose-Einstein Condensate and the Efimov Effect. Phys. Rev. Lett. 2015, 115, 125302. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; Zhai, H.; Cui, X. Visualizing the Efimov Correlation in Bose Polarons. Phys. Rev. Lett. 2017, 119, 013401. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Laing, W.B.; Stecher, J.; Esry, B.D. Efimov Physics in Heteronuclear Four-Body Systems. Phys. Rev. Lett. 2012, 108, 073201. [Google Scholar] [CrossRef] [PubMed]
- Casteels, W.; Tempere, J.; Devreese, J.T. Bipolarons and multipolarons consisting of impurity atoms in a Bose-Einstein condensate. Phys. Rev. A 2013, 88, 013613. [Google Scholar] [CrossRef] [Green Version]
- Blume, D.; Yan, Y. Generalized Efimov Scenario for Heavy-Light Mixtures. Phys. Rev. Lett. 2014, 113, 213201. [Google Scholar] [CrossRef] [Green Version]
- Shi, Z.Y.; Yoshida, S.M.; Parish, M.M.; Levinsen, J. Impurity-Induced Multibody Resonances in a Bose Gas. Phys. Rev. Lett. 2018, 121, 243401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoshida, S.M.; Shi, Z.Y.; Levinsen, J.; Parish, M.M. Few-body states of bosons interacting with a heavy quantum impurity. Phys. Rev. A 2018, 98, 062705. [Google Scholar] [CrossRef] [Green Version]
- Blume, D. Few-boson system with a single impurity: Universal bound states tied to Efimov trimers. Phys. Rev. A 2019, 99, 013613. [Google Scholar] [CrossRef] [Green Version]
- Jorgensen, N.B.; Wacker, L.; Skalmstang, K.T.; Parish, M.M.; Levinsen, J.; Christensen, R.S.; Bruun, G.M.; Arlt, J.J. Observation of Attractive and Repulsive Polarons in a Bose-Einstein Condensate. Phys. Rev. Lett. 2016, 117, 055302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, M.-G.; de Graaff, M.J.V.; Kedar, D.; Corson, J.P.; Cornell, E.A.; Jin, D.S. Bose Polarons in the Strongly Interacting Regime. Phys. Rev. Lett. 2016, 117, 055301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, Z.Z.; Ni, Y.; Robens, C.; Zwielein, M.W. Bose polarons near quantum criticality. Science 2020, 368, 190. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Levinsen, J.; Parish, M.M.; Christensen, R.S.; Arlt, J.J.; Bruun, G.M. Finite-temperature behavior of the Bose polaron. Phys. Rev. A 2017, 96, 063622. [Google Scholar] [CrossRef] [Green Version]
- Guenther, N.-E.; Massignan, P.; Lewenstein, M.; Bruun, G.M. Bose Polarons at Finite Temperature and Strong Coupling. Phys. Rev. Lett. 2018, 120, 050405. [Google Scholar] [CrossRef] [Green Version]
- Pastukhov, V. Polaron in the dilute critical Bose condensate. J. Phys. A Math. Theor. 2018, 51, 195003. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.E.; Levinsen, J.; Paris, M.M. Variational Approach for Impurity Dynamics at Finite Temperature. Phys. Rev. Lett. 2019, 122, 205301. [Google Scholar] [CrossRef] [Green Version]
- Field, B.; Levinsen, J.; Parish, M.M. Fate of the Bose polaron at finite temperature. Phys. Rev. A 2020, 101, 013623. [Google Scholar] [CrossRef] [Green Version]
- Pascual, G.; Boronat, J. Quasiparticle Nature of the Bose Polaron at Finite Temperature. Phys. Rev. Lett. 2021, 127, 205301. [Google Scholar] [CrossRef]
- Zinner, N.T. Efimov states of heavy impurities in a Bose-Einstein condensate. Europhys. Phys. Lett. 2013, 101, 60009. [Google Scholar] [CrossRef]
- Zinner, N.T. Spectral flow of trimer states of two heavy impurities and one light condensed boson. Europhys. Phys. J. D 2014, 68, 216. [Google Scholar] [CrossRef] [Green Version]
- Camacho-Guardian, A.; Ardila, L.A.P.; Pohl, T.; Bruun, G.M. Bipolarons in a Bose-Einstein Condensate. Phys. Rev. Lett. 2018, 121, 013401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Camacho-Guardian, A.; Bruun, G.M. Landau Effective Interaction between Quasiparticles in a Bose-Einstein Condensate. Phys. Rev. X 2018, 8, 031042. [Google Scholar] [CrossRef] [Green Version]
- Brauneis, F.; Hammer, H.-W.; Lemeshko, M.; Volosniev, A.G. Impurities in a one-dimensional Bose gas: The flow equation approach. SciPost Phys. 2021, 11, 008. [Google Scholar] [CrossRef]
- Petcovich, A.; Ristivojevic, Z. Mediated interaction between polarons in a one-dimensional Bose gas. arXiv 2021, arXiv:2103.08772. [Google Scholar]
- Pasek, M.; Orso, G. Induced pairing of fermionic impurities in a one-dimensional strongly correlated Bose gas. Phys. Rev. B 2019, 100, 245419. [Google Scholar] [CrossRef] [Green Version]
- Will, M.; Astrakharchik, G.E.; Fleischhauer, M. Polaron Interactions and Bipolarons in One-Dimensional Bose Gases in the Strong Coupling Regime. Phys. Rev. Lett. 2021, 127, 103401. [Google Scholar] [CrossRef]
- Dehkharghani, A.S.; Volosniev, A.G.; Zinner, N.T. Coalescence of Two Impurities in a Trapped One-dimensional Bose Gas. Phys. Rev. Lett. 2018, 121, 080405. [Google Scholar] [CrossRef] [Green Version]
- Mistakidis, S.I.; Volosniev, A.G.; Schmelcher, P. Induced correlations between impurities in a one-dimensional quenched Bose gas. Phys. Rev. Res. 2020, 2, 023154. [Google Scholar] [CrossRef]
- Naidon, P. Two Impurities in a Bose–Einstein Condensate: From Yukawa to Efimov Attracted Polarons. J. Phys. Soc. Jpn. 2018, 87, 043002. [Google Scholar] [CrossRef]
- Pastukhov, V. Polaron in dilute 2D Bose gas at low temperatures. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 155203. [Google Scholar] [CrossRef] [Green Version]
- Isaule, F.; Morera, I.; Massignan, P.; Juliá-Díaz, B. Renormalization-group study of Bose polarons. Phys. Rev. A 2021, 104, 023317. [Google Scholar] [CrossRef]
- Akaturk, E.; Tanatary, B. Two-dimensional Bose polaron using diffusion Monte Carlo method. Int. J. Mod. Phys. B 2019, 33, 1950238. [Google Scholar] [CrossRef] [Green Version]
- Ardila, L.A.P.; Astrakharchik, G.E.; Giorgini, S. Strong coupling Bose polarons in a two-dimensional gas. Phys. Rev. Res. 2020, 2, 023405. [Google Scholar] [CrossRef]
- Khan, M.M.; Tercas, H.; Mendonca, J.T.; Wehr, J.; Charalambous, C.; Lewenstein, M.; Garcia-March, M.A. Quantum dynamics of a Bose polaron in a d-dimensional Bose-Einstein condensate. Phys. Rev. A 2021, 103, 023303. [Google Scholar] [CrossRef]
- Kain, B.; Ling, H.Y. Analytical study of static beyond-Frohlich Bose polarons in one dimension. Phys. Rev. A 2018, 98, 033610. [Google Scholar] [CrossRef] [Green Version]
- Reichert, B.; Ristivojevic, Z.; Petkovic, A. The Casimir-like effect in a one-dimensional Bose gas. New J. Phys. 2019, 21, 053024. [Google Scholar] [CrossRef]
- Reichert, B.; Ristivojevic, Z.; Petkovic, A. Field-theoretical approach to the Casimir-like interaction in a one-dimensional Bose gas. Phys. Rev. B 2019, 99, 205414. [Google Scholar] [CrossRef] [Green Version]
- Panochko, G.; Pastukhov, V. Two- and three-body effective potentials between impurities in ideal BEC. J. Phys A Math. Theor. 2021, 54, 085001. [Google Scholar] [CrossRef]
- Drescher, M.; Salmhofer, M.; Enss, T. Quench Dynamics of the Ideal Bose Polaron at Zero and Nonzero Temperatures. Phys. Rev. A 2021, 103, 033317. [Google Scholar] [CrossRef]
- Levinsen, J.; Ardila, L.A.P.; Yoshida, S.M.; Parish, M.M. Quantum Behavior of a Heavy Impurity Strongly Coupled to a Bose Gas. Phys. Rev. Lett. 2021, 127, 033401. [Google Scholar] [CrossRef]
- Volosniev, A.G.; Hammer, H.-W.; Zinner, N.T. Real-time dynamics of an impurity in an ideal Bose gas in a trap. Phys. Rev. A 2015, 92, 023623. [Google Scholar] [CrossRef] [Green Version]
- Andersen, J.O. Theory of the weakly interacting Bose gas. Rev. Mod. Phys. 2004, 76, 599. [Google Scholar] [CrossRef] [Green Version]
- Salasnich, L.; Toigo, F. Zero-point energy of ultracold atoms. Phys. Rep. 2016, 640, 1. [Google Scholar] [CrossRef] [Green Version]
- Volosniev, A.G.; Hammer, H.-W. Analytical approach to the Bose-polaron problem in one dimension. Phys. Rev. A 2017, 96, 031601(R). [Google Scholar] [CrossRef] [Green Version]
- Pastukhov, V. Mean-field properties of impurity in Bose gas with three-body forces. Phys. Lett. A 2019, 383, 2610. [Google Scholar] [CrossRef] [Green Version]
- Panochko, G.; Pastukhov, V. Mean-field construction for spectrum of one-dimensional Bose polaron. Ann. Phys. 2019, 409, 167933. [Google Scholar] [CrossRef] [Green Version]
- Hryhorchak, O.; Panochko, G.; Pastukhov, V. Mean-field study of repulsive 2D and 3D Bose polarons. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 205302. [Google Scholar] [CrossRef]
- Hryhorchak, O.; Panochko, G.; Pastukhov, V. Impurity in a three-dimensional unitary Bose gas. Phys. Lett. A 2020, 384, 126934. [Google Scholar] [CrossRef]
- Massignan, P.; Yegovtsev, N.; Gurarie, V. Universal Aspects of a Strongly Interacting Impurity in a Dilute Bose Condensate. Phys. Rev. Lett. 2021, 126, 123403. [Google Scholar] [CrossRef] [PubMed]
- Jager, J.; Barnett, R.; Will, M.; Fleischhauer, M. Strong-coupling Bose polarons in one dimension: Condensate deformation and modified Bogoliubov phonons. Phys. Rev. Res. 2020, 2, 033142. [Google Scholar] [CrossRef]
- Mora, C.; Castin, Y. Ground State Energy of the Two-Dimensional Weakly Interacting Bose Gas: First Correction Beyond Bogoliubov Theory. Phys. Rev. Lett. 2009, 102, 180404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1964.
- Schmidt, R.; Enss, T. Self-stabilized Bose polarons. arXiv 2021, arXiv:2102.13616. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panochko, G.; Pastukhov, V. Static Impurities in a Weakly Interacting Bose Gas. Atoms 2022, 10, 19. https://doi.org/10.3390/atoms10010019
Panochko G, Pastukhov V. Static Impurities in a Weakly Interacting Bose Gas. Atoms. 2022; 10(1):19. https://doi.org/10.3390/atoms10010019
Chicago/Turabian StylePanochko, Galyna, and Volodymyr Pastukhov. 2022. "Static Impurities in a Weakly Interacting Bose Gas" Atoms 10, no. 1: 19. https://doi.org/10.3390/atoms10010019





