Photon Emission from Hollow Ions Near Surfaces
Abstract
:1. Introduction
2. Modeling Photon Emission from Hollow Ions
2.1. Photon Absorption and Emission
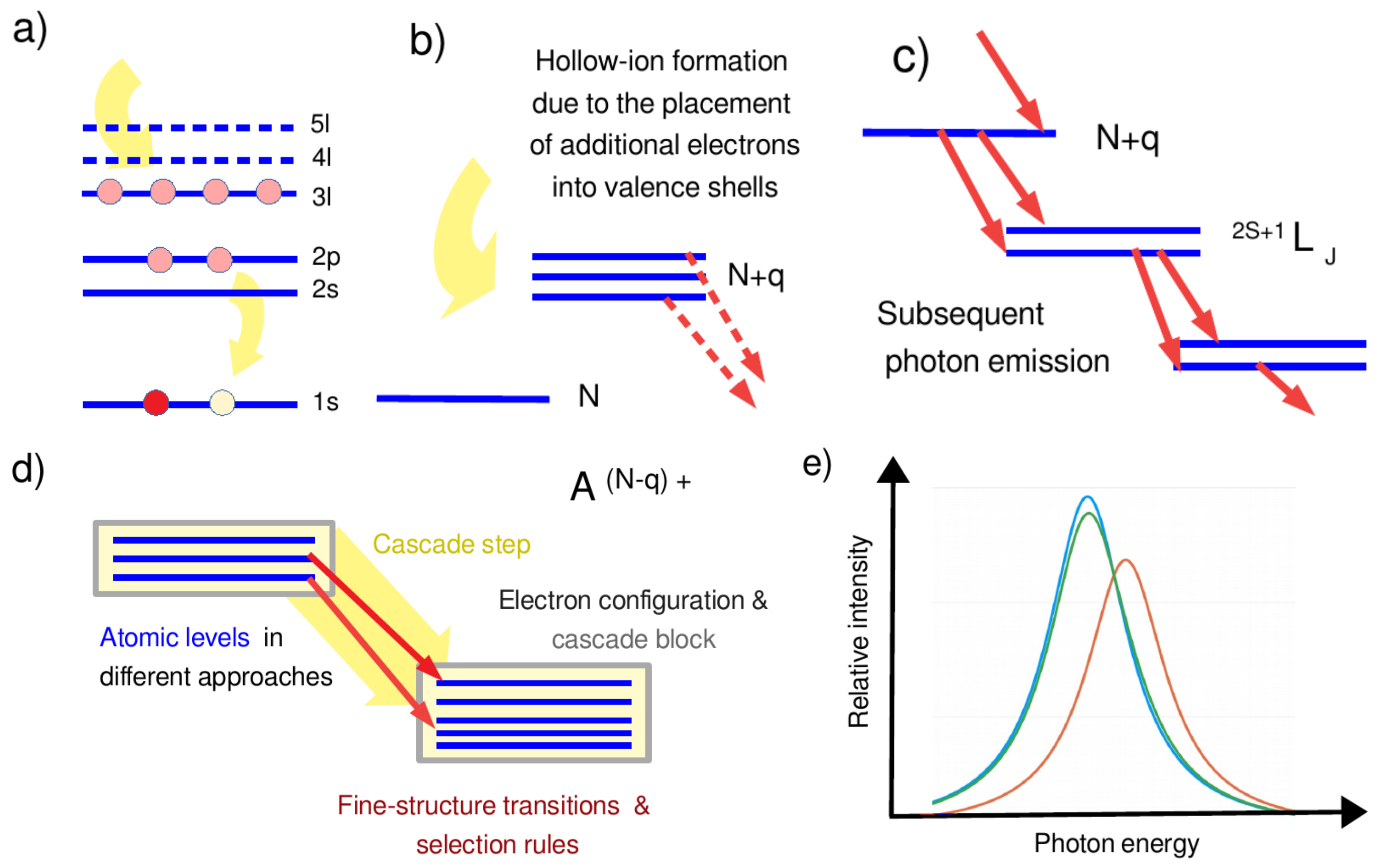
2.2. Photon Cascades and Spectra following Multiple Electron Capture
2.3. Implementation of Atomic Cascades
2.4. Data Types for Modeling Photon Spectra
3. Photon Satellite Emission from Hollow Ions
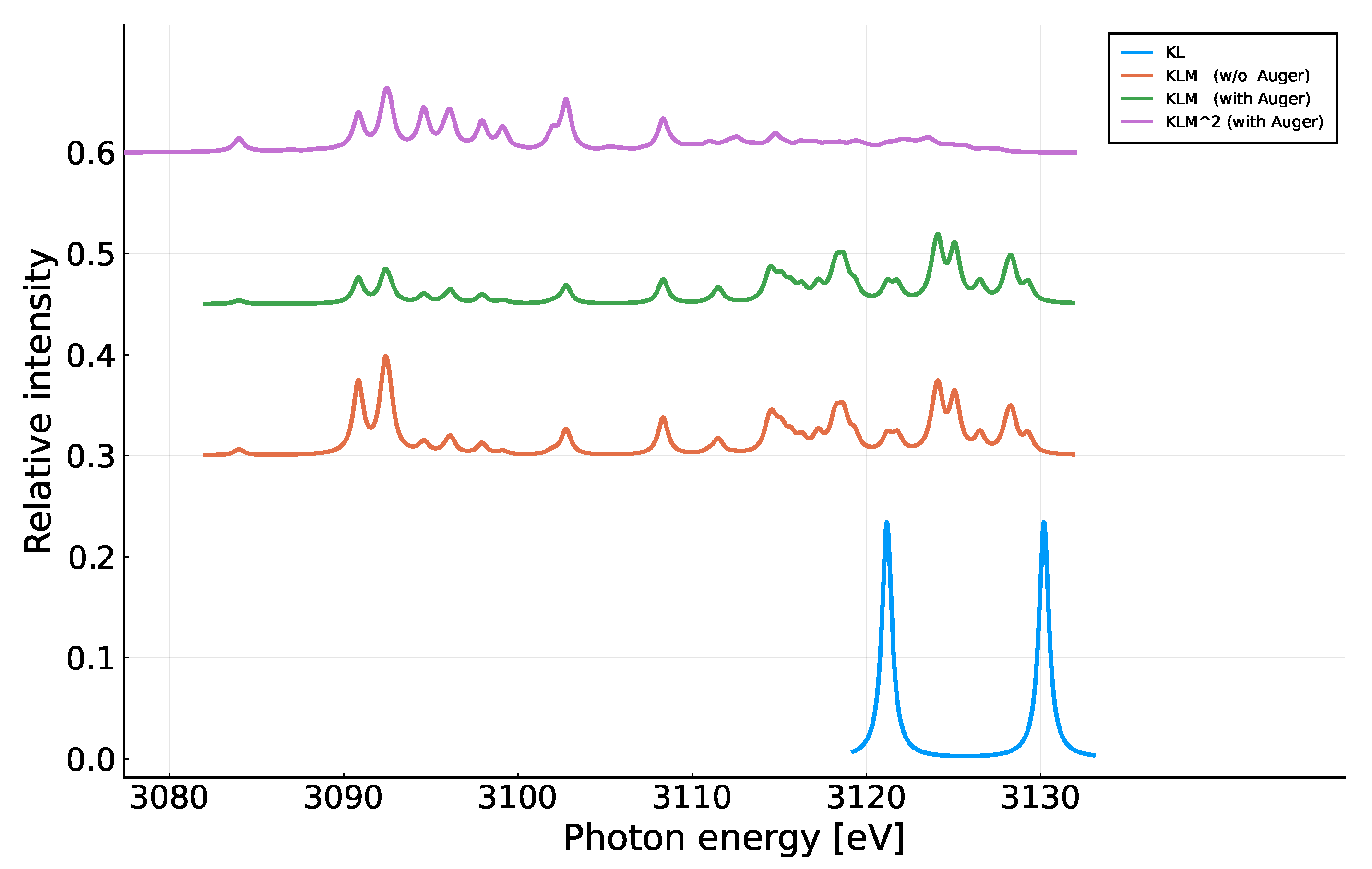
3.1. K Satellite Emission from KLM Configurations
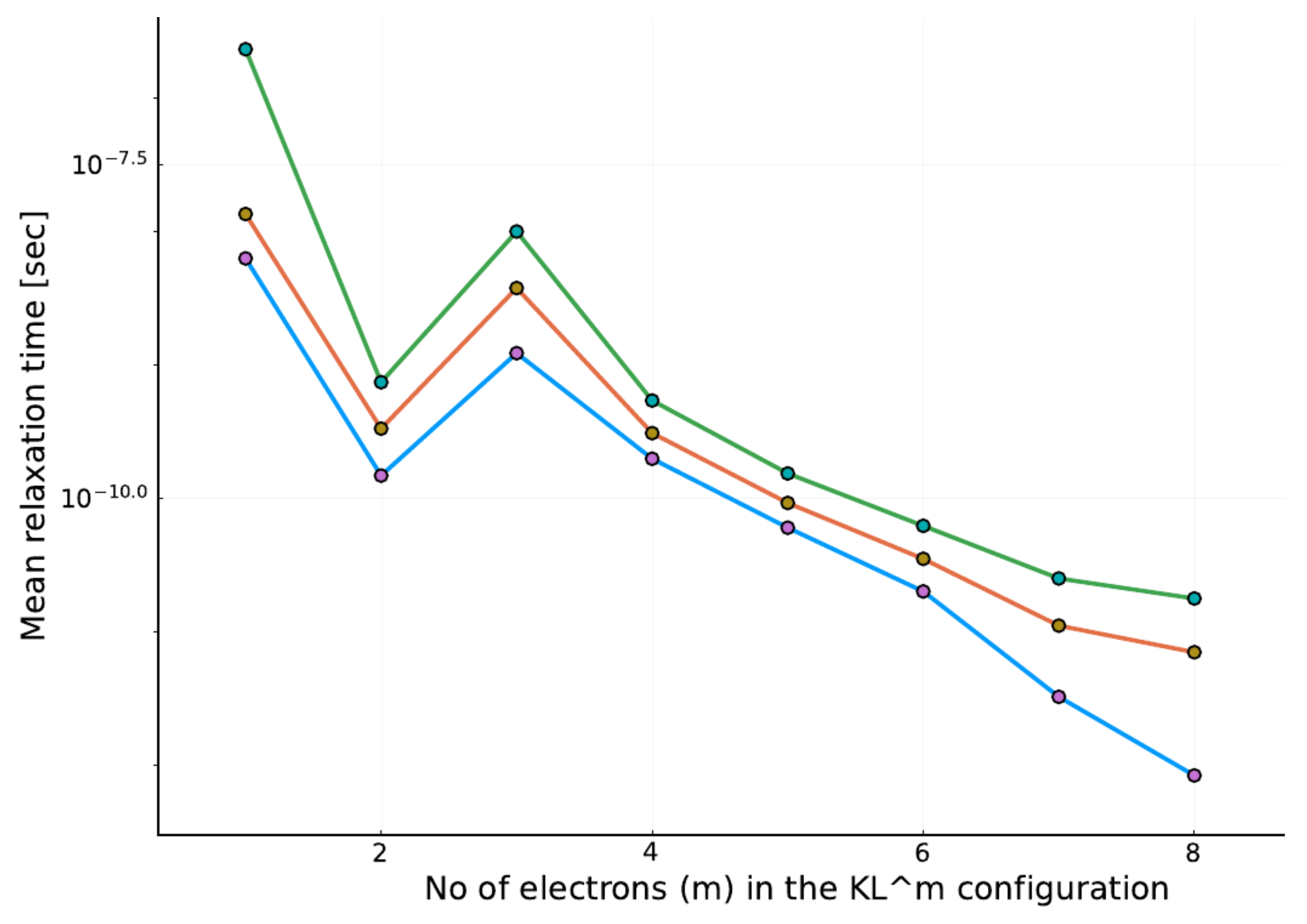
3.2. Mean Relaxation Time of KL Configurations
3.3. Analysis of Further Photon and Electron Spectra
- How can the effective electron capture be characterized for ions that swiftly collide with surfaces or rest-gas atoms? How can one model the relaxation dynamic of such ions that have been found to be inconsistent with prior measurements [12]?
- Which additional X-ray lines occur, and with which intensity, if electrons are placed into high-n Rydberg shells? Which of these lines contribute due to non-E1 (dipole) transitions? Such studies may have impacts on different kinds of precision measurements.
- How do the radiative (multipole) and Auger transition rates interplay with each other for muonic X-ray spectra following the capture of an muon by an atom?
- In two-step Auger cascades, a coherent summation over the individual decay paths from the first and second steps is known to be necessary in order to predict the angular distribution of the emitted Auger electrons if the fine-structure splitting of two or more intermediate levels is small or comparable to the natural line widths of these levels [38,39]. How can such a coherence transfer be treated efficiently, if needed, for a whole cascade?
- How do radiative and dielectronic capture compete with each other under different experimental conditions?
- A good understanding of astrophysical light curves helps resolve the chemical evolution of the early universe and, eventually, the formation and growth of galaxies. However, very little is known so far about the optical properties of the heavy r-process elements, and, hence, most previous light-curve models still utilize the opacities from the iron-group elements. How does a proper treatment of the opacities and atomic cascades affect the light curve as observed, for instance, from neutron-star mergers?
4. Summary and Conclusions
Funding
Conflicts of Interest
References
- Briand, J.-P.; de Billy, L.; Charles, P.; Essabaa, S.; Briand, P.; Geller, R.; Desclaux, P.; Bliman, S.; Ristori, C. Production of hollow atoms by the excitation of highly charged ions in interaction with a metallic surface. Phys. Rev. Lett. 1990, 65, 159. [Google Scholar] [CrossRef] [PubMed]
- Briand, J.-P.; Giardino, G.; Borsoni, G.; Froment, M.; Eddrief, M.; Sebenne, C.; Bardin, S.; Schneider, D.; Jin, J.; Khemliche, H.; et al. Decay of hollow atoms above and below a surface. Phys. Rev. A 1996, 54, 4136. [Google Scholar] [CrossRef] [PubMed]
- Palmeri, P.; Quinet, P.; Zitane, N.; Vaeck, N. Calculation of Auger rates for complex hollow-atom configurations. J. Phys. B 2001, 34, 4125. [Google Scholar] [CrossRef]
- Vaeck, N.; Hansen, J.E.; Palmeri, P.; Quinet, P.; Zitane, N.; Godefroid, M.; Fritzsche, S.; Kylstra, N. Hollow atoms: A theoretical challenge. Phys. Scr. 2001, T95, 68. [Google Scholar] [CrossRef]
- Tokesi, K.; Wirtz, L.; Lemell, C.; Burgdörfer, J. Hollow-ion formation in microcapillaries. Phys. Rev. A 2001, 64, 042902. [Google Scholar] [CrossRef] [Green Version]
- DuBois, R.D.; Tokesi, K.; Giglio, E. Charge deposition, redistribution, and decay properties of insulating surfaces obtained from guiding of low-energy ions through capillaries. Phys. Rev. A 2019, 99, 062704. [Google Scholar] [CrossRef] [Green Version]
- Schippers, S.; Martins, M.; Beerwerth, R.; Bari, S.; Holste, K.; Schubert, K.; Viefhaus, J.; Savin, D.W.; Fritzsche, S.; Müller, A.; et al. Near L-edge single and multiple photoionization of singly charged iron ions. Astrophys. J. 2017, 849, 5. [Google Scholar] [CrossRef] [Green Version]
- Beerwerth, R.; Buhr, T.; Perry-Sassmannshausen, A.; Stock, S.O.; Bari, S.; Holste, K.; Kilcoyne, A.L.D.; Reinwardt, S.; Ricz, S.; Savin, D.W.; et al. Near L-edge single and multiple photoionization of triply charged iron ions. Astrophys. J. 2019, 887, 189. [Google Scholar] [CrossRef] [Green Version]
- Hansen, S.B.; Colgan, J.; Faenov, A.Y.; Abdallah, J., Jr.; Pikuz, S.A.; Skobelev, I.Y.; Wagenaars, E.; Booth, N.; Culfa, O.; Dance, R.J.; et al. Detailed analysis of hollow ions spectra from dense matter pumped by X-ray emission of relativistic laser plasma. Phys. Plasma 2014, 887, 189. [Google Scholar] [CrossRef] [Green Version]
- Gillaspy, J.D. Precision spectroscopy of trapped highly charged heavy elements: Pushing the limits of theory and experiment. Phys. Scr. 2014, 89, 1114004. [Google Scholar] [CrossRef]
- Chantler, C.T.; Payne, A.T.; Gillaspy, J.D.; Hudson, L.T.; Smale, L.F.; Henins, A.; Kimpton, J.A.; Takacs, E. X-ray measurements in helium-like atoms increased discrepancy between experiment and theoretical QED. New J. Phys. 2014, 16, 123037. [Google Scholar] [CrossRef]
- Wilhelm, R.A.; Gruber, E.; Schwestka, J.; Kozubek, R.; Madeira, T.I.; Marques, J.P.; Kobus, J.; Krasheninnikov, A.V.; Schleberger, M.; Aumayr, F. Interatomic Coulombic decay: The mechanism for rapid deexcitation of hollow atoms. Phys. Rev. Lett. 2017, 119, 103401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sisourat, N.; Engin, S.; Gorfinkiel, J.; Kazandjian, S.; Kolorenc, P.; Miteva, T. On the computations of interatomic Coulombic decay widths with R-matrix method. J. Chem. Phys. 2017, 146, 244109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khokhlova, M.; Bahmanpour, L.; Bachhawat, N.; Cooper, B.; Averbukh, V. Interatomic Coulombic decay rate in endohedral complexes. J. Phys. 2020, B53, 184002. [Google Scholar] [CrossRef]
- Jakas, M.M.; Harrison, D.E., Jr. Many-body effects in atomic-collision cascades. Phys. Rev. Lett. 1985, 5, 1782. [Google Scholar] [CrossRef]
- Fritzsche, S. A fresh computational approach to atomic structures, processes and cascades. Comp. Phys. Commun. 2019, 240, 1. [Google Scholar] [CrossRef]
- Fritzsche, S.; Palmeri, P.; Schippers, S. Atomic cascade computations. Symmetry 2021, 13, 520. [Google Scholar] [CrossRef]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Johnson, W.R. Atomic Structure Theory: Lectures on Atomic Physics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Fritzsche, S. Large-scale accurate structure calculations for open-shell atoms and ions. Phys. Scr. 2002, T100, 37. [Google Scholar] [CrossRef]
- Grant, I.P. Relativistic Quantum Theory of Atoms and Molecules: Theory and Computation; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Fritzsche, S. The Ratip program for relativistic calculations of atomic transition, ionization and recombination properties. Comp. Phys. Commun. 2012, 183, 1525. [Google Scholar] [CrossRef]
- Perry-Sassmannshausen, A.; Buhr, T.; Borovik, A., Jr.; Martins, M.; Reinwardt, S.; Ricz, S.; Stock, S.O.; Trinter, F.; Muller, A.; Fritzsche, S.; et al. Multiple photodetachment of carbon anions via single and double core-hole creation. Phys. Rev. Lett. 2020, 124, 083203. [Google Scholar] [CrossRef] [Green Version]
- Sobel’man, I.I.; Vainshtein, L.; Yukov, E.A. Excitation of Atoms and Broadening of Spectral Lines; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Allen, F.I.; Biedermann, C.; Radtke, R.; Fussmann, G.; Fritzsche, S. Energy dependence of angular momentum capture states in charge exchange collisions between slow highly charged argon ions and argon neutrals. Phys. Rev. A 2008, 78, 032705. [Google Scholar] [CrossRef] [Green Version]
- Schippers, S.; Beerwerth, R.; Abrok, L.; Bari, S.; Buhr, T.; Martins, M.; Ricz, S.; Viefhaus, J.; Fritzsche, S.; Muller, A. Prominent role of multielectron processes in K-shell double and triple photodetachment of oxygen anions. Phys. Rev. A 2016, 94, 041401(R). [Google Scholar] [CrossRef] [Green Version]
- Schippers, S.; Buhr, T.; Borovik, A., Jr.; Holste, K.; Perry-Sassmannshausen, A.; Mertens, K.; Reinwardt, S.; Martins, M.; Klumpp, S.; Schubert, K.; et al. The photon-ion merged-beams experiment PIPE at PETRA III—The first five years. X-ray Spec. 2020, 49, 11. [Google Scholar] [CrossRef] [Green Version]
- Available online: https://docs.julialang.org/ (accessed on 10 February 2022).
- Bezanson, J.; Chen, J.; Chung, B.; Karpinski, S.; Shah, V.B.; Vitek, J.; Zoubritzky, J. Julia: Dynamism and performance reconciled by design. Proc. ACM Program. Lang. 2018, 2, 120. [Google Scholar] [CrossRef] [Green Version]
- Fritzsche, S. JAC: User Guide, Compendium & Theoretical Background. Available online: https://github.com/OpenJAC/JAC.jl (accessed on 10 February 2022).
- Fritzsche, S.; Fricke, B.; Sepp, W.D. Reduced L1 level-width and Coster-Kronig yields by relaxation and continuum interactions in atomic zinc. Phys. Rev. A 1992, 45, 1465. [Google Scholar] [CrossRef] [Green Version]
- Julia Comes with a Full-Featured Interactive and Command-Line REPL (Read-Eval-Print Loop) That is Built into the Executable of the Language. Available online: https://julialang.org/ (accessed on 10 February 2022).
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (ver. 5.8). 2021. Available online: https://physics.nist.gov/asd (accessed on 25 February 2022).
- Schippers, S.; Beerwerth, R.; Bari, S.; Buhr, T.; Holste, K.; Kilcoyne, A.L.D.; Perry-Saßmannshausen, A.; Phaneuf, R.A.; Reinwardt, S.; Savin, W.; et al. Near L-edge single and multiple photoionization of doubly charged iron ions. Astrophys. J. 2021, 908, 52. [Google Scholar] [CrossRef]
- Müller, A.; Martins, M.; Borovik, A., Jr.; Buhr, T.; Perry-Sassmannshausen, A.; Reinwardt, S.; Ricz, S.; Trinter, F.; Schippers, S.; Fritzsche, S.; et al. The role of L-shell single and double core-hole production and decay in m-fold (m = 1,2,…,6) photoionization of the Ar+ ion. Phys. Rev. A 2021, 104, 033105. [Google Scholar] [CrossRef]
- Lee, J.C.; Iwasawa, K.; Houck, J.C.; Fabian, A.C.; Marshall, H.L.; Canizares, C.R. The shape of the relativistic iron Kα line from MCG-6-30-15 measured with the Chandra HETGS and RXTE. Astrophys. J. 2002, 570, l47. [Google Scholar] [CrossRef] [Green Version]
- Hanke, M.; Wilms, J.; Nowak, M.A.; Pottschmidt, K.; Schulz, N.S.; Lee, J.C. Chandra X-ray spectroscopy of the focused wind in the Cygnus X-1 system I. The non-dip spectrum in the low/hard state. Astrophys. J. 2009, 690, 330. [Google Scholar] [CrossRef]
- Shimizu, Y.; Yoshida, H.; Okada, K.; Muramatsu, Y.; Saito, N.; Okashi, H.; Tamenori, Y.; Fritzsche, S.; Kabachnik, N.M.; Tanaka, H.; et al. Ultra-high resolution angle-resolved measurement of Auger emission from the photoexcited 1s−1→3p state of Ne. J. Phys. 2000, B33, L685. [Google Scholar]
- Ueda, K.; Shimizu, Y.; Chiba, H.; Kitajima, M.; Tanaka, H.; Fritzsche, S.; Kabachnik, N.M. Experimental and theoretical study of the Auger cascade following the 2p→4s photoexcitation in Ar. J. Phys. 2001, B34, 107. [Google Scholar] [CrossRef]



| Structures and Brief Explanation |
|---|
| Cascade.AbstractCascadeApproach: defines an abstract type for dealing with the cascade approach that is to be applied to the generation of all atomic levels and the evaluation of many-electron amplitudes. |
| Cascade.AbstractCascadeScheme: specifies an abstract data type to discriminate between different excitation, ionization and decay schemes of an atomic cascade; see Ref. [17] for a detailed discussion of different cascade schemes in Jac. |
| Cascade.AbstractSimulationProperty: defines an abstract type to deal with the property or distribution that is to be simulated, based on given cascade data; see below for several concrete types (properties). |
| Cascade.Computation: defines a data structure for the computation of a photoexcitation, photoionization, stepwise decay or hollow-ion cascade, and likely a few more in the future. |
| Cascade.Simulation: defines a structure to deal with cascade simulations of various kinds, based on given data from prior cascade computations. |
| Cascade.IonDistribution: defines a type to simulate the (final) ion or charge-state distribution, once all cascade computations are completed. |
| Cascade.PhotonIntensity: a type to simulate the photon intensities as applied and shown in Section 3; cf. also Cascade.ElectronIntensity. |
| Cascade.MeanRelaxationTime: a type to determine the mean relaxation times for given levels or configurations, i.e., the time, in which 70 %, 80 % or 90 % decay back to their ground configuration. |
| Cascade.DrRateCoefficients: a type to simulate the DR plasma rate coefficients as function of the plasma temperature. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fritzsche, S. Photon Emission from Hollow Ions Near Surfaces. Atoms 2022, 10, 37. https://doi.org/10.3390/atoms10020037
Fritzsche S. Photon Emission from Hollow Ions Near Surfaces. Atoms. 2022; 10(2):37. https://doi.org/10.3390/atoms10020037
Chicago/Turabian StyleFritzsche, Stephan. 2022. "Photon Emission from Hollow Ions Near Surfaces" Atoms 10, no. 2: 37. https://doi.org/10.3390/atoms10020037
APA StyleFritzsche, S. (2022). Photon Emission from Hollow Ions Near Surfaces. Atoms, 10(2), 37. https://doi.org/10.3390/atoms10020037






