Mass Spectrometry-Based Approach to Compute Electron-Impact Partial Ionization Cross-Sections of Methane, Water and Nitromethane from Threshold to 5 keV
Abstract
:1. Introduction
2. The BEB and Modified BEB Models
2.1. The BEB Model
2.2. The Modified BEB Model
3. Methodology and Computational Details
3.1. Methane (CH4)
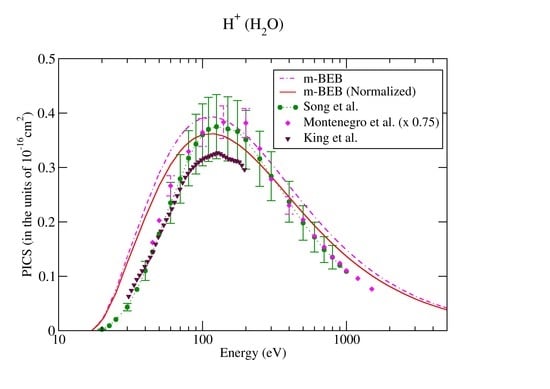
3.2. Water (H2O)
3.3. Nitromethane (CH3NO2)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
Abbreviations
| BEB | binary encounter Bethe |
| m-BEB | modified BEB |
| HF | Hartree–Fock |
| DFT | Density Functional Theory |
| ECP | Effective Core Potentials |
| EIMS | Electron Ionization Mass Spectrometry |
| DI | Dissociative Ionization |
| AE | Appearance Energy |
| IE | Ionization Energy |
| CC | Close Coupling |
| m/z | mass to charge ratio |
| eV | electron volt |
| au | atomic unit |
| RI | Relative Cation Intensity |
| BR | Branching Ratios |
References
- Janev, R.K. (Ed.) Atomic and Molecular Processes in Fusion Edge Plasmas; Plenum New York: New York, NY, USA, 1995. [Google Scholar]
- McMaster, M.C.; Hsu, W.L.; Coltrin, M.E.; Dandy, D.S.; Fox, C. Dependence of the gas composition in a microwave plasma-assisted diamond chemical vapor deposition reactor on the inlet carbon source: CH4 versus C2H2. Diam. Relat. Mater. 1995, 4, 1000. [Google Scholar] [CrossRef]
- Moos, H.W.; Clark, J.T. Detection of acetylene in the Saturnian atmosphere using the IUE satellite. Astrophys. J. 1979, 229, L107. [Google Scholar] [CrossRef]
- Owen, T.C.; Caldwel, J.; Rivolo, A.R.; Moore, V.; Lane, A.L.; Sagan, C.; Hunt, H.; Ponnamperuma, C. Observations of the spectrum of Jupiter from 1500 to 2000 A with the IUE. Astrophys. J. 1987, 236, 139. [Google Scholar] [CrossRef]
- Christophorou, L.G. (Ed.) Electron Molecule Interactions and Their Applications; Academic Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Christophorou, L.G.; Olthoff, J.K. Fundamental Electron Interactions with Plasma Processing Gases; Springer: Boston, MA, USA, 2004. [Google Scholar]
- Märk, T.D.; Dunn, G.H. (Eds.) Electron Impact Ionization; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Pitchford, L.C.; McKoy, B.V.; Chutjian, A.; Trajmar, S. (Eds.) Swarm Studies and Inelastic Electron-Molecule Collisions; Springer: New York, NY, USA, 1987. [Google Scholar]
- Mohr, J.P.; Wiese, W.L. (Eds.) Atomic and Molecular Data and their Applications; AIP Conference Proceedings; AIP: Woodbury, NY, USA, 1998; Volume 434. [Google Scholar]
- Morgan, W.L. A critical evaluation of low-energy electron impact cross sections for plasma processing modeling. II: Cl4, SiH4, and CH4. Plasma Chem. Plasma Process. 1992, 12, 477. [Google Scholar] [CrossRef]
- PKae-Nune, P.; Perrin, J.; Guillon, J.; Jolly, J. Mass spectrometry detection of radicals in SiH4-CH4-H2 glow discharge plasmas. Plasma Sources Sci. Technol. 1995, 4, 250. [Google Scholar] [CrossRef]
- Capitelli, M.; Celiberto, R.; Cocciatore, M. Needs for Cross Sections in Plasma Chemistry. Adv. At. Mol. Opt. Phys. 1994, 33, 321. [Google Scholar]
- Ratnavelu, K.; Brunger, M.J.; Buckman, S.J. Recommended Positron Scattering Cross Sections for Atomic Systems. J. Phys. Chem. Ref. Data 2019, 48, 023102. [Google Scholar] [CrossRef] [Green Version]
- Zammit, M.C.; Fursa, D.V.; Savage, J.S.; Bray, I. Electron– and positron–molecule scattering: Development of the molecular convergent close-coupling method. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 123001. [Google Scholar] [CrossRef]
- Pindzola, M.S.; Robicheaux, F.; Colgan, J. Electron-impact ionization of H2+ using a time-dependent close-coupling method. J. Phys. B At. Mol. Opt. Phys. 2005, 38, L285. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.K.; Rudd, M.E. Binary-encounter-dipole model for electron-impact ionization. Phys. Rev. A 1994, 50, 3954. [Google Scholar] [CrossRef] [Green Version]
- Deutsch, H.; Becker, K.; Matt, S.; Märk, T.D. Theoretical determination of absolute electron-impact ionization cross sections of molecules. Int. J. Mass Spectrom. 2000, 197, 37. [Google Scholar] [CrossRef]
- Khare, S.P. Introduction to the Theory of Collisions of Electrons with Atoms and Molecules; Physics of Atoms and Molecules Series; Springer: New York, NY, USA, 2001. [Google Scholar]
- Kumar, Y.; Kumar, M. Theoretical partial ionization cross sections by electron impact for production of cations from CH3OH, CO2 and NH3. Chem. Phys. Lett. 2020, 740, 137071. [Google Scholar] [CrossRef]
- Pal, S.; Kumar, J.; Märk, T.D. Differential, partial and total electron impact ionization cross sections for SF6. J. Chem. Phys. 2004, 120, 4658. [Google Scholar] [CrossRef]
- Pal, S.; Kumar, N. Electron-Collision-Induced Dissociative Ionization Cross Sections for Silane. Adv. Phys. Chem. 2009, 309292. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, H.; Brunger, M.J.; Campbell, L.; Kato, H.; Hoshino, M.; Rau, A.R.P. Scaled plane-wave Born cross sections for atoms and molecules. Rev. Mod. Phys. 2016, 88, 025004. [Google Scholar] [CrossRef]
- Graves, V.; Cooper, B.; Tennyson, J. The efficient calculation of electron impact ionization cross sections with effective core potentials. J. Chem. Phys. 2021, 154, 114104. [Google Scholar] [CrossRef]
- Kim, Y.K.; Santos, J.P.; Parentea, F. Extension of the binary-encounter-dipole model to relativistic incident electrons. Phys. Rev. A 2000, 62, 052710. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.A.; Kim, Y.-K. Ionization cross sections by electron impact on halogen atoms, diatomic halogen and hydrogen halide molecules. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 145202. [Google Scholar] [CrossRef]
- Graves, V.; Cooper, B.; Tennyson, J. Calculated electron impact ionisation fragmentation patterns. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 235203. [Google Scholar] [CrossRef]
- Fedus, K.; Karwasz, G.P. Electron scattering on molecules: Search for semi-empirical indications. Eur. Phys. J. D 2017, 71, 138. [Google Scholar] [CrossRef]
- Hwang, W.; Kim, Y.-K.; Rudd, M.E. New model for electron-impact ionization cross sections of molecules. J. Chem. Phys. 1996, 104, 2956. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.-K.; Hwang, W.; Weinberger, N.M.; Ali, M.A.; Rudd, M.E. Electron-impact ionization cross sections of atmospheric molecules. J. Chem. Phys. 1997, 106, 1026. [Google Scholar] [CrossRef] [Green Version]
- Scott, G.E.; Irikura, K.K. Performance of binary-encounter-Bethe (BEB) theory for electron-impact ionization cross sections of molecules containing heavy elements (Z > 10). Surf. Interface Anal. 2005, 37, 973. [Google Scholar] [CrossRef] [Green Version]
- Irikura, K.K.; Ali, M.A.; Kim, Y.-K. Electron-impact total ionization cross-sections of the chlorofluoromethanes. Int. J. Mass Spectrom. 2003, 222, 189. [Google Scholar] [CrossRef]
- Vriens, L. Electron exchange in binary encounter collision theory. Proc. Phys. Soc. Lond. 1966, 89, 13. [Google Scholar] [CrossRef]
- Kim, Y.-K.; Irikura, K.K.; Ali, M.A. Electron-impact total ionization cross sections of molecular ions. J. Res. Natl. Inst. Stand. Technol. 2000, 105, 285. [Google Scholar] [CrossRef]
- Irikura, K.K.; Kim, Y.-K.; Ali, M.A. Electron-impact total ionization cross sections of hydrocarbon ions. J. Res. Natl. Inst. Stand. Technol. 2002, 107, 63. [Google Scholar] [CrossRef]
- Huo, W.M.; Kim, Y.-K. Use of relativistic effective core potentials in the calculation of total electron-impact ionization cross-sections. Chem. Phys. Lett. 2000, 319, 576. [Google Scholar] [CrossRef]
- Gupta, D.; Choi, H.; Song, M.; Karwasz, G.P.; Yoon, J.-S. Electron impact ionization cross section studies of C2Fx (x = 1–6) and C3F x (x = 1–8) fluorocarbon species. Eur. Phys. J. D 2017, 71, 88. [Google Scholar] [CrossRef]
- Gupta, D.; Choi, H.; Singh, S.; Modal, P.; Antony, B.; Kwon, D.; Song, M.; Yoon, J.-S. Total Ionisation Cross sections of cyclic organic molecules. J. Chem. Phys. 2019, 150, 064313. [Google Scholar] [CrossRef]
- Huber, S.E.; Mauracher, A.; Süß, D.; Sukuba, I.; Urban, J.; Dmitry, D.; Probst, M. Total and partial electron impact ionization cross sections of fusion-relevant diatomic molecules. J. Chem. Phys. 2019, 150, 024306. [Google Scholar] [CrossRef] [PubMed]
- Goswami, K.; Luthra, M.; Bharadvaja, A.; Arora, A.K.; Baluja, K.L. Electron impact partial ionization cross sections of 1-butanol. Eur. Phys. D 2022, 76, 97. [Google Scholar] [CrossRef]
- Johnson, R.D., III (Ed.) Computational Chemistry Comparison and Benchmark Database, NIST Standard Reference Database Number 101, Release 21, August 2020. Available online: http://cccbdb.nist.gov/ (accessed on 20 March 2022).
- GAUSSIAN 03; Gaussian, Inc.: Wallingford, UK, 2003.
- Irikura, K.K. Semi-empirical estimation of ion-specific cross sections in electron ionization of molecules. J. Chem. Phys. 2016, 145, 224102. [Google Scholar] [CrossRef] [PubMed]
- Swain, R.; Vasisht, G.; Tinetti, G. The presence of methane in the atmosphere of an extrasolar planet. Nature 2008, 452, 329. [Google Scholar] [CrossRef] [PubMed]
- Mahaffy, R. Intensive Titan exploration begins. Science 2005, 308, 969. [Google Scholar] [CrossRef] [Green Version]
- Tian, C.C.; Vidal, C.R. Cross sections of the electron impact dissociative ionization of CO, CH4 and C2H2. J. Phys. B 1998, 31, 895. [Google Scholar] [CrossRef]
- Lindsay, B.G.; Rejoub, R.; Stebbings, R.F. Production of positive ion pairs by electron-impact ionization of CH4. J. Chem. Phys. 2001, 114, 10225. [Google Scholar] [CrossRef]
- Gadoum, A.; Benyoucef, D. Set of the electron collision cross sections for methane molecule. IEEE Trans. Plasma Sci. 2019, 47, 1505. [Google Scholar] [CrossRef]
- Song, M.-Y.; Yoon, J.; Cho, H.; Itikawa, Y.; Karwasz, G.P.; Kokoouline, V.; Nakamura, Y.; Tennyson, J. Cross sections for electron collisions with methane. J. Phys. Chem. Ref. Data 2015, 44, 023101. [Google Scholar] [CrossRef] [Green Version]
- Lindsay, B.G.; Mangan, M.A. Interactions of Photons and Electrons with Molecules; Landolt-Börnstein: Numerical Data and Functional Relationships in Science and Technology—New Series, Group I: Elementary Particles, Nuclei and Atoms; Martienssen, W., Ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2003; Volume 17C, p. 5001. [Google Scholar]
- Straub, C.; Lin, D.; Lindsay, B.G.; Smith, K.A.; Stebbings, R.F. Absolute partial cross sections for electron-impact ionization of CH4 from threshold to 1000 eV. Chem. Phys. 1997, 106, 4430. [Google Scholar] [CrossRef]
- NIST Chemistry WebBook, NIST Standard Reference Database Number 69. Available online: https://webbook.nist.gov/chemistry/ (accessed on 28 February 2022).
- Goswami, K.; Luthra, M.; Arora, A.K.; Bharadvaja, A.; Baluja, K.L. Electron-impact cross sections of acetylene up to 5 keV. Eur. Phys. J. D 2022, 76, 94. [Google Scholar] [CrossRef]
- Nixon, K.L.; Pires, W.A.D.; Neves, R.F.C.; Duque, H.V.; Jones, D.B.; Brunger, M.J.; Lopes, M.C.A. Electron impact ionisation and fragmentation of methanol and ethanol. Int. J. Mass Spectrom. 2016, 404, 48. [Google Scholar] [CrossRef]
- Arora, A.K.; Gupta, K.K.; Goswami, K.; Bharadvaja, A.; Baluja, K.L. A binary-encounter-Bethe approach to compute electron-impact partial ionization cross sections of plasma relevant molecules such as hexamethyldisiloxane and silane. Plasma Sour. Sci. Technol. 2022, 31, 015008. [Google Scholar] [CrossRef]
- Adamczyk, B.; Boerboom, A.J.H.; Schram, B.L.; Kistemaker, J. Partial ionization cross sections of He, Ne, H2, and CH4 for electrons from 20 to 500 eV. Chem. Phys. 1966, 44, 4640. [Google Scholar] [CrossRef]
- Orient, J.; Srivastava, S.K. Electron impact ionisation of H2O, CO, CO2 and CH4. J. Phys. B At. Mol. Opt. Phys. 1987, 20, 3923. [Google Scholar] [CrossRef]
- Chatham, H.; Hills, D.; Robertson, R.; Gallagher, A. Total and partial electron collisional ionization cross sections for CH4, C2H6, SiH4, and Si2H6. J. Chem. Phys. 1984, 81, 1770. [Google Scholar] [CrossRef]
- Tarnovsky, V.; Levin, A.; Deutsch, H.; Becker, K. Electron impact ionization of CDx (x = 1–4). J. Phys. B At. Mol. Opt. Phys. Phys. 1996, 29, 139. [Google Scholar] [CrossRef]
- Janev, R.K.; Reiter, D. Collision processes of CHy and CHy+ hydrocarbons with plasma electrons and protons. Phys. Plasmas 2002, 9, 4071. [Google Scholar] [CrossRef] [Green Version]
- Lindsay, G.; Mangan, M. Landolt-Bor¨nstein Group I: Elementary Particles Nuclei and Atoms; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2003; pp. 1–5. [Google Scholar]
- Bernath, P.F. The spectroscopy of water vapour: Experiment, theory and applications. Phys. Chem. Chem. Phys. 2002, 4, 1501. [Google Scholar] [CrossRef]
- Larsson, M.; Geppert, W.D.; Nyman, G. Ion chemistry in space. Rep. Prog. Phys. 2012, 75, 066901. [Google Scholar] [CrossRef]
- Savin, D.W.; Brickhouse, N.S.; Cowan, J.J.; Drake, R.P.; Federman, S.R.; Ferland, G.J.; Frank, A.; Gudipati, M.S.; Haxton, W.C.; Herbst, E.; et al. The impact of recent advances in laboratory astrophysics on our understanding of the cosmos. Rep. Prog. Phys. 2012, 75, 036901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hobbie, R.K.; Roth, B.J. Intermediate Physics for Medicine and Biology; Springer: New York, NY, USA, 2007. [Google Scholar]
- Byakov, V.M.; Stepanov, S.V. The mechanism for the primary biological effects of ionizing radiation. Phys. Usp. 2006, 49, 469. [Google Scholar] [CrossRef]
- Liu, D.X.; Bruggeman, P.; Iza, F.; Rong, M.Z.; Kong, M.G. Global model of low-temperature atmospheric-pressure He + H2O plasmas. Plasma Sources Sci. Technol. 2010, 19, 025018. [Google Scholar] [CrossRef]
- Tas, M.A.; van Veldhuizen, E.M.; Rutgers, W.R. Water is an active matrix of life for cell and molecular biology. J. Phys. D 1997, 30, 1636. [Google Scholar] [CrossRef] [Green Version]
- Uehara, S.; Nikjoo, H.; Goodhead, D.T. Comparison and Assessment of Electron Cross Sections for Monte Carlo Track Structure Codes. Rad. Res. 1999, 152, 202. [Google Scholar] [CrossRef]
- Kovtun, Y.V. Mean energy of water molecule ionization by electron impact. Technol. Phys. 2015, 60, 1110. [Google Scholar] [CrossRef]
- Straub, H.C.; Lindsay, B.G.; Smith, K.A.; Stebbings, R.F. Absolute partial cross sections for electron-impact ionization of H2O and D2O from threshold to 1000 eV. J. Chem. Phys. 1998, 108, 109. [Google Scholar] [CrossRef]
- Sahlaoui, M.; Bouamoud, M. Cross sections for electron-impact ionization of water molecules. Can. J. Phys. 2011, 89, 723. [Google Scholar] [CrossRef]
- Champion, C.; Hanssen, J.; Hervieux, P.A. Electron impact ionization of water molecule. J. Chem. Phys. 2002, 117. [Google Scholar] [CrossRef]
- Zavilopulo, A.N.; Chipev, F.F.; Shpenik, O.B. Ionization of water and carbon dioxide molecules by electron impact near threshold. Nuc. Instru. Meth. Phys. Res. B 2005, 233, 298. [Google Scholar] [CrossRef]
- Song, M.-Y.; Cho, H.; Karwasz, G.P.; Kokooulinea, V.; Nakamura, Y.; Tennyson, J.; Faure, A.; Mason, N.J.; Itikawa, Y. Cross Sections for Electron Collisions with H2O. J. Phys. Chem. Ref. Data 2021, 50, 023103. [Google Scholar] [CrossRef]
- Itikawa, Y.; Mason, N. Cross sections for electron collisions with water molecules. J. Phys. Chem. Ref. Data 2005, 34, 1. [Google Scholar] [CrossRef]
- King, S.J.; Price, S.D. Electron ionization of H2O. Int. J. Mass Spectrom. 2008, 277, 84. [Google Scholar] [CrossRef]
- Montenegro, E.C.; Scully, S.W.J.; Wyer, J.A.; Senthil, V.; Shah, M.B. Evaporation, fission and auto-dissociation of doubly charged water. J. Electron. Spectrosc. Relat. Phenom. 2007, 155, 81. [Google Scholar] [CrossRef]
- Cromer, D.T.; Ryan, R.R.; Schiferl, D. The structure of nitromethane at pressures of 0.3 to 6.0 GPa. J. Phys. Chem. 1989, 89, 2315. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Bauer, S.H. Modeling the Decomposition of Nitromethane, Induced by Shock Heating. J. Phys. Chem. B 1997, 101, 8717. [Google Scholar] [CrossRef]
- Winey, J.M.; Gupta, Y.M. Shock-Induced Chemical Changes in Neat Nitromethane: Use of Time-Resolved Raman Spectroscopy. J. Phys. Chem. B 1997, 101, 10733. [Google Scholar] [CrossRef]
- Winey, J.M.; Gupta, Y.M. UV-Visible Absorption Spectroscopy to Examine Shock-Induced Decomposition in Neat Nitromethane. J. Phys. Chem. A 1997, 101, 9333. [Google Scholar] [CrossRef]
- Bouyer, V.; Darbord, I.; Herve, P.; Baudin, G.; Gallic, C.L.; Clement, F.; Chavent, G. Shock-to-Detonation Transition of Nitro- methane: Time-Resolved Emission Spectroscopy Measurements. Combust. Flame 2006, 144, 139. [Google Scholar] [CrossRef]
- Gruzdkov, Y.A.; Gupta, Y.M. Emission and Fluorescence Spectroscopy To Examine Shock-Induced Decomposition in Nitromethane. J. Phys. Chem. 1998, 102, 8325. [Google Scholar] [CrossRef]
- Kelzenberg, S.; Eisenreich, N.; Eckl, W.; Weiser, V. Modelling Nitromethane Combustion. Propellants Explos. Pyrotech. 1999, 24, 189. [Google Scholar] [CrossRef]
- Boyer, E.; Kuo, K.K. Modeling of Nitromethane Flame Structure and Burning Behavior. Proc. Combust. Inst. 2007, 31, 2045. [Google Scholar] [CrossRef]
- Brill, T.B.; James, K.J. Kinetics and mechanisms of thermal decomposition of nitroaromatic explosives. Chem. Rev. 1993, 93, 2667. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, W.; Lin, D.C.; He, N.; Duan, Y. Influence of Nitromethane Concentration on Ignition Energy and Explosion Parameters in Gaseous Nitromethane/Air Mixtures. J. Hazard Mater. 2011, 185, 756. [Google Scholar] [CrossRef]
- Burger, A.; Parulkar, A.P. Relationships between chemical structure and biological activity. Annu. Rev. Pharmacol. 1966, 6, 19. [Google Scholar] [CrossRef]
- Kasemo, B. Biological surface science. Surf. Sci. 2002, 500, 656. [Google Scholar] [CrossRef]
- Jiao, C.Q.; DeJoseph, C.A., Jr.; Garscadden, A. Formation of Positive and Negative Ions in CH3NO2. J. Phys. Chem. A 2003, 107, 9040. [Google Scholar] [CrossRef]
- Kandel, R.J. Appearance Potential Studies. II. Nitromethane. J. Chem. Phys. 1955, 23, 84. [Google Scholar] [CrossRef]
- Hamilton, J.R.; Tennyson, J.; Huang, S.; Kushner, M.J. Calculated cross sections for electron collisions with NF3, NF2 and NF with applications to remote plasma sources. Plasma Sources Sci. Technol. 2017, 26, 065010. [Google Scholar] [CrossRef] [Green Version]
- Barnard, G.P. Modern Mass Spectrometry; Institute of Physics: London, UK, 1953. [Google Scholar]
- Ausloos, P.; Clifton, C.L.; Lias, S.G.; Mikaya, A.I.; Stein, S.E.; Tchekhovskoi, D.V.; Sparkman, O.D.; Zaikin, V.; Zhu, D. The critical evaluation of a comprehensive mass spectral library. J. Am. Soc. Mass Spectrom. 1999, 10, 287. [Google Scholar] [CrossRef] [Green Version]
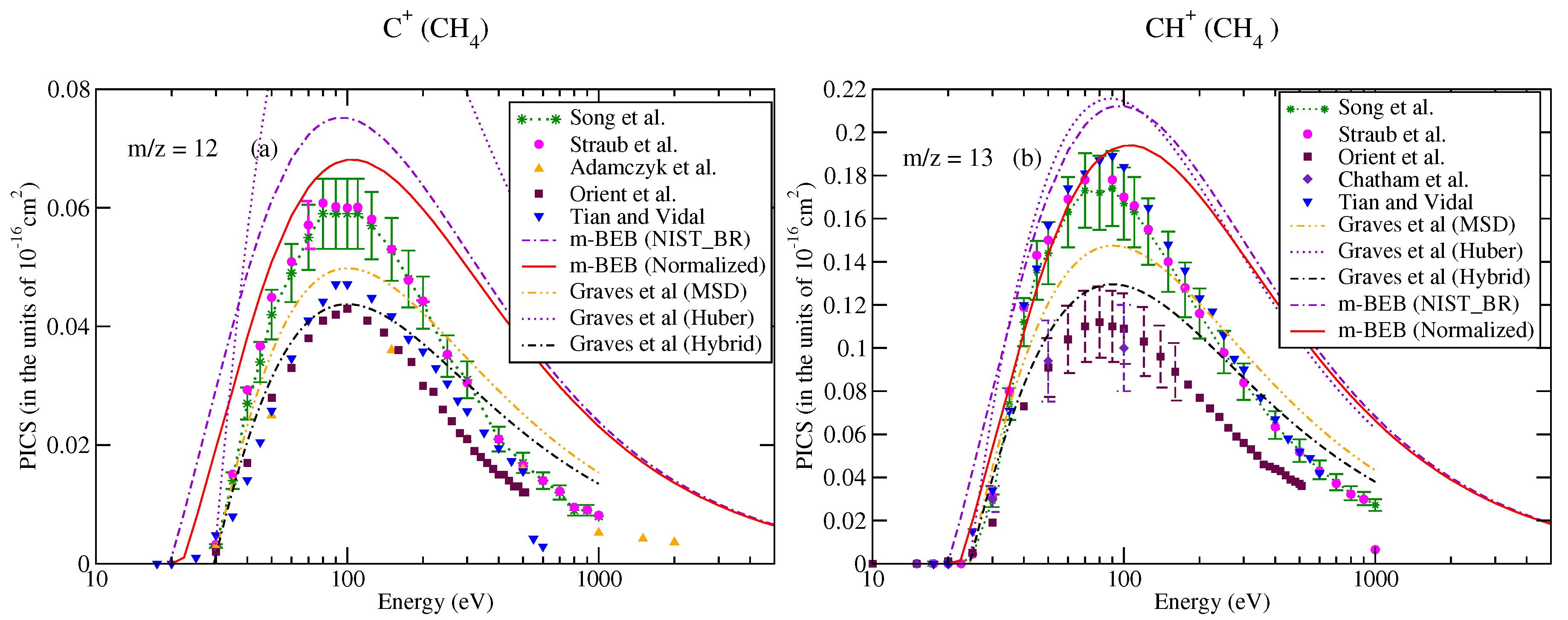
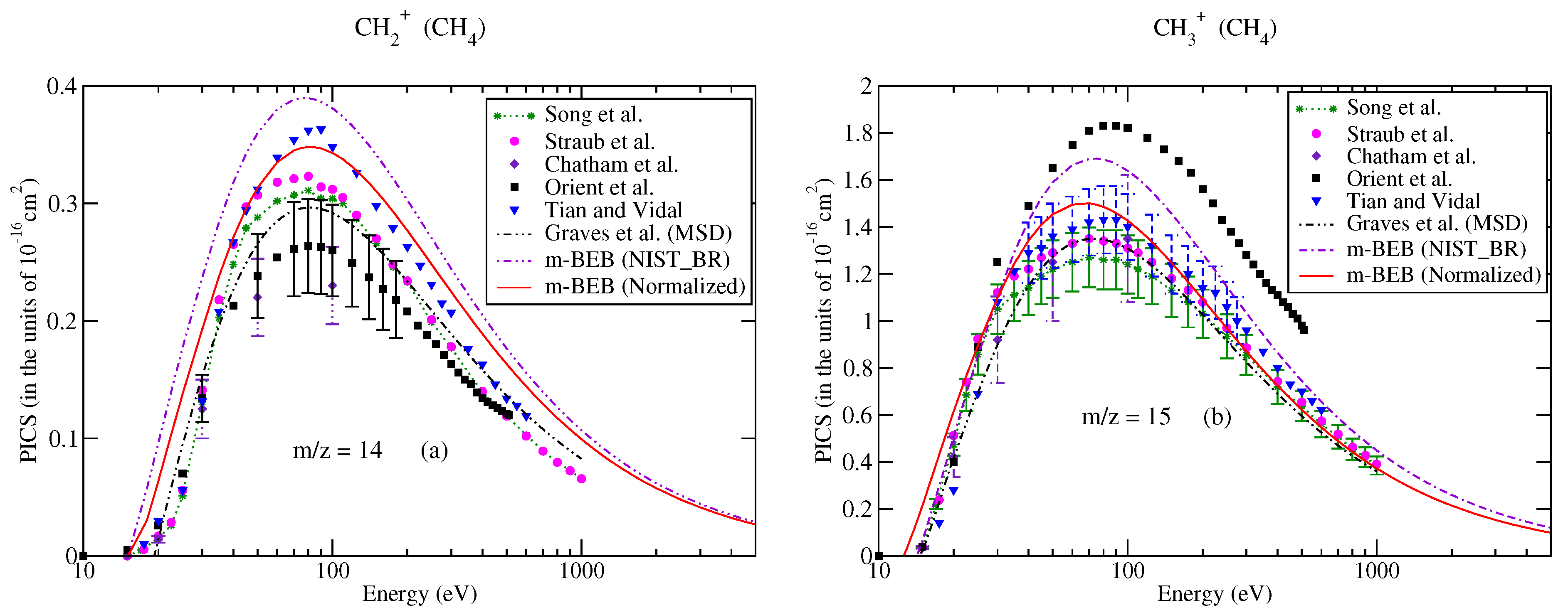
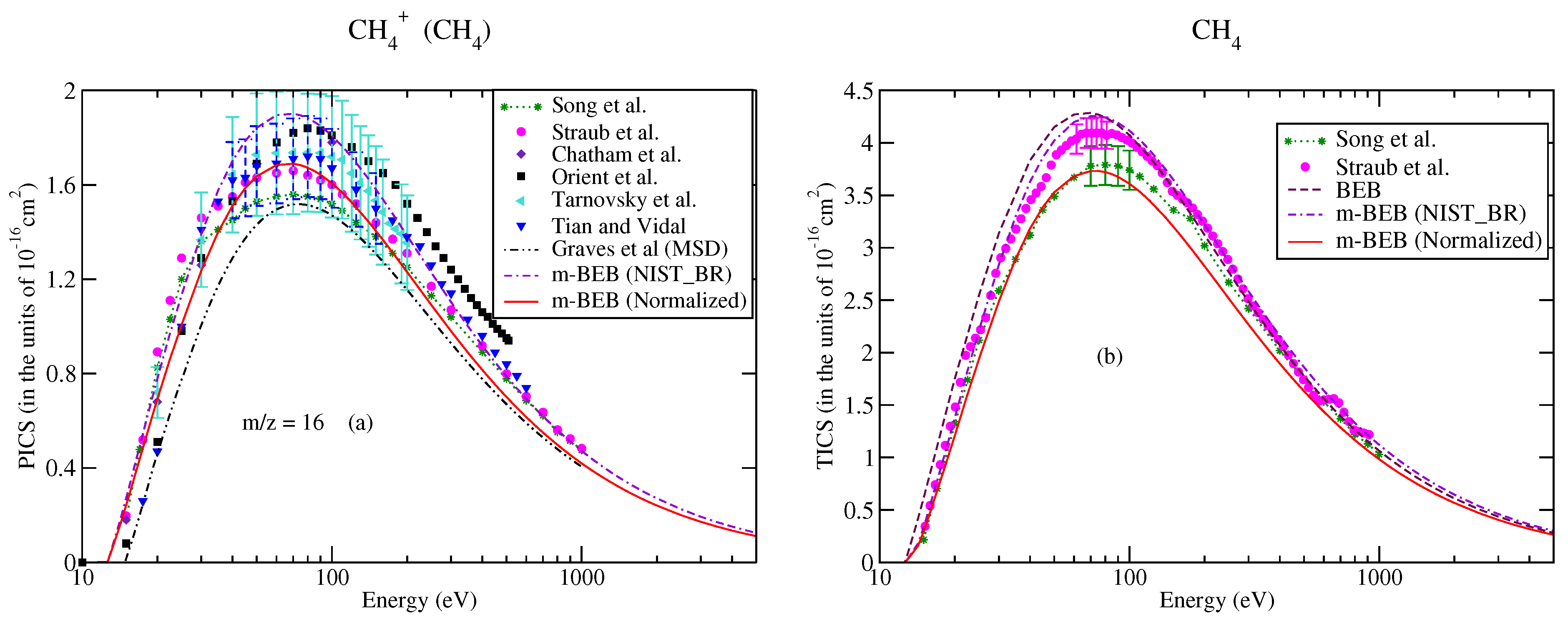

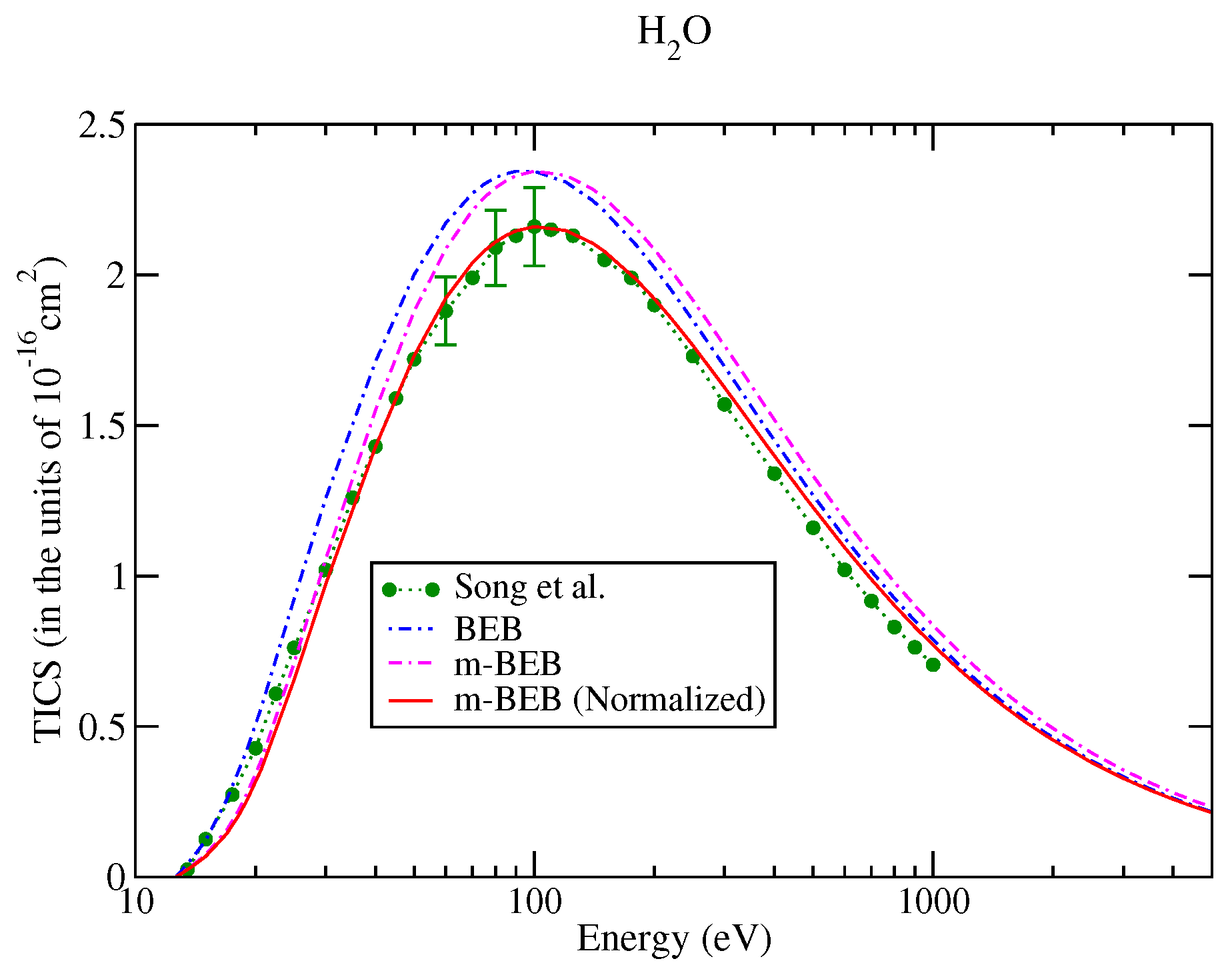


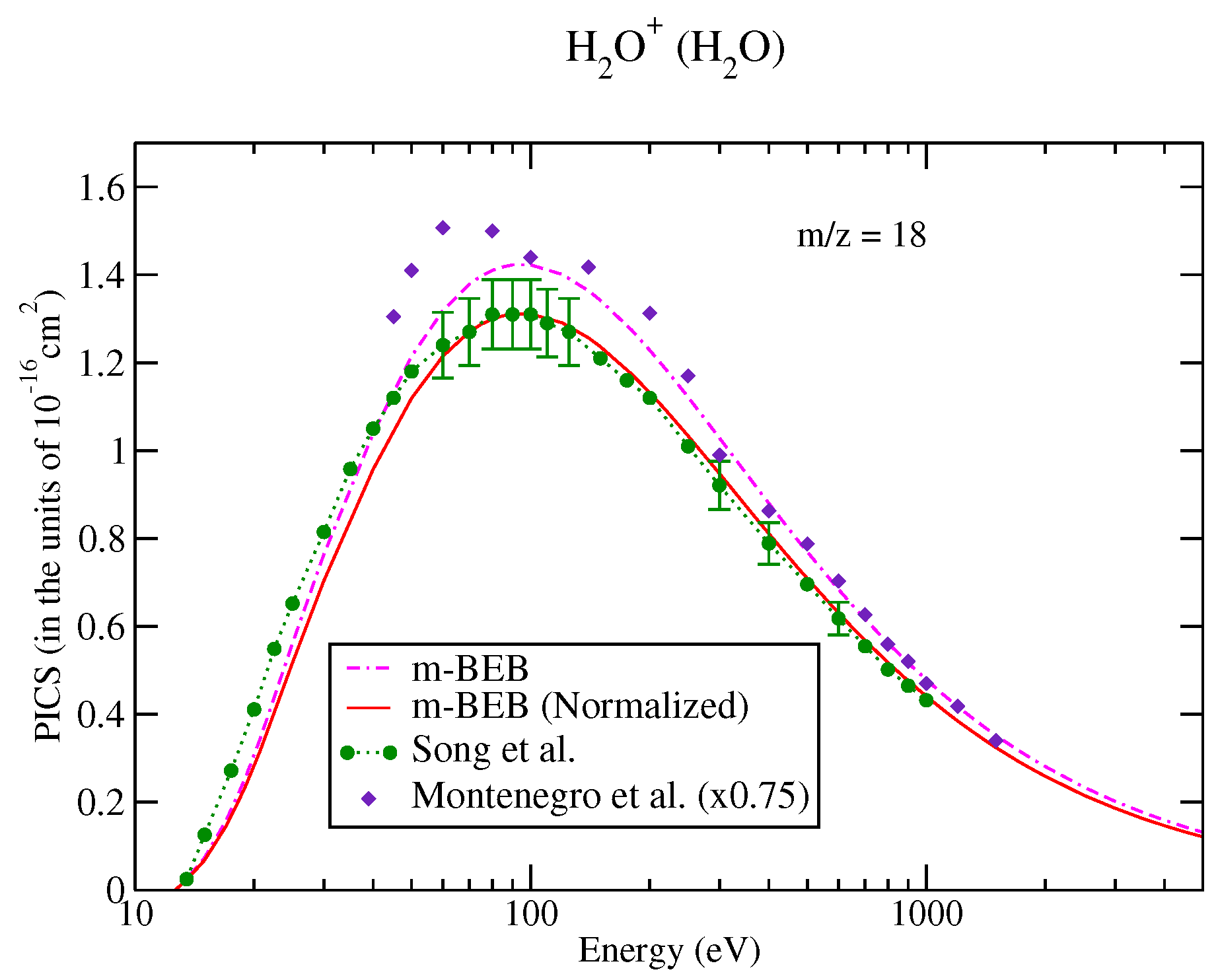

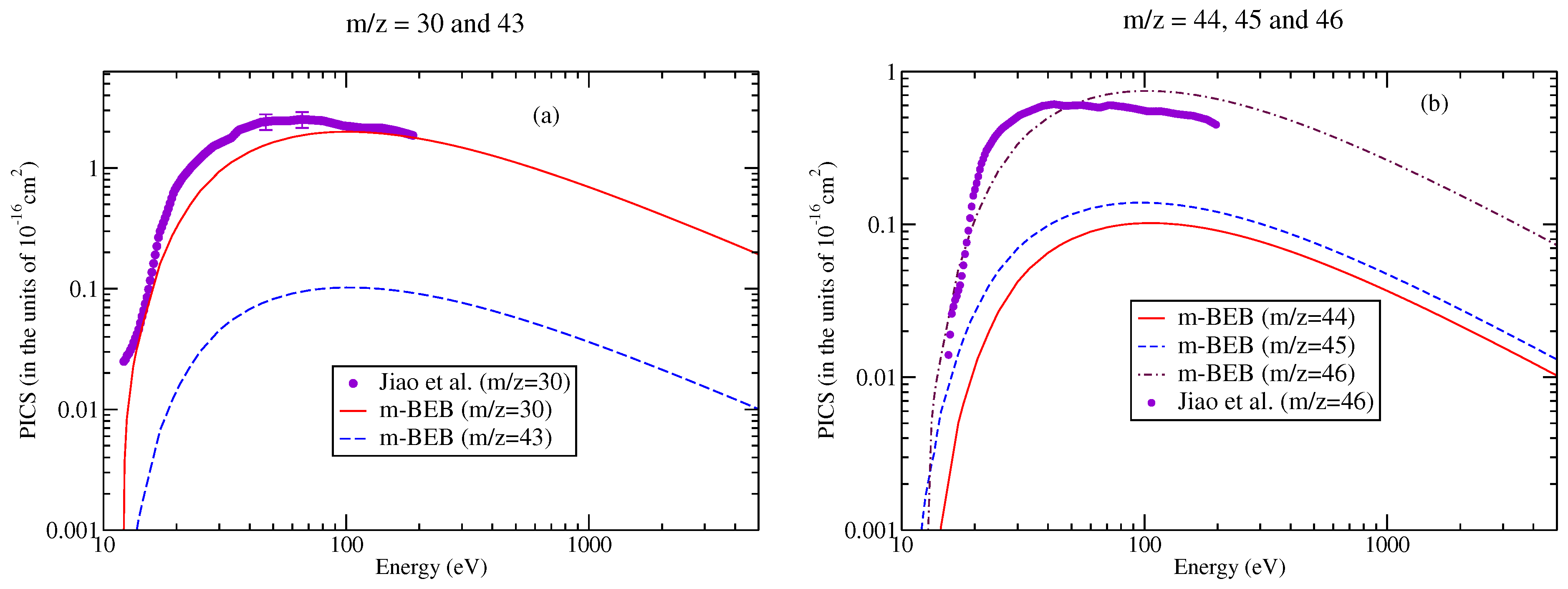
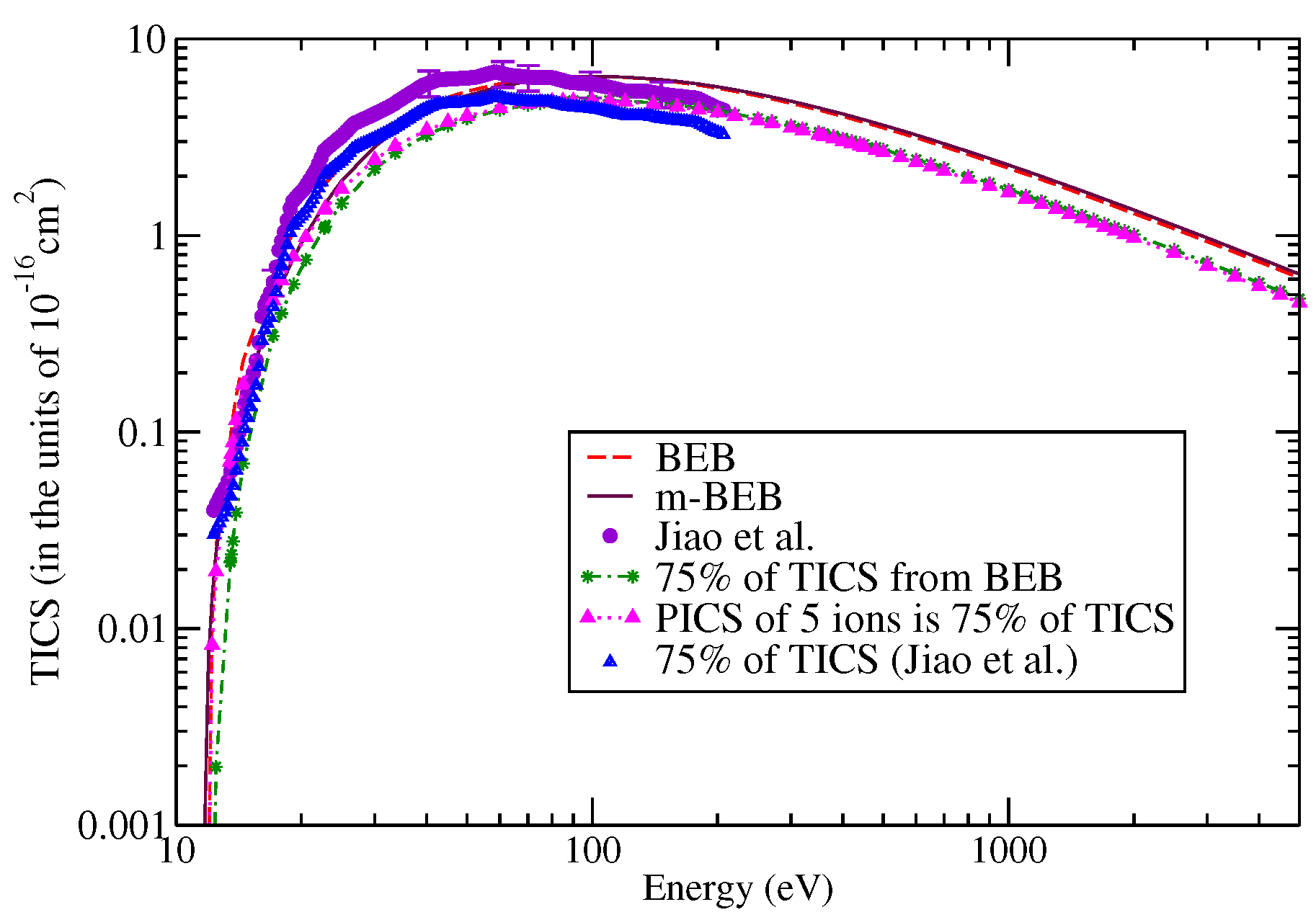
| Ions | Song et al. [48] | NIST Chemistry WebBook Database [51] | Song et al. (Renormalized) [48] | |
|---|---|---|---|---|
| 1 | 0.10053 | - | - | |
| 2 | 0.9260 (−2) | - | - | |
| 12 | 0.1455 (−1) | 0.1699 (−1) | 0.1634 (−1) | |
| 13 | 0.4577 (−1) | 0.4779 (−1) | 0.5141 (−1) | |
| 14 | 0.8122 (−1) | 0.9129 (−1) | 0.9123 (−1) | |
| 15 | 0.3360 | 0.3967 | 0.3774 | |
| 15 | 0.4127 | 0.4470 | 0.4636 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luthra, M.; Goswami, K.; Arora, A.K.; Bharadvaja, A.; Baluja, K.L. Mass Spectrometry-Based Approach to Compute Electron-Impact Partial Ionization Cross-Sections of Methane, Water and Nitromethane from Threshold to 5 keV. Atoms 2022, 10, 74. https://doi.org/10.3390/atoms10030074
Luthra M, Goswami K, Arora AK, Bharadvaja A, Baluja KL. Mass Spectrometry-Based Approach to Compute Electron-Impact Partial Ionization Cross-Sections of Methane, Water and Nitromethane from Threshold to 5 keV. Atoms. 2022; 10(3):74. https://doi.org/10.3390/atoms10030074
Chicago/Turabian StyleLuthra, Meetu, Kanupriya Goswami, Ajay Kumar Arora, Anand Bharadvaja, and Kasturi Lal Baluja. 2022. "Mass Spectrometry-Based Approach to Compute Electron-Impact Partial Ionization Cross-Sections of Methane, Water and Nitromethane from Threshold to 5 keV" Atoms 10, no. 3: 74. https://doi.org/10.3390/atoms10030074
APA StyleLuthra, M., Goswami, K., Arora, A. K., Bharadvaja, A., & Baluja, K. L. (2022). Mass Spectrometry-Based Approach to Compute Electron-Impact Partial Ionization Cross-Sections of Methane, Water and Nitromethane from Threshold to 5 keV. Atoms, 10(3), 74. https://doi.org/10.3390/atoms10030074