2. Basics
In the beginning of my lectures introducing atomic spectroscopy, I try to make the students aware of everyday phenomena that provide a mental scale for atomic phenomena. For example, from Avogadro’s number of about 6 × 10 particles per mole, at roughly ambient pressure in the reference volume of 22.3 l (that is, about 3 × 10 particles per cubic centimetre), one can easily estimate the volume that is available per particle (atom or molecule), that is, about 3.5 × 10 cm. This volume can have any shape, including that of a cylinder with a radius twice the Bohr radius of the hydrogen atom in its ground state (r≈ 0.5 Å); the round cylinder cross-section represents the geometric cross-section for collisions among such particles. In a collision scenario, the length of such a cylinder reaches to the next particle and, thus, represents an estimate of the mean free path (which is inversely proportional to density), which amounts to about 1.2 m at ambient pressure (A plasma physics rule-of-thumb says: at a pressure of 10 mTorr, the mean free path amounts to about 10 cm). At the temperature of our environment (T ≈ 293 K), the thermal energy corresponds to about 1/40 eV, and a nitrogen molecule travels at a velocity of roughly 300 m/s. Combining this velocity with the mean free path yields a typical time interval between collisions on the order of 5 ns and its inverse, the so-called collision frequency. Experimental physics measurements (discussed below) have shown that many excited levels in neutral atoms or molecules in our environment feature mean lives on the order of some 10 ns. Thus, by chance, the radiative lifetime and the typical time between collisions (under atmospheric conditions) are not so different. In fact, there are technical light sources (lamps) that operate at low pressure (say, 1/100 of atmospheric pressure) or high pressure (say, 100 times atmospheric pressure), the spectra of which show the influence of the collision frequency vs. the radiative lifetime, from the narrow-line (unperturbed) emission of low-pressure sodium vapour lamps to the massively broadened line emission of high-pressure sodium or mercury discharge lamps. These devices span roughly four orders of magnitude in pressure, and they use temperature (heating) to regulate the vapour pressure. A more fundamental entity than pressure would be the particle density. I want to discuss the interplay of atomic lifetime and density over about 25 orders of magnitude, in measurements of such atomic lifetimes or in using atomic lifetimes in the determination of density. The basics underlying the order-of-magnitude estimates of atomic parameters mentioned here have been explained in textbooks since the 1930s and do not need to be repeated here.
The density and mean free path estimates relate to neutral particles. As long as a charged ion approaches a neutral one, there is (in a simplistic view) no Coulomb interaction to change this situation. However, the positive ion charge interacts not just with the whole neutral atom, but also with its cloud of negative electrons, and a polarisation (distortion) of the cloud may lead to an electron (or more) being pulled over to the ion, a process called charge exchange (CX). Suddenly both collision partners are positively charged ions and repel each other. The Coulomb repulsion acts on a wider distance than the geometrical cross-section of the atom, and, therefore, the collision cross-section is much larger. Is then the mean free path much shorter? That depends on the density of given collision partners, of which in a mildly ionised plasma may be very few, but many in a hot, substantially ionised plasma. In a plasma, the free ions and electrons experience new phenomena, such as screening, which are better described by other (plasma physics) concepts than by individual collisions. For the scope and purpose of the present discussion, the parameter range of a neutral medium consisting of mostly neutral particles may serve sufficiently well for basic considerations. In the same vein, where applicable, (particle) density and electron density will not be explicitly distinguished, although, for example, the electron density in a carbon foil is six times that of the number density of nuclei, and in a solar coronal plasma some ions may be highly ionised and, thus, there may be as many free electrons per ion around—the dominant fraction is still hydrogen, respectively, protons and electrons in equal numbers.
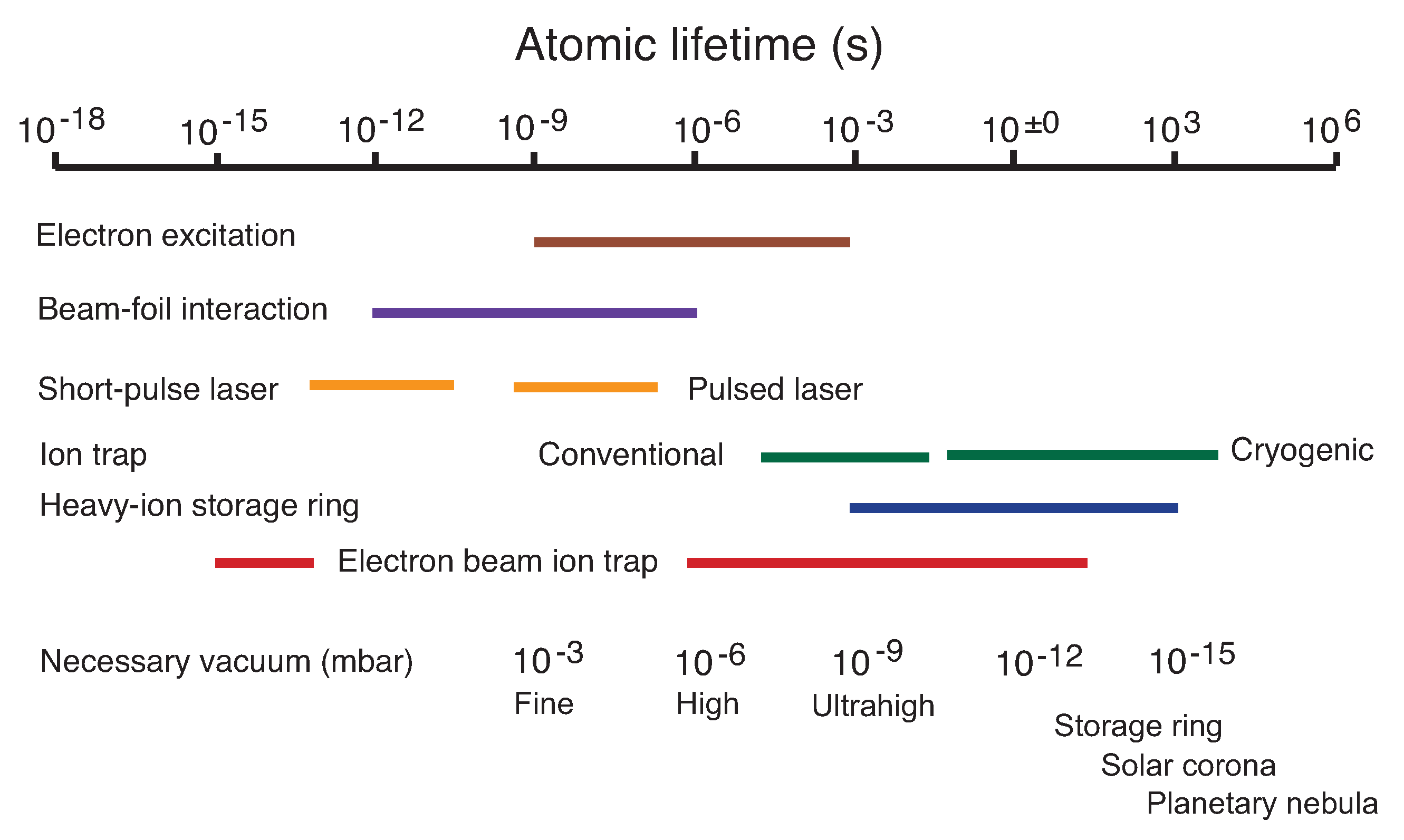
Figure 1 serves as an overview over the atomic lifetime and density (ambient pressure) ranges mentioned in this presentation, and of the devices/techniques used for atomic lifetime measurements. In
Table 1, I have listed atomic lifetime examples in the range from 10
s to 10
s, preferably of simple atomic systems. The arrangement is by lifetime in increasing order, not by any physical connection. Most of the shortest lifetimes relate to decays in the X-ray range (and vice versa), which has to be expected from the classical description of the transition rate as a function of oscillator strength and transition wavelength or energy. Correspondingly, most long-lived levels are long lived because they give rise to transitions of low energy (and thus long wavelength, e.g., in the infrared (IR)). However, there also are long-lived level decays in the vacuum ultraviolet (VUV) or extreme ultraviolet (EUV), if selection rules (spin conservation or parity; see He atoms and He-like ions) block an otherwise possible high-rate decay channel. Thus, very short and very long lived levels can often be found in a common given atom, for example in the He atom (spectrum He I), with its 2 h-lifetime of the 1s2s
S
level which decays via a relativistic
transition, and the nanosecond-lifetime of the 1s2p
P
resonance level (these lifetimes differ by 12 orders of magnitude) [
7,
8]. The
transition rate scales with the 10th power of the nuclear charge
Z; the heaviest element for which this level decay rate in a He-like ion has been measured is Xe (
), with a lifetime result of a few picoseconds. This decay rate has been studied along the isoelectronic sequence, with results spanning 15 orders of magnitude. In most of the lifetime experiments and elements addressed in He-like ions, the measured
transition rate eventually overlapped with the state-of-the-art prediction within the error bars (A notably difficult case was Ar
which at a lifetime of about 200 ns proved to be very challenging for fast-ion beam techniques). With many of the experimental results one would wish, in the next step, for a smaller uncertainty. Indeed, the experimental result with the tightest uncertainty estimate [
9] deviates by more than
from current theory [
10]. However, this is a single data point. More of such precise and, one hopes, accurate results are wanted to find out whether or not theory needs corrections in the high-
Z range of the data sample.
The examples in
Table 1 have been chosen to provide material for self-study via examples; approximate values are given instead of the latest research results. If one picks a didactic example from the middle of the aforementioned range, one may choose an atomic system with a lifetime of
10
s, which is the order of magnitude of the resonance level lifetimes of alkali atoms. Longer lifetimes are possible as a matter of small-term energy differences or particular combinations of level structure and symmetry (selection rules). So far the longest lifetime (of more than a year) has been measured in
Yb
, on a
level with an electric octupole (
) decay [
11], which had earlier on been estimated to amount to several years [
12]. In this case, the total angular momenta of the initial and final states differ by 3 units, and all dipole and quadrupole transitions are excluded; the octupole transition is the lowest multipole order that can bridge the gap, and
features the correct parity change. In highly charged ions, there are similar cases of high-multipole order transitions. For example, in Ni-like ions, an
decay was recognised in the very heavy highly charged ions Th
and U
[
13], corroborated by theory (pointing also to Pd-like ions) [
14], measured, with some time resolution, in much lighter ions [
15,
16], and then it was recognised to be affected by hyperfine effects and thus needing isotopically pure samples for proper lifetime data [
17] (see also
Section 4.3). Thus, listing a single (long) lifetime value for a particular high-
J level in a heavy ion may be misleading. Nevertheless, there are various high-
J levels of peculiar interest, as has been discussed elsewhere [
18]. However, it makes little sense to insist on “correct” individual lifetime data in
Table 1, while the discussion largely uses orders of magnitude.
We have started the practical estimates with level lifetimes encountered in our everyday environment that are of the order of 1.6 s, at a gas density of about 3 × 10 particles per cubic centimetre. Short atomic lifetimes, for example in the hydrogen-like spectrum Fm C (, all but one electron removed: very exotic, indeed, but predictable), are in the range of 1.6 s. This crude estimate neglects the considerable contribution of relativistic effects, due to which, at such a high value of Z, the “fine structure” of the levels is almost of the same order of magnitude as the gross structure. Thus the two 2p fine structure levels feature clearly different lifetimes for . A reminder: the Roman numerals in the labels of the spectra of highly charged ions indicate the number of positive charge units a valence electron “sees” when the screening of the nuclear charge by the inner electrons is taken into account (subtracted from the atomic number Z). Fm (Fermium) has an atomic number and, thus, 100 electrons as a neutral atom (spectrum Fm I); Fm C is the H-like ion in which a single electron stays with the nucleus after 99 electrons have been removed (ionised). The above relations point to a density of 3 × 10 particles per cubic centimetre at which density effects on the level lifetime might be notable. That is more than 10 times the density of solid matter. In terrestrial laboratories, such matter density is only reached in transients in high-pressure anvil cells (little chance to produce highly charged ions, because not enough energy is deposited in single atoms to shed almost 100 electrons) or in violent plasma experiments producing shock waves where (high) temperature is very important.
For example, so-called laser-fusion experiments (more correctly called inertial confinement fusion (ICF) experiments) attempt to reach nuclear fusion in a hydrogen isotope (D,T) sample that is compressed and heated by laser light. Facilities on this research path are, among others, OMEGA (USA), NIF (National Ignition Facility, USA), Laser Megajoule (F), and Orion (UK). In the indirect drive option, a centimetre-size hollow cylinder of high-Z material is irradiated by up to 192 (at NIF) powerful visible-light laser beams and heated so that the atoms are highly ionised (up to, say, q ≈ 40, with typical level lifetimes on the order of 10 s in the M and N shells) and emit X-rays that converge on a small (few-millimetre-size) fuel cell. The suddenly rising radiation pressure initialises a shock wave in the fuel and that, in turn, compresses part of the fuel up to about 1000 times solid state density. In the direct-drive version of the experiment, the lasers target the fuel cell directly. What about atomic lifetimes in the modelling of such a laser-ignition of ICF? The heavy-element liner used to convert visible laser light (by absorption and formation of a hot plasma) into X-rays does not quite reach the high density of the hydrogen fuel, since it is located on the outside, not in the centre of the implosion. The sheer density (neglecting the electric fields of highly charged ions) is not high enough to cause massive effects on the lifetimes of the excited levels in the heavy element ions. Thus, for the heavy element liner, our estimates of density and atomic lifetimes in highly charged ions apply. The high density in the nuclear fuel would affect transitions in cool hydrogen. However, the hydrogen fuel is compressed and heated far beyond the dissociation energy of atomic H (13.6 eV); the hydrogen is immediately turned into a hot plasma of protons/deuterons/tritons and free electrons. The continuum of black-body radiation and free-electron scattering should swamp the emission spectrum (with the fundamental transition Ly (Lyman-alpha) in the vacuum ultraviolet range), rather than the line radiation from H atoms.
Laboratories, such as NIF, cost billions of dollars and take many years to build. A much smaller experiment demonstrates spectra that bridge the physics context from a small laboratory device to the astrophysics of white dwarfs [
19]: in the laser-induced breakdown spectroscopy (LIBS) technique, of practically any material sample, a small plasma can be produced by an energetic, very short, well-focused laser light pulse from a table-top, show-box-size, pulsed Nd:YAG laser device. For example, the material sample can be pure hydrogen gas, and the line profiles (for example of the H
(Balmer-beta) line) can be studied for their similarity with astrophysical observations. Indeed, just as in the aforementioned fusion test plasma, a high degree of ionisation and the presence of many free electrons can be studied via spectroscopic means.
There are also experiments in which X-ray lasers interact with relatively cool matter. X-ray laser light can surely excite and ionise single atoms, but researchers want to find out which processes might explain the observed multiple excitation and ionisation, and whether density plays a role, that is, the proximity of other atoms. Highly charged ions in high-density matter are subject to rapid recombination. According to our simplistic estimate connecting typical atomic lifetimes, collision times, geometric cross sections, and mean free paths, the 2p level lifetime in H-like Ne X, of 1.6
s, corresponds to a density on the order of that of a solid, and not much higher. That looks like a valid ball park for experiments on, perhaps, micro-droplets of liquid Ne, to be exposed to X-ray laser light, as a follow-up to some of the ideas that have been discussed by Rohringer et al. [
20] and expanded into a productive suite of experiments. Apparently, those experiments can be modelled sensibly with basic atomic physics parameters “as known”. Of course, the real cross-sections of highly charged ions depend on the charges of the collision partners, but those “corrections” to the present ball park figures lie beyond the horizon of this discussion.
Another reminder of some basics: if X-rays or fast particles remove an inner electron, say, from the K-shell of the target, is not it difficult to compute the transition rate for K radiation in such a multi-electron ion? Actually, no. To a good approximation, p-electrons in the L shell see the nuclear Coulomb field shielded by the s-electrons of the K shell, while the outer electrons hardly matter, a result expected from potential theory of long before the discovery of electrons. Thus, the transition rate for K radiation in an atom with a single inner vacancy is about the same as that for a one-electron ion (represented by H-like ions in
Table 1).
2.1. H-like Ions
Atoms and ions with only one electron are, for all practical purposes, well described by quantum mechanics and quantum electrodynamical (QED) corrections. Half a century ago, Garcia and Mack [
21] calculated the level structure of the H-like atoms and ions of the first 20 elements with high precision. This work has since been expanded to cover all elements (see, for example, [
22]), and the QED calculations for highly charged ions (HCI) have developed into a cottage industry of their own. For general spectroscopic purposes (and unless interested in almost pure determinations of QED effects), the venerable calculation remains valid as a source of excellent and highly accurate reference data on wavelengths. Transition rates in such ions have been calculated for many decades (see [
23,
24], but one has to watch out for the tricky g-factor calculations on transition rates for multiplets, versus those simple ones for fine structure transitions). In contrast to calculations of the properties of single-electron atoms, experiments measuring level lifetimes have massive problems reaching a high accuracy. The 2s level lifetime in atomic hydrogen, for example, at 1/8 s is rather long for laboratory work of many types, and the 1.6 ns lifetime of the 2p levels has been considered to be rather short for a variety of experimental techniques. External fields influence the 2s–2p level mixing and hinder clean measurements (for a general introduction to atomic lifetime measurements, see, for example, the AMOP Handbook [
25] article by Curtis [
26]). Testing the H I 2p level lifetime experimentally has been so important that a measurement with a claimed uncertainty of only about one part in a thousand and finding agreement with theory had to be repeated (by others) when a mistake in theory was uncovered which spoiled the seeming (temporary) agreement.
Owing to the Lamb shift, the 2s
level in a hydrogen-like atom or ion lies very slightly above the 2p
level, but the transition energy is extremely small and, thus, an
transition within the
shell is of low probability. Alternatively, the 2s
level decays by
(two-photon transition, rate
[
27]) or
(single photon transition, rate
[
24]) decay. At low
Z, the two-photon decay channel dominates the 2s
level decay, whereas at high
Z the single-photon
channel does.
The rate of decay of the H I 2p levels to the 1s ground state results in an upper-level lifetime of about 1.6 ns (1.6 × 10 s). A crude estimate of the 3d level lifetime is 16 ns, and 160 ns for the 3s level. Of these, and in fact of all levels in atomic hydrogen, the 2p levels are the shortest-lived. In hydrogen-like ions, the electric dipole (E1) transition rates A (of transitions from level k to level i) scale with the square of the transition energy, which itself scales with the square of the nuclear charge: A ∼ , and A ∼ .
For transitions with , the oscillator strength f in a hydrogenic system is constant. while the energy differences scale as . For transitions with (in multi-electron systems), the oscillator strength scales as (for ions beyond the first few of an isoelectronic sequence, where the shell structure is not yet stratified). Consequently, the transition rate increases linearly with the screened nuclear charge = Z − (number of core electrons), that is, A∼. Such simple scaling rules render the concept of isoelectronic sequences attractive; ions of the same number of electrons show basically the same internal structure and dynamics, and the Z-dependences of various atomic parameters can be described by simple expressions.
2.2. He-like Atoms and Ions
Interesting options arise from the complexities of added electrons in atomic systems with two or more electrons. Of course, this is not new: Egil Hylleraas [
28,
29] has employed the then (around 1930) new quantum mechanics toolbox to look for regularities of various atomic structure parameters as a function of the ion charge, and he has developed series expansions in terms of
that provide useful isoelectronic estimates, enabling inter- and extrapolations once one knows suitable reference values. In terms of atomic lifetime measurements on multiply charged ions, recent reviews [
30,
31,
32,
33,
34,
35,
36,
37] point to a plethora of references.
A drastic change from the spectrum of atomic hydrogen is the electron–electron interaction that arises from the presence of a second electron in He-like atomic systems. Symmetries may hinder certain
transitions from occurring, while other transitions appear only now. Prominent examples are the
,
spin-changing (intercombination) transitions with
, the magnetic dipole (
), or the magnetic quadrupole (
) transitions. For atomic He, experiments have had immense problems with the measurement of some very long level lifetimes, and only recently has a set of experiments been successful in measuring the lifetimes of all
triplet levels with a meaningful accuracy [
7,
8]. At long last, highly accurate theoretical results have been corroborated by precise data. However, for atomic He, computation seems to be still ahead of experiment in accuracy.
The two-electron system helium is a well-calculated and measured prototype, and serves as a Rosetta stone that provides conceptual keys to studies of many ion species, including the rates of a variety of transitions. I remember how, in an atomic physics lecture, He was described as the almost perfect showpiece of the Russell–Saunders (LS) coupling, including spin conservation. What was not mentioned was that the transition rate of the
−
intercombination transition is not tiny at all; spectral tables list the intensity ratio of the resonance to the intercombination line in He I as about 40 (In the days before photoelectric detection, this value did not have much of a quantitative accuracy, and logarithmic estimates from the blackening of photographic emulsions dominated). The more recent NIST ASD tables [
38] list a line ratio of about 20, while the (well calculated) transition rates differ by about seven orders of magnitude. A warning: much more happens in a light source than meets the eye, and not all tabulations are clear about photoelectric (linear) or photographic (logarithmic) line intensities.
Intercombination (spin-changing) transitions are often described by the corresponding transition rate without spin change, with a mediating factor describing the multiplet mixing. At low Z, the multiplet-mixing matrix element scales with and is applied in quadrature. Thus, intercombination transition rates with a change of principal quantum number n scale with , whereas those for in-shell transitions () scale with . At low Z, the multiplet-mixing matrix element is often of order 1% (resulting in an intercombination transition rate that is a factor of about 10 smaller than the corresponding fully E1-allowed transition rate), where such transitions matter in low-charge ions, they extend the above nanosecond range of “regular” atomic level lifetimes to the millisecond range for levels with a dominant intercombination decay.
Higher-multipole order transitions
depend on the parities and the total angular momenta of the levels involved. The basic iso-electronic scaling rules for transition rates of various multipole orders have been obtained by Pasternack [
39]. Shorter versions are given in chapter 10 of Drake’s original AMOP Handbook [
25] (and in its successive issues, the latest version is in preparation right now), by Martin and Wiese [
40]; this material is also available on the web [
41]. Using their formulas as building blocks, one can, for example, derive the scaling behaviour of the rates for intercombination transitions (intra-shell or inter-shell transitions). In brief:
transition rate for a transition: f const, A→.
Intercombination () transition rate for a transition: .
transition rate for a transition: f, →.
Intercombination () transition rate for a transition: .
As is expected for higher-order terms in a multipole expansion of the radiation field, the amplitudes are generally smaller than those of the contribution, rendering most of the higher-order decays negligible—unless the decay of a given level is forbidden by parity and total angular momentum selection rules. The same applies to the higher orders, so that there are cases in which or decays are the dominant decay channels. The transition rates of these (-) forbidden transitions are very small for neutral atoms, but they scale steeply with Z, so that at high Z, these lines are competitive in line intensity with transitions.
Inside the ground configuration of a multi-electron ion there can be many levels of the same parity. Thus, only -forbidden transitions are possible, at rather low excitation energies (long transition wavelengths). However, transition rates scale steeply with the transition energy, which anyway scales more steeply with Z than that of the transitions mentioned above. For example, the level structure in such a term scales with (as the fine structure in hydrogen, a relativistic effect), and, consequently, the rates increase with and higher powers just because of the contribution of the transition energy.
transition rates rise ∼ (, within a given electron configuration, and thus () may increase ∼;
transition rates rise ∼ (, within a given electron configuration, thus () may increase ∼;
the relativistic rate in the He isoelectronic sequence increases steeply with Z: () ;
the transition rate for a transition increases not quite as steeply with Z: () ;
and so on. For further discussions of such systematics, see [
30,
42].
3. Examples of Methods and Techniques Applied in Specific Lifetime Ranges
Ideally, an atomic level that is to be measured for its decay properties is excited instantaneously and selectively, and then left to decay without further interactions, all the time being monitored for its decay that is detected with probability one. Actually, none of these requirements is perfectly fulfilled in reality. In the 1920s, Wilhelm Wien tried to measure atomic lifetimes using canal rays, but the geometry was too poorly defined to yield notable results. After all, atomic lifetimes in neutral atoms or low-charge state ions typically fall into the nanosecond range. Typical physics laboratory electronics (oscilloscopes with internal radio tubes) struggled with such fast signals well into the 1970s. If an atomic species was to be excited by electrons, the choice was between fast switching in electron energy (accelerating voltage), or current, or location of the electron beam. One standard experimental lay-out called for an atomic (molecular) beam crossing a well-collimated electron beam. The decay could be recorded by electronic timing of the detector signal after switching the electron beam off, or by moving the detector along the atomic beam, and taking the distance from the interaction zone as a measure of time after excitation (or by evaluating the phase shift of an oscillating signal after an oscillatory modulation of the excitation). These basic alternatives—as well as several of their technical implications—reappeared as soon as lasers entered the field. A few numerical examples show the lifetime range accessible with fast atomic or ion beams: N atoms or ions of 1 keV kinetic energy travel about 1 mm in 10 ns, thus permitting a time resolution of about 10 ns when interacting with a crossing electron beam of 1 mm width. At 100 keV, a beam energy available at many laboratories in the late 1960s, this would improve to about 1 ns. The same particle species travelling at 10 MeV has a speed of about 1 mm per 100 ps; in beam–foil spectroscopy, the interaction zone (a thin foil of high electron density) would be passed through in a few femtoseconds, and the time resolution would be limited by the geometry of the detection system (usually on the order of many picoseconds, see section below).
The excitation of a level requires an energy transfer that at least matches the excitation energy. However, at threshold, the excitation cross section is small and, thus, the signal is poor. Bennett and Kindlmann [
43] demonstrated that at electron beam energies higher than the threshold the signal may be much brighter, helped by cascade feeding through higher-lying levels that were simultaneously excited, but the decay curves then show distortions (multi-exponential decay curves) that render the data evaluation cumbersome or even impossible. The signal is poorest, but also cleanest, just above the threshold. The same insight, the need for selective excitation, eventually pointed to narrowband laser excitation. However, while lasers can serve the study of all neutral atoms, even nowadays, some 60 years after their introduction, they are not able to reach most levels in multiply ionised atoms, neither from the ground state, nor from metastable excited levels.
Some 45 years ago, Imhof and Read [
44] reviewed a multitude of techniques for lifetime measurements in atoms, molecules, and ions, including the findings by Bennett and Kindlmann [
43]. They also recite beam–foil spectroscopy and the then new-fangled fast-ion laser experiments, both addressing mainly the nanosecond lifetime. I am not repeating this task here, but jump to another specific technique of electron beam excitation, one that tried to beat the fast switching problem of an electron beam while maximising the signal.
3.1. High-Frequency Deflection Technique
The high-frequency deflection (HFD) technique avoided very-fast electronic switching by employing slower switching (oscillation) in a combination with geometry. An electron beam was scanned/swept across a narrow aperture, and the electron beam would reach its target particles behind the aperture only during one short time interval in each sweep. The real-life comparison is with a lighthouse and its rotating optical system; the light is continually on, but the distant observer sees only a flash, when the sweeping beam points her/his way. Thus, the electron beam current could be chosen high and constant, and the time range of microseconds—mostly in molecular ions, such as N
, O
, CO
—was addressed. These small molecules and radicals are of particular interest in atmospheric physics. Their spectroscopic signatures were clearly confirmed in observations on the “other side of the wall” with that small aperture. For a survey and representative experiments, see the work by Peter Erman and colleagues [
45,
46,
47]. Unfortunately, some of the experiments resulted in lifetime values so much shorter than predicted that systematic errors had to be assumed. They turned out to result from what had been assumed to be a strength of the arrangement, the high electron beam current. In the interaction zone of the fast electrons with the gas (beyond the aperture), the electrons would ionize and excite the ambient gas particles so efficiently (in high numbers) that the charged particles would feel each other’s Coulomb field and, thus, be mutually repelled and leave the observation zone. The more efficient the ionisation-cum-excitation arrangement, the stronger the mutual repulsion and the steeper the slope of the observed decay curve, misleading the evaluation to a much shorter apparent lifetime value. So this experiment suffered from a specific problem of density, not of the ambient gas, but of charged particles: a Coulomb explosion of the very ion sample produced.
In order to keep the particles confined to the observation volume for the duration of the atomic lifetime, Möhlmann and de Heer [
48] in their experiments introduced a particle confinement by moderate magnetic fields, and then obtained level lifetimes commensurate with the range of predicted values. Their atomic and molecular lifetime findings agreed with the results beam–foil work of the time performed at Lyon [
49], which, at the time, also included molecular ion studies. The Lyon laboratory operated their small ion accelerator at a voltage on the order of 100 kV. They had no Coulomb explosion problem, because their accelerated ions were much more energetic than those in the HFD experiments to begin with, and the particle density in such ion beams is very low. In beam–foil experiments, the ions pass through very thin carbon foils for ionisation and excitation, foils of a thickness that is on the order of 10 nm (and sometimes more). The geometric cross section of the ion beam is on the order of a few square millimetres, and the ion beam current amounts to, say, 1
A. One can easily estimate that along the beam the typical distance between ions is much larger than the foil thickness, so that at a given time rarely more than a single beam ion is inside the foil, while the lateral distance usually amounts to millimetres—on an atomic scale, the travelling ions are far away from any of their peers.
A cleaner experiment than the ionisation-cum-excitation of molecules in “open space” and the provisional confinement of an expanding ion cloud by magnetic fields can be done in an ion trap, at much lower particle densities and, thus, weaker interactions between the charged particles. By chance I became part of such an effort during a research visit to Harvard College Observatory [
50]. No, this experiment was not successful. Among several other problems it turned out that a preceding worker on the ion trap had removed the cryogenic baffle on top of the oil diffusion pump that should have provided the high vacuum for the ion trap. Without that, the radiofrequency ion trap became contaminated by oil vapour and the vacuum stayed too poor (the gas density too high) to measure relatively long atomic lifetimes, in this case on OH
ions. A proper measurement would have required a vacuum pressure better than 10
mbar, which we probably missed by two orders of magnitude. In earlier, cleaner days, the same apparatus did deliver useful lifetime data in the microsecond range [
51,
52,
53]. Eventually many substantially longer lifetimes wanted to be measured (elsewhere), which required much improved ion storage and trapping conditions (see sections below).
3.2. Beam–Foil Excitation
A fast ion beam from an accelerator can be passed through magnetic or electric fields to change the trajectory or the speed of the ions, or it can be sent through a photon field (laser beam) to excite the ions, or through matter to affect the ions by changing their charge state and excite them as well, by collisions with atoms and/or electrons. If the interaction zone is spatially well determined, this corresponds to a well-defined time signal in the rest frame of the speedy ions. In principle, the beam–foil interaction technique is suitable for almost all atomic lifetimes up to many nanoseconds. The short-time limit is given by the mechanical translation (displacement) of the foil or the detector by a few micrometers, which corresponds to an ion time-of-flight of several picoseconds. The standard technique of measuring the light (or electron) emission from the beam as a function distance from the foil (time after excitation) has been described many times before (see, for example, [
2]).
Even shorter lifetimes are associated with the inner-shell vacancies of heavy ions. As stated above, the lifetimes of K-shell vacancies are not very different from those of levels in one-electron ions that decay to the
level, that is the Lyman level series. A numerical example is the Ar XVIII 2p level (
) in
Table 1, which provides guidance in discussing the experiments of the Betz group [
54,
55] who addressed K radiation in highly charged S (
) ions. Betz et al. measured the X-rays from the fast ions while they traversed thin foils of different thickness. They expected level lifetimes on the order of 10
s. This is slightly longer than the ions take to pass through such an exciter foil. The ions from the ion source and ion accelerator arrived after a travel time of microseconds, and, thus, would not carry inner-shell vacancies. Upon entering the exciter foil, the fast ions (of MeV energies) encounter a dense sea of electrons that to the ions appear as almost free (binding energies of eV to less than 1 keV), and ion cores contributing to some scattering. The foil electrons and the projectile electrons scatter most efficiently from each other. Rapid electron excitation, loss, and capture result in a new equilibrium of the charge state distribution of the projectile beam after passing through a certain amount of matter (usually described as an areal density of a few
g/cm
). In the process, inner vacancies occur in the projectile ions, their number increasing with the particle penetration depth and decreasing by radiative decay. Betz et al. used foils of areal densities ranging from a few
g/cm
to about 100
g/cm
, and by some modelling they deduced K-shell vacancy lifetimes of the expected order of magnitude from the slope of the X-ray yield curves as a function of foil thickness. They were able to distinguish decays of different rates from each other.
Clearly, the evaluation of such data depends on the knowledge of the foil thickness. Foil thickness or areal density (typical writing paper has 80 g/m and is about a thousand times thicker than the typical exciter foils used in these experiments) has been a concern of nuclear scientists before, because ion beams traversing such a foil lose part of their energy, and the collision energy is a crucial parameter in many nuclear reactions. Additionally, in beam–foil spectroscopy, knowledge of the ion velocity after the experience of energy loss in the foil is crucial in the conversion of distance from the foil into time after excitation, the essence of an atomic lifetime measurement. Naively, one might assume the density of carbon to be known, so that a measure of area and weight might do the job. Incidentally, in the 1970s the Jülich Nuclear Research Centre (Germany), in the course of their work on a high-temperature (pebble bed) reactor, assembled a library of some 100,000 modifications of graphite and their structure, as obtained by electron transmission microscopy. When our institute asked for their judgement on C foils (including some of them modified by laser heating for longer endurance, etc.), the response was “these samples of ‘turbostratic’ graphite are new to us”. There are various methods to produce such thin foils, by vapour deposition from a heated graphite sample or from carbohydrates, by sputtering, and so on, and they all result in different distributions of inner voids. Laser annealing changes the void distribution, and so does ion irradiation. The internal restructuring causes tensions, and the foils rupture eventually under ion-beam irradiation. A key problem for the density determination is that the foils are “mostly surface, little bulk”. Traditional density measurement methods, such as floating a specimen in oil, fail drastically. Apparently the most reliable technique is the measurement of the energy loss that energetic -particles suffer in a foil. Foil production results vary, and, therefore, samples of each batch have to be tested. Of course, this appears to imply a circular argument, testing a nuclear physics tool by itself, but the interaction of -particles with matter has been studied for decades, with reliable energy measurements performed by mass spectroscopy, and the technique can be calibrated very well. Still, this energy loss in the exciter foil remains a significant contribution to the error budget in beam–foil lifetime measurements.
This note triggers me to remember an anecdote from Oxford late in the 1970s. Working in an office in the Nuclear Physics building on a Sunday, my senior colleague H.J. Rose (a German fellow of St. Johns college) dropped in and reported his latest find. He had been working on nuclear lifetimes using a method that relies on observing the fast moving and then completely stopped nuclear reaction products in matter (As long as the particle moves, its ray emission is Doppler shifted; comparing the shifted and unshifted ray peaks yields a ratio that tells a nuclear lifetime, if the time for decelerating and actually stopping the particle is known—physically the problem is related to the aforementioned energy loss of fast particles in matter). The laboratory computer that held the toolbox of handy programs for data evaluation was down for service. Therefore, Rose did the calculations by hand. He found a discrepancy with other results: his key formula for the nuclear stopping differed from the computer version by a factor of two. “Just thinking, I now could write a paper telling how about one hundred publications from this laboratory are wrong!”
3.3. Laser Excitation
Laser excitation often is perceived as a near-magical all-purpose tool. However, closer to reality is the snippet that each laser experiment needs its own type of laser. For atomic lifetime measurements, the first lasers of sufficient intensity were pulsed ones. A short pulse duration is linked to a wide spectral range. Truly selective excitation thus asks for cw lasers, and for additional features to enable time resolution. For example, experiments on fast ion beams are combined with a cw laser beam that crosses the ion trajectory, and tuning into resonance is achieved by a variation of the crossing angle. The lifetime measurement is achieved by moving the detector along the direction of the ion beam—a truly challenging geometrical problem. Other experiments on traditional single-pass ion beams or on straight sections of ion storage rings use a collinear arrangement with collinear or counter-propagating ion and laser beams; tuning is sometimes achieved by local modulations of the ion velocity to provide a short zone in which the resonance condition is met. Transitions in the visible spectral range and geometries of ion beams usually ‘conspire’ to lifetime measurements in the nanosecond range. The accuracy of lifetime measurements with the beam-laser technique has repeatedly reached uncertainties better than 1% [
36].
Additionally, in the nanosecond range are experiments that attempt to reach nuclear fusion in a hydrogen isotope (D,T) sample compressed and heated by laser light (Inertial confinement fusion ICF, mentioned in
Section 2 above). The Lawson criterion describes a product of density, temperature, and time that should correspond to the threshold necessary to ignite nuclear fusion. Incidentally, the present experiments work with laser pulse lengths in the nanosecond range. Actually, the light energy deposited in the fuel pellet is on the order of a few MJ, as is the chemical energy of a hamburger or the average daily food intake of a human. The processing power lies in the short duration in which the energy is deposited. Shortening that time further appears to be counterproductive, since the fusion process is mediated by a hot plasma and its statistical processes, not by a single quantum jump (see the time component of the Lawson criterion). Our simple estimates on density and atomic lifetimes suggest that the modellers of the ICF experiments do not need to worry about density corrections to their assumed atomic lifetimes. However, laser-produced plasmas are not light sources that one would use for measuring atomic lifetimes, because these plasmas are dominated by rapid plasma processes (heating/heat loss, expansion, etc.) that would likely spoil atomic lifetime measurements.
Short-pulse lasers of much shorter pulse lengths than a nanosecond are available. For example, Carlsson and Sturesson [
56,
57] used a mode-locked Ar ion laser powering a dye laser with 6 ps long pulses and measured the Li I 2p resonance level lifetime of 27.22 ns with an uncertainty of better than 1%. This was one of the most accurate such lifetime measurements (meanwhile corroborated by technically very different and even more precise work [
58,
59]). Li atoms were prepared as an atomic beam, but this had nothing to do with the timing, which solely depended on electronics measuring the delay between the laser pulse and the atomic emission. There are short-lived phenomena in solid state and biological systems (often associated with light in the infrared range), and there are short-lived levels in multiply charged ions. The latter are connected to short-wavelength light absorption and emission. ‘Traditional’ lasers exist that work in the VUV, EUV, or soft-X-ray ranges (some in the form of high-harmonic generation from intensive laser light in matter), but the tuneability and, thus, also the practical use for atomic lifetime measurements is limited. In the extreme, short light wave trains can be produced with durations in the sub-femtosecond range, but these attosecond-range experiments so far target the dynamics of fast phenomena, not the lifetimes of atomic levels in the attosecond range (which typically belong to highly ionized systems).
Classically, lasers employ a cavity (a space between two mirrors) in which the laser light runs back and forth through the lasing medium and, thus, builds up intensity. This scheme largely fails in the soft-X-ray (SXR) range, because normal-incidence mirrors (for example, multilayer mirrors) may have some reflectivity (much lower than the near-perfectly reflecting mirrors for visible light), but the radiation cannot escape through the material. The scheme there changes to a single pass through the lasing medium (a plasma), the so-called SASE scheme (self-amplified spontaneous emission). This brings us to other schemes of producing coherent SXR or even X-ray light. There are tuneable light sources that in recent years have matured to provide brilliant coherent light over a wide range of wavelengths, in the common field of synchrotron radiation (SR) and free-electron lasers (FEL). Both synchrotrons and FELs depend on electron beams with a speed close to that of the speed of light. Synchrotron light is emitted when the electrons are accelerated sideways, originally by the bending magnets of the beam transport system, and meanwhile by so-called insertion devices. The sharper the bend, the more light is produced, and at shorter wavelengths. Alternating magnetic fields of high spatial frequency multiply the amount of light accordingly (the device is called a wiggler); if the spacing is so short and the electron velocity tuned properly, the synchrotron light emitted in forward direction from the individual bends (of what is now called an undulator) can interfere which other wave packets and multiply the intensity again.
The former high-energy linear electron accelerator at Stanford has found a new life (under the name Linac Coherent Light Source (LCLS)) at much lower electron beam energies, but now serving the electrons as the medium for a bright source of X-rays. The accelerator works with high frequency modules that modulate the electron bunches and, thus, the X-ray pulses with the same high repetition frequency. Coherence can be expected only within a bunch. Therefore, the X-ray light bunch is split into two sections (for example, by reflection off a split crystal) that can be directed onto almost the same trajectory, but with an adjustable delay between the partial pulses. When these interact with the same target, they can effect pump–probe experiments for levels with femtosecond lifetimes. Such an experiment has been tried (unsuccessfully so far) by the Livermore and Heidelberg electron beam ion trap groups [
6]. The experiment aimed at two levels in Fe XVII that are expected to have level lifetimes of 44 fs and 166 fs, respectively (the purple 2s
2p
3d levels in
Figure 2). The idea was to cut the two pulses (of the pump–probe scheme) by mechanical means out of a single electron bunch, by introducing a mask with two slits. The fast electron beam has practically the speed of light, and a time difference of 100 fs then corresponds to a displacement by 30
m, less than half the width of a human hair. Maybe it is not so surprising that our first try with such a scheme did not immediately succeed. Meanwhile, a pulse splitter based on the split crystal scheme has been constructed by another group. Maybe somebody can try again?
The same LCLS X-ray “laser” has been used on micro-droplets of, for example, Ne [
20]. The X-ray light is able to effect inner-shell ionisation and excitation in the atoms of such clusters. Thus, one can study how ionisation and excitation proceed, and how they depend on target density. This is fundamentally different from the aforementioned irradiation by visible or IR laser light which cannot ionise the atoms directly (except by the absorption of several photons at once), but only successively, by first producing a hot plasma in which, then, fast electrons cause ionisation and excitation. This special field has become a veritable playground for physicists.
For the field of atomic lifetime measurements, the multi-particle environment may seem to be too complex to analyse in terms of individual level lifetimes. However, the Heidelberg electron beam ion trap group has combined high spectral resolution and a fast multichannel photon detector for the purpose of background reduction [
4,
5]. It might be possible to adapt such a system for atomic lifetime measurements in the femtosecond range. In these experiments the X-ray light is not required to make highly charged ions “from scratch” (the neutral atomic species). The highly charged ions are produced by successive collisions with an intense electron beam in an electron beam ion trap. In this arrangement the charge state distribution in the cloud of trapped ions can be manipulated in terms of the maximum charge state present (by the electron beam energy), and, in some cases, also in the width of the distribution, if atomic shell closures can be exploited. The X-ray laser thus serves for the resonance excitation in the specific target ion only, starting from the ground or metastable level of an ion prepared by/in an electron beam ion trap (with its extremely good vacuum).
5. Long-Lived Ions in Traps and in Space
So far, the atomic systems discussed have level lifetimes shorter than about 1 ms. Many of the lifetime measurements on the long side of 1 s make use of electron beam ion traps, because highly charged ions need to be produced without transferring too much kinetic energy onto the particles of interest, so that Doppler broadening remains under control. At the same time, an ion under study must be kept in the observation volume, which is more easily achieved at low kinetic energies than at higher energies. In addition, the ambient gas density has to be very low so that the collision rate stays low. In short, the laboratory situation requires ion traps and ultra-high vacuum. Consequently, many laboratory ion traps (the basic types Kingdon, Penning, Paul (-Straubel) radiofrequency (RF), EBIT, Zaijfman, and heavy-ion storage ring have been discussed in textbooks by now) rely on cryogenic operations for achieving an extremely good vacuum (cryogenic EBIT, cryogenic Penning trap, ion storage rings ASTRID, DESIREE, CSR, and so on), as well as for reducing the perturbation of weakly bound atomic systems by the blackbody radiation of the vacuum vessel.
In space, there are no tight physical bounds to the mostly low-charge ions at moderate to low temperatures. The ambient density is very low, indeed. Observations need a large optical depth to have optical access to what happens inside a cloud. Observations succeed only with a sufficiently large sample of atoms or ions seen, usually within a narrow solid angle. Factoring-in the large distances from the observer to the object, the object volume often is vast. This implies that sudden changes cannot affect many particles at once, and in practice variations on the time scale of an atomic level lifetime are not directly observable. However, the radiative transition rate still matters in the competition with collision rates. This competition shows up in line (intensity) ratios that depend (according to collisional-radiative models) on ambient density and temperature. Whatever processes are employed in the laboratory to prepare the atomic or molecular ions of interest, if one wants to mimic the astrophysical environment, one has to spend quite some time to let the particles cool down and de-excite their inner degrees of freedom. In space, the ambient temperature often is not much higher than that of the cosmic microwave background radiation (roughly 3 K), and the particles have plenty of time to reach levels close to their ground state. Consequently, the target temperature of devices, such as the Cryogenic Storage Ring CSR at Heidelberg, has been chosen about 10 K.
Actually, the low particle density in the solar corona was not recognised in the 19th century as the key ingredient when trying to understand why various mystery lines in the solar spectrum at eclipses could not be reproduced in the laboratory. Helium was initially missed, but then found on Earth after all, within a few decades after the first solar observations, as a reaction product of the radioactive decay of heavy elements. The hypothetical element Coronium was supplanted by Grotrian’s suggestion [
95] and Edlén’s experiments [
96] about 70 years after the spectral investigation of solar eclipses, finding that its spectral lines originated from
-forbidden transitions in highly charged ions of the iron group elements, instead. The hypothetical element Nebulium “existed” for about half a century, from the observation of strong emission from planetary nebulae [
97] over various serious theoretical and experimental studies [
98,
99] to the recognition by Ira S. Bowen [
100] that the lines of interest were actually fine structure transitions in relatively light ions, which could only be observed if the time between collisions was longer than the extremely long radiative level lifetimes of such low-
Z ions. Indeed, the astrophysical examples of interest include several very long lived levels which might be exploited in the density diagnostics of dilute astrophysical plasmas, such as planetary nebulae (discussed below). The lifetimes of interest span a range from the aforementioned milliseconds to a week or so, some nine orders of magnitude. As an example of such lifetimes, consider the lifetime predictions for the 3s
3p
P
and
D
levels of S II, which amount to a few seconds and about an hour, respectively (see the discussion and references in [
101,
102]).
Many lifetime data have been obtained on decays in the range of level lifetimes of 1 s and higher. Many of these measurements have been reviewed elsewhere, and, therefore, such reviews are cited in order to avoid an extra-long reference list here.
The majority of the data can be grouped into the following topical sets:
- (a)
Multiply charged ions of the iron group (discussed below in
Section 5.1);
- (b)
Singly charged ions of the iron group and (mostly) singly charged ions of astrophysical abundance (discussed in
Section 5.2).
Density enters the stage of some of these measurements via a back entrance. One such aspect is the appearance of satellite lines near the diagram (major) lines in the X-ray spectra of H- and He-like ions. These lines originate from few-electron ions with inner-shell vacancies, and thus they may be described as relatives to the diagram lines, with some shielding of the nuclear Coulomb field caused by spectator electrons (that do not actively participate in a transition). First scientifically described by Edlén and Tyrén [
103] in the late 1930s, these satellite lines have become of interest for plasma diagnostics since the 1960s [
104,
105]. The additional outer electrons (in comparison to the singly excited one- and two-electron systems) feature many coupling options with different influences of radiative decay and auto-ionisation, and the level populations being sensitive to di-electronic recombination and to collisional excitation. Although, in many spectra, not all of the satellite lines can be resolved, the overall envelope of the line distribution can be interpreted in terms of density and temperature. From the dense group of satellites one line sticks out by its longer lifetime, that is, the decay of the 1s2s2p
P
level [
18,
106,
107]. In the 1s2p
P state, the three fine structure levels evolve differently along the isoelectronic sequence, thus yielding information about the different
Z-dependences of the individual decay channels, as has been measured by beam–foil spectroscopy [
108]. Similar core-excited ions are models for many negative ions. Negative ions have been studied for photo-detachment and level lifetimes mostly using the storage rings at Aarhus (for examples of the wide range of these measurements, see [
109,
110]); these interesting and influential ions (consider the massive role of H
ions in the Sun), however, lie outside the scope of this manuscript.
5.1. Multiply Charged Ions of the Iron Group
Electric-dipole (
) forbidden transitions in multiply charged ions of the iron group have been identified as the origin of much of the corona spectrum observed during solar eclipses. Many of these lines can be used for plasma diagnostics, but the full interpretation of such spectra requires knowledge of the transition rates of various
,
, or
transitions. Most of the data available by now have been measured at an electron cyclotron resonance ion source (ECRIS) (for example at Reno, NV) [
111,
112,
113], the heavy-ion test storage ring TSR (at Heidelberg), the Gaithersburg EBIT, the Livermore EBITs, or one of the Heidelberg EBITs (for reviews and citations of the original work, see, for example, [
30,
31,
34,
35,
36,
114,
115]).
With growing experience, the error margins of such measurements have shrunk over time (see, for example, the discussions in [
113,
116,
117,
118]). However, there also is the question of systematic error (accuracy), and the comparison to established theory. Some of the measurement results fall onto the short side of predicted lifetimes, as would happen, if charge exchange (CX), that is, collisions of highly charge ions with the neutral particles of the residual gas, removed excited ions from the sample. One can estimate that the vacuum in an ECRIS is poorer than that in a cryogenic EBIT or a heavy-ion storage ring, and experiments that measure and correct for CX seem to do better. The systematic trend seemed to be violated by a peculiar lifetime result obtained at TSR, a single result clearly shorter than expected, but from an experiment with excellent vacuum. However, the Heidelberg heavy-ion storage ring experiments used ions from an ion source and passed them through a charge-changing stripper in the accelerator before feeding the ion beam into the TSR heavy-ion storage ring with its excellent UHV conditions. Here, it was recognised that the problem did not relate to CX in the storage ring, but to the (intentionally) higher particle density in the gas or foil stripper in the accelerator high voltage terminal. Just like in beam–foil spectroscopy (discussed above), collisions of the ion beam particles with electrons in the stripper (non-selectively) populate also high levels, which, in turn, may decay to any lower levels. If these cascades reach long-lived levels, the data analysis has to be aware of decay curve contributions from cascades. In the case of Al-like ions, the 3s3p3d
F
level has been identified as the likely culprit that affects lifetime measurements of the 3s
3p
P
ground state level [
35,
36]. In this case, the effect on the decay curve is difficult to see, because the lifetimes of primary and cascade level are rather similar, but they follow slightly different iso-electronic trends. In P- and S-like ions there are several long-lived 3d levels above the 3p levels of the ground configuration [
114,
115], and their cascades show up strongly and clearly, limiting the accuracy with which the lifetimes of the ground state fine structure levels in those ions can be measured.
It would be interesting to combine an EBIT (as a source of highly charged ions, produced under excellent vacuum conditions) with a heavy-ion storage ring (that separates ions of different charge states) in order to investigate the systematic error limits of atomic lifetime measurements. In two laboratories (Stockholm and Heidelberg), the proximity of their EBIT to their storage ring should have made such an experiment feasible. However, local perceptions and local policies were not in favour of such an enterprise, and by now both heavy-ion storage rings have moved away from the EBIT laboratories, Cryring to GSI Darmstadt (the CRYRING@ESR project at the high-energy heavy-ion accelerator complex [
119]), and TSR to Geneva and REX-Isolde (for isotope studies).
The structure of Al-like ions as just discussed seems very similar to that of B-like ions, but in the latter no corresponding long-lived cascade level has been identified in corresponding experiments [
111,
120,
121,
122]. Consequently, Ar XIV may be a system in which the transition rate of the
(with a small
admixture) transition between the fine structure levels of the ground state may be measured with particularly high accuracy, and very recent publications from the Heidelberg EBIT group show that this path is being pursued. The physics challenge here relates to the electron anomalous magnetic moment (EAMM), a QED correction of uncommon magnitude, which may indicate possible processes beyond the reach of the Standard Model. In the course of an experiment at the Heidelberg electron beam ion trap [
121,
122], veteran theory expert Walter Johnson remembered that in the 1950s somebody had estimated this correction to
transition amplitudes (and he cites textbook knowledge of 1980). Apparently, this insight had been largely forgotten since. The EAMM correction amounts to about 0.45% of the non-QED value of the
transition amplitude (for details, see [
123]) and, thus, is important in studies that aim to determine
transition rates (and thus level lifetimes) to 0.1% or better. Indeed, some experiments have reached this high precision, but a test of the EAMM contribution is hampered by the status of the insufficient accuracy of many-body quantum mechanics determining the non-QED part of atomic structure and dynamics. Another detail presently discussed is the
line ratio (two transitions of the same transition energy). The
branch is sensitive to the EAMM contribution of about 0.45%, whereas the
branch possibly is not. This makes for a small systematic correction that may be measurable.
5.2. Singly Charged Ions of Astrophysical Abundance
The Cryring heavy-ion storage ring at Stockholm was equipped with two ion sources, one of them an EBIT (used for collision experiments, but apparently never for atomic lifetime measurements), the other a source for singly charged ions. Such singly charged ions, with a fraction of them excited by collisions inside the ion source, were moderately accelerated towards the ring, stored there, and then probed by laser for surviving populated excited levels. The excitation should ideally be level-selective (not pursued here), whereas the probe might be more effective if the (few) surviving excited ions were ionised and then detected (with high efficiency) as particles. Varying the time after excitation, the final quenching event yields a single data point. Many such data points yield a decay curve. The Stockholm group specialised in the lifetime range from seconds to minutes that is found in the singly ionised atoms of elements of the iron group, because such singly charged ions are observed in many astrophysical objects (for a few of the many measurements, see [
124,
125,
126,
127,
128,
129]). The group activities have since moved on to the DESIREE ion beam trap.
A different class of objects are molecules, which have also been observed in outer space. Molecules have additional degrees of freedom beyond those of atoms, such as vibration and rotation. Collisions can modify the “mechanical” state of a molecule. The molecules in outer space have plenty of time to de-excite towards a thermodynamic equilibrium with the cosmic background radiation. Experiments in the laboratory, therefore, have to strive for extremely low densities, as well as very low temperatures, and freshly produced molecules have to be given sufficient time to quieten down. Only then can the lifetimes of low-lying molecular states be determined. Various ion traps, notably at Aarhus and Stockholm, have implemented schemes to cool the vacuum vessel in order to reduce black body radiation (in particular for the study of negative ions); the cryogenic storage ring CSR at Heidelberg [
130] aims at operations at a temperature of 10 K and has reported evidence for the cooling process of stored molecules [
131].
6. Extremely Long Lifetimes in Low Charge State Ions of Not-So-Heavy Elements
In the 1920s, Ira S. Bowen recognised the low-density atomic physics that resulted in the peculiar spectra of planetary nebulae and, later joined by Donald Menzel, explained the role of (
-) forbidden transitions in astrophysics [
132,
133,
134,
135,
136]. After World War II the age of electronic computing began, and in the late 1940s the first atomic structure codes began to evolve (Numerical Coulomb approximation, etc.). In the 1960s, Czyzak and Krueger [
137] introduced the process of computer modelling to the description of the spectra of planetary nebulae. They discussed which atomic structure features could be fruitfully exploited to learn about the environmental parameters, for example the relatively small ground state fine structure in the 2p
ground configurations of C(O)-like ions for density, and the higher-energy ground state transitions in N-like ions (which have a 2p
single-level ground state) for temperature. Czyzak stayed in this field for at least a quarter of a century [
138], and many colleagues joined the effort (For a timeline and examples of C-like ions, see [
139,
140,
141,
142,
143,
144,
145,
146]).
In those times of very limited computer resources and a considerable scatter of the results, Harry Nussbaumer earned a reputation for obtaining reliable results from insightfully chosen wave functions. When I joined the field of beam–foil spectroscopy and atomic lifetime measurements in the 1970s, Nussbaumer’s results on multiply charged ions turned out close to the experimental findings more often than some others. Those were atomic lifetimes of dozens to hundreds of picoseconds (in multiply charged ions of Si and so on). When looking for isoelectronic trends, I found out that the computations often started with very low charge states (O II, O III, and so on) and with level lifetimes in the range of seconds or even hours, which was not just many orders of magnitude, but seemingly more than a “world apart” from what appeared to be ever measurable by my toolbox. Actually, some of the aforementioned experiments have by now obtained atomic lifetime data up to the range of minutes. The remaining section deals with some perspectives of going farther.
6.1. Lifetime Measurements Almost in Reach
Atomic lifetime measurements on low-charge ions—as they appear in so many astrophysical objects—are surely desirable. Atomic structure theory has problems with near-neutral systems, because typical computational approaches converge haltingly in such cases without a dominant central Coulomb potential. Consequently, many early computations have not used the full range of tools, and this may explain why the results have scattered notably [
102]. Although more recent efforts are expanding, this is not a guaranteed path to success. The early lifetime predictions (of 50 and more years ago) scattered considerably, and one should expect that with growing computing power the scatter would eventually be reduced significantly. The evidence does not really encourage this hope (see [
101,
102] and references therein), and results that scatter on the order of 20% are still not unusual.
On the experimental side, one might think of single-ion trapping to reduce mutual perturbations of the ions in a stored ion cloud, of cooler environments and a better vacuum—all of these considerations are helpful, but there are other factors that block a straight path of development. Some of this has been discussed elsewhere [
101], and, thus, the discussion can be shorter here.
For example, the singly charged (P-like) sulphur ion S (spectrum S II) resembles N-like systems with a single ground level (3pS) and four other levels (P and D) in the same ground configuration. All transitions within this configuration are -forbidden and transitions. The predicted lifetimes of the P levels lie in the range of a few seconds, which can easily be measured, but have not been. The problems lie in the atomic structure. The decay branch to the ground level is in a convenient spectral range (wavelength near 400 nm) for which efficient photomultipliers exist, but the branching fraction is unfavourably minor. The major decay branch toward the D levels dominates by far, but for wavelengths just above 1000 nm an infrared (IR) detector is needed. Such detectors have immensely improved over recent decades, but in an ion trap experiment (especially with a single ion), single photon detection is necessary, and that requires cooling beyond the temperature of liquid nitrogen. This should be doable, but apparently it has not been done yet on such a measurement problem. Obviously it would be good to also cool the ion trap for a reduction in the background radiation. However, the two P levels are not of primary interest, but they might serve as a test bed for the next example.
More interesting for density diagnostics of planetary nebulae are the two decays of the
D
levels to ground, near 672 nm. The level lifetimes are predicted as about half an hour and a full hour or more, respectively. The detector problem is not quite as demanding as in the IR, since efficient detectors for red light have been around since decades—but they usually come with a high dark rate, again, requiring hard cooling. One might boost the signal rate by keeping many ions trapped (which might perturb each other, as mentioned above). However, the signal has to be followed into the detector noise in order to establish the shape of the decay curve and the height of the background level. For atomic lifetimes on the scale of an hour, the duty cycle of the experiment poses a serious practical problem. Therefore, alternative detection means have to be considered. There are technically demanding (expensive) techniques of active interrogation of a level population (some are discussed in [
101], see also the measurement of a level lifetime of about 1 year by a laser interrogation technique [
11]). Here, I prefer to juxtapose just two technical options, optical and non-optical detection.
Simply waiting for photons from the radiative decays of the excited ground configuration levels of interest is very inefficient, since the noise rate of any known detector for 670 nm light is many orders of magnitude higher than the expected signal rate. Moreover, any practical light collection system would cover a solid angle of detection that amounts to no more than only a small fraction of 4
. A light collection system of aperture ratio f/2.8 (
Figure 3) collects about 1% of the light emission. For a single ion in the trap and a level lifetime of about 5000 s (such as the S II 3s
3p
D
level), one can then expect an optical signal rate of 1 event per week. How to identify that event in the (overwhelming) presence of similarly-looking detector noise?
A completely different detection scheme has most recently become available from mass spectrometry of single ions in a Penning trap. Ground state and excited ions differ by the excitation energy, which, in S
ions, amounts to about 2 eV compared to the total mass of a mass-32 ion of about 32 GeV/c
. Thus, a ‘weighing’ process with a relative resolution of
should be able to discriminate between the ground state and the excited state S
ion. This goal has, in fact, recently been achieved on stored Re ions in a cryogenic Penning trap, and a very long-lived metastable level has been detected this way [
147]. The time after excitation that the ion remains excited contributes a data point to a decay curve; when the ion de-excites, the resonance frequency shifts accordingly, and the excitation system can be triggered to begin a new measurement cycle. Since the sensing of an ion in the one or the other state is done non-destructively by many interrogations of the trap frequencies, this is not a noise source contributing to an otherwise indistinguishable detector signal. However, misidentifications may contribute to a certain background distribution. It should be straightforward to disentangle the joint decay curve in terms of the two individual contributions. The detection is not limited by the geometry (solid angle) of a detection system as discussed above. Without that limitation, a single trapped S
ion could generate about 100 signal cycles per week, and within a few months a counting statistics reliability of the atomic lifetime result on the order of 3% might be achieved. This is still very demanding in terms of trap performance and measurement time (as well as personnel and equipment cost!), but it seems feasible. In the same ion, the aforementioned
P
levels with their lifetimes of a few seconds could serve as a much less demanding (and much less costly in terms of operating time) specimen that might be compared with results from optical data taking as a control. The relative uncertainties of theory are about the same for both terms.
6.2. Lifetime Measurements out of Reach, But …
If the hour-long atomic lifetimes of the 3pD levels in the ground configuration of S II are presently an enormous challenge to measurement techniques, what about the even longer lifetimes (because of smaller fine structure intervals) in the ground terms of C- and O-like ions? Or the decays of the 2s2pD levels to the P levels? All transitions within this configuration are -forbidden and transitions. These transitions originate from the same upper level, and, therefore, the line ratios do not depend on the environmental density. The upper level lifetime may be out of experimental reach in the foreseeable future, but the line ratios are immediately accessible from astrophysical observations (and possibly in the laboratory, because the upper level is the same). What does theory say, and is it reliable?
As it happens, the N II 2s
2p
P
–
D
lines bracket the astrophysically very prominent H
line. The predicted branching ratio is close to 3.00, but how reliable is such a prediction? According to a literature search by Dojčinović et al. [
148], most of the predictions say 2.96, with only a small scatter by 1 or 2%. For example, the extensive computations by Tachiev and Froese Fischer [
146] agree with LR 2.96. However, at the same time the predicted transition rates (the sum of which is the inverse of the upper level lifetime) scatter by some 20%. Is the reproducibility of the line ratio a proof of the high quality of theoretical prediction, or is the much larger scatter of the individual transition rates pointing to intrinsic problems?
Although the lifetime is too long to be measured directly at present, a measure of the line ratio should be straightforward from archival astrophysical data. For this purpose, Dojčinović et al. have evaluated spectra of active galactic nuclei (AGN). Planetary nebulae should do as well, for which ample data of high statistical reliability are available. The data mining by Dojčinović et al. has yielded line ratios a little higher (by some 3%) than most predictions. This may seem surprising in the light of so many earlier predictions that seemed to agree perfectly with each other. However, one has to be aware of the substance of such predictions. Basically, the prediction of such M1 transition rates consists of combining the transition energy and a factor from Racah algebra. The wavelengths are well known (from observation), and Racah algebra is mathematically strict, often with simple fractions of small integers that appear to leave little leeway for uncertainty. However, computations of the transition energy (or of the fine structure splittings) often do not agree with the precisely known experimental wavelength data, which is why “predictions” often are adjusted “semi-empirically”. Moreover, the seemingly exact, simple Racah factors apply to a single-configuration model. The above example deals with transitions between the five fine structure levels in the ground configuration of a C-like ion, and it has to be expected that a single-configuration ansatz may be insufficient. Indeed, recent multi-configuration computations, such as performed by Storey and Zeippen (with the SUPERSTRUCTURE code) [
145] yield a transition rate ratio of 3.07, in good agreement with the analysis of the AGN observations [
148] (3.05). Those authors, indeed, suggest to employ such observational astrophysical data in order to test the quality of some theoretical predictions.
Claudio Mendoza and colleagues (Claude Zeippen, Pete Storey, and various others) repeatedly have pointed out that many computations neglect higher-order and/or relativistic corrections to certain transition operators, and that relativistic corrections may be important even for line ratios in the lowest members of isoelectronic sequences in which early computations often differed from observation. This view underlines the above findings.
In the above example, the closeness of the lines of interest to the usually prominent H
line makes the lines easy to find, but they may also be blended with or even be drowned by the line wings of H
. There also are studies of the H
line profile which discuss distortions by the N II lines [
149]. O III has similar lines in the blue range of the visible spectrum and with a wider line separation [
150]. It seems intriguing to be able to look at archival data from astrophysical observations without time resolution, in order to extract information on atomic levels that are too long lived to be measured for their lifetime, and to learn something about computations that differ notably from each other in outcome, although a certain ratio of transition rate results (the line ratio) appears to be highly reproducible.