Pseudo-Relativistic Hartree–Fock and Fully Relativistic Dirac–Hartree–Fock Calculations of Radiative Parameters in the Fifth Spectrum of Lutetium (Lu V)
Abstract
:1. Introduction
2. Atomic Structure and Radiative Rate Calculations
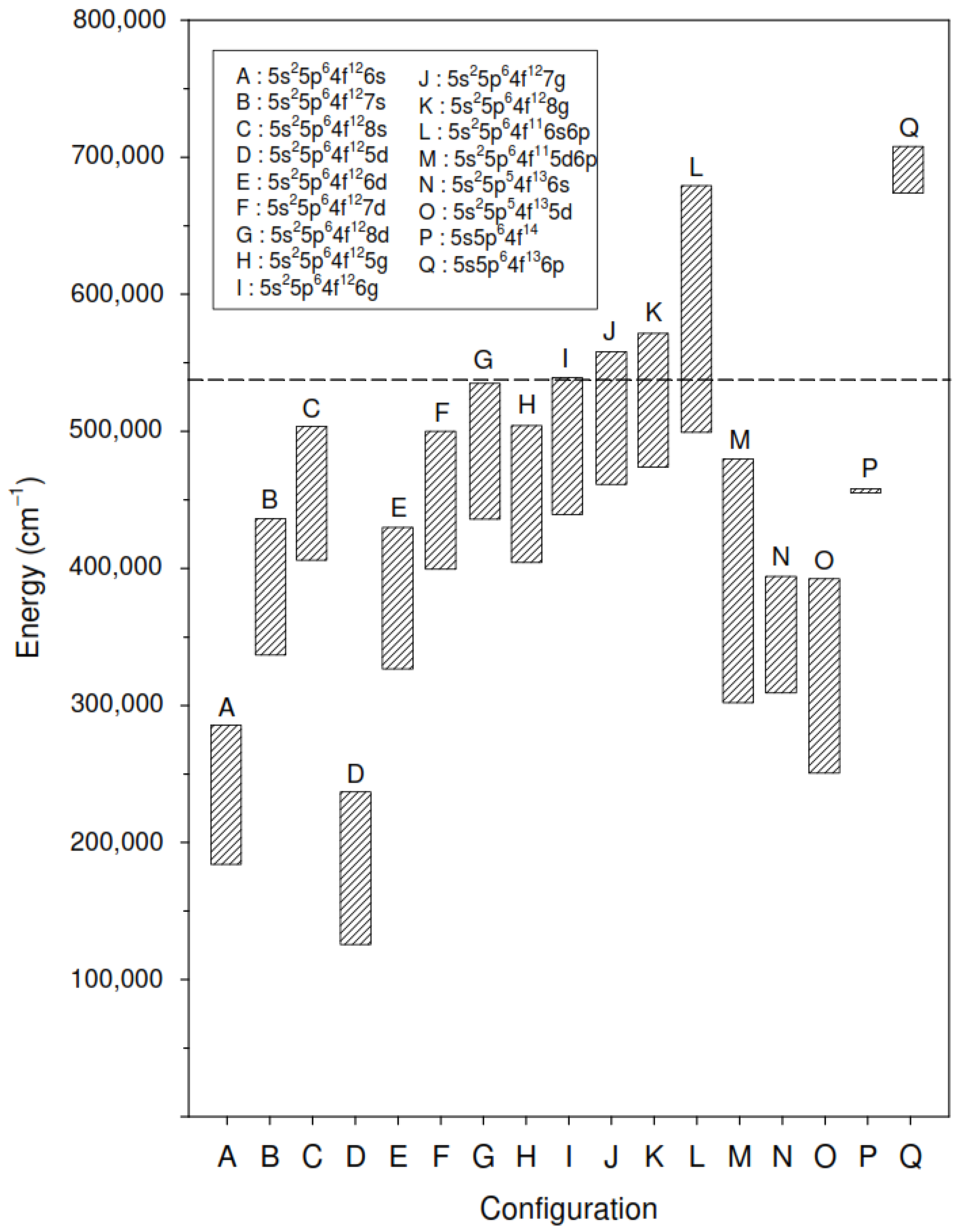
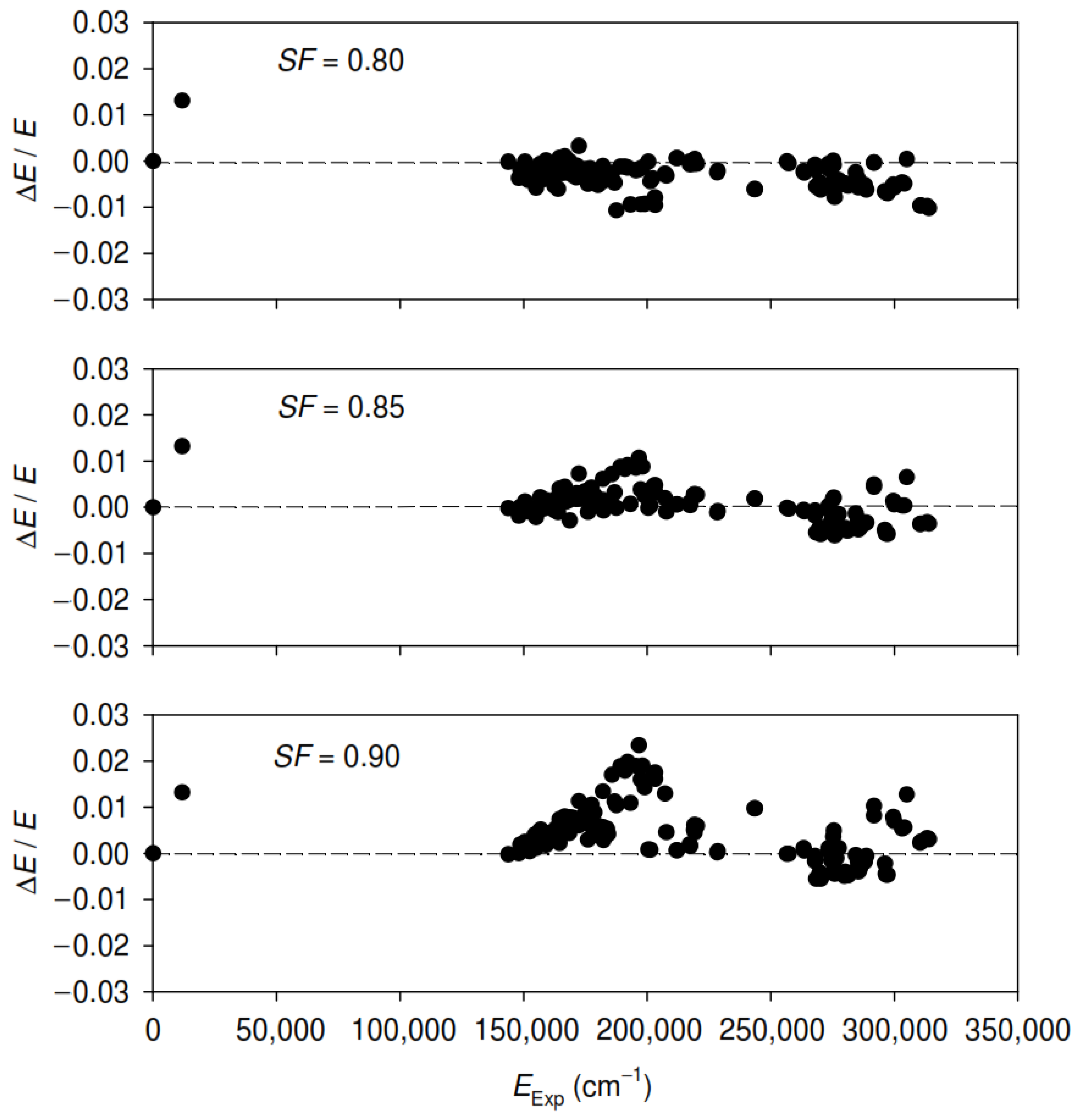
2.1. Pseudo-Relativistic Hartree–Fock Method
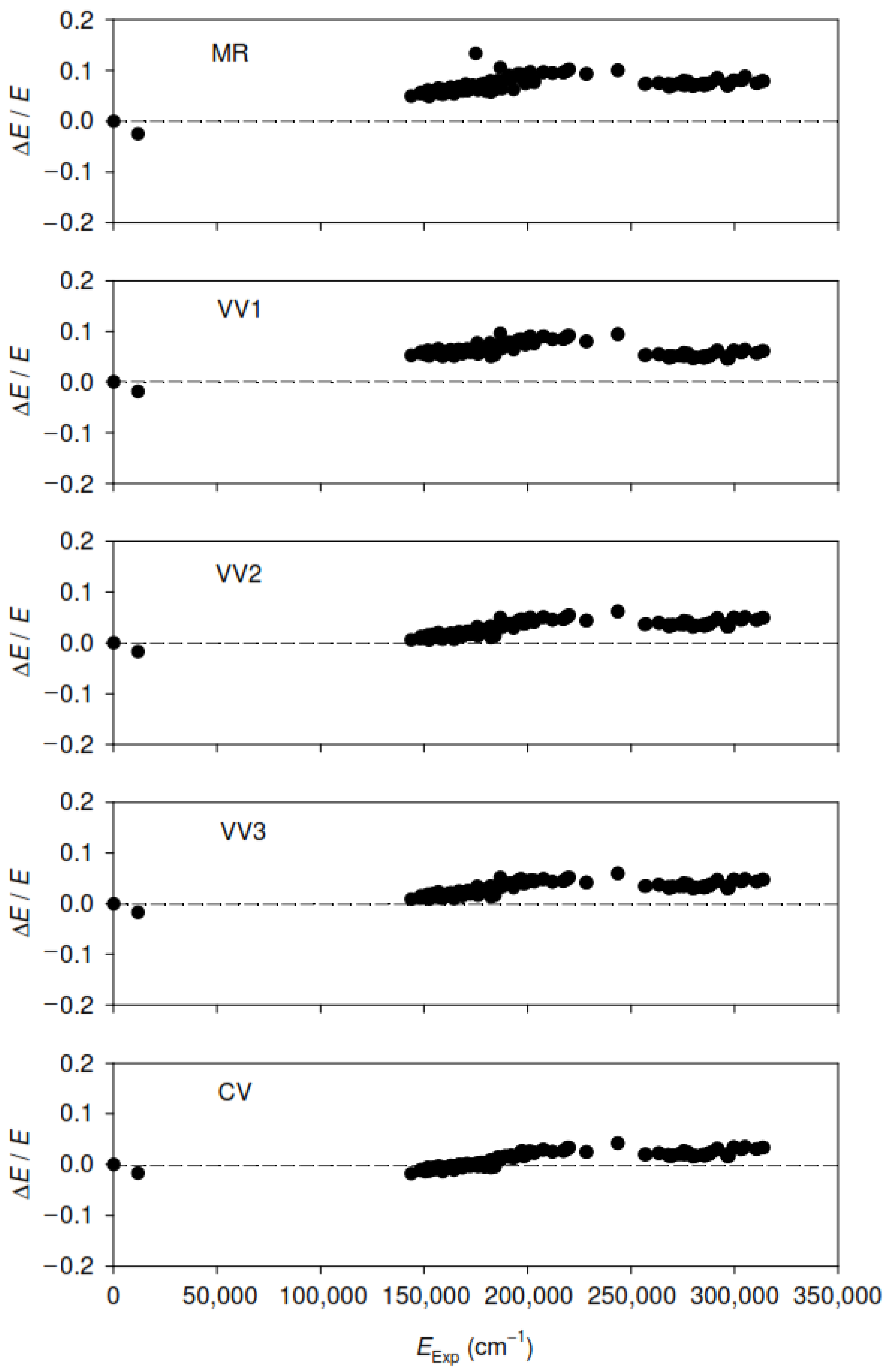
2.2. Fully Relativistic Multiconfiguration Dirac–Hartree–Fock Method
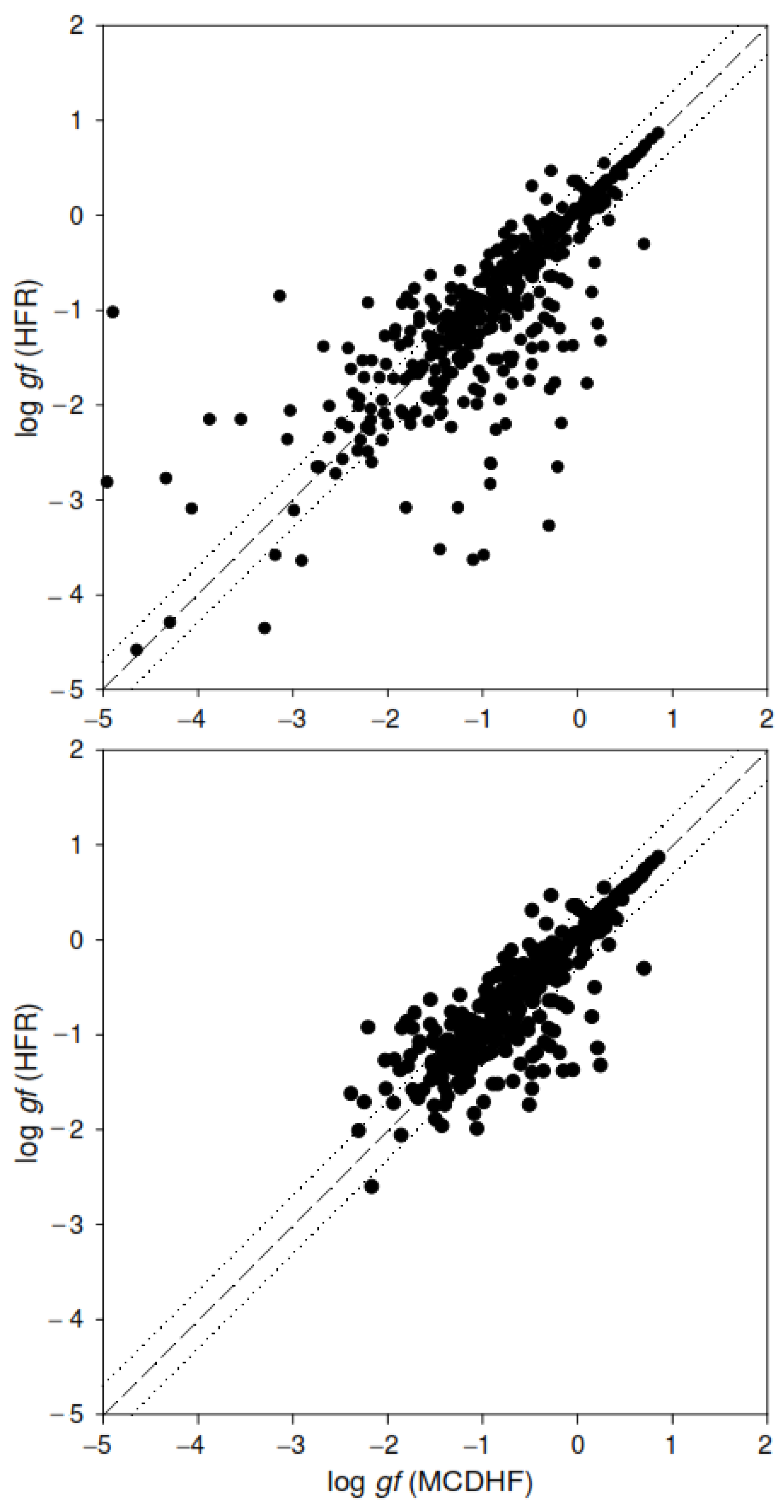
3. Transition Probabilities and Oscillator Strengths
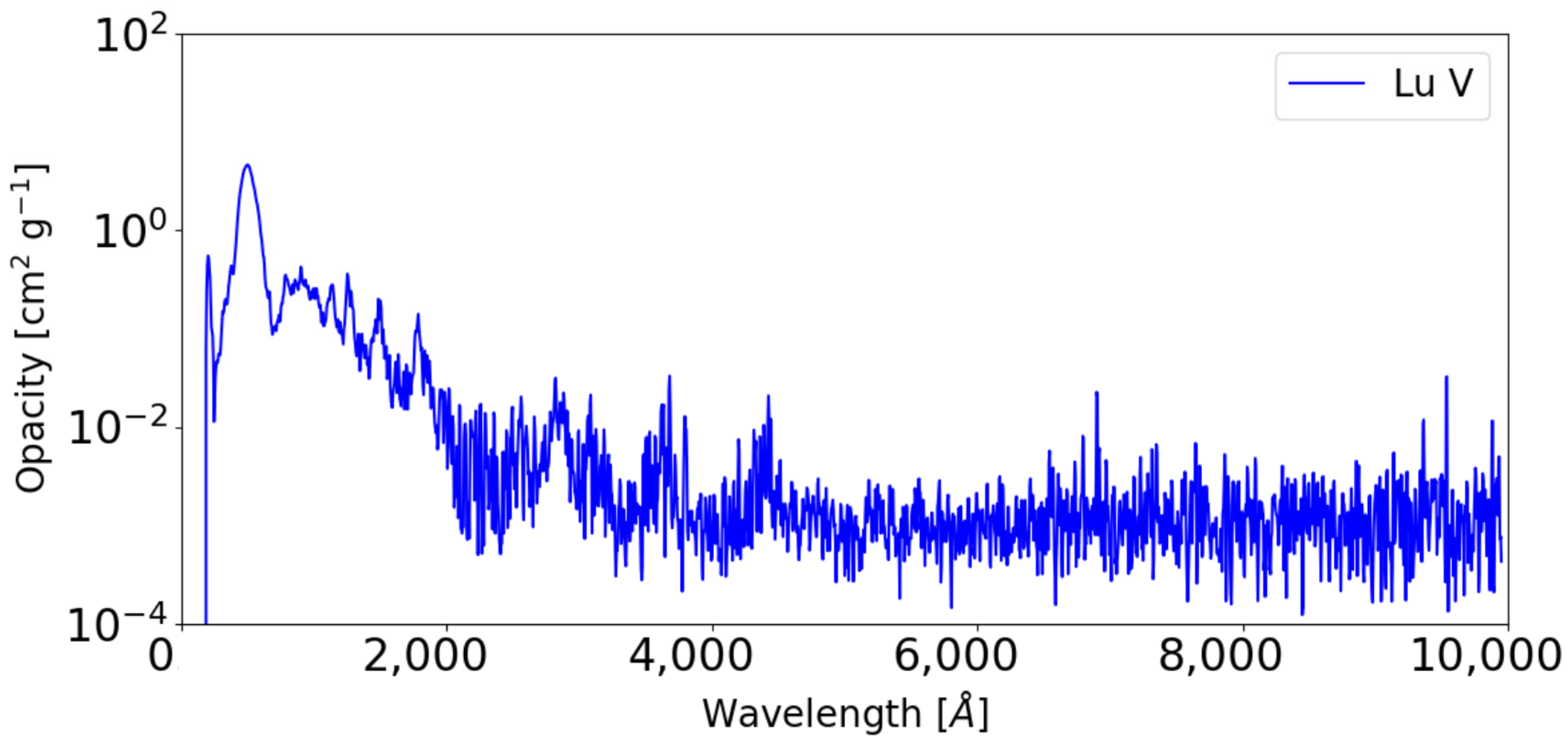
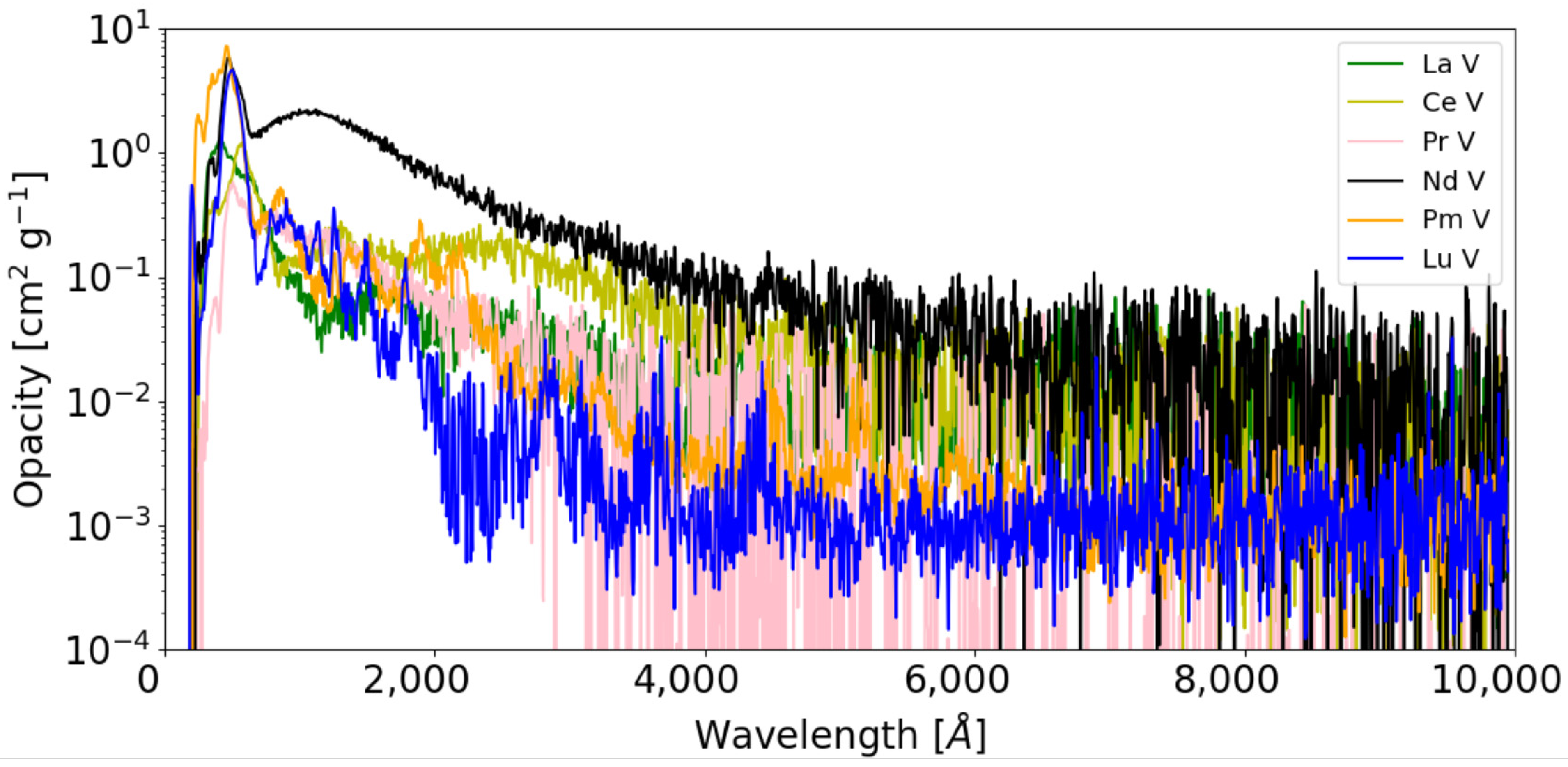
4. Applications to Opacity Calculations for Kilonovae
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022. Available online: http://physics.nist.gov/asd (accessed on 28 August 2022).
- Kaufman, V.; Sugar, J. Analysis of the spectrum of four-times-ionized lutetium (Lu V). J. Opt. Soc. Am. 1978, 68, 1529–1541. [Google Scholar] [CrossRef]
- Racah, G. Theory of complex spectra II. Phys. Rev. 1942, 62, 438–462. [Google Scholar] [CrossRef]
- Ryabtsev, A.; Kononov, E.; Kildiyarova, R.; Tchang-Brillet, W.-Ü.L.; Wyart, J.-F.; Champion, R.; Blaess, C. Spectra of W VIII and W IX in the EUV region. Atoms 2015, 3, 273. [Google Scholar] [CrossRef] [Green Version]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Kaufman, V.; Sugar, J. National Institute of Standards and Technology, Gaithersburg, MD, USA. 1980; Unpublished line list. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational waves and gamma-rays from a binary neutron star merger: GW170817 and GRB 170817A. Astrophys. J. 2017, 848, L13. [Google Scholar] [CrossRef] [Green Version]
- Kasen, D.; Metzger, B.; Barnes, J.; Quataert, E.; Ramirez-Ruiz, E. Origin of the heavy elements in binary neutron-star mergers from a gravitational-wave event. Nature 2017, 551, 80. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carvajal Gallego, H.; Berengut, J.C.; Palmeri, P.; Quinet, P. Atomic data and opacity calculations in La V-X ions for the investigation of kilonova emission spectra. Mon. Not. R. Astron. Soc. 2022, 513, 2302. [Google Scholar] [CrossRef]
- Carvajal Gallego, H.; Berengut, J.C.; Palmeri, P.; Quinet, P. Large scale atomic data calculations in Ce V-X ions for application to early kilonova emission from neutron star mergers. Mon. Not. R. Astron. Soc. 2022, 509, 6138. [Google Scholar] [CrossRef]
- Carvajal Gallego, H.; Deprince, J.; Berengut, J.; Palmeri, P.; Quinet, P. Opacity calculations in four to nine times ionized Pr, Nd and Pm atoms for the spectral analysis of kilonovae. Mon. Not. R. Astron. Soc. 2022. submitted. [Google Scholar]
- Quinet, P.; Palmeri, P.; Biémont, E. On the use of Cowan’s code for atomic structure calculations in singly ionized lanthanides. J. Quant. Spectrosc. Radiat. Transf. 1999, 62, 625. [Google Scholar] [CrossRef]
- Quinet, P.; Palmeri, P.; Biémont, E.; McCurdy, M.M.; Rieger, G.; Pinnington, E.H.; Wickliffe, M.E.; Lawler, J.E. Experimental and theoretical lifetimes, branching fractions and oscillator strengths in Lu II. Mon. Not. R. Astron. Soc. 1999, 307, 934. [Google Scholar] [CrossRef]
- Quinet, P.; Palmeri, P.; Biémont, E.; Li, Z.S.; Zhang, Z.G.; Svanberg, S. Radiative lifetime measurements and transition probability calculations in lanthanide ions. J. Alloys Compd. 2002, 344, 255. [Google Scholar] [CrossRef]
- Grant, I.P. Relativistic Quantum Theory of Atoms and Molecules; Springer: New York, NY, USA, 2007. [Google Scholar]
- Froese Fischer, C.; Godefroid, M.R.; Brage, T.; Jönsson, P.; Gaigalas, G. Advanced multiconfiguration methods for complex atoms: I. Energies and wave functions. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 182004. [Google Scholar] [CrossRef] [Green Version]
- Froese Fischer, C.; Gaigalas, G.; Jönsson, P. GRASP2018—A Fortran 95 version of the General Relativistic Atomic Structure Package. Comput. Phys. Commun. 2019, 237, 184. [Google Scholar] [CrossRef]
- Ekman, J.; Godefroid, M.R.; Hartman, H. Validation and implementation of uncertainty estimates of calculated transition Rates. Atoms 2014, 2, 215. [Google Scholar] [CrossRef]
- Grant, I.P. Gauge invariance and relativistic radiative transitions. J. Phys. B 1974, 7, 1458. [Google Scholar] [CrossRef]
- Bokamba Motoumba, E.; Enzonga Yoca, S.; Quinet, P.; Palmeri, P. Calculations of transition rates in erbium-like ions Lu IV, Hf V and Ta VI using the ab initio MCDHF-RCI and semi-empirical HFR methods. At. Data Nucl. Data Table 2020, 133–134, 101340. [Google Scholar] [CrossRef]
- Sobolev, V.V. Moving Envelopes of Stars; Harvard University Press: Cambridge, UK, 1960. [Google Scholar]
- Banerjee, S.; Tanaka, M.; Kawaguchi, K.; Kato, D.; Gaigalas, G. Simulations of early kilonova emission from neutron star mergers. Astrophys. J. Suppl. Ser. 2020, 901, 29. [Google Scholar] [CrossRef]


| Lower Level b | Upper Level b | gA (s−1) c | log gf c | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| λ (Å) a | E (cm−1) | (P) | J | E (cm−1) | (P) | J | HFR d | MCDHF e | HFR d | MCDHF e |
| 504.825 | 0 | (o) | 7/2 | 198,089 | (e) | 7/2 | 2.43 × 108 * | 1.80 × 108 | −2.04 * | −2.18 |
| 508.374 | 0 | (o) | 7/2 | 196,706 | (e) | 5/2 | 2.96 × 108 * | 7.75 × 108 | −1.95 * | −1.54 |
| 511.664 | 0 | (o) | 7/2 | 195,441 | (e) | 5/2 | 1.43 × 109 | 1.43 × 109 | −1.26 | −1.27 |
| 520.559 | 0 | (o) | 7/2 | 192,100 | (e) | 9/2 | 5.63 × 107 * | 4.56 × 107 # | −2.65 * | −2.75 # |
| 523.569 | 0 | (o) | 7/2 | 190,994 | (e) | 5/2 | 1.25 × 109 | 1.51 × 109 | −1.30 | −1.22 |
| 528.571 | 0 | (o) | 7/2 | 189,188 | (e) | 7/2 | 8.00 × 107 * | 1.18 × 108 # | −2.48 * | −2.32 # |
| 535.277 | 0 | (o) | 7/2 | 186,818 | (e) | 5/2 | 1.51 × 109 | 1.38 × 109 | −1.19 | −1.23 |
| 536.778 | 11,793 | (o) | 5/2 | 198,089 | (e) | 7/2 | 5.22 × 107 * | 4.53 × 107 # | −2.65 * | −2.72 # |
| 538.398 | 0 | (o) | 7/2 | 185,736 | (e) | 7/2 | 3.99 × 107 * | 1.09 × 106 # | −2.77 * | −4.34 # |
| 540.794 | 11,793 | (o) | 5/2 | 196,706 | (e) | 5/2 | 1.19 × 108 * | 1.59 × 105 # | −2.29 * | −5.18 # |
| 544.518 | 0 | (o) | 7/2 | 183,649 | (e) | 9/2 | 9.56 × 108 | 6.61 × 108 # | −1.37 | −1.53 # |
| 11,793 | (o) | 5/2 | 195,441 | (e) | 5/2 | 1.91 × 109 | 1.54 × 109 | −1.08 | −1.18 | |
| 549.375 | 0 | (o) | 7/2 | 182,025 | (e) | 5/2 | 1.93 × 108 * | 2.08 × 107 | −2.06 * | −3.03 |
| 549.772 | 0 | (o) | 7/2 | 181,894 | (e) | 7/2 | 5.14 × 108 * | 6.97 × 108 | −1.63 * | −1.50 |
| 555.444 | 0 | (o) | 7/2 | 180,036 | (e) | 7/2 | 2.69 × 109 | 4.00 × 109 | −0.91 | −0.73 |
| 558.024 | 0 | (o) | 7/2 | 179,203 | (e) | 5/2 | 3.15 × 107 * | 2.58 × 109 | −2.83 * | −0.92 |
| 11,793 | (o) | 5/2 | 190,994 | (e) | 5/2 | 2.57 × 108 * | 1.12 × 108 | −1.93 * | −2.30 | |
| 563.723 | 0 | (o) | 7/2 | 177,396 | (e) | 9/2 | 3.88 × 108 | 3.17 × 108 # | −1.73 | −1.82 # |
| 0 | (o) | 7/2 | 177,390 | (e) | 5/2 | 2.93 × 109 | 3.39 × 108 | −0.86 | −1.80 | |
| 11,793 | (o) | 5/2 | 189,188 | (e) | 7/2 | 5.53 × 106 * | 1.39 × 107 # | −3.58 * | −3.19 # | |
| 569.300 | 0 | (o) | 7/2 | 175,654 | (e) | 7/2 | 1.59 × 109 | 1.95 × 109 | −1.11 | −1.03 |
| 571.346 | 11,793 | (o) | 5/2 | 186,818 | (e) | 5/2 | 7.06 × 109 | 6.40 × 109 | −0.46 | −0.51 |
| 574.902 | 11,793 | (o) | 5/2 | 185,736 | (e) | 7/2 | 1.19 × 108 * | 7.90 × 107 # | −2.23 * | −2.42 # |
| 576.300 | 0 | (o) | 7/2 | 173,520 | (e) | 7/2 | 2.17 × 109 | 1.18 × 109 | −0.97 | −1.23 |
| 580.580 | 0 | (o) | 9/2 | 172,242 | (e) | 9/2 | 4.23 × 108 | 4.08 × 108 | −1.67 | −1.68 |
| 583.746 | 0 | (o) | 7/2 | 171,307 | (e) | 7/2 | 1.67 × 109 | 1.22 × 109 | −1.07 | −1.21 |
| 584.778 | 0 | (o) | 7/2 | 171,005 | (e) | 5/2 | 1.68 × 108 * | 3.81 × 108 | −2.07 * | −1.71 |
| 587.432 | 11,793 | (o) | 5/2 | 182,025 | (e) | 5/2 | 9.16 × 108 | 1.46 × 109 | −1.33 | −1.13 |
| 587.887 | 11,793 | (o) | 5/2 | 181,894 | (e) | 7/2 | 8.62 × 105 * | 9.55 × 106 # | −4.35 * | −3.30 # |
| 588.156 | 0 | (o) | 7/2 | 170,023 | (e) | 5/2 | 5.66 × 108 * | 1.30 × 108 | −1.53 * | −2.17 |
| 594.380 | 11,793 | (o) | 5/2 | 180,036 | (e) | 7/2 | 2.04 × 109 | 1.68 × 109 | −0.97 | −1.05 |
| 597.338 | 11,793 | (o) | 5/2 | 179,203 | (e) | 5/2 | 7.72 × 108 | 3.85 × 107 # | −1.38 | −2.68 # |
| 598.004 | 0 | (o) | 7/2 | 167,223 | (e) | 5/2 | 1.33 × 108 * | 5.25 × 106 | −2.15 * | −3.55 |
| 600.328 | 0 | (o) | 7/2 | 166,577 | (e) | 5/2 | 1.63 × 108 | 2.56 × 108 | −2.06 | −1.86 |
| 600.470 | 0 | (o) | 7/2 | 166,535 | (e) | 7/2 | 1.02 × 108 * | 1.18 × 108 | −2.26 * | −2.19 |
| 601.537 | 0 | (o) | 7/2 | 166,240 | (e) | 9/2 | 1.44 × 109 | 9.59 × 108 | −1.11 | −1.28 |
| 609.013 | 0 | (o) | 7/2 | 164,198 | (e) | 7/2 | 1.06 × 108 * | 1.69 × 105 # | −2.23 * | −5.02 # |
| 610.275 | 11,793 | (o) | 5/2 | 175,654 | (e) | 7/2 | 7.69 × 107 * | 1.58 × 108 | −2.37 * | −2.06 |
| 614.226 | 0 | (o) | 7/2 | 162,806 | (e) | 9/2 | 2.12 × 109 | 1.47 × 109 | −0.92 | −1.07 |
| 615.162 | 0 | (o) | 7/2 | 162,558 | (e) | 7/2 | 8.44 × 108 | 7.14 × 108 | −1.32 | −1.39 |
| 615.447 | 0 | (o) | 7/2 | 162,483 | (e) | 9/2 | 1.40 × 108 * | 6.17 × 108 | −2.10 * | −1.45 |
| 617.384 | 0 | (o) | 7/2 | 161,973 | (e) | 5/2 | 7.39 × 107 * | 8.93 × 107 # | −2.37 * | −2.29 # |
| 618.330 | 11,793 | (o) | 5/2 | 173,520 | (e) | 7/2 | 4.18 × 108 * | 3.99 × 108 | −1.62 * | −1.64 |
| 626.285 | 11,793 | (o) | 5/2 | 171,465 | (e) | 3/2 | 1.19 × 108 * | 1.12 × 108 | −2.16 * | −2.18 |
| 628.091 | 11,793 | (o) | 5/2 | 171,005 | (e) | 5/2 | 3.33 × 108 | 9.45 × 107 | −1.71 | −2.25 |
| 628.793 | 0 | (o) | 7/2 | 159,035 | (e) | 7/2 | 7.29 × 108 * | 7.47 × 108 | −1.37 * | −1.35 |
| 628.998 | 0 | (o) | 7/2 | 158,983 | (e) | 5/2 | 7.72 × 107 | 3.89 × 107 # | −2.34 | −2.62 # |
| 637.437 | 11,793 | (o) | 5/2 | 168,671 | (e) | 7/2 | 1.03 × 108 * | 1.63 × 108 | −2.20 * | −2.00 |
| 637.531 | 0 | (o) | 7/2 | 156,855 | (e) | 9/2 | 4.46 × 108 | 1.57 × 108 | −1.57 | −2.02 |
| 640.120 | 0 | (o) | 7/2 | 156,219 | (e) | 7/2 | 7.18 × 107 * | 1.41 × 107 # | −2.36 * | −3.06 # |
| 643.374 | 11,793 | (o) | 5/2 | 167,223 | (e) | 5/2 | 2.15 × 108 * | 6.96 × 107 | −1.88 * | −2.37 |
| 645.219 | 0 | (o) | 7/2 | 154,985 | (e) | 9/2 | 2.86 × 108 | 4.81 × 108 | −1.75 | −1.51 |
| 646.060 | 11,793 | (o) | 5/2 | 166,577 | (e) | 5/2 | 1.01 × 108 * | 2.75 × 108 | −2.20 * | −1.76 |
| 646.238 | 11,793 | (o) | 5/2 | 166,535 | (e) | 7/2 | 1.03 × 108 * | 5.21 × 107 # | −2.19 * | −2.49 # |
| 647.581 | 0 | (o) | 7/2 | 154,421 | (e) | 5/2 | 2.66 × 102 * | 1.64 × 106 | −7.77 * | −3.98 |
| 656.146 | 11,793 | (o) | 5/2 | 164,198 | (e) | 7/2 | 1.52 × 108 | 7.50 × 107 | −2.01 | −2.31 |
| 659.711 | 147,970 | (e) | 15/2 | 299,551 | (o) | 13/2 | 8.03 × 105 * | 8.85 × 105 # | −4.29 * | −4.30 # |
| 663.292 | 11,793 | (o) | 5/2 | 162,558 | (e) | 7/2 | 1.22 × 108 * | 2.18 × 108 | −2.09 * | −1.84 |
| 664.182 | 0 | (o) | 7/2 | 150,561 | (e) | 7/2 | 1.23 × 108 * | 1.34 × 108 | −2.09 * | −2.04 |
| 665.863 | 11,793 | (o) | 5/2 | 161,973 | (e) | 5/2 | 1.16 × 107 * | 1.51 × 107 | −3.11 * | −2.99 |
| 699.848 | 156,663 | (e) | 15/2 | 299,551 | (o) | 13/2 | 3.58 × 105 * | 3.53 × 105 # | −4.58 * | −4.65 # |
| 701.121 | 11,793 | (o) | 5/2 | 154,421 | (e) | 5/2 | 2.59 × 107 * | 3.80 × 107 | −2.72 * | −2.55 |
| 711.861 | 159,402 | (e) | 13/2 | 299,879 | (o) | 11/2 | 7.36 × 104 * | 8.15 × 105 # | −5.25 * | −4.28 # |
| 718.842 | 171,307 | (e) | 7/2 | 310,420 | (o) | 9/2 | 3.21 × 107 | 9.84 × 107 | −2.60 | −2.17 |
| 757.646 | 143,721 | (e) | 9/2 | 275,709 | (o) | 9/2 | 1.44 × 108 | 4.13 × 108 | −1.89 | −1.50 |
| 786.582 | 160,846 | (e) | 3/2 | 287,980 | (o) | 5/2 | 7.85 × 107 * | 2.09 × 108 | −2.13 * | −1.77 |
| 790.958 | 143,721 | (e) | 9/2 | 270,150 | (o) | 11/2 | 1.16 × 109 | 1.64 × 109 | −0.96 | −0.86 |
| 791.571 | 154,985 | (e) | 9/2 | 281,316 | (o) | 11/2 | 3.38 × 108 | 8.23 × 108 | −1.49 | −1.15 |
| 793.168 | 143,721 | (e) | 9/2 | 269,797 | (o) | 9/2 | 1.02 × 108 * | 2.84 × 107 # | −2.01 * | −2.62 # |
| 798.330 | 162,806 | (e) | 9/2 | 288,068 | (o) | 9/2 | 6.79 × 108 | 7.94 × 108 | −1.18 | −1.17 |
| 798.984 | 162,909 | (e) | 11/2 | 288,068 | (o) | 9/2 | 5.63 × 108 | 8.03 × 108 | −1.26 | −1.16 |
| 803.460 | 156,855 | (e) | 9/2 | 281,316 | (o) | 11/2 | 1.22 × 109 | 9.96 × 108 | −0.92 | −1.05 |
| 804.510 | 157,016 | (e) | 13/2 | 281,316 | (o) | 11/2 | 5.71 × 108 | 7.00 × 108 | −1.25 | −1.21 |
| 804.715 | 143,721 | (e) | 9/2 | 267,988 | (o) | 11/2 | 1.12 × 109 | 3.63 × 108 | −0.96 | −1.50 |
| 805.483 | 151,786 | (e) | 13/2 | 275,935 | (o) | 11/2 | 8.48 × 108 | 1.09 × 109 | −1.07 | −1.02 |
| 806.043 | 160,846 | (e) | 3/2 | 284,908 | (o) | 5/2 | 5.67 × 108 | 1.06 × 109 | −1.25 | −1.03 |
| 807.412 | 150,561 | (e) | 7/2 | 274,413 | (o) | 5/2 | 5.23 × 108 | 3.44 × 108 | −1.28 | −1.53 |
| 808.779 | 162,558 | (e) | 7/2 | 286,201 | (o) | 9/2 | 1.94 × 108 * | 9.12 × 107 | −1.71 * | −2.09 |
| 811.908 | 154,421 | (e) | 5/2 | 277,587 | (o) | 5/2 | 3.29 × 107 * | 7.04 × 107 | −2.49 * | −2.21 |
| 813.433 | 161,973 | (e) | 5/2 | 284,908 | (o) | 5/2 | 4.34 × 108 | 5.82 × 108 | −1.36 | −1.28 |
| 814.355 | 157,016 | (e) | 13/2 | 279,813 | (o) | 13/2 | 9.82 × 108 | 9.72 × 108 | −1.00 | −1.05 |
| 817.741 | 147,970 | (e) | 15/2 | 270,258 | (o) | 13/2 | 2.36 × 109 | 2.18 × 109 | −0.62 | −0.70 |
| 818.952 | 166,535 | (e) | 7/2 | 288,642 | (o) | 7/2 | 3.86 × 108 | 3.40 × 108 | −1.40 | −1.51 |
| 819.642 | 164,198 | (e) | 7/2 | 286,201 | (o) | 9/2 | 2.64 × 108 | 6.54 × 108 | −1.56 | −1.23 |
| 820.249 | 159,402 | (e) | 13/2 | 281,316 | (o) | 11/2 | 2.06 × 109 | 1.78 × 109 | −0.67 | −0.79 |
| 821.643 | 148,551 | (e) | 11/2 | 270,258 | (o) | 13/2 | 5.15 × 109 | 5.44 × 109 | −0.27 | −0.30 |
| 821.750 | 163,804 | (e) | 13/2 | 285,495 | (o) | 11/2 | 7.95 × 108 * | 1.32 × 109 | −1.09 * | −0.91 |
| 822.378 | 148,551 | (e) | 11/2 | 270,150 | (o) | 11/2 | 1.47 × 108 * | 3.97 × 108 | −1.82 * | −1.44 |
| 822.497 | 154,985 | (e) | 9/2 | 276,567 | (o) | 7/2 | 8.08 × 108 * | 4.11 × 108 | −2.08 * | −1.43 |
| 822.821 | 166,535 | (e) | 7/2 | 288,068 | (o) | 9/2 | 4.68 × 108 | 5.58 × 108 | −1.31 | −1.29 |
| 822.936 | 167,125 | (e) | 9/2 | 288,642 | (o) | 7/2 | 2.64 × 108 | 4.40 × 108 | −1.56 | −1.40 |
| 823.595 | 167,223 | (e) | 5/2 | 288,642 | (o) | 7/2 | 4.54 × 108 | 5.19 × 108 | −1.33 | −1.33 |
| 825.428 | 166,240 | (e) | 9/2 | 287,390 | (o) | 7/2 | 6.33 × 108 | 1.38 × 109 | −1.18 | −0.90 |
| 825.652 | 158,983 | (e) | 5/2 | 280,099 | (o) | 7/2 | 2.23 × 109 | 2.24 × 109 | −0.63 | −0.69 |
| 825.910 | 182,025 | (e) | 5/2 | 303,103 | (o) | 5/2 | 4.75 × 108 | 3.18 × 108 | −1.31 | −1.54 |
| 826.794 | 154,985 | (e) | 9/2 | 275,935 | (o) | 11/2 | 1.15 × 109 | 7.40 × 108 | −0.92 | −1.17 |
| 827.260 | 155,054 | (e) | 11/2 | 275,935 | (o) | 11/2 | 2.49 × 109 | 1.73 × 109 | −0.58 | −0.79 |
| 827.442 | 166,535 | (e) | 7/2 | 287,390 | (o) | 7/2 | 5.19 × 108 | 5.02 × 108 | −1.26 | −1.33 |
| 828.845 | 165,551 | (e) | 11/2 | 286,201 | (o) | 9/2 | 5.45 × 108 | 8.28 × 108 | −1.24 | −1.11 |
| 829.830 | 176,019 | (e) | 11/2 | 296,526 | (o) | 11/2 | 1.51 × 109 | 1.36 × 109 | −0.80 | −0.89 |
| 830.408 | 147,970 | (e) | 15/2 | 268,393 | (o) | 15/2 | 2.51 × 109 | 1.96 × 109 | −0.58 | −0.74 |
| 830.492 | 159,402 | (e) | 13/2 | 279,813 | (o) | 13/2 | 8.43 × 108 | 4.48 × 108 | −1.05 | −1.37 |
| 831.499 | 167,125 | (e) | 9/2 | 287,390 | (o) | 7/2 | 1.36 × 109 | 7.20 × 108 | −0.84 | −1.17 |
| 832.149 | 154,985 | (e) | 9/2 | 275,157 | (o) | 7/2 | 1.24 × 109 | 5.01 × 108 | −0.89 | −1.33 |
| 833.538 | 168,671 | (e) | 7/2 | 288,642 | (o) | 7/2 | 7.69 × 108 | 3.35 × 108 | −1.09 | −1.51 |
| 833.931 | 177,396 | (e) | 9/2 | 297,310 | (o) | 9/2 | 6.54 × 108 | 7.71 × 108 | −1.15 | −1.13 |
| 834.694 | 143,721 | (e) | 9/2 | 263,525 | (o) | 9/2 | 5.08 × 108 | 5.92 × 108 | −1.27 | −1.27 |
| 836.108 | 143,721 | (e) | 9/2 | 263,323 | (o) | 7/2 | 2.52 × 108 | 2.59 × 108 | −1.58 | −1.63 |
| 836.289 | 168,491 | (e) | 11/2 | 288,068 | (o) | 9/2 | 2.61 × 109 | 2.67 × 109 | −0.55 | −0.60 |
| 837.382 | 166,535 | (e) | 7/2 | 285,954 | (o) | 7/2 | 2.40 × 106 * | 1.05 × 109 | −3.58 * | −0.99 |
| 838.674 | 150,561 | (e) | 7/2 | 269,797 | (o) | 9/2 | 2.13 × 106 * | 8.43 × 108 | −3.63 * | −1.10 |
| 839.780 | 156,855 | (e) | 9/2 | 275,935 | (o) | 11/2 | 3.31 × 108 | 6.59 × 108 | −1.44 | −1.20 |
| 840.916 | 157,016 | (e) | 13/2 | 275,935 | (o) | 11/2 | 3.60 × 109 | 3.29 × 109 | −0.41 | −0.51 |
| 841.366 | 156,855 | (e) | 9/2 | 275,709 | (o) | 9/2 | 2.61 × 108 * | 6.26 × 108 | −1.55 * | −1.22 |
| 841.544 | 167,125 | (e) | 9/2 | 285,954 | (o) | 7/2 | 2.25 × 107 * | 1.24 × 109 | −2.61 * | −0.92 |
| 843.058 | 168,671 | (e) | 7/2 | 287,287 | (o) | 5/2 | 5.50 × 108 | 1.80 × 108 | −1.22 | −1.76 |
| 843.503 | 159,035 | (e) | 7/2 | 277,587 | (o) | 5/2 | 7.23 × 107 * | 1.65 × 108 | −3.08 * | −1.81 |
| 843.810 | 162,806 | (e) | 9/2 | 281,316 | (o) | 11/2 | 1.05 × 109 | 6.92 × 108 | −0.94 | −1.17 |
| 844.079 | 151,786 | (e) | 13/2 | 270,258 | (o) | 13/2 | 1.89 × 109 | 2.13 × 109 | −0.69 | −0.68 |
| 844.543 | 162,909 | (e) | 11/2 | 281,316 | (o) | 11/2 | 1.05 × 109 | 1.37 × 109 | −0.94 | −0.87 |
| 844.852 | 151,786 | (e) | 13/2 | 270,150 | (o) | 11/2 | 4.06 × 108 * | 9.00 × 108 | −1.35 * | −1.06 |
| 845.296 | 156,855 | (e) | 9/2 | 275,157 | (o) | 7/2 | 2.09 × 106 * | 1.27 × 107 # | −3.64 * | −2.91 # |
| 846.067 | 156,219 | (e) | 7/2 | 274,413 | (o) | 5/2 | 4.55 × 108 | 3.72 × 108 | −1.31 | −1.45 |
| 847.460 | 162,806 | (e) | 9/2 | 280,805 | (o) | 9/2 | 2.83 × 108 * | 5.63 × 108 | −1.50 * | −1.26 |
| 848.206 | 162,909 | (e) | 11/2 | 280,805 | (o) | 9/2 | 1.81 × 109 | 1.35 × 109 | −0.70 | −0.87 |
| 848.824 | 158,125 | (e) | 11/2 | 275,935 | (o) | 11/2 | 1.16 × 109 | 1.49 × 109 | −0.89 | −0.84 |
| 849.545 | 168,491 | (e) | 11/2 | 286,201 | (o) | 9/2 | 7.14 × 108 | 8.26 × 108 | −1.10 | −1.09 |
| 849.723 | 167,223 | (e) | 5/2 | 284,908 | (o) | 5/2 | 1.17 × 109 | 2.85 × 108 | −0.89 | −1.55 |
| 850.057 | 193,214 | (e) | 17/2 | 310,853 | (o) | 15/2 | 3.38 × 1010 | 3.52 × 1010 | 0.57 | 0.53 |
| 850.458 | 158,983 | (e) | 5/2 | 276,567 | (o) | 7/2 | 2.20 × 108 | 4.31 × 107 | −1.62 | −2.39 |
| 158,125 | (e) | 11/2 | 275,709 | (o) | 9/2 | 7.59 × 108 | 4.04 × 108 | −1.08 | −1.40 | |
| 850.836 | 159,035 | (e) | 7/2 | 276,567 | (o) | 7/2 | 7.50 × 106 * | 5.68 × 108 | −3.08 * | −1.26 |
| 850.976 | 163,804 | (e) | 13/2 | 281,316 | (o) | 11/2 | 2.77 × 108 | 5.47 × 108 | −1.51 | −1.26 |
| 851.580 | 170,639 | (e) | 9/2 | 288,068 | (o) | 9/2 | 3.55 × 109 | 4.09 × 109 | −0.40 | −0.39 |
| 852.001 | 150,561 | (e) | 7/2 | 267,932 | (o) | 9/2 | 5.39 × 109 | 5.64 × 109 | −0.23 | −0.26 |
| 185,736 | (e) | 7/2 | 303,103 | (o) | 5/2 | 6.13 × 108 | 1.77 × 109 | −1.17 | −0.76 | |
| 852.267 | 171,307 | (e) | 7/2 | 288,642 | (o) | 7/2 | 1.11 × 109 | 9.69 × 108 | −0.91 | −1.03 |
| 852.709 | 180,036 | (e) | 7/2 | 297,310 | (o) | 9/2 | 1.41 × 109 | 1.25 × 109 | −0.80 | −0.90 |
| 853.379 | 156,219 | (e) | 7/2 | 273,400 | (o) | 9/2 | 5.94 × 108 | 3.87 × 108 | −1.19 | −1.42 |
| 855.408 | 162,909 | (e) | 11/2 | 279,813 | (o) | 13/2 | 1.15 × 109 | 9.32 × 108 # | −0.89 | −1.02 # |
| 856.592 | 160,846 | (e) | 3/2 | 277,587 | (o) | 5/2 | 3.15 × 108 | 3.61 × 108 | −1.46 | −1.46 |
| 857.582 | 151,786 | (e) | 13/2 | 268,393 | (o) | 15/2 | 1.71 × 109 | 1.31 × 109 # | −0.71 | −0.88 # |
| 164,198 | (e) | 7/2 | 280,805 | (o) | 9/2 | 3.05 × 109 | 2.07 × 109 | −0.46 | −0.69 | |
| 858.039 | 156,855 | (e) | 9/2 | 273,400 | (o) | 9/2 | 7.71 × 108 | 6.13 × 108 | −1.07 | −1.21 |
| 858.128 | 159,402 | (e) | 13/2 | 275,935 | (o) | 11/2 | 1.07 × 109 | 1.18 × 109 | −0.92 | −0.93 |
| 859.109 | 172,242 | (e) | 9/2 | 288,642 | (o) | 7/2 | 1.91 × 109 | 2.11 × 109 | −0.67 | −0.69 |
| 859.849 | 158,983 | (e) | 5/2 | 275,283 | (o) | 5/2 | 1.00 × 109 | 1.21 × 109 | −0.96 | −0.93 |
| 860.567 | 151,786 | (e) | 13/2 | 267,988 | (o) | 11/2 | 2.35 × 109 | 1.97 × 109 | −0.58 | −0.70 |
| 860.781 | 158,983 | (e) | 5/2 | 275,157 | (o) | 7/2 | 2.11 × 109 | 2.15 × 109 | −0.62 | −0.68 |
| 861.164 | 159,035 | (e) | 7/2 | 275,157 | (o) | 7/2 | 2.01 × 109 | 1.07 × 109 | −0.64 | −0.97 |
| 861.455 | 171,307 | (e) | 7/2 | 287,390 | (o) | 7/2 | 9.56 × 108 | 1.86 × 109 | −0.96 | −0.73 |
| 861.924 | 152,373 | (e) | 17/2 | 268,393 | (o) | 15/2 | 3.27 × 1010 | 3.36 × 1010 | 0.57 | 0.53 |
| 862.222 | 171,307 | (e) | 7/2 | 287,287 | (o) | 5/2 | 3.52 × 109 | 4.33 × 109 | −0.40 | −0.36 |
| 862.798 | 164,198 | (e) | 7/2 | 280,099 | (o) | 7/2 | 1.26 × 109 | 1.47 × 109 | −0.84 | −0.83 |
| 863.370 | 172,242 | (e) | 9/2 | 288,068 | (o) | 9/2 | 2.30 × 108 | 1.80 × 108 | −1.58 | −1.74 |
| 866.324 | 158,983 | (e) | 5/2 | 274,413 | (o) | 5/2 | 1.29 × 109 | 5.88 × 108 | −0.83 | −1.24 |
| 866.928 | 164,463 | (e) | 15/2 | 279,813 | (o) | 13/2 | 2.85 × 1010 | 2.89 × 1010 | 0.52 | 0.47 |
| 867.487 | 158,125 | (e) | 11/2 | 273,400 | (o) | 9/2 | 1.22 × 108 * | 9.24 × 108 | −1.86 * | −1.03 |
| 868.023 | 155,054 | (e) | 11/2 | 270,258 | (o) | 13/2 | 1.40 × 109 | 1.40 × 109 | −0.79 | −0.84 |
| 868.327 | 154,985 | (e) | 9/2 | 270,150 | (o) | 11/2 | 7.81 × 108 | 2.30 × 109 | −1.05 | −0.63 |
| 868.447 | 172,242 | (e) | 9/2 | 287,390 | (o) | 7/2 | 2.02 × 109 | 1.95 × 109 | −0.63 | −0.70 |
| 868.652 | 173,520 | (e) | 7/2 | 288,642 | (o) | 7/2 | 1.17 × 109 | 2.15 × 109 | −0.87 | −0.66 |
| 868.841 | 172,885 | (e) | 5/2 | 287,980 | (o) | 5/2 | 1.04 × 109 | 6.06 × 107 | −0.92 | −2.21 |
| 155,054 | (e) | 11/2 | 270,150 | (o) | 11/2 | 2.00 × 109 | 4.91 × 109 | −0.64 | −0.30 | |
| 868.993 | 166,240 | (e) | 9/2 | 281,316 | (o) | 11/2 | 1.82 × 109 | 2.19 × 109 | −0.67 | −0.65 |
| 869.347 | 162,558 | (e) | 7/2 | 277,587 | (o) | 5/2 | 3.73 × 108 | 1.37 × 108 | −1.37 | −1.87 |
| 869.760 | 148,551 | (e) | 11/2 | 263,525 | (o) | 9/2 | 1.11 × 109 | 1.03 × 109 | −0.90 | −0.99 |
| 869.949 | 171,005 | (e) | 5/2 | 285,954 | (o) | 7/2 | 8.89 × 108 | 2.07 × 109 | −0.99 | −0.67 |
| 870.436 | 170,023 | (e) | 5/2 | 284,908 | (o) | 5/2 | 3.43 × 108 | 3.18 × 109 | −1.40 | −0.48 |
| 870.836 | 189,188 | (e) | 7/2 | 304,021 | (o) | 7/2 | 7.51 × 108 | 2.86 × 108 | −1.06 | −1.53 |
| 870.990 | 154,985 | (e) | 9/2 | 269,797 | (o) | 9/2 | 5.30 × 100 * | 5.26 × 108 | −9.21 * | −1.27 |
| 181,894 | (e) | 7/2 | 296,706 | (o) | 7/2 | 7.02 × 109 | 6.94 × 109 | −0.08 | −0.14 | |
| 872.194 | 161,055 | (e) | 11/2 | 275,709 | (o) | 9/2 | 3.39 × 109 | 6.90 × 109 | −0.40 | −0.15 |
| 872.647 | 161,973 | (e) | 5/2 | 276,567 | (o) | 7/2 | 2.62 × 108 | 1.26 × 109 | −1.52 | −0.89 |
| 872.869 | 166,240 | (e) | 9/2 | 280,805 | (o) | 9/2 | 3.15 × 109 | 5.83 × 109 | −0.43 | −0.22 |
| 873.323 | 172,885 | (e) | 5/2 | 287,390 | (o) | 7/2 | 1.25 × 109 | 1.38 × 109 | −0.83 | −0.85 |
| 873.840 | 158,983 | (e) | 5/2 | 273,421 | (o) | 7/2 | 2.76 × 109 | 3.92 × 109 | −0.50 | −0.40 |
| 874.237 | 159,035 | (e) | 7/2 | 273,421 | (o) | 7/2 | 7.85 × 108 | 7.96 × 108 | −1.05 | −1.09 |
| 874.319 | 198,972 | (e) | 9/2 | 313,347 | (o) | 11/2 | 7.06 × 109 | 6.97 × 109 | −0.08 | −0.15 |
| 874.638 | 181,894 | (e) | 7/2 | 296,226 | (o) | 5/2 | 1.45 × 109 | 1.84 × 109 | −0.77 | −1.72 |
| 875.121 | 166,535 | (e) | 7/2 | 280,805 | (o) | 9/2 | 1.21 × 109 | 6.93 × 108 | −0.84 | −1.13 |
| 875.645 | 182,025 | (e) | 5/2 | 296,226 | (o) | 5/2 | 4.35 × 109 | 4.58 × 109 | −0.28 | −0.31 |
| 875.724 | 167,125 | (e) | 9/2 | 281,316 | (o) | 11/2 | 1.00 × 109 | 1.36 × 108 | −0.93 | −1.85 |
| 875.892 | 182,357 | (e) | 13/2 | 296,526 | (o) | 11/2 | 2.41 × 1010 | 2.42 × 1010 | 0.45 | 0.40 |
| 876.449 | 174,544 | (e) | 9/2 | 288,642 | (o) | 7/2 | 4.57 × 108 * | 2.59 × 108 | −1.27 * | −1.58 |
| 876.548 | 162,483 | (e) | 9/2 | 276,567 | (o) | 7/2 | 3.61 × 108 | 4.24 × 109 | −1.38 | −0.36 |
| 877.127 | 162,558 | (e) | 7/2 | 276,567 | (o) | 7/2 | 5.78 × 107 * | 2.63 × 108 | −2.17 * | −1.57 |
| 877.501 | 172,242 | (e) | 9/2 | 286,201 | (o) | 9/2 | 3.39 × 109 | 4.81 × 109 | −0.40 | −0.30 |
| 877.848 | 189,188 | (e) | 7/2 | 303,103 | (o) | 5/2 | 9.81 × 109 | 8.98 × 109 | 0.07 | −0.03 |
| 877.933 | 171,005 | (e) | 5/2 | 284,908 | (o) | 5/2 | 3.48 × 109 | 1.34 × 109 | −0.38 | −0.85 |
| 878.199 | 173,520 | (e) | 7/2 | 287,390 | (o) | 7/2 | 9.46 × 108 | 6.49 × 108 | −0.95 | −1.17 |
| 878.279 | 166,240 | (e) | 9/2 | 280,099 | (o) | 7/2 | 1.86 × 108 * | 4.60 × 108 | −1.66 * | −1.32 |
| 879.409 | 172,242 | (e) | 9/2 | 285,954 | (o) | 7/2 | 1.89 × 107 * | 5.85 × 109 | −2.65 * | −0.21 |
| 879.666 | 167,125 | (e) | 9/2 | 280,805 | (o) | 9/2 | 3.26 × 109 | 1.10 × 109 | −0.41 | −0.93 |
| 880.316 | 156,663 | (e) | 15/2 | 270,258 | (o) | 13/2 | 1.80 × 1010 | 1.77 × 1010 | 0.33 | 0.27 |
| 880.457 | 156,219 | (e) | 7/2 | 269,797 | (o) | 9/2 | 1.61 × 108 | 1.08 × 108 | −1.72 | −1.94 |
| 880.543 | 166,535 | (e) | 7/2 | 280,099 | (o) | 7/2 | 5.51 × 109 | 4.98 × 109 | −0.18 | −0.27 |
| 160,846 | (e) | 3/2 | 274,413 | (o) | 5/2 | 4.44 × 109 | 3.84 × 109 | −0.28 | −0.40 | |
| 880.610 | 161,973 | (e) | 5/2 | 275,530 | (o) | 3/2 | 7.55 × 108 | 7.48 × 108 | −1.06 | −1.12 |
| 880.873 | 174,544 | (e) | 9/2 | 288,068 | (o) | 9/2 | 2.73 × 109 | 2.10 × 109 | −0.49 | −0.66 |
| 881.434 | 162,483 | (e) | 9/2 | 275,935 | (o) | 11/2 | 7.92 × 108 | 6.92 × 108 | −1.02 | −1.14 |
| 881.497 | 171,465 | (e) | 3/2 | 284,908 | (o) | 5/2 | 3.81 × 109 | 3.57 × 109 | −0.34 | −0.42 |
| 882.537 | 161,973 | (e) | 5/2 | 275,283 | (o) | 5/2 | 5.39 × 108 | 4.41 × 108 | −1.20 | −1.34 |
| 882.654 | 156,855 | (e) | 9/2 | 270,150 | (o) | 11/2 | 3.90 × 108 | 4.61 × 108 | −1.33 | −1.31 |
| 882.963 | 172,242 | (e) | 9/2 | 285,495 | (o) | 11/2 | 5.55 × 108 | 5.07 × 108 | −1.17 | −1.27 |
| 883.065 | 157,016 | (e) | 13/2 | 270,258 | (o) | 13/2 | 6.32 × 109 | 6.04 × 109 | −0.12 | −0.20 |
| 883.520 | 161,973 | (e) | 5/2 | 275,157 | (o) | 7/2 | 2.44 × 109 | 1.69 × 109 | −0.54 | −0.75 |
| 883.609 | 174,895 | (e) | 7/2 | 288,068 | (o) | 9/2 | 2.78 × 108 | 2.64 × 108 | −1.48 | −1.55 |
| 883.914 | 157,016 | (e) | 13/2 | 270,150 | (o) | 11/2 | 1.98 × 107 * | 1.18 × 109 | −2.62 * | −0.91 |
| 884.111 | 164,479 | (e) | 3/2 | 277,587 | (o) | 5/2 | 9.11 × 107 | 3.62 × 108 | −1.96 | −1.43 |
| 884.207 | 184,215 | (e) | 11/2 | 297,310 | (o) | 9/2 | 1.36 × 1010 | 1.37 × 1010 | 0.22 | 0.16 |
| 884.290 | 174,895 | (e) | 7/2 | 287,980 | (o) | 5/2 | 1.08 × 109 | 1.91 × 109 | −0.88 | −0.70 |
| 171,307 | (e) | 7/2 | 284,393 | (o) | 9/2 | 5.01 × 107 * | 5.51 × 107 | −2.23 * | −2.23 | |
| 884.512 | 183,649 | (e) | 9/2 | 296,706 | (o) | 7/2 | 6.39 × 109 | 6.35 × 109 | −0.11 | −0.17 |
| 884.747 | 190,994 | (e) | 5/2 | 304,021 | (o) | 7/2 | 1.91 × 108 | 1.92 × 108 | −1.64 | −1.70 |
| 884.928 | 154,985 | (e) | 9/2 | 267,988 | (o) | 11/2 | 1.51 × 109 | 1.22 × 109 | −0.75 | −0.89 |
| 885.057 | 175,654 | (e) | 7/2 | 288,642 | (o) | 7/2 | 1.11 × 109 | 7.33 × 108 | −0.88 | −1.11 |
| 885.160 | 167,125 | (e) | 9/2 | 280,099 | (o) | 7/2 | 2.43 × 108 * | 5.04 × 107 # | −1.53 * | −2.27 # |
| 885.235 | 150,561 | (e) | 7/2 | 263,525 | (o) | 9/2 | 2.96 × 109 | 3.67 × 109 | −0.46 | −0.42 |
| 885.394 | 156,855 | (e) | 9/2 | 269,797 | (o) | 9/2 | 4.56 × 107 * | 1.29 × 109 | −2.26 * | −0.86 |
| 885.720 | 162,806 | (e) | 9/2 | 275,709 | (o) | 9/2 | 4.85 × 107 * | 4.49 × 108 | −2.23 * | −1.33 |
| 885.923 | 183,649 | (e) | 9/2 | 296,526 | (o) | 11/2 | 9.45 × 108 | 7.70 × 108 # | −0.94 | −1.08 # |
| 886.160 | 143,721 | (e) | 9/2 | 256,566 | (o) | 11/2 | 1.41 × 1010 | 1.58 × 1010 | 0.22 | 0.21 |
| 174,544 | (e) | 9/2 | 287,390 | (o) | 7/2 | 9.68 × 109 | 9.37 × 109 | 0.07 | 0.00 | |
| 886.322 | 168,491 | (e) | 11/2 | 281,316 | (o) | 11/2 | 8.07 × 109 | 7.82 × 109 | −0.01 | −0.08 |
| 886.438 | 168,506 | (e) | 13/2 | 281,316 | (o) | 11/2 | 1.47 × 1010 | 1.42 × 1010 | 0.25 | 0.18 |
| 886.533 | 162,909 | (e) | 11/2 | 275,709 | (o) | 9/2 | 1.03 × 109 | 1.53 × 109 | −0.90 | −0.79 |
| 886.824 | 150,561 | (e) | 7/2 | 263,323 | (o) | 7/2 | 3.79 × 109 | 3.33 × 109 | −0.35 | −0.47 |
| 887.517 | 162,483 | (e) | 9/2 | 275,157 | (o) | 7/2 | 7.37 × 109 | 2.95 × 109 | −0.05 | −0.51 |
| 888.110 | 162,558 | (e) | 7/2 | 275,157 | (o) | 7/2 | 5.19 × 109 | 5.54 × 109 | −0.21 | −0.23 |
| 888.932 | 174,895 | (e) | 7/2 | 287,390 | (o) | 7/2 | 1.92 × 109 | 1.85 × 109 | −0.63 | −0.70 |
| 889.359 | 161,973 | (e) | 5/2 | 274,413 | (o) | 5/2 | 1.98 × 109 | 2.18 × 109 | −0.62 | −0.64 |
| 889.410 | 173,520 | (e) | 7/2 | 285,954 | (o) | 7/2 | 1.89 × 104 * | 1.57 × 109 | −5.64 * | −0.77 |
| 889.923 | 164,198 | (e) | 7/2 | 276,567 | (o) | 7/2 | 1.92 × 109 | 1.74 × 109 | −0.64 | −0.74 |
| 890.068 | 162,806 | (e) | 9/2 | 275,157 | (o) | 7/2 | 2.22 × 108 | 3.13 × 109 | −1.57 | −0.48 |
| 890.114 | 161,055 | (e) | 11/2 | 273,400 | (o) | 9/2 | 1.00 × 1010 | 6.44 × 109 | 0.08 | −0.16 |
| 890.360 | 168,491 | (e) | 11/2 | 280,805 | (o) | 9/2 | 8.28 × 109 | 8.48 × 109 | 0.01 | −0.04 |
| 891.814 | 163,804 | (e) | 13/2 | 275,935 | (o) | 11/2 | 1.81 × 1010 | 1.77 × 1010 | 0.34 | 0.28 |
| 891.991 | 190,994 | (e) | 5/2 | 303,103 | (o) | 5/2 | 3.21 × 109 | 3.14 × 109 | −0.41 | −0.47 |
| 892.556 | 201,310 | (e) | 11/2 | 313,347 | (o) | 11/2 | 3.44 × 108 | 6.52 × 109 | −1.38 | −0.15 |
| 892.656 | 158,125 | (e) | 11/2 | 270,150 | (o) | 11/2 | 2.18 × 109 | 3.23 × 109 | −0.57 | −0.46 |
| 187,526 | (e) | 15/2 | 299,551 | (o) | 13/2 | 2.39 × 1010 | 2.71 × 1010 | 0.45 | 0.45 | |
| 893.489 | 192,100 | (e) | 9/2 | 304,021 | (o) | 7/2 | 1.60 × 1010 | 1.61 × 1010 | 0.30 | 0.24 |
| 894.013 | 162,558 | (e) | 7/2 | 274,413 | (o) | 5/2 | 2.34 × 109 | 2.10 × 109 | −0.54 | −0.65 |
| 895.014 | 156,663 | (e) | 15/2 | 268,393 | (o) | 15/2 | 9.30 × 109 | 9.46 × 109 | 0.06 | 0.02 |
| 895.152 | 156,219 | (e) | 7/2 | 267,932 | (o) | 9/2 | 6.94 × 109 | 6.23 × 109 | −0.08 | −0.17 |
| 895.470 | 158,125 | (e) | 11/2 | 269,797 | (o) | 9/2 | 4.04 × 108 | 2.31 × 109 | −1.31 | −0.60 |
| 897.282 | 161,973 | (e) | 5/2 | 273,421 | (o) | 7/2 | 2.80 × 109 | 2.70 × 109 | −0.47 | −0.54 |
| 198,972 | (e) | 9/2 | 310,420 | (o) | 9/2 | 9.60 × 109 | 9.79 × 109 | 0.08 | 0.03 | |
| 897.422 | 168,671 | (e) | 7/2 | 280,099 | (o) | 7/2 | 2.55 × 108 | 5.16 × 108 | −1.50 | −1.24 |
| 897.766 | 173,520 | (e) | 7/2 | 284,908 | (o) | 5/2 | 1.26 × 109 | 1.46 × 109 | −0.81 | −0.79 |
| 897.857 | 157,016 | (e) | 13/2 | 268,393 | (o) | 15/2 | 5.63 × 108 | 4.44 × 108 # | −1.16 | −1.31 # |
| 898.301 | 168,491 | (e) | 11/2 | 279,813 | (o) | 13/2 | 7.09 × 108 | 5.11 × 108 # | −1.05 | −1.25 # |
| 898.415 | 168,506 | (e) | 13/2 | 279,813 | (o) | 13/2 | 8.10 × 109 | 7.96 × 109 | 0.01 | −0.05 |
| 898.918 | 177,396 | (e) | 9/2 | 288,642 | (o) | 7/2 | 4.54 × 109 | 2.54 × 109 | −0.25 | −0.57 |
| 898.980 | 176,831 | (e) | 11/2 | 288,068 | (o) | 9/2 | 1.59 × 1010 | 1.58 × 1010 | 0.30 | 0.24 |
| 899.489 | 202,173 | (e) | 11/2 | 313,347 | (o) | 11/2 | 1.25 × 1010 | 7.02 × 109 | −0.71 | −0.11 |
| 899.817 | 156,855 | (e) | 9/2 | 267,988 | (o) | 11/2 | 2.42 × 109 | 9.66 × 108 | −0.53 | −0.97 |
| 900.213 | 164,198 | (e) | 7/2 | 275,283 | (o) | 5/2 | 1.64 × 109 | 9.93 × 108 | −0.70 | −0.98 |
| 900.271 | 156,855 | (e) | 9/2 | 267,932 | (o) | 9/2 | 7.55 × 109 | 4.84 × 109 | −0.03 | −0.27 |
| 900.812 | 166,577 | (e) | 5/2 | 277,587 | (o) | 5/2 | 9.59 × 108 | 1.71 × 108 | −0.93 | −1.74 |
| 901.126 | 157,016 | (e) | 13/2 | 267,988 | (o) | 11/2 | 1.22 × 1010 | 1.25 × 1010 | 0.17 | 0.13 |
| 901.232 | 164,198 | (e) | 7/2 | 275,157 | (o) | 7/2 | 6.54 × 106 * | 7.98 × 105 # | −3.09 * | −4.07 # |
| 901.582 | 162,483 | (e) | 9/2 | 273,400 | (o) | 9/2 | 3.62 × 109 | 1.33 × 109 | −0.36 | −0.84 |
| 902.185 | 162,558 | (e) | 7/2 | 273,400 | (o) | 9/2 | 1.37 × 109 | 5.60 × 108 | −0.78 | −1.22 |
| 902.499 | 164,479 | (e) | 3/2 | 275,283 | (o) | 5/2 | 2.98 × 109 | 2.90 × 109 | −0.44 | −0.51 |
| 902.833 | 203,211 | (e) | 15/2 | 313,974 | (o) | 13/2 | 1.60 × 1010 | 1.56 × 1010 | 0.30 | 0.24 |
| 902.954 | 159,402 | (e) | 13/2 | 270,150 | (o) | 11/2 | 1.48 × 1010 | 1.10 × 1010 | 0.27 | 0.08 |
| 904.594 | 175,654 | (e) | 7/2 | 286,201 | (o) | 9/2 | 3.44 × 108 | 6.51 × 108 | −1.36 | −1.13 |
| 905.047 | 162,909 | (e) | 11/2 | 273,400 | (o) | 9/2 | 5.55 × 108 | 4.20 × 108 | −1.16 | −1.33 |
| 906.082 | 167,223 | (e) | 5/2 | 277,587 | (o) | 5/2 | 6.45 × 108 | 1.55 × 109 | −1.09 | −0.77 |
| 906.619 | 175,654 | (e) | 7/2 | 285,954 | (o) | 7/2 | 2.54 × 108 * | 1.63 × 109 | −1.49 * | −0.73 |
| 907.554 | 203,161 | (e) | 13/2 | 313,347 | (o) | 11/2 | 9.02 × 109 | 8.47 × 109 | 0.06 | −0.02 |
| 907.718 | 170,639 | (e) | 9/2 | 280,805 | (o) | 9/2 | 2.30 × 109 | 1.40 × 109 | −0.53 | −0.79 |
| 908.460 | 170,023 | (e) | 5/2 | 280,099 | (o) | 7/2 | 1.06 × 109 | 7.55 × 108 | −0.87 | −1.07 |
| 908.988 | 178,629 | (e) | 9/2 | 288,642 | (o) | 7/2 | 8.44 × 109 | 1.02 × 1010 | 0.03 | 0.06 |
| 909.637 | 164,479 | (e) | 3/2 | 274,413 | (o) | 5/2 | 7.91 × 108 | 1.16 × 109 | −1.00 | −0.89 |
| 909.941 | 177,390 | (e) | 5/2 | 287,287 | (o) | 5/2 | 4.22 × 108 | 8.32 × 107 | −1.27 | −2.03 |
| 910.156 | 181,894 | (e) | 7/2 | 291,764 | (o) | 5/2 | 1.89 × 109 | 3.05 × 109 | −0.64 | −0.49 |
| 910.220 | 158,125 | (e) | 11/2 | 267,988 | (o) | 11/2 | 6.20 × 109 | 3.15 × 109 | −0.11 | −0.45 |
| 910.683 | 158,125 | (e) | 11/2 | 267,932 | (o) | 9/2 | 4.78 × 109 | 3.48 × 109 | −0.22 | −0.41 |
| 911.242 | 182,025 | (e) | 5/2 | 291,764 | (o) | 5/2 | 5.07 × 108 | 1.09 × 108 # | −1.20 | −1.92 # |
| 911.509 | 182,025 | (e) | 5/2 | 291,733 | (o) | 3/2 | 1.69 × 109 | 1.34 × 109 | −0.68 | −0.83 |
| 912.834 | 195,441 | (e) | 5/2 | 304,990 | (o) | 5/2 | 2.27 × 109 | 2.73 × 109 | −0.55 | −0.52 |
| 913.569 | 170,639 | (e) | 9/2 | 280,099 | (o) | 7/2 | 4.32 × 109 | 4.30 × 109 | −0.25 | −0.30 |
| 913.729 | 167,125 | (e) | 9/2 | 276,567 | (o) | 7/2 | 4.30 × 109 | 1.84 × 109 | −0.26 | −0.69 |
| 914.012 | 186,818 | (e) | 5/2 | 296,226 | (o) | 5/2 | 2.72 × 108 | 3.22 × 108 | −1.45 | −1.43 |
| 914.326 | 176,831 | (e) | 11/2 | 286,201 | (o) | 9/2 | 8.56 × 108 | 5.34 × 108 | −0.95 | −1.21 |
| 914.719 | 147,970 | (e) | 15/2 | 257,293 | (o) | 13/2 | 2.21 × 1010 | 2.44 × 1010 | 0.44 | 0.43 |
| 915.730 | 164,198 | (e) | 7/2 | 273,400 | (o) | 9/2 | 5.04 × 108 | 1.04 × 109 | −1.20 | −0.94 |
| 161,055 | (e) | 11/2 | 270,258 | (o) | 13/2 | 8.65 × 107 | 7.62 × 107 # | −1.95 | −2.06 # | |
| 916.503 | 201,310 | (e) | 11/2 | 310,420 | (o) | 9/2 | 1.31 × 108 * | 1.75 × 109 | −1.77 * | −0.69 |
| 917.821 | 166,577 | (e) | 5/2 | 275,530 | (o) | 3/2 | 1.12 × 109 | 6.51 × 106 # | −0.85 | −3.14 # |
| 918.131 | 166,240 | (e) | 9/2 | 275,157 | (o) | 7/2 | 2.34 × 106 * | 3.19 × 108 | −3.52 * | −1.45 |
| 918.260 | 154,421 | (e) | 5/2 | 263,323 | (o) | 7/2 | 7.01 × 109 | 7.17 × 109 | −0.05 | −0.10 |
| 919.071 | 177,396 | (e) | 9/2 | 286,201 | (o) | 9/2 | 3.62 × 108 | 1.40 × 108 | −1.33 | −1.79 |
| 919.557 | 166,535 | (e) | 7/2 | 275,283 | (o) | 5/2 | 2.33 × 109 | 3.09 × 109 | −0.53 | −0.46 |
| 919.607 | 148,551 | (e) | 11/2 | 257,293 | (o) | 13/2 | 3.36 × 109 | 3.25 × 109 | −0.37 | −0.44 |
| 919.909 | 166,577 | (e) | 5/2 | 275,283 | (o) | 5/2 | 2.33 × 109 | 9.97 × 108 | −0.53 | −0.95 |
| 920.269 | 176,831 | (e) | 11/2 | 285,495 | (o) | 11/2 | 7.09 × 108 | 7.06 × 108 | −1.03 | −1.08 |
| 920.621 | 166,535 | (e) | 7/2 | 275,157 | (o) | 7/2 | 1.70 × 108 | 3.73 × 108 | −1.65 | −1.37 |
| 920.925 | 159,402 | (e) | 13/2 | 267,988 | (o) | 11/2 | 1.68 × 109 | 5.87 × 109 | −0.67 | −0.17 |
| 921.116 | 172,242 | (e) | 9/2 | 280,805 | (o) | 9/2 | 3.85 × 108 | 4.09 × 108 | −1.30 | −1.32 |
| 921.319 | 154,985 | (e) | 9/2 | 263,525 | (o) | 9/2 | 6.60 × 109 | 6.09 × 109 | −0.08 | −0.17 |
| 921.898 | 155,054 | (e) | 11/2 | 263,525 | (o) | 9/2 | 1.15 × 1010 | 1.07 × 1010 | 0.17 | 0.08 |
| 922.727 | 176,019 | (e) | 11/2 | 284,393 | (o) | 9/2 | 5.51 × 109 | 1.06 × 1010 | −0.15 | 0.08 |
| 923.042 | 154,985 | (e) | 9/2 | 263,323 | (o) | 7/2 | 3.50 × 109 | 2.45 × 109 | −0.35 | −0.56 |
| 923.492 | 196,706 | (e) | 5/2 | 304,990 | (o) | 5/2 | 5.80 × 108 | 1.87 × 108 | −1.13 | −1.67 |
| 923.812 | 202,173 | (e) | 11/2 | 310,420 | (o) | 9/2 | 3.73 × 109 | 1.79 × 109 | −0.31 | −0.68 |
| 925.408 | 167,223 | (e) | 5/2 | 275,283 | (o) | 5/2 | 2.52 × 108 | 1.83 × 109 | −1.49 | −0.68 |
| 925.655 | 167,125 | (e) | 9/2 | 275,157 | (o) | 7/2 | 1.75 × 108 * | 1.46 × 109 | −1.64 * | −0.78 |
| 925.787 | 148,551 | (e) | 11/2 | 256,566 | (o) | 11/2 | 9.95 × 109 | 1.10 × 1010 | 0.11 | 0.10 |
| 926.489 | 167,223 | (e) | 5/2 | 275,157 | (o) | 7/2 | 1.49 × 108 | 8.72 × 108 | −1.71 | −0.99 |
| 926.815 | 168,671 | (e) | 7/2 | 276,567 | (o) | 7/2 | 1.37 × 108 | 3.45 × 108 | −1.74 | −1.40 |
| 926.999 | 177,396 | (e) | 9/2 | 285,271 | (o) | 7/2 | 4.06 × 106 * | 4.26 × 109 | −3.27 * | −0.30 |
| 927.222 | 165,551 | (e) | 11/2 | 273,400 | (o) | 9/2 | 4.39 × 109 | 9.01 × 109 | −0.24 | 0.02 |
| 929.005 | 203,211 | (e) | 15/2 | 310,853 | (o) | 15/2 | 9.66 × 109 | 9.64 × 109 # | 0.11 | 0.06 # |
| 929.606 | 178,629 | (e) | 9/2 | 286,201 | (o) | 9/2 | 3.61 × 109 | 2.53 × 109 | −0.32 | −0.52 |
| 929.670 | 170,023 | (e) | 5/2 | 277,587 | (o) | 5/2 | 1.98 × 109 | 5.06 × 108 | −0.58 | −1.24 |
| 931.584 | 162,806 | (e) | 9/2 | 270,150 | (o) | 11/2 | 2.81 × 109 | 2.14 × 109 | −0.43 | −0.60 |
| 931.917 | 156,219 | (e) | 7/2 | 263,525 | (o) | 9/2 | 4.16 × 108 | 5.04 × 108 | −1.27 | −1.24 |
| 932.915 | 167,223 | (e) | 5/2 | 274,413 | (o) | 5/2 | 4.10 × 108 | 1.01 × 108 | −1.26 | −1.93 |
| 933.007 | 166,240 | (e) | 9/2 | 273,421 | (o) | 7/2 | 2.97 × 109 | 1.55 × 109 | −0.41 | −0.74 |
| 933.182 | 166,240 | (e) | 9/2 | 273,400 | (o) | 9/2 | 2.15 × 109 | 1.43 × 109 | −0.55 | −0.78 |
| 933.672 | 156,219 | (e) | 7/2 | 263,323 | (o) | 7/2 | 3.57 × 109 | 4.48 × 109 | −0.33 | −0.29 |
| 934.647 | 162,806 | (e) | 9/2 | 269,797 | (o) | 9/2 | 6.69 × 109 | 4.95 × 109 | −0.05 | −0.23 |
| 935.448 | 198,089 | (e) | 7/2 | 304,990 | (o) | 5/2 | 5.38 × 109 | 4.42 × 109 | −0.15 | −0.30 |
| 935.559 | 162,909 | (e) | 11/2 | 269,797 | (o) | 9/2 | 4.46 × 109 | 3.02 × 109 | −0.22 | −0.44 |
| 937.466 | 156,855 | (e) | 9/2 | 263,525 | (o) | 9/2 | 8.31 × 108 | 2.05 × 109 | −0.96 | −0.62 |
| 937.713 | 178,629 | (e) | 9/2 | 285,271 | (o) | 7/2 | 1.68 × 108 * | 7.58 × 108 | −1.64 * | −1.04 |
| 938.578 | 170,023 | (e) | 5/2 | 276,567 | (o) | 7/2 | 6.32 × 108 | 3.89 × 108 | −1.07 | −1.34 |
| 939.097 | 168,671 | (e) | 7/2 | 275,157 | (o) | 7/2 | 2.93 × 108 | 3.17 × 107 # | −1.40 | −2.42 # |
| 940.328 | 163,804 | (e) | 13/2 | 270,150 | (o) | 11/2 | 3.36 × 108 | 3.96 × 108 | −1.34 | −1.32 |
| 940.775 | 167,125 | (e) | 9/2 | 273,421 | (o) | 7/2 | 1.00 × 109 | 2.57 × 109 | −0.88 | −0.52 |
| 941.636 | 167,223 | (e) | 5/2 | 273,421 | (o) | 7/2 | 1.88 × 109 | 1.14 × 109 | −0.60 | −0.87 |
| 947.805 | 151,786 | (e) | 13/2 | 257,293 | (o) | 13/2 | 9.74 × 109 | 1.03 × 1010 | 0.12 | 0.09 |
| 948.762 | 158,125 | (e) | 11/2 | 263,525 | (o) | 9/2 | 1.64 × 109 | 2.83 × 109 | −0.65 | −0.47 |
| 950.032 | 170,023 | (e) | 5/2 | 275,283 | (o) | 5/2 | 1.28 × 109 | 3.95 × 108 | −0.76 | −1.33 |
| 950.246 | 180,036 | (e) | 7/2 | 285,271 | (o) | 7/2 | 4.67 × 108 | 5.21 × 109 | −1.19 | −0.19 |
| 950.729 | 162,806 | (e) | 9/2 | 267,988 | (o) | 11/2 | 7.93 × 107 * | 5.22 × 108 | −1.97 * | −1.20 |
| 951.237 | 162,806 | (e) | 9/2 | 267,932 | (o) | 9/2 | 4.63 × 107 * | 1.42 × 109 | −2.20 * | −0.76 |
| 951.662 | 162,909 | (e) | 11/2 | 267,988 | (o) | 11/2 | 1.65 × 109 | 4.43 × 109 | −0.64 | −0.26 |
| 952.173 | 162,909 | (e) | 11/2 | 267,932 | (o) | 9/2 | 2.05 × 108 * | 1.62 × 109 | −1.55 * | −0.70 |
| 952.873 | 186,818 | (e) | 5/2 | 291,764 | (o) | 5/2 | 2.70 × 109 | 2.80 × 109 | −0.44 | −0.48 |
| 953.165 | 186,818 | (e) | 5/2 | 291,733 | (o) | 3/2 | 1.58 × 109 | 1.45 × 109 | −0.68 | −0.77 |
| 954.374 | 151,786 | (e) | 13/2 | 256,566 | (o) | 11/2 | 5.49 × 109 | 5.57 × 109 | −0.13 | −0.17 |
| 956.772 | 170,639 | (e) | 9/2 | 275,157 | (o) | 7/2 | 8.14 × 107 * | 1.22 × 109 | −1.94 * | −0.82 |
| 958.970 | 171,005 | (e) | 5/2 | 275,283 | (o) | 5/2 | 2.17 × 108 | 1.19 × 109 | −1.52 | −0.84 |
| 960.921 | 173,520 | (e) | 7/2 | 277,587 | (o) | 5/2 | 1.93 × 109 | 2.36 × 109 | −0.57 | −0.54 |
| 963.227 | 171,465 | (e) | 3/2 | 275,283 | (o) | 5/2 | 9.93 × 108 | 1.33 × 109 | −0.86 | −0.79 |
| 965.653 | 166,240 | (e) | 9/2 | 269,797 | (o) | 9/2 | 7.30 × 108 | 1.13 × 109 | −0.98 | −0.85 |
| 974.890 | 189,188 | (e) | 7/2 | 291,764 | (o) | 5/2 | 9.79 × 108 | 5.43 × 108 | −0.85 | −1.16 |
| 197,304 | (e) | 13/2 | 299,879 | (o) | 11/2 | 5.16 × 109 | 4.92 × 109 | −0.13 | −0.19 | |
| 978.015 | 197,304 | (e) | 13/2 | 299,551 | (o) | 13/2 | 8.87 × 109 | 9.56 × 109 | 0.11 | 0.10 |
| 979.306 | 171,307 | (e) | 7/2 | 273,421 | (o) | 7/2 | 1.44 × 109 | 1.22 × 109 | −0.68 | −0.80 |
| 1002.891 | 156,855 | (e) | 9/2 | 256,566 | (o) | 11/2 | 7.45 × 108 | 8.86 × 108 | −0.95 | −0.92 |
| 1008.394 | 158,125 | (e) | 11/2 | 257,293 | (o) | 13/2 | 6.14 × 108 | 6.54 × 108 | −1.03 | −1.05 |
| 1015.829 | 158,125 | (e) | 11/2 | 256,566 | (o) | 11/2 | 5.73 × 108 | 6.75 × 108 | −1.05 | −1.03 |
| 1236.607 | 187,526 | (e) | 15/2 | 268,393 | (o) | 15/2 | 1.76 × 104 * | 9.56 × 103 # | −5.38 * | −5.68 # |
| 1247.456 | 217,147 | (e) | 7/2 | 297,310 | (o) | 9/2 | 1.10 × 107 * | 1.39 × 107 | −2.57 * | −2.48 |
| 1290.447 | 207,779 | (e) | 7/2 | 285,271 | (o) | 7/2 | 2.83 × 107 * | 5.16 × 105 # | −2.15 * | −3.88 # |
| 1420.023 | 243,552 | (e) | 11/2 | 313,974 | (o) | 13/2 | 5.36 × 109 | 5.00 × 109 | 0.23 | 0.18 |
| 1429.209 | 217,422 | (e) | 9/2 | 287,390 | (o) | 7/2 | 4.96 × 106 * | 3.62 × 104 # | −2.81 * | −4.96 # |
| 1432.500 | 243,539 | (e) | 13/2 | 313,347 | (o) | 11/2 | 2.51 × 109 | 2.15 × 109 | −0.09 | −0.18 |
| 207,779 | (e) | 7/2 | 277,587 | (o) | 5/2 | 1.78 × 109 | 2.49 × 109 | −0.26 | −0.12 | |
| 1432.771 | 243,552 | (e) | 11/2 | 313,347 | (o) | 11/2 | 1.46 × 1010 | 1.54 × 1010 | 0.67 | 0.67 |
| 1435.556 | 218,982 | (e) | 5/2 | 288,642 | (o) | 7/2 | 2.21 × 109 | 1.21 × 109 | −0.15 | −0.43 |
| 1441.761 | 211,957 | (e) | 11/2 | 281,316 | (o) | 11/2 | 1.12 × 1010 | 1.14 × 1010 | 0.56 | 0.56 |
| 1441.952 | 207,216 | (e) | 9/2 | 276,567 | (o) | 7/2 | 4.50 × 107 * | 1.61 × 109 | −1.83 * | −0.29 |
| 1443.641 | 212,047 | (e) | 9/2 | 281,316 | (o) | 11/2 | 5.57 × 109 | 5.16 × 109 | 0.26 | 0.21 |
| 1448.138 | 217,147 | (e) | 7/2 | 286,201 | (o) | 9/2 | 3.46 × 109 | 4.37 × 109 | 0.06 | 0.14 |
| 1449.324 | 218,982 | (e) | 5/2 | 287,980 | (o) | 5/2 | 2.93 × 108 | 3.94 × 104 # | −1.02 | −4.90 # |
| 1450.356 | 201,310 | (e) | 11/2 | 270,258 | (o) | 13/2 | 6.31 × 109 | 3.27 × 109 | 0.32 | 0.02 |
| 1450.686 | 228,377 | (e) | 7/2 | 297,310 | (o) | 9/2 | 5.15 × 109 | 4.96 × 109 | 0.23 | 0.20 |
| 1452.469 | 211,957 | (e) | 11/2 | 280,805 | (o) | 9/2 | 2.51 × 109 | 2.19 × 109 | −0.08 | −0.15 |
| 1452.638 | 201,310 | (e) | 11/2 | 270,150 | (o) | 11/2 | 7.11 × 109 | 6.27 × 109 | 0.37 | 0.30 |
| 1453.353 | 219,261 | (e) | 7/2 | 288,068 | (o) | 9/2 | 1.33 × 1010 | 1.30 × 1010 | 0.64 | 0.62 |
| 1453.751 | 207,779 | (e) | 7/2 | 276,567 | (o) | 7/2 | 9.94 × 108 | 4.73 × 109 | −0.50 | 0.18 |
| 1453.910 | 217,422 | (e) | 9/2 | 286,201 | (o) | 9/2 | 5.42 × 109 | 7.26 × 109 | 0.25 | 0.37 |
| 1454.375 | 212,047 | (e) | 9/2 | 280,805 | (o) | 9/2 | 1.09 × 1010 | 1.09 × 1010 | 0.56 | 0.55 |
| 1455.214 | 207,216 | (e) | 9/2 | 275,935 | (o) | 11/2 | 1.47 × 109 | 1.57 × 1010 | −0.30 | 0.70 |
| 219,261 | (e) | 7/2 | 287,980 | (o) | 5/2 | 7.04 × 108 | 8.94 × 107 | −0.63 | −1.55 | |
| 1459.156 | 217,422 | (e) | 9/2 | 285,954 | (o) | 7/2 | 1.96 × 107 * | 2.06 × 109 | −2.19 * | −0.17 |
| 1460.113 | 201,310 | (e) | 11/2 | 269,797 | (o) | 9/2 | 3.64 × 109 | 4.63 × 109 | 0.08 | 0.18 |
| 1460.708 | 220,182 | (e) | 5/2 | 288,642 | (o) | 7/2 | 8.12 × 109 | 9.14 × 109 | 0.43 | 0.47 |
| 1461.825 | 218,982 | (e) | 5/2 | 287,390 | (o) | 7/2 | 4.63 × 109 | 4.81 × 109 | 0.19 | 0.20 |
| 1463.514 | 228,377 | (e) | 7/2 | 296,706 | (o) | 7/2 | 8.58 × 109 | 8.47 × 109 | 0.46 | 0.44 |
| 1464.031 | 218,982 | (e) | 5/2 | 287,287 | (o) | 5/2 | 4.67 × 109 | 5.23 × 109 | 0.20 | 0.23 |
| 1467.809 | 219,261 | (e) | 7/2 | 287,390 | (o) | 7/2 | 5.60 × 109 | 5.44 × 109 | 0.28 | 0.25 |
| 1468.749 | 202,173 | (e) | 11/2 | 270,258 | (o) | 13/2 | 1.24 × 108 | 2.72 × 109 | −1.37 | −0.05 |
| 219,202 | (e) | 3/2 | 287,287 | (o) | 5/2 | 1.91 × 109 | 5.06 × 108 | −0.19 | −0.77 | |
| 1468.991 | 217,422 | (e) | 9/2 | 285,495 | (o) | 11/2 | 1.62 × 1010 | 1.56 × 1010 | 0.74 | 0.71 |
| 1469.454 | 212,047 | (e) | 9/2 | 280,099 | (o) | 7/2 | 8.76 × 109 | 7.78 × 109 | 0.47 | 0.41 |
| 1470.045 | 219,261 | (e) | 7/2 | 287,287 | (o) | 5/2 | 1.39 × 109 | 1.96 × 109 | −0.33 | −0.19 |
| 1471.094 | 202,173 | (e) | 11/2 | 270,150 | (o) | 11/2 | 1.37 × 108 | 5.31 × 109 | −1.32 | 0.24 |
| 1471.203 | 228,554 | (e) | 9/2 | 296,526 | (o) | 11/2 | 1.60 × 1010 | 1.56 × 1010 | 0.73 | 0.71 |
| 1471.880 | 207,216 | (e) | 9/2 | 275,157 | (o) | 7/2 | 1.92 × 108 | 1.14 × 109 | −1.19 | −0.43 |
| 1472.120 | 207,779 | (e) | 7/2 | 275,709 | (o) | 9/2 | 3.56 × 109 | 5.14 × 109 | 0.08 | 0.23 |
| 1473.710 | 211,957 | (e) | 11/2 | 279,813 | (o) | 13/2 | 1.89 × 1010 | 1.82 × 1010 | 0.81 | 0.78 |
| 1475.774 | 217,147 | (e) | 7/2 | 284,908 | (o) | 5/2 | 7.15 × 109 | 6.85 × 109 | 0.39 | 0.36 |
| 1478.758 | 202,173 | (e) | 11/2 | 269,797 | (o) | 9/2 | 4.89 × 107 * | 3.81 × 109 | −1.77 * | 0.10 |
| 1484.176 | 207,779 | (e) | 7/2 | 275,157 | (o) | 7/2 | 6.76 × 109 | 2.95 × 109 | 0.36 | −0.01 |
| 1485.582 | 243,539 | (e) | 13/2 | 310,853 | (o) | 15/2 | 2.13 × 1010 | 2.07 × 1010 | 0.87 | 0.85 |
| 1487.908 | 220,182 | (e) | 5/2 | 287,390 | (o) | 7/2 | 5.69 × 108 | 2.65 × 108 | −0.70 | −1.04 |
| 1493.883 | 219,261 | (e) | 7/2 | 286,201 | (o) | 9/2 | 1.61 × 108 | 1.52 × 108 | −1.25 | −1.28 |
| 1499.728 | 201,310 | (e) | 11/2 | 267,988 | (o) | 11/2 | 6.00 × 109 | 9.72 × 108 | 0.31 | −0.48 |
| 1500.734 | 207,779 | (e) | 7/2 | 274,413 | (o) | 5/2 | 6.23 × 109 | 5.47 × 109 | 0.33 | 0.27 |
| 1500.995 | 201,310 | (e) | 11/2 | 267,932 | (o) | 9/2 | 8.65 × 109 | 1.55 × 109 | 0.47 | −0.28 |
| 1510.946 | 207,216 | (e) | 9/2 | 273,400 | (o) | 9/2 | 3.22 × 108 | 8.63 × 108 | −0.95 | −0.52 |
| 1516.850 | 218,982 | (e) | 5/2 | 284,908 | (o) | 5/2 | 2.62 × 108 | 1.72 × 108 | −1.02 | −1.20 |
| 1519.401 | 202,173 | (e) | 11/2 | 267,988 | (o) | 11/2 | 1.64 × 108 | 9.52 × 108 | −1.23 | −0.48 |
| 1520.695 | 202,173 | (e) | 11/2 | 267,932 | (o) | 9/2 | 2.13 × 108 | 1.49 × 109 | −1.12 | −0.29 |
| 1523.901 | 207,779 | (e) | 7/2 | 273,400 | (o) | 9/2 | 2.22 × 109 | 5.29 × 108 | −0.11 | −0.70 |
| 1536.335 | 220,182 | (e) | 5/2 | 285,271 | (o) | 7/2 | 2.30 × 108 | 5.68 × 107 | −1.07 | −1.67 |
| 1544.949 | 220,182 | (e) | 5/2 | 284,908 | (o) | 5/2 | 2.23 × 108 | 3.47 × 108 | −1.07 | −0.88 |
| 1584.538 | 212,047 | (e) | 9/2 | 275,157 | (o) | 7/2 | 3.00 × 108 | 1.32 × 109 | −0.93 | −0.31 |
| 1629.368 | 212,047 | (e) | 9/2 | 273,421 | (o) | 7/2 | 4.62 × 108 | 6.28 × 108 | −0.73 | −0.61 |
| 1647.007 | 207,216 | (e) | 9/2 | 267,932 | (o) | 9/2 | 2.44 × 107 | 2.06 × 108 | −1.99 | −1.06 |
| 1677.768 | 228,377 | (e) | 7/2 | 288,068 | (o) | 9/2 | 4.85 × 107 * | 4.61 × 107 | −1.68 * | −1.76 |
| 1709.023 | 217,422 | (e) | 9/2 | 275,935 | (o) | 11/2 | 2.58 × 107 * | 5.81 × 107 | −1.92 * | −1.59 |
| 1721.095 | 212,047 | (e) | 9/2 | 270,150 | (o) | 11/2 | 3.16 × 109 | 1.03 × 109 | 0.17 | −0.33 |
| 1723.849 | 217,147 | (e) | 7/2 | 275,157 | (o) | 7/2 | 3.35 × 107 * | 7.94 × 107 | −1.81 * | −1.45 |
| 1728.896 | 211,957 | (e) | 11/2 | 269,797 | (o) | 9/2 | 4.86 × 109 | 1.94 × 109 | 0.36 | −0.05 |
| 1731.593 | 212,047 | (e) | 9/2 | 269,797 | (o) | 9/2 | 1.15 × 109 | 4.77 × 108 | −0.27 | −0.66 |
| 1736.574 | 218,982 | (e) | 5/2 | 276,567 | (o) | 7/2 | 1.75 × 109 | 9.55 × 108 | −0.08 | −0.35 |
| 1741.985 | 220,182 | (e) | 5/2 | 277,587 | (o) | 5/2 | 1.45 × 109 | 1.37 × 109 | −0.17 | −0.19 |
| 1757.639 | 228,377 | (e) | 7/2 | 285,271 | (o) | 7/2 | 3.70 × 107 * | 1.25 × 109 | −1.76 * | −0.24 |
| 1760.697 | 200,497 | (e) | 13/2 | 257,293 | (o) | 13/2 | 3.79 × 109 | 3.50 × 109 | 0.25 | 0.21 |
| 1773.513 | 220,182 | (e) | 5/2 | 276,567 | (o) | 7/2 | 9.71 × 108 | 3.47 × 108 | −0.32 | −0.76 |
| 1775.340 | 243,552 | (e) | 11/2 | 299,879 | (o) | 11/2 | 1.23 × 109 | 1.06 × 109 | −0.23 | −0.30 |
| 1775.921 | 207,216 | (e) | 9/2 | 263,525 | (o) | 9/2 | 3.22 × 108 | 2.93 × 109 | −0.81 | 0.15 |
| 1776.176 | 218,982 | (e) | 5/2 | 275,283 | (o) | 5/2 | 1.50 × 109 | 1.38 × 109 | −0.15 | −0.18 |
| 1777.040 | 217,147 | (e) | 7/2 | 273,421 | (o) | 7/2 | 1.32 × 109 | 1.16 × 109 | −0.20 | −0.26 |
| 1777.677 | 217,147 | (e) | 7/2 | 273,400 | (o) | 9/2 | 2.83 × 109 | 4.10 × 109 | 0.13 | 0.29 |
| 1780.161 | 218,982 | (e) | 5/2 | 275,157 | (o) | 7/2 | 2.21 × 108 | 1.13 × 109 | −0.96 | −0.25 |
| 1783.126 | 219,202 | (e) | 3/2 | 275,283 | (o) | 5/2 | 2.64 × 108 | 1.46 × 108 # | −0.90 | −1.15 # |
| 1783.513 | 200,497 | (e) | 13/2 | 256,566 | (o) | 11/2 | 8.14 × 109 | 7.86 × 109 | 0.59 | 0.58 |
| 1784.713 | 211,957 | (e) | 11/2 | 267,988 | (o) | 11/2 | 1.58 × 109 | 2.36 × 109 | −0.12 | 0.06 |
| 1785.034 | 219,261 | (e) | 7/2 | 275,283 | (o) | 5/2 | 2.81 × 109 | 2.83 × 109 | 0.13 | 0.13 |
| 1785.199 | 228,377 | (e) | 7/2 | 284,393 | (o) | 9/2 | 3.13 × 109 | 4.04 × 109 | 0.18 | 0.29 |
| 1785.749 | 243,552 | (e) | 11/2 | 299,551 | (o) | 13/2 | 8.61 × 109 | 8.45 × 109 | 0.61 | 0.60 |
| 217,422 | (e) | 9/2 | 273,421 | (o) | 7/2 | 4.48 × 109 | 4.18 × 109 | 0.33 | 0.30 | |
| 1786.254 | 201,310 | (e) | 11/2 | 257,293 | (o) | 13/2 | 7.43 × 109 | 3.98 × 109 | 0.55 | 0.28 |
| 1786.411 | 217,422 | (e) | 9/2 | 273,400 | (o) | 9/2 | 1.91 × 109 | 2.45 × 109 | −0.04 | 0.07 |
| 1786.501 | 211,957 | (e) | 11/2 | 267,932 | (o) | 9/2 | 1.81 × 109 | 4.46 × 109 | −0.05 | 0.33 |
| 1787.584 | 212,047 | (e) | 9/2 | 267,988 | (o) | 11/2 | 3.44 × 109 | 5.29 × 109 | 0.22 | 0.41 |
| 1789.384 | 212,047 | (e) | 9/2 | 267,932 | (o) | 9/2 | 3.13 × 108 | 8.20 × 108 | −0.81 | −0.40 |
| 1789.056 | 219,261 | (e) | 7/2 | 275,157 | (o) | 7/2 | 1.66 × 108 | 9.00 × 108 | −1.08 | −0.35 |
| 1790.865 | 228,554 | (e) | 9/2 | 284,393 | (o) | 9/2 | 2.01 × 109 | 2.46 × 109 | −0.01 | 0.08 |
| 1793.854 | 207,779 | (e) | 7/2 | 263,525 | (o) | 9/2 | 4.22 × 109 | 3.84 × 109 | 0.31 | 0.27 |
| 1800.399 | 207,779 | (e) | 7/2 | 263,323 | (o) | 7/2 | 1.59 × 109 | 1.52 × 109 | −0.11 | −0.13 |
| 1809.730 | 201,310 | (e) | 11/2 | 256,566 | (o) | 11/2 | 1.49 × 109 | 7.05 × 108 | −0.13 | −0.46 |
| 1811.205 | 219,202 | (e) | 3/2 | 274,413 | (o) | 5/2 | 5.02 × 108 | 6.33 × 108 | −0.58 | −0.48 |
| 1814.240 | 202,173 | (e) | 11/2 | 257,293 | (o) | 13/2 | 1.42 × 108 | 3.30 × 109 | −1.14 | 0.21 |
| 1819.006 | 220,182 | (e) | 5/2 | 275,157 | (o) | 7/2 | 2.80 × 107 | 1.53 × 108 | −1.83 | −1.09 |
| 1838.460 | 202,173 | (e) | 11/2 | 256,566 | (o) | 11/2 | 3.49 × 107 | 6.11 × 108 | −1.74 | −0.51 |
| 1843.938 | 220,182 | (e) | 5/2 | 274,413 | (o) | 5/2 | 3.05 × 108 | 4.34 × 108 | −0.78 | −0.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maison, L.; Carvajal Gallego, H.; Quinet, P. Pseudo-Relativistic Hartree–Fock and Fully Relativistic Dirac–Hartree–Fock Calculations of Radiative Parameters in the Fifth Spectrum of Lutetium (Lu V). Atoms 2022, 10, 130. https://doi.org/10.3390/atoms10040130
Maison L, Carvajal Gallego H, Quinet P. Pseudo-Relativistic Hartree–Fock and Fully Relativistic Dirac–Hartree–Fock Calculations of Radiative Parameters in the Fifth Spectrum of Lutetium (Lu V). Atoms. 2022; 10(4):130. https://doi.org/10.3390/atoms10040130
Chicago/Turabian StyleMaison, Lucas, Helena Carvajal Gallego, and Pascal Quinet. 2022. "Pseudo-Relativistic Hartree–Fock and Fully Relativistic Dirac–Hartree–Fock Calculations of Radiative Parameters in the Fifth Spectrum of Lutetium (Lu V)" Atoms 10, no. 4: 130. https://doi.org/10.3390/atoms10040130
APA StyleMaison, L., Carvajal Gallego, H., & Quinet, P. (2022). Pseudo-Relativistic Hartree–Fock and Fully Relativistic Dirac–Hartree–Fock Calculations of Radiative Parameters in the Fifth Spectrum of Lutetium (Lu V). Atoms, 10(4), 130. https://doi.org/10.3390/atoms10040130







